1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 4, 2022

Прикладная математика и механика, 2022, T. 86, № 4, стр. 505-526

Собственные колебания усеченных конических оболочек, содержащих жидкость

С. А. Бочкарёв 1, *, С. В. Лекомцев 1, **, В. П. Матвеенко 1, ***

1 Институт механики сплошных сред УрО РАН
Пермь, Россия

* E-mail: bochkarev@icmm.ru
** E-mail: lekomtsev@icmm.ru
*** E-mail: mvp@icmm.ru

Поступила в редакцию 03.03.2022
После доработки 03.05.2022
Принята к публикации 15.05.2022

Полный текст (PDF)

Аннотация

Представлены результаты исследований собственных частот колебаний круговых усеченных конических оболочек, полностью заполненных идеальной сжимаемой жидкостью. Поведение упругой конструкции рассматривается в рамках классической теории оболочек, уравнения которой записываются в виде системы обыкновенных дифференциальных уравнений относительно новых неизвестных. Малые колебания жидкости описываются линеаризованными уравнениями Эйлера, которые в акустическом приближении сводятся к волновому уравнению относительно гидродинамического давления и записываются в сферической системе координат. Его преобразование к системе обыкновенных дифференциальных уравнений выполняется тремя способами: методом прямых, с помощью интерполяции сплайнами и методом дифференциальных квадратур. Решение сформулированной краевой задачи осуществляется методом ортогональной прогонки Годунова. Вычисление собственных частот колебаний выполняется с помощью пошаговой процедуры с последующим уточнением методом деления пополам. Достоверность получаемых результатов подтверждена сравнением с известными численно-аналитическими решениями. Для оболочек с разными комбинациями граничных условий и углами конусности оценена эффективность вычисления частот колебаний для различных методов преобразования волнового уравнения. Продемонстрировано, что использование обобщенного метода дифференциальных квадратур обеспечивает наиболее экономичное решение задачи с приемлемой точностью вычислений.

Ключевые слова: классическая теория оболочек, коническая оболочка, метод ортогональной прогонки Годунова, собственные колебания, идеальная сжимаемая жидкость, метод прямых, кубический сплайн, метод дифференциальных квадратур

1. Введение. Тонкостенные оболочки, содержащие жидкость или погруженные в нее, находят широкое применение в различных областях техники. При их моделировании построение аналитических решений возможно только для некоторых конфигураций цилиндрических оболочек. В этих частных случаях волновое уравнение, наиболее часто используемое для описания идеальной жидкости, допускает формирование явного выражения для гидродинамического давления, записываемого в функциях Бесселя. Численно-аналитические или численные методы решения каких-либо ограничений при этом не имеют. Универсальные численные алгоритмы, такие как метод конечных элементов или его комбинация с методом граничных элементов, применимы при произвольном расположении меридиана и могут быть использованы при анализе как конических, так и сферических оболочек. Однако отсутствие полноценных экспериментальных исследований не позволяет в полной мере оценить достоверность получаемых при этом результатов в широком диапазоне волновых чисел при низко- или высокочастотных колебаниях. В связи с этим, необходимость разработки альтернативных методов решения задач гидроупругости в случае произвольного меридиана является очевидной. Многообразие имеющихся решений может послужить косвенной оценкой достоверности результатов, получаемых в рамках того или иного подхода. В настоящей работе внимание будет сконцентрировано на конических оболочках, содержащих неподвижную жидкость, но описываемый ниже численный алгоритм применим и в случае сферических оболочек.

В первых публикациях [1, 2], где предметом исследований становится полная или усеченная коническая оболочка (полость), полностью или частично заполненная жидкостью, целью авторов ставится получение явных выражений для низших частот гидроупругих колебаний. В [1] принимается гипотеза плоского движения жидкости совместно с методом последовательных приближений. В [2] потенциал смещений жидкости вычисляется в виде суммы двух функций. Одна из них удовлетворяет граничным условиям на смоченной поверхности, а другая соответствует свободным колебаниям жидкости в жесткой полости. Решение строится с использованием метода Галёркина. В работах [3, 4] предлагается приближенный аналитический метод определения динамических характеристик упругой конической оболочки с жидкостью. Потенциал скорости ищется в виде разложения по координатным функциям, представляющим полиномы Лежандра в случае осесимметричных колебаний или присоединенные функции Лежандра для неосесимметричных. Вводится система функций в явной форме, точно удовлетворяющая естественным краевым условиям формулируемой вариационной задачи. На основе проведенных виброиспытаний конического бака, частично заполненного жидкостью, в статье [5] получены частоты двух первых осесимметричных мод. Отмечается, что результаты натурных испытаний удовлетворительно согласуются с расчетными данными. Возможно, что первые наиболее обстоятельные численные результаты расчета динамических характеристик конических оболочек вращения с жидкостью представлены в работе [6]. Здесь применяется метод, основанный на разложении потенциала смещений жидкости в ряд по собственным функциям гидродинамической задачи, которые в случае возможности разделения переменных записываются в явном виде в функциях Бесселя первого рода действительного и чисто мнимого аргумента. Коэффициенты разложения определяются из условий ортогональности этих функций на смоченной поверхности. Решение уравнений осуществляется методом ортогональной прогонки Годунова. В этой же работе приведены результаты экспериментальных исследований, в которых частоты определялись резонансным методом при электродинамическом возбуждении колебаний. Продемонстрировано, что расхождение теоретических и экспериментальных данных не превышает 11%. В конечно-элементной работе [7] используется элемент, в котором точные функции перемещений определяются непосредственно из уравнений теорий оболочек Сандерса. Из волнового уравнения, записанного в сферической системе координат, в результате разделения переменных и метода Фробениуса получено аналитическое выражение для потенциала скорости как функции угла при вершине и окружной гармоники. В численных примерах продемонстрировано влияние угла конусности, геометрических размеров и уровня заполнения жидкостью на динамические характеристики прямой и перевернутой свободно опертой конической оболочки. Аналогичный подход был использован в [8] при моделировании жидкости в конической части комбинированной оболочки. Уравнения Доннела–Муштари, включающие аналитическое выражение для гидродинамического давления, записанное в функциях Бесселя, используются в [9] для оценки влияния жидкости и угла при вершине на связанные частоты и соответствующие им формы колебаний жестко закрепленной конической оболочки. Корректность выбранного метода решения авторами не обсуждается. В работе [10] представлена аналитическая модель для описания низкочастотных колебаний усеченной конической оболочки, погруженной в сжимаемую жидкость. Вся конструкция разбивается по длине на ряд цилиндрических сегментов с постоянным радиусом, описываемых уравнениями Флюгге, в пределах которых внешнее гидродинамическое давление вычисляется по аналитической формуле с использованием функций Ганкеля. С помощью метода степенных рядов проанализированы частоты оболочек с различными граничными условиями. Аналогичный подход применяется также в работах [11–14]. В первых трех статьях исследуются подкрепленные оболочки, толщина которых изменяется линейно, параболически, ступенчато или остается неизменной. В [11, 13] теория оболочек и метод решения полностью аналогичны [10]. В [12] применяется метод передаточной матрицы. В работе [14] метод динамической жесткости используется для анализа свободных колебаний композитных оболочек, описываемых в рамках теории Рейснера–Нагди, погруженных в жидкость или содержащих ее. В последнем случае гидродинамическое давление формируется в функциях Бесселя. Исходя из того, что аргументом цилиндрических функций выступает меридиональное волновое число, определяемое исходя из граничных условий на входе и выходе в оболочку, корректность данного метода вряд ли можно считать физически обоснованной. В работах [15, 16] описывается новый вариант метода конечных элементов для расчета колебаний упругих оболочек вращения с произвольным меридианом, частично заполненных жидкостью. В качестве конечных элементов рассматриваются узкие кольцевые полоски оболочки с содержащимися в них слоями жидкости. В случае осесимметричных колебаний осевое перемещение жидкости в поперечном сечении представляется в виде суммы плоского вытеснения и депланации по форме параболы, а при неосесимметричных радиальные и окружные перемещения определяются из точного решения уравнения неразрывности с учетом граничного условия на смоченной поверхности. Оценка влияния гидростатического давления на связанные частоты колебаний резервуаров с жидкостью, в том числе конических, выполнена в [17]. Одно из немногочленных экспериментальных исследований конических оболочек с жидкостью представлено в [18]. Здесь на основе спектрального анализа данных, зарегистрированных посредством тензометрии, получены низшие частоты колебаний в случае частичного заполнения. При этом отличия от конечно-элементного решения задачи, осуществленного в коммерческом пакете ANSYS, не превышают 7%. В [19] для анализа оболочек с различными вариантами граничных условий предлагается комбинированный подход. Определяющие уравнения упругой конструкции получены в наиболее общем виде с помощью вариационного принципа. Они базируются на теории оболочек типа Тимошенко (first-order shear deformation theory, FSDT), учитывающей деформации поперечного сдвига [20]. Решение этих уравнений осуществляется с помощью метода Галёркина, где перемещения раскладываются в ряды Фурье со вспомогательными функциями. Волновое уравнение для несжимаемой жидкости, сведенное к слабой форме посредством метода Галёркина, решается методом конечных элементов. Связанная система уравнений формируется в результате удовлетворения условий на упругой поверхности оболочки. Композитные конструкции в виде комбинации трех оболочек (коническая-цилиндрическая-коническая), описываемых в рамках теории оболочек типа Тимошенко, исследуются в [21] с помощью метода передаточной матрицы. Для учета полного или частичного заполнения гидродинамическое давление формулируется в функциях Бесселя. Внимание на конической части при этом не акцентируется. Заполненные жидкостью резервуары конической формы, подвергающиеся вертикальным и горизонтальным возмущениям, эмулирующим землетрясение, изучаются с помощью метода конечных элементов в работах [22, 23]. Гидродинамическое давление интерполируется рядами различных функций формы, удовлетворяющих волновому уравнению. Оценено влияние начальных неправильностей формы конструкции на несущую способность конических резервуаров под действием гидродинамического давления, инициированного сейсмической нагрузкой. В [24] из волнового уравнения с использованием разделения переменных получено аналитическое выражение для потенциала скорости как функции угла при вершине и окружной гармоники. Для решения уравнений, основанных на классической теории оболочек, используется аппроксимация функций перемещений сплайнами третьего и пятого порядка и метод коллокаций. Выполнен параметрический анализ, в ходе которого оценено влияние относительной толщины слоя и геометрических размеров на частотный спектр двухслойных оболочек при различных комбинациях граничных условий. Аналогичный подход для описания жидкости был использован в [25], где метод дифференциальных квадратур применяется для решения системы уравнений, полученной из принципа Гамильтона и теории оболочек Донелла. Комбинированный метод, сочетающий применение метода конечных элементов для упругого тела и метода граничных элементов для моделирования жидкой среды используется в [26, 27]. Совместные перемещения оболочки и жидкости представляются в виде линейной комбинации собственных форм колебаний оболочки в вакууме. Потенциал скорости жидкости рассматривается в виде суммы двух компонент, одна из которых описывает движение в жестком сосуде и позволяет учитывать эффекты на свободной поверхности. Для оболочек отличных от цилиндрических, усилия авторов сосредоточены в основном на изучении плескательных мод колебаний жидкости в жестких контейнерах, в том числе подкрепленных жесткими или упругими перегородками. Теория оболочек типа Тимошенко (FSDT), балочные функции и метод Галёркина используются в [28] для анализа оболочек с различными граничными условиями, расположенных на упругом основании.

Анализ устойчивости конических оболочек с текущей внутри жидкостью или газом исследуется в работах [29–36]. Исходя из условия малой конусности, в [29, 30] волновое уравнение, описывающее сверхзвуковое течение газа, решается с помощью преобразования Лапласа. При восстановлении оригинала аэродинамического давления модифицированная функция Бесселя заменяется асимптотическим разложением. В конечно-элементных реализациях [31–33] волновое уравнение сводится к слабой форме с помощью метода Бубнова–Галёркина. В первой из них применяется теория оболочек типа Тимошенко (FSDT), а в других – классическая теория оболочек. Здесь же показано, что с увеличением угла конусности возможно изменение вида потери устойчивости с дивергенции на флаттер. В работах [34, 35] методы, предложенные этими же авторами для анализа неподвижной жидкости [7, 19], обобщаются на случай текущей. В [35] продемонстрировано, что угол конусности может оказывать как стабилизирующее, так и дестабилизирующее влияние. Нанокомпозитные усеченные конические оболочки, описываемые уравнениями теории оболочек Новожилова, изучаются в [36]. Метод обобщенных дифференциальных квадратур применяется как для численного решения волнового уравнения, так и всей задачи в целом. Оценено влияние объемных фракций углеродных нанотрубок на критические скорости флаттера и дивергенции.

В настоящей работе для решения сформулированной краевой задачи используется метод ортогональной прогонки Годунова (МОПГ) [37]. Помимо процитированных выше публикаций примеры применения этого метода для задач гидроупругости приведены в монографиях [38, 39]. Причем распространен подход, когда аналитическое решение волнового уравнения относительно потенциала скорости или давления записывается в членах функций Бесселя. Комбинированный способ, где волновое уравнение сводится к системе обыкновенных дифференциальных уравнений, которая решается совместно с системой уравнений для упругого тела, применяется редко [40–42]. В частности, в [40, 41] для анализа вынужденных колебаний коаксиальных оболочек, содержащих жидкость в кольцевом канале, предложено использовать процедуры сведения к замкнутой системе обыкновенных дифференциальных уравнений, основанные на кубической сплайн-аппроксимации (КС) и методе прямых (МП). При этом декларируется, что первый метод более эффективен, но какие-либо аргументы в пользу этого утверждения не приводятся. Исходя из этого, в данной работе для конической оболочки осуществляется сравнение различных способов сведения уравнений жидкости к системе обыкновенных дифференциальных уравнений с целью выбора наиболее производительного. Наряду с упомянутыми подходами будет также апробирован обобщенный метод дифференциальных квадратур (МДК) [43], который, как это отмечено в [44], не нашел широкого распространения у отечественных исследователей, несмотря на все свои преимущества.

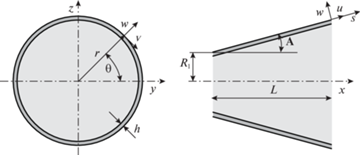
2. Постановка задачи. Рассматривается полностью заполненная неподвижной идеальной сжимаемой жидкостью усеченная коническая оболочка (рис. 1) с минимальным радиусом ${{R}_{1}}$, углом при вершине A, толщиной $h$ и длиной L. В работе ставится задача исследования различных методов сведения акустического волнового уравнения к системе обыкновенных дифференциальных уравнений и оценки их влияния на эффективность и точность вычислений связанных частот колебаний оболочки с жидкостью, имеющей различные комбинации граничных условий на краях.

Рис. 1.

Расчетная схема.

3. Основные соотношения

3.1. Коническая оболочка. Компоненты вектора деформации ${{{\text{E}}}_{{ij}}}$ в криволинейной системе координат $\left( {s,\theta ,z} \right)$ для классической теории оболочек, основанной на гипотезах Кирхгофа–Лява, записываются в виде [45]

${{{\rm E}}_{{11}}} = {{\varepsilon }_{{11}}} + z{{\kappa }_{{11}}},\quad {{{\rm E}}_{{22}}} = {{\varepsilon }_{{22}}} + z{{\kappa }_{{22}}},\quad {{{\rm E}}_{{12}}} = {{\varepsilon }_{{12}}} + 2z{{\kappa }_{{12}}},$
где

(3.1)
$\begin{gathered} {{\varepsilon }_{{11}}} = u{\kern 1pt} '\; + {{r}_{1}}w,\quad {{\varepsilon }_{{22}}} = {{{v}}^{\centerdot }} + \psi u + {{r}_{2}}w,\quad {{\varepsilon }_{{12}}} = v{\kern 1pt} '\; + {{u}^{\centerdot }} - \psi {v},\quad {{\kappa }_{{11}}} = \theta _{1}^{'} \\ {{\kappa }_{{22}}} = \theta _{2}^{\centerdot } + \psi {{\theta }_{1}},\quad {{\kappa }_{{12}}} = \theta _{1}^{\centerdot } - \psi {{\theta }_{2}} + {{r}_{2}}{v}{\kern 1pt} ',\quad {{\theta }_{1}} = - w{\kern 1pt} '\; + {{r}_{1}}u,\quad {{\theta }_{2}} = - {{w}^{\centerdot }} + {{r}_{2}}{v} \\ ( \ldots ){\kern 1pt} ' = \frac{1}{{{{A}_{1}}}}\frac{{\partial ( \ldots )}}{{\partial s}},\quad {{( \ldots )}^{\centerdot }} = \frac{1}{{{{A}_{2}}}}\frac{{\partial ( \ldots )}}{{\partial \theta }},\quad \psi = \frac{1}{{{{A}_{2}}}}A_{2}^{'} \\ \end{gathered} $

Здесь: ${{A}_{1}},{{A}_{2}}$ – коэффициенты Ламе; ${{r}_{1}},\;{{r}_{2}}$ – кривизны; u, ${v}$, w – меридиональная, окружная и нормальная составляющие вектора перемещений оболочки; ${{\theta }_{1}},\;{{\theta }_{2}}$ – углы поворота недеформируемой нормали.

Физические соотношения, устанавливающие связь между вектором усилий и моментов ${\mathbf{T}} = \{ {{T}_{{11}}},{{T}_{{22}}},S,{{M}_{{11}}}$, ${{M}_{{22}}},H{{\} }^{{\text{T}}}}$ и вектором обобщенных деформаций $\varepsilon = \{ {{\varepsilon }_{{11}}},{{\varepsilon }_{{22}}},{{\varepsilon }_{{12}}},{{\kappa }_{{11}}}$, ${{\kappa }_{{22}}},2{{\kappa }_{{12}}}{{\} }^{{\text{T}}}}$, в матричном виде записываются как

(3.2)
${\mathbf{T}} = {\mathbf{D}}\varepsilon = \left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {A}}}}&{{\mathbf{\bar {B}}}} \\ {{\mathbf{\bar {B}}}}&{{\mathbf{\bar {C}}}} \end{array}} \right]\varepsilon $

Здесь величины, составляющие матрицу жесткостей D, вычисляются по формулам

(3.3)
${{\bar {a}}_{{ij}}} = \int\limits_h {{{{\bar {Q}}}_{{ij}}}dz} ,\quad {{\bar {b}}_{{ij}}} = \int\limits_h {z{{{\bar {Q}}}_{{ij}}}dz,} \quad {{\bar {c}}_{{ij}}} = \int\limits_h {{{z}^{2}}{{{\bar {Q}}}_{{ij}}}dz} \quad (i,j = 1,2,3),$
где коэффициенты ${{\bar {Q}}_{{ij}}}$ определяются известным образом относительно модулей упругости (${{E}_{{11}}},{{E}_{{22}}}$), коэффициента Пуассона (${{\nu }_{{12}}}$) и модуля сдвига (${{G}_{{12}}}$) материала оболочки.

Уравнения движения оболочки

$T_{{11}}^{'} + \psi ({{T}_{{11}}} - {{T}_{{22}}}) + {{S}^{\centerdot }} + {{r}_{1}}({{Q}_{{11}}} - {{H}^{\centerdot }}) - {{\rho }_{0}}\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} = 0$
(3.4)
$\begin{gathered} S{\kern 1pt} '\; + 2\psi \left( {S + {{r}_{1}}H} \right) + T_{{22}}^{\centerdot } + {{r}_{2}}\left( {{{Q}_{{22}}} + H{\kern 1pt} '} \right) - {{\rho }_{0}}\frac{{{{\partial }^{2}}{v}}}{{\partial {{t}^{2}}}} = 0 \\ Q_{{11}}^{'} + \psi {{Q}_{{11}}} + Q_{{22}}^{\centerdot } - {{r}_{1}}{{T}_{{11}}} - {{r}_{2}}{{T}_{{22}}} - {{\rho }_{0}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + p = 0 \\ \end{gathered} $
$M_{{11}}^{'} + \psi \left( {{{M}_{{11}}} - {{M}_{{22}}}} \right) + {{H}^{\centerdot }} - {{Q}_{{11}}} = 0,\quad H{\kern 1pt} '\; + 2\psi H + M_{{22}}^{\centerdot } - {{Q}_{{22}}} = 0,$
где ${{Q}_{{ii}}}$ – поперечные силы, ${{\rho }_{0}} = \int_h {\rho dz} $, $\rho $ – плотность материала, p – гидродинамическое давление, действующее со стороны жидкости объема Vf  на поверхность оболочки.

Раскладывая все компоненты (3.1), (3.2) в ряды Фурье по окружной координате θ

$\begin{gathered} X(s,\theta ) = \sum\limits_{j = 0} {{{X}_{j}}(s)\cos (j\theta )} ,\quad Y(s,\theta ) = \sum\limits_{j = 0} {{{Y}_{j}}(s)\sin (j\theta )} \\ X = \{ u,w,{{\theta }_{1}},{{E}_{{11}}},{{E}_{{22}}},{{K}_{{11}}},{{K}_{{22}}},{{T}_{{11}}},{{T}_{{22}}},{{M}_{{11}}},{{M}_{{22}}},{{Q}_{{11}}},p\} \\ Y = \{ {v},{{\theta }_{2}},{{E}_{{12}}},{{K}_{{12}}},S,H,{{Q}_{{22}}}\} , \\ \end{gathered} $
сводим геометрические (3.1) и физические (3.2) соотношения, а также уравнения движения (3.4) к системе восьми обыкновенных дифференциальных уравнений первого порядка относительно новых неизвестных [45]

$\begin{gathered} {{y}_{1}} = {{T}_{{11}}},\quad {{y}_{2}} = S + 2{{r}_{2}}H,\quad {{y}_{3}} = {{M}_{{11}}},\quad {{y}_{4}} = {{Q}_{{11}}} + \bar {j}H \\ {{y}_{5}} = u,\quad {{y}_{6}} = {v},\quad {{y}_{7}} = w,\quad {{y}_{8}} = {{\theta }_{1}} \\ \end{gathered} $

Здесь j – номер гармоники при разложении в ряд Фурье, $\bar {j} = j{\text{/}}{{A}_{2}}$. С учетом этого и принимая во внимание ${\mathbf{y}}(t) = {\mathbf{y}}\exp (i\omega t)$, искомая система может быть записана следующим образом

(3.5)
${\mathbf{y}}{\kern 1pt} ' = {\mathbf{f}}\left( {j,\omega ,{\mathbf{y}}} \right),$
где

${{f}_{1}} = \bar {j}\left( {2{{r}_{2}}H - {{y}_{2}}} \right) - \psi \left( {{{y}_{1}} - {{T}_{{22}}}} \right) - {{r}_{1}}{{y}_{4}} - {{\omega }^{2}}{{\rho }_{0}}{{y}_{5}}$
${{f}_{2}} = \bar {j}{{T}_{{22}}} - 2\psi {{y}_{2}} - {{r}_{2}}{{Q}_{{22}}} - {{\omega }^{2}}{{\rho }_{0}}{{y}_{6}}$
(3.6)
${{f}_{3}} = {{y}_{4}} - \psi \left( {{{y}_{3}} - {{M}_{{22}}}} \right) - 2\bar {j}H$
${{f}_{4}} = {{r}_{1}}{{y}_{1}} - \psi {{y}_{4}} + {{r}_{2}}{{T}_{{22}}} - \bar {j}\left( {{{Q}_{{22}}} + 2\psi H} \right) - p - {{\omega }^{2}}{{\rho }_{0}}{{y}_{7}}$
${{f}_{5}} = {{\varepsilon }_{{11}}} - {{r}_{1}}{{y}_{7}},\quad {{f}_{6}} = {{\varepsilon }_{{12}}} + \psi {{y}_{6}} + \bar {j}{{y}_{5}},\quad {{f}_{7}} = - {{y}_{8}} + {{r}_{1}}{{y}_{5}},\quad {{f}_{8}} = {{\kappa }_{{11}}}$

Здесь ω – характеристический показатель, ${{i}^{2}} = - 1$. Входящие в выражения (3.6) величины вычисляются по следующим формулам

${{\varepsilon }_{{22}}} = \bar {j}{{y}_{6}} + {{r}_{2}}{{y}_{7}} + \psi {{y}_{5}},\quad {{\kappa }_{{22}}} = \bar {j}{{\theta }_{2}} + \psi {{y}_{8}},\quad {{\theta }_{2}} = {{r}_{2}}{{y}_{6}} + \bar {j}{{y}_{7}}$
$H = {{\bar {b}}_{{33}}}{{\varepsilon }_{{12}}} + 2{{\bar {c}}_{{33}}}{{\kappa }_{{12}}},\quad {{Q}_{{22}}} = - \bar {j}{{M}_{{22}}}$
${{\kappa }_{{11}}} = \left[ {{{{\bar {a}}}_{{11}}}\left( {{{y}_{3}} - {{{\bar {b}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {c}}}_{{12}}}{{\kappa }_{{22}}}} \right) - } \right.\left. {{{{\bar {b}}}_{{11}}}\left( {{{y}_{1}} - {{{\bar {a}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {b}}}_{{12}}}{{\kappa }_{{22}}}} \right)} \right]{\text{/}}({{\bar {a}}_{{11}}}{{\bar {c}}_{{11}}} - \bar {b}_{{11}}^{2})$
${{\varepsilon }_{{11}}} = \left( {{{y}_{1}} - {{{\bar {a}}}_{{12}}}{{\varepsilon }_{{22}}} - {{{\bar {b}}}_{{11}}}{{\kappa }_{{11}}} - {{{\bar {b}}}_{{12}}}{{\kappa }_{{22}}}} \right){\text{/}}{{\bar {a}}_{{11}}},\quad {{\kappa }_{{12}}} = {{r}_{2}}\left( {{{\varepsilon }_{{12}}} + \bar {j}{{y}_{5}}} \right) - \bar {j}\left( {{{y}_{8}} + \psi {{y}_{7}}} \right)$
${{T}_{{22}}} = {{\bar {a}}_{{12}}}{{\varepsilon }_{{11}}} + {{\bar {a}}_{{22}}}{{\varepsilon }_{{22}}} + {{\bar {b}}_{{12}}}{{\kappa }_{{11}}} + {{\bar {b}}_{{22}}}{{\kappa }_{{22}}},\quad {{M}_{{22}}} = {{\bar {b}}_{{12}}}{{\varepsilon }_{{11}}} + {{\bar {b}}_{{22}}}{{\varepsilon }_{{22}}} + {{\bar {c}}_{{12}}}{{\kappa }_{{11}}} + {{\bar {c}}_{{22}}}{{\kappa }_{{22}}}$
${{\varepsilon }_{{12}}} = \left[ {{{y}_{2}} - 2\left( {{{{\bar {b}}}_{{33}}} + 2{{r}_{2}}{{{\bar {c}}}_{{33}}}} \right)\bar {j}\left( {{{r}_{2}}{{y}_{5}} - {{y}_{8}} - \psi {{y}_{7}}} \right)} \right]{\text{/}}\left[ {{{{\bar {a}}}_{{33}}} + 4{{r}_{2}}\left( {{{{\bar {b}}}_{{33}}} + {{r}_{2}}{{{\bar {c}}}_{{33}}}} \right)} \right]$

3.2. Неподвижная сжимаемая жидкость. В случае конической оболочки акустическое волновое уравнение и соответствующие граничные условия записываются в сферической системе координат $(x,\alpha ,\theta )$

(3.7)
${{\nabla }^{2}}p = \frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{2}{x}\frac{{\partial p}}{{\partial x}} + \frac{1}{{{{x}^{2}}}}\left( {\frac{1}{{{{{\sin }}^{2}}\alpha }}\frac{{{{\partial }^{2}}p}}{{\partial {{\theta }^{2}}}} + \frac{1}{{\operatorname{tg} \alpha }}\frac{{\partial p}}{{\partial \alpha }} + \frac{{{{\partial }^{2}}p}}{{\partial {{\alpha }^{2}}}}} \right) = \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}}$

Здесь c – скорость звука в жидкости. На смоченной поверхности (α = Α), оси вращения оболочки (α = 0) и ее краях (x = 0, L) гидродинамическое давление p удовлетворяет следующим условиям:

(3.8)
${{\left. {\nabla p \cdot {\mathbf{n}}} \right|}_{{\alpha = {\rm A}}}} = {{\left. {\frac{1}{x}\frac{{\partial p}}{{\partial \alpha }}} \right|}_{{\alpha = {\rm A}}}} = - {{\rho }_{f}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}$
(3.9)
$\;{{\left. {\nabla p \cdot {\mathbf{n}}} \right|}_{{\alpha = 0}}} = {{\left. {\frac{{\partial p}}{{\partial \alpha }}} \right|}_{{\alpha = 0}}} = 0$
(3.10)
$x = 0{\kern 1pt} :\;\;\frac{{\partial p}}{{\partial x}} = 0,\quad x = L{\kern 1pt} :\;\;\frac{{\partial p}}{{\partial x}} = 0,$
где n – единичные внешние нормали к области жидкости Vf, ρf  – плотность жидкости.

Сведение уравнения (3.7) к системе обыкновенных дифференциальных уравнений осуществляется различными способами, описание которых представлено ниже.

3.2.1. Метод прямых. В методе прямых (дифференциально-разностный метод) [46] область жидкости делится на n равных углов и через точки деления проводится семейство лучей $\alpha = {{\alpha }_{i}}$ $(i = 1,n - 1)$. На каждом таком луче (прямой) дифференциальное уравнение (3.7) заменяется приближенным обыкновенным дифференциальным уравнением для функции $p(x,{{\alpha }_{i}})$. Для этого в выражении (3.7) производные по координате $\alpha $ заменяются на формулы численного дифференцирования

(3.11)
$\begin{gathered} {{\left. {\frac{{\partial p}}{{\partial \alpha }}} \right|}_{{\alpha = {{\alpha }_{i}}}}} = \frac{1}{{2t}}\left[ {p\left( {x,{{\alpha }_{{i + 1}}}} \right) - p\left( {x,{{\alpha }_{{i - 1}}}} \right)} \right] \\ {{\left. {\frac{{{{\partial }^{2}}p}}{{\partial {{\alpha }^{2}}}}} \right|}_{{\alpha = {{\alpha }_{i}}}}} = \frac{1}{{{{t}^{2}}}}\left[ {p\left( {x,{{\alpha }_{{i + 1}}}} \right) - 2p\left( {x,{{\alpha }_{i}}} \right) + p\left( {x,{{\alpha }_{{i - 1}}}} \right)} \right], \\ \end{gathered} $
где $t = {{\rm A} \mathord{\left/ {\vphantom {{\rm A} n}} \right. \kern-0em} n}$.

Для “крайних” прямых [47]:

(3.12)
$\begin{gathered} {{\left. {\frac{{\partial p}}{{\partial \alpha }}} \right|}_{{\alpha = 0}}} = \frac{1}{{2t}}\left[ {4p\left( {x,{{\alpha }_{1}}} \right) - p\left( {x,{{\alpha }_{2}}} \right) - 3p\left( {x,{{\alpha }_{0}}} \right)} \right] \\ {{\left. {\frac{{\partial p}}{{\partial \alpha }}} \right|}_{{\alpha = {\rm A}}}} = \frac{1}{{2t}}\left[ {3p\left( {x,{{\alpha }_{n}}} \right) - 4p\left( {x,{{\alpha }_{{n - 1}}}} \right) + p\left( {x,{{\alpha }_{{n - 2}}}} \right)} \right] \\ \end{gathered} $

Вводя сокращенные обозначения

$p\left( {x,{{\alpha }_{i}}} \right) = {{p}_{i}}\left( x \right),\quad \frac{{\partial p\left( {x,{{\alpha }_{i}}} \right)}}{{\partial x}} = p_{i}^{'}\left( x \right),\quad \frac{{{{\partial }^{2}}p\left( {x,{{\alpha }_{i}}} \right)}}{{\partial {{x}^{2}}}} = p_{i}^{{''}}\left( x \right)$
и подставляя формулы (3.11) в исходное уравнение (3.7), придем к системе $(n - 1)$ уравнений в обыкновенных производных
(3.13)
$p_{i}^{{''}}(x) = \beta _{1}^{i}{{p}_{i}}(x) - \beta _{2}^{i}{{p}_{{i + 1}}}(x) + \beta _{3}^{i}{{p}_{{i - 1}}}(x) + {{\beta }_{4}}p_{i}^{'}(x),$
где $\beta _{1}^{i} = \frac{2}{{{{x}^{2}}{{t}^{2}}}} + \frac{{{{j}^{2}}}}{{{{x}^{2}}{{{\sin }}^{2}}{{\alpha }_{i}}}} - \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}$, $\beta _{2}^{i} = \frac{1}{{2t{{x}^{2}}\operatorname{tg} {{\alpha }_{i}}}} + \frac{1}{{{{x}^{2}}{{t}^{2}}}}$, $\beta _{3}^{i} = \frac{1}{{2t{{x}^{2}}\operatorname{tg} {{\alpha }_{i}}}} - \frac{1}{{{{x}^{2}}{{t}^{2}}}}$, ${{\beta }_{4}} = \frac{2}{x}$. Эта система сводится к нормальному виду Коши следующим образом:

${{y}_{9}} = {{p}_{1}}(x),\quad y_{9}^{'} = {{y}_{{10}}},\quad y_{{10}}^{'} = \beta _{1}^{1}{{y}_{9}} - \beta _{2}^{1}{{y}_{{11}}} + \beta _{3}^{1}{{p}_{0}} - {{\beta }_{4}}{{y}_{{10}}}$
(3.14)
$\begin{gathered} {{y}_{{11}}} = {{p}_{2}}(x),\quad y_{{11}}^{'} = {{y}_{{12}}},\quad y_{{12}}^{'} = \beta _{1}^{2}{{y}_{{11}}} - \beta _{2}^{2}{{y}_{{13}}} + \beta _{3}^{2}{{y}_{9}} - {{\beta }_{4}}{{y}_{{12}}} \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ {{y}_{{7 + 2(n - 1)}}} = {{p}_{{n - 1}}}(x),\quad y_{{7 + 2(n - 1)}}^{'} = {{y}_{{8 + 2(n - 1)}}} \\ \end{gathered} $
$y_{{8 + 2(n - 1)}}^{'} = \beta _{1}^{{n - 1}}{{y}_{{7 + 2(n - 1)}}} - \beta _{2}^{{n - 1}}{{p}_{n}} + \beta _{3}^{{n - 1}}{{y}_{{5 + 2(n - 1)}}} - {{\beta }_{4}}{{y}_{{8 + 2(n - 1)}}}$

Значения p0 и pn в (3.14) определяются, исходя из условий (3.8)–(3.9) и уравнений для “крайних” прямых (3.12):

${{p}_{0}} = \frac{1}{3}\left( {4{{y}_{9}} - {{y}_{{11}}}} \right),\quad {{p}_{n}} = \frac{1}{3}\left( {2xt{{\rho }_{f}}{{\omega }^{2}}{{y}_{7}} + 4{{y}_{{7 + 2(n - 1)}}} - {{y}_{{5 + 2(n - 1)}}}} \right)$

Обратим внимание на то, что в соотношениях (3.4) p = pn. Таким образом, совокупное число неизвестных, определяемых системами уравнений (3.5) и (3.14), составляет $m = 8 + 2(n - 1)$.

3.2.2. Интерполяция кубическим сплайном. В этом методе задается сетка узлов $0 = {{\alpha }_{0}} < {{\alpha }_{1}}$… < ${{\alpha }_{{n - 1}}} < {{\alpha }_{n}} = {\rm A}$, на каждом сегменте которой $\left[ {{{\alpha }_{{i - 1}}},{{\alpha }_{i}}} \right]$, $i = \overline {1,n} $, для функции $p(x,\alpha )$ строится интерполяционный кубический сплайн [48, 49]

(3.15)
${{s}_{i}}(\alpha ) = {{c}_{{1i}}} + {{c}_{{2i}}}(\alpha - {{\alpha }_{i}}) + \frac{{{{c}_{{3i}}}}}{2}{{(\alpha - {{\alpha }_{i}})}^{2}} + \frac{{{{c}_{{4i}}}}}{6}{{(\alpha - {{\alpha }_{i}})}^{3}}$

По определению в каждом узле сетки выполняется условие $s({{\alpha }_{i}}) = p(x,{{\alpha }_{i}})$, $i = \overline {0,n} .$ Из выражения для сплайна (3.15), а также первой и второй производных

(3.16)
$s_{i}^{'}(\alpha ) = {{c}_{{2i}}} + {{c}_{{3i}}}(\alpha - {{\alpha }_{i}}) + \frac{{{{c}_{{4i}}}}}{2}{{(\alpha - {{\alpha }_{i}})}^{2}},\quad s_{i}^{{''}}(\alpha ) = {{c}_{{3i}}} + {{c}_{{4i}}}(\alpha - {{\alpha }_{i}}),$
следует

(3.17)
${{s}_{i}}({{\alpha }_{i}}) = {{c}_{{1i}}},\quad s_{i}^{'}({{\alpha }_{i}}) = {{c}_{{2i}}},\quad s_{i}^{{''}}({{\alpha }_{i}}) = {{c}_{{3i}}}$

Требование непрерывности сплайна ${{s}_{i}}(\alpha )$ на всем рассматриваемом диапазоне, как и его производных

(3.18)
${{s}_{i}}({{\alpha }_{{i - 1}}}) = {{c}_{{1i - 1}}},\quad s_{i}^{'}({{\alpha }_{{i - 1}}}) = {{c}_{{2i - 1}}},\quad s_{i}^{{''}}({{\alpha }_{{i - 1}}}) = {{c}_{{3i - 1}}},$
приводит к соотношениям
(3.19)
$\begin{gathered} {{c}_{{2i}}}{{t}_{i}} - \frac{{{{c}_{{3i}}}}}{2}t_{i}^{2} + \frac{{{{c}_{{4i}}}}}{6}t_{i}^{3} = p(x,{{\alpha }_{i}}) - p(x,{{\alpha }_{{i - 1}}});\quad i = \overline {1,n} \\ {{c}_{{3i}}}{{t}_{i}} - \frac{{{{c}_{{4i}}}}}{2}t_{i}^{2} = {{c}_{{2i}}} - {{c}_{{2i - 1}}},\quad {{c}_{{4i}}}{{t}_{i}} = {{c}_{{3i}}} - {{c}_{{3i - 1}}};\quad i = \overline {2,n} , \\ \end{gathered} $
где ${{t}_{i}} = {{\alpha }_{i}} - {{\alpha }_{{i - 1}}}$. С учетом граничных условий
(3.20)
${{c}_{{2n}}} = - x{{\rho }_{f}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}},\quad {{c}_{{20}}} = 0,$
следующих из (3.8), (3.9) и (3.17), с помощью операции редукции соотношения (3.19) можно выразить относительно коэффициентов ${{c}_{{3i}}}$, получив систему линейных уравнений, матрица которых является трехдиагональной. После решения этой системы методом прогонки, остальные коэффициенты определяются по рекуррентным формулам. Альтернативным вариантом является использование известных процедур вычисления коэффициентов кубического сплайна, например, таких как подпрограмма CUBSPL, описанная в монографии [50], или ее варианта CSDEC, реализованной в пакете математических функций IMSL.

С учетом того, что первая и вторая производные по координате α полностью определяются через коэффициенты сплайна, система обыкновенных дифференциальных уравнений формируется следующим образом

$\begin{gathered} {{y}_{9}} = {{p}_{1}}(x),\quad y_{9}^{'} = {{y}_{{10}}} \\ y_{{10}}^{'} = - \frac{{s_{1}^{{''}}({{\alpha }_{1}})}}{{{{x}^{2}}}} + {{y}_{9}}\left( {\frac{{{{j}^{2}}}}{{{{{\sin }}^{2}}{{\alpha }_{1}}}} - \frac{{s_{1}^{'}({{\alpha }_{1}})}}{{\operatorname{tg} {{\alpha }_{1}}}} - \frac{{{{x}^{2}}{{\omega }^{2}}}}{{{{c}^{2}}}}} \right){\text{/}}{{x}^{2}} - \frac{{2{{y}_{{10}}}}}{x} \\ \end{gathered} $
(3.21)
$\begin{gathered} {{y}_{{11}}} = {{p}_{2}}(x),\quad y_{{11}}^{'} = {{y}_{{12}}} \\ y_{{12}}^{'} = - \frac{{s_{2}^{{''}}({{\alpha }_{2}})}}{{{{x}^{2}}}} + {{y}_{{11}}}\left( {\frac{{{{j}^{2}}}}{{{{{\sin }}^{2}}{{\alpha }_{2}}}} - \frac{{s_{2}^{'}({{\alpha }_{2}})}}{{\operatorname{tg} {{\alpha }_{2}}}} - \frac{{{{x}^{2}}{{\omega }^{2}}}}{{{{c}^{2}}}}} \right){\text{/}}{{x}^{2}} - \frac{{2{{y}_{{12}}}}}{x} \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ \end{gathered} $
$\begin{gathered} {{y}_{{7 + 2n}}} = {{p}_{n}}(x),\quad y_{{7 + 2n}}^{'} = {{y}_{{8 + 2n}}} \\ y_{{8 + 2n}}^{'} = - \frac{{s_{n}^{{''}}({{\alpha }_{n}})}}{{{{x}^{2}}}} + {{y}_{{7 + 2n}}}\left( {\frac{{{{j}^{2}}}}{{{{{\sin }}^{2}}{{\alpha }_{n}}}} - \frac{{s_{n}^{'}({{\alpha }_{n}})}}{{\operatorname{tg} {{\alpha }_{n}}}} - \frac{{{{x}^{2}}{{\omega }^{2}}}}{{{{c}^{2}}}}} \right){\text{/}}{{x}^{2}} - \frac{{2{{y}_{{8 + 2n}}}}}{x} \\ \end{gathered} $

В случае интерполяции сплайном совокупное число неизвестных, определяемых системами уравнений (3.5) и (3.21), составляет $m = 8 + 2n$. Поскольку коэффициенты сплайна зависят от граничных условий (3.20), их перевычисление необходимо проводить на каждом шаге интегрирования по меридиональной координате.

3.2.3. Метод дифференциальных квадратур. Согласно этому методу область решения также дискретизируется n точками, а производные l-го порядка функции $p(x,\alpha )$ в любой точке ${{\alpha }_{i}}$ определяются как [43]

(3.22)
$\frac{{{{\partial }^{l}}p(x,{{\alpha }_{i}})}}{{\partial {{\alpha }^{l}}}} = \sum\limits_{k = 1}^n {c_{{ik}}^{{(l)}}p(x,{{\alpha }_{k}});} \quad i = \overline {1,n} ,\quad l = \overline {1,n - 1} ,$
где весовые коэффициенты $c_{{ik}}^{{(l)}}$ вычисляются по следующим рекуррентным формулам

$\left. {\begin{array}{*{20}{c}} {c_{{ik}}^{{(1)}} = \frac{{{{M}^{{(1)}}}({{\alpha }_{i}})}}{{{{M}^{{(1)}}}({{\alpha }_{k}})({{\alpha }_{i}} - {{\alpha }_{k}})}},\quad c_{{ii}}^{{(1)}} = - \sum\limits_{k = 1}^n {c_{{ik}}^{{(1)}}} ,\quad {{M}^{{(1)}}}({{\alpha }_{i}}) = \prod\limits_{k = 1}^n {({{\alpha }_{i}} - {{\alpha }_{k}})} } \\ {c_{{ik}}^{{(l)}} = l\left( {c_{{ik}}^{{(1)}}c_{{ii}}^{{(l - 1)}} - \frac{{c_{{ik}}^{{(l - 1)}}}}{{{{\alpha }_{i}} - {{\alpha }_{k}}}}} \right),\quad c_{{ii}}^{{(l)}} = - \sum\limits_{k = 1}^n {c_{{ik}}^{{(l)}}} } \end{array}} \right\}\quad i \ne k;\quad i,k = \overline {1,n} $

С учетом (3.22) граничные условия (3.8), (3.9) представим в виде

${{\left. {\frac{{\partial p(x,{{\alpha }_{n}})}}{{\partial \alpha }}} \right|}_{{\alpha = {\rm A}}}} = \sum\limits_{k = 1}^n {c_{{nk}}^{{(1)}}{{p}_{k}}(x)} + x{{\rho }_{f}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = 0,\quad {{\left. {\frac{{\partial p(x,{{\alpha }_{1}})}}{{\partial \alpha }}} \right|}_{{\alpha = 0}}} = \sum\limits_{k = 1}^n {c_{{1k}}^{{(1)}}{{p}_{k}}(x)} = 0,$
и, переписав их следующим образом
$\begin{gathered} c_{{n1}}^{{(1)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{nk}}^{{(1)}}{{p}_{k}}(x)} + c_{{nn}}^{{(1)}}{{p}_{n}}(x) + x{{\rho }_{f}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = 0 \\ c_{{11}}^{{(1)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{1k}}^{{(1)}}{{p}_{k}}(x)} + c_{{1n}}^{{(1)}}{{p}_{n}}(x) = 0, \\ \end{gathered} $
получим явные выражения для “ крайних” значений

$\begin{gathered} {{p}_{n}}(x) = \frac{{c_{{n1}}^{{(1)}}\sum\limits_{k = 2}^{n - 1} {c_{{1k}}^{{(1)}}{{p}_{k}}(x)} {\text{/}}c_{{11}}^{{(1)}} - \sum\limits_{k = 2}^{n - 1} {c_{{nk}}^{{(1)}}{{p}_{k}}} (x) - x{{\rho }_{f}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}}}{{c_{{nn}}^{{(1)}} - c_{{n1}}^{{(1)}}c_{{n1}}^{{(1)}}{\text{/}}c_{{11}}^{{(1)}}}} \\ {{p}_{1}}(x) = - \frac{{\sum\limits_{k = 2}^{n - 1} {c_{{1k}}^{{(1)}}{{p}_{k}}(x)} + c_{{1n}}^{{(1)}}{{p}_{n}}(x)}}{{c_{{11}}^{{(1)}}}} \\ \end{gathered} $

Тогда система обыкновенных дифференциальных уравнений примет вид

$p_{2}^{{(1)}}(x) = c_{{21}}^{{(1)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{2k}}^{{(1)}}{{y}_{{7 + 2(k - 1)}}}} + c_{{2n}}^{{(1)}}{{p}_{n}}(x)$
$p_{2}^{{(2)}}(x) = c_{{21}}^{{(2)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{2k}}^{{(2)}}{{y}_{{7 + 2(k - 1)}}}} + c_{{2n}}^{{(2)}}{{p}_{n}}(x)$
${{y}_{9}} = {{p}_{2}}(x),\quad y_{9}^{'} = {{y}_{{10}}}$
$y_{{10}}^{'} = - \frac{{p_{2}^{{(2)}}(x)}}{{{{x}^{2}}}} + {{y}_{9}}\left( {\frac{{{{j}^{2}}}}{{{{{\sin }}^{2}}{{\alpha }_{2}}}} - \frac{{p_{2}^{{(1)}}(x)}}{{\operatorname{tg} {{\alpha }_{2}}}} - \frac{{{{x}^{2}}{{\omega }^{2}}}}{{{{c}^{2}}}}} \right){\text{/}}{{x}^{2}} - \frac{{2{{y}_{{10}}}}}{x}$
$p_{3}^{{(1)}}(x) = c_{{31}}^{{(1)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{3k}}^{{(1)}}{{y}_{{7 + 2(k - 1)}}}} + c_{{3n}}^{{(1)}}{{p}_{n}}(x)$
$p_{3}^{{(2)}}(x) = c_{{31}}^{{(2)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{3k}}^{{(2)}}{{y}_{{7 + 2(k - 1)}}}} + c_{{3n}}^{{(2)}}{{p}_{n}}(x)$
(3.23)
${{y}_{{11}}} = {{p}_{3}}(x),\quad y_{{11}}^{'} = {{y}_{{12}}}$
$y_{{12}}^{'} = - \frac{{p_{3}^{{(2)}}(x)}}{{{{x}^{2}}}} + {{y}_{{11}}}\left( {\frac{{{{j}^{2}}}}{{{{{\sin }}^{2}}{{\alpha }_{3}}}} - \frac{{p_{3}^{{(1)}}(x)}}{{\operatorname{tg} {{\alpha }_{3}}}} - \frac{{{{x}^{2}}{{\omega }^{2}}}}{{{{c}^{2}}}}} \right){\text{/}}{{x}^{2}} - \frac{{2{{y}_{{12}}}}}{x}$
$ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots $
$p_{{n - 1}}^{{(1)}}(x) = c_{{n - 11}}^{{(1)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{n - 1k}}^{{(1)}}{{y}_{{7 + 2(k - 1)}}}} + c_{{n - 1n}}^{{(1)}}{{p}_{n}}(x)$
$p_{{n - 1}}^{{(2)}}(x) = c_{{n - 11}}^{{(2)}}{{p}_{1}}(x) + \sum\limits_{k = 2}^{n - 1} {c_{{n - 1k}}^{{(2)}}{{y}_{{7 + 2(k - 1)}}}} + c_{{n - 1n}}^{{(2)}}{{p}_{n}}(x)$
${{y}_{{7 + 2(n - 1)}}} = {{p}_{{n - 1}}}(x),\quad y_{{7 + 2(n - 1)}}^{'} = {{y}_{{8 + 2(n - 1)}}}$
$y_{{8 + 2(n - 1)}}^{'} = - \frac{{p_{{n - 1}}^{{(2)}}(x)}}{{{{x}^{2}}}} + {{y}_{{7 + 2(n - 1)}}}\left( {\frac{{{{j}^{2}}}}{{{{{\sin }}^{2}}{{\alpha }_{{n - 1}}}}} - \frac{{p_{{n - 1}}^{{(1)}}(x)}}{{\operatorname{tg} {{\alpha }_{{n - 1}}}}} - \frac{{{{x}^{2}}{{\omega }^{2}}}}{{{{c}^{2}}}}} \right){\text{/}}{{x}^{2}} - \frac{{2{{y}_{{8 + 2(n - 1)}}}}}{x}$

Таким образом, для данного метода совокупное число неизвестных, определяемых системами уравнений (3.5) и (3.23), также составляет $m = 8 + 2(n - 1)$. Отмечается [51], что МДК довольно часто обеспечивает более точное решение дифференциальных уравнений в случае неравномерных сеток, узлы которых определяются согласно распределению Чебышева–Гаусса–Лобатто. Однако для корректного сравнения с другими методами все расчеты осуществлялись на равномерной сетке, тем более, что для описанной реализации МДК преимущества неравномерной сетки выявлены не были.

4. Метод решения. Система уравнений (3.5) (в случае вычисления гидродинамического давления p по аналитической формуле) как и объединенные системы уравнений (3.5), (3.14), (3.5), (3.21) и (3.5), (3.23) решаются методом ортогональной прогонки Годунова [37] с численным интегрированием дифференциальных уравнений методом Рунге–Кутты четвертого порядка точности и соответствующими однородными граничными условиями, задаваемыми на краях оболочки

(4.1)
${{\left. {{{y}_{i}}} \right|}_{{s = 0}}}{{\delta }_{i}} + {{\left. {{{y}_{{i + 4}}}} \right|}_{{s = 0}}}\left( {1 - {{\delta }_{i}}} \right) = 0;\quad i = 1 \ldots 4$
(4.2)
${{\left. {{{y}_{i}}} \right|}_{{s = L}}}{{\delta }_{{i + 4}}} + {{\left. {{{y}_{{i + 4}}}} \right|}_{{s = L}}}\left( {1 - {{\delta }_{{i + 4}}}} \right) = 0;\quad i = 1 \ldots 4$
(4.3)
${{\left. {{{y}_{i}}} \right|}_{{x = 0}}} = 0;\quad i = 10,12 \ldots m{\text{/}}2$
(4.4)
${{\left. {{{y}_{i}}} \right|}_{{x = L}}} = 0;\quad i = 10,12 \ldots m{\text{/}}2,$
где ${{\delta }_{i}} = 0$, если заданы кинематические, и ${{\delta }_{i}} = 1$, если заданы статические граничные условия.

Общее решение систем представляется в виде

${\mathbf{y}} = \sum\limits_{k = 1}^{m/2} {{{C}_{k}}{{{\mathbf{y}}}_{k}}} ,$
где ${{C}_{k}}$ – некоторые константы и ${{{\mathbf{y}}}_{j}}$ – совокупность линейно независимых решений объединенных систем, удовлетворяющих граничным условиям (4.1), (4.3). В результате интегрирования по заданному интервалу и удовлетворения граничных условий (4.2), (4.4) получаем следующую алгебраическую систему для определения постоянных ${{C}_{k}}$

(4.5)
$\sum\limits_{k = 1}^{m/2} {{{C}_{k}}{{f}_{{ik}}}} = 0;\quad i = 1,m{\text{/}}2$

Искомая задача сводится к вычислению таких значений ω, при которых существует нетривиальное решение системы (4.5), необходимым условием которого является равенство нулю определителя матрицы $\left| {{{f}_{{ij}}}\left( \omega \right)} \right| = 0$. Для этой цели используется комбинация шаговой процедуры, посредством которой вычисляются значения ω, при которых происходит смена знака определителя $\left| {{{f}_{{ij}}}\left( \omega \right)} \right|$, с последующим уточнением ω в полученном диапазоне методом деления отрезка пополам.

5. Численные результаты. В численных примерах рассматриваются свободно опертые (${v} = w$ = ${{T}_{{11}}} = {{M}_{{11}}}$ = 0, SS), жестко защемленные ($u = {v} = w = {{\theta }_{1}}$ = 0, CC) на обоих краях или консольно закрепленные $({{T}_{{11}}} = 0$, $S + 2{{r}_{2}}H = 0$, ${{M}_{{11}}} = 0$, ${{Q}_{{11}}} + \bar {j}H = 0$, CF) конические оболочки.

Первоначально была исследована сходимость решения от степени дискретизации области жидкости n. На рисунках 2 и 3 представлены зависимости трех низших частот колебаний ω (Гц) жестко закрепленной оболочки от количества узлов (прямых) n, на которые разбивается область жидкости тремя описанными выше методами. Проверка сходимости решения осуществлена для оболочек с разными граничными условиями и углами конусности Α = 30° (рис. 2) и Α = 60° (рис. 3). Из приведенных данных следует, что наихудшей сходимостью обладает метод прямых, как это было отмечено в монографии [41]. Однако с вычислительной точки зрения данный метод обеспечивает наиболее эффективное решение при равном количестве точек разбиения. Интерполяция сплайнами является наименее экономичным методом из-за дополнительных вычислений, выполняемых на каждом шаге интегрирования. С ростом точек интегрирования относительно быстрая сходимость этого метода нивелируется более высокой скоростью решения метода прямых, поэтому при определенных условиях оба метода являются сопоставимыми. В процессе вычислений было также выявлено, что с ростом угла конусности для получения устойчивого решения при некоторых граничных условиях и окружных гармониках требуется повышение количества точек интегрирования, особенно в случае интерполяции сплайнами и метода прямых. С учетом высказанных замечаний преимущества метода дифференциальных квадратур благодаря исключительной сходимости являются неоспоримыми. При дальнейших расчетах количество прямых (узлов) n принимается равным 10, 20 и 50 для методов дифференциальных квадратур, интерполяции сплайнами и прямых соответственно.

Рис. 2.

Сходимость трех низших собственных частот ω (Гц) жестко закрепленной (CC) конической оболочки с жидкостью от количества узлов n для различных методов преобразования волнового уравнения: Α = 30°;  j = 5; 1 – МП, 2 – КС, 3 – МДК.

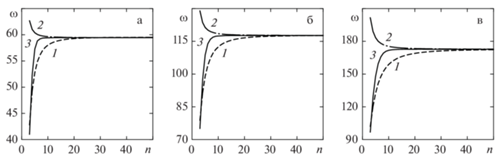
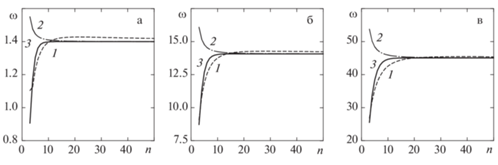
Рис. 3.

Сходимость трех низших собственных частот ω (Гц) консольно закрепленной (CF) конической оболочки с жидкостью от количества узлов n для различных методов преобразования волнового уравнения: Α = 60°;  j = 5; 1 – МП, 2 – КС, 3 – МДК.

Верификация результатов, получаемых в рамках описанного алгоритма, для пустых конических оболочек осуществлена в статье [52]. В случае оболочек с жидкостью сравнение с известными решениями производится для нескольких конфигураций. В первом примере рассматривается полностью заполненная несжимаемой жидкостью (ρf = = 1000 кг/м3) жестко закрепленная усеченная коническая оболочка (L = 0.56 м, R1 = = 0.15 м, h = 0.00053 м, Α = 15°), выполненная из материала АМГ-6 (E = 67.7 ГПа, ν = 0.29, ρ = 2648 кг/м3), экспериментальные и теоретические результаты для которой были опубликованы в работе [6]. За прошедшие десятилетия эти данные стали выступать в качестве эталона, сопоставление с которым является неотъемлемой частью большинства исследований, посвященных анализу конических оболочек, взаимодействующих с жидкостью. В таблице 1 приведены низшие частоты колебаний ω (Гц), полученные для ряда окружных гармоник j. Здесь введены обозначения для следующих источников данных: 1 – [6] (МОПГ), 2 – [6] (эксперимент), 3 – [16] (МКЭ), 4 – [37] (МОПГ), 5 – [53] (МКЭ), 6 – [54] (МКЭ), 7 – МОПГ и МП, 8 – МОПГ и КС, 9 – МОПГ и МДК. Из приведенной в таблице информации следует, что при небольшом угле конусности результаты, полученные в рамках как численно-аналитических, так и численных методов, хорошо согласуются не только между собой, но и с данными натурных наблюдений.

Таблица 1.

Сравнение собственных частот колебаний ω (Гц) жестко закрепленной (CC) конической оболочки, заполненной жидкостью

№ Номер гармоники  j
3 4 5 6 7 8 9 10
1 101.0 78.7 63.60 54.4 50.80 52.80 – 67.3
2 100.0 76.0 – – 51.00 54.00 – 69.8
3 101.63 79.16 63.82 54.41 50.70 52.44 – 66.86
4 101.76 79.29 63.99 54.64 51.02 52.87 – 67.51
5 100.86 78.7 63.55 54.23 50.52 52.24 58.20 –
6 96.34 75.5 61.07 53.22 50.12 52.14 58.21 –
7 100.95 78.54 63.29 53.95 50.28 51.98 57.83 66.12
8 100.91 78.56 63.36 54.07 50.46 52.26 58.26 66.75
9 100.91 78.55 63.34 54.05 50.42 52.19 58.17 66.61

В следующем примере рассматривается конфигурация (L = 0.9144 м, h = 0.0015 м, E = 207 ГПа, ν = 0.3, ρ = 7840 кг/м3), используемая для верификации результатов конечно-элементных решений во многих работах. Радиус оболочки, содержащей сжимаемую жидкость (ρf  = 1000 кг/м3, c = 1500 м/с), при 0.5L остается неизменным и равным 0.876 м. В таблицах 2–4 приведены низшие частоты колебаний ω (Гц) для первых 12 окружных гармоник, полученные для трех углов конусности при различных комбинациях граничных условий. Здесь источники данных обозначены следующим образом: 1 – [19] (МКЭ), 2 – [30] (МКЭ), 3 – [33] (МКЭ), 4 – МОПГ и МП, 5 – МОПГ и КС, 6 – МОПГ и МДК, 7 – [23] (сплайны).

Таблица 2.

Сравнение собственных частот колебаний ω (Гц) жестко закрепленной (CC) конической оболочки, заполненной жидкостью, при различных углах конусности Α

№ Номер гармоники  j
1 2 3 4 5 6 7 8 9 10 11 12
Угол конусности Α = 10°
1 99.55 107.35 98.92 88.03 77.99 69.35 62.10 56.18 51.57 48.32 46.53 46.29
2 98.37 105.96 99.52 88.01 78.46 70.28 62.71 57.41 52.56 49.69 48.03 48.34
3 95.43 103.73 95.56 85.06 75.69 67.42 60.75 54.91 50.94 47.64 45.78 45.78
4 99.95 107.46 98.66 87.59 77.47 68.80 61.55 55.62 51.01 47.74 45.92 45.63
5 99.88 107.46 98.69 87.66 77.59 68.97 61.77 55.90 51.34 48.13 46.38 46.18
6 97.19 107.43 98.66 87.62 77.53 68.89 61.67 55.77 51.18 47.93 46.11 45.82
Угол конусности Α = 30°
1 73.62 79.64 74.58 66.68 58.94 52.16 46.55 42.18 39.15 37.58 37.54 38.97
2 73.96 80.14 75.12 67.01 59.41 52.33 46.67 42.80 39.97 38.30 38.43 39.97
3 70.05 81.92 74.82 66.75 58.55 51.54 45.94 41.71 39.14 37.17 37.31 37.31
7 69.54 83.10 68.27 66.98 58.21 49.31 46.76 44.06 41.04 34.91 – –
4 80.79 85.50 77.63 68.09 59.51 52.31 46.47 41.98 38.88 37.26 37.16 38.52
5 80.55 85.29 77.47 68.00 59.49 52.34 46.56 42.13 39.08 37.52 37.50 38.96
6 78.61 85.25 77.44 67.95 59.42 52.27 46.47 42.01 38.93 37.32 37.22 38.56
Угол конусности Α = 60°
1 20.52 22.62 21.77 19.58 17.64 16.57 16.15 16.20 16.62 17.36 18.34 19.56
2 21.27 23.48 22.44 20.17 17.90 17.01 16.25 16.59 16.80 17.49 18.52 19.90
4 29.99 31.64 27.11 22.12 19.03 17.51 16.88 16.83 17.19 17.88 18.85 20.05
5 29.51 31.14 26.71 21.82 18.81 17.34 16.75 16.75 17.16 17.91 18.94 20.23
6 28.91 31.10 26.68 21.79 18.68 17.52 17.08 16.87 16.98 17.67 18.56 19.66
Таблица 3.

Сравнение собственных частот колебаний ω (Гц) консольно закрепленной (CF) конической оболочки, заполненной жидкостью, при различных углах конусности Α

№ Номер гармоники  j
1 2 3 4 5 6 7 8 9 10 11 12
Угол конусности Α = 10°
1 63.72 48.16 35.43 26.76 20.92 17.09 14.87 14.16 14.89 16.87 19.88 23.72
2 63.25 48.43 35.17 27.12 21.38 17.72 15.63 14.58 14.89 16.97 20.21 24.17
3 61.80 46.94 34.85 26.58 20.96 16.92 15.14 14.42 15.10 16.74 19.86 23.83
4 64.50 48.93 35.98 27.13 21.16 17.25 14.98 14.24 14.94 16.90 19.88 23.68
5 64.46 48.92 35.98 27.14 21.19 17.29 15.03 14.31 15.03 17.03 20.07 23.96
6 62.80 48.92 35.98 27.14 21.18 17.27 15.01 14.28 14.99 16.97 19.97 23.79
Угол конусности Α = 30°
1 34.36 23.58 16.74 12.45 9.74 8.19 7.66 8.12 9.42 11.36 13.77 16.56
2 34.12 23.86 16.63 12.92 10.09 8.72 7.95 8.24 9.42 11.48 13.63 16.86
3 35.71 25.37 18.34 13.48 10.69 8.98 8.15 8.74 9.98 11.72 14.24 16.87
4 38.10 26.15 18.44 13.60 10.57 8.82 8.20 8.64 9.98 12.00 14.52 17.42
5 37.98 26.08 18.40 13.58 10.56 8.82 8.22 8.67 10.04 12.09 14.65 17.62
6 37.11 26.08 18.39 13.58 10.55 8.81 8.20 8.65 10.00 12.02 14.54 17.44
Угол конусности Α = 60°
1 1.08 0.58 0.47 0.67 1.02 1.44 1.93 2.49 3.14 3.88 4.71 5.64
2 1.21 0.72 0.53 0.69 1.00 1.44 1.92 2.49 3.14 3.90 4.76 5.69
4 1.57 0.83 0.67 0.95 1.42 1.98 2.63 3.39 4.25 5.22 6.32 7.55
5 1.54 0.82 0.66 0.93 1.40 1.96 2.61 3.37 4.24 5.23 6.35 7.62
6 1.51 0.81 0.66 0.93 1.40 1.95 2.60 3.34 4.19 5.15 6.21 7.39
Таблица 4.

Сравнение собственных частот колебаний ω (Гц) свободно опертой (SS) конической оболочки, заполненной жидкостью, при различных углах конусности Α

№ Номер гармоники  j
1 2 3 4 5 6 7 8 9 10 11 12
Угол конусности Α = 10°
1 93.98 105.96 93.58 76.76 62.26 51.09 42.83 37.03 33.39 31.81 32.16 34.28
2 92.03 103.70 93.05 76.90 61.79 51.13 43.06 37.21 33.77 32.56 32.56 34.78
3 92.79 103.25 90.38 74.35 60.36 50.00 41.61 36.57 32.84 31.44 31.99 34.10
4 94.49 106.18 93.32 76.36 61.85 50.69 42.46 36.67 33.05 31.44 31.76 33.82
5 94.42 106.17 93.34 76.42 61.95 50.82 42.61 36.85 33.26 31.70 32.07 34.22
6 91.88 106.15 93.32 76.39 61.90 50.76 42.54 36.77 33.16 31.57 31.90 33.96
Угол конусности Α = 30°
1 61.09 77.56 69.52 55.79 44.32 35.95 30.22 26.74 25.32 25.79 27.81 30.95
2 – 76.81 69.16 55.81 44.54 36.11 30.67 27.55 25.87 26.12 28.32 31.68
3 62.02 81.36 70.12 56.21 44.10 35.70 30.38 26.62 24.85 25.01 27.40 30.51
4 67.11 83.63 72.00 56.67 44.63 36.03 30.19 26.65 25.19 25.61 27.58 30.66
5 66.90 83.42 71.85 56.60 44.61 36.05 30.25 26.74 25.32 25.79 27.83 31.01
6 65.28 83.39 71.82 56.56 44.57 36.00 30.18 26.66 25.22 25.65 27.62 30.68
Угол конусности Α = 60°
1 14.92 21.83 15.47 11.33 10.38 10.30 10.62 11.23 12.05 13.07 14.26 15.63
2 – 21.70 15.49 11.82 10.53 10.22 10.63 11.14 12.02 13.10 14.39 15.53
4 21.95 30.37 17.19 12.23 11.09 10.93 11.22 11.81 12.64 13.69 14.91 16.32
5 21.59 29.87 16.94 12.07 10.96 10.83 11.14 11.76 12.62 13.71 14.99 16.47
6 21.16 29.86 16.92 12.05 10.93 10.79 11.08 11.67 12.49 13.50 14.67 16.00

Из представленных в таблицах 2–4 данных видно, что полученные в работе результаты достаточно хорошо согласуются с конечно-элементными решениями с некоторыми исключениями. В частности, фактически для всех рассмотренных вариантов наиболее существенное расхождение имеет место в области низших гармоник. С повышением номера j низшая частота стремится к своему минимальному значению, а различие между разными методами решения нивелируется. Отметим, что о некоторых отличиях с результатами, полученными с использованием метода конечных элементов, в том числе в коммерческом пакете ANSYS, сообщается также в работах [9, 24, 25]. Причина этих расхождений не выявлена. Также подчеркнем, что во всех приведенных сравнениях результаты, вычисленные для различных способов сведения уравнений жидкости, практически идентичны.

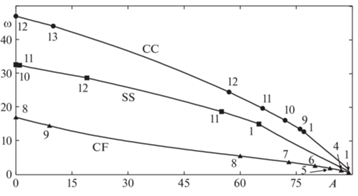
С помощью описанного алгоритма выполнен анализ влияния угла конусности Α на минимальную частоту колебаний ω. Параметры конструкции аналогичны предыдущему примеру за тем исключением, что минимальный радиус и длина образующей остаются неизменными и равными 0.876 м, 0.9144 м соответственно. Результаты исследования, выполненные с использованием метода дифференциальных квадратур, приведены на рисунке 4. Символами на графиках обозначены места смены формы колебаний с минимальной частотой, а цифрами указано число полуволн в окружном направлении j. Согласно представленным зависимостям рост угла конусности приводит к монотонному снижению низшей частоты колебаний. Отметим, что для свободно опертых и жестко закрепленных оболочек существует некоторое пороговое значение A, после которого частота снижается более существенно за счет реализации балочной моды.

Рис. 4.

Зависимости низших частот колебаний ω (Гц) от угла конусности Α, полученные для конических оболочек с различными граничными условиями.

Заключение. Представлены результаты численных исследований частотного спектра усеченных круговых конических оболочек, заполненных идеальной сжимаемой жидкостью. Решение краевой задачи выполняется методом ортогональной прогонки Годунова, в котором осуществляется интегрирование связанных систем обыкновенных дифференциальных уравнений для оболочки и жидкости. Для упругого тела такая система получена преобразованием уравнений классической теории оболочек относительно новых неизвестных, а для уравнений жидкости – в результате применения трех различных способов: метода прямых, интерполяции кубическим сплайном и обобщенного метода дифференциальных квадратур. Их точность и вычислительная эффективность оценена на ряде примеров. Продемонстрировано, что для анализа динамических характеристик конических оболочек с жидкостью целесообразно использование метода дифференциальных квадратур. Этот способ обеспечивает приемлемую точность вычислений и высокую скорость сходимости решения. Проанализировано влияние угла конусности на минимальную частоту собственных колебаний конструкции при различных граничных условиях.

Работа выполнена в рамках государственного задания; номер гос. регистрации темы АААА-А19-119012290100-8.

Список литературы

  1. Шклярчук Ф.Н. О приближенном методе расчета осесимметричных колебаний оболочек вращения с жидким заполнением // Изв. АН СССР. Механика. 1965. № 6. С. 123–129.

  2. Докучаев Л.В. Об уравнениях упругих колебаний полости, частично заполненной жидкостью // Изв. АН СССР. Механика. 1965. № 3. С. 149–153.

  3. Пожалостин А.А. Построение системы гармонических функций для неосесимметричных колебаний конического бака, заполненного жидкостью // Колебания упругих конструкций с жидкостью: Тр. II-го Всесоюзн. симп. Новосибирск: Изд. НЭТИ, 1974. С. 229–231.

  4. Пожалостин А.А. Неосесимметричные колебания конической оболочки, частично заполненной жидкостью // Динамика упругих и твердых тел, взаимодействующих с жидкостью: Тр. I Всесоюзн. сем. Томск: Изд. ТГУ, 1975. С. 85–93.

  5. Пожалостин А.А., Каменский О.А., Куликов В.З. Экспериментальное определение форм и частот осесимметричных колебаний конического бака, частично заполненного жидкостью // Тр. X Всесоюзн. конф. по теории оболочек и пластинок. Кутаиси, 1975. С. 178–180.

  6. Горбунов Ю.А., Новохатская Л.М., Шмаков В.П. Теоретическое и экспериментальное исследование спектра собственных неосесимметричных колебаний конической оболочки с жидкостью при наличии внутреннего давления // Динамика упругих и твердых тел, взаимодействующих с жидкостью. Томск: Томский ун-т, 1975. С. 47–52.

  7. Lakis A.A., van Dyke P., Ouriche H. Dynamic analysis of anisotropic fluid-filled conical shells // J. Fluids Struct. 1992. V. 6. № 2. P. 135–162.

  8. Kerboua Y., Lakis A.A. Dynamic behaviour of a rocket filled with liquid // Univ. J. Aeronaut. Aerosp. Sci. 2014. V. 2. P. 55–79.

  9. Jhung M.J., Jo J.C., Jeong K.H. Modal analysis of conical shell filled with fluid // J. Mech. Sci. Technol. 2006. V. 20. № 11. P. 1848–1862.

  10. Caresta M., Kessissoglou N.J. Vibration of fluid loaded conical shells // J. Acoust. Soc. Am. 2008. V. 124. № 4. P. 2068–2077.

  11. Liu M., Liu J., Cheng Y. Free vibration of a fluid loaded ring-stiffened conical shell with variable thickness // J. Vib. Acoust. 2014. V. 136. № 5. 051006.

  12. Liu J., Ye X., Liu M., Cheng Y., Wu L. A semi-analytical method of free vibration of fluid loaded ring-stiffened stepped conical shell // J. Mar. Eng. Technol. 2014. V. 13. № 2. P. 35–49.

  13. Xie K., Chen M., Deng N., Jia W. Free and forced vibration of submerged ring-stiffened conical shells with arbitrary boundary conditions // Thin-Walled Struct. 2015. V. 96. P. 240–255.

  14. Zhu H., Wu J. Free vibration of partially fluid-filled or fluid-surrounded composite shells using the dynamic stiffness method // Acta Mech. 2020. V. 231. P. 3961–3978.

  15. Шклярчук Ф.Н., Рей Ч. Расчет осесимметричных колебаний оболочек вращения с жидкостью методом конечных элементов // Вестн. МАИ. 2012. Т. 19. № 5. С. 197–204.

  16. Шклярчук Ф.Н., Рей Ч. Расчет неосесимметричных колебаний оболочек вращения с жидкостью методом конечных элементов // Вестн. МАИ. 2013. Т. 20. № 2. С. 49–58.

  17. Кирпиченко В.Н., Швейко Ю.Ю. О влиянии гидростатики на частоты колебаний оболочек топливных баков жидкостных ракет-носителей // Космонавтика и ракетостроение. 2014. № 3 (76). С. 46–51.

  18. Шупиков А.Н., Мисюра C.Ю., Ярещенко В.Г. Численное и экспериментальное исследование гидроупругих колебаний оболочек // Восточно-европейский журнал передовых технологий. 2014. № 6(7). С. 8–12.

  19. Rahmanian M., Firouz-Abadi R.D., Cigeroglu E. Free vibrations of moderately thick truncated conical shells filled with quiescent fluid // J. Fluids Struct. 2016. V. 63. P. 280–301.

  20. Бауэр С.М., Ермаков А.М., Каштанова С.В., Морозов Н.Ф. Применение неклассических моделей теории оболочек к исследованию механических параметров многослойных нанотрубок // Вестн. Санкт-Петербургского университета. Математика. Механика. Астрономия. 2011. № 1. С. 22–30.

  21. Hien V.Q., Thinh T.I., Cuong N.M. Free vibration analysis of joined composite conical-cylindrical-conical shells containing fluid // Vietnam J. Mech. 2016. V. 38. P. 249–265.

  22. Musa A., El Damatty A.A. Capacity of liquid steel conical tanks under hydrodynamic pressure due to horizontal ground excitations // Thin-Walled Struct. 2016. V. 103. P. 157–170.

  23. Musa A., El Damatty A.A. Capacity of liquid-filled steel conical tanks under vertical excitation // Thin-Walled Struct. 2016. V. 103. P. 199–210.

  24. Nurul Izyan M.D., Viswanathan K.K., Aziz Z.A. et al. Free vibration of layered truncated conical shells filled with quiescent fluid using spline method // Compos. Struct. 2017. V. 163. P. 385–398.

  25. Mohammadi N., Aghdam M.M., Asadi H. Instability analysis of conical shells filled with quiescent fluid using generalized differential quadrature method // The 26th Annual Int. Conf. of Iranian Soc. Mech. Eng.-ISME2018, 24–26 April, 2018, School of Mech. Engng., Semnan Univ., Semnan, Iran, ISME2018-1216.

  26. Огородник У.Е., Гнитько В.И. Методы граничных и конечных элементов для динамического анализа оболочек с жидкостью // Механика машин, механ. и матер. 2013. № 4(25). С. 65–69.

  27. Naumenko Y.V., Gnitko V.I., Strelnikova E.A. Liquid induced vibrations of truncated elastic conical shells with elastic and rigid bottoms // Int. J. Eng. Technol. 2018. V. 7(2.23). P. 335–339.

  28. Paknejad R., Ghasemi F.A., Malekzadeh F.K. Natural frequency analysis of multilayer truncated conical shells containing quiescent fluid on elastic foundation with different boundary conditions // Int. J. App. Mech. 2021. V. 13. № 7. 2150075.

  29. Кийко И.А. Постановка задачи об аэроупругих колебаниях конической оболочки малого раствора, внутри которой со сверхзвуковой скоростью протекает газ // Вестн. Моск. ун-та. Сер. 1. Матем. мех. 2004. № 3. С. 58–61.

  30. Кийко И.А., Наджафов М.А. Флаттер конической оболочки // Пробл. машиностр. и автом. 2009. № 4. С. 96–98.

  31. Senthil Kumar D., Ganesan N. Dynamic analysis of conical shells conveying fluid // J. Sound Vib. 2008. V. 310. № 1–2. P. 38–57.

  32. Бочкарёв С.А., Матвеенко В.П. Исследование устойчивости конических оболочек вращения с внутренним течением жидкости // Вестн. СамГУ. Естеств. сер. 2008. № 6(65). С. 225–237.

  33. Bochkarev S.A., Matveenko V.P. Natural vibrations and stability of shells of revolution interacting with an internal fluid flow // J. Sound Vib. 2011. V. 330. P. 3084–3101.

  34. Kerboua Y., Lakis A.A., Hmila M. Vibration analysis of truncated conical shells subjected to flowing fluid // Appl. Math. Model. 2010. V. 34. № 3. P. 791–809.

  35. Rahmanian M., Firouz-Abadi R.D., Cigeroglu E. Dynamics and stability of conical/cylindrical shells conveying subsonic compressible fluid flows with general boundary conditions // Int. J. Mech. Sci. 2017. V. 120. P. 42–61.

  36. Mohammadi N., Asadi H., Aghdam M.M. An efficient solver for fully coupled solution of interaction between incompressible fluid flow and nanocomposite truncated conical shells // Comput. Methods Appl. Mech. Eng. 2019. V. 351. P. 478–500.

  37. Годунов С.К. О численном решении краевых задач для систем линейных обыкновенных дифференциальных уравнений // Усп. матем. наук. 1961. Т. 16. № 3. С. 171–174.

  38. Горшков А.Г., Морозов В.И., Пономарев А.Т., Шклярчук Ф.Н. Аэрогидроупругость конструкций. М.: Физматлит, 2000. 591 с.

  39. Шмаков В.П. Избранные труды по гидроупругости и динамике упругих конструкций. М.: Изд-во МГТУ им. Н.Э. Баумана, 2011. 287 с.

  40. Юдин А.С., Амбалова Н.М. Вынужденные колебания коаксиальных подкрепленных цилиндрических оболочек при взаимодействии с жидкостью // Прикл. мех. 1989. Т. 25. № 12. С. 63–68.

  41. Юдин А.С., Сафроненко В.Г. Виброакустика структурно-неоднородных оболочек. Ростов н/Д: Изд-во ЮФУ, 2013. 424 с.

  42. Bochkarev S.A. Natural vibrations of a cylindrical shell with fluid partly resting on a two-parameter elastic foundation // Int. J. Struct. Stab. Dyn. 2022. V. 22. 2250071.

  43. Shu C. Differential Quadrature and Its Application in Engineering. London: Springer, 2000. 340 p.

  44. Барулина М.А. Применение обобщенного метода дифференциальных квадратур к решению двумерных задач механики // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2018. Т. 18. Вып. 2. С. 206–216.

  45. Кармишин А.В., Лясковец В.А., Мяченков В.И., Фролов А.Н. Статика и динамика тонкостенных оболочечных конструкций. М.: Машиностроение, 1975. 376 с.

  46. Березин И.С., Жидков Н.П. Методы вычислений. Том 2. М.: Физматлит, 1962. 620 с.

  47. Демидович Б.П., Марон И.А., Шувалова Е.З. Численные методы анализа. М.: Наука, 1967. 368 с.

  48. Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с.

  49. Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам. М.: Логос, 2004. 184 с.

  50. De Boor C. A Practical Guide to Splines. New York: Springer, 2001. 348 p.

  51. Bert C.W., Malik M. Differential quadrature method in computational mechanics: A review // ASME. Appl. Mech. Rev. 1996. V. 49. № 1. P. 1–28.

  52. Бочкарёв С.А. Собственные колебания усеченных конических оболочек переменной толщины // Вычисл. механика сплошных сред. 2020. Т. 13. № 4. С. 402–413.

  53. Бочкарёв С.А., Матвеенко В.П. Численное моделирование устойчивости нагруженных оболочек вращения при внутреннем течении жидкости // ПМТФ. 2008. Т. 49. № 2. С. 185–195.

  54. Григорьев В.Г. Методология исследования динамических свойств сложных упругих и гидроупругих систем / Дисс. на соискание ученой степени доктора техн. наук, М.: 2000, 326 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал