1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 4, 2022

Прикладная математика и механика, 2022, T. 86, № 4, стр. 451-469

Задачи Лэмба и родственные проблемы динамики. Обзор

В. А. Братов 1, 2, 3, С. В. Кузнецов 4, *, Н. Ф. Морозов 1, 2

1 Институт проблем машиноведения РАН
С. Петербург, Россия

2 СПб Государственный университет
С. Петербург, Россия

3 СПб Политехнический университет Петра Великого
С. Петербург, Россия

4 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: kuzn-sergey@yandex.ru

Поступила в редакцию 29.03.2022
После доработки 05.05.2022
Принята к публикации 15.05.2022

Полный текст (PDF)

Аннотация

Анализируется решение внутренней и внешней задач Лэмба от сосредоточенного силового воздействия, приложенного к свободной границе упругого полупространства (полуплоскости). Рассматриваются так же некоторые родственные задачи, в частности о приложении дуплетов и диполей в упругом полупространстве, о появлении высокочастотных волн, отвечающих волне Рэлея, при распространении волн Похгаммера–Кри и др. Анализируются решения задач о движущейся нагрузке, приложенной к границе полупространства или полуплоскости.

Ключевые слова: задача Лэмба, объемная волна, волна Рэлея, полупространство, полуплоскость

1. Задачи Лэмба. Интегральные преобразования. Лэмб [1] рассмотрел две внешних задачи о распространении волн в изотропном упругом полупространстве и изотропной упругой полуплоскости от сосредоточенного силового воздействия, приложенного нормально к свободной границе. В этой работе были рассмотрены также две внутренние задачи о волнах в упругом полупространстве и полуплоскости, вызванные центром расширения, находящимся на некоторой глубине под поверхностью. Решение этих задач было сведено [1] к интегральным уравнениям относительно скалярного и векторного потенциалов. Внутренняя и внешняя задачи были обобщены [2] на случай сосредоточенных нагрузок, движущихся с постоянной скоростью.

Надо отметить, что в случае произвольных по времени нагрузок [1, 2] замкнутое решение удалось построить лишь в пространстве изображений (по Фурье для пространственных переменных и по Лапласу для временной переменной). С помощью асимптотических оценок было показано [1], что в случае внешних плоской и пространственной задач основной вклад в поле смещений на свободной поверхности вносят рэлеевские волны. Помимо этого, было получено аналитическое решение [1] для плоской внешней задачи в случае нормальной нагрузки, изменяющейся во времени в виде ядра Пуассона.

Кроме того, показано, что в случае гармонического источника магнитуды рэлеевских волн на свободной поверхности на достаточном удалении от эпицентра в случае плоской задачи не зависят от $\left| {rx} \right|$, а в случае пространственной задачи убывают пропорционально ${{\left| {rx} \right|}^{{ - 1/2}}}$, где $\left| x \right|$ – расстояние от эпицентра, а $r$ – волновое число. Далее, в той же работе с помощью асимптотических оценок было найдено, что наряду с волнами Рэлея точечный источник вызывает появление объемных продольных (P) и поперечных (S) волн. Магнитуды этих волн в случае гармонического источника на достаточном удалении от него в случае плоской задачи убывают на поверхности пропорционально ${{\left| {rx} \right|}^{{ - 3/2}}}$, а в случае пространственной задачи – пропорционально ${{\left| {rx} \right|}^{{ - 2}}}$. Заметим, что при распространении объемных волн, порожденных точечным гармоническим источником в безграничной среде, убывание их магнитуд происходит медленнее. Например, в случае плоской задачи магнитуда убывает как ${{\left| {rx} \right|}^{{ - 1/2}}}$, а в случае пространственной задачи, как ${{\left| {rx} \right|}^{{ - 1}}}$ [3]. Таким образом, в [1] впервые было дано теоретическое обоснование утверждения Рэлея [4] о том, что поверхностные (рэлеевские) волны убывают медленнее объемных волн с увеличением расстояния от источника.

Для построения решений, уравнения движения Навье в [1, 2] записывались в форме Ламе–Клапейрона ([5], Sect. 59)

(1.1)
$\left( {\lambda + 2\mu } \right)\nabla \operatorname{div} {\mathbf{u}} - \mu \operatorname{rot} \operatorname{rot} {\mathbf{u}} + {\mathbf{b}} = \rho {\mathbf{\ddot {u}}}{\kern 1pt} {\kern 1pt} ,$
где $\lambda $ и $\mu $ – константы Ламе, ${\mathbf{u}}$ – поле перемещений, ${\mathbf{b}}$ – поле массовых сил, $\rho $ – плотность среды, использовалось представление Гельмгольца ([5], Sect. 67) для поля массовых сил
(1.2)
${\mathbf{b}} = - \nabla \alpha - \operatorname{rot} \beta {\kern 1pt} ,$
где $\alpha $ и $\beta $ – скалярный и векторный потенциалы и представление Ламе–Грина ([5], Sect. 67) для динамического поля перемещений
(1.3)
${\mathbf{u}} = \nabla \varphi + \operatorname{rot} \psi {\kern 1pt} ,$
где $\varphi $ – скалярный, а $\psi $ – векторный потенциалы. Представление (1.3) аналогично представлению Папковича–Нейбера для поля перемещений при решении уравнений статики. В качестве начальных условий в [1, 2] рассматривались однородные условия вида

(1.4)
${{\left. {{\mathbf{u}}({\mathbf{x}},t)} \right|}_{{t = 0}}} = 0,\quad {{\left. {{{\partial }_{t}}{\mathbf{u}}({\mathbf{x}},t)} \right|}_{{t = 0}}} = 0$

На внешней поверхности ${{\Pi }_{\nu }}$ полупространства или полуплоскости задавались условия второй краевой задачи (в напряжениях)

(1.5)
${{{\mathbf{t}}}_{\nu }} \equiv \left( {\lambda \,{\text{tr}}\,\left( \varepsilon \right){\mathbf{I}} + 2\mu \,\varepsilon } \right) \cdot \nu = p({\mathbf{x}}{\kern 1pt} ',t)\,\nu {\kern 1pt} ;\quad {\mathbf{x}}{\kern 1pt} ' \in {{\Pi }_{\nu }},$
где $\nu $ – вектор единичной внешней нормали к границе; ${\mathbf{I}}$ – единичная диагональная матрица, $\varepsilon $ – тензор (малых) деформаций; $p$ – нагрузка на свободной поверхности. В случае внутренней задачи Лэмба $p = 0$.

Подстановка представлений (1.2), (1.3) в уравнения движения и применение преобразования Лапласа по временной переменной (или предположение о гармоническом изменении во времени нагрузки) позволили свести уравнения движения к неоднородным уравнениям Гельмгольца для скалярного и векторного потенциалов

(1.6)
$\left( {\Delta + \tfrac{{{{\omega }^{2}}}}{{c_{1}^{2}}}} \right)\varphi {\kern 1pt} ' = \tfrac{1}{{\lambda + 2\mu }}\alpha {\kern 1pt} ',\quad \left( {\Delta + \tfrac{{{{\omega }^{2}}}}{{c_{2}^{2}}}} \right)\psi {\kern 1pt} ' = \tfrac{1}{\mu }\beta {\kern 1pt} '$

Штрихи у потенциалов в (1.4) означают освобождение от гармонического множителя ${{e}^{{i\omega t}}}$. При получении уравнений (1.6) использовались три легко проверяемых тождества ([5], Sect. 5)

(1.7)
${\text{rot}}\,{\text{rot}}\,{\text{rot}}\,\psi = - {\text{rot}}\,\Delta \psi ,\quad {\text{div}}\,{\text{rot}}\,\psi = 0,\quad {\text{rot}}\,\nabla \,\varphi = 0$

Далее, для построения решения пространственного уравнения Гельмгольца в [1, 2] использовалось фундаментальное решение

(1.8)
$\varphi {\kern 1pt} ' = - \frac{1}{{4\pi \left| {\mathbf{x}} \right|}}{{e}^{{i{{r}_{1}}\left| {\mathbf{x}} \right|}}};\quad {{r}_{1}} = \frac{\omega }{{{{c}_{1}}}}$

Аналогичный вид имеет фундаментальное решение $\psi {\kern 1pt} '$ векторного уравнения Гельмгольца с заменой r1 на r2 и c1 на c2, где ${{c}_{1}}$ и c2 – скорости продольной и поперечной объемных волн соответственно

(1.9)
${{c}_{1}} = \sqrt {\frac{{\lambda + 2\mu }}{\rho }} ,\quad {{c}_{2}} = \sqrt {\frac{\mu }{\rho }} $

В плоском случае фундаментальное решение скалярного уравнения Гельмгольца представимо в виде

(1.10)
$\varphi {\kern 1pt} ' = - \frac{i}{4}H_{0}^{{(1)}}\left( {{{r}_{1}}\left| {\mathbf{x}} \right|} \right);\quad {{r}_{1}} = \frac{\omega }{{{{c}_{1}}}},$
где $H_{0}^{{(1)}}$ – функция Ганкеля первого рода нулевого порядка. Аналогичный вид имеет фундаментальное решение $\psi {\kern 1pt} '$ для векторного уравнения. При решении задачи с нагрузкой, произвольно зависящей от времени, круговая частота $\omega $ в выражениях (1.8), (1.10) заменяется на параметр преобразования Лапласа. Далее, осуществлялось [1, 2] сужение потенциалов с ядром (1.8) или (1.10) на граничную поверхность. Надо отметить, что полученные интегральные представления оказались весьма сложными: в замкнутом виде решение удалось получить лишь для гармонической нагрузки. В случае произвольной зависимости от времени замкнутое решение было получено в пространстве изображений, точнее, решение на поверхности было представлено в виде несобственного интеграла от алгебраической функции.

В дальнейшем представление Гельмгольца (1.1) и потенциалы Ламе–Грина (1.3) использовались в большинстве подходов, связанных с решением внутренней и внешней задач Лэмба, однако техника вычисления сингулярных интегралов, появляющихся при сужении потенциалов на граничную поверхность, менялась. С помощью метода наискорейшего спуска Дебая были получены [6, 7] асимптотические оценки для компонент перемещений на границе для некоторых внутренних и внешних задач, обобщающих задачу Лэмба, например, рассматривалась нагрузка [6] под произвольным углом к поверхности. Исследовалась [7] плоская внутренняя задача о действии сосредоточенной силы в упругой полуплоскости. В этой работе на основании расчетов, выполненных по асимптотическим формулам, было найдено, что рэлеевские волны не образуются вблизи от эпицентра, на расстояниях $d$, удовлетворяющих условию

(1.11)
$d < \frac{{{{c}_{R}}h}}{{\sqrt {c_{1}^{2} - c_{R}^{2}} }},$
где ${{c}_{R}}$ – скорость волны Рэлея, а $h$ – глубина источника. При получении оценки (1.11) сделано упрощающее предположение о том, что две объемных волн и рэлеевская волна распространяются независимо друг от друга. На самом же деле рэлеевская волна формируется из двух объемных волн, начиная с момента прихода медленной объемной волны, см. ([3], p. 66). Не совсем понятное отсутствие рэлеевских волн в эпицентральной зоне, удовлетворяющей оценке (1.11), объяснялось [7] интерференцией с объемными волнами, полностью поглощающими рэлеевскую волну. В случае плоской внешней задачи Лэмба получены [8] асимптотические оценки, аналогичные [6, 7].

Для вычисления сингулярных интегралов, связанных с обращением преобразования Лапласа в задачах Лэмба, предложен [9, 10] особый путь интегрирования, связанный с деформацией контура интегрирования. Вместо деформации контура интегрирования предложено [11, 12] использовать многократное изменение порядка интегрирования, при этом использовался подход, развитый ранее [13, 14] и основанный на функционально-инвариантных решениях. Заметим, что с помощью функционально-инвариантных решений поле перемещений в среде удалось представить в виде однократного интеграла от алгебраической функции по некоторому контуру в комплексной плоскости. Предложенный метод вычисления интегралов [11, 12] позднее был применен для анализа поля перемещений в цилиндрических координатах в случае осевой симметрии [15]. Для нагрузки в виде временной функции Хэвисайда, действующей на поверхности [16] и внутри [17, 18] полупространства, получено замкнутое выражение для вертикальной компоненты перемещений и выражение, содержащее эллиптические интегралы, для горизонтальной компоненты. Результаты работ [16–18] обобщены [19] на другие виды нагрузок. Для “плоской” задачи Лэмба выбор пути в методе Каньяра был упрощен [20, 21], кроме того, объяснен кажущийся парадокс [21], связанный с особой дисперсией волн Рэлея. Надо отметить, что обнаруженная дисперсия рэлеевских волн [21] – весьма своеобразная: она обнаруживается только при изменении знака круговой частоты и, таким образом, проявляется лишь при обращении двусторонних интегральных преобразований, в которых параметры преобразования меняют знак. В работах [22–24] на основе асимптотических разложений получены численные значения напряжений и перемещений вблизи от источника. Дальние асимптотики поля перемещений для внешней пространственной задачи Лэмба в случае гармонической нагрузки, совпадающие с решением Рэлея, приведены в работах [25, 26].

С помощью фундаментального решения Стокса [27] (см. также ([5], Sect. 68)) в [28–30] внешняя задача Лэмба о гармонической нагрузке сведена к интегральным уравнениям Фредгольма второго рода относительно неизвестных перемещений на границе.

Приведены ([31], Гл. 1) и ([32], Sect. 6.1) результаты аналитического исследования поляризации гармонических поверхностных волн (с плоским фронтом), распространяющихся по границе упругого полупространства. На основании этих исследований оказалось, что для материала, удовлетворяющего условию Пуассона $\lambda = \mu $ вертикальная компонента на свободной поверхности приблизительно в полтора раза больше горизонтальной компоненты перемещений. Аналогичное соотношение между компонентами перемещений найдено несколько ранее [33]. Фактически, результаты [31–33], подтвердили расчеты, проведенные Рэлеем [4] для случая $\lambda = \mu $, в которых отношение вертикальной амплитуды перемещений к горизонтальной составило 1.4677.

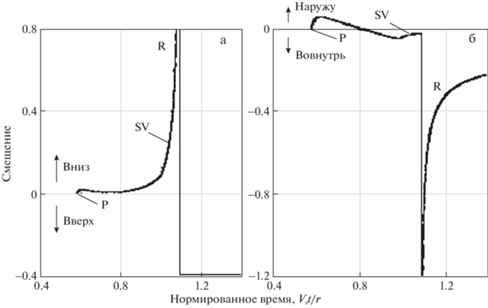
Интересные данные получены во внешней пространственной задаче Лэмба для случая импульсной нагрузки, заданной в виде временной функции Хэвисайда. Численный анализ решения [16] для этой задачи дал неожиданные результаты с точки зрения физической интерпретации. Например, вычисления, проведенные в [16] и повторенные в [34–38] с помощью различных вариантов метода [1, 2], показали, что в произвольной точке на поверхности вертикальная и горизонтальная компоненты перемещений претерпевают разрыв второго рода в момент, соответствующий приходу рэлеевской волны, рис. 1. При этом за фронтом рэлеевской волны решение [16] дает мгновенный выход на статическое решение Буссинеска для вертикальной компоненты, а для горизонтальной компоненты выход на статическое решение происходит асимптотически при $t \to \infty $. В этой связи интерес представляет сравнение аналитических (или аналитико-асимптотических) решений, рассмотренных в настоящем разделе, с расчетами, выполненными с помощью разностных методов.

Рис. 1.

Изменение во времени (а) вертикальной и (б) горизонтальной компонент вектора перемещений на границе полупространства для внешней пространственной задачи Лэмба при импульсной вертикальной нагрузке (при выполнении условия Пуассона $\lambda = \mu $) [36].

2. Разностные и вариационно-разностные методы. Решение внешней и внутренней задач Лэмба как в плоском, так и в пространственном случае, наталкиваются на определенные сложности, связанные с устойчивостью и схемной вязкостью явных разностных схем, а также появлением осцилляций в зонах за ударным фронтом, характерным для явных схем второго [39, 40] или более высокого порядка точности, или размытием ударных волновых фронтов, характерного для явных схем первого порядка [41] и неявных схем любого порядка точности [42]. Положение осложняет плохое распараллеливание вычислений в динамических задачах теории упругости, что делает малоэффективным применение современных кластерных и метакластерных вычислительных систем.

Частично недостатки разностных методов удается преодолеть с помощью разностных уравнений, записанных в окрестности характеристик. Явные разностные схемы в окрестности характеристик применены [43–45] для исследования распространения волн в упругих и упруго-пластических средах. Этот подход применен [46, 47] к решению плоской внешней задачи Лэмба для поверхностной нагрузки, заданной в виде временной функции Хэвисайда. Отмечено [47] хорошее совпадение с результатами, полученными методами интегральных преобразований [11, 12].

Для решения динамических задач, включая и внешнюю задачу Лэмба, предложен [48] гибридный подход, объединяющий конечноэлементный и конечноразностный методы. Использованные разностные схемы, разработаны в [49] позволяют получить конечноразностные уравнения второго порядка точности по временной переменной и четвертого порядка по пространственным переменным. Гибридный метод применен [50] к решению пространственной внешней задачи Лэмба. Численные эксперименты [51] показали, что гибридный метод оказался практически свободным от осцилляций за фронтом рэлеевской волны.

Для исследования распространения волн в задаче Лэмба применялся [52–54] спектральный метод (конечных) элементов (SEM). Этот метод фактически представляет собой метод конечных элементов высокого порядка точности, в котором пространственными элементами (базисными функциями) являются полиномы Лежандра.

Канонический метод конечных элементов с явными двухслойными разностными схемами при интегрировании по времени применялись для решения различных задач геомеханики, включая внутреннюю [55, 56] и внешнюю (пространственную) задачи Лэмба [57–59]. Сравнение данных расчета по методу конечных элементов с аналогичными результатами, выполненными с помощью интегральных преобразований, выявило [58] хорошее качественное совпадение магнитуд перемещений на свободной поверхности, вызванных действием гармонической нагрузки.

3. Анизотропные среды. По-видимому, впервые внешняя плоская задача Лэмба для трансверсально-изотропной полуплоскости исследовалась в [60] с помощью интегральных преобразований и вычислением сингулярных интегралов по методу [9, 10]. Эта техника была обобщена [61] для решения плоской внешней задачи Лэмба для упруго анизотропной полуплоскости с моноклинной симметрией. С помощью техники [60] для внутренней задачи Лэмба получены [62] выражения смещений на границе трансверсально-изотропной полуплоскости. Для построения решения внешней плоской задачи Лэмба в случае анизотропной полуплоскости с моноклинной симметрией применялся [63] метод, основанный на шестимерном комплексном формализме Стро [64]. С помощью этого метода получены [63] выражения для поля смещений в полуплоскости при внешнем гармоническом силовом воздействии.

Рассмотрена [65, 66] внешняя пространственная задача Лэмба для полупространства с произвольной упругой анизотропией. При решении этой задачи уравнения движения анизотропной среды записывались в виде

(3.1)
${\text{div}}\,{\mathbf{C}} \cdot \cdot \nabla {\mathbf{u}} = \rho \partial _{t}^{2}{\mathbf{u}}{\kern 1pt} ,$
где ${\mathbf{C}}$ – четырехвалентный тензор упругости. Предполагалось, что тензор упругости, рассматриваемый как оператор в пространстве симметричных тензоров второго ранга, положительно определен и симметричен. Объемные силы в [65, 66] отсутствовали, а на граничной плоскости полупространства ${{\Pi }_{\nu }}$ задавались условия в напряжениях

(3.2)
${{{\mathbf{t}}}_{\nu }} \equiv \nu \cdot {\mathbf{C}} \cdot \cdot \nabla {\mathbf{u}} = p({\mathbf{x}}{\kern 1pt} ',t)\nu ;\quad {\mathbf{x}}{\kern 1pt} ' \in {{\Pi }_{\nu }}$

Далее в этих работах использовалось преобразование Радона по пространственным переменным. Это позволило свести внешнюю задачу Лэмба к вычислению однократных интегралов по окружностям, появляющимся при обращении преобразования Радона. Преобразования Радона по пространственным переменным применялись [67–69] в дальнейшем при решении аналогичных задач.

Метод, основанный на преобразовании Фурье по пространственным переменным, применялся [70–75] для решения внешней и внутренней задач Лэмба. При этом перемещения на поверхности [74, 75] представлены в виде несобственных интегралов, появляющихся при сужении преобразованных по Фурье компонент перемещений и их производных на граничную плоскость.

4. Экспериментальные методы. По-видимому, впервые присутствие рэлеевских волн во внутренней задаче Лэмба было экспериментально зафиксировано [1] при анализе сейсмограмм от удаленного эпицентра землетрясения. В дальнейшем, результаты [1] подтверждались в различных исследованиях по решению геофизических задач [76–81], в том числе задач, связанных с анализом распространения волн Похгаммера–Кри и некоторых родственных волн [80]. Здесь надо отметить, что при исследовании волн Похгаммера–Кри удается обнаружить высокочастотные волны, отвечающие волнам Рэлея.

Надо отметить, что далеко не во всех геофизических исследованиях отмечено появление волн Рэлея. Например, в ([82], с. 268) дан анализ сейсмограмм, полученных при поверхностных взрывах, которые фактически, описываются решением внешней пространственной задачи Лэмба. По наблюдениям [82] волны Рэлея при поверхностных взрывах не обнаруживаются. Аналогичные данные приводятся в [83]. Определенный интерес представляет концепция анализа сейсмограмм землетрясений ([84], с. 25). В соответствии с этой концепцией, волны, возникающие при сейсмической активности, разделяются на два класса: объемные волны – это относительно короткие волны с периодом колебаний менее одной секунды, а поверхностные – это волны очень большой длины (от десятков до сотен километров), у которых период колебаний существенно превосходит одну секунду.

В экспериментальных модельных методах исследования задач Лэмба применялась в основном техника фотоупругости. С помощью этого метода исследовались [85–87] волны, распространяющиеся от точечного источника во внешних задачах Лэмба. Сравнение экспериментальных результатов, приведенных в этих работах, с данными теоретического анализа выявило хорошее качественное совпадение.

Среди других экспериментальных методов, применяемых для исследования волн, возникающих в задачах Лэмба, надо отметить метод глубинной акустической регистрации колебаний [88]. Для анализа смещений на поверхности полупространства во внешней задаче Лэмба (в случае малых масштабов) применяют также методы оптической интерферометрии [89, 90]. В этих случаях для возбуждения акустических волн обычно применяют мгновенный лазерный нагрев поверхности [89].

5. Задачи Лэмба о подвижной нагрузке. В одной из первых работ [6], обобщающих задачу Лэмба [2] о действии подвижной нагрузки, рассмотрены внешняя и внутренняя задачи о действии подвижной нагрузки, наклоненной под произвольным углом к поверхности полупространства (полуплоскости).

Помимо точных методов, основанных на применении интегральных преобразований, разрабатывались инженерные подходы, причем в этих подходах вместо полупространства или полуплоскости обычно рассматривались свободные балочные конструкции (описываемые теорией Бернулли–Эйлера или Тимошенко), а также балки, лежащие на упругом основании (в этом случае в качестве модели основания чаще всего применялась модель Винклера). При этом, инженерные подходы различались в зависимости от области применения. Так, специалисты по эксплуатации железных дорог и мостов в основном исследовали динамическую устойчивость упругих конструкций, несущих подвижные нагрузки [91–96]. В горной механике подвижные нагрузки возникали при исследовании динамики шахтного подъема, где используются канаты переменной длины [97–101]. Специфические методы разрабатывались в теории механизмов и машин для исследования динамической устойчивости гибких ветвей передач [102–104]. Предложен [105–107] объединенный подход для исследования различных задач с подвижными нагрузками на основе вариационного принципа Гамильтона–Остроградского. В этом подходе введено дополнительное нелинейное краевое условие, описывающее взаимовлияние движущегося объекта и колебаний упругой направляющей. Физический смысл последнего условия состоит в том, что при взаимодействии распределенной системы с движущимся сосредоточенным объектом возникают силы вибрационного давления. Надо отметить, что введение в расчет таких дополнительных сил, учитывающих движение нагрузки, предлагалось ранее [108, 109].

При исследовании пластин, нагруженных движущейся нагрузкой, обычно применяют теорию Бернулли–Эйлера, основанную на гипотезе плоских сечений. Эта теория позволяет получить динамические уравнения, аналогичные статическим уравнениям изгиба тонких пластин или уравнениям изгиба балок [110–113]. В дальнейшем методы [110–113] применялись при решении различных задач, связанных в основном с исследованием поведения ледяного покрова [114–116] а также колебаниям балок [117–120] при движущихся нагрузках.

Задачи для тел, нагруженных движущимися нагрузками, могут исследоваться с помощью конечноэлементных и конечноразностных методов. Задача о пластине, нагруженной движущейся нагрузкой, анализировалась [121–123] с помощью конечноэлементного метода с использованием двухслойных явных разностных схем второго порядка точности для интегрирования уравнений движения. Аналогичным методом исследовались [124, 125] колебания балок на упругом основании от действия движущихся нагрузок. Представлены [126] расчеты методом конечных элементов сложных систем, подверженных действию движущихся нагрузок. Численные исследования по колебаниям мостовых конструкций от движущихся нагрузок сопоставлены [127] с результатами натурных измерений. Это сопоставление выявило хорошее качественное и количественное совпадение частот и амплитуд колебаний. Решение уравнений движения для задач с подвижными нагрузками осуществлялось [128, 129] с помощью метода конечных разностей.

6. Родственные проблемы динамики. В случае внешних задач о действии нагрузки на границу упругой полуплоскости или полупространства, наряду с нормальным к границе воздействием [25], как отмечено выше, исследуют задачу о наклонной к поверхности нагрузке [6, 22]. Рассматриваются также задачи о штампе, контактирующим с упругим полупространством и совершающим горизонтальные гармонические колебания [130] и неосесимметричные вертикальные колебания [131]. Рассматривалась [132, 133] дипольная (моментная) гармоническая и импульсная нагрузка, приложенная на поверхности полупространства. Эта задача исследовалась с помощью преобразования Ханкеля по радиальной координате и преобразованием Лапласа по временной переменной. Численные анализ этой задачи показал [133], что на поверхности полупространства основной вклад от дипольной нагрузки вносят рэлеевские волны.

В случае внутренних задач, по-видимому, наибольший интерес представляют решения для дуплета (двойной силы без момента) [134–136] и диполя (сосредоточенного момента) [137]. В этих работах построение решений для соответствующих внутренних (пространственных) задач осуществлялось с помощью метода Лэмба и выбора контура интегрирования по методу [9, 10]. Построено [138] решение для внутренней пространственной задачи о действии горизонтальной гармонической силы в упругом трансверсально-изотропном полупространстве. Заметим, что плоские внутренние задачи о диполе и дуплете, по-видимому, не исследовались.

Исследовались [139, 140] решения внутренних задач Лэмба, связанные с появлением истекающих волн (волн, амплитуда которых не убывает по глубине). Построение и анализ соответствующих решений в [140] проводились методами [9, 10].

Список литературы

  1. Lamb H. On the propagation of tremors over the surface of an elastic solid // Phil. Trans. Roy. Soc. London. Ser. A. 1904. V. 203. P. 1–42.

  2. Lamb H. On waves due to a travelling disturbance, with an application to waves in superposed fluids // Phil. Mag. 1916. V. 13. P. 386–399; 539–548.

  3. Ewing W.M., Jardetzky W.S., Press F. Elastic Waves in Layered Media. New York: McGraw-Hill, 1957.

  4. Strutt J.W. (Lord Rayleigh) On wave propagating along the plane surface of an elastic solid // Proc. London Math. Soc. 1885. V. 17. P. 4 – 11.

  5. Gurtin M.E. The Linear theory of elasticity // in: Handbuch der Physik, Vol. VIaII/ Ed. by Truesdell C. Berlin: Springer, P. 1–296.

  6. Nakano H. Some problems concerning the propagations of the disturbances in and on semi-infinite elastic solid // Geophys. Mag. 1930. V. 2. P. 189–348.

  7. Nakano H. On Rayleigh waves // Japan J. Astron.&Geophys. 1925. V. 2. P. 233–326.

  8. Lapwood E.R. The disturbance due to a line source in a semiinfinite elastic medium // Philos. Trans. R. Soc. London. Ser. A. 1949. V. 242. P. 63–100.

  9. Cagniard L. Reflexion et refraction des ondes seismiques progressives. Paris: Gauthier-Villard, 1939. 255 p.

  10. de Hoop A.T. A modification of Cagniard’s method for solving seismic pulse problems // Appl. Sci. Res. Sect. Ser. B. 1960. V. 8. № 4. P. 349–356.

  11. Петрашень Г.И. О задаче Лэмба в случае упругого полупространства // Докл. АН СССР. 1949. Т. 64. С. 649–652.

  12. Петрашень Г.И., Марчук Г.И., Огурцов К.И. О задаче Лэмба в случае полупространства // Уч. зап. ЛГУ. Сер. Мат. 1950. № 135. Bып. 21. С. 71–118.

  13. Смирнов В.И., Соболев С.Л. Новый метод решения плоской задачи упругих колебаний // Тр. Сейсмол. ин-та АН СССР. 1932. № 20. 37 с.

  14. Смирнов В.И., Соболев С.Л. О применении нового метода к изучению упругих колебаний в пространстве при наличии осевой симметрии // Тр. Сейсмол. ин-та АН СССР. 1933. № 29. С. 43–51.

  15. Огурцов К.И., Петрашень Г.И. Динамические задачи для упругого полупространства в случае осевой симметрии // Уч. зап. ЛГУ. Сер. Мат. 1951. № 149. Bып. 24. С. 3–117.

  16. Pekeris C.L. The seismic surface pulse // Proc. Nat. Acad. Sci. USA. 1955. V. 41. P. 469–480.

  17. Pekeris C.L. The seismic buried pulse // Proc. Nat. Acad. Sci. USA. 1955. V. 41. P. 629–639.

  18. Pekeris C.L., Lifson H. Motion of the surface of a uniform elastic half-space produced by a burried pulse // J. Acoust. Soc. Am. 1957. V. 29. P. 1233–1238.

  19. Richards P.G. Elementary solutions to Lamb’s problem for a point source and their relevance to three-dimensional studies of spontaneous crack propagation // Bull. Seism. Soc. Amer. 1979. V. 69. P. 947–956.

  20. Поручиков В.Б. Методы динамической теории упругости. М.: Наука, 1986.

  21. Перегудов Д.В. Двумерная задача Лэмба. Метод Каньяра // Выч. сейсмол. 2000. Bып. 31. С. 120–137.

  22. Шемякин Е.И., Файншмидт В.Л. Распространение волн в упругом полупространстве, возбужденном поверхностной касательной силой // Уч. зап. ЛГУ. 1954. № 177. Bып. 28. С. 148–179.

  23. Никифоровский В.С. Исследование динамического поля напряжений в упругом полупространстве в окрестности точки приложения поверхностной нагрузки // ПМТФ. 1962. № 2. С. 85–94.

  24. Никифоровский В.С., Шемякин Е.И. Динамическое разрушение твердых тел. Новосибирск: Наука, 1979.

  25. Нарышкина Е.А. Колебания полупространства при любых начальных условиях // Тр. Сейсмологич. ин-та АН СССР. 1934. № 45. 71 с.

  26. Гоголадзе В.Г. Отражение и преломление упругих волн. Общая теория граничных волн Рэлея // Тр. Сейсмологич. ин-та АН СССР. 1947. № 125. 43 с.

  27. Stokes G.G. On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids // Trans. Cambridge Phil. Soc. 1849. V. 8. P. 287–319.

  28. Шерман Д.И. Колебания упругого полупространства при заданных смещениях или внешних силах на границе // Тр. Сейсмологического ин-та АН СССР. 1946. № 118. 47 с.

  29. Шаташвили С.Х. Приведение одной смешанной задачи теории установившихся упругих колебаний к интегральным уравнениям Фредгольма // Сообщ. Акад. наук Груз. ССР. 1953. Т. XIV. № 5. С. 257–260.

  30. Шаташвили С.Х. Об одной смешанной задаче теории установившихся колебаний упругого полупространства // Тр. Груз. политехн. ин-т. 1956. № 1. С. 77–80.

  31. Викторов И.А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике. М.: Наука, 1966. 168 с.

  32. Graff K.P. Wave Motion in Elastic Solids. Oxford: Clarendon, 1975. 682 p.

  33. Frederick J.R. Ultrasonic Engineering. New York: Wiley, 1965. 382 p.

  34. Lang H.A. Surface displacements in an elastic half-space // Z. Angew Math. Mech. 1961. V. 41. P. 141–153.

  35. Mitra M. Disturbance produced in an elastic half-space by impulsive normal pressure // Proc. Camb. Phil. Soc. Math. Phys. Sci. 1961. V. 60. P. 683–696.

  36. Mooney H.M. Some numerical solutions for Lamb’s problem // Bull. Seismol. Soc. Am. 1974. V. 64. № 2. P. 473–491.

  37. Richards P.G. Elementary solutions to Lamb’s problem for a point source and their relevance to three-dimensional studies of spontaneous crack propagation // Bull. Seismol. Soc. Am. 1979. V. 69. № 4. P. 947–956.

  38. Kausel E. Fundamental Solutions of Elastodynamics. New York: Cambridge Univ. Press, 2006. 251 p.

  39. Lax P.D., Wendroff B. Difference schemes for hyperbolic equations with high order of accuracy // Comm. Pure Appl. Math. 1964. V. 17. P. 381–398.

  40. Wendroff B. Theoretical Numerical Analysis. New York: Acad. Press, 1967.

  41. Годунов С.К. и др. Численное решение многомерных задач газовой динамики. М.: Наука, 1976. 400 с.

  42. Самарский А.А. Экономичные разностные схемы для гиперболической системы уравнений со смешанными производными и их применение для уравнений теории упругости // ЖВММФ. 1965. Т.5. № 1. С. 34–43.

  43. Clifton R.J. A difference method for plane problems in dynamic elasticity // Quart. Appl. Math. 1967. V. 25. № 1. P. 97–116.

  44. Сабодаш П.Ф., Череднеченко Р.А. Применение метода пространственных характеристик к решению задачи о распространении волн в упругой полуполосе // Изв. АН СССР. МТТ. 1972. № 6. С. 180–185.

  45. Кондауров В.И., Кукуджанов В.Н. Численное решение неодномерных задач динамики упруго-пластических сред // в кн.: Избранные проблемы прикладной механики. М.: ВИНИТИ, 1974.

  46. Кукуджанов В.Н. Численное решение неодномерных задач распространения волн напряжений в твердых телах // Сообщ. по прикл. матем. М.: ВЦ АН СССР, 1976. Вып. 6. 67 с.

  47. Веденяпин Е.Н., Кукуджанов В.Н. Метод численного интегрирования нестационарных задач динамики упругой среды // ЖВММФ. 1981. Т. 21. № 5. С. 1233–1248.

  48. Moczo P. et al. Hybrid modeling of P-SV seismic motion at inhomogeneous viscoelastic topographic structures // Bull. Seism. Soc. Am. 1997. V. 87. P. 1305–1323.

  49. Levander A.R. Fourth-order finite-difference P-SV seismograms // Geophys. 1988. V. 53. P. 1425–1436.

  50. Moczo P., Kristek J., Vavrycuk V., Archuleta R.J., Halada L. 3D heterogeneous staggered-grid finite-difference modeling of seismic motion with volume harmonic and arithmetic averaging of elastic moduli and densities // Bull. Seism. Soc. Am. 2002. V. 92. № 8. P. 3042–3066.

  51. Shuo M., Archuleta R.J., Liu P. Hybrid modeling of elastic P-SV wave motion: A combined finite-element and staggered-grid finite-difference approach // Bull. Seismol. Soc. Am. 2004. V. 94. № 4. P. 1557–1563.

  52. Komatitsch D., Tromp J. Introduction to the spectral-element method for 3-D seismic wave propagation // Geophys. J. Int. 1999. V. 139. P. 806–822.

  53. Komatitsch D., Tromp J. Spectral-element simulations of global seismic wave propagation. I. Validation // Geophys. J. Int. 2002. V. 149. № 2. P. 390–412.

  54. Komatitsch D., Tromp J. Spectral-element simulations of global seismic wave propagation. II. 3-D models, oceans, rotation, and self-gravitation // Geophys. J. Int. 2002. V. 150. № 1. P. 303–318.

  55. Olsen K.B., Archuleta R.J. Three-dimensional simulation of earthquakes on the Los Angeles fault system // Bull. Seism. Soc. Am. 1996. V. 86. P. 575–596.

  56. Kuznetsov S.V. SH-waves in laminated plates // Quart. Appl. Math. 2006. V. 64. P. 153–165.

  57. Kuznetsov S.V. Love waves in layered anisotropic media // JAMM. 2006. V. 70(1). P. 116–127.

  58. Ilyashenko A.V. et al. SH waves in anisotropic (monoclinic) media // Z. Angew. Math. Phys. 2018. V. 69. № 17. P. 1–11.

  59. Kuznetsov S.V. Seismic waves and seismic barriers // Acoust. Phys. 2011. V. 57. P. 420–426.

  60. Kraut E.A. Advances in the theory of elastic wave propagation // Rev. Geophys. 1963. V. 1. P. 401–448.

  61. Burridge R. Lamb’s problem for an ainisotropic halfspace // Q. J. Mech. Appl. Math. 1971. V. 24. № 1. P. 81–98.

  62. Payton R.G. Elastic Wave Propagation in Transversely Isotropic Media. The Hague: Martinus Nijhoff, 1983.

  63. Wu K.-C. Extension of Stroh’s formalism to self-similar problems in two-dimensional elastodynamics // Proc. R. Soc. London. Ser. A. 2000. V. 456. P. 869–890.

  64. Stroh A.N. Steady state problems in anisotropic elasticity // J. Math. Phys. 1962. V. 41. P. 77–103.

  65. Willis J.R. Self-similar problems in elastodynamics // Phil. Trans. Roy. Soc. London. 1973. V. A274. № 1240. P. 435–491.

  66. Bedding R.J., Willis J.R. The dynamic indentation of an elastic half-space // J. Elast. 1973. V. 3. P. 289–309.

  67. Willis J.R., Bedding R.J. Transient elastodynamic fields in anisotropic plates and layers // in: Modern Problems in Elastic Wave Propagation / Ed. by Miklowitz J., Achenbach J.D. New York: Wiley, 1978. P. 347–355.

  68. van der Hijden J.H.M.T. Propagation of Transient Elastic Waves in Stratified Anisotropic Media. Amsterdam: North-Holland, 1987.

  69. Wang C.-Y., Achenbach J.D. Lamb’s problem for solid of general anisotropy // Wave Motion. 1996. V. 24. P. 227–242.

  70. Mourad A., Deschamps M. Lamb’s problem for an anisotropic half-space studied by the Cagniard de Hoop method // J. Acoust. Soc. Am. 1995. V. 97. P. 3194–3197.

  71. Mourad A., Deschamps M., Castagnede B. Acoustic waves generated by a transient line source in an anisotropic half-space // Acustica. 1996. V. 82. P. 839–851.

  72. Eringen A.C., Suhubi E.S. Elastodynamics. V. 2. New York: Academic, 1975. P. 600–644.

  73. Spies M. Green’s tensor function for Lamb’s problem: The general anisotropic case // J. Acoust. Soc. Am. 1997. V. 102. P. 2438–2441.

  74. Every A.G., Kim K.Y., Maznev A.A. The elastodynamic response of a semi-infinite anisotropic solid to sudden surface loading // J. Acoust. Soc. Am. 1997. V. 102. P. 1346–1355.

  75. Every A.G., Kim K.Y., Maznev A.A. Surface dynamic response functions of anisotropic solids // Ultrasonics. 1998. V. 36. P. 349–353.

  76. Oldham R.D. On the propagation of earthquake motion to great distances // Phil. Trans. Roy. Soc. (London). Ser. A. 1900. V. 194. P. 135–174.

  77. Northwood T.D., Anderson D.V. Model Seismology // Bull. Seism. Soc. Am. 1953. V. 43. P. 239–246.

  78. Kuznetsov S.V., Terentjeva E.O. Planar internal Lamb problem: Waves in the epicentral zone of a vertical power source // Acoust. Phys. 2015. V. 61. P. 356–367.

  79. Kravtsov A.V. et al. Finite element models in Lamb’s problem // Mech. Solids. 2011. V. 46. P. 952–959.

  80. Ilyashenko A.V. et al. Pochhammer–Chree waves: polarization of the axially symmetric modes // Arch. Appl. Mech. 2018. V. 88. P. 1385–1394.

  81. Kanamori H., Given J.W. Lamb pulse observed in nature // Geophys. Res. Lett. 1983. V. 10. P. 373–376.

  82. Адушкин В.В., Спивак А.А. Геомеханика крупномасштабных взрывов. М.: Недра, 1993. 319 с.

  83. Родионов В.Н., Сизов И.А., Цветков В.М. Основы геомеханики. М.: Недра, 1986. 301 с.

  84. Магницкий В.А. Общая геофизика. М.: МГУ, 1995. 317 с.

  85. Dally J.W., Durrelli A.J., Riley W.F. Photoelastic study of stress wave propagation in large plates // Proc. Soc. Exp. Stress Analysis. 1960. V. 17. P. 33–50.

  86. Dally J.W., Thau S.A. Observations of stress wave propagation in a half-plane with boundary loading // Int. J. Solids Struct. 1967. V. 3. P. 293–307.

  87. Dally J.W. A dynamic photoelastic study of a doubly loaded half-plane // Develop. Mech. 1968. V. 4. P. 649–664.

  88. Glaser S.D., Weiss G.G., Johnson L.R. Body waves recorded inside an elastic half-space by an embedded, wideband velocity sensor // J. Acoust. Soc. Am. 1998. V. 104. Iss. 3. P. 1404–1412.

  89. Hsiao C.P., Kline R.A., Grasse K.A. A theoretical and experimental study of the propagation of acoustic emission signals in polymeric media // IEEE 1986 Ultrasonics Symp. 1986. P. 1005–1008.

  90. Huynh A. et al. Optical excitation and detection of terahertz acoustic waves with semiconductor superlattices // J. Phys. Conf. Ser. 2010. V. 214. https://doi.org/10.1088/1742-6596/214/1/012047

  91. Болотин В.В. Задача о колебаниях мостов под действием подвижной нагрузки // Изв. АН СССР. ОТН. 1961. № 4. С. 109–115.

  92. Тимошенко С.П. Прочность и колебание элементов конструкций. Избранные работы / Под ред. Григолюка Э.И. М.: Наука, 1975.

  93. Филиппов А.П., Кохманюк С.С., Воробьев Ю.С. Воздействие динамических нагрузок на элементы конструкций. Киев: Наукова думка, 1974.

  94. Энгелъбрехт Ю.К., Нигул У.К. Нелинейные волны деформации. М.: Наука, 1981.

  95. Якушев Н.З. Динамика деформируемых систем под действием движущихся нагрузок. Ч. I. Балки, стержни и арки под действием подвижных нагрузок // в кн.: Исследования по теории пластин и оболочек. Казань: Изд-во Казанск. ун-та, 1972. Вып. 8. С. 3–42.

  96. Якушев Н.З. Динамика деформируемых систем под действием движущихся нагрузок. Ч. П. Балки, стержни и арки под действием подвижных нагрузок // в кн.: Исследования по теории пластин и оболочек. Казань: Изд-во Казанск. ун-та, 1972. Вып. 9. С. 118–156.

  97. Горошко О.А., Савин Т.Н. Введение в механику деформируемых одномерных тел переменной длины. Киев: Наукова думка, 1971.

  98. Ишлинский А.Ю. Об уравнении продольных движений каната (упругой нити) переменной длины // Докл. АН СССР. 1954. Т. 95. № 5. С. 370–374.

  99. Неронов Н.П. Об упругих деформациях в подъемном канате // ПММ. 1937. Т. 1. № 1. С. 91–96.

  100. Неронов Н.П. Определение напряжений в подъемном канате // Докл. АН СССР. 1947. Т. 57. № 8. С. 765–768.

  101. Доценко П.Д. О нелинейных колебаниях движущейся струны // Самолетостроение и техн. возд. флота. 1971. № 25. С. 123–126.

  102. Кожегиник Я. Поперечные колебания напряженных гибких звеньев передач // в кн.: Теория машин и механизмов. М.: Наука, 1976.

  103. Раздольский А.Г., Заболотный Ю.В. К исследованию переходных процессов одномерных механических систем переменной длины // в кн.: Динамика машин. М.: Наука, 1974.

  104. Светлицкий В.А. Передачи с гибкой связью. М.: Машиностроение, 1967.

  105. Весницкий А.И., Лисенкова Е.Е. Частотно-энергетические соотношения для упругих волн в одномерных системах с движущимися объектами // Акустич. ж. 1995. Т. 41. № 2. С. 209–215.

  106. Весницкий А.И. Волны в системах с движущимися границами и нагрузками. М.: Физматлит, 2001. 320 с.

  107. Весницкий А.И., Катан Л.Э., Уткин Г.А. Законы изменения энергии и импульса для одномерных систем с движущимися закреплениями и нагрузками // ПММ. 1983. Т. 47. № 5. С. 863.

  108. Николаи Е.Л. Теоретическая механика. Ч. 2. Динамика. М.: Физматлит, 1962. 280 с.

  109. Thurman A.L., Mote C.D. (Jr) Free, periodic, nonlinear oscillation of an axially moving strip // Trans ASME. J. Appl. Mech. 1969. V. 36. № 1. P. 87–98.

  110. Бернштейн С.А. Ледяная железнодорожная переправа (работа, теория и расчет ледяного слоя). М.: Транспечать, 1929. 42 с.

  111. Коренев Б.Г. О движении нагрузки по пластинке, лежащей на упругом основании // Строит. мех. и расчет сооруж. 1967. № 3. С. 27–30.

  112. Бляхман Р.И. Колебания бесконечной пластинки на упругом полупространстве под действием подвижной нагрузки // Строит. мех. и расчет сооруж. 1967. № 3. С. 112–115.

  113. Муравский Г.Б. Действие движущейся системы сил на балку, лежащую на упругом основании // Изв. АН СССР. МТТ. 1975. № 3. С. 190–195.

  114. Козин В.М. и др. Прикладные задачи динамики ледяного покрова. М.: Изд. Акад. естеств., 2008.

  115. Жесткая В.Д., Джабраилов М.Р. Численное решение задачи о движении нагрузки по ледяному покрову с трещиной // ПМТФ. 2008. № 3. Т. 49. С. 151–156.

  116. Squire V.A., Hosking R.J., Kerr A.D., Langhorne P.J. Moving Loads on Ice Plates. New York: Kluver Acad. Publ., 1996.

  117. Wang R.T. Vibration of multi-span Timoshenko beams subjected to a concentrated moving force // J. Sound&Vibr. 1997. V. 207. P. 731–742.

  118. Hong S.W., Kim J.W. Modal analyses of multi span Timoshenko beams connected or supported by resilient joints with damping // J. Sound&Vibr. 1999. V. 227(4). P. 787–806.

  119. Ichikawa M., Miyakawa Y., Matsuda A. Vibration analysis of the continuous beam subjected to a moving mass // J. Sound&Vibr. 2000. V. 230(3). P. 493–506.

  120. Kim S.-M. Vibration and Stability of axial loaded beams on elastic foundation under moving harmonic loads // Engng. Struct. 2004. № 26. P. 95–105.

  121. Wu J.J., Whittaker A.R., Cartmell M.P. The use of finite element techniques for calculating the dynamic response of structures to moving loads // Comput.&Struct. 2000. V. 78. P. 789–799.

  122. Wu J.J., Whittaker A.R., Cartmell M.P. Dynamic responses of structures to moving bodies using combined finite element and analytical methods // Int. J. Mech. Sci. 2001. V. 43. P. 2555–2579.

  123. Wu J.J. Dynamic analysis of a rectangular plate under a moving line load using scale beams and scaling laws // Comput.&Struct. 2005. V. 83. P. 1646–1658.

  124. Kuznetsov S.V. Fundamental and singular solutions of Lamé equations for media with arbitrary elastic anisotropy // Quart. Appl. Math. 2005. V. 63. P. 455–467.

  125. Andersen L., Nielsen S.R.K., Kirkegaard P.H. Finite element modelling of infinite Euler beams on Kelvin foundations exposed to moving loads in convected coordinates // J. Sound&Vibr. 2001. V. 241. Iss. 4–5. P. 587–604.

  126. Kadivar M.H., Mohebpour S.R. Finite element dynamic analysis of unsymmetric composite laminated beams with shear effect and rotary inertia under the action of moving loads // Finite Elements in Anal.&Design. 1998. V. 29. P. 259–273.

  127. Hugul S. Vibration Analysis of Systems Subjected to Moving Loads by Using the Finite Element Method / PhD Thesis. Izmir: Dokuz Eylül Univ., 2005.

  128. Liu K., DeRoeck G., Reynders E. Experimental validation of the dynamic analysis of high speed composite railway bridge // EURODYN 2008. Southampton. UK. P. 1–16.

  129. Fryba L. Vibration of Solids and Structures under Moving Loads. Groningen: Noordhoff Int. Publ., 1972.

  130. Jonsson J.O. On Ground and Structural Vibrations Related to Railway Traffic / PhD Thesis. Sweden: Chalmers Univ. Technol., 2000.

  131. Шехтер О.Я. Вынужденные горизонтальные колебания круглого штампа на упругом полупространстве // в сб.: Основания, фундаменты и подземные сооружения. № 61. М.: Госстройиздат, 1971. С. 26–30.

  132. Сеймов В.М., Ермоленко Н.П., Зайцева Е.А. Неосесимметричные периодические и нестационарные колебания круглого штампа на упругом полупространстве // Прикл. мех. 1997. Т. 33. № 5. С. 41–48.

  133. Михайлюк B.С. Определение вертикальных перемещений точки поверхности грунта вне массивного фундамента при действии на него вращательного импульса // Сб. научн. тр. НИИОСП им. Н.М. Герсеванова. 2008. Вып. № 99. С. 95–100.

  134. Kawasaki I., Suzuki Y., Sato R. Seismic waves due to double couple source in a semi-infinite space, Part 1 // Zisin. 1972. V. 25. P. 207–217.

  135. Kawasaki I., Suzuki Y., Sato R. Seismic waves due to double couple source in a semi-infinite space, Part 2 // Zisin. 1972. V. 25. P. 333–342.

  136. Djeran-Maigre I. et al. Solitary SH waves in two-layered traction-free plates // Comptes Rendus. Mecanique. 2008. V. 336(1–2). P. 102–107.

  137. Johnson L.R. Green’s function for Lamb’s problem // Geophys. J. R. Astron. Soc. 1974. V. 37. P. 99–131.

  138. Pan Y.C., Chou T.W. Green’s function solutions for semi-infinite transversely isotropic materials // Int. J. Engng. Sci. 1979. V. 17. P. 545–551.

  139. Gupta U. On leaking modes // Pure&Appl. Geophys. 1970. V. 80. № 1. P. 27–37.

  140. Chapman C.H. Lamb’s problem and comments on the paper ‘on leaking modes’ by Usha Gupta // Pure&Appl. Geoph. 1972. V. 94. № 1. P. 233–247.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал