1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 4, 2022

Прикладная математика и механика, 2022, T. 86, № 4, стр. 595-611

К РАСЧЕТАМ ТЕХНОЛОГИЧЕСКОЙ ОПЕРАЦИИ СБОРКИ ГОРЯЧЕЙ ПОСАДКОЙ ЦИЛИНДРИЧЕСКИХ ДЕТАЛЕЙ

А. А. Буренин 1, *, А. В. Ткачева 1

1 Институт машиноведения и металлургии ДВО РАН
Комсомольск-на-Амуре, Россия

* E-mail: burenin@iacp.dvo.ru

Поступила в редакцию 06.04.2022
После доработки 02.05.2022
Принята к публикации 15.05.2022

Полный текст (PDF)

Аннотация

Рассчитываются изменения температурных напряжений, включая итоговые остаточные напряженные состояния и формируемый натяг в сборке, в процессе горячей посадки трубы на вал, изготовленные из материалов с упруговязкопластическими свойствами. Расчеты проводятся разрешением соответствующей осесимметричной задачи Гадолина, в которой детали сборки имеют одинаковую длину. Обращается внимание на возможную сингулярность в задании краевых условий задачи и предлагается способ исключения влияния данной особенности на результаты расчетов.

Ключевые слова: упругость, вязкопластичность, температурные напряжения, задача Гадолина, горячая посадка, сборка с натягом

1. Введение. Основная сложность в разрешении краевых задач упругопластичного деформирования с использованием теории течения в интенсивно деформируемых пластических областях [1] связана с тем, что в таких областях задача ставится в скоростях, а в области упругого деформирования – в перемещениях. С целью выполнения условий непрерывности перемещений на упругопластических границах следует определить распределение перемещений в пластической области, что может оказаться совсем не простой задачей [2]. Если же ограничиться выполнением на границах областей пластического течения только условий непрерывности напряжений и скоростей, то не исключается запись ошибочного решения [3].

Положение существенно упрощается, когда уравнение равновесия, записанное в скоростях в области пластического течения, удается проинтегрировать. Однако обеспечить это возможно только принятием существенных ограничений в задаваемой геометрии деформируемых тел и задаваемых внешних нагрузок. Иногда данной интегрируемости способствует принятие в качестве пластических потенциалов классических кусочно-линейных поверхностей нагружения [4, 5] в пространстве главных напряжений. Преимущественно таким способом получили свое решение одномерные задачи упругопластического и упруговязкопластического деформирования [6–15]. Среди подобных задач следует выделить такие, где изучается не только состояние упругопластического тела, но и эволюция таких состояний в зависимости от меняющегося во времени термомеханического воздействия, то есть упругопластические процессы [6, 11, 13–17]. Итогом завершения таких процессов после полной разгрузки и остывания оказывается новое состояние продеформированного тела, отличное от первоначального не только своей новой геометрией, но и присутствием в нем сформировавшегося распределения остаточных деформаций и напряжений. Именно итоговая геометрия и итоговое распределение остаточных напряжений часто являются главной целью при решении подобных задач. Это в полной мере относится к задачам, призванным обеспечить математическое моделирование технологической операции сборки цилиндрических деталей способом горячей посадки [18–24, 27]. В отечественной литературе [25–27] данную задачу теории температурных напряжений называют задачей Гадолина. Итоговое напряженное состояние после полного остывания обеспечивает требуемый натяг в сборке, необходимый для функционирования соединения.

Упругопластическое состояние элементов сборки возможно рассчитать аналитически [18, 21, 27]; операцию горячей посадки представляют последовательностью подобных состояний при изменениях температуры [21–24, 27]. Производством тепла за счет необратимого деформирования в таких задачах, как правило, пренебрегают, рассматривая их в рамках несвязанной теории температурных напряжений. Очевидно, что последовательность состояния элементов сборки в течение технологической операции удобнее рассматривать с помощью программно-технических средств, используя точное решение задачи о состоянии элементов сборки на каждом временном шаге расчетов. Данное решение возможно построить даже в случае зависимости предела текучести от температуры [21–24]. Когда вместе с пределом текучести зависимыми от температуры полагаются иные термомеханические постоянные (упругие модули, удельная теплоемкость и др.), то решение сводится [24] к интегрированию на каждом временном шаге расчетов совокупности систем обыкновенных дифференциальных уравнений для каждой из возможных областей обратимого и необратимого деформирования. В этом состоит основное преимущество, предоставляемое использованием кусочно-линейных условий пластического течения для решения одномерных краевых задач теории температурных напряжений в условиях плоских деформированных [19, 21, 27] или напряженных [20, 24] состояний.

В настоящей статье, сохраняя осевую симметрию, откажемся от одномерности задачи. Будем считать торцы элементов сборки свободными, а на контактной поверхности полагаем возможным осевое относительное смещение в материалах сопрягаемых деталей сборки.

2. Основные зависимости математической модели. Считаем, что допускаемые деформируемым материалом деформации являются малыми и для них

(2.1)
${\mathbf{d}} = {\mathbf{e}} + {\mathbf{p}} = \frac{1}{2}\left( {\nabla {\mathbf{u}} + {{\nabla }^{T}}{\mathbf{u}}} \right)$

В (2.1) ${\mathbf{d}}$, ${\mathbf{e}}$, ${\mathbf{p}}$ – полные деформации, упругие и пластические их составляющие, ${\mathbf{u}}$ – вектор перемещений. Следствием законов сохранения импульса и энергии являются дифференциальные зависимости

(2.2)
$\nabla \sigma = 0$
(2.3)
$\rho \frac{{d\xi }}{{dt}} + \operatorname{div} {\mathbf{q}} = \sigma \cdot \cdot \,\varepsilon $

Следствие закона сохранения импульса (2.2) записано здесь в форме уравнений равновесия, то есть силами инерции и массовыми силами в (2.2) пренебрегатся. В (2.2) $\sigma $ тензор напряжений. В скалярном уравнении баланса внутренней энергией (2.3), которое является следствием закона сохранения энергии $\xi $ – массовая плотность распределения внутренней энергии, $\varepsilon $ – тензор скорости деформации Эйлера, $t$ – время, $\rho $ – плотность, ${\mathbf{q}}$ – вектор потока тепла. В рассматриваемом случае следствием (2.3) и второго закона термодинамики оказываются соотношения

(2.4)
$\sigma = \rho \frac{{\partial \psi }}{{\partial {\mathbf{e}}}}$
$\psi = \xi - sT,\quad \frac{{\partial \psi }}{{\partial T}} = - s,\quad \frac{{\partial \xi }}{{\partial s}} = T;\quad \xi = \xi \left( {{\mathbf{e}},s} \right),\quad \psi = \psi \left( {{\mathbf{e}},T} \right)$
(2.5)
$\frac{{\partial \left( {\rho s} \right)}}{{\partial t}} = - \operatorname{div} {\mathbf{J}} + \frac{1}{T}\sigma \cdot \cdot \,{{\varepsilon }^{p}} - \frac{1}{{{{T}^{2}}}}{\mathbf{q}} \cdot \nabla T$
${\mathbf{J}} = \rho sv + {{T}^{{ - 1}}}q,\quad {{\varepsilon }^{p}} = \frac{{dp}}{{dt}},\quad {{\varepsilon }^{e}} = \frac{{d{\mathbf{e}}}}{{dt}}$

Зависимость (2.4) называют формулой Мурнагана [4, 6], соотношение (2.5) – уравнением баланса энтропии [6, 28]. В нем $s$ – плотность распределения энтропии, $T$ – температура, ${\mathbf{J}}$ – вектор потока энтропии. Консервативные и диссипативные составляющие процесса деформирования возможно разделить, если принять, что термодинамический потенциал (свободная энергия) является функцией только обратимых (упругих) деформаций, то есть принять гипотезу, что $\psi = \psi \left( {{\mathbf{e}},T} \right)$. Именно в условиях принятия такой гипотезы записаны соотношения (2.4) и (2.5), и именно функция $\psi \left( {{\mathbf{e}},T} \right)$ задает консервативную составляющую процесса деформирования. Задание диссипативной составляющей процесса деформирования связано с заданием пластического потенциала, роль которого выполняет поверхность нагружения $f\left( {\sigma ,k} \right) = 0$ ($k$ – предел текучести) в шестимерном пространстве напряжений.

В простейшем случае задания функции $\psi = \psi \left( {{\mathbf{e}},T} \right)$ в форме квадратичной функции инвариантов тензора ${\mathbf{e}}$ (материал изотропен) из (2.4) следуют известные зависимости закона Дюамеля–Неймана [28]

(2.6)
$\begin{gathered} \sigma = \left( {\lambda \operatorname{tr} {\mathbf{e}} - 3\alpha {{T}_{0}}K\theta } \right){\mathbf{I}} + 2\mu {\mathbf{e}} \\ \theta = \frac{{T - {{T}_{0}}}}{{{{T}_{0}}}} \\ \end{gathered} $

Здесь $\lambda $, $\mu $ – упругие постоянные Ламе, $\alpha $ – коэффициент линейного расширения, ${{T}_{0}}$ – температура свободного состояния тела (комнатная температура), $K = \lambda + \frac{2}{3}\mu $ – коэффициент всестороннего сжатия, ${\mathbf{I}}$ – единичный тензор второго ранга.

Если в уравнении баланса энтропии (2.5) принять условия изотропии термомеханических свойств деформируемого тела и связать поток тепла с температурной законом Фурье, то в простейшем случае, возможно записать [6] уравнение теплопроводности в виде

(2.7)
$\frac{{\partial \theta }}{{\partial t}} = a\Delta \theta - \frac{1}{{c{{T}_{0}}}}\left( {\delta \operatorname{tr} {{\varepsilon }^{e}} - \sigma \cdot \cdot \,{{\varepsilon }^{p}}} \right) + w\left( {{\mathbf{x}},t} \right)$

В (2.7) $c$ – удельная теплоемкость деформируемого материала, $a$ – коэффициент температуропроводности, $\delta $ – коэффициент связанности, $w\left( {x,t} \right)$ задаваемые источники тепла в теле (${\mathbf{x}}$ – радиус вектор места рассматриваемой точки тела). Если в (2.7) пренебречь теплом, производимым за счет деформирования по сравнению с теплом, поступающих от внешних источников, то будем иметь

(2.8)
$\frac{{\partial \theta }}{{\partial t}} = a\Delta \theta + w\left( {{\mathbf{x}},t} \right)$

Когда распределение температуры рассчитывается согласно (2.8) независимо от процесса деформирования, то такая несвязанная теория называется теорией температурных напряжений. Дальнейший расчет будем проводить в рамках такой теории.

Необратимые (пластические) деформации в теле производятся только при напряжениях, соответствующих поверхности нагружения (текучести) $f\left( {\sigma ,k} \right) = 0$, где $k = k\left( \theta \right)$ – предел текучести материала, соответствующий местной температуре $\theta \left( {{\mathbf{x}},t} \right)$. При принятии условий принципа максимума Мизеса [4, 5] функция $f\left( {\sigma ,k} \right)$ оказывается пластическим потенциалом и следует ассоциированный закон пластического течения

(2.9)
$d{{{\mathbf{e}}}^{p}} = d\zeta \frac{{\partial f\left( {\sigma ,k} \right)}}{{\partial \sigma }};\quad d\zeta > 0$

В качестве условия пластического течения (уравнения поверхности нагружения) далее будем использовать условие максимальных октаэдрических напряжений (условие Мизеса [4])

(2.10)
$\left( {\tau - \eta {{\varepsilon }^{p}}} \right) \cdot \cdot \left( {\tau - \eta {{\varepsilon }^{p}}} \right) = 2{{k}^{2}}$

В пространстве главных напряжений ${{\sigma }_{j}}$ уравнение (2.10) задает цилиндрическую поверхность наклонного цилиндра Мизеса [5], осью которого является гидростатическая ось ${{\sigma }_{1}} = {{\sigma }_{2}} = {{\sigma }_{3}}$; $\eta $ – коэффициент вязкости в условиях вязкопластического течения.

Зависимость предела текучести от температуры принимаем в форме

(2.11)
$k = k\left( \theta \right) = {{k}_{0}}y;\quad y = {{\left( {\frac{{{{\theta }_{r}} - \theta }}{{{{\theta }_{r}}}}} \right)}^{2}};\quad {{\theta }_{r}} = \frac{{{{T}_{r}} - T}}{{{{T}_{0}}}}$

В (2.11) ${{T}_{r}}$ – температура плавления материла. В ряде случаев для зависимости предела текучести от температуры принимается более простая линейная функция [18–21].

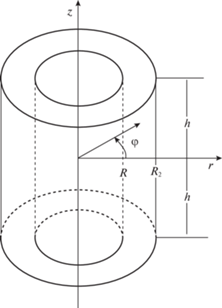
3. Сборка горячей посадкой. Деталями предстоящей сборки считаем сплошной цилиндр (вал) длинной 2$h$ и радиуса ${{r}_{0}}$ и полый цилиндр той же длины, ограниченный в цилиндрической системе координат $r,\varphi ,z$ поверхностями $r = {{R}_{1}}$, $r = {{R}_{2}}$ $\left( {{{r}_{0}} \leqslant {{R}_{1}} < {{R}_{2}}} \right)$. Вал называем охватываемой деталью сборки, а полый цилиндр – охватывающей деталью. Охватывающую деталь сборки нагреваем до некоторой назначаемой температуры $\theta = {{\theta }_{*}}$ и помещаем в нее охватываемую. Геометрические размеры ${{r}_{0}}$ и ${{R}_{1}}$ подбирают так, чтобы детали сборки непосредственно за моментом посадки получили бы общую граничную поверхность $r = R$ (рис. 1).

Рис. 1

Материалы элементов сборки могут быть одинаковыми, но могут и различаться. Уравнение теплопроводности (2.8) запишем в цилиндрической системе координат, учитывая осевую симметрию задачи

(3.1)
$\frac{{\partial {{\theta }_{m}}}}{{\partial t}} = {{a}_{m}}\left( {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}{{\theta }_{m}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}}{{\theta }_{m}}} \right)$

Здесь и далее $m = 1,2$; $m = 1$ для охватываемой и $m = 2$ для охватывающей детали сборки. Внутренние задаваемые источники тепла считаем отсутствующими. Начальными условиями температурной задачи становятся

(3.2)
$\begin{gathered} {{\theta }_{1}}\left( {r,z,0} \right) = 0\quad {\text{при}}\quad 0 \leqslant r \leqslant R,\quad - h \leqslant z \leqslant h \\ {{\theta }_{2}}\left( {r,z,0} \right) = {{\theta }_{*}}\quad {\text{при}}\quad R \leqslant r \leqslant {{R}_{1}},\quad - h \leqslant z \leqslant h \\ \end{gathered} $

Граничные условия обеспечивают теплообмен между деталями сборки и окружающей средой. Следовательно, при $t > 0$ имеем на поверхности контакта $r = R$

(3.3)
${{\theta }_{1}}\left( {R,z,t} \right) = {{\theta }_{2}}\left( {R,z,t} \right),\quad {{\chi }_{1}}\frac{{\partial {{\theta }_{1}}\left( {R,z,t} \right)}}{{\partial r}} = {{\chi }_{2}}\frac{{\partial {{\theta }_{2}}\left( {R,z,t} \right)}}{{\partial r}}\quad {\text{при}}\quad - {\kern 1pt} h \leqslant z \leqslant h$

Здесь ${{\chi }_{1}}$ и ${{\chi }_{2}}$ – коэффициент теплопроводности материалов сопрягаемых деталей сборки. На свободных поверхностях сборки задается теплообмен с окружающей средой. На боковой поверхности $r = {{R}_{2}}$ охватывающей детали имеем

(3.4)
${{\chi }_{2}}\frac{{\partial {{\theta }_{2}}\left( {{{R}_{2}},z,t} \right)}}{{\partial z}} = {{\beta }_{2}}{{\theta }_{2}}\left( {{{R}_{2}},z,t} \right)\quad {\text{при}}\quad - {\kern 1pt} h \leqslant z \leqslant h$

В (3.4) ${{\beta }_{2}}$ – коэффициент теплоотдачи от поверхности охватываемой детали сборки в окружающую среду, находящуюся при комнатной температуре $\theta = 0$. Далее принимаем ${{\beta }_{2}} = \operatorname{const} $. Подобную теплоотдачу задаем и на торцевых плоскостях сборки $z = \pm h$. Считаем при этом, что коэффициент теплоотдачи от материала охватываемой детали также постоянен и равен ${{\beta }_{1}}$

(3.5)
$\begin{gathered} {{\chi }_{1}}\frac{{\partial {{\theta }_{1}}\left( {r, \pm h,t} \right)}}{{\partial z}} = {{\beta }_{1}}{{\theta }_{1}}\quad {\text{при}}\quad 0 \leqslant r \leqslant R \\ {{\chi }_{2}}\frac{{\partial {{\theta }_{2}}\left( {r, \pm h,t} \right)}}{{\partial z}} = {{\beta }_{2}}{{\theta }_{2}}\quad {\text{при}}\quad R \leqslant r \leqslant {{R}_{1}} \\ \end{gathered} $

Замыкаем задачу, вследствие ее симметрии, требованием

(3.6)
$\frac{{\partial {{\theta }_{1}}\left( {r,0,t} \right)}}{{\partial z}} = \frac{{\partial {{\theta }_{2}}\left( {r,0,t} \right)}}{{\partial z}} = 0$

Областью расчетов, следовательно, является (рис. 1) верхняя половина сборки. Дополнительных трудностей такие расчеты не содержат, разработаны и апробированы соответствующие алгоритмы, имеются пользовательские программы расчетов. Не останавливаясь здесь на этом считаем, что распределение температуры в материалах сборки известно (рассчитано) в каждый момент времени после посадки, вплоть до полного остывания, когда температура выровняется и сравняется с комнатной температурой.

4. Температурные напряжения. В рассматриваемом случае осевой симметрии независимыми переменными задачи остаются пространственные координаты $r$, $z$ и время $t$. Искомыми зависимыми переменными являются компоненты вектора перемещений ${{u}_{r}} = {{u}_{r}}\left( {r,z,t} \right)$, ${{u}_{z}} = {{u}_{z}}\left( {r,z,t} \right)$ и тензора напряжений ${{\sigma }_{{rr}}} = {{\sigma }_{{rr}}}\left( {r,z,t} \right)$, ${{\sigma }_{{rz}}} = {{\sigma }_{{rz}}}\left( {r,z,t} \right)$, ${{\sigma }_{{\varphi \varphi }}} = {{\sigma }_{{\varphi \varphi }}}\left( {r,z,t} \right)$. Для полных деформаций (2.1) имеем

(4.1)
${{d}_{{rr}}} = {{u}_{{r,r}}},\quad {{d}_{{zz}}} = {{u}_{{z,z}}},\quad {{d}_{{\varphi \varphi }}} = \frac{{{{u}_{r}}}}{r},\quad {{d}_{{rz}}} = \frac{1}{2}\left( {{{u}_{{r,z}}} + {{u}_{{z,r}}}} \right)$

Уравнения равновесия, следующие из (2.1), в рассматриваемом случае цилиндрических координат запишутся в форме

(4.2)
$\begin{gathered} \sigma _{{rr,r}}^{{(m)}} + \sigma _{{rz,z}}^{{(m)}} + {{r}^{{ - 1}}}\left( {\sigma _{{rr}}^{{(m)}} - \sigma _{{\varphi \varphi }}^{{(m)}}} \right) = 0 \\ \sigma _{{rz,r}}^{{(m)}} + \sigma _{{zz,z}}^{{(m)}} = 0 \\ \end{gathered} $

Здесь, также как и ранее, $m = 1$ для охватываемой детали сборки, $m = 2$ для охватывающей детали. Напряжения вычисляется через распределения деформации и температуры зависимостями закона Дюамеля–Неймана (2.6). В цилиндрической системе координат они принимают вид

$\sigma _{{rr}}^{{(m)}} = \left( {{{\lambda }_{m}} + 2{{\mu }_{m}}} \right)\left( {u_{{r,r}}^{{(m)}} - p_{{rr}}^{{(m)}}} \right) + {{\lambda }_{m}}\left( {{{r}^{{ - 1}}}u_{r}^{{(m)}} + u_{{z,z}}^{{(m)}} - p_{{\varphi \varphi }}^{{(m)}} - p_{{zz}}^{{(m)}}} \right) - 3{{\alpha }_{m}}{{K}_{m}}{{T}_{0}}{{\theta }_{m}}$
(4.3)
$\begin{gathered} \sigma _{{\varphi \varphi }}^{{(m)}} = \left( {{{\lambda }_{m}} + 2{{\mu }_{m}}} \right)\left( {{{r}^{{ - 1}}}u_{r}^{{(m)}} - p_{{\varphi \varphi }}^{{(m)}}} \right) + {{\lambda }_{m}}\left( {u_{{r,r}}^{{(m)}} + u_{{z,z}}^{{(m)}} - p_{{rr}}^{{(m)}} - p_{{zz}}^{{(m)}}} \right) - 3{{\alpha }_{m}}{{K}_{m}}{{T}_{0}}{{\theta }_{m}} \\ \sigma _{{rr}}^{{(m)}} = \left( {{{\lambda }_{m}} + 2{{\mu }_{m}}} \right)\left( {u_{{z,z}}^{{(m)}} - p_{{zz}}^{{(m)}}} \right) + {{\lambda }_{m}}\left( {{{r}^{{ - 1}}}u_{r}^{{(m)}} + u_{{r,r}}^{{(m)}} - p_{{\varphi \varphi }}^{{(m)}} - p_{{rr}}^{{(m)}}} \right) - 3{{\alpha }_{m}}{{K}_{m}}{{T}_{0}}{{\theta }_{m}} \\ \end{gathered} $
$\sigma _{{rz}}^{{(m)}} = 2{{\mu }_{m}}\left( {\frac{1}{2}\left( {u_{{z,r}}^{{(m)}} + u_{{r,z}}^{{(m)}}} \right) - p_{{rz}}^{{(m)}}} \right)$

Первоначально с развитием процесса деформирования пластические деформации в материалах сборки отсутствуют и в (3.3) компоненты тензора пластических деформаций следует положить равными нулю. Они развиваются только при достижении напряжениями поверхности нагружения (2.10), то есть при выполнении условия

(4.4)
${{\left( {\sigma _{{rr}}^{{(m)}} - \sigma _{{\varphi \varphi }}^{{(m)}}} \right)}^{2}} + {{\left( {\sigma _{{\varphi \varphi }}^{{(m)}} - \sigma _{{zz}}^{{(m)}}} \right)}^{2}} + {{\left( {\sigma _{{zz}}^{{(m)}} - \sigma _{{rr}}^{{(m)}}} \right)}^{2}} + 6{{\left( {\sigma _{{rz}}^{{(m)}}} \right)}^{2}} = \frac{8}{3}{{k}^{2}}$

Соотношение (4.4) служит начальным условием для дальнейшего роста пластических деформаций в развивающейся области пластического течения. В данной области вязкопластического течения из (2.10) следуют зависимости, задающие скорости пластических деформаций $\varepsilon _{m}^{p}$.

(4.5)
$\begin{gathered} \varepsilon _{m}^{p} = \frac{1}{\eta }\frac{{{{\Sigma }_{m}} - {{k}_{m}}}}{{{{\sum }_{m}}}}{{\tau }^{{(m)}}},\quad \zeta = \frac{1}{\eta }\left( {\frac{{{{\Sigma }_{m}}}}{{{{k}_{m}}}} - 1} \right) \\ \Sigma _{m}^{2} = {{\tau }^{{(m)}}} \cdot \cdot \,{{\tau }^{{(m)}}} = \frac{3}{2}\left( {{{{\left( {\sigma _{{rr}}^{{(m)}} - \sigma _{{\varphi \varphi }}^{{(m)}}} \right)}}^{2}} + {{{\left( {\sigma _{{\varphi \varphi }}^{{(m)}} - \sigma _{{zz}}^{{(m)}}} \right)}}^{2}} + {{{\left( {\sigma _{{zz}}^{{(m)}} - \sigma _{{rr}}^{{(m)}}} \right)}}^{2}} + 6{{{\left( {\sigma _{{rz}}^{{(m)}}} \right)}}^{2}}} \right) \\ \end{gathered} $

Если считать, что в некоторый текущий момент времени пластические деформации достигли уровня $\tilde {p}_{{rr}}^{{(m)}}$, $\tilde {p}_{{\varphi \varphi }}^{{(m)}}$, $\tilde {p}_{{zz}}^{{(m)}}$ и $\tilde {p}_{{rz}}^{{(m)}}$, то для их расчета на последующем временном шаге можно использовать зависимости, следующие из ассоциированного закона пластического течения

$p_{{rr}}^{{(m)}} = \left( {2\sigma _{{rr}}^{{(m)}} - \sigma _{{\varphi \varphi }}^{{(m)}} - \sigma _{{zz}}^{{(m)}}} \right)d\zeta \Delta t + \tilde {p}_{{rr}}^{{(m)}}$
(4.6)
$\begin{gathered} p_{{\varphi \varphi }}^{{(m)}} = \left( {2\sigma _{{\varphi \varphi }}^{{(m)}} - \sigma _{{rr}}^{{(m)}} - \sigma _{{zz}}^{{(m)}}} \right)d\zeta \Delta t + \tilde {p}_{{\varphi \varphi }}^{{(m)}} \\ p_{{zz}}^{{(m)}} = \left( {2\sigma _{{zz}}^{{(m)}} - \sigma _{{rr}}^{{(m)}} - \sigma _{{\varphi \varphi }}^{{(m)}}} \right)d\zeta \Delta t + \tilde {p}_{{zz}}^{{(m)}} \\ \end{gathered} $
$p_{{rz}}^{{(m)}} = 12\sigma _{{rz}}^{{(m)}}d\zeta \Delta t + \tilde {p}_{{rz}}^{{(m)}}$

В (4.6) $\Delta t$ – шаг по времени, $d\zeta > 0$.

Следует иметь в виду, что при повторном (обратным) пластическом течении [6, 21, 23, 27], которое с неизбежностью возникает в случае значительного первоначального нагрева охватываемой детали сборки, пластические деформации правой части (4.6) обязаны включать в себя необратимые деформации, накопленные при активном пластическом течении. Для этой цели алгоритмически следует предусмотреть формирование массива накапливаемых необратимых деформаций [21], его хранение и использование в продолжающихся дальнейших расчетах. При расчетах повторных вязкопластических течений в условиях остывания сборки согласно (4.6) это совершенно необходимо.

Когда в расчетах изменяющихся напряженных состояний используются кусочно-линейные условия пластического течения, то повторное пластическое течение при остывании сборки соответствует, как правило, грани поверхности текучести, противоположной той грани, в условиях которой протекало пластическое течение при активном процессе термодеформирования. Отметим в этой связи публикацию [15], где при использовании условия пластичности максимальных касательных напряжений Треска–Сен-Венана показано, что в условиях ускоренного и после замедленного вращения упругопластического цилиндра возникают области течения, соответствующие всем граням и ребрам наклонной призмы Треска: трем граням и трем ребрам при ускоренном вращении и тем оставшимся граням и трем оставшимся ребрам при замедлении вращения. Использование кусочно-линейных пластических потенциалов приводит к разделению области пластического течения на части, в которых течение подчинено разным граням и ребрам поверхности текучести [17, 21–24, 27]. В рассматриваемом случае гладкой поверхности нагружения (боковая поверхность наклонного цилиндра Мизесса [4]) положение значительно упрощается, но все же формированию массива данных о накапливаемых пластических деформациях в условиях активного пластического течения должное внимание следует уделить. Сведения о повторных пластических течениях, которые могут возникнуть в остывающей сборке, можно получить из [23], где подобная по постановке задача решается с использованием кусочно-линейного условия пластического течения максимальных приведенных напряжений (условия Ишлинского–Ивлева) [5]. В областях обратимого (упругого) деформирования при разгрузке компоненты пластических деформаций в (4.3) в рассматриваемом случае остаются постоянными.

Обратимся к постановке граничных условий механической части задачи. На внешних поверхностях формирующейся сборки имеем однородные краевые условия

$\sigma _{{zz}}^{{(1)}}\left( {r,h,t} \right) = \sigma _{{zz}}^{{(1)}}\left( {r, - h,t} \right) = 0,\quad \sigma _{{rz}}^{{(1)}}\left( {r,h,t} \right) = \sigma _{{rz}}^{{(1)}}\left( {r, - h,t} \right) = 0\quad {\text{при}}\quad 0 \leqslant r \leqslant R$
(4.7)
$\sigma _{{zz}}^{{(2)}}\left( {r,h,t} \right) = \sigma _{{zz}}^{{(2)}}\left( {r, - h,t} \right) = 0,\quad \sigma _{{rz}}^{{(2)}}\left( {r,h,t} \right) = \sigma _{{rz}}^{{(2)}}\left( {r, - h,t} \right) = 0\quad {\text{при}}\quad R \leqslant r \leqslant {{R}_{2}}$
$\sigma _{{rr}}^{{(2)}}\left( {{{R}_{2}},z,t} \right) = \sigma _{{rr}}^{{(2)}}\left( {{{R}_{2}},z,t} \right) = 0\quad {\text{при}}\quad - h \leqslant z \leqslant h$

На контактной поверхности $r = R$ полагаем непрерывными радиальные компоненты вектора перемещений и тензора напряжений

(4.8)
$u_{r}^{{(1)}}\left( {R,z,t} \right) = u_{r}^{{(2)}}\left( {R,z,t} \right),\quad \sigma _{{rr}}^{{(1)}}\left( {R,z,t} \right) = \sigma _{{rr}}^{{(2)}}\left( {R,z,t} \right)$

Возможность проскальзывания материалов элементов сборки на их общей поверхности $r = R$ и возникающее при этом трение зададим зависимостями

(4.9)
$\sigma _{{rz}}^{{(1)}}\left( {R,z,t} \right) = \sigma _{{rz}}^{{(2)}}\left( {R,z,t} \right),\quad u_{z}^{{(1)}}\left( {R,z,t} \right) = u_{z}^{{(2)}}\left( {R,z,t} \right),$
при $\left| {\sigma _{{rz}}^{{(2)}}\left( {R,z,t} \right)} \right| \leqslant g\left( {z,t} \right)$
(4.10)
$\begin{gathered} \sigma _{{rz}}^{{(1)}}\left( {R,z,t} \right) = - \sigma _{{rz}}^{{(2)}}\left( {R,z,t} \right) = f\left( {z,t} \right)\left| {\sigma _{{rr}}^{{(2)}}\left( {R,z,t} \right)} \right| + \\ + \;\phi \left( {z,t} \right)\left| {{v}_{z}^{{(1)}}\left( {R,z,t} \right) - {v}_{z}^{{(2)}}\left( {R,z,t} \right)} \right|, \\ \end{gathered} $
при $\left| {\sigma _{{rz}}^{{(2)}}\left( {R,z,t} \right)} \right| > g\left( {z,t} \right)$

В (4.9) и (4.10) $g\left( {z,t} \right)$, $f\left( {z,t} \right)$ и $\phi \left( {z,t} \right)$ – задаваемые параметры трения. Первый из них $g\left( {z,t} \right)$ – параметр Прандтля, второй $f\left( {z,t} \right)$ – параметр (коэффициент) сухого трения скольжения и $\phi \left( {z,t} \right)$ – коэффициент вязкого трения. Зависимость их от пространственной координаты $z$ и времени $t$ определяется зависимостью их от местной температуры $\theta \left( {z,t} \right)$.

(4.11)
$\begin{gathered} g\left( {z,t} \right) = {{g}_{0}}y,\quad f\left( {z,t} \right) = {{f}_{0}}y,\quad \phi = {{\phi }_{0}}y \\ y = {{\left( {\frac{{{{\theta }_{r}} - \theta }}{{{{\theta }_{r}}}}} \right)}^{2}},\quad {{\theta }_{r}} = \frac{{{{T}_{r}} - {{T}_{0}}}}{{{{T}_{0}}}} \\ \end{gathered} $

Здесь ${{g}_{0}}$, ${{f}_{0}}$, ${{\xi }_{0}}$ – значения параметров при комнатной температуре, ${{\theta }_{r}}$ – безразмерная температура плавления, наименьшее для материалов сопрягаемых деталей.

На линиях $z = \pm h$ и $r = R$ присутствует сингулярность в граничных условиях. Это с необходимостью приведет к соответствующим следствиям в расчетах. С целью избежать данных особенностей воспользуемся искусственным отходом от этих линий, предполагая, что в окрестностях их $h - \delta \leqslant z \leqslant h$ и $ - h \leqslant z \leqslant - h + \delta $ зависимости (4.11) дополняются соответственно сомножителями

(4.12)
$\begin{gathered} {{\psi }^{ + }}\left( z \right) = 1 - {{\left( {\frac{{z - h + \delta }}{\delta }} \right)}^{2}}\quad {\text{при}}\quad h - \delta \leqslant z \leqslant h \\ {{\psi }^{ - }}\left( z \right) = - \frac{{\left( {z + h} \right)\left( {z + h - 2\delta } \right)}}{{{{\delta }^{2}}}}\quad {\text{при}}\quad - h \leqslant z \leqslant - h + \delta \\ \end{gathered} $
(4.13)
$g\left( {z,t} \right) = {{g}_{0}}y{{\psi }^{ \pm }}\left( {z,\delta } \right)$; $f\left( {z,t} \right) = {{f}_{0}}y{{\psi }^{ \pm }}\left( {z,\delta } \right)$; $\phi = {{\phi }_{0}}y{{\psi }^{ \pm }}\left( {z,\delta } \right)$

Зависимости (4.13) сохраняют симметрию сборки относительно плоскости $z = 0$. Таким способом в качестве расчетной области имеем возможность принять половину $z \geqslant 0$ сборки. На плоскости симметрии $z = 0$ потребуем

(4.14)
$u_{z}^{{(1)}}\left( {r,0,t} \right) = u_{z}^{{(2)}}\left( {r,0,t} \right) = 0,\quad \sigma _{{rz}}^{{(1)}}\left( {r,0,t} \right) = \sigma _{{rz}}^{{(2)}}\left( {r,0,t} \right) = 0$

Также следует иметь ввиду, что на оси симметрии $r = 0$ выполняются условия

(4.15)
$u_{r}^{{(1)}}\left( {0,z,t} \right) = 0;\quad \sigma _{{rz}}^{{(1)}}\left( {0,z,t} \right) = 0$

5. Результаты расчетов. Приближенные численные расчеты проводились следуя конечно-разностному аналогу записанных выше дифференциальных уравнений. Область расчетов ($0 \leqslant r \leqslant {{R}_{1}}$; $0 \leqslant z \leqslant h$) разбивалась сеткой, составленной из четырехугольных элементов. Искомые величины аппроксимировались в узлах сетки конечными разностями. В тех узлах, которые примыкают к границам элементов сборки, или к поверхности их соединения, или к продвигающимся поверхностям упруговязкопластических границ, для разностных представлений искомых значений зависимых неизвестных последовательно использовались приведенные ранее граничные условия и условия непрерывности радиальных компонент перемещений и напряжений на упругопластических границах. После разрешения полученной таким способом системы алгебраических уравнений, производился последующий шаг по времени. На каждом таком временном шаге отслеживалось возможное возникновение области вязкопластического течения, последующее продвижение границы данной области, включая смену направления движения такой упруговязкопластической границы и исчезновение области пластического течения. В условиях остывания сборки при обратимом деформировании ее деталей отслеживался момент возможного возникновения повторного (обратного) пластического течения [23, 27]. Накопленные в активном процессе пластические деформации учитывались при расчетах повторных течений за счет внесения их в последние слагаемые правых частей равенств (4.8). В этом случае они не меняются со временем, но разные в каждой точке деформируемых деталей сборки.

При проведении расчетов будем считать, что упругие модули (коэффициенты Ламе) материалов частей сборки ${{\lambda }_{m}}$ и ${{\mu }_{m}}$, коэффициенты их теплопроводности ${{\chi }_{m}}$ в законе теплопроводности Фурье, коэффициенты ${{\beta }_{m}}$ теплоотдачи в окружающую среду являются постоянными, не зависящими от температуры. Заметим, что такое предположение делается только для упрощения расчетов. Его можно обосновать тем, что до настоящего времени не существует надежных экспериментальных данных о таких зависимостях. В таблице 1 приведены принимаемые значения постоянных для некоторых материалов, процессы соединения элементов сборки из которых иллюстрируются далее графически.

Таблица 1
  ${{k}_{0}}$, МПа $\lambda $, МПа $\mu $, МПа α × 106 a × 10–6, м2/с $\chi $, Вт/(мК) ${{T}_{p}}$, °C $\beta $, Вт/(мК)
сталь 360 97.06 82.68 11.1     17.35     67.78 1400 7.5
латунь 290 58.26 38.84 19.1     35.68     113 937 7.5
дюраль 255 41.53 27.70 22.9     50     188 660 10.0

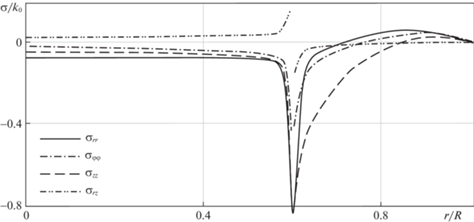
Анализ результатов численных расчетов начинаем с представления графических зависимостей о распределении остаточных напряжений в сборке после ее остывания до комнатной температуры. Так на рис. 2 указано такое распределение для сборки из двух стальных деталей, термомеханические параметры которых одинаковы (таблица 1) и охватывающая деталь ($RR_{1}^{{ - 1}} = 0.6$) сборки до момента посадки нагревалась до температуры 600°С.

Рис. 2.

Распределение остаточных напряжений в сборке (${{T}_{0}}$ = 600°C, ${{g}_{0}} = 0.06{{k}_{0}}$, ${{f}_{0}} = 0.22$, ${{\phi }_{0}} = 0.8\sqrt {\rho {{k}_{0}}} $, $RR_{2}^{{ - 1}} = 0.6$) после ее остывания.

Совершенно необходимо заметить, что значение параметра ${{q}_{0}}$ (${{q}_{0}} = 0.06{{k}_{0}}$), задающего момент проскальзывания материалов на поверхности контакта $r = R$, мало сказывается на уровень и распределение как итоговых остаточных напряжений, так и текущих напряжений в процессе посадки. Проскальзывание наступает непосредственно за моментом посадки из-за значительной разности температур сопрягаемых деталей сборки и, как следствие, быстрого роста контактных напряжений. Вследствие малых скоростей проскальзывание совершенно незначительным оказывается влияние вязкого трения, то есть значений коэффициента ${{\phi }_{0}}$. В то же время уровень температурных напряжений удивительно чувствителен к изменениям в значениях коэффициента сухого трения скольжения Кулона ${{f}_{0}}$. Для сравнения приведем распределения остаточных напряжений, изменив ${{f}_{0}}$ со значения ${{f}_{0}} = 0.22$ (рис. 2) до значения ${{f}_{0}} = 0.35$ (рис. 3). Итоговый натяг в сборке увеличивается при этом почти вдвое (сравни рис. 3 и рис. 2).

Рис. 3.

Остаточные напряжения при ${{f}_{0}} = 0.35$.

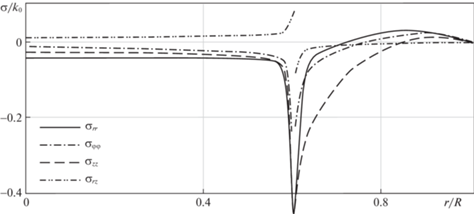
Изменения в геометрии сопрягаемых деталей и их материалах иллюстрируют графические зависимости на рис. 4 и 5. На первом из них (рис. 4) охватывающая деталь сборки считается существенно более тонкой в сравнении с охватываемой, на втором (рис. 5) – наоборот. Начальное значение коэффициента трения скольжения в таких расчетах принималось одинаковым (${{f}_{0}} = 0.26$). В первом случае на массивный стальной вал насаживалась труба, изготовленная из латуни (таблица 1, ${{T}_{0}}$ = 600°С); во втором охватываемый вал из дюралюминия сжимался массивной стальной трубой (таблица 1, ${{T}_{0}}$ = 600°С).

Рис. 4.

Распределение остаточных напряжений в сборке: сталь-латунь ${{f}_{0}} = 0.26$, $RR_{2}^{{ - 1}} = 0.8$.

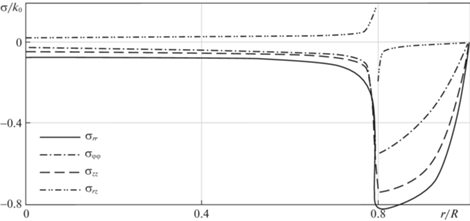
Рис. 5.

Распределение остаточных напряжений в сборке: дюралюминий – сталь ${{f}_{0}} = 0.26$, $RR_{2}^{{ - 1}} = 0.2$.

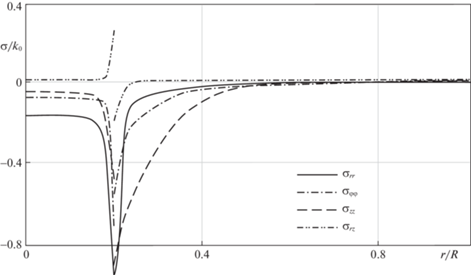
На плоскости $z = h$ напряжение ${{\sigma }_{{rz}}}\left( {r,h} \right) = 0$, а на поверхности $r = R$ ${{\sigma }_{{rz}}}\left( {r,h} \right) \ne 0$. Следовательно, на линии $r = R$ и $z = h$ имеется разрыв в граничных условиях. С целью избавления от подобной сингулярности в краевых условиях (4.9) и (4.10), задающих трение на поверхности контакта $r = R$, в $\delta $ – окрестностях торцов $z = \pm h$ параметры трения уточнялись с помощью зависимостей (4.12) и (4.13). Таким способом значения $\delta $ оказывалось еще одним задаваемым параметром в расчетах. При построении графических зависимостей рис. 2–5 этот параметр полагался одинаковым и равным $0.01h$ ($\delta = 0.01h$). Если термомеханические и геометрические параметры оставить теми же, что и при получении зависимостей рис. 2, то натяг в сборке и иные остаточные контактные напряжения по оси $z$ распределены согласно графическим зависимостям рис. 6.

Рис. 6.

Остаточные напряжения на поверхности $r = R$ в зависимости от координаты $z$ (торцевой эффект) (${{T}_{0}}$ = 600°C, ${{g}_{0}} = 0.06{{k}_{0}}$, ${{f}_{0}} = 0.22$, ${{\phi }_{0}} = 0.8\sqrt {\rho {{k}_{0}}} $, $RR_{2}^{{ - 1}} = 0.6$) и $\delta = 0.01h$.

Следуя рис. 6, контактные напряжения в сборке практически не меняются с изменением координаты $z$. Только имеет место ярко выраженный торцевой эффект падения натяга и абсолютных значений иных контактных напряжений. Такое падение в значениях напряжений ${{\sigma }_{{rr}}}$ и ${{\sigma }_{{rz}}}$ до нуля при $z = \pm h$ диктуется граничными условиями, при этом натяг ${{\sigma }_{{rr}}}\left( {R,h} \right) < 0$ и ${{\sigma }_{{\varphi \varphi }}}\left( {R,h} \right) < 0$ сохраняется не нулевым, но при уменьшенных по абсолютной величине значениях (рис. 6). В настоящее время достаточно устойчиво сформировалось противоположное заключение о торцевом эффекте, состоящее в том, что в условиях горячей посадки или иной посадки с натягом наоборот на торцах формируется максимальный натяг в сравнении с натягом во внутренних точках поверхности сопряжения $r = R$. Тревожит, что последний вывод иногда без сомнений воспринимается технологической практикой [30–34]. Подкрепляется такой вывод многочисленными расчетами преимущественно с помощью метода конечных элементов [30, 31, 33] или посредством пакетов пользовательских программ [32, 34]. Ошибочность результатов подобных расчетов связана именно с игнорированием сингулярности в задании граничных условий на линии $r = R$ и $z = h$. Действительно, если в расчетах уровня и распределения остаточных напряжений, представленных графическими зависимостями рис. 2 и рис. 6, положить $\delta = 0$, то вместо зависимостей рис. 6 будем иметь рис. 7.

Рис. 7.

Остаточные напряжения на поверхности $r = R$ в зависимости от координаты $z$ (торцевой эффект) (${{T}_{0}}$ = 600°C, ${{g}_{0}} = 0.06{{k}_{0}}$, ${{f}_{0}} = 0.22$, ${{\phi }_{0}} = 0.8\sqrt {\rho {{k}_{0}}} $, $RR_{2}^{{ - 1}} = 0.6$) и $\delta = 0$.

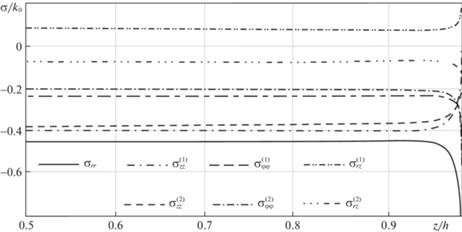
Торцевой эффект в таком случае ($\delta = 0$ на рис. 7) противоположен показанному на рис. 2. При приближении к торцу $z = h$ напряжения ${{\sigma }_{{rr}}}$ и ${{\sigma }_{{\varphi \varphi }}}$ увеличиваются по абсолютной величине, что отмечалось в [30–34]. Графические зависимости рис. 7 качественно совпадают с аналогичными зависимостями, представленными в [32, 33]. В [30, 31, 34] отмечен подобный эффект возрастания температурных напряжений в местах сингулярностей в задании граничных условий, объяснить который иначе чем некорректным использованием таких особенностей в задании краевых условий невозможно.

При проведении расчетов предпринимались попытки еще более уменьшить $\delta $, считая, например, $\delta = 0.001h$. В этом случае наблюдали при приближении $z$ к значению $z = h$ рост напряжений по абсолютной величине и их последующее уменьшение. Измельчением сетки не удается избавиться от такого немонотонного изменения в натяге в приторцевой области. Настолько определяющим оказывается влияние сингулярности в граничных условиях на линии $r = R$ и $z = h$.

Ранее [21–23, 27] для расчетов итогового натяга и распределения остаточных напряжений в сборке нами предлагалось использовать численно-аналитические решения соответствующей задачи Гадолина о горячей посадке. В рассматриваемом случае упругопластических свойств материалов сопрягаемых деталей сборки при использовании кусочно-линейных пластических потенциалов (условий пластического течения Треска–Сен-Венана или Ишлинского–Ивлева), когда только и возможны отмеченные численно-аналитические решения, получили в качестве результатов расчетов следствия: натяг в сборке в местах удаленных от торцевой меньше рассчитываемых значений, полученных здесь, при использовании условия пластичности максимальных касательных напряжений и больше при использовании условия максимальных приведенных напряжений. Это вполне согласуется с выводами, полученными в [8], где температурные напряжения в трубе, полученные при условии пластического течения максимальных октаэдрических напряжений (Мизеса), оказались полусуммой напряжений, рассчитанных при использовании кусочно-линейных условий пластического течения. Данное обстоятельство находит свое подтверждение и в рассматриваемом случае. Следовательно, построенные [22, 27], по-существу, аналитические решения задач посадки цилиндрических деталей вполне могут использоваться в расчетах технологических задач о посадке с натягом, включая операцию горячей посадки.

Заключение. Здесь не учитывалось упрочнение в материалах сопрягаемых деталей сборки; для его учета не имеется труднопреодолимых препятствий алгоритмического и вычислительного свойства. Предполагалось дать ответ в использовании для моделирования технологической операции горячей посадки существенно упрощенных расчетов решением одномерных задач, предполагающих плоские и обобщенно плоские деформированные состояния. Решения, получены в таких условиях, являются наиболее простыми, численно-аналитическими, но позволяют прогнозировать натяг в сборке в случае неизменно возникающих областей необратимого деформирования материалов элементов сборки. Численно-аналитические расчеты в таком случае свободны от сингулярностей в задаваемых граничных условиях. Оказалось, что неверный учет подобных особенностей в задании граничных условий может приводить не только к количественным, но и к качественным ошибкам в расчетах. Используемый здесь прием выделения областей, примыкающих к местам разрывов в поставленных граничных условиях, является безусловно искусственным. Таким способом здесь продемонстрирована необходимость внимательного отношения к существованию отмечаемых сингулярностей в постановках краевых задач при их численных решениях, включая популярные метод конечных элементов и предлагаемые многочисленные пакеты программ.

Для исключения сингулярностей в постановках граничных условий возможно воспользоваться приспособленным для этой цели методом граничных состояний В.Б. Пенькова [35]. Совершенно необходимо отметить метод расчетов на основе быстрых разложений, предложенный А.Д. Чернышовым [36, 37], свободный от влияния сингулярностей подобного свойства на процесс расчетов и их результаты.

Работа выполнена в рамках государственно задания Хабаровского Федерального научного центра Дальневосточного отделения Российской академии наук № 075-00742-22-00, с использованием ресурсов ЦКПН “Центр обработки и хранения научных данных ДВО РАН”, финансируемых Российской Федерацией в лице Министерства науки и высшего образования Российской Федерации по проекту № 075-15-2021-663.

Список литературы

  1. Галин Л.А. Упругопластические задачи. М.: Наука, 1984. 232 с.

  2. Ивлев Д.Д. Об определении перемещений в упругопластических задачах теории идеальной пластичности // в сб.: Успехи механики деформируемых сред. М.: 1975. С. 236–240.

  3. Ивлев Д.Д. Из истории дискуссий в механике. Три дискуссии // в сб.: Теоретическая и прикладная механика. Минск: БИТУ, 2012. Вып. 27. С. 5–10.

  4. Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.

  5. Ишлинский А.Д., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.

  6. Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации и упругое последействие. Владивосток: Дальнаука, 2013. 312 с.

  7. Alexandrov S.E. Elastic/Plastic Disc under Plane Stress Conditions. New York; London: Springer, 2015. 113 p.

  8. Дац Е.П., Мурашкин Е.В., Ткачева А.В., Щербатюк Г.А. Температурные напряжения в упругопластической трубе в зависимости от выбора условия пластичности // Изв. РАН. МТТ. 2018. № 1. С. 32–43.

  9. Александров С.Е., Ломакин Е.В., Дзенг Й.-Р. Решение термоупругопластической задачи для тонкого диска, подверженного термическому нагружению // Докл. РАН. 2012. Т. 443. № 3. С. 310–312.

  10. Фирсов С.В., Прокудин А.Н., Буренин А.А. Ползучесть и пластическое течение во вращающемся цилиндре с жестким включением // СибЖИМ. 2019. Т. 22. № 4. С. 121–133.

  11. Begun A.S., Burenin A.A., Kovtanyuk L.V., Lemza A.O. On the mechanismus of production of large irreversible strains in materials with elastic, viscous and plastic properties // Arch. Appl. Mech. 2020. V. 90. P. 829–845.

  12. Севастьянов Г.М., Буренин А.А. О больших деформациях при кручении несжимаемого упругопластического цилиндра // Докл. РАН. 2018. Т. 482. № 482. № 3. С. 285–287.

  13. Eraslan A.N., Akis T. On the plane strain and plane stress solutions of functionally graded rotating solid shaft and solid disk problems // Acta Mech. 2006. V. 181. P. 43–63.

  14. Antoni N. Contact separation and failure analysis of a rotating thermoelasticplastic shink-fik assembly // Appl. Math. Model. 2013. V. 37. P. 2352–2363.

  15. Prokudin A.N. Exact elastoplastic analysis of a rotating cylinder with a rigid inclusion under mechanical loading and unloading // ZAMM – J. Appl. Math.&Mech. 2020. V. 100. № 3. e201900213.

  16. Begun A.S., Burenin A.A., Kovtanyuk L.V., Prokudin A.N. Irreversible deformation of a rotating disk having angular acceleration // Acta Mech. 2021. V. 232. № 5. P. 1917–1931.

  17. Прокудин А.Н., Буренин А.А. Упругопластическое деформирование вращающегося сплошного цилиндра из линейно-упрочняющегося материала // ПММ. 2021. Т. 85. № 2. С. 172–192.

  18. Mack W. Thermal assembly of an elastic-plastic hub and a solid shaft // Arch. Appl. Mech. 1993. V. 63 P. 42–50.

  19. Bengeri M., Mack W. The influence of the temperature dependence of the yield stress on the stress distribution in a thermally assembled elastic-plastic shrink fit // Acta Mech. 1994. V. 103. P. 243–257.

  20. Kovacs A. Residual Stresses in thermally loaded shrink fits // Periodica Polytechn. Ser. Mech. Eng. 1996. V. 40. № 2. P. 103–112.

  21. Буренин А.А., Ткачева А.В., Щербатюк Г.А. К расчету неустоявшихся температурных напряжений в упругопластических телах // Вычисл. мех. сплошн. сред. 2017. Т. 10. № 3. С. 245–259.

  22. Буренин А.А., Ткачева А.В. О сборке двухслойной металлической трубы способом горячей посадки // Изв. РАН. МТТ. 2019. № 3. С. 86–99.

  23. Буренин А.А., Матвеенко В.П., Ткачева А.В. Температурные напряжения в процессе сборки двухслойного вала способом горячей посадки // Уч. зап. КнАГТУ. 2018. № 3 (35). С. 31–41.

  24. Буренин А.А., Каинг М., Ткачева А.В. К расчету плоских напряженных состояний в теории неустановившихся температурных напряжений в упругопластических телах // ДВМЖ. 2018. Т. 18. № 2. С. 131–146.

  25. Гадолин А.В. Теория орудий, скрепленных обручами // Артилл. ж. 1861. № 12. С. 1033–1071.

  26. Попов А.Л., Челюбеев Д.А., Бухалов В.И. Задача Гадолина в упругопластической постановке // ПММ. 2018. Т. 82. № 6. С. 804–812.

  27. Буренин А.А., Ткачева А.В. Эволюция температурных напряжений в задаче Гадолина о сборке двухслойной упругопластической трубы // Вестн. ПНИПУ. Сер. Мех. 2020. № 3. С. 20–31.

  28. Хаазе Р. Термодинамика необратимых процессов. М.: Мир, 1967. 438 с.

  29. Боли Б., Уэйнер Дж. Теория температурных напряжений. М.: Мир, 1964. 512 с.

  30. Gaul L., Schmidt A. Finite element simulation and experiments on rotor damping assembled disc shrink fits // Mech. Syst.&Signal Proc. 2019. V. 127. P. 412–422.

  31. Erena D., Vazquez J., Navarro C., Talemi R. Numerical study on the influence of artificial internal stress relief groove on fretting fatigue in a shrink-fitted assembly // Tribol. Int. 2020. V. 151. P. 1–9.

  32. Buczkowski R., Kleiber M. A study of the surface roughness in elasto-plastic shrink fitted joint // Tribol. Int. 2016. V. 98. P. 125–132.

  33. Őzel A., Temiz S., Aydin M.D., Sen S. Stress analysis of shrink-fitted joints for various fit formas via finite element // Mater.&Design. 2005. V. 26. P. 281–289.

  34. Потянихин Д.А., Дубенко Е.М. Расчет напряженно-деформированного состояния заклепочного соединения, полученного с помощью азотного охлаждения заклепки // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Мех. пред. сост. 2018. № 3 (37). С. 134–144.

  35. Пеньков В.Б., Поликарпов М.В. Сосредоточенные силовые воздействия в методе граничных состояний // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Мех. пред. состяния. 2020. № 1(43). С. 34–44.

  36. Чернышов А.Д. Метод быстрых разложений для решения нелинейных дифференциальных уравнений // ЖВММФ. 2014. Т. 54. № 1. С. 13–24.

  37. Горяйнов В.В., Попов М.И., Чернышов А.Д. Решение задачи о напряжениях в остром клиновидном режущем инструменте методом быстрых разложений и проблема согласования граничных условий // Изв. РАН. МТТ. 2019. № 5. С. 113–130.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал