Прикладная математика и механика, 2022, T. 86, № 4, стр. 488-495

1. Введение. Решение задач, связанных с расчетом предельных допустимых напряжений в материалах в условиях динамического нагружения, является актуальной научной проблемой. До сих пор не выработано общепринятого подхода по определению прочностных свойств и прогнозированию поведения материалов при высокоинтенсивных воздействиях. В течение последних десятилетий многочисленные динамические испытания четко фиксируют наличие скоростной зависимости прочности, то есть роста предельного уровня напряжений в момент разрушения при увеличении скорости деформации образца [1–3]. Первоначально делались попытки объяснить рост напряжений в момент разрушения наличием некоторой степенной зависимости прочности от скорости нагружения, которая бы являлась свойством материалов [4]. Главным недостатком такого подхода является то, что для разных материалов, а также для различных экспериментальных схем значения показателя степени варьировались от 0.05–0.33. Достаточно большой разброс значений указывает на то, что такое объяснение скоростной зависимости прочности является скорее численной аппроксимацией, чем некоторой феноменологической моделью, предсказывающей условия разрушения материала в динамике. Также был предложен интегральный критерий разрушения Тулера–Бутчера (Tuler&Butcher), в котором учитывается, что разрушение не происходит мгновенно, и что это процесс, развивающийся во времени [5]. К недостаткам этого критерия можно отнести отсутствие даже гипотетического мысленного эксперимента, позволяющего измерить значения констант материала.

В настоящей работе рассмотрены два подхода к описанию динамической прочности материала. В их основе, в отличии от упомянутых выше методов, лежит определённая идея и физический смысл. Один из подходов основан на полуэмпирической модели Пэливола–Рэмиша (Paliwal B. and Ramesh K.T, P–R модель), рассматривающей сплошную среду с дефектной структурой [6, 7]. Анализ роста микротрещин при одноосном сжатии в зависимости от скорости нагружения позволил вычислить характеристические параметры материала, определяющие его скоростную зависимость прочности. Другой, структурно-временной подход основан на критерии инкубационного времени [8, 9], основная идея которого, также как и в подходе Тулера–Бутчера (Tuler&Butcher), заключается в том, что процесс разрушения не мгновенный. Главным отличием структурно-временного подхода является предположение о том, что существует временной интервал, называемый инкубационным временем разрушения, который может трактоваться как характерное время релаксации подготовительных процессов микроразрушения, предваряющих разрыв материала на макроскопическом уровне. При этом для определения условий возникновения разрушения также принципиальное значение имеют не только амплитудные характеристики, но и история поля напряжений в течение инкубационного периода.

2. Описание моделей и анализ взаимосвязей. В рамках P–R модели Пэливола–Рэмеша было получено следующее нормировочное соотношение, описывающее скоростную зависимость прочности материалов:

где ${{\sigma }_{f}}$ – предельный уровень напряжений в момент разрушения, $\dot {\varepsilon }$ – скорость деформации, параметры материала ${{\sigma }_{0}}$ и ${{\dot {\varepsilon }}_{0}}$ – характеристические напряжение и скорость деформации соответственно. Значения ${{\sigma }_{0}}$ и ${{\dot {\varepsilon }}_{0}}$ могут быть вычислены согласно микроструктурной модели, рассматривающей рост и развитие микродефектов в хрупких средах. Для расчета ${{\sigma }_{0}}$ и ${{\dot {\varepsilon }}_{0}}$ используются такие параметры структуры среды, как средний размер и средняя плотность дефектов, а также такие макропараметры, как упругие константы Ламе, плотность и трещиностойкость. Стоит отметить, что сама зависимость (2.1) была получена полуэмперическим путем, как аппроксимация результатов численных экспериментов. При испытании различных материалов был определен диапазон возможных значений параметров модели Паливола–Рэмеша. Затем в рамках этой модели был вычислен предельный уровень напряжений в зависимости от скорости деформации для виртуальных материалов со случайно выбранными комбинациями значений модельных параметров из выявленного ранее диапазона. В результате получилось, что вычисленная таким образом скоростная зависимость прочности может быть хорошо описана нормировочным соотношением (2.1).

Как было упомянуто выше, в основе другого подхода лежит критерий инкубационного времени:

где $\sigma \left( s \right)$ – временной профиль нагружающего воздействия, $\tau $ – инкубационное время, а ${{\sigma }_{c}}$ – критическое напряжение разрушения. Стоит отметить, что в основе критерия инкубационного времени лежит феноменологическая концепция, согласно которой, для развития любого переходного процесса требуется некоторое время, продолжительность которого определяется значением параметра инкубационного времени, а также интенсивностью нагрузки. Скоростная зависимость в случае постоянной скорости деформации $\dot {\varepsilon }$ будет описываться следующим соотношением: $k = \frac{{2{{\sigma }_{c}}}}{E}$ безразмерный параметр, где $E$ – модуль Юнга. Таким образом, структурно-временная модель также содержит два параметра прочности материала, как и нормировочное соотношение, предложенное Кимберли, Рэмешом и Дапхалапуркаром (Kimberley J., Ramesh K.T., Daphalapurkar N.P.). При этом можно утверждать, что параметры ${{\sigma }_{0}}$ и ${{\sigma }_{с}}$ имеют примерно один и тот же физический смысл и можно полагать, что они совпадают, в то время как ${{\dot {\varepsilon }}_{0}}$ и $\tau $ принципиально отличаются несмотря на схожесть их размерностей $\left[ {1{\text{/}}c} \right]$ и $\left[ c \right]$ соответственно. Более того из соотношения (2.3) видно, что в структурно-временном подходе также появляется характерная скорость деформации ${{\dot {\varepsilon }}_{с}} = \frac{k}{\tau } = \frac{{2{{\sigma }_{c}}}}{{E\tau }}$, которая однозначно определяется параметрами модели. На диаграмме скоростной зависимости прочности ${{\dot {\varepsilon }}_{с}}$ условно разделяет статическую и динамическую ветви прочности, то есть участок, на котором уровень критических напряжений слабо меняется от скорости деформации от области с явно выраженным ростом напряжений в момент разрушения.

При предположении тождественности параметров ${{\sigma }_{0}}$ и ${{\sigma }_{с}}$, можно приравнять правые части выражений (2.1) и (2.3) и установить связь между ${{\dot {\varepsilon }}_{0}}$ и $\tau $:

Соотношение (2.4) показывает, что параметр нормировочного соотношения ${{\dot {\varepsilon }}_{0}}$ может быть выражен через инкубационное время $\tau $ только в зависимости от скорости деформации материала $\dot {\varepsilon }$. Интересной особенностью выражения (2.4) является то, что для скорости деформации $\dot {\varepsilon } = {{\dot {\varepsilon }}_{с}} = \frac{k}{\tau }$, значение параметра ${{\dot {\varepsilon }}_{0}}$ совпадает с ${{\dot {\varepsilon }}_{с}}$:

Таким образом, получается, что в структурно-временном подходе также возможна нормировка кривой скоростной зависимости прочности, но только неравномерная, в отличие от подхода, основанного на P–R модели Пэливола–Рэмеша.

3. Оценка значений модельных параметров. Важной проблемой при расчете скоростной зависимости прочности для конкретного материала является задача оценки значений параметров модели. В случае нормировочного соотношения эти значения могут быть вычислены согласно формулам (3.1), полученным в рамках структурной P–R модели:

где ${{K}_{{IC}}}$ – критическое значение трещиностойкости, $\bar {s}$ и $\eta $ – средний размер и средняя плотность дефектов, ${{c}_{d}} = \sqrt {\left( {\lambda + 2\mu } \right){\text{/}}\rho } $ – максимальная скорость распространения волн в среде, $\lambda $ и $\mu $ – упругие постоянные Ламе, $\rho $ – массовая плотность.

Для определения значений параметров критерия инкубационного времени использовался метод знаковозмущенных сумм (Sign-Perturbed Sums) [10]. Ранее было показано, что зависимость вида (2.3) полностью удовлетворяет условиям применимости этого метода [11, 12]. При этом экспериментальные результаты измерения скоростной зависимости прочности $({{\sigma }_{*}}_{i},{{\dot {\varepsilon }}_{*}}{{{\kern 1pt} }_{i}})$ представляются в виде следующей модели наблюдений со случайным шумом ${{{v}}_{i}}$:

где функция $\varphi \left( {\tau ,\dot {\varepsilon }} \right)$ определяется согласно структурно-временному подходу соотношением (2.3). Предполагается, что случайный шум имеет симметричное распределение с нулевым математическим ожиданием. Результатом обработки метода SPS является доверительный интервал T, содержащий истинное значение $\tau {\kern 1pt} *$ инкубационного времени с заранее выбранным уровнем вероятности:

Параметры алгоритма $M$ и $q$ выбираются согласно требуемому уровню достоверности.

Рандомизированная часть алгоритма состоит в формировании $M - 1$ комплектов из $N$ случайных знаков $\beta = \pm 1$ согласно схеме испытаний Бернулли. Сгенерированный набор знаков позволяет для пробного значения $\tau $ вычислить последовательность знаковозмущенных сумм ${{H}_{j}}\left( \tau \right)$:

Сумма ${{H}_{0}}\left( \tau \right)$ вычисляется для полностью положительного набора знаков $\beta = + 1$:

Равенство нулю правой части выражения (3.5) эквивалентно необходимому условию минимума среднеквадратичного отклонения расчётной кривой для пробного значения $\tau $ от последовательности экспериментальных значений. Суть метода SPS заключается в том, что если пробное значение $\tau $ достаточно близко к истинному значению $\tau {\kern 1pt} *$, то величина $\left| {{{H}_{0}}\left( \tau \right)} \right|$ будет соизмерима со знакопеременными суммами $\left| {{{H}_{j}}\left( \tau \right)} \right|.$ В противном случае $\left| {{{H}_{0}}\left( \tau \right)} \right|$ будет мажорировать суммы $\left| {{{H}_{j}}\left( \tau \right)} \right|$, что будет означать, что проверяемое значение $\tau $ не принадлежит доверительному интервалу T. Формально шаги этой процедуры показаны в таблице 1.

Результаты расчета скоростных зависимостей прочности, приведенные в следующем разделе, рассчитаны для значений инкубационного времени $\tau $, которые соответствуют границам 80%-го доверительного интервала T.

4. Результаты расчета скоростных зависимостей. В рамках рассмотренных моделей были вычислены скоростные зависимости прочности для некоторых материалов.

На рис. 1 показаны результаты, полученные при обработке данных эксперимента (круглые точки – 1) по ударному сжатию керамического материала SiC-N [13]. Кривая 2 соответствует результатам расчета согласно нормировочному соотношению (2.1) при следующих значениях параметров ${{\dot {\varepsilon }}_{0}} = 5000.1{\text{/c}}$ и ${{\sigma }_{0}} = 5.4$ ГПа. Видно, что данный подход позволяет лишь качественно показать начало роста предельного уровня напряжений при динамическом нагружении. Для количественного описания этих данных Холландом (Holland C.C.) была сделана поправка нормировочного соотношения [14]:

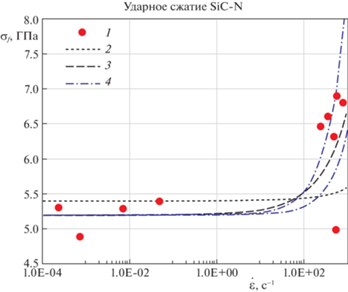
Кривая 3 показывает расчетную зависимость согласно выражению (4.1) при значениях ${{\dot {\varepsilon }}_{0}} = 131.~1{\text{/с}}$ и ${{\sigma }_{0}} = 5.2$ ГПа. Последняя кривая уже достаточно хорошо описывает экспериментальную зависимость, однако остается непонятным, каким образом получается существенный перерасчет параметра ${{\dot {\varepsilon }}_{0}}$ и почему возникает множитель 0.1. Кривые 4 получены в рамках структурно-временного подхода для следующих значений модельных параметров $\tau \in \left[ {5.4;\;14.5} \right]$ мкс и ${{\sigma }_{с}} = 5.2$ ГПа. Рис. 1 демонстрирует, что для этих кривых также наблюдается хорошее соответствие с экспериментальными данными, и при этом не требуется никаких дополнительных поправок.

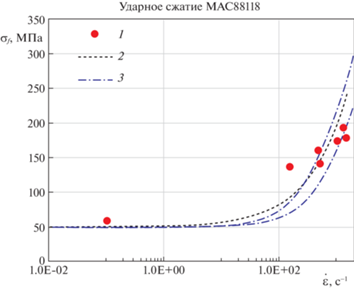
Дополнительно было проведено сравнение рассматриваемых подходов на примере испытаний по ударному сжатию метеоритного камня MAC88118 [15]. Результаты расчетов представлены на рис. 2. Кривая 2 соответствует нормировочному соотношению, вычисленному для параметров ${{\dot {\varepsilon }}_{0}} = 200.1{\text{/с}}$ и ${{\sigma }_{0}} = 50$ МПа, а кривые 3 построены согласно критерию инкубационного времени при $\tau \in \left[ {82.5;\;124.4} \right]$ мкс и ${{\sigma }_{с}} = 50$ МПа. Можно отметить, что для камня MAC88118 оба подхода позволяют получить хорошее совпадение расчетных кривых с экспериментальными данными.

Заключение. Проведенное сравнение двух теоретических подходов к описанию прочности материалов при динамическом нагружении показало, что скоростная зависимость может быть качественно описана с помощью и того и другого метода. Однако феноменологическая основа структурно-временного подхода дает ему несомненные преимущества. Введение характерного времени $\tau $, как параметра прочности материала, и самого принципа развития процесса разрушения в условиях высокоскоростного нагружения позволяет рассчитать скоростную зависимость прочности для любого материала. В то время как, нормировочное соотношение не всегда предоставляет хорошее количественное совпадение с экспериментальными результатами и требует ничем необоснованных исправлений, что наблюдалось для керамики SiC-N. Соотношение (2.4) связывающее временные параметры двух подходов, показывает, что в струтурно-временном подходе нормировка скорости деформации формально происходит неравномерно, что и позволяет достигать хорошего количественного соответствия с экспериментом безо всяких поправок. При этом совпадение нормирующего значения скорости деформации при нагружении с этой же скоростью, соотношение (2.5), позволяет сделать вывод о неплохом качественном совпадении рассматриваемых методов в некоторых случаях.

Работа выполнена при поддержке РФФИ (проект 20-01-00291). Разделы 2, 3 были выполнены Г.А. Волковым при поддержке Российского научного фонда (РНФ № 20-79-10078).