Программирование, 2019, № 1, стр. 52-58

1. ВВЕДЕНИЕ

Развитие средств R-функционального моделирования (RFM) для аналитического построения сложных геометрических моделей [1–4], а также появление метода функционально-воксельного моделирования таких моделей на компьютере [5–10] ставит перед разработчиками средств компьютерного проектирования новые задачи, приводящие процесс описания сложных функциональных зависимостей к традиционным способам конструирования.

Описанный функцией на выбранной области геометрический объект, где нулевым значением функции является его граница, представляет собой максимально полную и точную геометрическую модель на локальном уровне ее представления.

Метод (RFM), достаточно широко представленный в монографии К.В. Максименко-Шейко [11], получил свое развитие в вопросах описания сложных геометрических моделей и описывает конструктивные средства теоретико-множественных операций над функциями-предикатами:

где ${{\varpi }_{1}} = f({{x}_{n}}),$ ${{\varpi }_{2}} = g({{x}_{n}}).$

Однако метод RFM является средством математического описания объекта и требует приличной математической подготовки для применения в инженерных задачах. К тому же компьютерный расчет значений в точках области аналитических объектов RFM напрямую зависит от сложности вычисляемых выражений и требует значительных ресурсов для хранения и обработки такой информации. Попытки аппроксимации таких моделей полигонами сводят к минимуму существующие преимущества аналитической модели перед традиционными компьютерными представлениями геометрического объекта.

Метод функционально-воксельного моделирования (ФВМ), описанный в монографии А.В. Толока [12, 13], позволяет организовать компьютерное представление области функции соразмерными воксельными образами на основе разложения функции на локальные геометрические характеристики в каждой точке воксельного пространства. На рисунке 1 демонстрируется функционально-воксельная модель для тригонометрической функции вида

Такой подход обеспечивает приведение сложной функциональной зависимости, описывающей геометрический объект к однородной локальной функции линейного типа для каждой точки на рассматриваемой области существования этого объекта. При этом функционально-воксельное представление области функции значительно упрощает дальнейшую компьютерную обработку применительно к задачам компьютерного геометрического моделирования с сохранением преимуществ полноты представления геометрии объекта.

Следующим шагом в развитии средств автоматизированного проектирования на основе описания областью функций является разработка конструкторских инструментов, позволяющих традиционно просто проектировать сложные геометрические объекты. Одним из основных конструкторских инструментов проектирования является моделирование кривых и поверхностей, заданных управляющими точками [14]. Далее предлагается рассмотреть основные принципы построения функциональной области для кривой Безье и реализации ее функционально-воксельной модели на некоторой выделяемой области.

2. ОПИСАНИЕ ФУНКЦИОНАЛЬНОЙ ОБЛАСТИ НА ОСНОВЕ МНОГОЧЛЕНА БЕРНШТЕЙНА

Кривая Бернштейна (больше известная как кривая Безье) строится на основе применения полиномов С.Н. Берштейна [15]:

где $\left( \begin{gathered} n \\ i \\ \end{gathered} \right) = \frac{{n!}}{{i!(n - i)!}}$ – число сочетаний из $n$ по $i,$ $n$ – степень полинома, i – порядковый номер опорной вершины.

Квадратичная кривая $(n = 2)$ принимает следующее описание с применением трех опорных точек $({{P}_{0}},{{P}_{1}},{{P}_{2}})$:

Параметр $t$ в таком случае выражается через координаты опорных точек t = = $\frac{{{{P}_{0}}\, - \,{{P}_{1}}\, \pm \,\sqrt {({{P}_{0}}\, - \,2{{P}_{1}}\, + \,{{P}_{2}})} B\, + \,P_{1}^{2}\, - \,{{P}_{0}}{{P}_{2}}}}{{{{P}_{0}} - 2{{P}_{1}} + {{P}_{2}}}},$ при P₀ – 2P₁ + + ${{P}_{2}} \ne 0;$

$t = \frac{{B - {{P}_{0}}}}{{2({{P}_{1}} - {{P}_{0}})}},$ при ${{P}_{0}} - 2{{P}_{1}} + {{P}_{2}} = 0$ и ${{P}_{1}} \ne {{P}_{0}};$

$t = \sqrt {\frac{{B - {{P}_{0}}}}{{{{P}_{2}} - {{P}_{1}}}}} ,$ при ${{P}_{0}} = {{P}_{1}} \ne {{P}_{2}},$ $B$ – текущая точка кривой.

Чтобы построить область функции $z = f(x,y)$ для представленной квадратичной кривой достаточно описать, например, выражение:

при условии, что: ${{x}_{0}} - 2{{x}_{1}} + {{x}_{2}} \ne 0.$

При выполнении поставленного условия получим квадратично гладкую поверхность $z = f(x,y),$ ограниченную заданной областью, где $f(x,y) = 0$ определяет кривую Безье, выражаемую уравнением $y = g(x).$

Для построения области $z = f(x,y)$ воспользуемся системой РАНОК 2D, используемой для построения плоской функционально-воксельной модели [5]. Система имеет встроенный формульный интерпретатор и осуществляет линейную аппроксимацию на области определения функции для получения образов функционально-воксельной модели. При этом существует возможность выделения цветом положительной области функции, а также управления точностью аппроксимации габаритами выводимого графического образа. В целом система RANOK 2D многофункциональна и применяется для исследования возможностей применения функционально-воксельных моделей в различных расчетных приложениях.

На языке интерпретатора системы РАНОК 2D получим следующий вид описания функции:

RECTANGLE(0,0,1,1) // область определения функции

RECTBMP(400,400) // область графического вывода изображения

ARGUMENT x,y // аргументы области определения функции

CONSTANT $X0 = 0.$ // задание координат опорных точек

CONSTANT $Y0 = 0.$

CONSTANT $X1 = 0.7$

CONSTANT $Y1 = 1.$

CONSTANT $X2 = 1.$

CONSTANT $Y2 = 0.$

// Расчет параметра $t$, выраженный через аргумент $x$ и опорные точки

FUNCTION t = (X0 – X1 + ((X0 – 2*X1 + X2)*x + + X1^2 – X0*X2)^0.5)/(X0 – 2*X1 + X2)

// Расчет области значений функции

FUNCTION z = y – (1 – t)^2*X0 + 2*t*(1 – t)*X1 + + t^2*X2

RETURN z

Результат построения функции z по заданным в примере опорным точкам $({{x}_{0}} = 0,$ ${{y}_{0}} = 0,$ ${{x}_{1}}$ = = 0.7, ${{y}_{1}} = 1,$ ${{x}_{2}} = 1,$ ${{y}_{2}} = 0)$ на области $x \in [0,1]$ $y \in [0,1]$ представлен на рисунке 2. Плавное изменение градации серого тона на всей области изображения говорит о гладкости полученной поверхности z. Более темная зона закраски (в цветном варианте синяя) выделяет положительную область значений функции z, демонстрируя изгиб кривой Безье по своей границе, где значение z = 0. Прямыми линиями соединены опорные точки кривой Безье.

Такой способ построения области функции возможен, но требует сложных вычислений для параметра t. Действительно, если квадратичная кривая предусматривает подкорневые выражения при вычислении формулы (1), то кубическая кривая на порядок увеличит степень подкорневого выражения и так далее.

3. ПОСТРОЕНИЕ КРИВОЙ СОЧЕТАНИЕМ ЛИНЕЙНЫХ МНОГОЧЛЕНОВ БЕРНШТЕЙНА

Рассмотрим алгоритм построения той же кривой Безье, на который обратил в свое время внимание Поль де Кастельджо [13]. Он интересен тем, что позволяет конструировать из простых линейных многочленов Бернштейна кривую любого порядка. Например, квадратичная кривая моделируется на основе сочетания двух линейных многочленов:

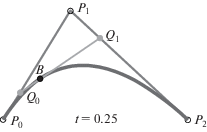
Геометрический смысл такого сочетания демонстрируется на рисунке 3 [13].

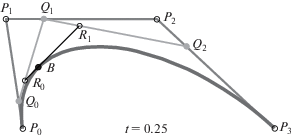
В свою очередь кубическая кривая строится по тому же принципу с нарастанием элементов (рис. 4)

что говорит о конструктивности алгоритма и применимости его в автоматизации.

Построим алгоритм определения области функции z на основе сочетания линейных многочленов Бернштейна.

Из построения квадратичной кривой (рис. 3) видно, что прямая $({{Q}_{0}}{{Q}_{1}})$ является касательной к кривой Безье при текущем параметре t.

Выразим параметр $t$ через аргумент x на промежутке $[{{x}_{0}},{{x}_{2}}]$

Тогда построение квадратичной кривой Безье по трем заданным точкам ${{P}_{0}},{{P}_{1}},{{P}_{2}}$ можно описать как

Доказательство адекватности такого алгоритма приводится на рисунке 5, где дополненные построения наглядно демонстрируют пропорциональное соответствие аргумента $x$ для точки $B$ на прямой ${{Q}_{0}}{{Q}_{1}}$ с параметром $t.$

Остается рассмотреть общий случай построения такой кривой с учетом поставленного условия.

Утверждение. Всегда можно определить такой поворот системы координат, чтобы для рассматриваемых трех точек ${{P}_{0}},{{P}_{1}},{{P}_{2}}$ выполнялось условие ${{x}_{1}} - {{x}_{0}} = {{x}_{2}} - {{x}_{1}}.$

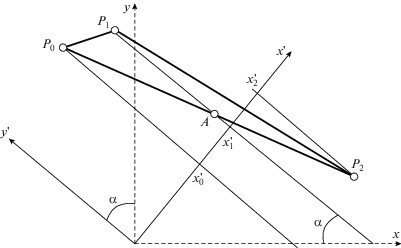
Доказательство. В пространстве $xOy$ рассмотрим треугольник, образуемый тремя точками P₀, ${{P}_{1}},{{P}_{2}}.$ Разделив отрезок $[{{P}_{0}}{{P}_{2}}]$ пополам получим точку A, доопределяющую прямую $A{{P}_{1}},$ направление которой должно совпасть с направлением оси $Oy{\text{'}}$ (рис. 6). В таком случае прямая $(A{{P}_{1}})$ делит также отрезок координатной оси $[x_{0}^{'}x_{2}^{'}]$ пополам, выполняя условие $x_{1}^{'} - x_{0}^{'} = x_{2}^{'} - x_{1}^{'}$. Что и требовалось доказать.

Исходя из утверждения, рассмотрим описание алгоритма в общем случае построения кривой Безье по трем точкам:

1 шаг: Определение координат для точки A на отрезке $[{{P}_{0}}{{P}_{2}}]$

2 шаг: Определение параметров поворота системы координат:

3 шаг: Поворот системы координат на угол $\alpha $ со сдвигом в точку A:

4 шаг: Построение сегмента кривой Безье:

На рисунке 7 демонстрируются примеры построения области функции, описывающей кривую Безье в нулевых значениях z. Более темной областью (в цветном варианте синим) выделена положительная зона.

Такой алгоритм вполне реализуем для построения кривых более высокого порядка. Для примера рассмотрим построение поверхности функции $z = f(x,y)$ для кубической кривой Безье, задаваемой четырьмя точками на основе сочетания линейных многочленов Бернштейна.

Допустим, что заданы четыре точки ${{P}_{0}},{{P}_{1}},{{P}_{2}},{{P}_{3}}$ в пространстве $xOy.$ Суть выполнения задачи сводится к последовательному приведению алгоритма к уже рассмотренному для точек ${{Q}_{0}},{{Q}_{1}}$ (рис. 3).

На рисунке 5 видно, что алгоритм применим при каждом определении пар точек ${{Q}_{0}},{{Q}_{1}}$ и ${{Q}_{1}},{{Q}_{2}}$ при рассмотрении соответственно тройки точек ${{P}_{0}},{{P}_{1}},{{P}_{2}}$ и ${{P}_{1}},{{P}_{2}},{{P}_{3}},$ а затем по тому же принципу определяются точки ${{R}_{0}},{{R}_{1}}$ через тройку точек Q₀, ${{Q}_{1}},{{Q}_{2}}.$ Функция $z = f(x,y)$ будет выражаться как

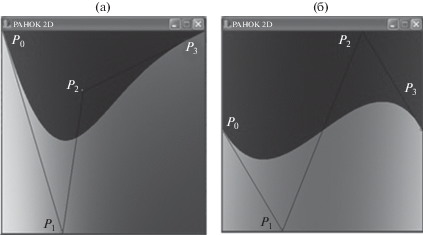
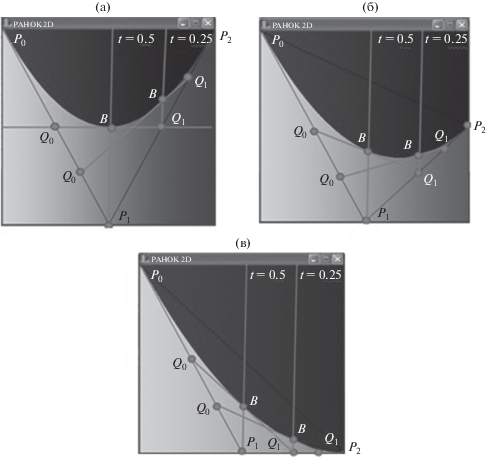
На рисунке 8 демонстрируются некоторые варианты кубической кривой Безье, построенной предложенным подходом.

4. ЗАКЛЮЧЕНИЕ

Приведенный алгоритм позволяет моделировать кривую Безье в виде области криволинейной поверхности аналитической функции $z = f({{x}_{n}})$. Он обеспечивает применение традиционных способов конструирования кривых по опорным точкам в комплексе средств моделирования аналитических объектов, которые предназначены для дальнейшего использования R-функциональном моделировании (RFM) и построении функционально-воксельных моделей (ФВМ) без привлечения сложных описаний аналитическими выражениями.