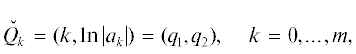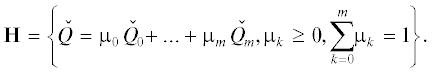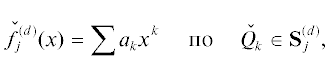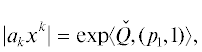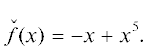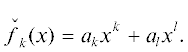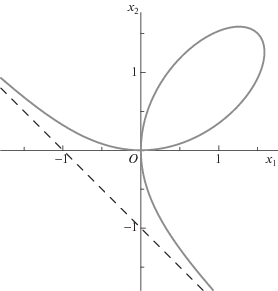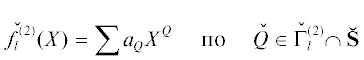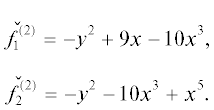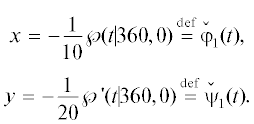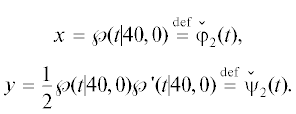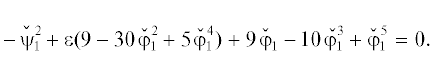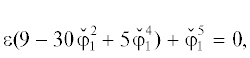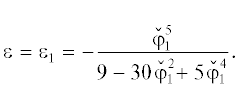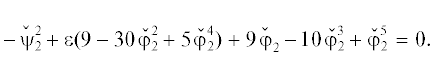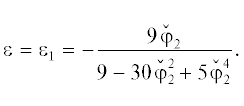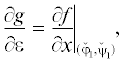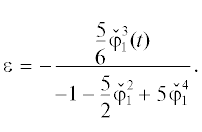Программирование, 2019, № 1, стр. 59-72
Алгоритмы решения одного алгебраического уравнения
А. Д. Брюно *
Институт прикладной математики им. М.В. Келдыша
125047 Москва, Миусская пл., 4, Россия
* E-mail: abruno@keldysh.ru
Поступила в редакцию 02.09.2018
После доработки 02.09.2018
Принята к публикации 12.09.2018
Аннотация
Для нахождения глобальных приближенных решений алгебраического уравнения с n неизвестными при n = 1 предлагается ломаная Адамара, а при n = 2 – многогранник Адамара. Найденные решения переводятся в координатное подпространство: для n = 1 – сдвигом, а для n = 2 – заменой координат, использующей униформизацию кривой. Затем излагаются алгоритмы локального решения алгебраического уравнения вблизи особой (критической) точки для n = 2 и n = 3 для получения асимптотических разложений одномерных и двумерных ветвей. С помощью многоугольника Ньютона (при n = 2), многогранника Ньютона (при n = 3) и степенных преобразований эта задача сводится к ситуациям, аналогичным теореме о неявной функции. В частности, при локальном анализе решений одного уравнения от трех неизвестных приходим к задаче об униформизации плоской алгебраической кривой и преобразовании ее в координатную ось. После этого вблизи этой оси можно получить асимптотическое разложение куска изучаемой поверхности. Приведены примеры таких вычислений.
1. ВВЕДЕНИЕ
Несмотря на большой рост и усложнение математики, некоторые основные ее задачи остаются нерешенными. К таким задачам относится решение алгебраического уравнения с одним или несколькими неизвестными.
Пусть задан многочлен $f(X)$ с вещественными или комплексными коэффициентами, где X = = $({{x}_{1}}, \ldots ,{{x}_{n}})$. Требуется найти решение уравнения
для $X \in {{\mathbb{R}}^{n}}$ или ${{\mathbb{C}}^{n}}$ в виде либо функций $X = \Phi (\Xi )$ от параметров Ξ, либо набора асимптотических разложений по параметрамПри этом множество решений уравнения (1) образует алгебраическое многообразие $\mathcal{F}$ и может состоять из нескольких компонент (ветвей) разных размерностей в вещественном случае. Для каждой компоненты надо найти свое разложение (2).
Здесь опишем алгоритмы решения этой задачи и их компьютерную реализацию. Изложение проведем по возрастанию размерности n этой задачи.
КРАТКОЕ СОДЕРЖАНИЕ СТАТЬИ
Сначала напоминается алгоритм выделения значений наибольших скалярных произведений на множестве точек в ${{\mathbb{R}}^{n}}$ (§ 2). Затем излагаются алгоритмы глобального решения алгебраического уравнения для n = 1 (корни многочлена) и n = 2 (униформизация кривой) (§ 3 и 4 соответственно). Для нахождения приближенных решений при n = 1 предлагается ломаная Адамара, а при n = 2 – многогранник Адамара. Найденные решения переводятся в координатное подпространство: для n = 1 – сдвигом, а для n = 2 – заменой координат, использующей униформизацию кривой. Затем излагаются алгоритмы локального решения алгебраического уравнения вблизи особой (критической) точки для n = 2 и n = 3 (§§ 5 и 7 соответственно). Цель – получение асимптотических разложений одномерных и двумерных ветвей. С помощью многоугольника Ньютона (при n = 2), многогранника Ньютона (при n = 3) и степенных преобразований эта задача сводится к ситуациям, аналогичным теореме о неявной функции (§ 6). В частности, при локальном анализе решений одного уравнения от трех неизвестных приходим к задаче об униформизации плоской алгебраической кривой и преобразовании ее в координатную ось. После этого вблизи этой оси можно получить асимптотическое разложение куска изучаемой поверхности. Приведены примеры таких вычислений.
2. МНОГОГРАННИК И НОРМАЛЬНЫЕ КОНУСЫ
Пусть в ${{\mathbb{R}}^{n}}$ задано несколько точек 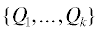 = S. Здесь Q = (q1, ..., qn). Их выпуклая оболочка
= S. Здесь Q = (q1, ..., qn). Их выпуклая оболочка
(3)
$\begin{gathered} {\mathbf{U}}_{j}^{{(d)}} = \left\{ {P:\left\langle {P,Q{\text{'}}} \right\rangle = \left\langle {P,Q{\text{''}}} \right\rangle > \left\langle {P,Q{\text{'''}}} \right\rangle \;{\text{д л я }}\;} \right. \\ Q{\text{'}},Q{\text{''}} \in \Gamma _{j}^{{(d)}},Q{\text{'''}} \in \Gamma {\backslash }\Gamma _{j}^{{(d)}}\} . \\ \end{gathered} $При этом вектор P лежит в пространстве $\mathbb{R}_{ * }^{n}$, двойственном пространству ${{\mathbb{R}}^{n}}$. Вообще, здесь мы находимся в ситуации аффинной геометрии.
Все векторы нормального конуса ${\mathbf{U}}_{j}^{{(d)}}$ ортогональны грани $\Gamma _{j}^{{(d)}}$. В силу однородности нормальных конусов достаточно рассмотреть их пересечения с двумя
гиперплоскостями (скажем, ${{p}_{n}} = \pm 1$) и отмечать на них пересечения 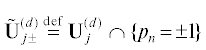 , которые назовем приведенными нормальными конусами. Имеются стандартные программы как для вычисления выпуклых оболочек, так и для вычисления
их нормальных конусов [1, 2]. В частности, они имеются в системе Maple.
, которые назовем приведенными нормальными конусами. Имеются стандартные программы как для вычисления выпуклых оболочек, так и для вычисления
их нормальных конусов [1, 2]. В частности, они имеются в системе Maple.
3. ГЛОБАЛЬНЫЙ АНАЛИЗ ДЛЯ n = 1
Для многочлена
с вещественными или комплексными коэффициентами ${{a}_{k}}$ его корни всегда выражаются в радикалах, если m ≤ 4 (формулы Кардано и Феррари – XVI век).Согласно Абелю и Галуа (1830) общее уравнение ${{f}_{m}}(x) = 0$ с $m > 4$ неразрешимо в радикалах от его коэффициентов. Для уравнения пятой степени Эрмит, Кронекер и Бриоски (1858) показали, что его корни могут быть выражены через тета-функции Якоби [3]. При $m > 6$ известно, в каких сложных функциях от коэффициентов ${{a}_{k}}$ оно разрешается [4], но явных формул, пригодных для вычисления, пока нет. Имеются различные способы определения числа вещественных корней на заданном интервале $x \in [a,b]$ и их приближенных значений.
Опишем новый способ вычисления приближенных значений корней многочлена (4). Для этого на вещественную плоскость ${{q}_{1}},{{q}_{2}}$ наносятся точки
образующие суперноситель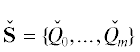 , и строится их выпуклая оболочка
, и строится их выпуклая оболочка
Граница $\partial {\mathbf{H}}$ является ломаной линией. Каждому ребру $\Gamma _{j}^{{(1)}}$ и вершине $\Gamma _{j}^{{(0)}}$ этой границы $\partial {\mathbf{H}}$ соответствует граничное подмножество ${\mathbf{S}}_{j}^{{(d)}}$ точек 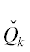 , лежащих на $\Gamma _{j}^{{(d)}}$, и укороченный многочлен
, лежащих на $\Gamma _{j}^{{(d)}}$, и укороченный многочлен
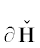 границы $\partial {\mathbf{H}}$ – это ломанная Адамара (J. Hadamard, 1893) [5], [6, гл. IV, п. 2.1]. Нормальные конусы её рёбер имеют p2 > 0. Для таких рёбер в укороченный многочлен входят те и только те слагаемые ${{a}_{k}}{{x}^{k}}$, у которых модуль ${\text{|}}{{a}_{k}}{{x}^{k}}{\text{|}}$ наибольший при фиксированном ${\text{|}}x{\text{|}}:ln{\text{|}}x{\text{|}} = {{p}_{1}}$, ибо тогда
а экспонента – монотонная функция.
границы $\partial {\mathbf{H}}$ – это ломанная Адамара (J. Hadamard, 1893) [5], [6, гл. IV, п. 2.1]. Нормальные конусы её рёбер имеют p2 > 0. Для таких рёбер в укороченный многочлен входят те и только те слагаемые ${{a}_{k}}{{x}^{k}}$, у которых модуль ${\text{|}}{{a}_{k}}{{x}^{k}}{\text{|}}$ наибольший при фиксированном ${\text{|}}x{\text{|}}:ln{\text{|}}x{\text{|}} = {{p}_{1}}$, ибо тогда
а экспонента – монотонная функция.
Пример 1. Рассмотрим многочлен
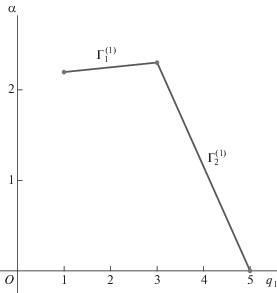
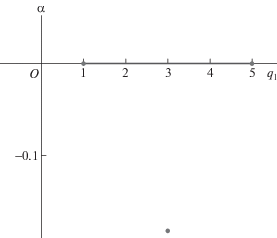
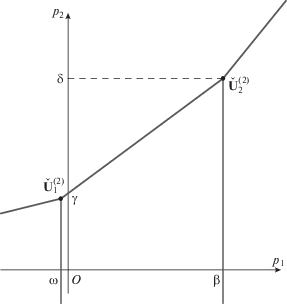
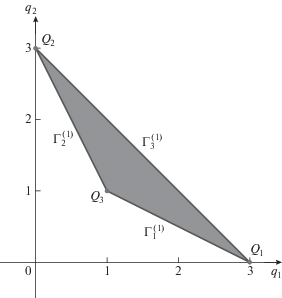
с корнями $x_{k}^{0} = 0, \pm 1, \pm 3$. Его ломаная Адамара натянута на три вершины $(1,ln9)$, $(3,ln10)$, (5, 0) и показана на рис. 1. Она имеет два ребра $\Gamma _{1}^{{(1)}}$ и $\Gamma _{2}^{{(2)}}$.Их приведенные нормальные конусы ω = = ${\mathbf{\tilde {U}}}_{{1 + }}^{{(1)}}\, = \,{\text{ln}}\sqrt {0.9} \approx $ –0.05268 и β = ${\mathbf{\tilde {U}}}_{{2 + }}^{{(1)}}\, = \,{\text{ln}}\sqrt {10} $ ≈ ≈ 1.15129 показаны на рис. 2.
Ребрам $\Gamma _{1}^{{(1)}}$ и $\Gamma _{2}^{{(2)}}$ соответствуют укороченные многочлены 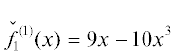 и
и 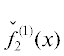 = –10x3 + + 9x5, корни которых x1 = 0, x2, 3 = $ \pm \sqrt {0.9} $ ≈ ≈ ±0.948683 и x4, 5 = $ \pm \sqrt {10} \approx \pm 3.162278$ дают приближенные значения ненулевых корней полного многочлена $f(x)$. Для их уточнения можно использовать метод Ньютона, т.е. искать разложение корня
${{x}^{0}} = x + {{\varepsilon }_{1}} + {{\varepsilon }_{2}} + \ldots $ Для первых добавок ${{\varepsilon }_{1}}$ из уравнения $f(x) + {{\varepsilon }_{1}}f{\kern 1pt} {\text{'}}(x) = 0$ получаем значение ${{\varepsilon }_{1}} = - f(x){\text{/}}f{\kern 1pt} {\text{'}}(x)$. Значения добавок ${{\varepsilon }_{1}}$ в ${{x}_{k}}$, $k = 2, \ldots ,5$, и уточненных значений ${{x}_{k}} + {{\varepsilon }_{1}}$ показаны в табл. 1.
= –10x3 + + 9x5, корни которых x1 = 0, x2, 3 = $ \pm \sqrt {0.9} $ ≈ ≈ ±0.948683 и x4, 5 = $ \pm \sqrt {10} \approx \pm 3.162278$ дают приближенные значения ненулевых корней полного многочлена $f(x)$. Для их уточнения можно использовать метод Ньютона, т.е. искать разложение корня
${{x}^{0}} = x + {{\varepsilon }_{1}} + {{\varepsilon }_{2}} + \ldots $ Для первых добавок ${{\varepsilon }_{1}}$ из уравнения $f(x) + {{\varepsilon }_{1}}f{\kern 1pt} {\text{'}}(x) = 0$ получаем значение ${{\varepsilon }_{1}} = - f(x){\text{/}}f{\kern 1pt} {\text{'}}(x)$. Значения добавок ${{\varepsilon }_{1}}$ в ${{x}_{k}}$, $k = 2, \ldots ,5$, и уточненных значений ${{x}_{k}} + {{\varepsilon }_{1}}$ показаны в табл. 1.
Таблица 1.
Поправки к корням
| k | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| xk | 0.948683 | −0.948683 | 3.162278 | −3.162278 |
| ε1 | 0.055085 | −0.055085 | −0.136175 | 0.136175 |
| xk + ε1 | 1.003768 | −1.003768 | 3.026103 | −3.026103 |
| $x_{k}^{0}$ | 1 | −1 | 3 | −3 |
Пример 2. Рассмотрим многочлен
(9)
$f(x) = - x - \frac{5}{6}{{x}^{3}} + {{x}^{5}} = x\left( {1 + \frac{3}{2}{{x}^{2}}} \right)\left( {1 - \frac{2}{3}{{x}^{2}}} \right).$Его точные корни суть
(10)
$\begin{gathered} {{x}^{0}} = 0,\quad \pm i\sqrt {2{\text{/}}3} \approx \pm 0.81648i, \\ \pm \sqrt {3{\text{/}}2} \approx \pm 1.2247. \\ \end{gathered} $Его суперноситель 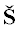 и многоугольник Адамара
и многоугольник Адамара 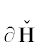 показаны на рис. 3. Он натянут на 2 вершины (1, 0), (5, 0).
показаны на рис. 3. Он натянут на 2 вершины (1, 0), (5, 0).
Он имеет одно ребро $1 \leqslant {{q}_{1}} = k \leqslant 5$, q2 = α = ln|ak| = 0 с приведенным нормальным конусом – точкой ${{p}_{1}} = p_{1}^{0}$ = 0. Ему соответствует укороченный многочлен
Его ненулевые корни суть ${{x}_{{2,3}}} = \pm i,{{x}_{{4,5}}} = \pm 1$. Для них всех $ln{\text{|}}{{x}_{k}}{\text{|}} = 0 = p_{1}^{0} = \omega $. Они дают приближенные значения корней (10) полного многочлена (9). Поправки ${{\varepsilon }_{1}} = - f({{x}_{k}}){\text{/}}f{\kern 1pt} {\text{'}}({{x}_{k}})$ метода Ньютона к ним приведены в табл. 2.
Таблица 2.
Поправки к корням
| k | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| xk | +i | −i | +1 | −1 |
| ε1 | −0.12821i | 0.12821i | 0.55556 | −0.55556 |
| xk + ε1 | 0.871795i | −0.871795i | 1.555556 | −1.555556 |
| $x_{k}^{0}$ | 0.816497i | −0.816497i | 1.224745 | −1.224745 |
Пример 3. С помощью ломанной Адамара найдем приближенные значения корней многочлена
(12)
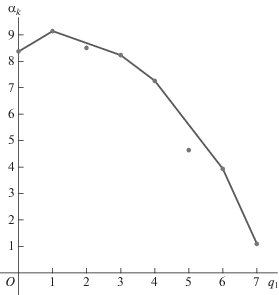
$\begin{gathered} f(x)\mathop = \limits^{{\text{def}}} \, - {\kern 1pt} 4320 - 9336x - 4972{{x}^{2}} - 3754{{x}^{3}} - \\ \, - 1426{{x}^{4}} + 104{{x}^{5}} + 51{{x}^{6}} + 3{{x}^{7}}. \\ \end{gathered} $Значения его коэффициентов ak приведены во второй строке таблицы 3. В третьей строке даны значения ${{\alpha }_{k}} = ln{\text{|}}{{a}_{k}}{\text{|}}$. На рис. 4 показаны точки 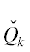 = = (k, αk) и их огибающая – ломаная Адамара
= = (k, αk) и их огибающая – ломаная Адамара 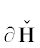 .
.
Таблица 3.
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| ak | −4320 | −9336 | −4972 | −3754 | −1426 | 104 | 51 | 3 |
| αk | 8.371 | 9.142 | 8.511 | 8.230 | 7.262 | 4.644 | 3.932 | 1.098 |
| xk | −.4627 | 1.577i | −1.577i | −2.633 | 5.288 | −5.288 | −17 | |
| 2εk | −.1157 | .0439− | .0439+ | .36 | −.032 | 1.82 | 1.78 | |
| −.0633i | +.0633i | |||||||
| 2${{\tilde {x}}_{k}}$ | −10.5+ | −10.5− | ||||||
| +2.9i | −2.9i | |||||||
| 2${{\tilde {\varepsilon }}_{k}}$ | 0.578− | 0.578+ | ||||||
| −0.762i | +0.762i | |||||||
| xk + εk | −.5784 | .0439+ | .0439− | −2.2725 | 5.2558 | −9.922+ | −9.922− | |
| +1.514i | −1.514i | +2.138i | −2.138i | |||||
| 2*$x_{k}^{0}$ | −.5819 | .0519+ | .0519− | −2.0984 | 5.2551 | −9.8393+ | −9.8393− | |
| +1.5148i | −1.5148i | +.931i | −.931i |
Для всех k, кроме k = 2 и k = 5, точки 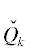 = (k, αk) являются вершинами ломанной
= (k, αk) являются вершинами ломанной 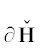 . Паре соседних вершин $(k,{{\alpha }_{k}})$ и $(l,{{\alpha }_{l}})$, $k < l$, соответствует укороченный многочлен
. Паре соседних вершин $(k,{{\alpha }_{k}})$ и $(l,{{\alpha }_{l}})$, $k < l$, соответствует укороченный многочлен
Его ненулевые корни обозначим ${{x}_{{k + 1}}}$, если l = k + 1, или ${{x}_{{k + 1}}},{{x}_{{k + 2}}}$, если $l = k + 2$. Их значения приведены в четвертой строке таблицы 3. В каждой из этих точек вычислены значения $f({{x}_{k}})$ и $f{\kern 1pt} {\text{'}}({{x}_{k}})$.
Вычисленные по методу Ньютона поправки ${{\varepsilon }_{k}} = - f({{x}_{k}}){\text{/}}f{\kern 1pt} {\text{'}}({{x}_{k}})$ к потенциальным приближенным корням ${{x}_{k}}$ приведены в пятой строке таблицы 3. Для k < 6 модули поправок ${\text{|}}{{\varepsilon }_{k}}{\text{|}} < 0.5$, а для k = 6 и 7 эти модули больше 1.5. Следовательно, значения ${{x}_{6}}$ и ${{x}_{7}}$ требуют уточнения. Они получены из укороченных многочленов, содержащих ${{a}_{4}}{{x}^{4}}$, ${{a}_{6}}{{x}^{6}}$ и ${{a}_{7}}{{x}^{7}}$. Поэтому в качестве приближенного к $f(x)$ рассмотрим многочлен
т.е. многочлен третьей степениДля него значение ${{x}_{5}} \approx 5.2$ является приближенным корнем. Более точным является значение x = 4. Деля многочлен h на $x - 4$, получаем многочлен второй степени
и –2 в остатке. Корни ${{\tilde {x}}_{6}}$ и ${{\tilde {x}}_{7}}$ многочлена (13) суть $ - 10.5\, \pm \,2.9i$. Они приведены в шестой строке таблицы 3. Соответствующие поправки ${{\tilde {\varepsilon }}_{k}}\, = \, - {\kern 1pt} f({{\tilde {x}}_{k}}){\text{/}}f{\kern 1pt} {\text{'}}({{\tilde {x}}_{k}})$ приведены в седьмой строке, при этом оба ${\text{|}}{{\tilde {\varepsilon }}_{k}}{\text{|}} < 1$. В восьмой строке приведены уточненные значения ${{x}_{k}} + {{\varepsilon }_{k}}$ для k < 6 и ${{\tilde {x}}_{k}} + {{\tilde {\varepsilon }}_{k}}$ для $k = 6,7$. Наконец, в девятой строке приведены точные значения $x_{k}^{0}$ корней. Полученные приближенные значения корней многочлена $f(x)$ пригодны для уточнения по методу Ньютона.В целом метод ломанной Адамара состоит в том, что исходный многочлен заменяется набором более простых многочленов, корни которых вычисляются просто и дают такие приближения корней исходного многочлена, которые достаточно хороши для численного уточнения пометоду Ньютона.
4. ГЛОБАЛЬНЫЙ АНАЛИЗ ДЛЯ n = 2
Предположим сначала, что многочлен f(X) = = $f({{x}_{1}},{{x}_{2}})$ не распадается на множители. Тогда его корневое множество $\mathcal{F}$ – это плоская алгебраическая кривая. Для комплексных значений ${{x}_{1}},{{x}_{2}}$ кривая $\mathcal{F}$ – это двумерная поверхность в четырехмерном пространстве ${\text{Re}}{{x}_{1}},{\text{Im}}{{x}_{1}},{\text{Re}}{{x}_{2}},{\text{Im}}{{x}_{2}}$. Если к этому пространству добавить бесконечно удаленные точки, то кривая $\mathcal{F}$ станет топологически эквивалентна сфере с $\mathfrak{g}$ ручками, $\mathfrak{g} \geqslant 0$ (Риман, 1840).
• Если $\mathfrak{g} = 0$, то это обычная сфера (поверхность колобка).
• Если $\mathfrak{g} = 1$, то это поверхность тора (бублика).
• Если $\mathfrak{g} = 2$, то это поверхность кренделя и т.д.
Итак, алгебраическая кривая $\mathcal{F}$ имеет целочисленный топологический инвариант – род $\mathfrak{g} \geqslant 0$, $\mathfrak{g} \in \mathbb{Z}$. Рассмотрим ситуации для различных значений $\mathfrak{g}$.
4.1. Случай $\mathfrak{g} = 0$
Тогда кривая $\mathcal{F}$ бирационально эквивалентна прямой, т.е. существует параметризация
(14)
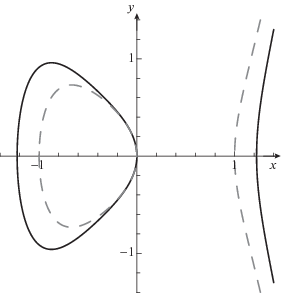
${{x}_{1}} = {{\varphi }_{1}}(t),\quad {{x}_{2}} = {{\varphi }_{2}}(t),\quad t = \eta ({{x}_{1}},{{x}_{2}}),$Пример 4. Для листа Декарта
(15)
$f({{x}_{1}},{{x}_{2}})\mathop = \limits^{{\text{def}}} x_{1}^{3} + x_{2}^{3} - 3{{x}_{1}}{{x}_{2}} = 0$(16)
${{x}_{1}} = \frac{{3t}}{{1 + {{t}^{3}}}},\quad {{x}_{2}} = \frac{{3{{t}^{2}}}}{{1 + {{t}^{3}}}},\quad t = {{x}_{2}}{\text{/}}{{x}_{1}}.$На вещественной плоскости ${{x}_{1}},{{x}_{2}}$ лист Декарта показан на рис. 5.
4.2. Случай $\mathfrak{g} = 1$ [7]
Тогда кривая $f(X) = 0$ называется эллиптической. Посредством бирациональной замены ${{x}_{1}},{{x}_{2}} \leftrightarrow {{y}_{1}},{{y}_{2}}$ она приводится к нормальной форме Вейерштрасса
где ${{g}_{2}}$ и ${{g}_{3}}$ – постоянные (модули).Униформизацию нормальной формы кривой дает функция Вейерштрасса $\wp (t)$, которая является решением дифференциального уравнения
(18)
$\mathop {\left[ {\wp {\text{'}}(t)} \right]}\nolimits^2 = 4{{\wp }^{3}}(t) - {{g}_{2}}\wp (t) - {{g}_{3}},$(19)
$\wp (t) = \frac{1}{{{{t}^{2}}}} + \sum\limits_{k = 1}^\infty {{b}_{k}}{{t}^{{2k}}},\quad {{b}_{k}} = {\text{const}}.$Итак, получаем униформизацию
4.3. Гиперэллиптический случай с $\mathfrak{g} > 1$ [7, гл. 13]
В этом случае с помощью бирационального преобразования ${{x}_{1}},{{x}_{2}} \leftrightarrow {{y}_{1}},{{y}_{2}}$ уравнение кривой приводится к нормальной форме
где $R({{y}_{1}})$ – многочлен степени $2\mathfrak{g} + 1$ или $2\mathfrak{g} + 2$ без кратных корней. Решения этого уравнения можно записать в виде ${{y}_{1}} = \varphi (t)$, ${{y}_{2}} = \psi (t)$, где автоморфные функции $\varphi (t)$ и $\psi (t)$ определенным образом выражаются через тета-функции. Если $\mathfrak{g} = 2$, то кривая всегда является гиперэллиптической (см. примеры в [8–14]), но при $\mathfrak{g} > 2$ существуют не гиперэллиптические кривые [15].4.4. Суперэллиптический случай с $\mathfrak{g} > 2$
В этом случае бирациональной заменой координат уравнение приводится к нормальной форме
где натуральное $m \geqslant 3$, а $R({{y}_{1}})$ – многочлен. Здесь также существует униформизация через тэта-функции. Но как ее находить, пока неясно [16, 17].По-видимому, существуют кривые, которые не являются суперэллиптическими. Но для них пока нет нормальной формы.
Пример 5. Рассмотрим кривую Ферма
Ее род $\mathfrak{g} = n(n - 3{\text{)/}}2 + 1$. Эти значения приведены в таблице 4.
Только при n = 2 эта кривая рациональна. Помимо случая n = 3, ее униформизации также известны при n = 4 и 8 [10].
4.5. Общий случай
Для произвольной кривой $f({{x}_{1}},{{x}_{2}}) = 0$ известна только теорема о существовании ее глобальной униформизации ${{x}_{1}} = \varphi (t)$, ${{x}_{2}} = \psi (t)$, но нет аналитического алгоритма ее вычисления. К настоящему времени при $\mathfrak{g}$ > 1 явные униформизации известны только для кривых, имеющих достаточно большую группу симметрий, т.е. бирациональных автоморфизмов [8–10]. Более того, даже для гиперэллиптических кривых такая униформизация находится преимущественно в случаях наличия дополнительных симметрий [8–12].
В [18, 19] предложен алгоритм униформизации алгебраической кривой с помощью радикалов. В частности, он позволяет найти униформизации кривых рода $\mathfrak{g} \leqslant 6$, а также некоторых специальных кривых с $\mathfrak{g}$ > 6. Например, для эллиптической кривой $y_{2}^{2} = 4y_{1}^{3} - {{g}_{2}}{{y}_{1}} - {{g}_{3}}$ униформизация в радикалах – это
Для общей кривой рода $\mathfrak{g} > 6$ униформизация в радикалах невозможна. Так же как невозможно решение в радикалах общего уравнения от одной неизвестной степени больше 4.
4.6. Имплементация
Все локальные вычисления пунктов 4.1, 4.2, 4.3 имеются в системе компьютерной алгебры Maple. С помощью пакета algcurves можно вычислить род кривой $\mathfrak{g}$. Если $\mathfrak{g}$ = 0 или 1, то можно найти соответствующую бирациональную замену координат. Если $\mathfrak{g}$ > 2, то можно выяснить, является ли кривая гиперэллиптической или нет. Для гиперэллиптической кривой можно найти бирациональное преобразование к нормальной форме, алгоритма поиска униформизации там нет. Вопросы, связанные с суперэллиптическими кривыми, в Maple не рассматриваются.
Пример 6. В статье [13] дана униформизация кривой
гдеВычисления в системе Maple показали, что род этой кривой равен 2, а ее нормальная форма есть ${{y}^{2}} = {{x}^{6}} - 3{{a}^{2}}{{x}^{4}} + 3{{a}^{4}}{{x}^{2}} - 2{{a}^{4}} + {{a}^{2}}$.
4.7. Метод многогранника Адамара
Если для кривой $\mathcal{F}:f({{x}_{1}},{{x}_{2}}) = 0$ не удалось найти параметризацию, то можно найти несколько более простых приближенных
кривых 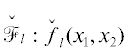 = = 0, $l = 1, \ldots ,m$, которые приближают исходную кривую в своем множестве ${{\mathcal{W}}_{l}}$ пространства ${{\mathbb{R}}^{2}}$ или ${{\mathbb{C}}^{2}}$.
= = 0, $l = 1, \ldots ,m$, которые приближают исходную кривую в своем множестве ${{\mathcal{W}}_{l}}$ пространства ${{\mathbb{R}}^{2}}$ или ${{\mathbb{C}}^{2}}$.
Может случиться, что кривая 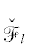 параметризуема:
параметризуема: 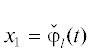 ,
, 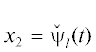 . Для исходной кривой $\mathcal{F}$ эту параметризацию можно уточнить.
. Для исходной кривой $\mathcal{F}$ эту параметризацию можно уточнить.
Пусть 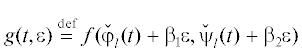 , где βi = ${\text{const}},{\text{|}}{{\beta }_{1}}{\text{|}} + \,{\text{|}}{{\beta }_{2}}{\text{|}} \ne 0$. Находим $\varepsilon $ по методу Ньютона: из уравнения
, где βi = ${\text{const}},{\text{|}}{{\beta }_{1}}{\text{|}} + \,{\text{|}}{{\beta }_{2}}{\text{|}} \ne 0$. Находим $\varepsilon $ по методу Ньютона: из уравнения 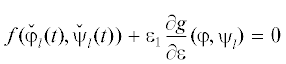 получаем ${{\varepsilon }_{1}}$. При этом все последовательные добавки ${{\varepsilon }_{1}},{{\varepsilon }_{2}}, \ldots $ являются рациональными функциями от
получаем ${{\varepsilon }_{1}}$. При этом все последовательные добавки ${{\varepsilon }_{1}},{{\varepsilon }_{2}}, \ldots $ являются рациональными функциями от 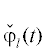 и
и 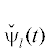 .
.
Находить эти кривые 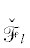 можно так. Пусть
можно так. Пусть
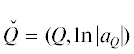 в ${{\mathbb{R}}^{3}}$. Их совокупность образует суперноситель
в ${{\mathbb{R}}^{3}}$. Их совокупность образует суперноситель 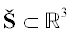 . Его выпуклая оболочка – H. Верхняя часть
. Его выпуклая оболочка – H. Верхняя часть 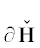 его границы $\partial {\mathbf{H}}$ – это многогранник Адамара. Каждой его грани
его границы $\partial {\mathbf{H}}$ – это многогранник Адамара. Каждой его грани 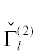 соответствует укороченный многочлен
соответствует укороченный многочлен
и p3 > 0 у её нормального конуса
Для нормальной формы суперэллиптической кривой $x_{2}^{m} = R({{x}_{1}})$ в множествах ${{\mathcal{W}}_{l}}$ ограничены только значения ${{x}_{1}}$, а значения ${{x}_{2}}$ там произвольны. Точность приближения 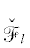 к $\mathcal{F}$ можно оценить по точности приближения корней уравнения
к $\mathcal{F}$ можно оценить по точности приближения корней уравнения 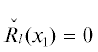 к корням уравнения $R({{x}_{1}}) = 0$.
к корням уравнения $R({{x}_{1}}) = 0$.
Пример 7 (продолжение примера 1). Рассмотрим кривую $\mathcal{F}$:
(26)
$f\mathop = \limits^{{\text{def}}} \, - {\kern 1pt} {{y}^{2}} + 9x - 10{{x}^{3}} + {{x}^{5}} = 0.$Ее род равен 2. Согласно [10] кривая (26) имеет униформизацию в тэта-функциях
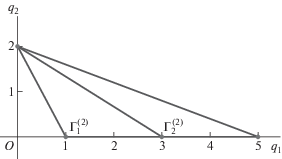
Ее многогранник Адамара 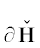 натянут на 4 вершины (0, 2, 0), $(1,0,ln9)$, $(3,0,ln10)$, (5, 0, 0) и при ${{q}_{2}} = 0$ изображен на рис. 1. Проекция многогранника
натянут на 4 вершины (0, 2, 0), $(1,0,ln9)$, $(3,0,ln10)$, (5, 0, 0) и при ${{q}_{2}} = 0$ изображен на рис. 1. Проекция многогранника 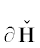 на плоскость ${{q}_{1}},{{q}_{2}}$ показана на рис. 6.
на плоскость ${{q}_{1}},{{q}_{2}}$ показана на рис. 6.
Из него видно, что многогранник H имеет точно две верхние двумерные грани $\Gamma _{1}^{{(2)}}$ и $\Gamma _{2}^{{(2)}}$. Им соответствуют два укороченных многочлена
Их приведенные нормальные конусы являются точками ${\mathbf{\tilde {U}}}_{{1 + }}^{{(2)}} = (\omega ,\gamma )$ и ${\mathbf{\tilde {U}}}_{{2 + }}^{{(2)}} = (\beta ,\delta )$, где $\omega \, = \,{\text{ln}}\sqrt {0.9} $ ≈ ≈ –0.0568, $\gamma = (3{\text{ln}}9 - {\text{ln}}10){\text{/}}4 \approx 1.07227$, β = ${\text{ln}}\sqrt {10} $ ≈ ≈ 1.15129, $\delta = (5{\text{ln}}10{\text{)/}}4$ ≈ 2.87231, показаны на рис. 7.
Будем считать, что область ${{\mathcal{W}}_{1}}$ = {x, y : ln|x| < < $(\omega + \beta ){\text{/}}2 \approx 0.5493$, т.е. ${\text{|}}x{\text{|}} < 1.73204$, y – любое}, а ${{\mathcal{W}}_{2}}$ = ${\{ }x,y:ln{\text{|}}x{\text{|}} > (\omega + \beta ){\text{/}}2 \approx 0.5493$, т.е. ${\text{|}}x{\text{|}}$ > > 1.73204, y – любое}. Кривые 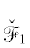 и
и 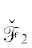 имеют род 1.
имеют род 1.
Преобразование ${{x}_{1}} = - 10x,{{y}_{1}} = - 20y$ приводит уравнение 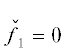 к нормальной форме Вейерштрасса
к нормальной форме Вейерштрасса
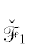 униформизируется так:
униформизируется так:
Преобразование $x = {{x}_{2}},y = {{x}_{2}}{{y}_{2}}{\text{/}}2$ приводит уравнение 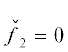 к нормальной форме Вейерштрасса
к нормальной форме Вейерштрасса
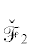 униформизируется так:
униформизируется так:
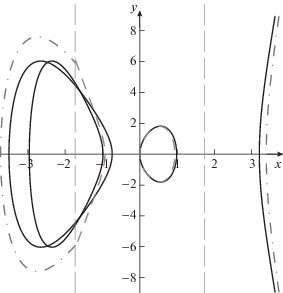
Кривые 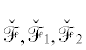 показаны на рис. 8.
показаны на рис. 8.
Рис. 8.
Кривые примера 7: $\mathcal{F}$ (сплошная), ${{\mathcal{F}}_{1}}$ (пунктир), ${{\mathcal{F}}_{2}}$ (штрих-пунктир). Кривые 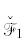 ,
, 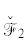 изображены только в своих областях ${{\mathcal{W}}_{1}}$, ${{\mathcal{W}}_{2}}$.
изображены только в своих областях ${{\mathcal{W}}_{1}}$, ${{\mathcal{W}}_{2}}$.
Уточним кривую (27) как приближение к кривой (26). Для этого положим 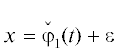 , y =
, y = 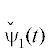 . Тогда по методу Ньютона для $\varepsilon $ получаем уравнение
. Тогда по методу Ньютона для $\varepsilon $ получаем уравнение
Из уравнения кривой 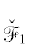 получаем, что
получаем, что
Можно вычислить и дальнейшие поправки.
Аналогично уточним кривую (28) как приближение кривой (26). Для этого положим x = = 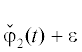 ,
, 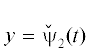 . Тогда в первом приближении по $\varepsilon $ получаем
. Тогда в первом приближении по $\varepsilon $ получаем
Но теперь 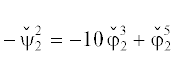 , поэтому
, поэтому
Пример 8 (продолжение примера 2). Рассмотрим кривую $\mathcal{F}$:
(29)
$f\mathop = \limits^{{\text{def}}} \, - {\kern 1pt} {{y}^{2}} - x - \frac{5}{6}{{x}^{3}} + {{x}^{5}} = 0.$Ее род равен двум и параметризация неизвестна. Ее суперноситель 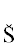 состоит из четырех точек (0, 2, 0), (1, 0, 0), $(3,0,ln(5{\text{/}}6)),(5,0,0)$. Многогранник H имеет сверху только одну грань $\Gamma _{1}^{{(2)}}$, содержащую точки $(0,2,0)$, $(1,0,0)$, $(5,0,0)$, с приведенным нормальным конусом ${\mathbf{\tilde {U}}}_{{1 + }}^{{(2)}} = (0,0)$. Ей соответствует одно укороченное уравнение
состоит из четырех точек (0, 2, 0), (1, 0, 0), $(3,0,ln(5{\text{/}}6)),(5,0,0)$. Многогранник H имеет сверху только одну грань $\Gamma _{1}^{{(2)}}$, содержащую точки $(0,2,0)$, $(1,0,0)$, $(5,0,0)$, с приведенным нормальным конусом ${\mathbf{\tilde {U}}}_{{1 + }}^{{(2)}} = (0,0)$. Ей соответствует одно укороченное уравнение
Это кривая Бернсайда, ее явная параметризация 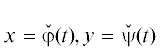 в функциях $\wp $ и $\wp {\text{'}}$ приведена в сложной формуле (3) статьи [9]. Найдем поправку $\varepsilon $ к кривой
в функциях $\wp $ и $\wp {\text{'}}$ приведена в сложной формуле (3) статьи [9]. Найдем поправку $\varepsilon $ к кривой 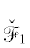 . Положим
. Положим 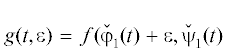 ). Тогда
). Тогда
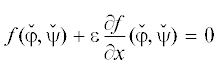 , т.е.
, т.е.
Эту процедуру можно продолжить и получить дальнейшие добавки ${{\varepsilon }_{2}},{{\varepsilon }_{3}}$, … как рациональные функции от 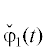 и
и 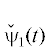 . Здесь область ${{\mathcal{W}}_{1}}$ совпадает со всем пространством.
. Здесь область ${{\mathcal{W}}_{1}}$ совпадает со всем пространством.
При этом подходе приходим к задаче параметризации кривых вида
Они могут быть любого рода (см. пример 5), но у них много симметрий, т.е. бирациональных автоморфизмов.
4.8. Преобразование кривой в координатную ось
Пусть кривая $\mathcal{F}$, заданная алгебраическим уравнением $f({{x}_{1}},{{x}_{2}}) = 0$, имеет параметризацию ${{x}_{1}} = \varphi (t)$, ${{x}_{2}} = \psi (t)$. Для того чтобы перевести кривую $\mathcal{F}$ в координатную ось, сделаем замену координат
где ${{\beta }_{1}}$ и ${{\beta }_{2}}$ – такие постоянные, что ${\text{|}}{{\beta }_{1}}{\text{|}} + \,{\text{|}}{{\beta }_{2}}{\text{|}} \ne 0$. Тогда многочлен $f({{x}_{1}},{{x}_{2}})$ переходит в функцию $h(t,z)$, которая при z = 0 тождественно равна нулю, а ее производная $\partial{ \tilde {f}}{\text{/}}\partial z\not { \equiv }0$ при z = 0.Пример 9 (продолжение примера 4). В многочлене $f({{x}_{1}},{{x}_{2}}) = x_{1}^{3} + x_{2}^{3} - 3{{x}_{1}}{{x}_{2}}$ сделаем подстановку
(31)
${{x}_{1}} = \frac{{3t}}{{1 + {{t}^{3}}}} + 3z,\quad {{x}_{2}} = \frac{{3{{t}^{2}}}}{{1 + {{t}^{3}}}}.$После умножения на общий знаменатель ${{(1 + {{t}^{3}})}^{3}}$ получим многочлен
(32)
$\tilde {f}(t,z) = {{(1 + {{t}^{3}})}^{2}}{{z}^{3}} + 3{{z}^{2}}t(1 + {{t}^{3}}) + z{{t}^{2}}(2 - {{t}^{3}}),$Эта производная обращается в ноль при $t = {{t}_{0}} = 0$ (что соответствует двойной точке ${{x}_{1}} = {{x}_{2}} = 0$, ей же соответствует $t = \infty $) и при $t = {{t}_{1}} = \sqrt[3]{2}$. В этой последней точке $\partial f{\text{/}}\partial {{x}_{1}} = 0$ на $f = 0$. Точку ${{t}_{1}}$ можно убрать, если вместо (31) сделать замену (30) с другим набором чисел ${{\beta }_{1}}$, ${{\beta }_{2}}$. Но тогда получится другая точка ${{t}_{2}} \ne 0,\infty $, где $\partial{ \tilde {f}}{\text{/}}\partial z = 0$ при z = 0.
Замечание 1. Аналогичная техника применима и при n = 3 для глобальной параметризации двумерного алгебраического многообразия, заданного одним многочленом от трех переменных. Если такая глобальная параметризация не находится, то ее можно заменить несколькими приближенными параметризациями, которые находятся с помощью верхней границы четырехмерного многогранника.
Замечание 2. Униформизация двумерных алгебраических поверхностей с помощью радикалов рассматривается в [19].
5. ЛОКАЛЬНЫЙ АНАЛИЗ ДЛЯ n = 2
Точка $X = {{X}^{0}}$, $f({{X}^{0}}) = 0$ называется простой точкой кривой $\mathcal{F}$, если в ней вектор $(\partial f{\text{/}}\partial {{x}_{1}},\partial f{\text{/}}\partial {{x}_{2}})$ не нулевой. В противном случае точка ${{X}^{0}}$ называется особой или критической. Сдвигом перенесем точку ${{X}^{0}}$ в начало координат.
5.1. Локальный анализ простой точки
Теорема 1 (Коши [22]). Если при ${{X}^{0}} = 0$ производная $\partial f{\text{/}}\partial {{x}_{2}} \ne 0$, то все решения уравнения (1) вблизи точки ${{X}^{0}} = 0$ содержатся в разложении
где ${{b}_{k}}$ – постоянные.5.2. Локальный анализ особой точки ${{X}^{0}} = 0$ [6, гл. I, пар. 2], [23], гл. II
Запишем многочлен $f(X)$ в виде
(35)
$f(X) = \sum {{{a}_{Q}}{{X}^{Q}}\quad {\text{п о }}\quad Q \geqslant 0,\quad Q \in {{\mathbb{Z}}^{n}}} ,$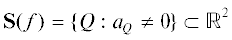 . Множество S называется носителем (support) многочлена $f(X)$. Пусть оно состоит из точек ${{Q}_{1}}, \ldots ,{{Q}_{k}}$. Выпуклая оболочка носителя ${\mathbf{S}}(f)$ – это множество
. Множество S называется носителем (support) многочлена $f(X)$. Пусть оно состоит из точек ${{Q}_{1}}, \ldots ,{{Q}_{k}}$. Выпуклая оболочка носителя ${\mathbf{S}}(f)$ – это множество
(36)
${\mathbf{N}}(f) = \left\{ {Q = \sum\limits_{j = 1}^k \,{{\mu }_{j}}{{Q}_{j}},{{\mu }_{j}} \geqslant 0,\sum\limits_{j = 1}^k \,{{\mu }_{j}} = 1} \right\},$Каждому ребру $\Gamma _{i}^{{(1)}}$ соответствуют его граничное подмножество ${\mathbf{S}}_{i}^{{(1)}} = {\mathbf{S}} \cap \Gamma _{i}^{{(1)}}$, укороченный многочлен
(37)
$\hat {f}_{i}^{{(1)}}(X) = \sum {{{a}_{i}}{{X}^{Q}}\quad {\text{п о }}\quad Q \in {\mathbf{S}}_{i}^{{(1)}}} $(38)
$\begin{gathered} {\mathbf{U}}_{i}^{{(1)}} = \left\{ {P:\left\langle {P,Q{\text{'}}} \right\rangle = \left\langle {P,Q{\text{''}}} \right\rangle > \left\langle {P,Q{\text{'''}}} \right\rangle ,} \right. \\ Q{\text{'}},Q{\text{''}} \in \Gamma _{i}^{{(1)}},Q{\text{'''}} \in \Gamma {\backslash }\Gamma _{i}^{{(1)}}\} , \\ \end{gathered} $Лемма 1. Вблизи особой точки ${{X}^{0}} = 0$ все решения уравнения $f(X) = 0$ образуют ветви вида
(39)
${{x}_{i}} = \sum\limits_{k = 1}^\infty {{b}_{{ik}}}{{\tau }^{{{{r}_{{ik}}}}}},\quad i = 1,2,\quad \tau \to 0,\quad {{r}_{{ik}}} < {{r}_{{ik + 1}}}$Из этой леммы следует, что в разложениях (39) отношения ${{r}_{{ik}}}{\text{/}}{{r}_{{i1}}}$, $i = 1,2$, суть рациональные числа. Более того, при правильной параметризации все числа ${{r}_{{ik}}}$ – целые.
Аналогично устроены ветви кривой (1) вблизи точки ${{X}^{0}} = (\infty ,\infty )$, только там надо ограничиться ребрами $\Gamma _{i}^{{(1)}}$ с нормальными конусами ${\mathbf{U}}_{i}^{{(1)}}$, лежащими в первом квадранте ${{p}_{1}},{{p}_{2}} > 0$ плоскости $\mathbb{R}_{ * }^{2}$. Наконец, так же устроены ветви кривой (1) вблизи точки ${{X}^{0}} = (0,\infty )$, только там нормальные конусы ${\mathbf{U}}_{i}^{{(1)}}$ лежат во втором квадранте ${{p}_{1}} < 0$, ${{p}_{2}} > 0$ (в конусе задачи).
5.3. Степенное преобразование
Теперь заметим, что степенное преобразование
(40)
$\left( {\begin{array}{*{20}{c}} {ln{{x}_{1}}} \\ {ln{{x}_{2}}} \end{array}} \right) = \alpha \left( {\begin{array}{*{20}{c}} {ln{{y}_{1}}} \\ {ln{{y}_{2}}} \end{array}} \right),$(41)
$\tilde {Q}{\text{*}} = \alpha {\text{*}}Q{\text{*}}\quad {\text{и }}\quad \tilde {P}{\text{*}} = {{\alpha }^{{ - 1}}}P{\text{*}},$В дальнейшем можно ограничиться только унимодулярными матрицами $\alpha = ({{\alpha }_{{ij}}})$, т.е. ${{\alpha }_{{ij}}}$ – целые и $det\alpha = \pm 1$.
Лемма 2 [6, гл. I, пар. 2]. Для каждого ребра $\Gamma _{j}^{{(1)}}$ существует степенное преобразование (40) с унимодулярной матрицей $\alpha $, которое переводит многочлен $f(X)$ в многочлен $g(Y)$. При этом ребру $\Gamma _{i}^{{(1)}} \subset \partial {\mathbf{N}}(f)$ соответствует вертикальное ребро $\tilde {\Gamma }_{i}^{{(1)}} \subset \partial {\mathbf{N}}(g)$.
Теперь для вычисления разложений, соответствующих ребру $\Gamma _{i}^{{(1)}}$, надо найти ненулевые корни ${{y}_{2}} = y_{2}^{0}$ уравнения $y_{1}^{q}{{\tilde {g}}_{i}}({{y}_{2}}) = 0$, где $y_{1}^{q}{{\tilde {g}}_{i}}({{y}_{2}})$ – укорочение многочлена $g({{y}_{1}},{{y}_{2}})$, соответствующее вертикальному ребру $\tilde {\Gamma }_{i}^{{(1)}}$. Пусть $y_{2}^{0} \ne 0$ – такой корень. Если он прост, то теорема 1 о неявной функции дает разложение ветви, проходящей через точку ${{y}_{1}} = 0$, ${{y}_{2}} = y_{2}^{0}$. Если $y_{2}^{0}$ – кратный корень многочлена ${{\tilde {g}}_{i}}({{y}_{2}})$, то делаем сдвиг y2 = $y_{2}^{0} + {{z}_{2}}$ и исследуем окрестность точки ${{y}_{1}} = {{z}_{2}} = 0$ тем же способом. Так получаются все ветви исходной кривой.
Пример 10. Лист Декарта
(43)
$f({{x}_{1}},{{x}_{2}})\mathop = \limits^{{\text{def}}} x_{1}^{3} + x_{2}^{3} - 3{{x}_{1}}{{x}_{2}} = 0$1. Ребру $\Gamma _{1}^{{(1)}}$ соответствуют укороченный многочлен
и ветвь ${{x}_{2}} = \frac{1}{3}x_{1}^{2} + \varphi ({{x}_{1}})$.
2. Ребру $\Gamma _{2}^{{(1)}}$ соответствуют укорочение
и ветвь ${{x}_{1}} = \frac{1}{3}x_{2}^{2} + \varphi ({{x}_{2}})$. Обе эти ветви пересекаются в особой точке ${{X}^{0}} = 0$.
3. Ребру $\Gamma _{3}^{{(1)}}$ соответствуют укорочение
и ветвь ${{x}_{2}} = - {{x}_{1}} - 1 + \ldots $ в бесконечности (рис. 5).
6. МОДИФИЦИРОВАННЫЕ ТЕОРЕМЫ О НЕЯВНОЙ ФУНКЦИИ ДЛЯ n = 3
Теорема 2 (Коши [22]). Пусть при ${{X}^{0}} = 0$ имеем $f(X) = 0$ и $\partial f{\text{/}}\partial {{x}_{3}} \ne 0$, тогда вблизи точки $X = {{X}^{0}}$ все решения уравнения $f(X) = 0$ имеют вид
где $X' = ({{x}_{1}},{{x}_{2}})$, $Q' = ({{q}_{1}},{{q}_{2}})$, ${{b}_{{Q'}}} = {\text{const}}$. где ${{a}_{Q}} = {\text{const}}$,(46)
$\begin{gathered} {{q}_{1}} - {{\lambda }_{1}}{{q}_{2}} < 0,\quad {{q}_{1}} - {{\lambda }_{2}}{{q}_{2}} < 0, \\ 0 \leqslant Q \in {{\mathbb{Z}}^{3}},\quad {{\lambda }_{1}},{{\lambda }_{2}} = {\text{const}} \\ \end{gathered} $Теорема 4 ([23, гл. 2, пар. 1, теорема 1.1]). Пусть
где сумма конечна, $0 \leqslant {{q}_{2}},{{q}_{3}} \in \mathbb{Z}$, а ${{a}_{{{{q}_{2}}{{q}_{3}}}}}({{x}_{1}})$ – некоторые функции от x1, кроме тогоТогда решение уравнения $f(X) = 0$ имеет вид
где коэффициенты ${{b}_{k}}$ суть функции от ${{x}_{1}}$, являющиеся многочленами от ${{a}_{{{{q}_{2}}{{q}_{3}}}}}({{x}_{1}})$ с ${{q}_{2}} + {{q}_{3}} \leqslant k$, деленными на $a_{{10}}^{{2k - 1}}$. Такое разложение единственно.В русском издании книги [23] имеется опечатка в формулировке этой теоремы. Она исправлена в ее английском издании. Кроме того, в [23] она сформулирована вблизи точки X = 0, но она справедлива вблизи оси ${{x}_{1}}$, т. е. прямой ${{x}_{2}} = {{x}_{3}}$ = 0.
Имплементация имеется только для теорем 2 и 3 в Maple и в [20].
7. ЛОКАЛЬНЫЙ АНАЛИЗ ДЛЯ n = 3
Точка $X = {{X}^{0}}$, $f({{X}^{0}}) = 0$ называется простой, если в ней вектор $(\partial f{\text{/}}\partial {{x}_{1}}$, $\partial f{\text{/}}\partial {{x}_{2}}$, $\partial f{\text{/}}\partial {{x}_{3}})$ ненулевой. В противном случае точка $X = {{X}^{0}}$ называется особой или критической. Сдвигом $X = {{X}^{0}} + \tilde {X}$ перенесем точку ${{X}^{0}}$ в начало координат. Если в этой точке производная $\partial f{\text{/}}\partial {{x}_{3}} \ne 0$, то согласно теореме 2 о неявной функции вблизи ${{X}^{0}}$ все решения уравнения $f(X) = 0$ имеют вид (44).
7.1. Многогранник Ньютона
Пусть точка ${{X}^{0}} = 0$ – особая. Записываем многочлен в виде $f(X) = \sum {{{a}_{Q}}{{X}^{Q}}} $ (35) с n = 3 и строим его многогранник Ньютона. То есть: носитель 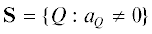 , многогранник Ньютона ${\mathbf{N}}$ как выпуклую оболочку носителя, находим его границу $\partial {\mathbf{N}}$ и ее обобщенные грани $\Gamma _{j}^{{(d)}}$, т.е. вершины с d = 0, ребра с d = 1 и обычные грани с d = 2. Для каждой из них вычисляем граничное множество ${\mathbf{S}}_{j}^{{(d)}} = {\mathbf{S}} \cap \Gamma _{j}^{{(d)}}$, укороченный многочлен
, многогранник Ньютона ${\mathbf{N}}$ как выпуклую оболочку носителя, находим его границу $\partial {\mathbf{N}}$ и ее обобщенные грани $\Gamma _{j}^{{(d)}}$, т.е. вершины с d = 0, ребра с d = 1 и обычные грани с d = 2. Для каждой из них вычисляем граничное множество ${\mathbf{S}}_{j}^{{(d)}} = {\mathbf{S}} \cap \Gamma _{j}^{{(d)}}$, укороченный многочлен
(50)
$\hat {f}_{j}^{{(d)}}(X) = \sum {{{a}_{Q}}{{X}^{Q}}\quad {\text{п о }}\quad Q \in {\mathbf{S}}_{j}^{{(d)}}} $7.2. Степенные преобразования [23]
Введем степенные преобразования
где $lnX = (ln{{x}_{1}},ln{{x}_{2}},ln{{x}_{3}}){\text{*}}$, lnY = $({\text{ln}}{{y}_{1}},{\text{ln}}{{y}_{2}},{\text{ln}}{{y}_{3}}){\text{*}}$, $\alpha $ – невырожденная квадратная 3 × 3 матрица $({{\alpha }_{{ij}}})$ с рациональными элементами ${{\alpha }_{{ij}}}$ (зачастую они будут целыми). При степенном преобразовании (52) моном ${{X}^{Q}}$ переходит в моном ${{Y}^{{\widetilde Q}}}$, гдеСтепенное преобразование (52) в двойственном пространстве $\mathbb{R}_{ * }^{3}$ индуцирует линейное преобразование
Матрица $B$ называется унимодулярной, если все ее элементы целые и $detB = \pm 1$. Очевидно, для унимодулярной матрицы $B$ обратная матрица ${{B}^{{ - 1}}}$ также унимодулярна.
Теорема 5 [20, теорема 2]. Для грани $\Gamma _{j}^{{(d)}}$ существует степенное преобразование (52) с унимодулярной матрицей $\alpha $, которое переводит укороченную сумму $\hat {f}_{j}^{{(d)}}(X)$ в сумму от $d$ координат, т.е.
где $h(Y) = h({{y}_{1}})$, если $d = 1$, и $h(Y) = h({{y}_{1}},{{y}_{2}})$, если d = 2. Здесь $R = ({{r}_{1}},{{r}_{2}},{{r}_{3}}) \in {{\mathbb{R}}^{3}}$. При этом дополнительные координаты ${{y}_{2}}$, ${{y}_{3}}$ при d = 1 и ${{y}_{3}}$ при d = 2 являются локальными, и для многочлена $\hat {f}_{j}^{{(d)}}(X)$ сумма $h(Y)$ также будет многочленом.Умножению многочлена $f(X)$ на ${{X}^{P}}$ соответствует параллельный перенос носителя ${\mathbf{S}}(f)$ и многогранника $\Gamma (f)$ на вектор $P$. Поэтому если после степенного преобразования (52), примененного к многочлену $f(X)$, получаем конечную сумму $g(Y)$, содержащую отрицательные степени координат ${{y}_{1}}$, ${{y}_{2}}$ или ${{y}_{3}}$, то существует такой вектор $P$, что произведение ${{Y}^{P}}g(Y)$ является многочленом, т.е. все показатели степени его мономов неотрицательны.
Структура решений полного уравнения, стремящихся к решениям укороченного уравнения, определяется размерностью d соответствующей обобщенной грани. Рассмотрим эти случаи по отдельности.
7.3. Случай ребра, т.е. d = 1 [23]
В этом случае по теореме 5 существует степенное преобразование и сокращение, приводящее многочлен $f(X)$ к виду (45), (46). При этом образ ребра $\Gamma _{j}^{{(1)}}$ находится на оси ${{q}_{3}}$, т.е. ${{q}_{1}} = {{q}_{2}} = 0$. Соответствующее укорочение является многочленом $h({{y}_{3}})$. Пусть ${{y}_{3}} = y_{3}^{0}$ – его корень. Если это простой корень, то применима теорема 3, которая дает решение полного уравнения $f(X) = 0$ в виде
$Q{\text{'}} = ({{q}_{1}},{{q}_{2}})$ с неравенствамиЕсли $y_{3}^{0}$ – кратный корень, то сдвигом y3 = = $y_{3}^{0} + \mathop {\tilde {y}}\nolimits_3 $ переводим его в начало координат; получаем новый многочлен $g({{y}_{1}},{{y}_{2}},\mathop {\tilde {y}}\nolimits_3 )$ и ищем его корни с помощью построения многогранника Ньютона, как описано выше.
7.4. Случай грани, т.е. $d = 2$
В этом случае согласно теореме 5 с помощью степенного преобразования и сокращения приводим многочлен $f(X)$ к виду $g(Y)$, где $g(Y) = h({{y}_{1}},{{y}_{2}})$ при ${{y}_{3}} = 0$. Уравнение $h({{y}_{1}},{{y}_{2}}) = 0$ определяет плоскую алгебраическую кривую. Пусть $\tilde {h}({{y}_{1}},{{y}_{2}})$ – неприводимый сомножитель многочлена $h({{y}_{1}},{{y}_{2}})$ и $\mathfrak{g}$ – род соответствующей кривой $\mathcal{G}$.
Так или иначе находим униформизацию кривой $\mathcal{G}$. Затем алгоритмом п. 4. переводим эту кривую в координатную ось, т.е. делаем рациональную замену координат
где ${{\beta }_{1}}$ и ${{\beta }_{2}}$ – такие постоянные, что ${\text{|}}{{\beta }_{1}}{\text{|}} + \,{\text{|}}{{\beta }_{2}}{\text{|}} \ne 0$. Тогда многочлен $\tilde {h}({{y}_{1}},{{y}_{2}})$ переходит в многочлен $H(t,z)$, который при z = 0 тождественно равен нулю, а его производная $\partial H{\text{/}}\partial z\not { \equiv }0$ при z = 0. При замене (57) во всем многочлене $g(Y)$ он переходит в функцию $G(Z)$, где ${{z}_{1}} = t$, ${{z}_{2}} = z$, ${{z}_{3}} = {{y}_{3}}$. Если $\tilde {h}({{y}_{1}},{{y}_{2}})$ – простой множитель многочлена $h({{y}_{1}},{{y}_{2}})$, то применяем теорему 4 и получаем решение – ветвь вида (49) где ${{b}_{k}}({{z}_{1}})$ суть рациональные функции от коэффициентов многочлена $G(Z)$.Если $\tilde {h}({{y}_{1}},{{y}_{2}})$ – кратный множитель в $h({{y}_{1}},{{y}_{2}})$, то после замены (57) надо для полученного многочлена снова строить многогранник Ньютона и т.д. Аналогично, для каждой из особых точек многочлена $h({{y}_{1}},{{y}_{2}})$: надо сдвигать ее в начало координат по ${{y}_{1}}$, ${{y}_{2}}$ и строить многогранник Ньютона. Примеры таких вычислений см. в [24].
Список литературы
Fukuda K. Exact algorithms and software in optimization and polyhedral computation // Proceed. ISSAC’08 of XXI International Symposium on Symbolic and Algebraic Computations, ACM NY, USA, 2008. P. 333–334.
Barber C.B., Dobkin D.P., Huhdanpaa H.T. The Quickhull algorithm for convex hulls // ACM Transactions on Mathematical Software. Dec. 1996. V. 22. № 4. P. 469–483. http://www.qhull.org.
King R.B. Beyond the quartic equation. Birkhäser, Boston, 1996.
Умемура Х. Решение алгебраических уравнений с помощью тэта-констант. В кн. Мамфорд Д. Лекции о тэта-функциях. М.: Мир, 1988. С. 360–370.
Hadamard J. Etude sur les proprietes des fonctions entieres et en particulier d’une fonction consideree par Riemann // Journal de mathematiques pures et appliques, 1893. V. 9. № 2. P. 171–215.
Брюно А.Д. Локальный метод нелинейного анализа дифференциальных уравнений. М.: Наука. 1979. // Bruno A.D. Local Methods in Nonlinear Differential Equations. Springer-Verlag: Berlin-Heidelberg-New York-London-Paris-Tokyo, 1989.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. М.: Наука, 1967. Т. 3. // Bateman H. and Erdélyi A. Higher Transcendal Functions. V. 3. McGraw-Hill, 1955.
Brezhnev Yu.V. On the uniformization of algebraic curves // Moscow Mathematical Journal, 2008. V. 8. № 2. P. 233–271.
Brezhnev Yu.V. On uniformization of Burnside’s curve ${{y}^{2}} = {{x}^{5}} - x$ // Journal of Mathematical Physics. 2009. V. 50. № 10.
Brezhnev Yu.V. The sixth Painlevé transcendent and uniformization of algebraic curves // Journal Differential Equations. 2016. V. 260. № 3. P. 2507–2556.
Belokolos E.D., Enolskii V.Z. Reduction of Abelian functions and completely integrable equations // Journal of Mathematical Sciences. 2001. V. 106. № 6. P. 3395–3486 (Part I) and 2002. V. 108. № 3. P. 295–374 (Part II).
Ônishi Y. Complex multiplication formulae for hyperelliptic curves of genus three // Tokyo Journal Mathematics. 1998. V. 21. P. 381–431.
Аптекарев А.И., Туляков Д.Н., Ятцелев М.Л. (О параметризации одной комплексной алгебраической кривой рода 2 // Матем. заметки. 2015. Т. 95. № 5. С. 782–785. // Aptekarev A.I., Toulyakov D.N. and Yattselev M.L. On the parametrization of a certain algebraic curve of genus 2 / / Math. Notes. 2015. V. 95. № 5. P. 843–846.
Aptekarev A.I., Toulyakov D.N., Van Assche W. Hyperelliptic uniformization of algebraic curves of third order // Journal Computational and Applied Mathematics. 2015. V. 284. P. 38–49.
Уокер Р. Алгебраические кривые. Пер. с англ. М.: Книжный дом “Либроком”. 2009. = Walker R.J. Algebraic Curves. Princeton, New Jersy, 1950.
Eilbeck J.C., Enolski V. Z., Matsutani S., Ônishi Y., Previato E. Abelian functions for trigonal curves of genus three // International Mathematics Research Notices. 2007. V. 2007. Article ID rnm140.
Eilbeck J.C. Weierstrass functions for higher genus curves // http://www.ma.hw.ac.uk/Weierstrass
Sendra J.R., Sevilla D. Radical parametrizations of algebraic curves by adjoint curves // Journal of Symbolic Computation. 2011. V. 46. P. 1030–1038.
Harrison M. Explicit solution by radicals, gonal maps and plane models of algebraic curves of genus 5 or 6 // Journal of Symbolic Computation. 2013. V. 51. P. 3–21.
Брюно А.Д., Батхин А.Б. Разрешение алгебраической сингулярности алгоритмами степенной геометрии // Программирование. – 2012. – Т. 38, № 2. С. 12–30. = Bruno A.D., Batkhin A.B. (курсивом) Resolution of algebraic singularity by algorithms of Power Geometry // Programming and Computer Software. 2012. V. 38. № 2. P. 57–72.
Sendra J.R., Sevilla D. First step towards radical parametrization of algebraic surfaces // Computer Aided Geometric Design. 2013. V. 30. P. 374–388.
Гурса Э. Курс математического анализа. – М.-Л.: ГТТИ, 1933. Т. 1, Ч. 2. = Goursat E. Course of Mathematical Analusis. Dover Publ. Inc., New York. 1959.
Power Geometry in Algebraic and Differential Equations. Elsevier Science (North-Holland), Amsterdam, 2000.
Bruno A.D. Asymptotic solving essentially nonlinear problems // Mathematics and Statistics. 2016. V. 4. № 1. P. 27–39.
Дополнительные материалы отсутствуют.
Инструменты
Программирование