Программирование, 2019, № 2, стр. 17-31
ВЫЧИСЛЕНИЕ ОСНОВНЫХ ЕДИНИЦ ЧИСЛОВЫХ КОЛЕЦ С ПОМОЩЬЮ ОБОБЩЕННОЙ ЦЕПНОЙ ДРОБИ
А. Д. Брюно *
Институт прикладной математики им. М.В. Келдыша
125047 Москва, Миусская пл., 4, Россия
* E-mail: abruno@keldysh.ru
Поступила в редакцию 30.07.2018
После доработки 02.09.2018
Принята к публикации 20.09.2018
Аннотация
Предлагается глобальное обобщение цепной дроби, основанное на компьютерной алгебре и дающее наилучшие диофантовы приближения. На нем базируется способ вычисления основных единиц алгебраических колец и нахождение всех решений некоторого класса диофантовых уравнений. Приведены примеры в размерностях 2, 3, 4.
I. ВВЕДЕНИЕ
Пусть в вещественном $n$-мерном пространстве ${{\mathbb{R}}^{n}} = \{ X\} $ задано m однородных вещественных форм ${{f}_{i}}(X)$, $i = 1,\; \ldots ,\;m$, $2 \leqslant m \leqslant n$. Выпуклая оболочка множества значений G(X) = (| f1(X)|, ..., ${\text{|}}{{f}_{m}}(X){\text{|}}) \in \mathbb{R}_{ + }^{m}$ для целочисленных $X \in {{\mathbb{Z}}^{n}}$ во многих случаях является выпуклым многогранным множеством, граница которого для $\left\| X \right\| < {\text{const}}$ вычисляется с помощью стандартной программы компьютерной алгебры. Точки $X \in {{\mathbb{Z}}^{n}}$, для которых значения $G(X)$ лежат на этой границе, названы граничными. Они являются наилучшими диофантовыми приближениями для корневых множеств указанных форм. Их вычисление дает глобальное обобщение цепной дроби (раздел III). Для n = 3 обобщить цепную дробь безуспешно пытались Эйлер, Якоби, Дирихле, Эрмит, Пуанкаре, Гурвиц, Клейн, Минковский, Брун, Арнольд и многие другие.
Пусть $p(\xi )$ – целый неприводимый в $\mathbb{Q}$ многочлен степени n и λ – его корень. Набор основных единиц кольца $\mathbb{Z}[\lambda ]$ можно вычислить по граничным точкам некоторой совокупности линейных и квадратичных форм, построенных по корням многочлена $p(\xi )$ (раздел IV). До сих пор эти единицы вычислялись только для n = 2 (с помощью обычных цепных дробей [1, гл. II, § 7]), n = 3 (с помощью алгоритмов Вороного [2]) и n = 4, когда комплексны все четыре корня многочлена $p(\xi )$, Парусниковым [3], но большинство найденных им единиц не являются основными. Каждая единица определяет как автоморфизм граничных точек $X \in {{\mathbb{R}}^{n}}$, так и автоморфизм соответствующих точек $G(X) \in \mathbb{R}_{ + }^{m}$. В логарифмической проекции положительного ортанта $\mathbb{R}_{ + }^{m}$ на ${{\mathbb{R}}^{{m - 1}}}$ можно найти фундаментальную область для группы автоморфизмов, соответствующих единицам (раздел V).
С помощью этих конструкций можно находить целочисленные решения диофантовых уравнений специального вида (раздел VI). Аналогично вычисляются все указанные объекты для других колец поля $\mathbb{Q}(\lambda )$ (раздел VII). В разделе VIII перечислены предшествующие вычисления основных единиц. Приведены примеры для $n = 2,3$ и 4 (разделы IX–XII).
Наш подход обобщает цепную дробь, позволяет вычислить наилучшие совместные приближения, основные единицы алгебраических колец поля $Q(\lambda )$ и все решения некоторого класса диофантовых уравнений для любого n.
II. ЦЕПНАЯ ДРОБЬ
Пусть ${{\alpha }_{0}}$ и ${{\alpha }_{1}}$ – натуральные числа. Для нахождения их наибольшего общего делителя используется алгоритм Евклида последовательного деления с остатком:
(2)
$\left( {\begin{array}{*{20}{c}} {{{\alpha }_{{k + 1}}}} \\ {{{\alpha }_{{k + 2}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&1 \\ 1&{ - {{a}_{k}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\alpha }_{k}}} \\ {{{\alpha }_{{k + 1}}}} \end{array}} \right),\quad {{a}_{k}} = [{{\alpha }_{k}}{\text{/}}{{\alpha }_{{k + 1}}}].$Если разложение (1) оборвать на ${{a}_{k}}$ и свернуть эту оборванную цепную дробь в рациональное число ${{p}_{k}}{\text{/}}{{q}_{k}}$, то получается подходящая дробь, которая дает наилучшее рациональное приближение к числу $\alpha $. При этом
(3)
$\begin{gathered} \left( {\begin{array}{*{20}{c}} {{{p}_{k}}}&{{{p}_{{k - 1}}}} \\ {{{q}_{k}}}&{{{q}_{{k - 1}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{p}_{{k - 1}}}}&{{{p}_{{k - 2}}}} \\ {{{q}_{{k - 1}}}}&{{{q}_{{k - 2}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{a}_{k}}}&1 \\ 1&0 \end{array}} \right), \\ \mathop {\left( {\begin{array}{*{20}{c}} {{{a}_{k}}}&1 \\ 1&0 \end{array}} \right)}\nolimits^{ - 1} = \left( {\begin{array}{*{20}{c}} 0&1 \\ 1&{ - {{a}_{k}}} \end{array}} \right),\quad det\left( {\begin{array}{*{20}{c}} {{{p}_{k}}}&{{{p}_{{k - 1}}}} \\ {{{q}_{k}}}&{{{q}_{{k - 1}}}} \end{array}} \right) = \pm 1, \\ \end{gathered} $Итак, разложение числа в цепную дробь:
• просто;
•дает наилучшие рациональные приближения к числу;
• конечно для рационального числа;
•периодично для квадратичных иррациональностей [4, § 10];
• устроено как для почти всех чисел [4, гл. III] для кубических иррациональностей [5].
Кроме того, оно обладает еще рядом замечательных свойств.
III. ГЛОБАЛЬНОЕ ОБОБЩЕНИЕ ЦЕПНОЙ ДРОБИ И НАИЛУЧШИЕ ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ
Обобщить цепную дробь для векторов безуспешно пытались Эйлер, Якоби, Дирихле, Эрмит, Пуанкаре, Гурвиц, Клейн, Минковский, Брун, Арнольд и многие другие [6, 7, п. 1.2]. Только пошаговые алгоритмы Вороного [2] безотказны, но сложны.
В [7–9] предложено следующее обобщение цепной дроби.
Пусть в n-мерном вещественном пространстве ${{\mathbb{R}}^{n}}$ с координатами $X = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$ заданы $m$ однородных вещественных форм (т.е. многочленов от переменных) ${{f}_{1}}(X)$, …, ${{f}_{m}}(X)$, $2 \leqslant m \leqslant n$.
Модули ${{g}_{i}}(X) = \left| {{{f}_{i}}(X)} \right|$ форм ${{f}_{i}}(X)$, $i = 1,\; \ldots ,\;m$, задают отображение $G(X) = ({{g}_{1}}(X), \ldots ,{{g}_{m}}(X))$ пространства ${{\mathbb{R}}^{n}}$ в положительный ортант ${\mathbf{S}}\;\mathop = \limits^{{\text{def}}} \;\mathbb{R}_{ + }^{m}$ в m-мерном пространстве ${{\mathbb{R}}^{m}}$ с координатами S = = $({{s}_{1}}, \ldots ,{{s}_{m}})$: ${{s}_{i}} = {{g}_{i}}(X) = \left| {{{f}_{i}}(X)} \right|$, $i = 1, \ldots ,m$. При этом целочисленная решетка ${{\mathbb{Z}}^{n}} \subset {{\mathbb{R}}^{n}}$ отображается в некоторое множество ${\mathbf{Z}} \subset {\mathbf{S}}$. Замыкание выпуклой оболочки ${\mathbf{H}}$ множества ${\mathbf{Z}}{\backslash }0$ является выпуклым множеством. Все целочисленные точки $X \in {{\mathbb{Z}}^{n}}{\backslash }0$, отображающиеся на границу $\partial {\mathbf{H}}$ множества ${\mathbf{H}}$, назовем граничными.
Задача 1. Найти все граничные точки X.
Решение задачи 1. В дальнейшем ограничимся случаями, когда выпуклое множество ${\mathbf{H}}$ является многогранным, т.е. его граница $\partial {\mathbf{H}}$ состоит из вершин, ребер, граней различных размерностей и не содержит непрерывных “кривых” частей. В этих случаях граница $\partial {\mathbf{H}}$ вычисляется с помощью стандартных программ компьютерной алгебры, предназначенных для вычисления выпуклых многогранных оболочек [10, 11]. Это и дает алгоритмическое обобщение цепной дроби на любую размерность. Примеры см. в [7].
В частности, это дает возможность вычислить наилучшие совместные рациональные приближения ${{q}_{1}}{\text{/}}{{q}_{0}}$, …, ${{q}_{l}}{\text{/}}{{q}_{0}}$ к вещественным числам ${{\beta }_{1}}, \ldots ,{{\beta }_{l}}$, где ${{q}_{0}},{{q}_{1}}, \ldots ,{{q}_{l}} \in \mathbb{Z}$ и ${{f}_{0}}({{q}_{0}}) = {{q}_{0}}$, ${{f}_{i}}({{q}_{0}},{{q}_{i}})$ = = q0βi – qi, $i = 1,\; \ldots ,\;l$. Здесь $n = m = l + 1$. Если l = 1, то получаем одно число ${{\beta }_{1}}$, тогда выпуклый многогранник ${\mathbf{H}}$ – это выпуклый многоугольник на плоскости с координатами ${\text{|}}{{q}_{0}}{\text{|}},\;{\text{|}}{{q}_{0}}{{\beta }_{1}} - {{q}_{1}}{\text{|}}$. Его граница $\partial {\mathbf{H}}$ – это ломаная линия, вершины которой соответствуют подходящим дробям ${{q}_{1}}{\text{/}}{{q}_{0}}$ цепной дроби числа ${{\beta }_{1}}$.
Гипотеза 1. Если все ${{f}_{1}},\; \ldots ,\;{{f}_{m}}$ суть линейные и квадратичные формы, то граница $\partial {\mathbf{H}}$ не имеет непрерывных кривых участков, т.е. является многогранной.
Более того, до сих пор неизвестно ни одного набора форм ${{f}_{1}},\; \ldots ,\;{{f}_{m}}$, для которого граница $\partial {\mathbf{H}}$ не была бы многогранной.
IV. ОСНОВНЫЕ ЕДИНИЦЫ КОЛЬЦА $\mathbb{Z}[\lambda ]$
Пусть дан целый неприводимый в $\mathbb{Q}$ вещественный многочлен
с целыми коэффициентами ${{b}_{i}}$, т.е. он не разлагается в произведение двух нетривиальных многочленов с коэффициентами из $\mathbb{Q}$. Ему соответствует кольцо $\mathbb{Z}[\lambda ]$ чисел вида с целыми коэффициентами ${{x}_{i}}$, где $\lambda $ – корень многочлена (4) и $X = ({{x}_{1}},\; \ldots ,\;{{x}_{n}}) \in {{\mathbb{Z}}^{n}}$. Каждому числу (5) соответствует квадратная матрица D(ξ) = $({{d}_{{ij}}})$:(6)
${{\lambda }^{i}}\xi (X) = \sum\limits_{j = 0}^{n - 1} \,{{d}_{{ij}}}{{\lambda }^{j}},\quad i = 0,1,\; \ldots ,\;n - 1.$Определитель $detD(\xi )$ называется нормой числа (5) и обозначается $N(\xi )$. Норма произведения чисел равна произведению их норм: $N({{\xi }_{1}} \cdot {{\xi }_{2}})$ = = $N({{\xi }_{1}}) \cdot N({{\xi }_{2}})$. Те числа (5), у которых норма $N(\xi ) = \pm 1$, называются единицами [1, гл. II]. В дальнейшем предполагаем, что среди корней многочлена $p(\xi )$ нет единиц, т.е. ${\text{|}}{{b}_{n}}{\text{|}} \ne 1$. Этим исключается кручение в абелевой группе единиц. Существует такой набор единиц $\Sigma = ({{\varepsilon }_{1}},\; \ldots ,\;{{\varepsilon }_{r}})$, что всякая единица $\varepsilon \in \mathbb{Z}[\lambda ]$ однозначно представляется в виде
где ${{a}_{i}}$ – целые числа. Эти единицы ${{\varepsilon }_{1}},\; \ldots ,\;{{\varepsilon }_{r}}$ называются основными.Задача 2. Для фиксированного многочлена (4) найти набор основных единиц кольца $\mathbb{Z}[\lambda ]$.
Решение задачи 2. Пусть неприводимый в $\mathbb{Q}$ многочлен (4) имеет $l$ вещественных корней ${{\lambda }_{1}}$, ..., ${{\lambda }_{l}}$ и $k$ пар комплексно сопряженных корней ${{\lambda }_{{l + 1}}}$, ..., ${{\lambda }_{{l + k}}}$, ${{\bar {a}}_{{l + 1}}}$, ..., ${{\bar {\lambda }}_{{l + k}}}$, $l + 2k = n$. Здесь $l \geqslant 0$, $k \geqslant 0$. Рассмотрим $m = k + l$ форм
(9)
${{f}_{{l + j}}}(X) = \left\langle {{{K}_{{l + j}}},X} \right\rangle \left\langle {\mathop {\bar {K}}\nolimits_{l + j} ,X} \right\rangle ,\quad j = 1,\; \ldots ,\;k,$(11)
$\left\langle {{{L}_{i}},X} \right\rangle = {{x}_{1}} + {{\lambda }_{i}}{{x}_{2}} + \ldots + \lambda _{i}^{{n - 1}}{{x}_{n}},$(12)
${{K}_{{l + j}}} = (1,{{\lambda }_{{l + j}}},\lambda _{{l + j}}^{2},\; \ldots ,\;\lambda _{{l + j}}^{{n - 1}}),$(13)
${{\bar {K}}_{{l + j}}} = (1,{{\bar {\lambda }}_{{l + j}}},\bar {\lambda }_{{l + j}}^{2},\; \ldots ,\;\bar {\lambda }_{{l + j}}^{{n - 1}}).$По теореме Дирихле [1, гл. II, § 4, п. 3] для многочлена (4) число основных единиц $r = k + l - 1$. Далее предполагаем, что $m = k + l \geqslant 2$. Ибо если $k + l \leqslant 1$, то $r \leqslant 0$ и по теореме Дирихле основные единицы отсутствуют.
Теорема 1. ([1, гл. II, § 1, п. 2]). Для чисел (5) с $X = ({{x}_{1}}, \ldots ,{{x}_{n}}) \in {{\mathbb{R}}^{n}}$
Поэтому для всех единиц вида (5)
(15)
$f(X) = \pm 1\quad {\text{и }}\quad g(X)\;\mathop = \limits^{{\text{def}}} \;\left| {f(X)} \right| = 1.$Пусть 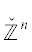 – множество точек $X \in {{\mathbb{Z}}^{n}}$ со свойством (15). Рассмотрим для него (т.е. для
– множество точек $X \in {{\mathbb{Z}}^{n}}$ со свойством (15). Рассмотрим для него (т.е. для 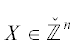 ) конструкции раздела III: множество
) конструкции раздела III: множество 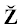 значений
значений
(16)
$G(X) = \left( {{{g}_{1}}(X),\; \ldots ,\;{{g}_{m}}(X)} \right) \subset {\mathbf{S}} = \mathbb{R}_{ + }^{m},$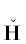 множества
множества 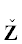 и ее границу
и ее границу 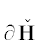 . Граница
. Граница 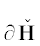 имеет размерность $m - 1 = r$, не имеет кривых участков и состоит из вершин, ребер и граней.
имеет размерность $m - 1 = r$, не имеет кривых участков и состоит из вершин, ребер и граней.
Гипотеза 2. Все грани границы  являются симплексами, а значение ${{G}_{0}} = (1,1,\; \ldots ,\;1)$ является ее вершиной.
являются симплексами, а значение ${{G}_{0}} = (1,1,\; \ldots ,\;1)$ является ее вершиной.
Пусть Δ – некоторая $(m - 1)$-мерная грань границы 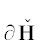 , содержащая вершину ${{G}_{0}} = (1,1,\; \ldots ,\;1)$, а ${{R}_{1}},\; \ldots ,\;{{R}_{{m - 1}}}$ – ее ребра, содержащие ${{G}_{0}}$.
, содержащая вершину ${{G}_{0}} = (1,1,\; \ldots ,\;1)$, а ${{R}_{1}},\; \ldots ,\;{{R}_{{m - 1}}}$ – ее ребра, содержащие ${{G}_{0}}$.
Теорема 2. Пусть ${{G}_{i}}$ – вторая вершина ребра ${{R}_{i}}$, отличная от вершины G0, $i = 1,\; \ldots ,\;m - 1$. Числа (5), у которых $G(X) = {{G}_{i}}$, $i = 1,\; \ldots ,\;m - 1$, образуют набор основных единиц кольца $\mathbb{Z}[\lambda ]$.
Следовательно, для вычисления основных единиц надо на некотором ограниченном множестве
$\left\| X \right\| < {\text{const}}$, 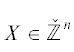 вычислить кусок границы
вычислить кусок границы 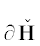 , содержащий $(m - 1)$-мерную грань $\Delta $.
, содержащий $(m - 1)$-мерную грань $\Delta $.
Каждому числу (5) соответствует матрица
где E – единичная, а B – это матрица, сопровождающая многочлен (4):(18)
$B = \left( \begin{gathered} \begin{array}{*{20}{c}} 0&{\;\,1}&{\;\;\;\;0}&{\;\; \cdots }&{\;0}&{\;\;0} \\ {\;0\;}&{\;\;0}&{\;\;\;\;1}&{\;\; \cdots }&{\;0}&{\;\;0} \end{array} \hfill \\ ...................................... \hfill \\ \begin{array}{*{20}{c}} 0&0&0& \cdots &0&1 \\ { - {{b}_{n}}}&{ - {{b}_{{n - 1}}}}&{ - {{b}_{{n - 2}}}}& \cdots &{ - {{b}_{2}}}&{ - {{b}_{1}}} \end{array} \hfill \\ \end{gathered} \right).$Если число (5) является единицей, то матрица $T(\xi )$ унимодулярна и линейное преобразование $X{\text{*}} = T(\xi )X$ в ${{\mathbb{R}}^{n}}$ индуцирует автоморфизм
множества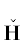 в ${\mathbf{S}} = \mathbb{R}_{ + }^{m}$. Следовательно, каждой единице $\varepsilon $ соответствуют два автоморфизма: граничных точек в ${{\mathbb{R}}^{n}}$ и многогранника ${\mathbf{H}}$ в $\mathbb{R}_{ + }^{m}$, т.е. $T(\varepsilon )$ – это период обобщенной цепной дроби. Количество независимых периодов равно m – 1. Это – обобщение теоремы Лагранжа [4, § 10], доказанной для $n = l = 2$, $k = 0$, т.е. $m = k + l = 2$.
в ${\mathbf{S}} = \mathbb{R}_{ + }^{m}$. Следовательно, каждой единице $\varepsilon $ соответствуют два автоморфизма: граничных точек в ${{\mathbb{R}}^{n}}$ и многогранника ${\mathbf{H}}$ в $\mathbb{R}_{ + }^{m}$, т.е. $T(\varepsilon )$ – это период обобщенной цепной дроби. Количество независимых периодов равно m – 1. Это – обобщение теоремы Лагранжа [4, § 10], доказанной для $n = l = 2$, $k = 0$, т.е. $m = k + l = 2$.
V. ФУНДАМЕНТАЛЬНАЯ ОБЛАСТЬ
В поле $\mathbb{Q}(\lambda )$ всякая целая степень $t \geqslant n$ числа $\xi $ из (5) однозначно записывается в виде многочлена от $\lambda $ степени $n - 1$, ибо
(20)
${{\lambda }^{n}} = - ({{b}_{n}} + {{b}_{{n - 1}}}\lambda + \ldots + {{b}_{1}}{{\lambda }^{{n - 1}}}).$Поэтому отношение двух многочленов от $\lambda $ однозначно записывается в виде многочлена от $\lambda $ степени $n - 1$.
Теорема 3. Пусть $X = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$, Y = $({{y}_{1}}, \ldots ,{{y}_{n}})$, $Z = ({{z}_{1}},\; \ldots ,\;{{z}_{n}}) \in {{\mathbb{Q}}^{n}}$ и $\xi (X) \cdot \xi (Y) = \xi (Z)$, тогда ${{f}_{i}}(X) \cdot {{f}_{i}}(Y) = {{f}_{i}}(Z)$, $i = 1,\; \ldots ,\;m$.
Следствие 1. В условиях теоремы 3 ${{g}_{i}}(X) \cdot {{g}_{i}}(Y)$ = = gi(Z), $i = 1,\; \ldots ,\;m$.
Логарифмическая замена
(21)
$\begin{gathered} {{h}_{i}}(X) = ln{{g}_{i}}(X),\quad i = 1,\;...,\;m, \\ H\;\mathop = \limits^{{\text{def}}} \;({{h}_{1}},\; \ldots ,\;{{h}_{m}}) \\ \end{gathered} $На ${{\mathbb{R}}^{{m - 1}}}$ автоморфизм (19) принимает вид
т.е. является параллельным переносом. Единицы кольца $\mathbb{Z}[\lambda ]$ образуют абелеву группу по умножению. По теореме 3 их логарифмы $H$ образуют абелеву группу по сложению. В ${{\mathbb{R}}^{{m - 1}}}$ имеется фундаментальная область $\mathcal{F}$ относительно сдвигов (22) этой группы. Пусть $m$-мерные векторы ${{G}_{i}}$, i = = $1, \ldots ,m - 1$, соответствующие основным единицам теоремы 2, имеют вид ${{G}_{i}} = ({{g}_{{1i}}},\; \ldots ,\;{{g}_{{mi}}})$. Положим(23)
${{\Gamma }_{i}} = (ln{{g}_{{1i}}}, \ldots ,ln{{g}_{{m - 1,i}}}),\quad i = 1,\; \ldots ,\;m - 1.$Теорема 4. В ${{\mathbb{R}}^{{m - 1}}}$ фундаментальная область относительно сдвигов (22), (23) – это $(m - 1)$-мерный “куб”
(24)
$\begin{gathered} \mathcal{F} = \{ H' = {{\mu }_{1}}{{\Gamma }_{1}} + \ldots + {{\mu }_{{m - 1}}}{{\Gamma }_{{m - 1}}}, \\ 0 \leqslant {{\mu }_{i}} \leqslant 1,\;i = 1,\; \ldots ,\;m - 1\} . \\ \end{gathered} $При вычислении границы выпуклой оболочки некоторого множества точек трудности возрастают вместе с ростом количества точек. Чтобы уменьшить эти трудности, можно вычисления разбить на следующие 6 шагов.
Шаг 1. Сначала в кольце $\mathbb{Z}[\lambda ]$ находим все единицы с $X \in {{\mathbb{Z}}^{n}}$ из области ||X|| < const, вычисляя значения $g(X)$ в этих X.
Шаг 2. Затем на множестве единиц {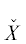 } надо вычислить границу
} надо вычислить границу 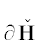 их выпуклой оболочки
их выпуклой оболочки 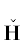 .
.
Шаг 3. По теореме 2 из 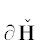 выделяем набор основных единиц, представленных в ${\mathbf{S}}$ вершинами ${{G}_{0}},{{G}_{1}},\; \ldots ,\;{{G}_{{m - 1}}}$.
выделяем набор основных единиц, представленных в ${\mathbf{S}}$ вершинами ${{G}_{0}},{{G}_{1}},\; \ldots ,\;{{G}_{{m - 1}}}$.
Шаг 4. По теореме 4 находим фундаментальную область (24).
Шаг 5. Теперь выпуклая оболочка значений $G(X)$ с $\xi (X) \in \mathbb{Z}[\lambda ]$ вычисляется только по тем X, у которых $H{\kern 1pt} {\text{'}}(X)$ попадают в фундаментальную область (24) и ее близкую окрестность.
Шаг 6. По этой части границы $\partial {\mathbf{H}}$ восстанавливается вся граница $\partial {\mathbf{H}}$ с помощью периодов ${{G}_{i}}$, $i = 1, \ldots ,m - 1$, соответствующих основным единицам, или с помощью сдвигов (22).
VI. ДИОФАНТОВЫ УРАВНЕНИЯ
Многочлену $p(\xi )$ степени $n$ из (4) соответствует форма $f(X)$ из (14) степени n от n переменных $X = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$. Ее коэффициенты являются многочленами от коэффициентов ${{b}_{i}}$ многочлена (4). Так, при n = 2
при n = 3(26)
$\begin{gathered} f(X) = x_{1}^{3} - {{b}_{1}}x_{1}^{2}{{x}_{2}} + {{b}_{2}}{{x}_{1}}x_{2}^{2} - {{b}_{3}}x_{2}^{3} + \\ + \;(b_{1}^{2} - 2{{b}_{2}})x_{1}^{2}{{x}_{3}} + (3{{b}_{3}} - {{b}_{1}}{{b}_{2}}){{x}_{1}}{{x}_{2}}{{x}_{3}} + \\ + \;{{b}_{1}}{{b}_{2}}x_{2}^{2}{{x}_{3}} + (b_{2}^{2} - 2{{b}_{1}}{{b}_{3}}){{x}_{1}}x_{3}^{2} - {{b}_{2}}{{b}_{3}}{{x}_{2}}x_{3}^{2} + b_{3}^{2}x_{3}^{3}, \\ \end{gathered} $Для любого n при ${{x}_{3}} = \ldots = {{x}_{n}} = 0$ имеем
Задача 3. Для заданного многочлена (4) найти все решения (5) с $\xi \in \mathbb{Z}[\lambda ]$ уравнения
где число $\beta $ рационально, $\beta \ne \pm 1$.Решение задачи 3.
Теорема 5. ([1, гл. II, § 5, теорема 1]). Все решения (5) с $\xi \in \mathbb{Z}[\lambda ]$ уравнения (48) имеют вид
(29)
$\xi = \xi _{j}^{0}\varepsilon _{1}^{{{{a}_{1}}}} \cdots \varepsilon _{r}^{{{{a}_{r}}}},\quad j = 1,\; \ldots ,\;J,$Далее дается набросок конструктивного доказательства этой теоремы, позволяющий вычислять соответствующие постоянные и выделенные решения $\xi _{1}^{0}$, …, $\xi _{J}^{0}$.
Согласно предыдущим разделам находим набор основных единиц $\Sigma = ({{\varepsilon }_{1}},\; \ldots ,\;{{\varepsilon }_{{m - 1}}})$ кольца $\mathbb{Z}[\lambda ]$ и по ним строим фундаментальную область $\mathcal{F}$ в координатах $H'\;\mathop = \limits^{{\text{def}}} \;({{h}_{1}},\; \ldots ,\;{{h}_{{m - 1}}})$.
Лемма 1. Для всех точек $X \in {{\mathbb{R}}^{n}}$, у которых логарифмические проекции $H' = ({{h}_{1}},\; \ldots ,\;{{h}_{{m - 1}}})$ лежат в фундаментальной области $\mathcal{F}$, справедливы оценки
где $0 < {{\mu }_{i}} < {{\nu }_{i}}$ – вещественные числа.Лемма 2. Для всех точек $X$, у которых $H' \in \mathcal{F}$ и выполнено равенство $g(X) = \left| \beta \right|$, справедливы оценки
где $0 < {{\mu }_{m}} < {{\nu }_{m}}$ – вещественные числа.Нижние оценки в (30) нужны для получения верхней оценки в (31).
Поскольку $\left\langle {K,X} \right\rangle = \left\langle {{\text{Re}}K,X} \right\rangle + i\left\langle {{\text{Im}}K,X} \right\rangle $, то
(32)
$\left\langle {K,X} \right\rangle \left\langle {\bar {K},X} \right\rangle = \mathop {\left\langle {{\text{Re}}K,X} \right\rangle }\nolimits^2 + \mathop {\left\langle {{\text{Im}}K,X} \right\rangle }\nolimits^2 .$Лемма 3. Если
(33)
$\begin{gathered} \gamma \;\mathop = \limits^{{\text{def}}} \;det({{\Lambda }_{1}},\; \ldots ,\;{{\Lambda }_{l}},{\text{Re}}{{K}_{{l + 1}}}, \\ {\text{Im}}{{K}_{{l + 1}}},\; \ldots ,\;{\text{Re}}{{K}_{{l + k}}},{\text{Im}}{{K}_{{l + k}}}) \ne 0, \\ \end{gathered} $Поскольку
(34)
$\gamma = \frac{1}{{{{{( - 2i)}}^{k}}}}det({{\Lambda }_{1}}, \ldots ,{{\Lambda }_{l}},{{K}_{{l + 1}}},{{\bar {K}}_{{l + 1}}}, \ldots ,{{K}_{{l + k}}},{{\bar {K}}_{{l + k}}}),$ненулевым множителем, то условие (33) эквивалентно условию, что у многочлена (4) нет кратных корней. Но это так по условию, что многочлен (4) неприводим в $\mathbb{Q}$.
Неравенства (30), (31) выделяют в ${{\mathbb{R}}^{n}}$ всего ${{2}^{m}}$ ограниченных областей вида
(35)
${{\mu }_{i}}_{i} \leqslant {{\varkappa }_{i}}{{f}_{i}}(X) \leqslant {{\nu }_{i}},\quad {{\varkappa }_{i}} = \pm 1,\quad i = 1,\; \ldots ,\;m.$В каждой из них количество целочисленных точек $X \in {{\mathbb{Z}}^{n}}$ конечно. В каждой из этих точек можно вычислить $f(X)$ и отобрать те ${{X}_{i}}$, в которых выполнено уравнение (28). Наконец, среди этих точек ${{X}_{i}}$ оставляем только те $X_{1}^{0},\; \ldots ,\;X_{J}^{0}$, для которых отношения $\xi (X_{i}^{0}){\text{/}}\xi (X_{j}^{0})$ по $j \ne i$ не лежат в $\mathbb{Z}{\kern 1pt} [\lambda ]$. Тогда $\xi _{j}^{0} = \xi (X_{j}^{0})$, $j = 1,\; \ldots ,\;J$, являются выделенными решениями уравнения (48) и все решения этого уравнения имеют вид (49).
Это первый способ. Он заключается в том, что в каждом ортанте пространства ${{\mathbb{R}}^{n}} = \{ X\} $ кусок множества значений $X:f(X) = \beta $ заключается в некоторый параллелепипед. В каждом из них перебираются все точки X решетки ${{\mathbb{Z}}^{n}}$ и находятся те, которые удовлетворяют уравнению (28). Затем среди всех этих точек всех ортантов оставляются все выделенные решения.
Второй способ. Все искомые точки решетки лежат в множестве $ - {{\nu }_{i}} \leqslant {{f}_{i}}(X) \leqslant {{\nu }_{i}}$, $i = 1,\; \ldots ,\;m$. Найдем все точки пересечения поверхностей
и для каждого ${{x}_{j}}$ выберем значение ${{z}_{j}} = max\left| {{{x}_{j}}} \right|$ среди этих точек пересечения. Затем среди точек X решетки, для которых найдем все те, которые удовлетворяют уравнению (48). Затем, вычисляя их попарные отношения, находим множество выделенных решений. Этот способ удобнее для вычислений на компьютере, но дает много лишних решений, которые не являются выделенными.VII. ОБОБЩЕНИЯ
A. Единицы с положительной нормой
Для единицы $\varepsilon $ норма $N(\varepsilon ) = \pm 1$. Иногда нужны только единицы, у которых норма положительна. Чтобы при четном $n$ найти базисный набор таких (квазиосновных) единиц $\hat {\Sigma } = ({{\hat {\varepsilon }}_{1}}, \ldots ,{{\hat {\varepsilon }}_{{m - 1}}})$, надо в описанной процедуре раздела 4 оставлять только те точки 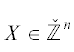 , для которых $f(X) = + 1$, и по ним указанным выше способом выделить мультипликативный базис. При нечетном
$n$ всякой единице $\varepsilon $ соответствует единица $\varepsilon '$ с $N(\varepsilon ') = 1$: это либо $\varepsilon $, либо $ - \varepsilon $, т.е. в записи (5) X заменяется на –X.
, для которых $f(X) = + 1$, и по ним указанным выше способом выделить мультипликативный базис. При нечетном
$n$ всякой единице $\varepsilon $ соответствует единица $\varepsilon '$ с $N(\varepsilon ') = 1$: это либо $\varepsilon $, либо $ - \varepsilon $, т.е. в записи (5) X заменяется на –X.
B. Произвольный порядок
Согласно [1, гл. II, § 2] полный модуль в поле $\mathbb{Q}(\lambda )$, содержащий число 1 и являющийся кольцом, называется порядком поля $\mathbb{Q}(\lambda )$. Очевидно, что кольцо $\mathbb{Z}[\lambda ]$ является порядком поля $\mathbb{Q}(\lambda )$. Но в этом поле могут быть и другие порядки. Например, если в записи (5) все ${{x}_{2}}$ – четные, то получим подкольцо кольца $\mathbb{Z}[\lambda ]$. Все результаты разделов IV–VI, доказанные для порядка $\mathbb{Z}[\lambda ]$, справедливы для любого порядка $\Omega $ поля $\mathbb{Q}(\lambda )$. Пусть ${{\omega }_{1}},\; \ldots ,\;{{\omega }_{n}}$ – базис порядка $\Omega $, т.е. все числа $\alpha \in \Omega $ имеют вид
(36)
$\alpha = {{y}_{1}}{{\omega }_{1}} + {{y}_{2}}{{\omega }_{2}} + \ldots + {{y}_{n}}{{\omega }_{n}},\quad {{y}_{i}} \in \mathbb{Z}.$При записи этих чисел в виде (5) коэффициенты ${{x}_{i}}$ могут быть рациональными числами.
Отметим отличия, возникающие для произвольного порядка $\Omega $. Единицы (5) этого порядка могут иметь рациональные коэффициенты ${{x}_{i}}$. Существует такой набор единиц ${{\varepsilon }_{1}},\; \ldots ,\;{{\varepsilon }_{r}} \in \Omega $, что все единицы поля имеют вид (7). Назовем эти единицы основными. Для них справедливы
все конструкции и теоремы разделов IV–VI. Только матрица периода $T(\varepsilon )$ может иметь рациональные элементы, но $detT(\varepsilon ) = N(\varepsilon ) = \pm 1$. Поэтому для отыскания основных единиц порядка надо вычислять $f(X)$ на решетке чисел (56), записанных в виде (5) с рациональными ${{x}_{i}}$. Дальнейшие вычисления такие же, как для кольца $\mathbb{Z}[\lambda ]$. Мультипликативный базис единиц с положительной нормой образует набор квазиосновных
единиц $\hat {\Sigma } = ({{\hat {\varepsilon }}_{1}}, \ldots ,{{\hat {\varepsilon }}_{{m - 1}}})$ с положительной нормой. Здесь также можно найти фундаментальные области $\mathcal{F}$ и 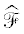 , соответствующие наборам $\Sigma $ и $\widehat \Sigma $.
, соответствующие наборам $\Sigma $ и $\widehat \Sigma $.
С. Максимальный порядок
В поле $\mathbb{Q}(\lambda )$ имеется максимальный порядок $\widetilde \Omega $. Его базис $\mathop {\tilde {\omega }}\nolimits_1 ,\; \ldots ,\;\mathop {\tilde {\omega }}\nolimits_r $ называется фундаментальным, о его вычислении см. [1, гл. II, § 2]. Все сказанное для порядка $\mathbb{Z}[\lambda ]$ справедливо и для максимального порядка. В частности, он имеет набор основных единиц
$\Sigma = ({{\varepsilon }_{1}}, \ldots ,{{\varepsilon }_{r}})$, набор квазиосновных единиц $\hat {\Sigma } = ({{\hat {\varepsilon }}_{1}}, \ldots ,{{\hat {\varepsilon }}_{r}})$ с положительными нормами и соответствующие им фундаментальные области $\mathcal{F}$ и 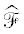 .
.
VIII. ПРЕДШЕСТВЕННИКИ И ДИСКРИМИНАНТЫ
Для $n = 2$, $k = 0$, $l = 2$, когда $m = 2$ и $r = 1$, т.е. для вещественных квадратичных полей способ вычисления основной единицы максимального порядка $\widetilde \Omega $, основанный на разложении в цепную дробь, описан в книге [1, гл. II, § 7]. В конце этой книги в табл. 1 приведены значения основных единиц $\varepsilon > 1$ максимальных порядков полей $\mathbb{Q}(\sqrt d )$ для $2 \leqslant d \leqslant 101$, $d \in \mathbb{Z}$.
Таблица 1.
Решения уравнения (28) (71), β = 4 в параллелепипеде (78)
| No. | ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ |
|---|---|---|---|
| 1 | –14 | +5 | +4 |
| 2 | –14 | –25 | +9 |
| 3 | –13 | –19 | –6 |
| 4 | –11 | –2 | +1 |
| 5 | –8 | –1 | +1 |
| 6 | –6 | –1 | +1 |
| 7 | –4 | –9 | –7 |
| 8 | –3 | –10 | +1 |
| 9 | –3 | –2 | +1 |
| 10 | –2 | –1 | –11 |
| 11 | –2 | –1 | +0 |
| 12 | –1 | –1 | +0 |
| 13 | +0 | +3 | –5 |
| 14 | +0 | –2 | +1 |
| 15 | +0 | –1 | +1 |
| 16 | +0 | +3 | +1 |
| 17 | +1 | +2 | +1 |
| 18 | +2 | +3 | +1 |
| 19 | +3 | +9 | –2 |
| 20 | +3 | –1 | +0 |
| 21 | +4 | –1 | –1 |
| 22 | +4 | +4 | +1 |
| 23 | +9 | –6 | +1 |
Для $n = 3$, $m = 2$ ($r = 1$) и $n = 3$, $m = 3$ ($r = 2$) основные единицы максимальных порядков вычислял Вороной [2] с помощью своих пошаговых обобщений цепной дроби. В [6, 7, 12] вычислены многоугольники и многогранники $\partial {\mathbf{H}}$ с помощью других обобщений.
Для $n = 4$, $k = 2$, l = 0, т.е. $m = 2$ ($r = 1$), Парусников [3] вычислил единицы максимальных порядков полей $\mathbb{Q}(\lambda )$ для 41 многочлена (4) с помощью пошагового алгоритма. Но большинство найденных им единиц не являются основными, а являются лишь их целыми степенями.
Напомним, как определить число l вещественных и число k пар комплексно сопряженных корней многочлена (4) в случае, когда нет кратных корней, т.е. дискриминант многочлена $D$ отличен от нуля.
Случай $n = 2$. Тогда $D = b_{1}^{2} - 4{{b}_{2}}$. Имеем l = 2, $k = 0$, если $D > 0$; $k = 1$, если $D < 0$.
Случай $n = 3$. Тогда D = $ - 4b_{1}^{2}{{b}_{3}}\, + \,b_{1}^{2}b_{2}^{2}\, + \,18{{b}_{1}}{{b}_{2}}{{b}_{3}}$ – – $4b_{2}^{2}$ – $27b_{3}^{2}$. Имеем $l = 3,k = 0$, если $D > 0$; l = 1, $k = 1$, если $D < 0$.
Случай $n = 4$. Тогда
Здесь ${{D}_{1}}$ и ${{D}_{2}}$ – субдискриминанты многочлена (4).
$l = 2,$ $k = 1,$ если $D < 0$;
$l = 0,$ $k = 2,$ если $D > 0$ и либо ${{D}_{1}} = {{D}_{2}} = 0$, либо хотя бы один из ${{D}_{1}}$ и ${{D}_{2}}$ отрицателен;
$l = 4,$ $k = 0,$ если все $D,{{D}_{1}},{{D}_{2}}$ положительны [14, 15].
IX. ПРИМЕР СЛУЧАЯ $n = 2,$ $l = 2,$ $k = 0$
Пусть $p(\xi ) = {{\xi }^{2}} - 5$. Тогда $n = 2$, а корни многочлена $p(\xi )$ суть $\lambda = \pm \sqrt 5 \approx \pm 2.23605$. Поэтому $k = 0$, $l = 2$, $m = k + l = 2$ и $r = m - 1 = 1$. Разложение $\sqrt 5 $ в цепную дробь имеет вид
Подходящие дроби суть
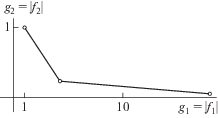
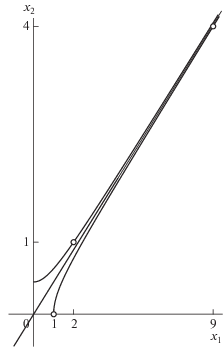
На рис. 1 показаны: прямая ${{x}_{2}} = {{x}_{1}}{\text{/}}\sqrt 5 $, кривые $x_{1}^{2} - 5x_{2}^{2}$ = ±1 и лежащие на них точки $({{x}_{1}},{{x}_{2}}):(1,0)$, (2, 1), (9, 4), соответствующие подходящим дробям. На рис. 1 масштабы по осям разные. Здесь ${{f}_{1}}(X)\, = \,{{x}_{1}}\, + \,{{x}_{2}}\sqrt 5 $, ${{f}_{2}}(X) = {{x}_{1}} - {{x}_{2}}\sqrt 5 $ и f(X) = $x_{1}^{2}\, - \,5x_{2}^{2}$. В координатах ${{g}_{i}}(X) = \left| {{{f}_{i}}(X)} \right|$, $i = 1,2$, для целочисленных X получаем ломаную линию, показанную на рис. 2. Ее вершины соответствуют подходящим дробям. Вообще, если ${{\lambda }_{1}} > 0$ – корень квадратного уравнения, то подходящим дробям цепной дроби числа ${{\lambda }_{1}}$ соответствуют вершины ломаной $\partial {\mathbf{H}}$.
Рис. 1.
Прямая ${{x}_{2}} = {{x}_{1}}{\text{/}}\sqrt 5 $, кривые $x_{1}^{2} - 5x_{2}^{2} = \pm 1$ и точки, соответствующие подходящим дробям цепной дроби $\sqrt 5 $. Масштабы по осям разные.
Основная единица максимального порядка $\widetilde \Omega $ есть $\varepsilon \, = \,(1\, + \,\lambda ){\text{/}}2\, \approx \,1.61803$, т.е. в записи (5) ${{x}_{1}}\, = \,{{x}_{2}}$ = = 1/2. Поскольку $N(X) = x_{1}^{2} - 5x_{2}^{2}$, то $N(\varepsilon ) = - 1$ и квазиосновная единица порядка $\widetilde \Omega $ есть $\hat {\varepsilon } = {{\varepsilon }^{2}} = (3 + \lambda ){\text{/}}2$ ≈ 2.61803. Основная единица кольца $\mathbb{Z}[\lambda ]$ есть ${{\varepsilon }^{3}}\, = \,2\, + \,\lambda \, \approx \,4.23605$ с нормой $N({{\varepsilon }^{3}})$ = = –1. Наконец, квазиосновная единица этого кольца есть $\hat {\varepsilon } = {{\varepsilon }^{6}} = 9 + 4\lambda \approx 17.94421$.
Уравнение (48) здесь имеет вид $x_{1}^{2} - 5x_{2}^{2} = \beta $. Положим $\beta = 4$ и найдем все целочисленные решения $({{x}_{1}},{{x}_{2}})$ уравнения
т.е. $\xi ({{x}_{1}},{{x}_{2}}) = {{x}_{1}} + {{x}_{2}}\sqrt 5 \in \mathbb{Z}(\sqrt 5 )$. Ограничимся решениями ${{x}_{1}},{{x}_{2}} \geqslant 0$, остальные решения получаются изменением знаков. Поэтому наша основная единица – это $\hat {\varepsilon } = {{\varepsilon }^{6}} = 9 + 4\sqrt 5 $ ≈ 17.94421 < 18. Фундаментальная область в координатах ${{x}_{1}},\;{{x}_{2}}$ – это
в координатах ${{x}_{1}},\;{{x}_{2}}$ – это
(39)
$1 \leqslant {{f}_{1}}\;\mathop = \limits^{{\text{def}}} \;{{x}_{1}} + {{x}_{2}}\sqrt 5 \leqslant \hat {\varepsilon } < 18.$На кривой (66) над  выполнены неравенства $4{\text{/}}\hat {\varepsilon } \leqslant {{f}_{2}}\;\mathop = \limits^{{\text{def}}} \;{{x}_{1}} - {{x}_{2}}\sqrt 5 \leqslant 4$, т.е.
выполнены неравенства $4{\text{/}}\hat {\varepsilon } \leqslant {{f}_{2}}\;\mathop = \limits^{{\text{def}}} \;{{x}_{1}} - {{x}_{2}}\sqrt 5 \leqslant 4$, т.е.
На плоскости $({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}$ неравенства (39), (40) выделяют четырехугольник, ограниченный прямыми ${{f}_{1}} = 1$, ${{f}_{1}} = 18$, ${{f}_{2}} = 2{\text{/}}9$, ${{f}_{2}} = 4$ и показанный на рис. 3. На нем показана ветвь кривой $f(X) = 4$ и три выделенных точки на ней.
Рис. 3.
Область в ${{\mathbb{R}}^{2}}$, где содержатся все выделенные решения $\xi _{i}^{0}$, заштрихована. Показана кривая $x_{1}^{2} - 5x_{2}^{2}$ = 4 и выделенные точки на ней.
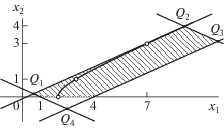
Вершины этого четырехугольника суть
(41)
$\begin{gathered} {{Q}_{1}} = \left( {\frac{1}{2} + \frac{1}{9},\frac{1}{{2\sqrt 5 }} - \frac{1}{{9\sqrt 5 }}} \right) \approx (0.61111,\,\,0.17392), \\ {{Q}_{2}} = \left( {9 + \frac{1}{9},\frac{9}{{\sqrt 5 }} - \frac{1}{{9\sqrt 5 }}} \right) \approx (9.11111,\,\,3.97524), \\ {{Q}_{3}} = \left( {11,\frac{7}{{\sqrt 5 }}} \right) \approx (11,3.13051), \\ {{Q}_{4}} = \left( {\frac{5}{2}, - \frac{{3\sqrt 5 }}{{10}}} \right) \approx (2.5, - 0.67082). \\ \end{gathered} $Теперь для каждого целого ${{x}_{2}}:0 \leqslant {{x}_{2}} \leqslant 3$ переберем все целые ${{x}_{1}}:1 \leqslant {{x}_{1}} < 11$ и выберем среди таких точек $({{x}_{1}},{{x}_{2}})$ решения уравнения (66). Получаем точки $(2,0)$, $(3,1)$, $(7,3)$. Поскольку отношения $(3 + \sqrt 5 ){\text{/}}2$, $(7 + 3\sqrt 5 ){\text{/}}2$, $\tfrac{{7 + 3\sqrt 5 }}{{3 + \sqrt 5 }} = \tfrac{{3 + \sqrt 5 }}{2}$ не лежат в $\mathbb{Z}[\sqrt 5 ]$, то получим три выделенных решения $\xi _{1}^{0} = 2$, $\xi _{2}^{0} = 3 + \sqrt 5 $, $\xi _{3}^{0} = 7 + 3\sqrt 5 $. По теореме 5 все решения с ${{x}_{1}},{{x}_{2}} \geqslant 0$ имеют вид
10. ПРИМЕР СЛУЧАЯ $n = 3,l = 3,k = 0$
Пусть $p(\xi ) = {{\xi }^{3}} - 7\xi - 2$, все его корни вещественны:
Здесь $n = m = l = 3$, $k = 0$, $r = m - 1 = 2$. Фундаментальный базис максимального порядка $\widetilde \Omega $ есть $1,\lambda ,(\lambda + {{\lambda }^{2}}){\text{/}}2$. Здесь ${{b}_{1}} = 0,$ ${{b}_{2}} = - 7,$ ${{b}_{3}} = - 2$ и согласно разделу VI
(43)
$\begin{gathered} f(X) = x_{1}^{3} - 7{{x}_{1}}x_{2}^{2} + 2x_{2}^{3} + 14x_{1}^{2}{{x}_{2}} - \\ - \;6{{x}_{1}}{{x}_{2}}{{x}_{3}} + 49{{x}_{1}}x_{3}^{2} - 14{{x}_{2}}x_{3}^{2} - 8x_{3}^{3}. \\ \end{gathered} $Вычисления проведем в 6 шагов раздела V.
Шаг 1. Вычисляя значения $g(Y)$ на точках ξ = = ${{y}_{1}} + {{y}_{2}}\lambda + {{y}_{3}}(\lambda + {{\lambda }^{2}}){\text{/}}2$ с целыми ${{y}_{i}}$, находим единицы ${{\varepsilon }_{i}} = ({{y}_{1}},{{y}_{2}},{{y}_{3}})$: ${{\varepsilon }_{1}} = (0,0,1)$, ${{\varepsilon }_{2}} = (1,2,2)$, ${{\varepsilon }_{3}} = ( - 2,0,1)$, ${{\varepsilon }_{4}} = ( - 10, - 2,3)$, ${{\varepsilon }_{5}} = (5,2, - 2)$, ε6 = = $(0,2, - 1)$.
Шаг 2. Вычисляем выпуклую оболочку соответствующих точек ${{G}_{0}},{{G}_{i}} = G({{Y}_{i}})$, $i = 1,\; \ldots ,\;6$, и получаем у нее 6 двумерных граней. Их логарифмические проекции на плоскость ${{h}_{1}},\;{{h}_{2}}$ показаны на рис. 4. На нем логарифмические проекции ребер показаны прямыми отрезками, хотя они являются криволинейными. Заметим, что ${{\varepsilon }_{{i + 3}}} = \varepsilon _{i}^{{ - 1}}$, i = 1, 2, 3.
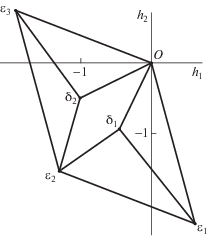
Рис. 4.
Логарифмическая проекция вершин, ребер и граней многогранника $\partial {\mathbf{\tilde {H}}}$. Показаны проекции единиц, близкие к нулю. Проекции ребер выпрямлены.
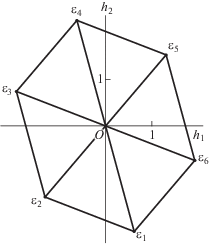
Шаг 3. Здесь любая пара ${{\varepsilon }_{i}}$ и ${{\varepsilon }_{j}} \ne \varepsilon _{i}^{{ \pm 1}}$ (i, j = = $1, \ldots ,6$) образует набор фундаментальных единиц.
Шаг 4. Для пары ${{\varepsilon }_{1}}$, ${{\varepsilon }_{3}}$ фундаментальная область $\mathcal{F}$ – четырехугольник с вершинами 0, ε1, ${{\varepsilon }_{2}},{{\varepsilon }_{3}}$.
Шаг 5. Логарифмическая проекция границы выпуклой оболочки значений $G(Y)$ по $Y \in {{\mathbb{Z}}^{3}}$ с $H'(Y) \in \mathcal{F}$ показана на рис. 5. Тут имеются две новые вершины: ${{\delta }_{1}} = (0,1,1)$ и ${{\delta }_{2}} = (1,1,1)$. На них $g(Y)$ = 2. Имеется четырехугольная грань с вершинами $0,\;{{\delta }_{1}},\;{{\varepsilon }_{2}},\;{{\delta }_{2}}$.
Шаг 6. Сдвигая фундаментальную область рис. 5 на целочисленные линейные комбинации логарифмов известных единиц, получаем схематическую проекцию всего многогранника $\partial {\mathbf{H}}$ на плоскость ${{h}_{1}},\;{{h}_{2}}$, показанную на рис. 6. На рис. 7 показана точная логарифмическая проекция многогранника $\partial {\mathbf{H}}$ на плоскость ${{h}_{1}},\;{{h}_{2}}$; проекции ребер криволинейны. Отрезки в ромбах – это ошибки: их не должно быть. Этот рисунок взят из [7], куда он попал из [13].
Рис. 6.
Логарифмическая проекция многогранника $\partial {\mathbf{H}}$ на часть плоскости ${{h}_{1}},{{h}_{2}}$.
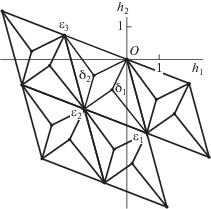
Рис. 7.
Аналог рис. 6 с точными проекциями ребер. Ребра, разделяющие ромбы на треугольники, ошибочны.
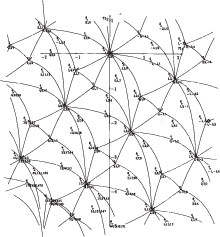
Этот пример взят у Вороного [2, § 59, пример]. Там найдены две пары основных единиц ${{\varepsilon }_{2}},\;{{\varepsilon }_{3}}$ и ${{\varepsilon }_{2}},\;{{\varepsilon }_{4}}$, но нет аналогов наших рисунков. На самом деле, в этом примере граница $\partial {\mathbf{H}}$ вычисляется сразу как выпуклая оболочка значений $G(Y)$ по $Y \in {{\mathbb{Z}}^{3}}$, ибо размерность задачи n = 3 невелика. Но здесь показано разбиение на шаги, которое может быть полезным при больших размерностях $n$ и m.
Найдем все решения $X$ с $\xi (X) \in \widetilde \Omega $ уравнения (48) с $\beta = 4$. В единице ${{\varepsilon }_{1}}$ формы
В единице ${{\varepsilon }_{3}}$ формы
Используем второй способ нахождения выделенных решений. Согласно рис. 4 фундаментальная область $\mathcal{F}$ лежит внутри квадрата
(46)
$\begin{gathered} \mathcal{G} = \{ \ln (0.147) \leqslant {{h}_{1}} \leqslant \ln (1.853), \\ \ln (0.102) \leqslant {{h}_{2}} \leqslant \ln (2.102)\} . \\ \end{gathered} $Над этим квадратом лемма 1 принимает вид
(47)
$\begin{gathered} 0.147 \leqslant {{g}_{1}}(X) \leqslant 1.853, \\ 0.102 \leqslant {{g}_{2}}(X) \leqslant 2.102. \\ \end{gathered} $Для решения уравнения $g(X) = 4$ имеем
Поэтому для этих решений над квадратом $G$
Теперь согласно (75) все выделенные решения находятся в области
(48)
$\begin{gathered} - 1.853 \leqslant {{f}_{1}}(X) \leqslant 1.853, \\ - 2.102 \leqslant {{f}_{2}}(X) \leqslant 2.102, \\ \end{gathered} $Максимальные значения модулей координат этих точек суть
В параллелепипеде
имеется 23 решения нашего уравнения (28), приведенные в табл. 1.
Из них отберем те, отношения которых не лежат в решетке: ${{x}_{1}} \in \mathbb{Z}$, $2{{x}_{3}} \in \mathbb{Z}$, ${{x}_{2}} \in \mathbb{Z}$, если ${{x}_{3}} \in \mathbb{Z}$, и $2{{x}_{2}} \in \mathbb{Z}$, если ${{x}_{3}}\not { \in }\mathbb{Z}$. В $\mathbb{Q}(\lambda )$ отношение двух чисел $X{\text{/}}Y = Z$, если
(51)
$\begin{gathered} X = {{x}_{1}} + {{x}_{2}}\lambda + {{x}_{3}}{{\lambda }^{2}} = \\ = \;({{y}_{1}} + {{y}_{2}}\lambda + {{y}_{3}}{{\lambda }^{2}})({{z}_{1}} + {{z}_{2}}\lambda + {{z}_{3}}{{\lambda }^{3}}), \\ \end{gathered} $Результат показан в табл. 2.
Таблица 2.
Точки $\xi _{1}^{0},\;...,\;\xi _{5}^{0}$
| No. | ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ |
|---|---|---|---|
| 1 | –14 | –25 | 9 |
| 2 | –14 | 5 | 4 |
| 3 | –13 | –19 | –6 |
| 4 | –11 | –2 | 1 |
| 5 | –8 | –1 | 1 |
Согласно теореме 4 все решения $\xi \in \widetilde \Omega $ уравнения (48) суть
XI. ПРИМЕРЫ СЛУЧАЯ $n = 3,l = 1,k = 1$
Пусть $p(\xi ) = {{\lambda }^{3}} + 22{{\lambda }^{2}} + 11\lambda + 25$. Этот пример взят из [12, табл. 2]. Здесь
Здесь ${{b}_{1}} = 22$, ${{b}_{2}} = 11$, ${{b}_{3}} = 25$ и согласно разделу VI
Результаты вычисления выпуклой ломаной $\partial {\mathbf{H}}$ для $\xi \in \mathbb{Z}(\lambda )$ на плоскости ${{g}_{1}}(X) = \left| {{{f}_{1}}(X)} \right|$, g2(X) = = $\left| {{{f}_{2}}(X)} \right|$ приведены в табл. 3. Каждая ее строка соответствует вершине ломаной $\partial {\mathbf{H}}$ и содержит x1, ${{x}_{2}},{{x}_{3}},$ $g(X) = \left| {f(X)} \right|,$ ${{g}_{1}}(X)$, ${{g}_{2}}(X)$, $ln{{g}_{1}}$, $ln{{g}_{2}}$.
Таблица 3.
Вершины ломаной $\partial {\mathbf{H}}$ для $p(\xi ) = {{\lambda }^{3}} + 22{{\lambda }^{2}} + 11\lambda + 25$
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ | $g(X)$ | ${{g}_{1}}(X)$ | ${{g}_{2}}(X)$ | $ln{{g}_{1}}$ | $ln{{g}_{2}}$ |
|---|---|---|---|---|---|---|---|
| 29 | –171 | –8 | 1 | 2.711e-05 | 3.689e+04 | –10.52 | 10.52 |
| 96 | 26 | 1 | 109 | 0.01261 | 8645 | –4.373 | 9.065 |
| 8 | 65 | 3 | 113 | 0.02463 | 4587 | –3.704 | 8.431 |
| 43 | 2 | 0 | 157 | 0.08653 | 1814 | –2.447 | 7.503 |
| 10 | 22 | 1 | 85 | 0.1605 | 529.7 | –1.83 | 6.272 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 109 | 465.1 | 0.2344 | 6.142 | –1.451 |
| 2 | 1 | 2 | 113 | 908.7 | 0.1244 | 6.812 | –2.085 |
| 8 | 3 | 7 | 157 | 3192 | 0.04918 | 8.068 | –3.012 |
| 15 | 6 | 13 | 85 | 5919 | 0.01436 | 8.686 | –4.243 |
| 94 | 37 | 81 | 1 | 3.689e+04 | 2.711e-05 | 10.52 | –10.52 |
В верхней и нижней строках таблицы стоят основные единицы $\varepsilon = 29 - 171\lambda - 8{{\lambda }^{2}}$ и $\varepsilon \, = \,94\, + \,37\lambda $ + + 81λ2. Видна периодичность значений $g(X)$ на этих вершинах.
Аналогичные вычисления вершин ломаной $\partial {\mathbf{H}}$ были проделаны и для других случаев n = 3, $D < 0$ из статьи [12, таблицы 3–7]. Их результаты приводятся ниже в виде таблиц 4–8.
Таблица 4.
Вершины ломаной $\partial {\mathbf{H}}$ для $p(\xi ) = {{\xi }^{3}} + 19{{\xi }^{2}} + 11\xi + 18$
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ | $g(X)$ | ${{g}_{1}}(X)$ | ${{g}_{2}}(X)$ | $ln{{g}_{1}}$ | $ln{{g}_{2}}$ |
|---|---|---|---|---|---|---|---|
| 49 | –145 | –8 | 1 | 3.723e-05 | 2.686e+04 | –10.2 | 10.2 |
| 67 | 59 | 3 | 64 | 0.01203 | 5319 | –4.42 | 8.579 |
| 10 | 19 | 1 | 8 | 0.02475 | 323.2 | –3.699 | 5.778 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 64 | 323.2 | 0.198 | 5.778 | –1.619 |
| 2 | 1 | 2 | 8 | 664.9 | 0.01203 | 6.5 | –4.42 |
| 79 | 44 | 81 | 1 | 2.686e+04 | 3.723e-05 | 10.2 | –10.2 |
Таблица 5.
Вершины ломаной $\partial {\mathbf{H}}$ для $p(\xi ) = {{\xi }^{3}} + 16{{\xi }^{2}} + 8\xi + 20$
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ | $g(X)$ | ${{g}_{1}}(X)$ | ${{g}_{2}}(X)$ | $ln{{g}_{1}}$ | $ln{{g}_{2}}$ |
|---|---|---|---|---|---|---|---|
| 29 | 33 | 2 | 1 | 0.0006028 | 1659 | –7.414 | 7.414 |
| 9 | –15 | –1 | 65 | 0.1467 | 443.1 | –1.919 | 6.094 |
| 7 | 16 | 1 | 87 | 0.2846 | 305.7 | –1.257 | 5.722 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 65 | 243.4 | 0.2671 | 5.495 | –1.32 |
| 3 | 1 | 2 | 87 | 472.2 | 0.1842 | 6.157 | –1.691 |
| 9 | 3 | 7 | 1 | 1659 | 0.0006028 | 7.414 | –7.414 |
Таблица 6.
Вершины ломаной $\partial {\mathbf{H}}$ для $p(\xi ) = {{\xi }^{3}} - 4{{\xi }^{2}} + 25\xi + 17$
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ | $g(X)$ | ${{g}_{1}}(X)$ | ${{g}_{2}}(X)$ | $ln{{g}_{1}}$ | $ln{{g}_{2}}$ |
|---|---|---|---|---|---|---|---|
| 121 | 396 | 324 | 1 | 9.91e-09 | 1.009e+08 | –18.43 | 18.43 |
| –317 | –479 | 65 | 11 | 1.535e-06 | 7.167e+06 | –13.39 | 15.79 |
| 11 | 40 | 36 | 27 | 2.212e-05 | 1.221e+06 | –10.72 | 14.01 |
| –11 | –29 | –18 | 13 | 3.871e-05 | 3.359e+05 | –10.16 | 12.72 |
| –11 | –18 | 0 | 1 | 9.953e-05 | 1.005e+04 | –9.215 | 9.215 |
| 1 | 1 | –1 | 11 | 0.01542 | 713.4 | –4.172 | 6.57 |
| –1 | –2 | 0 | 27 | 0.2222 | 121.5 | –1.504 | 4.8 |
| 1 | 1 | 0 | 13 | 0.3889 | 33.43 | –0.9445 | 3.509 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
Таблица 7.
Вершины ломаной $\partial {\mathbf{H}}$ для $p(\xi ) = {{\xi }^{3}} - 8{{\xi }^{2}} + 21\xi + 13$
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ | $g(X)$ | ${{g}_{1}}(X)$ | ${{g}_{2}}(X)$ | $ln{{g}_{1}}$ | $ln{{g}_{2}}$ |
|---|---|---|---|---|---|---|---|
| 170 | 243 | –173 | 3 | 2.628e-07 | 1.142e+07 | –15.15 | 16.25 |
| 91 | 135 | –83 | 13 | 5.365e-06 | 2.423e+06 | –12.14 | 14.7 |
| 12 | 27 | 7 | 1 | 1.047e-05 | 9.554e+04 | –11.47 | 11.47 |
| 1 | 4 | 4 | 9 | 0.0006305 | 1.427e+04 | –7.369 | 9.566 |
| –10 | –19 | 1 | 9 | 0.00125 | 7197 | –6.684 | 8.881 |
| –9 | –15 | 5 | 11 | 0.001881 | 5848 | –6.276 | 8.674 |
| 9 | 16 | –3 | 29 | 0.01099 | 2639 | –4.511 | 7.878 |
| –1 | –2 | 0 | 3 | 0.02511 | 119.5 | –3.685 | 4.783 |
| 0 | –1 | 0 | 13 | 0.5126 | 25.36 | –0.6683 | 3.233 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 51 | –17 | 2 | 9 | 60.24 | 0.1494 | 4.098 | –1.901 |
| 101 | –34 | 4 | 9 | 119.5 | 0.07533 | 4.783 | –2.586 |
| 152 | –51 | 6 | 11 | 179.7 | 0.06121 | 5.191 | –2.793 |
| 888 | –298 | 35 | 29 | 1050 | 0.02762 | 6.956 | –3.589 |
| 2029 | –681 | 80 | 3 | 2399 | 0.00125 | 7.783 | –6.684 |
$p(\xi ) = {{\xi }^{3}} + 19{{\xi }^{2}} + 11\xi + 18$; ${{\lambda }_{1}} \approx - 18.4568$, λ2,3 ≈ ≈ $ - 0.27517 \pm 0.94947i$. Табл. 4.
$p(\xi ) = {{\xi }^{3}} + 16{{\xi }^{2}} + 8\xi + 20$; ${{\lambda }_{1}} \approx - 15.56866$, λ2 ≈ ≈ $ - 0.215669 \pm 1.1127078i$. Табл. 5.
$p(\xi )\, = \,{{\xi }^{3}} - 4{{\xi }^{2}}\, + \,25\xi \, + \,17$; ${{\lambda }_{1}} \approx - 0.6111166$, λ2,3 ≈ ≈ $2.305558 \pm 4.74366i$. Табл. 6.
$p(\xi )\, = \,{{\xi }^{3}} - 8{{\xi }^{2}} + 21\xi + 13$; ${{\lambda }_{1}} \approx - 0.5125546$, λ2,3 ≈ ≈ $4.256277 \pm 2.692072i$. Табл. 7.
$p(\xi ) = {{\xi }^{3}} - 5{{\xi }^{2}} + 11\xi + 9$; ${{\lambda }_{1}} \approx - 0.6210714$, λ2,3 ≈ ≈ $2.8105357 \pm 2.567484i$. Табл. 8.
Таблица 8.
Вершины ломаной $\partial {\mathbf{H}}$ для p(ξ) = ξ3 – $5{{\xi }^{2}} + 11\xi $ + 9
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ | $g(X)$ | ${{g}_{1}}(X)$ | ${{g}_{2}}(X)$ | $ln{{g}_{1}}$ | $ln{{g}_{2}}$ |
|---|---|---|---|---|---|---|---|
| –1 | –1 | 1 | 1 | 0.006801 | 147 | –4.991 | 4.991 |
| 1 | 1 | 0 | 8 | 0.3789 | 21.11 | –0.9704 | 3.05 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 44 | –17 | 3 | 8 | 55.72 | 0.1436 | 4.02 | –1.941 |
| 116 | –45 | 8 | 1 | 147 | 0.006801 | 4.991 | –4.991 |
XII. ПРИМЕРЫ СЛУЧАЯ $n = 4,\;l = 0,\;k = 2$
В препринте [3] В.И. Парусников вычислил по паре единиц для 41 многочлена (5) с $n = 4$ и двумя парами комплексных корней ${{\lambda }_{1}},\;{{\lambda }_{2}},\;{{\bar {\lambda }}_{1}},\;{{\bar {\lambda }}_{2}}$. По теореме Дирихле в этих случаях имеется ровно одна фундаментальная единица. Здесь получаем две формы
Таблица 9.
Основные единицы для многочленов 4-й степени
| N | p(ξ) | D2 | D1 | D | ε(λ) | V | μ2 | μ3 |
| 1 | ${{\xi }^{4}} - 2{{\xi }^{2}} + 2$ | 16 | –64 | 512 | $1 + \lambda - {{\lambda }^{2}} - {{\lambda }^{3}}$ | 0 | ${{\varepsilon }^{2}}( - \lambda )$ | $ - {{\varepsilon }^{{ - 3}}}(\lambda )$ |
| 2 | ${{\xi }^{4}} - {{\xi }^{2}} + 2$ | 8 | –56 | 1568 | $1 - {{\lambda }^{2}} - {{\lambda }^{3}}$ | 1 | ${{\varepsilon }^{3}}(\lambda )$ | ${{\varepsilon }^{{ - 3}}}(\lambda )$ |
| 3 | ${{\xi }^{4}} - {{\xi }^{2}} + \xi + 2$ | 8 | –92 | 1257 | $ - 1 + {{\lambda }^{2}} - {{\lambda }^{3}}$ | 0 | $ - {{\varepsilon }^{{ - 1}}}(\lambda )$ | $ - {{\varepsilon }^{{ - 1}}}(\lambda )$ |
| 4 | ${{\xi }^{4}} + 2$ | 0 | 0 | 2048 | $1 - {{\lambda }^{2}} - {{\lambda }^{3}}$ | 0 | $ - \varepsilon (\lambda )$ | $ - \varepsilon (\lambda )$ |
| 5 | ${{\xi }^{4}} + \xi + 2$ | 0 | –36 | 2021 | $3 - \lambda + {{\lambda }^{3}}$ | 1 | ${{\varepsilon }^{4}}(\lambda )$ | |
| 6 | ${{\xi }^{4}} + 2\xi + 2$ | 0 | –144 | 1616 | $1 + \lambda - {{\lambda }^{2}} + {{\lambda }^{3}}$ | 0 | $ - \varepsilon (\lambda )$ | $ - \varepsilon (\lambda )$ |
| 7 | ${{\xi }^{4}} + {{\xi }^{2}} + 2$ | –8 | 56 | 1568 | $1 + \lambda + {{\lambda }^{2}}$ | 0 | $ - {{\varepsilon }^{{ - 3}}}(\lambda )$ | |
| 8 | ${{\xi }^{4}} + {{\xi }^{2}} + \xi + 2$ | –8 | 20 | 1825 | $ - 1 - \lambda + {{\lambda }^{2}} - {{\lambda }^{3}}$ | 0 | ${{\varepsilon }^{5}}(\lambda )$ | $ - {{\varepsilon }^{3}}(\lambda )$ |
| 9 | ${{\xi }^{4}} + {{\xi }^{2}} + 2\xi + 2$ | –8 | –88 | 2272 | $1 - 3\lambda + 2{{\lambda }^{2}} - {{\lambda }^{3}}$ | 2 | ||
| 10 | ${{\xi }^{4}} + 2{{\xi }^{2}} + 2$ | –16 | 64 | 512 | $1 - \lambda - {{\lambda }^{3}}$ | 0 | ${{\varepsilon }^{{ - 4}}}(\lambda )$ | ? |
| 11 | ${{\xi }^{4}} + 2{{\xi }^{2}} + 2\xi + 2$ | –16 | –80 | 5526 | $ - 3 - \lambda - {{\lambda }^{3}}$ | 1 | ${{\varepsilon }^{4}}(\lambda )$ | ${{\varepsilon }^{3}}(\lambda )$ |
| 12 | ${{\xi }^{4}} + {{\xi }^{3}} - 2{{\xi }^{2}} - \xi + 2$ | 19 | –54 | 257 | $1 - \lambda - {{\lambda }^{2}}$ | 0 | ${{\varepsilon }^{{ - 2}}}(\lambda )$ | ${{\varepsilon }^{{ - 4}}}(\lambda )$ |
| 13 | ${{\xi }^{4}} + {{\xi }^{3}} - {{\xi }^{2}} - 2\xi + 2$ | 11 | –154 | 1384 | $1 - \lambda - 2{{\lambda }^{2}} - {{\lambda }^{3}}$ | 0 | $ - {{\varepsilon }^{{ - 1}}}(\lambda )$ | $ - {{\varepsilon }^{{ - 1}}}(\lambda )$ |
| 14 | ${{\xi }^{4}} + {{\xi }^{3}} - {{\xi }^{2}} - \xi + 2$ | 11 | –80 | 1556 | $1 - \lambda - 2{{\lambda }^{2}} - {{\lambda }^{3}}$ | 1 | ${{\varepsilon }^{{ - 6}}}(\lambda )$ | ${{\varepsilon }^{{ - 3}}}(\lambda )$ |
| 15 | ${{\xi }^{4}} + {{\xi }^{3}} - {{\xi }^{2}} + 2$ | 11 | –892 | 892 | 1 + λ | 0 | ${{\varepsilon }^{{ - 8}}}(\lambda )$ | ${{\varepsilon }^{{ - 4}}}(\lambda )$ |
Для уравнения с n = 10 найденная Парусниковым единица ${{\mu }_{3}}$ является столь большой (или малой) степенью основной единицы $\varepsilon $, что оказалась вне просчитанной части ломаной $\partial {\mathbf{H}}$. В этом месте поставлен знак вопроса. Пустые места для ${{\mu }_{2}}$ при n = 5, для ${{\mu }_{3}}$ при $n = 7$ и для ${{\mu }_{2}},{{\mu }_{3}}$ при $n = 9$ означают, что Парусников не привел этих значений.
Замечание. Если единица $\varepsilon (\lambda ) = {{x}_{1}} + {{x}_{2}}\lambda + {{x}_{3}}{{\lambda }^{2}}$ + + x4λ3, то обычно число –ε(λ) = $ - {{x}_{1}} - {{x}_{2}}\lambda - {{x}_{3}}{{\lambda }^{2}}$ – – x4λ3 является также единицей. Но для биквадратного многочлена $p(\xi )$ число ε(–λ) = x1 – ${{x}_{2}}\lambda \, + \,{{x}_{3}}{{\lambda }^{2}}$ – – x4λ3 также является единицей с той же нормой, ибо вместе с корнем $\lambda $ многочлен $p(\xi )$ имеет корень $ - \lambda $. В табл. 9 такими являются многочлены для $n = 1,2,4,7,10$.
XIII. ПЕРСПЕКТИВЫ
Алгоритм разложения в обычную цепную дробь является пошаговым, и каждый шаг однозначен. Алгоритм вычисления обобщенной цепной дроби является глобальным, он не разбивается на шаги и требует большого объема вычислений.
Пример. Марков [18] вычислил фундаментальную единицу
кольца $\mathbb{Z}[\lambda ]$ с ${{\lambda }^{3}} = 23$. Для ее вычисления по алгоритму раздела VI требуется перебор значений нормы для $\left| {{{x}_{i}}} \right| \leqslant {{10}^{{11}}}$, $i = 1,2,3$. Правда, Вороной [2, отдел II] вычислил к ней обратную фундаментальную единицу за 21 шаг своего алгоритма. Для ее вычисления алгоритмом раздела VI требуется перебор значений нормы (81) для $\left| {{{x}_{i}}} \right| \leqslant {{10}^{6}}$, $i = 1,2,3$.Поэтому для разных n и m желательно найти более простые алгоритмы последовательного вычисления вершин многогранника H. Здесь возможны два следующих подхода.
Подход 1. Пусть известны все вершины ${{V}_{1}}, \ldots ,{{V}_{s}}$ некоторой гиперграни $H_{j}^{{(m - 1)}}$ многогранника H. Надо найти все вершины примыкающих к ней гиперграней многогранника H. При этом можно различать несколько случаев и делать некоторый перебор. Такие алгоритмы для n = 3, $m = 1$ и n = 3, $m = 2$ были предложены автором и В.И. Парусниковым в [6, 12, 19–21].
Подход 2. Вместе с многогранником ${\mathbf{H}}$ в ${{\mathbb{R}}^{n}}$ рассматривать сопряженный многогранник ${{{\mathbf{H}}}_{*}}$ в двойственном пространстве $\mathbb{R}_{*}^{n}$ и двигаться по ним одновременно в зависимости о взаимных свойств граней. Для $n = 3$, $m = 2$ несколько случаев таких пар многогранников описаны в [7, 13 ]. Отметим, что для обычной цепной дроби многогранники H и ${{{\mathbf{H}}}_{*}}$ совпадают, т.е. являются самосопряженными.
Для детальной разработки алгоритмов указанных двух подходов потребуется вычислить много разных примеров с помощью описанного алгоритма обобщенной цепной дроби. Кроме того, надо проверить гипотезу 2 и найти способ ее доказательства.
Список литературы
Боревич З.И., Шафаревич И.Р. Теория чисел. Наука, М. 1972.
Вороной Г.Ф. Об одном обобщении алгорифма непрерывных дробей, Из-во Варш. Ун-та, Варшава, 1896. Также: Собр. соч. в 3-х томах. Из-во АН УССР. Киев. 1952. Т. 1. С. 197–391.
Парусников В.И. Четырехмерное обобщение алгоритма цепных дробей. Препринты ИПМ им. М.В. Келдыша. 2011. № 78. 16 с. http://library.keldysh. ru/preprint.asp?id 11-78.
Хинчин А.Я. Цепные дроби. Физматгиз, М. 1961.
Брюно А.Д. Разложения алгебраических чисел в цепные дроби, Журнал вычислительной матем. и матем. физики. 1964. Т. 4. № 2. С. 211–221.
Bruno A.D. New generalizations of continued fraction. I, Functiones et Approximatio. 2010. V. 43. № 1. P. 55–104.
Брюно А.Д. Универсальное обобщение алгоритма цепной дроби. Чебышевский сборник (Тула). 2015. Т. 16. № 2. С. 35–65.
Брюно А.Д. Структура многомерных диофантовых приближений. ДАН. 2010. Т. 433. № 5. С. 587–589.
Bruno A.D. Structure of the best Diophantine approximations and multidimensional generalizations of the continued fraction, Чебышевский сборник (Тула). 2010. V. 11. № 1. P. 68–73.
Fukuda K. Exact algorithms and software in optimization and polyhedral computation, Proceed. ISSAC’08 of XXI International Symposium on Symbolic and Algebraic Computations, ACM NY, USA. 2008. P. 333–334.
Barber C.B., Dobkin D.P., Huhdanpaa H.T. The Quickhull algorithm for convex hulls, ACM Trans. on Mathematical Software. 1996. V. 22. № 4. P. 469–483. http://www.qhull.org.
Брюно А.Д. Обобщения цепной дроби. Чебышевский сборник (Тула). 2006. Т. 7. № 3. С. 4–71.
Брюно А.Д., Парусников В.И. Многогранники модулей троек линейных форм. Препринты ИПМ им. М.В. Келдыша, № 93 (2003). 20 с. URL: http://library.keldysh.ru/preprint.asp?id 03-93.
Basu S., Pollack R., Roy M.-F. Algorithms in Real Algebraic Geometry, Springer-Verlag, Berlin Heidelberg New York. 2006.
Батхин А.Б. Параметризация дискриминантного множества вещественного многочлена. Программирование. 2016. Т. 42. № 2. С. 8–21.
Брюно А.Д. От диофантовых приближений к диофантовым уравнениям. Препринты ИПМ им. М.В. Келдыша, № 1 (2016) 20 с. http://library.keldysh. ru/preprint.asp?id 16-1.
Брюно А.Д. Вычисление наилучших диофантовых приближений и основных единиц алгебраических полей, ДАН. 2016. Т. 468. № 1. С. 6–10.
Markov A.A. Sur les nombres entieres dependents d’une racine cubique d’un nombre entier ordinaire, Mémoires de l’Academie de St.-Petersburg, VII serie, 1892. V. 38. № 9. P. 4–32.
Bruno A.D., Parusnikov V.I. New generalizations of the continued fraction, Keldysh Institute Preprints. № 52, Moscow. 2005. 17 p.
Брюно А.Д., Парусников В.И. Дальнейшее обобщение цепной дроби, ДАН. 2006. Т. 410, № 1. С. 12–16.
Брюно А.Д., Парусников В.И. Двустороннее обобщение цепной дроби, ДАН. 2009. Т. 429, № 6. С. 727–730.
Дополнительные материалы отсутствуют.
Инструменты
Программирование