1. На главную
  2. Электронные версии
  3. Программирование
  4. № 2, 2019

Программирование, 2019, № 2, стр. 32-40

ПРИМЕНЕНИЕ МЕТОДОВ КОМПЬЮТЕРНОЙ АЛГЕБРЫ ДЛЯ ИССЛЕДОВАНИЯ ДИНАМИКИ СИСТЕМЫ ДВУХ СВЯЗАННЫХ ТЕЛ НА КРУГОВОЙ ОРБИТЕ

С. А. Гутник a, b, *, В. А. Сарычев c, **

a Московский государственный институт международных отношений
119454 Москва, проспект Вернадского, 76, Россия

b Московский физико-технический институт
141701 Долгопрудный, Институтский переулок, 9, Россия

c Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

* E-mail: s.gutnik@inno.mgimo.ru
** E-mail: vas31@rambler.ru

Поступила в редакцию 01.09.2018
После доработки 01.09.2018
Принята к публикации 20.09.2018

Полный текст (PDF)

Аннотация

С использованием методов компьютерной алгебры было проведено исследование свойств нелинейной алгебраической системы, определяющей равновесные ориентации системы двух тел соединенных сферическим шарниром, движущихся в центральном ньютоновом силовом поле по круговой орбите под действием гравитационного момента. Для определения равновесных ориентаций связки двух тел проводилась декомпозиция системы, состоящей из двенадцати алгебраических уравнений, с применением методов линейной алгебры и алгоритмов построения базисов Гребнера. Положения равновесия в зависимости от четырех параметров задачи определялись путем исследования числа действительных корней алгебраических уравнений из полученных базисов Гребнера. Проведен анализ эволюции условий существования различного числа равновесий в пространстве безразмерных параметров задачи. Рассматриваются вопросы эффективности алгоритмов построения базисов Гребнера от числа параметров на примере представленной задачи.

I. ВВЕДЕНИЕ

В работе представлены результаты применения методов компьютерной алгебры для исследования динамики движения системы двух тел (спутник-стабилизатор), соединенных сферическим шарниром, движущихся в центральном ньютоновом силовом поле по круговой орбите. Определение положений равновесия связки тел на круговой орбите представляет практический интерес для создания составных схем гравитационной системы ориентации спутников, которые могут функционировать на орбите продолжительное время без расходования энергии. Подробное рассмотрение динамики различных типов составных схем гравитационной системы ориентации спутник-стабилизатор представлено в [1].

В данной работе проведено исследование пространственных положений равновесия (равновесных ориентаций) системы спутник-стабилизатор в орбитальной системе координат при заданных значениях главных центральных моментов инерции тел системы. Действие стабилизатора на спутник позволяет получить новые положения равновесия системы двух тел и ввести диссипацию в систему.

Положения равновесия системы спутник–стабилизатор определяются действительными корнями системы алгебраических уравнений. Для определения равновесных решений проводилась декомпозиция системы алгебраических уравнений с применением методов линейной алгебры и алгоритмов построения базисов Гребнера. Некоторые классы равновесных решений были получены явно из алгебраических уравнений, входящих в базис Гребнера. Найдены значения параметров, при которых изменяется число положений равновесия системы спутник–стабилизатор. Проведен символьно-численный анализ изменения областей существования различного числа равновесий в пространстве безразмерных параметров.

Рассмотрены вопросы эффективности алгоритмов построения базисов Гребнера в зависимости от числа параметров задачи. Исследование проводилось с использованием системы компьютерной алгебры Maple [9].

Алгебраические методы определения положений равновесия системы двух тел, изложенные в данной работе, ранее успешно применялись при анализе динамики спутника-гиростата [2], [3] и динамики спутника с аэродинамической системой ориентации [4]. Исследование полиномиальных систем в задачах механики с применением символьных вычислений является широко используемым приложением компьютерной алгебры. Примеры алгоритмов компьютерной алгебры для решения такого рода задач представлены в [13], [15].

II. УРАВНЕНИЯ ДВИЖЕНИЯ

Рассмотрим задачу о движении системы двух тел, соединенных сферическим шарниром, на круговой орбите [5].

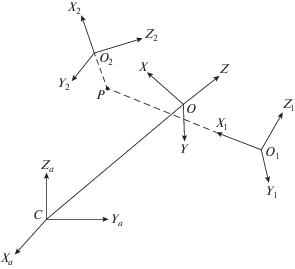
Для записи уравнений движения двух тел введем следующие правые декартовы системы координат (рис. 1): $C{{X}_{a}}{{Y}_{a}}{{Z}_{a}}$ – абсолютная система координат с началом в центре масс Земли С; плоскость $C{{X}_{a}}{{Y}_{a}}$ совпадает с плоскостью экватора, ось $C{{Z}_{a}}$ совпадает с осью вращения Земли. $OXYZ$ – орбитальная система координат. Ось OZ направлена вдоль радиуса-вектора, соединяющего центр масс Земли C и центр масс системы двух тел O; ось $OX$ направлена вдоль вектора линейной скорости центра масс O, ось OY направлена по нормали к плоскости орбиты. ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$ – связанная с i-м телом система координат ($i = 1,2$); ${{O}_{i}}{{x}_{i}}$, ${{O}_{i}}{{y}_{i}}$, ${{O}_{i}}{{z}_{i}}$ – главные центральные оси инерции i-го тела. Ориентацию системы координат ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$ относительно орбитальной системы координат определим с использованием самолетных углов тангажа ${{\alpha }_{i}}$, рыскания ${{\beta }_{i}}$ и крена ${{\gamma }_{i}}$ [1]

Рис. 1.

Основные системы координат.

$\begin{gathered} a_{{11}}^{{(i)}} = cos{{\alpha }_{i}}cos{{\beta }_{i}}, \\ a_{{12}}^{{(i)}} = sin{{\alpha }_{i}}sin{{\gamma }_{i}} - cos{{\alpha }_{i}}sin{{\beta }_{i}}cos{{\gamma }_{i}}, \\ a_{{13}}^{{(i)}} = sin{{\alpha }_{i}}cos{{\gamma }_{i}} + cos{{\alpha }_{i}}sin{{\beta }_{i}}sin{{\gamma }_{i}}, \\ \end{gathered} $
(1)
$\begin{gathered} a_{{21}}^{{(i)}} = sin{{\beta }_{i}},\quad a_{{22}}^{{(i)}} = cos{{\beta }_{i}}cos{{\gamma }_{i}}, \\ a_{{23}}^{{(i)}} = - cos{{\beta }_{i}}sin{{\gamma }_{i}}, \\ \end{gathered} $
$\begin{gathered} a_{{31}}^{{(i)}} = - sin{{\alpha }_{i}}cos{{\beta }_{i}}, \\ a_{{32}}^{{(i)}} = cos{{\alpha }_{i}}sin{{\gamma }_{i}} + sin{{\alpha }_{i}}sin{{\beta }_{i}}cos{{\gamma }_{i}}, \\ a_{{33}}^{{(i)}} = cos{{\alpha }_{i}}cos{{\beta }_{i}} - sin{{\alpha }_{i}}sin{{\beta }_{i}}sin{{\gamma }_{i}}. \\ \end{gathered} $

Пусть $({{a}_{i}},0,0)$ – координаты сферического шарнира P в связанной с телом системе координат ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$; ${{A}_{i}},{{B}_{i}},{{C}_{i}}$ – главные центральные моменты инерции; M = ${{M}_{1}}{{M}_{2}}{\text{/}}({{M}_{1}} + {{M}_{2}})$; Mi – масса i-го тела; ${{p}_{i}}$, ${{q}_{i}}$, ${{r}_{i}}$ – проекции абсолютной угловой скорости i-го тела на оси $O{{x}_{i}}$, $O{{y}_{i}}$, $O{{z}_{i}}$; ${{\omega }_{0}}$ – угловая скорость движения центра масс системы тел по круговой орбите. Тогда, используя выражения для кинетической энергии и силовой функции, определяющей действие гравитационного поля Земли на систему двух тел, соединенных шарниром [1], уравнения движения этой системы можно записать в форме уравнений Лагранжа второго рода, используя возможности символьного дифференцирования в системе Maple, в следующем виде:

${{A}_{i}}\mathop {\dot {p}}\nolimits_i + ({{C}_{i}} - {{B}_{i}}){{q}_{i}}{{r}_{i}} - 3\omega _{0}^{2}({{C}_{i}} - {{B}_{i}})a_{{32}}^{{(i)}}a_{{33}}^{{(i)}} = 0,$
$\begin{gathered} ({{B}_{i}} + Ma_{i}^{2})\mathop {\dot {q}}\nolimits_i - M{{a}_{i}}{{a}_{j}}(a_{{13}}^{{(i)}}a_{{13}}^{{(j)}} + a_{{23}}^{{(i)}}a_{{23}}^{{(j)}} + a_{{33}}^{{(i)}}a_{{33}}^{{(j)}})\mathop {\dot {q}}\nolimits_j + \\ + \;M{{a}_{i}}{{a}_{j}}(a_{{13}}^{{(i)}}a_{{12}}^{{(j)}} + a_{{23}}^{{(i)}}a_{{22}}^{{(j)}} + a_{{33}}^{{(i)}}a_{{32}}^{{(j)}})\mathop {\dot {r}}\nolimits_j + \\ + \;M{{a}_{i}}{{a}_{j}}(a_{{13}}^{{(i)}}({{r}_{j}}({{p}_{j}}a_{{13}}^{{(j)}} - {{r}_{j}}a_{{11}}^{{(j)}}) - \\ - \;{{q}_{j}}({{q}_{j}}a_{{11}}^{{(j)}} - {{p}_{j}}a_{{12}}^{{(j)}})) + \\ \end{gathered} $
(2)
$\begin{gathered} + \;a_{{23}}^{{(i)}}({{r}_{j}}({{p}_{j}}a_{{23}}^{{(j)}} - {{r}_{j}}a_{{21}}^{{(j)}}) - {{q}_{j}}({{q}_{j}}a_{{21}}^{{(j)}} - {{p}_{j}}a_{{22}}^{{(j)}})) + \\ + \;a_{{33}}^{{(i)}}({{r}_{j}}({{p}_{j}}a_{{33}}^{{(j)}} - {{r}_{j}}a_{{31}}^{{(j)}}) - {{q}_{j}}({{q}_{j}}a_{{31}}^{{(j)}} - {{p}_{j}}a_{{32}}^{{(j)}}))) + \\ + \;M{{a}_{i}}\omega _{0}^{2}({{a}_{j}}(a_{{13}}^{{(i)}}a_{{11}}^{{(j)}} + a_{{23}}^{{(i)}}a_{{21}}^{{(j)}} + a_{{33}}^{{(i)}}a_{{31}}^{{(j)}}) + \\ + \;3a_{{33}}^{{(i)}}({{a}_{i}}a_{{31}}^{{(i)}} - {{a}_{j}}a_{{31}}^{{(j)}})) + \\ + \;(({{A}_{i}} - {{C}_{i}}) - Ma_{i}^{2}){{r}_{i}}{{p}_{i}} - 3\omega _{0}^{2}({{A}_{i}} - {{C}_{i}})a_{{33}}^{{(i)}}a_{{31}}^{{(i)}} = 0, \\ \end{gathered} $
$\begin{gathered} ({{C}_{i}} + Ma_{i}^{2})\mathop {\dot {r}}\nolimits_i + M{{a}_{i}}{{a}_{j}}(a_{{12}}^{{(i)}}a_{{13}}^{{(j)}} + a_{{22}}^{{(i)}}a_{{23}}^{{(j)}} + a_{{32}}^{{(i)}}a_{{33}}^{{(j)}})\mathop {\dot {q}}\nolimits_j - \\ - \;M{{a}_{i}}{{a}_{j}}(a_{{12}}^{{(i)}}a_{{12}}^{{(j)}} + a_{{22}}^{{(i)}}a_{{22}}^{{(j)}} + a_{{32}}^{{(i)}}a_{{32}}^{{(j)}})\mathop {\dot {r}}\nolimits_j - \\ - \;M{{a}_{i}}{{a}_{j}}(a_{{12}}^{{(i)}}({{r}_{j}}({{p}_{j}}a_{{13}}^{{(j)}} - {{r}_{j}}a_{{11}}^{{(j)}}) - \\ - \;{{q}_{j}}({{q}_{j}}a_{{11}}^{{(j)}} - {{p}_{j}}a_{{12}}^{{(j)}})) + \\ \end{gathered} $
$\begin{gathered} + \;a_{{22}}^{{(i)}}({{r}_{j}}({{p}_{j}}a_{{23}}^{{(j)}} - {{r}_{j}}a_{{21}}^{{(j)}}) - {{q}_{j}}({{q}_{j}}a_{{21}}^{{(j)}} - {{p}_{j}}a_{{22}}^{{(j)}})) + \\ + \;a_{{32}}^{{(i)}}({{r}_{j}}({{p}_{j}}a_{{33}}^{{(j)}} - {{r}_{j}}a_{{31}}^{{(j)}}) - {{q}_{j}}({{q}_{j}}a_{{31}}^{{(j)}} - {{p}_{j}}a_{{32}}^{{(j)}}))) - \\ - \;M{{a}_{i}}\omega _{0}^{2}({{a}_{j}}(a_{{12}}^{{(i)}}a_{{11}}^{{(j)}} + a_{{22}}^{{(i)}}a_{{21}}^{{(j)}} + a_{{32}}^{{(i)}}a_{{31}}^{{(j)}}) + \\ + \;3a_{{32}}^{{(i)}}({{a}_{i}}a_{{31}}^{{(i)}} - {{a}_{j}}a_{{31}}^{{(j)}})) + \\ + \;(({{B}_{i}} - {{A}_{i}}) + Ma_{i}^{2}){{p}_{i}}{{q}_{i}} - 3\omega _{0}^{2}({{B}_{i}} - {{A}_{i}})a_{{31}}^{{(i)}}a_{{32}}^{{(i)}} = 0. \\ \end{gathered} $

Здесь

(3)
$\begin{gathered} {{p}_{i}} = ({{\alpha }_{i}} + {{\omega }_{0}})a_{{21}}^{{(i)}} + {{\gamma }_{i}}, \\ {{q}_{i}} = ({{\alpha }_{i}} + {{\omega }_{0}})a_{{22}}^{{(i)}} + {{\beta }_{i}}sin{{\gamma }_{i}}, \\ {{r}_{i}} = ({{\alpha }_{i}} + {{\omega }_{0}})a_{{23}}^{{(i)}} + {{\beta }_{i}}cos{{\gamma }_{i}}. \\ \end{gathered} $

В первых трех уравнениях (2) индекс i = 1, индекс $j = 2$, а в последующих трех уравнениях (2) индекс i = 2, индекс $j = 1$. В уравнениях (3) $i = 1,2$. В уравнениях (2), (3) точкой обозначено дифференцирование по времени t.

III. ПОЛОЖЕНИЯ РАВНОВЕСИЯ

Положив в уравнениях (2) и (3) ${{\alpha }_{i}} = {{\alpha }_{{i0}}}$ = = const, ${{\beta }_{i}} = {{\beta }_{{i0}}} = {\text{const}}$, ${{\gamma }_{i}} = {{\gamma }_{{0i}}} = {\text{const}}$ и вводя для удобства обозначения $a_{{ij}}^{{(1)}} = {{a}_{{ij}}}$, $a_{{ij}}^{{(2)}} = {{b}_{{ij}}}$, получим при условиях ${{A}_{i}} \ne {{B}_{i}} \ne {{C}_{i}}$ уравнения

(4)
$\begin{gathered} {{a}_{{22}}}{{a}_{{23}}} + 3{{a}_{{32}}}{{a}_{{33}}} = 0, \\ {{m}_{1}}({{a}_{{23}}}{{a}_{{21}}} - 3{{a}_{{33}}}{{a}_{{31}}}) + {{a}_{{23}}}{{b}_{{21}}} - 3{{a}_{{33}}}{{b}_{{31}}} = 0, \\ {{n}_{1}}({{a}_{{22}}}{{a}_{{21}}} - 3{{a}_{{32}}}{{a}_{{31}}}) - {{a}_{{22}}}{{b}_{{21}}} + 3{{a}_{{32}}}{{b}_{{31}}} = 0, \\ {{b}_{{22}}}{{b}_{{23}}} - {{b}_{{32}}}{{b}_{{33}}} = 0, \\ {{b}_{{23}}}{{a}_{{21}}} - 3{{b}_{{33}}}{{a}_{{31}}} + {{m}_{2}}({{b}_{{23}}}{{b}_{{21}}} - 3{{b}_{{33}}}{{b}_{{31}}}) = 0, \\ - \;{{b}_{{22}}}{{a}_{{21}}} + 3{{b}_{{32}}}{{a}_{{31}}} + {{n}_{2}}({{b}_{{22}}}{{b}_{{21}}} - 3{{b}_{{32}}}{{b}_{{31}}}) = 0, \\ \end{gathered} $
позволяющие определить положения равновесия системы двух тел, соединенных сферическим шарниром, в орбитальной системе координат. В уравнениях (4) введены следующие обозначения: m1 = $(({{A}_{1}} - {{C}_{1}}) - Ma_{1}^{2}){\text{/}}M{{a}_{1}}{{a}_{2}}$; m2 = ((A2 – C2) – – $Ma_{2}^{2}){\text{/}}M{{a}_{1}}{{a}_{2}}$; n1 = $(({{B}_{1}} - {{A}_{1}}) - Ma_{1}^{2}){\text{/}}M{{a}_{1}}{{a}_{2}}$; n2 = = ((B2 – A2) – $Ma_{2}^{2}){\text{/}}M{{a}_{1}}{{a}_{2}}$. С учетом выражений для направляющих косинусов из (1) систему (4) можно рассматривать как систему шести уравнений с шестью неизвестными ${{\alpha }_{i}}$, ${{\beta }_{i}}$ и ${{\gamma }_{i}}$ ($i = 1,2$).

Другой более удобный для исследования способ замыкания уравнений (4) заключается в добавлении шести условий ортогональности направляющих косинусов

$\begin{gathered} a_{{21}}^{2} + a_{{22}}^{2} + a_{{23}}^{2} - 1 = 0, \\ a_{{31}}^{2} + a_{{32}}^{2} + a_{{33}}^{2} - 1 = 0, \\ \end{gathered} $
(5)
$\begin{gathered} {{a}_{{21}}}{{a}_{{31}}} + {{a}_{{22}}}{{a}_{{32}}} + {{a}_{{23}}}{{a}_{{33}}} = 0, \\ b_{{21}}^{2} + b_{{22}}^{2} + b_{{23}}^{2} - 1 = 0, \\ \end{gathered} $
$\begin{gathered} b_{{31}}^{2} + b_{{32}}^{2} + b_{{33}}^{2} - 1 = 0, \\ {{b}_{{21}}}{{a}_{{31}}} + {{b}_{{22}}}{{b}_{{32}}} + {{b}_{{23}}}{{b}_{{33}}} = 0. \\ \end{gathered} $

Уравнения (4) и (5) образуют замкнутую алгебраическую систему уравнений относительно 12 неизвестных направляющих косинусов, определяющих положения равновесия системы двух тел. Для этой системы ставится следующая задача: для заданных ${{m}_{1}}$, ${{n}_{1}}$, ${{m}_{2}}$, ${{n}_{2}}$ требуется определить все двенадцать направляющих косинусов. Остальные шесть направляющих косинуса ${{a}_{{11}}}$, ${{a}_{{12}}}$, ${{a}_{{13}}}$ и ${{b}_{{11}}}$, ${{b}_{{12}}}$, ${{b}_{{13}}}$ могут быть получены из условий ортогональности.

Основное внимание в данной работе уделено символьным методам исследования равновесных решений, определяемых алгебраическими уравнениями (4) и (5).

IV. ИССЛЕДОВАНИЕ ПОЛОЖЕНИЙ РАВНОВЕСИЯ СИСТЕМЫ ДВУХ ТЕЛ С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ КОМПЬЮТЕРНОЙ АЛГЕБРЫ

Проведем подробное исследование решений системы алгебраических уравнений (4) и (5).

Для нахождения решений алгебраической системы (4), (5) рассматривалась возможность применения различных алгоритмов построения базисов Гребнера [8]. Метод построения базиса Гребнера представляет собой алгоритмическую процедуру для полного приведения задачи в случае системы полиномов от многих переменных к рассмотрению полинома от одной переменной.

Исследование проводилось с использованием реализованного в системе компьютерной алгебры Maple 17 [9], [10] пакета построения базисов Гребнера Groebner[Вasis]. В пакете Groebner[Вasis] используется комбинация пяти алгоритмов для вычисления базисов Гребнера для различных порядков мономов и областей значений коэффициентов полиномов. Тип алгоритма задается специальной опцией method=meth. Опция method=direct выполняет самый быстрый, реализованный на данный момент, универсальный прямой метод.

Построение базиса Гребнера для системы (4), (5), состоящей из 12 алгебраических уравнений второго порядка, коэффициенты которых зависят от четырех параметров, представляет собой очень сложную алгоритмическую задачу.

При исследовании системы (4), (5) применялись следующие алгоритмы: 1) method=mapleF4 выполняет алгоритм F4, разработанный Д.С. Фожером (Faugere) и реализованный на языке Maple. Алгоритм F4 поддерживает все порядки мономов и типы коэффициентов полиномов из любого поля, а также вычисления в некоммутативных алгебрах Оре; 2) method=fglm выполняет алгоритм построения базиса Гребнера FGLM, разработанный Фожером, Джиани, Лазардом и Морой (Faugere, Gianni, Lazard, Mora) [11]; 3) method=walk выполняет алгоритм Walk, который разработан Коллартом, Калкбренером и Моллом (Collart, Kalkbrener, Mall), поддерживает все коммутативные поля и порядки мономов и производит преобразование базиса Гребнера из одного порядка мономов в другой [12].

Построить базис Гребнера для 12 полиномов ${{f}_{i}}$ $(i = 1,2,...,12)$, которые представляют собой левые части уравнений системы (4), (5) с 12 переменными направляющими косинусами ${{a}_{{ij}}}$, ${{b}_{{ij}}}$ $(i = 2,3$, j = = 1, 2, 3), используя опцию лексикографического упорядочения по переменным plex, в общем случае не удается.

Приведем результаты построения базисов Гребнера системы (4), (5) для некоторых частных случаев.

Используя команду Maple–infolevel[GroebnerBasis] := 2, были получены данные по типу используемого алгоритма и времени его выполнения. Все вычисления проводились на персональном компьютере с 8 гигабайт оперативной памяти и процессором Intel Core i7 2,4 ГГц.

Случай 1: ${{m}_{1}} = {{n}_{1}} = {{m}_{2}} = {{n}_{2}} = m$. В этом случае с применением алгоритма F4 с опцией упорядочивания переменных по степеням $tdeg$ был построен базис Гребнера. Время вычисления базиса Гребнера для порядка $tdeg$ с применением алгоритма F4 составило около 2 часов машинного времени – 7124.35 сек, размер файла, содержащего полиномы базиса, составил 3668 Кбайт. Пересчитать полученный базис для порядка $plex$ на основе алгоритма FGLM не удалось в связи с прерыванием программы из-за превышения допустимого размера памяти, который использует система Maple. Сообщение об ошибке имеет следующий вид: Error, (in Groebner:-Basis) object too large.

Случай 2: ${{m}_{1}} = {{n}_{1}} = m;{{m}_{2}} = {{n}_{2}} = 1$. Этот случай более простой по сравнению со случаем 1. Здесь так же был построен базис Гребнера с применением алгоритма F4 с опцией упорядочивания переменных по степеням tdeg. Время вычисления базиса Гребнера для степенного порядка с применением алгоритма F4 составило 5503.5 сек, размер файла, содержащего полиномы базиса, составил 3375 Кбайт. Пересчитать полученный базис для порядка $plex$ на основе алгоритма FGLM не удалось в связи прерыванием программы из-за превышения допустимого размера памяти. Система Maple завершила работу через 5952 сек.

Случай 3: ${{m}_{1}} = m,{{n}_{1}} = {{m}_{2}} = {{n}_{2}} = 1$, еще более простой по сравнению со случаями 1 и 2. Здесь был построен базис Гребнера с применением алгоритма Walk для 12 полиномов ${{f}_{i}}$ $(i = 1,2,\;...\;12)$, которые представляют собой левые части уравнений системы (4), (5) с 12 переменными ${{a}_{{ij}}}$, ${{b}_{{ij}}}$ $(i = 2,3$,  j = 1, 2, 3), c использованием опции лексикографического упорядочения по переменным $plex$

G:=map(factor,Groebner[Basis]([f1, … f12], plex(b21, …, a33))).

Процедура вычисления базиса Гребнера состояла из двух этапов. Вначале выполнялся алгоритм F4, время работы которого составило – 3017.5 сек. Далее выполнялся алгоритм Walk. Общее время вычисления базиса составило 12 324 сек. Число полиномов в построенном базисе Гребнера равнялось 170, а количество строк в базисе превысило один миллион. Тем не менее, в данном базисе Гребнера был выделен полином, зависящий только от одной переменной $x = a_{{33}}^{2}$, который имеет следующий вид:

(6)
$P(x) = {{P}_{1}}(x){{P}_{2}}(x){{P}_{3}}(x){{P}_{4}}(x){{P}_{5}}(x){{P}_{6}}(x) = 0.$

Здесь

$\begin{gathered} {{P}_{1}}(x) = x(x - 1), \\ {{P}_{2}}(x) = 16({{m}^{2}} - 1){{x}^{2}} - \\ - \;40({{m}^{2}} - 1)x + 49{{m}^{2}} - 25 = 0, \\ \end{gathered} $
$\begin{gathered} {{P}_{3}}(x) = 64{{m}^{2}}(4m - 1){{x}^{2}} - \\ - \;32(2{{m}^{2}} - 1)(4m - 1)x + 7m + 5 = 0, \\ \end{gathered} $
$\begin{gathered} {{P}_{4}}(x) = 64{{m}^{2}}(4m + 1){{x}^{2}} - \\ - \;32(2{{m}^{2}} - 1)(4m + 1)x + 7m - 5 = 0, \\ \end{gathered} $
$\begin{gathered} {{P}_{5}}(x) = 18{{(m + 1)}^{4}}(m - 1){{x}^{2}} + \\ + \;12{{(m + 1)}^{2}}(m - 1)({{m}^{2}} - 3m - 1)x + \\ + \;(7m + 5)(7{{m}^{2}} - 1)(5{{m}^{2}} - 2) = 0, \\ {{P}_{6}}(x) = {{m}^{2}}x - {{m}^{2}} + 1 = 0. \\ \end{gathered} $

Для определения равновесных решений необходимо рассмотреть отдельно шесть случаев равенства нулю квадратичных полиномов Pi = 0, (i = 1, 2, ..., 6). Отсюда получим значения ${{a}_{{33}}}$, зависящие только от параметра m. Значение для направляющего косинуса ${{a}_{{32}}}$ можно получить из второго полинома, входящего в базис Гребнера, а ${{a}_{{31}}}$ получим из условий ортогональности (5). Значения остальных направляющих косинусов могут быть получены из системы уравнений (4).

Следует отметить, что более эффективным способом построения базисов Гребнера для случая 3 оказался двухступенчатый алгоритм вычисления базиса Гребнера с опцией лексикографического упорядочивания переменных – сначала для степенного порядка $tdeg$, а затем путем пересчета полученного базиса для лексикографического порядка plex на основе алгоритма FGLM. Время вычисления базиса Гребнера для порядка $tdeg$ с применением алгоритма F4 составляет 630.125 сек, количество полиномов в базисе равнялось 490. Пересчет этого базиса для порядка plex на основе алгоритма FGLM выполнялся за 1823.4 сек, количество полиномов в базисе равнялось 170. Общее время работы программы на основе двухступенчатого алгоритма составило 2453.525 сек, что в пять раз быстрее по сравнению с временем работы алгоритма Walk для этого же случая. Максимальное время вычисления базиса Гребнера из всех вышеперечисленных способов было получено для исключающего блочного порядка $lexdeg$ при явном указании метода работы алгоритма – method=walk.

Случай равновесных решений, когда конфигурация связки двух тел находится в плоскости орбиты при ${{\beta }_{i}} = 0$, ${{\gamma }_{i}} = 0$ и ${{\alpha }_{i}} \ne 0$. рассматривался в работах [6] и [7]. В плоском случае система (4) и (5) имеет следующие 4 типа простых решений

(7)
$\begin{gathered} sin{{\alpha }_{1}} = 0,\quad sin{{\alpha }_{2}} = 0, \\ cos{{\alpha }_{1}} = 0,\quad cos{{\alpha }_{2}} = 0, \\ cos{{\alpha }_{1}} = 0,\quad (sin{{\alpha }_{1}} + {{m}_{2}}sin{{\alpha }_{2}}) = 0, \\ cos{{\alpha }_{2}} = 0,\quad ({{m}_{1}}sin{{\alpha }_{1}} + sin{{\alpha }_{2}}) = 0. \\ \end{gathered} $

В [7] рассмотрены плоские колебания системы двух тел, определены все положения равновесия (7) и получены достаточные условия устойчивости положений равновесия с использованием интеграла энергии в качестве функции Ляпунова.

Из приведенных результатов расчетов следует, что прямым способом применения методов построения базисов Гребнера решить систему алгебраических уравнений (4), (5) в общем случае не удается. Далее рассмотрим комбинированный способ решения данной задачи.

V. КОМБИНИРОВАННЫЙ МЕТОД РЕШЕНИЯ

Рассмотрим второе, третье, пятое и шестое уравнения системы (4) относительно переменных ${{a}_{{21}}}$, ${{a}_{{31}}}$, ${{b}_{{21}}}$, ${{b}_{{31}}}$. Эти уравнения образуют однородную подсистему

(8)
$\begin{gathered} ({{m}_{1}}{{a}_{{23}}}){{a}_{{21}}} - (3{{m}_{1}}{{a}_{{33}}}){{a}_{{31}}} + ({{a}_{{23}}}){{b}_{{21}}} - (3{{a}_{{33}}}){{b}_{{31}}} = 0, \\ ({{n}_{1}}{{a}_{{22}}}){{a}_{{21}}} - (3{{n}_{1}}{{a}_{{32}}}){{a}_{{31}}} - ({{a}_{{22}}}){{b}_{{21}}} + (3{{a}_{{32}}}){{b}_{{31}}} = 0, \\ ({{b}_{{23}}}){{a}_{{21}}} - (3{{b}_{{33}}}){{a}_{{31}}} + ({{m}_{2}}{{b}_{{23}}}){{b}_{{21}}} - (3{{m}_{2}}{{b}_{{33}}}){{b}_{{31}}} = 0, \\ - \;({{b}_{{22}}}){{a}_{{21}}} + (3{{b}_{{32}}}){{a}_{{31}}} + ({{n}_{2}}{{b}_{{22}}}){{b}_{{21}}} - (3{{n}_{2}}{{b}_{{32}}}){{b}_{{31}}} = 0. \\ \end{gathered} $

Определитель системы (8) имеет вид:

$\begin{gathered} \Delta = ({{m}_{1}}{{n}_{1}}{{m}_{2}}{{n}_{2}} + 1){{a}_{{11}}}{{b}_{{11}}} - \\ - \;({{m}_{1}}{{m}_{2}} + {{n}_{1}}{{n}_{2}})({{a}_{{22}}}{{b}_{{33}}} - {{a}_{{32}}}{{b}_{{23}}}) \times \\ \times \;({{a}_{{33}}}{{b}_{{22}}} - {{a}_{{23}}}{{b}_{{32}}}) + \\ + \;({{m}_{1}}{{n}_{1}} + {{m}_{2}}{{n}_{1}})({{a}_{{22}}}{{b}_{{32}}} - {{a}_{{32}}}{{b}_{{22}}})({{a}_{{23}}}{{b}_{{33}}} - {{a}_{{33}}}{{b}_{{23}}}). \\ \end{gathered} $

Если $\Delta \ne 0$, то ${{a}_{{21}}} = {{a}_{{31}}} = {{b}_{{21}}} = {{b}_{{31}}} = 0$ и система (8) разделяется на две подсистемы

(9)
$\begin{gathered} {{a}_{{22}}}{{a}_{{23}}} - 3{{a}_{{32}}}{{a}_{{33}}} = 0,\quad {{b}_{{22}}}{{b}_{{23}}} - 3{{b}_{{32}}}{{b}_{{33}}} = 0, \\ a_{{22}}^{2} + a_{{23}}^{2} = 1,\quad b_{{22}}^{2} + b_{{23}}^{2} = 1, \\ a_{{32}}^{2} + a_{{33}}^{2} = 1,\quad b_{{32}}^{2} + b_{{33}}^{2} = 1, \\ {{a}_{{22}}}{{a}_{{32}}} + {{a}_{{23}}}{{a}_{{33}}} = 0,\quad {{b}_{{22}}}{{b}_{{32}}} + {{b}_{{23}}}{{b}_{{33}}} = 0. \\ \end{gathered} $

Решения системы (9) можно получить с использованием метода построения базиса Гребнера. Построим базис Гребнера с применением алгоритма FGLM для 8 полиномов ${{f}_{i}}$ $(i = 1,2,\;...,\;8)$, которые представляют собой левые части уравнений системы (9) с 8 переменными ${{a}_{{ij}}}$, ${{b}_{{ij}}}$ $(i = 2,3$, j = 2, 3), c использованием опции лексикографического упорядочения по переменным $plex$. Общее время вычисления базиса составило 0.05 сек. Число полиномов в построенном базисе Гребнера равнялось 18. Выпишем из построенного базиса Гребнера некоторые полиномы, которые зависит от переменных и ${{a}_{{22}}}$ и ${{a}_{{33}}}$: ${{a}_{{22}}}(a_{{22}}^{2} - 1)$, ${{a}_{{33}}}(a_{{33}}^{2}$ – 1), $a_{{22}}^{2} - a_{{33}}^{2}$. Решения системы (9) из построенного базиса Гребнера можно получить в следующем виде:

(10)
$\begin{gathered} a_{{22}}^{2} = 1,\quad {{a}_{{23}}} = 0,\quad {{a}_{{32}}} = 0,\quad a_{{33}}^{2} = 1, \\ b_{{22}}^{2} = 1,\quad {{b}_{{23}}} = 0,\quad {{b}_{{32}}} = 0,\quad b_{{33}}^{2} = 1; \\ \end{gathered} $
(11)
$\begin{gathered} {{a}_{{22}}} = 0,\quad a_{{23}}^{2} = 1,\quad a_{{32}}^{2} = 1,\quad {{a}_{{33}}} = 0, \\ {{b}_{{22}}} = 0,\quad b_{{23}}^{2} = 1,\quad b_{{32}}^{2} = 1,\quad {{b}_{{33}}} = 0. \\ \end{gathered} $

Имеем всего 8 различных решений: четыре решения, когда $a_{{22}}^{2} = 1$, $a_{{33}}^{2} = 1$ (решения (10)) и четыре решения, когда $a_{{23}}^{2} = 1$, $a_{{32}}^{2} = 1$ (решения (11)). Условие $\Delta \ne 0$, например, для решения, когда ${{a}_{{22}}} = {{a}_{{33}}} = {{b}_{{22}}} = {{b}_{{33}}}$ = 1, выполняются при следующих ограничениях на параметры системы: ${{m}_{1}}{{m}_{2}}({{n}_{1}}{{n}_{2}} - 1) + ({{m}_{1}} - {{n}_{1}}){{n}_{2}} + {{m}_{2}}{{n}_{1}} \ne 0$. При Δ = 0 получим случай параметрических решений системы (8) [14].

Рассмотрим теперь первое и второе уравнения системы (4). Они образуют однородную подсистему относительно переменных ${{a}_{{23}}}$ и ${{a}_{{33}}}$

(12)
$\begin{gathered} ({{a}_{{22}}}){{a}_{{23}}} - (3{{a}_{{32}}}){{a}_{{33}}} = 0, \\ ({{m}_{1}}{{a}_{{21}}} + {{b}_{{21}}}){{a}_{{23}}} - 3({{m}_{1}}{{a}_{{31}}} + {{b}_{{31}}}){{a}_{{33}}} = 0. \\ \end{gathered} $

Если определитель системы (12) ${{\Delta }_{1}}$ = a22b31 – a32b21 – – ${{m}_{1}}({{a}_{{21}}}{{a}_{{32}}} - {{a}_{{22}}}{{a}_{{31}}}) \ne 0,$ то ${{a}_{{23}}} = 0$, a33 = 0.

Уравнения 4 и 5 системы (4) так же образуют однородную подсистему относительно переменных ${{b}_{{23}}}$ и ${{b}_{{33}}}$

(13)
$\begin{gathered} ({{b}_{{22}}}){{b}_{{23}}} - (3{{b}_{{32}}}){{b}_{{33}}} = 0, \\ ({{m}_{2}}{{b}_{{21}}} + {{a}_{{21}}}){{b}_{{23}}} - 3({{m}_{2}}{{b}_{{31}}} + {{a}_{{31}}}){{b}_{{33}}} = 0. \\ \end{gathered} $

Если определитель системы (13) ${{\Delta }_{2}}$ = b22a31 – ‒ ${{b}_{{32}}}{{a}_{{21}}} - {{m}_{2}}({{b}_{{21}}}{{b}_{{32}}} - {{b}_{{22}}}{{b}_{{31}}}) \ne 0,$ то ${{b}_{{23}}} = 0$ и ${{b}_{{33}}}$ = 0. Если определители ${{\Delta }_{1}} \ne 0$, ${{\Delta }_{2}} \ne 0$, то ${{a}_{{23}}} = 0$, ${{a}_{{33}}}$ = 0, ${{b}_{{23}}} = 0$, ${{b}_{{33}}} = 0$ и система (4) в этом случае примет вид

(14)
$\begin{gathered} {{n}_{1}}({{a}_{{21}}}{{a}_{{22}}} - 3{{a}_{{31}}}{{a}_{{32}}}) - {{b}_{{21}}}{{a}_{{22}}} + 3{{b}_{{31}}}{{a}_{{32}}} = 0, \\ {{n}_{2}}({{b}_{{21}}}{{b}_{{22}}} - 3{{b}_{{31}}}{{b}_{{32}}}) - {{a}_{{21}}}{{b}_{{22}}} + 3{{a}_{{31}}}{{b}_{{32}}} = 0, \\ a_{{21}}^{2} + a_{{22}}^{2} - 1 = 0,\quad b_{{21}}^{2} + b_{{22}}^{2} - 1 = 0, \\ a_{{31}}^{2} + a_{{32}}^{2} - 1 = 0,\quad b_{{31}}^{2} + b_{{32}}^{2} - 1 = 0, \\ {{a}_{{21}}}{{a}_{{31}}} + {{a}_{{22}}}{{a}_{{32}}} = 0,\quad {{b}_{{21}}}{{b}_{{31}}} + {{b}_{{22}}}{{b}_{{32}}} = 0. \\ \end{gathered} $

Решения системы (14) можно получить с использованием методов построения базиса Гребнера. Построим базис Гребнера с применением алгоритма FGLM для 8 полиномов fi $(i = 1,2,\;...\;8)$, которые представляют собой левые части уравнений системы (14) с 8 переменными ${{a}_{{ij}}}$, ${{b}_{{ij}}}$ $(i = 2,3$, j = 1, 2), c использованием опции лексикографического упорядочения по переменным

G:=map(factor,Groebner[Basis]([f1, … f8], plex(b21,…,a32))).

Общее время вычисления базиса составило 0.125 сек. Число полиномов в построенном базисе Гребнера равнялось 27. Выпишем из построенного базиса Гребнера для системы (14) полином, который зависит только от одной переменной ${{a}_{{32}}}$,

(15)
$P({{a}_{{32}}}) = {{P}_{7}}({{a}_{{32}}}){{P}_{8}}({{n}_{1}},{{n}_{2}},{{a}_{{32}}}) = 0.$

Здесь

$\begin{gathered} {{P}_{7}}({{a}_{{32}}}) = {{a}_{{32}}}(a_{{32}}^{2} - 1), \\ {{P}_{8}}({{a}_{{32}}}) = 64n_{1}^{2}(4n_{1}^{2}n_{2}^{2} - 1)(n_{1}^{2}n_{2}^{2} - 1)a_{{32}}^{4} - \\ - \;32(2n_{1}^{2} - 1)(4n_{1}^{2}n_{2}^{2} - 1)(n_{1}^{2}n_{2}^{2} - 1)a_{{32}}^{2} + \\ + \;({{(4n_{1}^{2}n_{2}^{2} - 1)}^{2}} - 9{{({{n}_{1}} + {{n}_{2}})}^{2}}) = 0. \\ \end{gathered} $

Кроме того, из построенного базиса Гребнера следуют соотношения

(16)
$a_{{21}}^{2} = a_{{32}}^{2},\quad a_{{22}}^{2} = a_{{31}}^{2},\quad b_{{21}}^{2} = b_{{32}}^{2},\quad b_{{22}}^{2} = b_{{31}}^{2}.$

Систему (14) с учетом соотношений (16) можно переписать в более простом виде

(17)
$\begin{gathered} 4{{n}_{1}}{{a}_{{21}}}{{a}_{{22}}} - {{b}_{{21}}}{{a}_{{22}}} - 3{{b}_{{22}}}{{a}_{{21}}} = 0, \\ 4{{n}_{2}}{{b}_{{21}}}{{b}_{{22}}} - {{a}_{{21}}}{{b}_{{22}}} - 3{{a}_{{22}}}{{b}_{{21}}} = 0, \\ a_{{21}}^{2} + a_{{22}}^{2} - 1 = 0,\quad b_{{21}}^{2} + b_{{22}}^{2} - 1 = 0. \\ \end{gathered} $

Решение системы (17) сводится к решению биквадратного уравнения из (15).

Используя соотношения (15) и (16) выпишем все решения системы (14).

1. Решения, которые получены из условия ${{P}_{7}}({{a}_{{32}}}) = 0$ (${{a}_{{32}}} = 0$) имеют следующий вид:

(18)
$\begin{gathered} {{a}_{{32}}} = 0,\quad a_{{31}}^{2} = 1,\quad a_{{22}}^{2} = 1,\quad {{a}_{{21}}} = 0, \\ b_{{22}}^{2} = 1,\quad {{b}_{{21}}} = 0,\quad {{b}_{{32}}} = 0,\quad b_{{31}}^{2} = 1. \\ \end{gathered} $

Решения (18) существуют при выполнении условий ${{\Delta }_{1}}$ = $({{b}_{{31}}} - {{m}_{1}}{{a}_{{31}}}) \ne 0,$ $({\text{|}}{{m}_{1}}{\text{|}} \ne 1)$; ${{\Delta }_{2}}$ = (a31 –‒ ${{m}_{2}}{{b}_{{31}}}) \ne 0,$ $({\text{|}}{{m}_{2}}{\text{|}} \ne 1)$.

2. Решения, которые получаются из условия ${{P}_{7}}({{a}_{{32}}}) = 0$ $(a_{{32}}^{2} = 1)$,

(19)
$\begin{gathered} a_{{32}}^{2} = 1,\quad {{a}_{{31}}} = 0,\quad a_{{21}}^{2} = 1,\quad {{a}_{{22}}} = 0, \\ b_{{21}}^{2} = 1,\quad {{b}_{{22}}} = 0,\quad {{b}_{{31}}} = 0,\quad b_{{32}}^{2} = 1. \\ \end{gathered} $

Решения (19) существуют при выполнении условий ${{\Delta }_{1}}$ = $({{b}_{{21}}} + {{m}_{1}}{{a}_{{21}}}) \ne 0,$ $({\text{|}}{{m}_{1}}{\text{|}} \ne 1)$; ${{\Delta }_{2}}$ = (a21 + + ${{m}_{2}}{{b}_{{21}}}) \ne 0,$ $({\text{|}}{{m}_{2}}{\text{|}} \ne 1)$.

3. В третьем случае $({{P}_{8}}({{n}_{1}},{{n}_{2}},{{a}_{{32}}}) = 0)$ система (14) имеет следующие решения при ${{\Delta }_{1}} \ne 0$ и ${{\Delta }_{2}} \ne 0$:

$\begin{gathered} a_{{32}}^{2} = \frac{{n_{1}^{2} - 1}}{{4n_{1}^{2}}} \pm \\ \pm \;\frac{{(8n_{1}^{3}{{n}_{2}} - 5{{n}_{1}}({{n}_{1}} + {{n}_{2}}) + 2)\sqrt {(4{{n}_{1}}{{n}_{2}} - 1)({{n}_{1}}{{n}_{2}} - 1)} }}{{8n_{1}^{2}(4{{n}_{1}}{{n}_{2}} - 1)({{n}_{1}}{{n}_{2}} - 1)}}, \\ \end{gathered} $
(20)
$\begin{gathered} a_{{31}}^{2} = 1 - a_{{32}}^{2},\quad {{a}_{{33}}} = 0, \\ a_{{21}}^{2} = a_{{32}}^{2},\quad a_{{22}}^{2} = a_{{31}}^{2},\quad {{a}_{{23}}} = 0, \\ b_{{32}}^{2} = \frac{{n_{2}^{2} - 1}}{{4n_{2}^{2}}} \pm \\ \pm \;\frac{{(8n_{2}^{3}{{n}_{1}} - 5{{n}_{2}}({{n}_{1}} + {{n}_{2}}) + 2)\sqrt {(4{{n}_{1}}{{n}_{2}} - 1)({{n}_{1}}{{n}_{2}} - 1)} }}{{8n_{2}^{2}(4{{n}_{1}}{{n}_{2}} - 1)({{n}_{1}}{{n}_{2}} - 1)}}, \\ \end{gathered} $
$\begin{gathered} b_{{31}}^{2} = 1 - b_{{32}}^{2},\quad {{b}_{{33}}} = 0, \\ b_{{21}}^{2} = b_{{32}}^{2},\quad b_{{22}}^{2} = b_{{31}}^{2},\quad {{b}_{{23}}} = 0. \\ \end{gathered} $

Решения (20) существуют при выполнении условий ${{n}_{1}}{{n}_{2}} < 1{\text{/}}4$, ${{n}_{1}}{{n}_{2}} > 1$.

Далее, аналогично предыдущему случаю, рассмотрим первое и третье уравнения системы (4) относительно переменных ${{a}_{{22}}}$ и ${{a}_{{32}}}$ и четвертое и шестое уравнения системы (4) относительно переменных ${{b}_{{22}}}$ и ${{b}_{{32}}}$. Если определитель первой подсистемы относительно переменных ${{a}_{{22}}}$ и ${{a}_{{32}}}$, ${{\Delta }_{3}}$ = ${{a}_{{33}}}{{b}_{{21}}} - {{a}_{{23}}}{{b}_{{31}}} + {{n}_{1}}({{a}_{{23}}}{{a}_{{31}}} - {{a}_{{21}}}{{a}_{{33}}}) \ne 0,$ то ${{a}_{{22}}} = 0$, ${{a}_{{32}}}$ = 0. Если определитель второй подсистемы относительно переменных ${{b}_{{22}}}$ и ${{b}_{{32}}}$ ${{\Delta }_{4}}$ = a21b33 – ‒ ${{b}_{{23}}}{{a}_{{31}}} + {{n}_{2}}({{b}_{{23}}}{{b}_{{31}}} - {{b}_{{21}}}{{b}_{{33}}}) \ne 0,$ то ${{b}_{{22}}} = 0$ и ${{b}_{{32}}}$ = 0. Если определители ${{\Delta }_{3}} \ne 0$ и ${{\Delta }_{4}} \ne 0$, то ${{a}_{{22}}}$ = 0, ${{a}_{{32}}}$ = 0, ${{b}_{{22}}} = 0$, ${{b}_{{32}}} = 0$ и тогда система (4) примет следующий вид:

(21)
$\begin{gathered} {{m}_{1}}({{a}_{{23}}}{{a}_{{21}}} - 3{{a}_{{33}}}{{a}_{{31}}}) + {{b}_{{21}}}{{a}_{{23}}} - 3{{b}_{{31}}}{{a}_{{33}}} = 0, \\ {{m}_{2}}({{b}_{{23}}}{{b}_{{21}}} - 3{{b}_{{33}}}{{b}_{{31}}}) + {{a}_{{21}}}{{b}_{{23}}} - 3{{a}_{{31}}}{{b}_{{33}}} = 0, \\ a_{{21}}^{2} + a_{{23}}^{2} - 1 = 0,\quad b_{{21}}^{2} + b_{{23}}^{2} - 1 = 0, \\ a_{{31}}^{2} + a_{{33}}^{2} - 1 = 0,\quad b_{{31}}^{2} + b_{{33}}^{2} - 1 = 0, \\ {{a}_{{21}}}{{a}_{{31}}} + {{a}_{{23}}}{{a}_{{33}}} = 0,\quad {{b}_{{21}}}{{b}_{{31}}} + {{b}_{{23}}}{{b}_{{33}}} = 0. \\ \end{gathered} $

Решения системы (21), также как и в предыдущем случае, получим с использованием алгоритма построения базиса Гребнера для системы полиномов (22) с применением алгоритма FGLM для 8 полиномов  fi $(i = 1,2,\;...,\;8)$, которые представляют собой левые части уравнений системы (21) с 8 переменными ${{a}_{{ij}}}$, ${{b}_{{ij}}}$ $(i = 2,3,j = 1,3)$, с опцией лексикографического упорядочивания переменных $plex$. Общее время вычисления базиса составило 0.172 сек. Число полиномов в построенном базисе Гребнера равнялось 27.

Выпишем из построенного базиса Гребнера полином, который зависит только от одной переменной ${{a}_{{33}}}$ в виде

(22)
$P({{a}_{{33}}}) = {{P}_{9}}({{a}_{{33}}}){{P}_{{10}}}({{m}_{1}},{{m}_{2}},{{a}_{{33}}}) = 0.$

Здесь

$\begin{gathered} {{P}_{9}}({{a}_{{33}}}) = {{a}_{{33}}}(a_{{33}}^{2} - 1), \\ {{P}_{{10}}}({{a}_{{33}}}) = 256m_{1}^{2}{{(2{{m}_{1}}{{m}_{2}} + 1)}^{2}}a_{{33}}^{4} - \\ - \;8(2{{m}_{1}}{{m}_{2}} + 1)(64m_{1}^{3}{{m}_{2}} + 32{{m}_{1}}({{m}_{1}} - {{m}_{2}}) - 25)a_{{33}}^{2} + \\ + \;({{(8{{m}_{1}}{{m}_{2}} - 5)}^{2}} - 36{{({{m}_{1}} - {{m}_{2}})}^{2}}) = 0. \\ \end{gathered} $

Кроме того, из построенного базиса Гребнера следуют следующие соотношения:

(23)
$a_{{21}}^{2} = a_{{33}}^{2},\quad a_{{23}}^{2} = a_{{31}}^{2},\quad b_{{21}}^{2} = b_{{33}}^{2},\quad b_{{23}}^{2} = b_{{31}}^{2}.$

Используя соотношения (22) и (23), выпишем все решения системы (21).

4. Решения, которые получены из условия ${{P}_{9}}({{a}_{{33}}})$ = 0 (${{a}_{{33}}} = 0$), имеют следующий вид:

(24)
$\begin{gathered} {{a}_{{33}}} = 0,\quad a_{{31}}^{2} = 1,\quad a_{{23}}^{2} = 1,\quad {{a}_{{21}}} = 0, \\ b_{{23}}^{2} = 1,\quad {{b}_{{21}}} = 0,\quad {{b}_{{33}}} = 0,\quad b_{{31}}^{2} = 1. \\ \end{gathered} $

Эти решения существуют при выполнении условий ${{\Delta }_{3}}$ = $({{b}_{{31}}} - {{n}_{1}}{{a}_{{31}}}) \ne 0,$ $({\text{|}}{{n}_{1}}{\text{|}} \ne 1)$; ${{\Delta }_{4}}$ = (a31 –‒ ${{n}_{2}}{{b}_{{31}}}) \ne 0,$ $({\text{|}}{{n}_{2}}{\text{|}} \ne 1)$.

5. Решения, которые получены из условия $a_{{33}}^{2}$ = 1 имеют вид

(25)
$\begin{gathered} a_{{33}}^{2} = 1,\quad {{a}_{{31}}} = 0,\quad a_{{21}}^{2} = 1,\quad {{a}_{{23}}} = 0, \\ b_{{21}}^{2} = 1,\quad {{b}_{{23}}} = 0,\quad {{b}_{{31}}} = 0,\quad b_{{33}}^{2} = 1. \\ \end{gathered} $

Эти решения существуют при выполнении условий ${{\Delta }_{3}}$ = $({{b}_{{21}}} + {{n}_{1}}{{a}_{{21}}}) \ne 0,$ $({\text{|}}{{n}_{1}}{\text{|}} \ne 1)$; ${{\Delta }_{4}}$ = (a21 –‒ ${{n}_{2}}{{b}_{{21}}}) \ne 0,$ $({\text{|}}{{n}_{2}}{\text{|}} \ne 1)$.

6. В случае, когда ${{P}_{{10}}}({{m}_{1}},{{m}_{2}},{{a}_{{33}}}) = 0$ система (21) имеет следующие решения при ${{\Delta }_{3}} \ne 0$ и ${{\Delta }_{4}} \ne 0$:

$\begin{gathered} a_{{33}}^{2} = \frac{1}{2} - \frac{{32{{m}_{1}}{{m}_{2}} + 25}}{{64m_{1}^{2}(2{{m}_{1}}{{m}_{2}} + 1)}} \pm \\ \pm \;\frac{{(8m_{1}^{2} - 5)\sqrt {64{{m}_{1}}{{m}_{2}}({{m}_{1}}{{m}_{2}} + 1) + 25} }}{{64m_{1}^{2}(2{{m}_{1}}{{m}_{2}} + 1)}}, \\ \end{gathered} $
(26)
$\begin{gathered} a_{{31}}^{2} = 1 - a_{{33}}^{2},\quad {{a}_{{32}}} = 0, \\ a_{{21}}^{2} = a_{{33}}^{2},\quad a_{{23}}^{2} = a_{{31}}^{2},\quad {{a}_{{22}}} = 0, \\ b_{{33}}^{2} = \frac{1}{2} - \frac{{32{{m}_{1}}{{m}_{2}} + 25}}{{64m_{2}^{2}(2{{m}_{1}}{{m}_{2}} + 1)}} \pm \\ \pm \;\frac{{(8m_{2}^{2} - 5)\sqrt {64{{m}_{1}}{{m}_{2}}({{m}_{1}}{{m}_{2}} + 1) + 25} }}{{64m_{2}^{2}(2{{m}_{1}}{{m}_{2}} + 1)}}, \\ \end{gathered} $
$\begin{gathered} b_{{31}}^{2} = 1 - b_{{33}}^{2},\quad {{b}_{{32}}} = 0,\quad b_{{21}}^{2} = b_{{33}}^{2}, \\ b_{{23}}^{2} = b_{{31}}^{2},\quad {{b}_{{22}}} = 0,\quad (2{{m}_{1}}{{m}_{2}} \ne - 1). \\ \end{gathered} $

Выражение $64{{m}_{1}}{{m}_{2}}({{m}_{1}}{{m}_{2}} + 1) + 25$ неотрицательно для любых ${{m}_{1}},{{m}_{2}}$.

Таким образом, мы получили для общего случая семейства равновесных решений (10), (11), (18), (19), (20), (24), (25), (26) исходной системы 12 алгебраических уравнений (4) и (5) при ограничениях $\Delta \ne 0$, ${{\Delta }_{1}} \ne 0$, ${{\Delta }_{2}} \ne 0$, ${{\Delta }_{3}} \ne 0$ и ${{\Delta }_{4}} \ne 0$. Условия выполнения данных ограничений можно проверить численно для каждого набора параметров системы.

В заключение следует отметить, что комбинация методов компьютерной и линейной алгебры позволяет провести исследование широкого класса равновесных решений системы двух тел, соединенным сферическим шарниром, на круговой орбите при определенных ограничениях на параметры задачи. На основании полученных в данной работе результатов с использованием символьных методов показано, что на круговой орбите могут существовать как плоские так и пространственные конфигурации системы двух тел, находящихся в положении равновесия.

Традиционно для отыскания стационарных конфигураций используют численные методы отыскания корней систем нелинейных алгебраических уравнений такие как, методы итераций (метод простой итерации и метод Зейделя), метод Ньютона, методы спуска, метод секущих, метод Стеффенсена [16], [17], [18], [19], [20]. Недостатки этого подхода хорошо известны. Одной из наиболее трудных проблем, возникающих при численном решении систем нелинейных уравнений, является задача локализации решения гарантирующего сходимость метода и нахождения всех действительных корней. В случае зависимости коэффициентов алгебраических уравнений от параметров, что имеет место в нашей задаче, применение численных методов не позволяет определить характер поведения корней в пространстве параметров.

В настоящей работе используется другой подход, основанный на символьных методах решения системы нелинейных алгебраических уравнений. Это позволило получить следующие новые результаты: привести систему состоящей из 12 алгебраических уравнений второго порядка к рассмотрению полинома от одной переменной, найти аналитическое решение и исследовать условия существования решений в пространстве параметров задачи.

Список литературы

  1. Сарычев В.А. Вопросы ориентации искусственных спутников. Итоги науки и техники. Серия Исследование космического пространства. М.: ВИНИТИ, 1978. Т. 11. 224 с.

  2. Гутник С.А., Сарычев В.А. Символьно-численные методы исследования положений равновесия спутника-гиростата. Программирование, 2014. № 3. С. 49–58.

  3. Гутник С.А., Сарычев В.А. Применение методов компьютерной алгебры для исследования стационарных движений спутника-гиростата. Программирование, 2017. № 2. С. 35–44.

  4. Gutnik S.A., Sarychev V.A.: A symbolic investigation of the influence of aerodynamic forces on satellite equilibria, Lect. Notes Comput. Sci. 2016. V. 9890. P. 243–254.

  5. Сарычев В.А., Гутник С.А. Положения равновесия системы двух тел, связанных сферическим шарниром. Тезисы докладов XL Академических чтений по космонавтике 26–29 января 2016. Сборник тезисов. М.: МГТУ им. Н.Э. Баумана, 2016. С. 90

  6. Сарычев В.А. Исследование динамики системы гравитационной стабилизации. Сб. “Искусств. Спутники Земли”. М.: Изд. АН СССР, 1963. № 16. С. 10–33

  7. Сарычев В.А. Положения относительного равновесия двух тел, соединенных сферическим шарниром, на круговой орбите. Космические исследования. 1967. Т. 5. № 3. С. 360–364.

  8. Buchberger B. Theoretical basis for the reduction of polynomials to canonical forms, SIGSAM Bulletin, 1976. P. 19–29.

  9. Char B.W., Geddes K.O., Gonnet G.H., Monagan M.B., Watt S.M. Maple Reference Manual, Watcom Publications Limitid, Waterloo, Canada, 1992.

  10. Maple online help. http://www.maplesoft.com/support/help/

  11. Faugere J., Gianni P., Lazard P., Mora T. Efficient computation of zero-dimensional Grobner bases by change of ordering, Journal of Symbolic Computation. 1993. V. 16. P. 329–344.

  12. Collart S., Kalkbrener M., Mall D. Converting Bases with the Grobner Walk, Journal of Symbolic Computation. 1997. V. 3. № 4. P. 465–469.

  13. Chen C., Maza M.M. Semi-algebraic description of the equilibria of dynamical systems. In: Gerdt V.P., Koepf W., Mayr E.W., and Vorozhtsov E.V. (eds.) CASC 2011, LNCS. 2011. V. 6885. P. 101–125. Springer, Heidelberg.

  14. Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2010.

  15. Батхин A.Б. Параметризация дискриминантного множества многочлена. Программирование, 2016. № 2. С. 8–21.

  16. Бахвалов Н.С., Жидков Н.П., Кобельков Г.Г. Численные методы. М.: БИНОМ. Лаборатория знаний, 2011. 636 с.

  17. Калиткин Н.П. Численные методы. М.: Наука, 1978. 512 с.

  18. Крылов В.И., Бобков В.В., Монастырский П.И. Вычислительные методы, 1978. Т. 1. М.: Наука, 584 с.

  19. Амосов А.А., Дубинский Ю.А., Копченова Н.П. Вычислительные методы для инженеров. М.: Высшая школа, 1994. 544 с.

  20. Турчак Л.И., Плотников П.В. Основы численных методов. М.: Физматлит, 2005. 352 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал