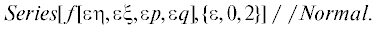1. На главную
  2. Электронные версии
  3. Программирование
  4. № 2, 2019

Программирование, 2019, № 2, стр. 58-65

ПРИМЕНЕНИЕ КОМПЬЮТЕРНОЙ АЛГЕБРЫ В ИССЛЕДОВАНИЯХ ДВУХПЛАНЕТНОЙ ЗАДАЧИ ТРЕХ ТЕЛ С ПЕРЕМЕННЫМИ МАССАМИ

А. Н. Прокопеня a, *, М. Дж. Минглибаев b, c, С. А. Шомшекова b, c

a Варшавский университет естественных наук
02-776 Варшава, ул. Новоурсыновска, 159, Польша

b Казахский национальный университет им. аль-Фараби
050040 Алматы, пр. аль-Фараби, 71, Казахстан

c Астрофизический институт им. В.Г. Фесенкова
050020 Алматы, Обсерватория, 23, Казахстан

* E-mail: Alexander_prokopenya@sggw.pl

Поступила в редакцию 27.08.2018
После доработки 27.08.2018
Принята к публикации 20.09.2018

Полный текст (PDF)

Аннотация

Рассматривается классическая двухпланетная задача трех тел переменной массы в общем случае, когда массы тел изменяются неизотропно с различными скоростями. Получены дифференциальные уравнения движения в оскулирующих элементах апериодического движения по квазиконическим сечениям. Обсуждается алгоритм вычисления возмущающей функции в виде степенных рядов по малым параметрам и получение дифференциальных уравнений, определяющих вековые возмущения орбитальных элементов. Все необходимые символьные вычисления выполняются с использованием системы компьютерной алгебры Mathematica.

I. ВВЕДЕНИЕ

Классическая проблема трех тел является базовой моделью небесной механики и имеет многочисленные приложения (см., напр., [1, 2]). В простейшем случае она описывает движение трех материальных точек постоянной массы, взаимодействующих друг с другом в соответствии с законом всемирного тяготения. Дифференциальные уравнения, определяющие движение тел, могут быть легко выписаны, но получить общее решение этих уравнений в виде конечных аналитических выражений до сих пор не удалось. Некоторые классы решений можно построить в виде степенных и тригонометрических рядов (см., напр., [3–5]). Построение и исследование таких решений обычно связано с выполнением весьма громоздких символьных вычислений, что стимулировало разработку соответствующих аналитических и численно-аналитических методов и алгоритмов [6–14]. Эти методы успешно используются при исследовании более сложных моделей [15–22].

Следует отметить, что реальные небесные тела не являются стационарными и такие их характеристики как масса, размеры, форма и внутренняя структура могут с течением времени изменяться (см. [23–25]). Учет зависимости параметров системы от времени существенно усложняет модель и даже задача двух тел переменной массы, общее решение которой при постоянных массах хорошо известно, допускает аналитическое решение только в специальных случаях (см. [26, 28]).

Проблема трех тел является неинтегрируемой даже при постоянных массах и для ее исследования обычно применяют теорию возмущений, используя в качестве нулевого приближения точное решение задачи двух тел. Такой подход оказался весьма успешным, например, при исследовании движения планеты или спутника в системе звезда–планета или двойная звезда [2, 29–31]. Поскольку массы небесных тел с течением времени изменяются [23, 24, 26, 27], представляет интерес исследовать влияние таких изменений на орбитальные параметры в рамках задачи трех тел. Специальный случай этой задачи, когда массы двух тел изменяются изотропно одинаковым образом, рассмотрен в работах [32–34].

Целью данной работы является исследование проблемы трех тел с переменными массами в общем случае, когда массы тел изменяются неизотропно с различными скоростями. Хотя уравнения движения системы получены в общем виде и могут быть использованы при исследовании проблемы трех тел с переменными массами в различных постановках, мы ограничиваемся наиболее изученным случаем двухпланетной проблемы трех тел [27, 33]. Основное внимание уделяется обсуждению вычислительных задач, возникающих при получении разложения возмущающей функции в степенной ряд по малым параметрам и определении эволюционных уравнений, для решения которых лучше всего использовать системы компьютерной алгебры. В данной работе все символьные вычисления выполняются с помощью системы компьютерной алгебры Mathematica [35], которая имеет удобный интерфейс и позволяет легко комбинировать различные виды вычислений. Поскольку для использования системы Mathematica требуется лицензия, для выполнения описанных в работе вычислений можно воспользоваться и другой системой компьютерной алгебы в зависимости от предпочтений исследователей.

II. УРАВНЕНИЯ ДВИЖЕНИЯ

Предполагая, что наиболее массивное тело P0 находится в начале координат, и используя относительные декартовы координаты ${{\vec {R}}_{i}} = ({{X}_{i}},{{Y}_{i}},{{Z}_{i}})$, уравнения движения тел ${{P}_{1}}$, ${{P}_{2}}$ можно записать в виде (см. [21, 26, 27])

(1)
${{\ddot {\vec {R}}}_{1}} + G({{m}_{0}} + {{m}_{1}})\frac{{{{{\vec {R}}}_{1}}}}{{R_{1}^{3}}} - \frac{{\mathop {\ddot {\gamma }}\nolimits_1 }}{{{{\gamma }_{1}}}}{{\vec {R}}_{1}} = {{\vec {\nabla }}_{{\mathop {\vec {R}}\nolimits_1 }}}{{W}_{1}},$
(2)
${{\ddot {\vec {R}}}_{2}} + G({{m}_{0}} + {{m}_{2}})\frac{{\mathop {\vec {R}}\nolimits_2 }}{{R_{2}^{3}}} - \frac{{\mathop {\ddot {\gamma }}\nolimits_2 }}{{{{\gamma }_{2}}}}{{\vec {R}}_{2}} = {{\vec {\nabla }}_{{\mathop {\vec {R}}\nolimits_2 }}}{{W}_{2}},$
где ${{m}_{0}} = {{m}_{0}}(t)$, ${{m}_{1}} = {{m}_{1}}(t)$, ${{m}_{2}} = {{m}_{2}}(t)$ – массы тел ${{P}_{0}}$, ${{P}_{1}}$ и ${{P}_{2}}$ соответственно, G – гравитационная постоянная,
${{R}_{{ij}}} = \sqrt {{{{({{X}_{j}} - {{X}_{i}})}}^{2}} + {{{({{Y}_{j}} - {{Y}_{i}})}}^{2}} + {{{({{Z}_{j}} - {{Z}_{i}})}}^{2}}} ,$
${{R}_{i}} = \sqrt {X_{i}^{2} + Y_{i}^{2} + Z_{i}^{2}} ,\quad (i,j = 1,2),$
а возмущающие функции ${{W}_{1}}$, ${{W}_{2}}$, приводящие к неинтегрируемости уравнений (1), (2), имеют вид (см. [26, 27])

${{W}_{1}} = G{{m}_{2}}\left( {\frac{1}{{{{R}_{{12}}}}} - \frac{{{{{\vec {R}}}_{1}} \cdot {{{\vec {R}}}_{2}}}}{{R_{2}^{3}}}} \right) - \frac{{\mathop {\ddot {\gamma }}\nolimits_1 }}{{2{{\gamma }_{1}}}}\vec {R}_{1}^{2} + {{\vec {F}}_{1}} \cdot {{\vec {R}}_{1}},$
${{W}_{2}} = G{{m}_{1}}\left( {\frac{1}{{{{R}_{{12}}}}} - \frac{{{{{\vec {R}}}_{1}} \cdot {{{\vec {R}}}_{2}}}}{{R_{1}^{3}}}} \right) - \frac{{\mathop {\ddot {\gamma }}\nolimits_2 }}{{2{{\gamma }_{2}}}}\vec {R}_{2}^{2} + {{\vec {F}}_{2}} \cdot {{\vec {R}}_{2}}.$

Точка над символом в уравнениях (1), (2) означает полную производную соответствующей функции по времени. Дважды непрерывно дифференцируемые функции ${{\gamma }_{1}}(t)$ и ${{\gamma }_{2}}(t)$ определяются соотношениями

${{\gamma }_{1}}(t) = \frac{{{{m}_{{00}}} + {{m}_{{10}}}}}{{{{m}_{0}}(t) + {{m}_{1}}(t)}},\quad {{\gamma }_{2}}(t) = \frac{{{{m}_{{00}}} + {{m}_{{20}}}}}{{{{m}_{0}}(t) + {{m}_{2}}(t)}},$
где ${{m}_{{00}}} = {{m}_{0}}(0)$, ${{m}_{{10}}} = {{m}_{1}}(0)$, ${{m}_{{20}}} = {{m}_{2}}(0)$ – значения масс тел в начальный момент времени. Реактивные силы ${{\vec {F}}_{1}}$ и ${{\vec {F}}_{2}}$, которые возникают вследствие неизотропности изменения массы тел, можно представить в виде
(3)
${{\vec {F}}_{i}} = \frac{{{{{\dot {m}}}_{i}}}}{{{{m}_{i}}}}{{\vec {V}}_{i}} - \frac{{{{{\dot {m}}}_{0}}}}{{{{m}_{0}}}}{{\vec {V}}_{0}},\quad (i = 1,2),$
где относительные скорости ${{\vec {V}}_{j}}$, ($j = 0,1,2$) частиц, покидающих тело ${{P}_{j}}$ или осаждающихся на нем, являются заданными функциями времени. Законы изменения масс во времени ${{m}_{j}}(t)$, (j = 0, 1, 2) определяются на основе наблюдений за движением небесных тел и также считаются известными. Потому далее будем считать, что реактивные силы ${{\vec {F}}_{1}}$ и ${{\vec {F}}_{2}}$ являются заданными функциями времени.

Поскольку получить общее решение уравнений (1), (2) не представляется возможным, для исследования динамики системы воспользуемся теорией возмущений. Отметим, что в случае ${{W}_{1}} = {{W}_{2}}$ = 0 оба уравнения (1), (2) являются интегрируемыми и определяют движение тел ${{P}_{1}}$ и ${{P}_{2}}$ вокруг тела P0 по квазиконическим сечениям (см. [26]). Соответствующие точные решения, которые будем использовать в качестве нулевого приближения, можно представить в виде

${{X}_{j}} = {{\gamma }_{j}}{{\rho }_{j}}(cos{{u}_{j}}cos{{\Omega }_{j}} - sin{{u}_{j}}sin{{\Omega }_{j}}cos{{i}_{j}}),$
${{Y}_{j}} = {{\gamma }_{j}}{{\rho }_{j}}(cos{{u}_{j}}sin{{\Omega }_{j}} + sin{{u}_{j}}cos{{\Omega }_{j}}cos{{i}_{j}}),$
(4)
${{Z}_{j}} = {{\gamma }_{j}}{{\rho }_{j}}sin{{u}_{j}}sin{{i}_{j}},$
где ${{u}_{j}} = {{\text{v}}_{j}} + {{\omega }_{j}}$,
(5)
${{\rho }_{j}} = \frac{{{{a}_{j}}(1 - e_{j}^{2})}}{{1 + {{e}_{j}}\cos {{\text{v}}_{j}}}},\quad (j = 1,2),$
а параметры ${{a}_{j}}$, ${{e}_{j}}$, ${{i}_{j}}$, ${{\omega }_{j}}$, ${{\Omega }_{j}}$, определяемые из начальных условий движения, соответствуют известным из классической задачи двух тел кеплеровским орбитальным элементам и являются аналогами большой полуоси, эксцентриситета, наклонения, долготы перицентра и долготы восходящего узла невозмущенной квазиэллиптической орбиты каждого из тел ${{P}_{1}}$ и ${{P}_{2}}$ (см. [1, 2, 26, 36]). Истинная аномалия ${{\text{v}}_{j}}$ характеризует положение тела на орбите и определяется уравнением
(6)
$\begin{gathered} \int\limits_0^{{{\text{v}}_{j}}} {\frac{{d{{\text{v}}_{j}}}}{{{{{(1 + {{e}_{j}}\cos {{\text{v}}_{j}})}}^{2}}}}} = \frac{1}{{{{{(1 - e_{j}^{2})}}^{{3/2}}}}}({{E}_{j}} - {{e}_{j}}sin{{E}_{j}}) = \\ = \;\frac{{{{M}_{j}}}}{{{{{(1 - e_{j}^{2})}}^{{3/2}}}}} = \frac{{\sqrt {{{K}_{{j0}}}} }}{{a_{j}^{{3/2}}{{{(1 - e_{j}^{2})}}^{{3/2}}}}}({{\Phi }_{j}}(t) - {{\Phi }_{j}}({{\tau }_{j}})), \\ \end{gathered} $
где ${{\tau }_{j}}$ – время прохождения тела ${{P}_{j}}$ через перицентр, ${{M}_{j}}$ – средняя аномалия,
${{\Phi }_{j}}(t) = \int\limits_0^t {\frac{{dt}}{{\gamma _{j}^{2}(t)}}} ,\quad {{K}_{{j0}}} = G({{m}_{{00}}} + {{m}_{{j0}}}),\quad (j = 1,2),$
а эксцентрическая аномалия ${{E}_{j}}$ связана с истинной аномалией соотношением

(7)
${\text{tg}}\frac{{{{\text{v}}_{j}}}}{2} = \sqrt {\frac{{1 + {{e}_{j}}}}{{1 - {{e}_{j}}}}} {\text{tg}}\frac{{{{E}_{j}}}}{2}.$

Легко видеть, что при заданных орбитальных параметрах ${{a}_{j}}$, ${{e}_{j}}$, ${{i}_{j}}$, ${{\omega }_{j}}$, ${{\Omega }_{j}}$, ${{\tau }_{j}}$ каждого из тел ${{P}_{1}}$ и ${{P}_{2}}$, а также известных функциях ${{\gamma }_{1}}(t)$, ${{\gamma }_{2}}(t)$, которые зависят от законов изменения масс всех трех тел, уравнение (6) позволяет найти средние аномалии Mj как функции времени. Решая затем уравнение Кеплера,

(8)
${{E}_{j}} - {{e}_{j}}sin{{E}_{j}} = {{M}_{j}},$
находим эксцентрические аномалии ${{E}_{j}}$ и, используя соотношение (7), вычисляем истинные аномалии ${{\text{v}}_{j}}$. В результате соотношения (4), (5) позволяют вычислить относительные декартовы координаты тел ${{P}_{1}}$ и ${{P}_{2}}$ и полностью описать их невозмущенное движение.

Следует отметить, что в случае постоянных масс, когда ${{\gamma }_{j}}(t) \equiv 1$, уравнения (4)–(7) определяют движение тел ${{P}_{1}}$ и ${{P}_{2}}$ вокруг тела ${{P}_{0}}$ по коническим сечениям. Наличие в выражениях (4) масштабного множителя ${{\gamma }_{j}}(t)$, зависящего от времени, приводит к деформации конических сечений и непериодичности движения. Поэтому говорят, что решения уравнений движения (1), (2) в случае ${{W}_{1}} = {{W}_{2}} = 0$ описывают апериодическое движение тел по квазиконическим сечениям (см. [26]).

В рассматриваемом случае двухпланетной задачи трех тел предполагается, что масса центрального тела ${{P}_{0}}$ значительно превышает массы тел ${{P}_{1}}$ и ${{P}_{2}}$. Потому их орбиты будут квазиконическими сечениями, определяемыми уравнениями (4)–(7), с малыми отклонениями, которые возникают вследствие взаимного гравитационного притяжения тел ${{P}_{1}}$ и ${{P}_{2}}$. Кроме того, изменение массы тел и возникающие при этом реактивные силы также будут влиять на изменение орбитальных параметров. Все эти факторы определяются возмущающими функциями ${{W}_{1}} \ne 0$ и ${{W}_{2}} \ne 0$, градиенты которых находятся в правых частях уравнений (1), (2). Чтобы получить дифференциальные уравнения, определяющие временную эволюцию орбитальных параметров, удобно перейти к новым каноническим переменным, известным как элементы Делоне и переписать уравнения (1), (2) в канонической форме (см. [2, 26, 36]). Используя решение (4) и выполняя стандартные, но довольно громоздкие символьные преобразования (см., напр., [34]), определяем три пары канонически сопряженных координат и импульсов $({{l}_{j}},{{L}_{j}})$, $({{g}_{j}},{{G}_{j}})$, $({{h}_{j}},{{H}_{j}})$ для каждого из тел ${{P}_{1}}$ и ${{P}_{2}}$, которые связаны с аналогами кеплеровских элементов орбиты соотношениями

${{l}_{j}} = {{M}_{j}},\quad {{L}_{j}} = \sqrt {{{K}_{{j0}}}{{a}_{j}}} ,$
${{g}_{j}} = {{\omega }_{j}},\quad {{G}_{j}} = \sqrt {{{K}_{{j0}}}{{a}_{j}}(1 - e_{j}^{2})} ,$
(9)
${{h}_{j}} = {{\Omega }_{j}},\quad {{H}_{j}} = \sqrt {{{K}_{{j0}}}{{a}_{j}}(1 - e_{j}^{2})} cos{{i}_{j}}.$

Соответствующие функции Гамильтона имеют вид

(10)
${{\mathcal{H}}_{j}} = - \frac{{K_{{j0}}^{2}}}{{2\gamma _{j}^{2}L_{j}^{2}}} - {{W}_{j}},\quad (j = 1,2),$
где возмущающие функции ${{W}_{1}}$, ${{W}_{2}}$ были введены ранее в уравнениях (1), (2).

Далее будем предполагать, что во время движения выполняются условия ${{i}_{j}} \ll 1$ и ${{e}_{j}} \ll 1$, т.е. тела движутся вблизи экваториальной плоскости по траекториям с малым эксцентриситетом. В этом приближении уравнения движения тел можно упростить, выбирая новые канонические переменные таким образом, чтобы во время движения некоторые из них оставались малыми величинами, и заменяя возмущающие функции их разложениями в степенные ряды по малым параметрам. Такие переменные, образующие три пары канонически сопряженных координат и импульсов $({{\lambda }_{j}},{{\Lambda }_{j}})$, $({{\eta }_{j}},{{\xi }_{j}})$, $({{q}_{j}},{{p}_{j}})$, известны в литературе как вторая система элементов Пуанкаре (см. [2, 26, 36]) и определяются через элементы Делоне (9) соотношениями

${{\lambda }_{j}} = {{l}_{j}} + {{g}_{j}} + {{h}_{j}},\quad {{\Lambda }_{j}} = {{L}_{j}},$
${{\eta }_{j}} = \sqrt {2{{\Gamma }_{j}}} sin{{\pi }_{j}},\quad {{\xi }_{j}} = \sqrt {2{{\Gamma }_{j}}} cos{{\pi }_{j}},$
(11)
${{q}_{j}} = \sqrt {2{{Z}_{j}}} sin{{z}_{j}},\quad {{p}_{j}} = \sqrt {2{{Z}_{j}}} cos{{z}_{j}},$
где

${{\Gamma }_{j}} = {{\Lambda }_{j}}(1 - \sqrt {1 - e_{j}^{2}} ),$
${{Z}_{j}} = {{\Lambda }_{j}}\sqrt {1 - e_{j}^{2}} (1 - cos{{i}_{j}}),$
(12)
${{\pi }_{j}} = - {{g}_{j}} - {{h}_{j}},\quad {{z}_{j}} = - {{h}_{j}}.$

При этом функции Гамильтона сохраняют вид (10), а уравнения Гамильтона принимают вид

${{\dot {\lambda }}_{j}} = \frac{{\partial {{\mathcal{H}}_{j}}}}{{\partial {{\Lambda }_{j}}}} = \frac{{K_{{j0}}^{2}}}{{\gamma _{j}^{2}\Lambda _{j}^{3}}} - \frac{{\partial {{W}_{j}}}}{{\partial {{\Lambda }_{j}}}},\mathop {\quad \dot {\Lambda }}\nolimits_j = - \frac{{\partial {{\mathcal{H}}_{j}}}}{{\partial {{\lambda }_{j}}}} = \frac{{\partial {{W}_{j}}}}{{\partial {{\lambda }_{j}}}},$
(13)
${{\dot {\eta }}_{j}} = \frac{{\partial {{\mathcal{H}}_{j}}}}{{\partial {{\xi }_{j}}}} = - \frac{{\partial {{W}_{j}}}}{{\partial {{\xi }_{j}}}},\quad \mathop {\dot {\xi }}\nolimits_j = - \frac{{\partial {{\mathcal{H}}_{j}}}}{{\partial {{\eta }_{j}}}} = \frac{{\partial {{W}_{j}}}}{{\partial {{\eta }_{j}}}},$
$\mathop {\dot {q}}\nolimits_j = \frac{{\partial {{\mathcal{H}}_{j}}}}{{\partial {{p}_{j}}}} = - \frac{{\partial {{W}_{j}}}}{{\partial {{p}_{j}}}},\quad \mathop {\dot {p}}\nolimits_j = - \frac{{\partial {{\mathcal{H}}_{j}}}}{{\partial {{q}_{j}}}} = \frac{{\partial {{W}_{j}}}}{{\partial {{q}_{j}}}}.$

Отметим, что возмущающие функции ${{W}_{1}}$, ${{W}_{2}}$ в уравнениях (13) должны быть выражены через новые канонические переменные.

III. РАЗЛОЖЕНИЕ ВОЗМУЩАЮЩИХ ФУНКЦИЙ

Уравнения движения (13) показывают, что в отсутствие возмущений (${{W}_{1}} = {{W}_{2}} = 0$) канонические переменные Пуанкаре ${{\Lambda }_{j}}$, ${{\eta }_{j}}$, ${{\xi }_{j}}$, ${{q}_{j}}$, ${{p}_{j}}$, а также орбитальные элементы ${{a}_{j}}$, ${{e}_{j}}$, ${{i}_{j}}$, ${{\omega }_{j}}$, ${{\Omega }_{j}}$, остаются постоянными, а средняя долгота ${{\lambda }_{j}}$ и средняя аномалия Mj являются возрастающими функциями времени (см. (6), (9), (11)). Гравитационное взаимодействие тел ${{P}_{1}}$ и ${{P}_{2}}$, а также изменения масс всех трех тел, описываемые возмущающими функциями ${{W}_{1}}$, ${{W}_{2}}$, приводят к изменениям орбитальных параметров. Для исследования их зависимости от времени возмущающие функции обычно заменяют их разложениями в ряды по малым параметрам с требуемой точностью (см. [2]), что позволяет найти приближенные решения уравнений (13). Следует отметить, что разложение возмущающих функций ${{W}_{1}}$, ${{W}_{2}}$ в ряды требует выполнения довольно громоздких символьных вычислений и представляет собой нетривиальную задачу, которая весьма эффективно решается при помощи систем компьютерной алгебры.

Напомним, что в рассматриваемом случае эксцентриситеты ${{e}_{j}}$ и наклонения ${{i}_{j}}$ орбит являются малыми величинами. Соответственно малыми величинами будут и две пары переменных Пуанкаре $({{\eta }_{j}},{{\xi }_{j}})$, $({{q}_{j}},{{p}_{j}})$. Действительно, из соотношений (11), (12) получаем

(14)
$e_{j}^{2} = \frac{{\eta _{j}^{2} + \xi _{j}^{2}}}{{{{\Lambda }_{j}}}}\left( {1 - \frac{{\xi _{j}^{2} + \xi _{j}^{2}}}{{4{{\Lambda }_{j}}}}} \right),$
(15)
$\frac{{p_{j}^{2} + q_{j}^{2}}}{{2{{\Lambda }_{j}}}} = 1 - cos{{i}_{j}} = 2si{{n}^{2}}\frac{{{{i}_{j}}}}{2}.$

Таким образом, при ${{e}_{j}} \ll 1$, ${{i}_{j}} \ll 1$ переменные ${{\eta }_{j}}$, ${{\xi }_{j}}$ и эксцентриситет ${{e}_{j}}$, а также переменные ${{q}_{j}}$, ${{p}_{j}}$ и наклонение ${{i}_{j}}$ являются величинами одного порядка. Выполняя в (11), (12), (14), (15) необходимые разложения с точностью до второго порядка по ${{\eta }_{j}}$, ${{\xi }_{j}}$, ${{q}_{j}}$ и ${{p}_{j}}$ включительно, получаем следующие соотношения:

(16)
${{e}_{j}}cos{{\pi }_{j}} = \frac{{{{\xi }_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }},\quad {{e}_{j}}sin{{\pi }_{j}} = \frac{{{{\eta }_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }},$
(17)
$sin{{i}_{j}}cos{{z}_{j}} = \frac{{{{p}_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }},\quad sin{{i}_{j}}sin{{z}_{j}} = \frac{{{{q}_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }}.$

При ${{e}_{j}} \ll 1$ решение уравнения Кеплера (8) также можно записать в виде сходящегося степенного ряда (см. [2]), что с точностью до второго порядка по ${{e}_{j}}$ дает

(18)
${{E}_{j}} = {{M}_{j}} + {{e}_{j}}sin{{M}_{j}} + \frac{{{{e}^{2}}}}{2}sin(2{{M}_{j}}) + ....$

Принимая во внимание соотношения Mj = = ${{\lambda }_{j}} + {{\pi }_{j}}$, ${{\omega }_{j}} = {{z}_{j}} - {{\pi }_{j}}$, ${{\Omega }_{j}} = - {{z}_{j}}$ (см. (9), (11), (12)) и используя разложения (16)–(18), выражения (4) для декартовых координат тел ${{P}_{1}}$ и ${{P}_{2}}$ с точностью до второго порядка по переменным Пуанкаре ${{\eta }_{j}}$, ${{\xi }_{j}}$, ${{q}_{j}}$, ${{p}_{j}}$ получаем в виде

$\frac{{{{X}_{j}}}}{{{{\gamma }_{j}}{{a}_{j}}}} = cos{{\lambda }_{j}} - \frac{{{{\xi }_{j}}}}{{2\sqrt {{{\Lambda }_{j}}} }}\left( {3 - cos(2{{\lambda }_{j}})} \right) - $
$ - \;\frac{{{{\eta }_{j}}}}{{2\sqrt {{{\Lambda }_{j}}} }}sin(2{{\lambda }_{j}}) + \frac{{3\xi _{j}^{2}}}{{8{{\Lambda }_{j}}}}\left( {cos(3{{\lambda }_{j}}) - cos{{\lambda }_{j}}} \right) - $
$ - \;\frac{{{{\xi }_{j}}{{\eta }_{j}}}}{{4{{\Lambda }_{j}}}}\left( {3sin(3{{\lambda }_{j}}) + sin{{\lambda }_{j}}} \right) - \frac{{\eta _{j}^{2}}}{{8{{\Lambda }_{j}}}}\left( {3cos(3{{\lambda }_{j}})} \right. + $
$ + \;\left. {5cos{{\lambda }_{j}}} \right) - \frac{{{{p}_{j}}{{q}_{j}}}}{{2{{\Lambda }_{j}}}}sin{{\lambda }_{j}} - \frac{{q_{j}^{2}}}{{2{{\Lambda }_{j}}}}cos{{\lambda }_{j}},$
$\frac{{{{Y}_{j}}}}{{{{\gamma }_{j}}{{a}_{j}}}} = sin{{\lambda }_{j}} + \frac{{{{\eta }_{j}}}}{{2\sqrt {{{\Lambda }_{j}}} }}(3 + cos(2{{\lambda }_{j}})) + $
$ + \;\frac{{{{\xi }_{j}}}}{{2\sqrt {{{\Lambda }_{j}}} }}sin(2{{\lambda }_{j}}) - \frac{{3\eta _{j}^{2}}}{{8{{\Lambda }_{j}}}}(sin(3{{\lambda }_{j}}) + sin{{\lambda }_{j}}) + $
$ + \;\frac{{{{\xi }_{j}}{{\eta }_{j}}}}{{4{{\Lambda }_{j}}}}\left( {3cos(3{{\lambda }_{j}}} \right) - cos{{\lambda }_{j}}) + \frac{{\xi _{j}^{2}}}{{8{{\Lambda }_{j}}}}\left( {3sin(3{{\lambda }_{j}})} \right. - $
$ - \;5sin{{\lambda }_{j}}) - \frac{{{{p}_{j}}{{q}_{j}}}}{{2{{\Lambda }_{j}}}}cos{{\lambda }_{j}} - \frac{{p_{j}^{2}}}{{2{{\Lambda }_{j}}}}sin{{\lambda }_{j}},$
$\frac{{{{Z}_{j}}}}{{{{\gamma }_{j}}{{a}_{j}}}} = \frac{{{{p}_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }}sin{{\lambda }_{j}} + \frac{{{{q}_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }}cos{{\lambda }_{j}} + $
$ + \;\frac{{{{\xi }_{j}}{{p}_{j}}}}{{2{{\Lambda }_{j}}}}sin(2{{\lambda }_{j}}) - \frac{{{{\xi }_{j}}{{q}_{j}}}}{{2{{\Lambda }_{j}}}}\left( {3 - cos(2{{\lambda }_{j}})} \right) + $
(19)
$ + \;\frac{{{{\eta }_{j}}{{p}_{j}}}}{{2{{\Lambda }_{j}}}}\left( {3 + {\text{cos}}(2{{\lambda }_{j}})} \right) - \frac{{{{\eta }_{j}}{{q}_{j}}}}{{2{{\Lambda }_{j}}}}sin(2{{\lambda }_{j}}).$

Заметим, что использование встроенной в систему Mathematica функции Series (см. [35]) существенно упрощает вычисление разложений (19). Поскольку каждая из функций (4) разлагается в ряд по четырем переменным ${{\eta }_{j}}$, ${{\xi }_{j}}$, ${{p}_{j}}$, ${{q}_{j}}$ в окрестности точки ${{\eta }_{j}} = {{\xi }_{j}} = {{p}_{j}} = {{q}_{j}} = 0$, при выполнении вычислений удобно воспользоваться следующим приемом: добавляем множитель $\varepsilon $ у каждой из четырех переменных и выполняем разложение функции по $\varepsilon $ в окрестности нуля с точностью до второго порядка. Соответствующая команда в системе $Mathematica$ имеет вид:

В результате получаем следующее разложение:

$f[0,0,0,0] + \varepsilon (q{{f}^{{(0,0,0,1)}}}[0,0,0,0] + $
$ + \;p{{f}^{{(0,0,1,0)}}}[0,0,0,0] + \xi {{f}^{{(0,1,0,0)}}}[0,0,0,0] + $
$\, + \eta {{f}^{{(1,0,0,0)}}}[0,0,0,0]) + \frac{1}{2}{{\varepsilon }^{2}}({{q}^{2}}{{f}^{{(0,0,0,2)}}}[0,0,0,0] + $
$ + \;2pq{{f}^{{(0,0,1,1)}}}[0,0,0,0] + {{p}^{2}}{{f}^{{(0,0,2,0)}}}[0,0,0,0] + $
$ + \;2q\xi {{f}^{{(0,1,0,1)}}}[0,0,0,0] + 2p\xi {{f}^{{(0,1,1,0)}}}[0,0,0,0] + $
$ + \;{{\xi }^{2}}{{f}^{{(0,2,0,0)}}}[0,0,0,0] + 2q\eta {{f}^{{(1,0,0,1)}}}[0,0,0,0] + $
$ + \;2p\eta {{f}^{{(1,0,1,0)}}}[0,0,0,0] + 2\eta \xi {{f}^{{(1,1,0,0)}}}[0,0,0,0] + $
$ + \;{{\eta }^{2}}{{f}^{{(2,0,0,0)}}}[0,0,0,0]).$

Полагая $\varepsilon = 1$, получаем искомый полином второй степени, причем функция Series используется только один раз, а степень полинома определяется точностью разложения по ε.

Применение функции Series позволяет также получить следующие выражения, которые будут использованы при вычислении разложений возмущающих функций ${{W}_{1}}$ и ${{W}_{2}}$:

(20)
$\begin{gathered} \frac{{R_{j}^{2}}}{{\gamma _{j}^{2}a_{j}^{2}}} = 1 + \frac{2}{{\sqrt {{{\Lambda }_{j}}} }}\left( {{{\eta }_{j}}sin{{\lambda }_{j}} - {{\xi }_{j}}cos{{\lambda }_{j}}} \right) + \\ + \;\frac{{\eta _{j}^{2}}}{{2{{\Lambda }_{j}}}}\left( {3 + cos(2{{\lambda }_{j}})} \right) + \frac{{{{\eta }_{j}}{{\xi }_{j}}}}{{{{\Lambda }_{j}}}}sin(2{{\lambda }_{j}}) + \\ + \;\frac{{\xi _{j}^{2}}}{{2{{\Lambda }_{j}}}}\left( {3 - cos(2{{\lambda }_{j}})} \right), \\ \end{gathered} $
(21)
$\begin{gathered} \frac{{\gamma _{j}^{3}a_{j}^{3}}}{{R_{j}^{3}}} = 1 - \frac{{3{{\eta }_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }}sin{{\lambda }_{j}} + \frac{{3{{\xi }_{j}}}}{{\sqrt {{{\Lambda }_{j}}} }}cos{{\lambda }_{j}} + \\ + \;\frac{{3\eta _{j}^{2}}}{{2{{\Lambda }_{j}}}}\left( {1 - 3cos(2{{\lambda }_{j}})} \right) - \frac{{9{{\eta }_{j}}{{\xi }_{j}}}}{{{{\Lambda }_{j}}}}sin(2{{\lambda }_{j}}) + \\ + \;\frac{{3\xi _{j}^{2}}}{{2{{\Lambda }_{j}}}}\left( {1 - 3cos(2{{\lambda }_{j}})} \right),\quad (j = 1,2). \\ \end{gathered} $

Аналогичным образом вычисляется разложение выражения $1{\text{/}}{{R}_{{12}}}$, которое описывает возмущения, связанные с гравитационным взаимодействием тел ${{P}_{1}}$ и ${{P}_{2}}$. Поскольку получаемое выражение более громоздко, мы его не приводим. Отметим только, что в результате получается многочлен второго порядка относительно переменных Пуанкаре ${{\eta }_{j}}$, ${{\xi }_{j}}$, ${{q}_{j}}$, ${{p}_{j}}$, коэффициенты которого являются периодическими функциями средних долгот ${{\lambda }_{1}}$, ${{\lambda }_{2}}$ и представляют собой рациональные выражения, в числителях которых содержатся тригонометрические функции $sin(k{{\lambda }_{j}})$, ${\text{cos}}(k{{\lambda }_{j}})$, ${\text{sin}}(k{{\lambda }_{1}}\, \pm \,n{{\lambda }_{2}})$, ${\text{cos}}(k{{\lambda }_{1}}\, \pm \,n{{\lambda }_{2}})$, (k, n = 1, 2, 3), а знаменатели содержат выражения ${{\Delta }_{0}}$, $\Delta _{0}^{3}$, $\Delta _{0}^{5}$, где

${{\Delta }_{0}} = {{(1 + {{\alpha }^{2}} - 2\alpha cos({{\lambda }_{1}} - {{\lambda }_{2}}))}^{{1/2}}},$
и введен параметр

$\alpha = \frac{{{{\gamma }_{1}}{{a}_{1}}}}{{{{\gamma }_{2}}{{a}_{2}}}} < 1.$

Ограничение на величину параметра $\alpha $ является следствием предположения, что траектория планеты ${{P}_{1}}$ располагается внутри траектории планеты ${{P}_{2}}$, т.е. в любой момент времени выполняется условие ${{R}_{1}} < {{R}_{2}}$.

Поскольку ${{\Delta }_{0}}$ является периодической функцией параметра $({{\lambda }_{1}} - {{\lambda }_{2}})$, имеют место следующие разложения в ряды Фурье (см. [2]):

$\frac{1}{{{{\Delta }_{0}}}} = \frac{1}{2}\sum\limits_{k = - \infty }^{ + \infty } {{A}_{k}}cos\left( {k({{\lambda }_{1}} - {{\lambda }_{2}})} \right),$
(22)
$\frac{{{{\gamma }_{1}}{{\gamma }_{2}}{{a}_{1}}{{a}_{2}}}}{{\Delta _{0}^{3}}} = \frac{1}{2}\sum\limits_{k = - \infty }^{ + \infty } {{B}_{k}}cos\left( {k({{\lambda }_{1}} - {{\lambda }_{2}})} \right),$
$\frac{{\gamma _{1}^{2}\gamma _{2}^{2}a_{1}^{2}a_{2}^{2}}}{{\Delta _{0}^{5}}} = \frac{1}{2}\sum\limits_{k = - \infty }^{ + \infty } {{C}_{k}}cos\left( {k({{\lambda }_{1}} - {{\lambda }_{2}})} \right),$
причем коэффициенты ${{A}_{k}}$, ${{B}_{k}}$, ${{C}_{k}}$ связаны между собой рекуррентными соотношениями и выражаются через два коэффициента ${{A}_{0}}$ и ${{A}_{1}}$, которые определяются выражениями

$\begin{gathered} {{A}_{0}} = \frac{2}{{\pi {{a}_{2}}{{\gamma }_{2}}}}\int\limits_0^\pi {\frac{{d\lambda }}{{{{{(1 + {{\alpha }^{2}} - 2\alpha cos\lambda )}}^{{1/2}}}}}} = \\ = \;\frac{4}{{\pi {{a}_{2}}{{\gamma }_{2}}(1 + \alpha )}}K\left( {\frac{{4\alpha }}{{{{{(1 + \alpha )}}^{2}}}}} \right), \\ \end{gathered} $
(23)
$\begin{gathered} {{A}_{1}} = \frac{2}{{\pi {{a}_{2}}{{\gamma }_{2}}}}\int\limits_0^\pi {\frac{{cos\lambda d\lambda }}{{{{{(1 + {{\alpha }^{2}} - 2\alpha cos\lambda )}}^{{1/2}}}}}} = \\ = \;\frac{2}{{\pi {{a}_{2}}{{\gamma }_{2}}\alpha (1 + \alpha )}}\left( {(1 + {{\alpha }^{2}})K\left( {\frac{{4\alpha }}{{{{{(1 + \alpha )}}^{2}}}}} \right)} \right. - \\ \left. { - \;{{{(1 + \alpha )}}^{2}}E\left( {\frac{{4\alpha }}{{{{{(1 + \alpha )}}^{2}}}}} \right)} \right). \\ \end{gathered} $

Функции $K(4\alpha {\text{/}}{{(1 + \alpha )}^{2}})$ и $E(4\alpha {\text{/}}{{(1 + \alpha )}^{2}})$ в (23) обозначают соответственно эллиптические интегралы первого и второго рода.

Используя выражения (19)–(22) и выполняя необходимые символьные вычисления, мы получаем разложение возмущающих функций ${{W}_{1}}$ и ${{W}_{2}}$ в ряды по степеням переменных Пуанкаре ${{\eta }_{j}}$, ${{\xi }_{j}}$, ${{q}_{j}}$, ${{p}_{j}}$, ($j = 1,2$) с точностью до второго порядка включительно. Полученное выражение весьма громоздко и потому мы его не приводим. Отметим только, что коэффициенты полученного полинома содержат синусы и косинусы переменных ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$, которые представляют собой быстро изменяющиеся величины. Поскольку нас интересует влияние изменений масс тел на эволюцию орбитальных параметров тел ${{P}_{1}}$ и ${{P}_{2}}$ на больших интервалах времени, короткопериодические возмущения, связанные с движением тел ${{P}_{1}}$, ${{P}_{2}}$, следует устранить путем усреднения возмущающих функций по средним долготам ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$ (см. [2, 29]). Фактически это означает, что в полученных разложениях следует оставить только члены, не зависящие от ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$. При этом предполагается, что в разложениях возмущающих функций отсутствуют резонансные члены, т.е. отсутствует соизмеримость средних движений тел ${{P}_{1}}$ и ${{P}_{2}}$. В результате получим следующие вековые части возмущающих функций:

$\begin{gathered} W_{1}^{{(sec)}} = G{{m}_{2}}\left( {\frac{{{{A}_{0}}}}{2} + {{\Pi }_{{11}}}\frac{{\eta _{1}^{2} + \xi _{1}^{2}}}{{2{{\Lambda }_{1}}}} + } \right. \\ + \;{{\Pi }_{{12}}}\frac{{{{\eta }_{1}}{{\eta }_{2}} + {{\xi }_{1}}{{\xi }_{2}}}}{{\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }} + {{\Pi }_{{22}}}\frac{{\eta _{2}^{2} + \xi _{2}^{2}}}{{2{{\Lambda }_{2}}}} - \\ \end{gathered} $
(24)
$\begin{gathered} \left. { - {{B}_{1}}\left( {\frac{{p_{1}^{2} + q_{1}^{2}}}{{8{{\Lambda }_{1}}}} - \frac{{{{p}_{1}}{{p}_{2}} + {{q}_{1}}{{q}_{2}}}}{{4\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }} + \frac{{p_{2}^{2} + q_{2}^{2}}}{{8{{\Lambda }_{2}}}}} \right)} \right) - \\ - \;\frac{{\mathop {\ddot {\gamma }}\nolimits_1 \Lambda _{1}^{4}}}{{2{{\gamma }_{1}}K_{{10}}^{2}}}\left( {1 + \frac{3}{{2{{\Lambda }_{1}}}}(\xi _{1}^{2} + \eta _{1}^{2})} \right) + \\ \end{gathered} $
$ + \frac{{3{{\gamma }_{1}}\Lambda _{1}^{2}}}{{2{{K}_{{10}}}}}\left( { - {{F}_{{1x}}}\frac{{{{\xi }_{1}}}}{{\sqrt {{{\Lambda }_{1}}} }} + {{F}_{{1y}}}\frac{{{{\eta }_{1}}}}{{\sqrt {{{\Lambda }_{1}}} }}} \right. + \left. {{{F}_{{1z}}}\frac{{{{p}_{1}}{{\eta }_{1}} - {{q}_{1}}{{\xi }_{1}}}}{{{{\Lambda }_{1}}}}} \right),$
$\begin{gathered} W_{2}^{{(sec)}} = G{{m}_{1}}\left( {\frac{{{{A}_{0}}}}{2} + {{\Pi }_{{11}}}\frac{{\eta _{1}^{2} + \xi _{1}^{2}}}{{2{{\Lambda }_{1}}}} + } \right. \hfill \\ + \;{{\Pi }_{{12}}}\frac{{{{\eta }_{1}}{{\eta }_{2}} + {{\xi }_{1}}{{\xi }_{2}}}}{{\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }} + {{\Pi }_{{22}}}\frac{{\eta _{2}^{2} + \xi _{2}^{2}}}{{2{{\Lambda }_{2}}}} - \hfill \\ \end{gathered} $
(25)
$\begin{gathered} \left. { - {{B}_{1}}\left( {\frac{{p_{1}^{2} + q_{1}^{2}}}{{8{{\Lambda }_{1}}}} - \frac{{{{p}_{1}}{{p}_{2}} + {{q}_{1}}{{q}_{2}}}}{{4\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }} + \frac{{p_{2}^{2} + q_{2}^{2}}}{{8{{\Lambda }_{2}}}}} \right)} \right) - \\ - \;\frac{{\mathop {\ddot {\gamma }}\nolimits_2 \Lambda _{2}^{4}}}{{2{{\gamma }_{2}}K_{{20}}^{2}}}\left( {1 + \frac{3}{{2{{\Lambda }_{2}}}}(\xi _{2}^{2} + \eta _{2}^{2})} \right) + \\ \end{gathered} $
$ + \frac{{3{{\gamma }_{2}}\Lambda _{2}^{2}}}{{2{{K}_{{20}}}}}\left( { - {{F}_{{2x}}}\frac{{{{\xi }_{2}}}}{{\sqrt {{{\Lambda }_{2}}} }} + {{F}_{{2y}}}\frac{{{{\eta }_{2}}}}{{\sqrt {{{\Lambda }_{2}}} }}} \right. + \left. {{{F}_{{2z}}}\frac{{{{p}_{2}}{{\eta }_{2}} - {{q}_{2}}{{\xi }_{2}}}}{{{{\Lambda }_{2}}}}} \right),$
где

${{\Pi }_{{11}}} = - \frac{{3\alpha }}{4}{{B}_{0}} - \frac{1}{2}{{B}_{1}} + \frac{{15 + 6{{\alpha }^{2}}}}{8}{{C}_{0}} - \frac{{3\alpha }}{2}{{C}_{1}} - \frac{9}{8}{{C}_{2}},$
$\begin{gathered} {{\Pi }_{{12}}} = \frac{1}{8}(9{{B}_{0}} + {{B}_{2}}) - \frac{{9(1 + {{\alpha }^{2}})}}{{8\alpha }}{{C}_{0}} + \\ + \;\frac{{21}}{{16}}{{C}_{1}} + \frac{{3(1 + {{\alpha }^{2}})}}{{8\alpha }}{{C}_{2}} + \frac{3}{{16}}{{C}_{3}}, \\ \end{gathered} $
${{\Pi }_{{22}}} = - \frac{3}{{4\alpha }}{{B}_{0}} - \frac{1}{2}{{B}_{1}} + \frac{{15{{\alpha }^{2}} + 6}}{{8{{\alpha }^{2}}}}{{C}_{0}} - \frac{3}{{2\alpha }}{{C}_{1}} - \frac{9}{8}{{C}_{2}}.$

IV. ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ

Эволюционные уравнения, определяющие поведение орбитальных параметров на больших интервалах времени, получаются из уравнений движения (13), если вместо возмущающих функций ${{W}_{1}}$, ${{W}_{2}}$ подставить их усредненные разложения (24), (25). Поскольку $W_{1}^{{(sec)}}$, $W_{2}^{{(sec)}}$ не зависят от координат ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, соответствующие им канонические импульсы ${{\Lambda }_{1}}$, ${{\Lambda }_{2}}$, а также большие полуоси ${{a}_{j}} = \Lambda _{j}^{2}{\text{/}}{{K}_{{j0}}}$, ($j = 1,2$), не зависят от времени.

Вековые возмущения элеметнов Пуанкаре ${{\eta }_{j}}$, ${{\xi }_{j}}$, ${{q}_{j}}$, ${{p}_{j}}$ ($j = 1,2$) определяются как решения следующей системы дифференциальных уравнений:

$\begin{gathered} \mathop {\dot {\eta }}\nolimits_1 = - \frac{{\partial W_{1}^{{(sec)}}}}{{\partial {{\xi }_{1}}}} = - \left( {\frac{{G{{m}_{2}}{{\Pi }_{{11}}}}}{{{{\Lambda }_{1}}}} - \frac{{3\mathop {\ddot {\gamma }}\nolimits_1 \Lambda _{1}^{3}}}{{2{{\gamma }_{1}}K_{{10}}^{2}}}} \right){{\xi }_{1}} - \\ - \;\frac{{G{{m}_{2}}{{\Pi }_{{12}}}}}{{\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }}{{\xi }_{2}} + \frac{{3{{\gamma }_{1}}\Lambda _{1}^{{3/2}}}}{{2{{K}_{{10}}}}}{{F}_{{1x}}} + \frac{{3{{\gamma }_{1}}{{\Lambda }_{1}}}}{{2{{K}_{{10}}}}}{{F}_{{1z}}}{{q}_{1}}, \\ \end{gathered} $
$\begin{gathered} \mathop {\dot {\xi }}\nolimits_1 = \frac{{\partial W_{1}^{{(sec)}}}}{{\partial {{\eta }_{1}}}} = \left( {\frac{{G{{m}_{2}}{{\Pi }_{{11}}}}}{{{{\Lambda }_{1}}}} - \frac{{3\mathop {\ddot {\gamma }}\nolimits_1 \Lambda _{1}^{3}}}{{2{{\gamma }_{1}}K_{{10}}^{2}}}} \right){{\eta }_{1}} + \\ + \;\frac{{G{{m}_{2}}{{\Pi }_{{12}}}}}{{\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }}{{\eta }_{2}} + \frac{{3{{\gamma }_{1}}\Lambda _{1}^{{3/2}}}}{{2{{K}_{{10}}}}}{{F}_{{1y}}} + \frac{{3{{\gamma }_{1}}{{\Lambda }_{1}}}}{{2{{K}_{{10}}}}}{{F}_{{1z}}}{{p}_{1}}, \\ \end{gathered} $
$\begin{gathered} \mathop {\dot {\eta }}\nolimits_2 = - \frac{{\partial W_{2}^{{(sec)}}}}{{\partial {{\xi }_{2}}}} = - \left( {\frac{{G{{m}_{1}}{{\Pi }_{{22}}}}}{{{{\Lambda }_{2}}}} - \frac{{3\mathop {\ddot {\gamma }}\nolimits_2 \Lambda _{2}^{3}}}{{2{{\gamma }_{2}}K_{{20}}^{2}}}} \right){{\xi }_{2}} - \\ - \;\frac{{G{{m}_{1}}{{\Pi }_{{12}}}}}{{\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }}{{\xi }_{1}} + \frac{{3{{\gamma }_{2}}\Lambda _{2}^{{3/2}}}}{{2{{K}_{{20}}}}}{{F}_{{2x}}} + \frac{{3{{\gamma }_{2}}{{\Lambda }_{2}}}}{{2{{K}_{{20}}}}}{{F}_{{2z}}}{{q}_{2}}, \\ \end{gathered} $
$\begin{gathered} \mathop {\dot {\xi }}\nolimits_2 = \frac{{\partial W_{2}^{{(sec)}}}}{{\partial {{\eta }_{2}}}} = \left( {\frac{{G{{m}_{1}}{{\Pi }_{{22}}}}}{{{{\Lambda }_{2}}}} - \frac{{3\mathop {\ddot {\gamma }}\nolimits_2 \Lambda _{2}^{3}}}{{2{{\gamma }_{2}}K_{{20}}^{2}}}} \right){{\eta }_{2}} + \\ + \;\frac{{G{{m}_{1}}{{\Pi }_{{12}}}}}{{\sqrt {{{\Lambda }_{1}}{{\Lambda }_{2}}} }}{{\eta }_{1}} + \frac{{3{{\gamma }_{2}}\Lambda _{2}^{{3/2}}}}{{2{{K}_{{20}}}}}{{F}_{{2y}}} + \frac{{3{{\gamma }_{2}}{{\Lambda }_{2}}}}{{2{{K}_{{20}}}}}{{F}_{{2z}}}{{p}_{2}}, \\ \end{gathered} $
$\mathop {\dot {q}}\nolimits_1 = - \frac{{\partial W_{1}^{{(sec)}}}}{{\partial {{p}_{1}}}} = \frac{{G{{m}_{2}}{{B}_{1}}}}{{4\sqrt {{{\Lambda }_{1}}} }}\left( {\frac{{{{p}_{1}}}}{{\sqrt {{{\Lambda }_{1}}} }} - \frac{{{{p}_{2}}}}{{\sqrt {{{\Lambda }_{2}}} }}} \right) - \frac{{3{{\gamma }_{1}}{{\Lambda }_{1}}}}{{2{{K}_{{10}}}}}{{F}_{{1z}}}{{\eta }_{1}},$
$\mathop {\dot {p}}\nolimits_1 = \frac{{\partial W_{1}^{{(sec)}}}}{{\partial {{q}_{1}}}} = - \frac{{G{{m}_{2}}{{B}_{1}}}}{{4\sqrt {{{\Lambda }_{1}}} }}\left( {\frac{{{{q}_{1}}}}{{\sqrt {{{\Lambda }_{1}}} }} - \frac{{{{q}_{2}}}}{{\sqrt {{{\Lambda }_{2}}} }}} \right) - \frac{{3{{\gamma }_{1}}{{\Lambda }_{1}}}}{{2{{K}_{{10}}}}}{{F}_{{1z}}}{{\xi }_{1}},$
$\mathop {\dot {q}}\nolimits_2 = - \frac{{G{{m}_{1}}{{B}_{1}}}}{{4\sqrt {{{\Lambda }_{2}}} }}\left( {\frac{{{{p}_{1}}}}{{\sqrt {{{\Lambda }_{1}}} }} - \frac{{{{p}_{2}}}}{{\sqrt {{{\Lambda }_{2}}} }}} \right) - \frac{{3{{\gamma }_{2}}{{\Lambda }_{2}}}}{{2{{K}_{{20}}}}}{{F}_{{2z}}}{{\eta }_{2}},$
$\mathop {\dot {p}}\nolimits_2 = \frac{{G{{m}_{1}}{{B}_{1}}}}{{4\sqrt {{{\Lambda }_{2}}} }}\left( {\frac{{{{q}_{1}}}}{{\sqrt {{{\Lambda }_{1}}} }} - \frac{{{{q}_{2}}}}{{\sqrt {{{\Lambda }_{2}}} }}} \right) - \frac{{3{{\gamma }_{2}}{{\Lambda }_{2}}}}{{2{{K}_{{20}}}}}{{F}_{{2z}}}{{\xi }_{2}}.$

Напомним, что массы тел ${{m}_{j}}(t)$, ($j = 0,1,2$) и реактивные силы $({{F}_{{jx}}}(t),{{F}_{{jy}}}(t),{{F}_{{jz}}}(t))$, (j = 1, 2) являются функциями времени. Следовательно, зависят от времени и отношения масс ${{\gamma }_{1}}(t)$, ${{\gamma }_{2}}(t)$, а также параметр $\alpha (t)$ и коэффициенты Лапласа ${{B}_{0}}$, ${{B}_{1}}$, ${{B}_{2}}$, ${{C}_{0}}$, ${{C}_{1}}$, ${{C}_{2}}$, ${{C}_{3}}$. Поэтому коэффициенты полученной системы из восьми линейных дифференциальных уравнений являются довольно сложными функциями от времени, и записать общее решение этой системы в символьной форме не представляется возможным. Однако эту систему можно решать численно, задавая различные законы изменения масс и реактивные силы и исследуя их влияние на вековые возмущения орбитальных элементов.

Отметим также, что вычисление правой части первого дифференциального уравнения системы (13), определяеющего зависимость от времени средних долгот ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, которое принимает вид

$\mathop {\dot {\lambda }}\nolimits_j = \frac{{K_{{j0}}^{2}}}{{\gamma _{j}^{2}\Lambda _{j}^{3}}} - \frac{{\partial W_{j}^{{(sec)}}}}{{\partial {{\Lambda }_{j}}}},$
требует весьма громоздких символьных вычислений, поскольку возмущающие функции (24), (25) зависят от импульсов ${{\Lambda }_{j}}$ как явным образом, так и посредством зависимости от ${{\Lambda }_{j}}$ параметра $\alpha $ и коэффициентов Лапласа ${{B}_{0}}$, ${{B}_{1}}$, ${{B}_{2}}$, ${{C}_{0}}$, ${{C}_{1}}$, ${{C}_{2}}$, ${{C}_{3}}$. Тем не менее, это уравнение также допускает численное интегрирование.

V. ЗАКЛЮЧЕНИЕ

В настоящей работе обсуждается классическая двухпланетная задача трех тел переменной массы в общем случае, когда массы тел изменяются неизотропно с различными скоростями, что приводит к появлению реактивных сил. Поскольку дифференциальные уравнения движения являются неинтегрируемыми, проблема исследуется в рамках теории возмущений, причем в качестве нулевого приближения используется точное решение задачи двух тел с переменными массами, описывающее апериодическое движение тел по квазиконическим сечениям. Подробно описаны основные типы вычислений, связанных с разложением возмущающих функций в степенные ряды, и получены выражения для возмущающих функций с точностью до второго порядка по эксцентриситетам и наклонениям. Получены эволюционные уравнения, определяющие вековые возмущения орбитальных элементов, которые допускают численное интегрирование при заданных законах изменения масс тел.

Отметим, что все описанные символьные вычисления реализованы в системе компьютерной алгебры Mathematica.

Список литературы

  1. Рой А.Э. Движение по орбитам. М.: Мир, 1981. 544 с.

  2. Мюррей К., Дермотт С. Динамика Солнечной системы / Пер. с англ. под ред. И.И. Шевченко. М.: Физматлит, 2010. 588 с.

  3. Мерман Г.А. О представлении общего решения задачи трех тел сходящимися рядами // Бюлл. ин-та теор. астрономии. 1958. Т. 6. С. 713–732.

  4. Брумберг В.А. Ряды полиномов в задаче трех тел // Бюлл. ин-та теор. астрономии. 1963. Т. 9. № 4. С. 234–256.

  5. Борунов В.П., Рябов Ю.А. Построение численно-аналитического тригонометрического решения задачи трех тел в ССВ Mathematica и Maple. Применение систем Mathematica и Maple в научных исследованиях. М.: ВЦ РАН, 2001. С. 63–77.

  6. Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Наука, 1978. 312 с.

  7. Брумберг В.А. Аналитические алгоритмы в небесной механике. М.: Наука, 1980. 208 с.

  8. Абрамов С.А., Зима Е.Б., Ростовцев В.А. Компьютерная алгебра // Программирование. 1992. № 5. С. 4–25.

  9. Васильев Н.Н., Еднерал В.Ф. Компьютерная алгебра в физических и математических приложениях // Программирование. 1994. № 1. С. 70–82.

  10. Прокопеня А.Н. Некоторые алгоритмы символьных вычислений в исследованиях проблем космической динамики // Программирование. 2006. Т. 32. № 2. С. 16–22.

  11. Prokopenya A.N. Determination of the stability boundaries for the Hamiltonian systems with periodic coefficients // Math. Modelling and Analysis. 2005. V. 10. № 2. P. 191–204.

  12. Prokopenya A.N. Computing the stability boundaries for the Lagrange triangular solutions in the elliptic restricted three-body problem // Math. Modelling and Analysis. 2006. V. 11. № 1. P. 95–104.

  13. Прокопеня А.Н. Символьные вычисления в исследованиях устойчивости решений линейных систем дифференциальных уравнений с периодическими коэффициентами // Программирование. 2007. Т. 33. № 2. С. 9–16.

  14. Прокопеня А.Н. Нормализация гамильтониана в ограниченной задаче многих тел методами компьютерной алгебры // Программирование. 2012. Т. 38. № 3. С. 65–78.

  15. Будько Д.А., Прокопеня А.Н. Символьно-численный анализ равновесных решений в ограниченной задаче четырех тел // Программирование. 2010. Т. 3. № 2. С. 13–20.

  16. Будько Д.А., Прокопеня А.Н. Символьно-численные методы поиска положений равновесия в ограниченной задаче четырех тел // Программирование. 2013. Т. 39. № 2. С. 30–37.

  17. Schmidt D., Vidal C. Stability of the planar equiibrium solutions of a restricted 1+N body problem // Regular Chaotic Dyn. 2014. V. 19. № 5. P. 533–547.

  18. Prokopenya A.N., Minglibayev M.Zh., Beketauov B.A. Secular perturbations of quasi-elliptic orbits in the restricted three-body problem with variable masses // Int. J. Non-Linear Mechanics. 2015. V. 73. P. 58–63.

  19. Prokopenya A.N. Symbolic-numerical analysis of the relative equilibria stability in the planar circular restricted four-body problem. Computer Algebra in Scientific Computing/CASC’2017 / Gerdt V.P., Koepf  W., Seiler W.M., Vorozhtsov E.V. Eds. LNCS 10490. Berlin: Springer-Verlag, 2017. P. 329–345.

  20. Прокопеня А.Н., Минглибаев М.Дж., Маемерова Г.М., Иманова Ж.У. Исследование ограниченной задачи трех тел с переменными массами методами компьютерной алгебры // Программирование. 2017. Т. 435. С. 18–23.

  21. Minglibayev M.Zh., Prokopenya A.N., Mayemerova G.M., Imanova Zh.U. Three-body problem with variable masses that change anisotropically at different rates // Mathematics in Computer Sci. 2017. V. 11. № 3З4. P. 383–391.

  22. Prokopenya A.N. Numerical-symbolic methods for searching relative equilibria in the restricted problem of four bodies // Math. Modelling and Analysis. 2018. V. 23. № 3. P. 507–525.

  23. Bekov A.A., Omarov T.B. The theory of orbits in non-stationary stellar systems // Astron. Astrophys. Trans. 2003. V. 22. № 2. P. 145–153.

  24. Eggleton P. Evolutionary processes in binary and multiple stars. Cambridge University Press, 2006. 332 p.

  25. Veras D., Hadjidemetriou J.D., Tout C.A. An exoplanet’s response to anisotropic stellar mass-loss during birth and death // Mon. Not. R. Astron. Soc. 2013. V. 435. № 3. P. 2416–2430.

  26. Минглибаев М.Дж. Динамика гравитирующих тел с переменными массами и размерами. LAP LAMBERT Academic Publ., 2012. 224 с.

  27. Минглибаев М.Дж., Маемерова Г.М., Шомшекова С.А. Дифферециальные уравнения относительного движения нестационарных экзопланетных систем // Вестник Казахского Национального педагогического университета им. Абая. Серия “Физ.-мат. науки”. 2017. Т. 57. № 1. С. 147–152. http://kaznpu.kz/docs/vestnik/fizika_matematika/1.2017-ilovepdf-compressed_1.pdf

  28. Berkovič L.M. Gylden-Meščerski problem // Celestial Mechanics. 1981. V. 24. P. 407–429.

  29. Лидов М.Л., Вашковьяк М.А. О квазиспутниковых орбитах в ограниченной эллиптической задаче трех тел // Письма в Астрон. журн. 1994. Т. 20. № 10. С. 781–795.

  30. Ford E.B., Kozinsky B., Rasio F.A. Secular evolution of hierarchical triple star systems // Astron. J. 2000. V. 535. P. 385–401.

  31. Вашковьяк М.А., Вашковьяк С.Н., Емельянов Н.В. О разложении вековой части возмущающей функции взаимного притяжения в спутниковой системе планеты // Астрон. вестник. 2013. Т. 47. № 1. С. 32–39.

  32. Minglibayev M.Zh., Mayemerova G.M. Investigation of the evolutionary equations of the three-body problem with variable masses // Appl. Math. Sci. 2013. V. 7. № 89. P. 4439–4454.

  33. Minglibayev M.Zh., Mayemerova G.M. Evolution of the orbital-plane orientations in the two-protoplanet three-body problem with variable masses // Astron. Rep. 2014. V. 58. № 9. P. 667–677.

  34. Прокопеня А.Н., Минглибаев М.Дж., Маемерова Г.М. Символьные вычисления в исследованиях проблемы трех тел с переменными массами // Программирование. 2014. Т. 40. № 2. С. 51–59.

  35. Wolfram S. An elementary introduction to the Wolfram Language. Wolfram Media, Inc., 2016.

  36. Субботин М.Ф. Введение в теоретическую астрономию. М.: Наука, 1968. 800 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал