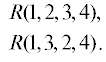Программирование, 2019, № 2, стр. 66-72

КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОЛИНОМИАЛЬНЫХ ВЫРАЖЕНИЙ С ИНДЕКСАМИ

Г. Б. Шпиз^a, *, А. П. Крюков^a

^a Московский государственный университет имени М.В. Ломоносова
119991 ГСП-1, Москва, Ленинские горы, 1, Россия

Поступила в редакцию 16.07.2018
После доработки 16.07.2018
Принята к публикации 31.08.2018

DOI: 10.1134/S0132347419020110

Аннотация

Методы компьютерной алгебры широко применяются в различных областях математики, физики и других наук. Одним из важных случаев является упрощение алгебраических выражений, содержащих индексы. Наиболее типичный пример таких выражений тензорные выражения. В настоящей работе кратко описаны основные методы приведения выражений с индексами к каноническому виду. Основное внимание уделяется учету свойств симметрий по отношению к различным перестановкам индексов внутри элементарных символов, симметрий, связанных с переименованием индексов суммирования, а также линейным соотношениям между ними общего вида. В настоящей работе дается определение канонического представления для полиномиальных (мультипликативных) выражений от переменных с абстрактными индексами, которое является результатом усреднения исходного выражения по действию некоторой конечной группы (стабилизатору сигнатуры). В практических случаях, например для выражений от тензоров кривизны Римана, предложенные алгоритмы, демонстрируют высокую эффективность.

I. ВВЕДЕНИЕ

Задача упрощения математических выражений, содержащих индексы, часто встречается в математике, физике и других естественных науках. В данной работе рассматриваются индексные выражения абстрактного вида. В качестве типичного случая таких выражений приведем тензоры и выражения, построенные из них. Тензоры, как правило, обладают различными свойствами симметрии по отношению с перестановкам своих индексов, а произведение одинаковых тензоров может давать дополнительные симметрии в силу коммутативности операции умножения. Дополнительно свертка индексов приводит к появлению симметрии, связанной с переименованием индексов суммирования.

Задача упрощения таких выражений должна учитывать все богатство свойств выражений с индексами для повышения эффективности работы с ними.

В работе мы будем придерживаться обозначений Эйнштейна, когда наличие пары одинаковых индексов означает сумму по всем значениям данной пары:

$T(i,i) \equiv \sum\limits_{i = 1}^{i = n} T(i,i).$

Структура статьи следующая. В разделе II мы кратко остановимся на типах вычислений выражений с индексами в компьютерной алгебре. В разделе III дадим постановку задачи и краткий обзор смежных работ. Во разделе IV дадим более строгое определение выражений с абстрактными индексами и их свойств. В этом же разделе дадим строгое определение оператора приведения к каноническому виду. В заключение укажем возможное развитие предложенных методов.

II. ТИПЫ ВЫЧИСЛЕНИЙ ВЫРАЖЕНИЙ С ИНДЕКСАМИ

Вычисление выражений с индексами можно разделить на три основных типа:

• покомпонентные вычисления;

• вычисления с абстрактными индексами;

• абстрактные вычисления.

Рассмотрим случай покомпонентных вычислений на примере тензорных выражений. В этом случае тензоры представляют собой набор отдельных компонент, которые заданы в некотором фиксированном базисе. Таким образом, вычисление тензорного выражения сводится с скалярным вычислениям набора компонент результирующего тензора.

В качестве примера таких вычислений можно указать программы xAct [1], DifferentialGeometry [2], GRTensor [3], Atlas 2 [4], CTENSOR [9].

Недостатком такого подхода является громоздкость вычислений. Так, если у вас есть тензорное выражение, имеющее 4 индекса, а каждый индекс пробегает значения от 0 до 3, то необходимо вычислить ${{4}^{4}} = 256$ компонент. К тому же, данный подход не позволяет автоматически учесть свойства симметрии, которыми часто обладают тензоры. Сильной стороной покомпонентных вычислений является то, что в прикладных областях конечный результат, как правило, надо получить в конкретном базисе и покомпонентно.

На другом полюсе вычислений выражений с индексами находятся полностью абстрактные вычисления, когда выражение записывается в абстрактном виде без индексов. В качестве таких вычислений укажем внешнюю алгебру. Примером системы компьютерной алгебры, где реализованы такие вычисления может являться система xAct [1], в которой реализован пакет xTerior [5], или пакет ITENSOR [9] в системе MAXIMA [10]. Подобные вычисления, как правило, используются в математике, редко применяются в физике и других естественных науках [6]. В данной работе мы не будем рассматривать такой тип вычислений.

Наиболее частым случаем является вычисление выражений с абстрактными индексами. В этом случае упрощение выражений основывается на свойствах симметрии по отношению как к перестановкам индексов в выражении, так и симметрии, связанные с переименованием индексов суммирования. Дополнительно к выше названным симметриям, существуют линейные соотношения между элементарными выражениями с абстрактными индексами общего вида. Их учет существенно усложняет задачу приведения выражения к каноническому виду.

Что касается конкретных систем компьютерной алгебры, где такие вычисления применяются, то можно упомянуть пакет ATENSOR [9] в системе MAXIMA [10], систему Cadabra [11] и ряд других. Эти системы неоднократно рассматривались на семинаре по компьютерной алгебре под руководством профессора С.А. Абрамова [7]. Дополнительные ссылки по теме можно найти в статье А.В. Корольковой и других [8]¹ ¹.

Заметим, что эффективного общего решения данной проблемы, в смысле полиномиального времени работы алгоритма, нет. В данной работе предлагается алгоритм, который эффективен для мономов с индексами разумного размера, которые встречается в практике вычислений. Алгоритм позволяет последовательно учесть все виды соотношений между элементарными выражениями с абстрактными индексами, включая линейные соотношения общего вида. Значительное сокращение времени работы достигается за счет использования усреднения по стабилизаторам сигнатур, размер которых достаточно небольшой. Частично схожие подходы к решению поставленных проблем использованы авторами системы Redberry [13] и в работе [14].

III. ПОСТАНОВКА ЗАДАЧИ И СМЕЖНЫЕ ИССЛЕДОВАНИЯ

Дадим предварительную постановку задачи. В качестве иллюстрации будем использовать тензор Римана. Так как мы не интересуемся его геометрическими свойствами, то будем считать, что это просто символ с абстрактными индексами $R(i,j$, k, l), который обладает некоторыми свойствами.

Во-первых, это свойства симметрии по отношению к перестановкам индексов:

$R(i,j,k,l) = - R(j,i,k,l);$

$R(k,l,i,j) = R(i,j,k,l).$

Во-вторых, по части индексов может быть произведено суммирование, что порождает дополнительные свойства симметрии:

$R({{i}_{1}},j,{{i}_{2}},j) = R({{i}_{2}},j,{{i}_{1}},j);$

$R(i,j,i,j) = R(j,i,j,i).$

В выражении (3), мы временно пометили индексы ${{i}_{1}}$ и ${{i}_{2}}$, чтобы продемонстрировать, возможность их перестановки в случае суммирования по ним.

Дополнительные симметрии появляются если рассмотреть мономы как произведение элементарных символов с одинаковыми именами:

$R(i,j,k,l) \cdot R(k,l,p,q) = R(k,l,p,q) \cdot R(i,j,k,l).$

Легко заметить, что все эти случаи являются симметриями, порожденными соответствующими подгруппами группы перестановок. Сложность задачи связана с тем, что если первый тип симметрии (1, 2) определяется свойствами элементарного символа и может быть задан априори, то симметрии связанные с индексами суммирования (3) и коммутативными свойствами умножения (5) возникают динамически в процессе работы с такими выражениями. Во-вторых, с мономами, содержащими много элементарных символов, связаны большие подгруппы группы перестановок, что приводит к большому объему вычислений.

Одной из первых работ, в которой была решена задача приведения подобных мономов к каноническому виду была работа А. Родионова и А. Таранова [15]. В ней проблема упрощения выражений с абстрактными индексами, была сведена к задаче построения двойного класса смежности $S{\backslash }T{\text{/}}D$ по двум подгруппам перестановок. Здесь подгруппа $S$ связана с перестановками индексов элементарного символа, а вторая подгруппа $D$ связана с подгруппой перестановок индексов суммирования. В дальнейшем эта техника использовалась в работе [21] и работах других исследователей. Общая теория этого вопроса изложена, например, в работах Г. Батлера [16] и М. Слатера [19].

К сожалению, на этом проблемы не кончаются. В дополнение к указанным выше свойствам симметрии существуют соотношения, которые являются линейными соотношениями между тремя и более элементарными символами. Примером таких соотношений является тождество Бьянки:

$R(i,j,k,l) + R(i,k,l,j) + R(i,l,j,k) = 0.$

Особенностью таких соотношений является то, что они разрушают групповую структуру выражений с индексами и требуют другого подхода для их упрощения.

Одна из попыток описать единым образом все виды симметрий и линейные соотношения общего вида была предпринята В. Ильиным и А. Крюковым [20] в 1996 году.

В этой работе было предложено рассматривать групповую алгебру, когда все возможные мономы, которые могут быть порождены с помощью всех перестановок индексов, как базис линейного пространства, в котором реализуются симметрии и линейные соотношения общего вида. Тогда совокупность этих соотношений определяет подпространство в этом пространстве, а подпространство, дополнительное к нему, можно рассматривать как пространство канонических элементов.

Таким образом, задача приведения к каноническому виду выражения с абстрактными индексами была сведена к задаче проектирования полинома, который рассматривается как линейная комбинация базисных векторов, на подпространство дополнительное к подпространству соотношений. Решение данной задачи эквивалентно решению линейной системы уравнений методом Гаусса.

Основной проблемой данного подхода является огромный размер этого линейного пространства равный $N!$, где N – число индексов в мономе. С практической точки зрения используя данный подход невозможно работать с выражениями, содержащими более десятка индексов. Тем не менее, данная идея оказалась полезной в дальнейшем.

IV. УПРОЩЕНИЕ ВЫРАЖЕНИЙ С АБСТРАКТНЫМИ ИНДЕКСАМИ

A. Соглашения и обозначения

Фиксируем два линейно упорядоченных множества: множество типов $\Theta $ и множество индексов ${\mathbf{I}}$. В множестве ${\mathbf{I}}$ фиксируем подмножество ${\mathbf{D}} \subset {\mathbf{I}}$ индексов суммирования.

Определение 1. Сигнатурой будем называть пару $(t,{\mathbf{i}})$, где $t \in \Theta $, и ${\mathbf{i}} = ({{i}_{1}},\; \ldots ,\;{{i}_{n}})$ неубывающая последовательность индексов.

Для любой конечной последовательности элементов ${\mathbf{i}} = {{i}_{1}},\; \ldots ,\;{{i}_{n}}$ будем обозначать ${\mathbf{\hat {i}}}$ результат сортировки i по возрастанию.

Определение 2. Элементарным символом порядка n будем называть выражение $e$ вида $e = t({\mathbf{i}})$, где $t \in \Theta $, ${\mathbf{i}} = ({{i}_{1}},\; \ldots ,\;{{i}_{n}})$, ${{i}_{k}} \in {\mathbf{I}}$.

Определение 3. Сигнатурой символа e = t(i₁, ..., ${{i}_{n}})$ будем называть пару $(t,{\mathbf{i}}{\text{'}})$, где $t \in \Theta $, и i' = = $(i_{i}^{'}, \ldots ,i_{n}^{'})$ упорядоченная по возрастанию последовательность индексов ${\mathbf{i}} = ({{i}_{1}},\; \ldots ,\;{{i}_{n}})$.

Обозначим S – множество всех сигнатур символов.

Множество последовательностей индексов линейно упорядочено относительно лексикографического порядка.

Множество сигнатур и множество элементарных символов также линейно упорядочены относительно лексикографического порядка.

Векторное пространство формальных линейных комбинаций элементарных символов будем обозначать Sym, а его элементы называть индексированными величинами.

Пусть $s = (t,{\mathbf{i}}) \in {\mathbf{S}}$ – сигнатура.

Через ${\mathbf{Sym}}(s) \subset {\mathbf{Sym}}$ будем обозначать векторное пространство, порожденное всеми элементарными символами с сигнатурой s, то есть из символов типа t и последовательностью индексов, получающихся из последовательности i = = $({{i}_{1}}, \ldots ,{{i}_{n}})$ некоторой перестановкой элементов.

Группа G перестановок множества индексов I естественным образом действует на множестве всех элементарных символов и, соответственно, на пространстве ${\mathbf{Sym}}$. В дальнейшем будем называть ее группой переименований индексов. Если $g \in G$, то ${\mathbf{Sym}}(ge) = g({\mathbf{Sym}}(e))$.

Очевидно, группа G переименований индексов переводит символы с одинаковой сигнатурой в символы с одинаковой сигнатурой и определено ее естественное действие на множестве сигнатур S.

Пусть $D \subset {\mathbf{I}}$ – некоторое подмножество индексов. Через ${\mathbf{G}}(D)$ будем обозначать подгруппу группы переименований индексов, переводящих множество D в себя оставляющих на месте индексы из дополнения к D.

Группу переименований индексов суммирования будем обозначать ${{{\mathbf{G}}}_{d}}$.

B. Соотношения между элементарными символами

Будем предполагать, что все соотношения между элементарными символами сводятся к некоторым линейным соотношениям между символами с одинаковой сигнатурой, причем множество соотношений инвариантно относительно группы переименований индексов.

Пусть $s = (t,{\mathbf{i}}) \in {\mathbf{S}}$ – некоторая сигнатура. Обозначим через $R(s)$ пространство всех (линейных) соотношений в пространстве ${\mathbf{Sym}}(s)$. Мы будем требовать, чтобы соответствие $s \to R(s)$ было инвариантно относительно переименования индексов.

Обозначим через R подпространство в S, порожденное всеми $R(s)$ в пространстве Sym. По построению R инвариантно относительно переименования индексов и ${\mathbf{R}}(s) = {\mathbf{Sym}}(s) \cap {\mathbf{R}}$.

Предложение 1. Пусть $s = (t,{\mathbf{i}}) \in {\mathbf{S}}$ – некоторая сигнатура. В пространстве ${\mathbf{Sym}}(s)$ существует единственная последовательность ${\mathbf{b}}(s) = {{e}_{1}}, \ldots ,{{e}_{k}}$ элементарных символов, образующая базис в факторпространстве ${\mathbf{V}}(s) = {\mathbf{Sym}}(s){\text{/}}{\mathbf{R}}(s)$, минимальная среди таких последовательностей в смысле лексикографического порядка.

Пространство, порожденное базисом ${\mathbf{b}}(s)$, естественно отождествляется с факторпространством ${\mathbf{Sym}}(s){\text{/}}{\mathbf{R}}(s)$ и будет обозначаться ${\mathbf{V}}(s)$.

Будем называть ${\mathbf{b}}(s)$ каноническим базисом, а элементы канонического базиса будем называть каноническими символами.

Пример. Пусть $s = (Ri,(1,2,3,4))$ сигнатура тензора Римана. Тогда канонический базис в ${\mathbf{V}}(s)$ состоит из двух символов: $Ri(1,2,3,4)$ и $Ri(1,3,2,4)$.

Поскольку пространство соотношений ${\mathbf{R}}(s)$ инвариантно относительно группы ${\mathbf{G}}(s)$ переименований индексов входящих в s, то эта группа действует в ${\mathbf{V}}(s) = {\mathbf{Sym}}(s){\text{/}}{\mathbf{R}}(s)$. Заметим, что при этом действии элементарный символ переходит, вообще говоря, в линейную комбинацию канонических символов.

C. Мономы и полиномы

Определение 4. Мономом будем называть формальное коммутативное произведение элементарных символов. Индексы, появляющиеся в мономе более одного раза называются индексами суммирования, остальные – простыми индексами. Мы будем требовать, чтобы индексы суммирования и только они лежали в множестве D.

Обозначим ${\mathbf{M}}$ множество всех мономов, а P – векторное пространство с базисом ${\mathbf{M}}$. Элементы пространства P естественно называются полиномами.

Сигнатурой ${\mathbf{s}}(m)$ монома $m = {{e}_{1}} \cdot \ldots \cdot {{e}_{k}}$ назовем последовательность сигнатур его сомножителей, упорядоченную по возрастанию.

Множество всех возможных сигнатур мономов будем обозначать ${{{\mathbf{S}}}_{{\mathbf{m}}}}$.

Пусть $S$ – некоторое множество сигнатур мономов. Обозначим ${\mathbf{M}}(S)$ множество всех мономов сигнатуры которых лежат в $S$ и ${\mathbf{P}}(S)$ векторное пространство с базисом ${\mathbf{M}}(S)$.

Пусть $m = {{e}_{1}} \cdot \ldots \cdot {{e}_{k}}$ – моном. Обозначим ${\mathbf{S}}(m)$ множество сигнатур всех мономов, получающихся из ${\mathbf{s}}(m)$ переименованием индексов суммирования, то есть орбиту ${\mathbf{s}}(m)$ относительно действия группы ${{{\mathbf{G}}}_{d}}$.

Между мономами существуют три типа линейных отношений.

1. Отношения порожденные отношениями внутри одного из сомножителей, при фиксированных остальных сомножителях.

2. Равенство мономов, полученных при перестановке сомножителей

3. Равенство мономов, полученных переименованием индексов суммирования (то есть действием группы ${{{\mathbf{G}}}_{d}}$).

Обозначим ${\mathbf{P}}(m)$ векторное пространство, порожденное всеми мономами сигнатуры которых лежат в ${\mathbf{S}}(m)$, а ${\mathbf{R}}(m) \subset {\mathbf{P}}(m)$ – подпространство порожденное соотношениями перечисленных типов. Подпространство порожденное отношениями типа 1 и 2 будем обозначать ${{{\mathbf{R}}}_{0}}(m)$.

Пространства ${\mathbf{P}}(m)$, ${\mathbf{R}}(m)$ и ${{{\mathbf{R}}}_{0}}(m)$ инвариантны относительно действия группы ${{{\mathbf{G}}}_{d}}$. В частности эта группа действует и на фактор-пространствах ${\mathbf{P}}(m){\text{/}}{{{\mathbf{R}}}_{0}}(m)$ и ${\mathbf{P}}(m){\text{/}}{\mathbf{R}}(m)$.

Определение 5. Моном назовем редуцированным, если все его сомножители являются каноническими символами и последовательность сомножителей упорядочена по возрастанию.

Пространство порожденное всеми редуцированными мономами из ${\mathbf{P}}(m)$ будем обозначать ${{{\mathbf{P}}}_{r}}(m)$.

Предложение 2. Всякий моном из пространства ${\mathbf{P}}(m)$ может быть представлен с точностью до соотношений из R₀(m) в виде линейной комбинации редуцированных мономов. Пространство ${{{\mathbf{P}}}_{r}}(m)$ естественно отождествляется с фактор-пространством ${\mathbf{P}}(m){\text{/}}{{{\mathbf{R}}}_{0}}(m)$.

Доказательство. Немедленно вытекает из определений.

Будем обозначать $\rho :{\mathbf{P}}(m) \to {{{\mathbf{P}}}_{r}}(m)$ естественный проектор на фактор-пространство ${\mathbf{P}}(m){\text{/}}{{{\mathbf{R}}}_{0}}(m)$.

Заметим, что образ $\rho (m)$ монома m, вообще говоря является полиномом.

V. ПРИВЕДЕНИЕ МОНОМА К КАНОНИЧЕСКОМУ ВИДУ

Определение 6. Каноническим представлением называется такой линейный оператор $\kappa :{\mathbf{P}} \to {\mathbf{P}}$, что $x = \kappa (x)mod({\mathbf{R}})$ и $\kappa (x) = \kappa (y)$ тогда и только тогда, когда $x = ymod({\mathbf{R}})$ при $x,y \in {\mathbf{P}}$.

Определим оператор $\alpha :{\mathbf{P}} \to {\mathbf{P}}$, полагая для произвольного $p \in {\mathbf{P}}$, что

$\alpha (p) = \frac{1}{N}\sum\limits_{g \in {{{\mathbf{G}}}_{d}}} g(p),$

где N – количество элементов в группе ${{{\mathbf{G}}}_{d}}$.

Предложение 3. Оператор $\alpha \rho = \rho \alpha $ является каноническим представлением.

К сожалению, это каноническое представление слишком громоздко для реальных вычислений. Поэтому мы модифицируем его конструкцию.

Множество ${{{\mathbf{S}}}_{{\mathbf{m}}}}$ сигнатур всех мономов является подмножеством множества конечных последовательностей сигнатур элементарных символов, линейно упорядоченного относительно лексикографического порядка. Соответственно, множество ${{{\mathbf{S}}}_{{\mathbf{m}}}}$ является линейно упорядоченным относительно унаследованного порядка.

Группа ${{{\mathbf{G}}}_{d}}$ переименований индексов суммирования естественным образом действует на множестве мономов и на множестве их сигнатур.

Минимальным элементом в орбите сигнатуры ${\mathbf{s}}(m)$ монома $m$ относительно действия группы ${{{\mathbf{G}}}_{d}}$ будем обозначать ${{{\mathbf{s}}}_{{min}}}(m)$.

Определение 7. Сигнатуру монома $m$ будем называть экстремальной, если она не может быть уменьшена никаким переименованием индексов суммирования, то есть совпадает с ${{{\mathbf{s}}}_{{min}}}(m)$.

Моном будем называть экстремальным, если его сигнатура экстремальна.

Пространство порожденное всеми экстремальными редуцированными мономами из ${\mathbf{P}}$ будем обозначать ${{{\mathbf{P}}}_{{min}}}$. Оно совпадает с подпространством в ${{{\mathbf{P}}}_{{min}}}(m)$ порожденным всеми мономами с сигнатурой ${{{\mathbf{s}}}_{{min}}}(m)$.

Предложение 4. Всякий моном $m \in {{{\mathbf{P}}}_{{min}}}$ может быть представлен с точностью до соотношений из ${\mathbf{R}}$ в виде линейной комбинации экстремальных редуцированных мономов с сигнатурой ${{{\mathbf{s}}}_{{min}}}(m)$.

Пусть множество мономов $M \in {{{\mathbf{P}}}_{{min}}}$ содержит по одному моному из ${{{\mathbf{P}}}_{{min}}}$ для каждой сигнатуры. Пространство ${{{\mathbf{P}}}_{{min}}}$ является прямой суммой

$\mathop \oplus \limits_{m \in M} {{{\mathbf{P}}}_{{min}}}(m)$

${\mathbf{R}} \cap {{{\mathbf{P}}}_{{min}}} = \mathop \oplus \limits_{m \in M} {\mathbf{R}} \cap {{{\mathbf{P}}}_{{min}}}(m).$

Доказательство. Немедленно вытекает из соотношений всех трех типов.

Для монома $m\, \in \,{\mathbf{P}}$ положим r(m) = $\{ x\, \in \,{{{\mathbf{P}}}_{{min}}}(m)$ : x = = mmod(R)}. Таким образом ${\mathbf{r}}(m)$ это множество всех полиномов из ${{{\mathbf{P}}}_{{min}}}(m)$, совпадающих с $m$ по модулю соотношений из R.

Обозначим ${\mathbf{k}}(m)$ среднее арифметическое элементов множества ${\mathbf{r}}(m)$.

Очевидно, функция ${\mathbf{k}}(m)$ продолжается до линейного оператора на пространстве P, который мы будем обозначать тем же символом ${\mathbf{k}}:{\mathbf{P}} \to {{{\mathbf{P}}}_{{min}}}$.

Предложение 5. Оператор ${\mathbf{k}}$ является каноническим представлением.

Вычисление значения ${\mathbf{k}}(m)$ на мономе m сводится к вычислению множества ${\mathbf{r}}(m)$ и вычислению его среднего арифметического. Множество ${\mathbf{r}}(m)$ является орбитой любого своего элемента относительно группы переименования индексов суммирования, сохраняющих сигнатуру ${{{\mathbf{s}}}_{{min}}}(m)$. Поэтому задача сводится к нахождению некоторого элемента группы ${{{\mathbf{G}}}_{d}}$, переводящего m в моном с сигнатурой ${{{\mathbf{s}}}_{{min}}}(m)$ и к нахождению стабилизатора сигнатуры ${{{\mathbf{s}}}_{{min}}}(m)$ в группе ${{{\mathbf{G}}}_{d}}$. В случае небольшого числа индексов суммирования обе эти задачи легко решаются прямым перебором группы переименований. В противном случае нужно использовать связь между структурой системы индексов суммирования и структурой некоторых цветных графов, связанных с сигнатурой монома.

Вершины таких графов соответствуют элементарным символам, являющимся сомножителями монома, цвета вершин сигнатурам соответствующих сомножителей из которых исключены индексы суммирования, а ребра соответствуют индексам суммирования.

Заметим, что размерность пространства ${{{\mathbf{P}}}_{{min}}}$ значительно меньше размерности пространства ${\mathbf{P}}$, а стабилизатор сигнатуры ${{{\mathbf{s}}}_{{min}}}(m)$ в группе ${{{\mathbf{G}}}_{d}}$ значительно меньше самой группы.

Так, если моном является m полной сверткой (то есть когда все индексы являются индексами суммирования), не распадающейся в обычное произведение пары мономов (это соответствует связности графа), пяти тензоров Римана и произвольного число симметричных и антисимметричных билинейных форм, то порядок группы ${{{\mathbf{G}}}_{d}}$ огромен, однако порядок стабилизатора ${{{\mathbf{s}}}_{{min}}}(m)$ как правило меньше 100, размерность пространства ${{{\mathbf{P}}}_{{min}}}(m)$ не больше 32 и не зависит от количества индексов суммирования.

VI. РАСШИРЕННЫЙ ПРИМЕР

Приведем к каноническому виду выражение

$(R(i,j,k,l) - R(i,k,j,l)) * \epsilon (i,j),$

где $R$ – тензор Римана, $\epsilon $ – кососимметрическая форма:

$\epsilon (i,j) = - \epsilon (j,i).$

Для удобства заменим индексы на их номера в прядке возрастания:

$i \to 1,\quad j \to 2,\quad k \to 3,\quad l \to 4.$

Также будем считать, что $\epsilon < R$ с точки зрения лексикографического порядка.

Тензор Римана удовлетворяет симметриям (1), (2), (6).

Канонический базис в пространстве тензоров Римана состоит из двух элементов:

Канонический базис в пространстве кососимметрических форм состоит из одного элемента

$\epsilon (1,2).$

Минимальная сигнатура для нашего примера

$\epsilon (1,2) * R(1,2,3,4),$

где (1, 2) индексы суммирования.

Стабилизатор этой сигнатуры в группе переименований индексов суммирования

$st = ((1,2),(2,1))$

и совпадает с самой группой переименований.

Раскроем скобки в выражении (8) и применим каждый элемент стабилизатора (11) к произведению $Q1 = \epsilon (1,2) * R(1,2,3,4)$:

$\begin{gathered} (1,2):\quad \epsilon (1,2) * R(1,2,3,4) \to \\ \to \;\epsilon (1,2) * R(1,2,3,4) \\ (2,1):\quad \epsilon (1,2) * R(1,2,3,4) \to \\ \to \;\epsilon (2,1) * R(2,1,3,4) = \\ = \;\epsilon (1,2) * R(1,2,3,4). \\ \end{gathered} $

Здесь мы каждый сомножитель привели к каноническому виду в соответствии с правилами (1), (2), (6) и (9).

Среднее арифметическое от $Q1$ равно:

$s1 = \epsilon (1,2) * R(1,2,3,4).$

Аналогично поступим со вторым членом Q2 = = $\epsilon (1,2) * R(1,3,2,4)$ выражения (8):

$\begin{gathered} (1,2):\quad \epsilon (1,2) * R(1,3,2,4) \to \\ \to \;\epsilon (1,2) * R(1,3,2,4) \\ (2,1):\quad \epsilon (1,2) * R(1,3,2,4) \to \\ \to \;\epsilon (2,1) * R(2,3,1,4) = \\ = \; - \epsilon (1,2) * R(1,4,2,3) = \\ = \; - \epsilon (1,2) * (R(1,3,2,4) - R(1,2,3,4)) \\ \end{gathered} $

Среднее арифметическое от $Q2$ равно:

$s2 = \frac{1}{2}\epsilon (1,2) * R(1,2,3,4).$

Окончательно, канонический вид выражения 8 равен

$\begin{gathered} s1 - s2 = \frac{1}{2}\varepsilon (1,2) * R(1,2,3,4) \to \\ \to \;\frac{1}{2}\epsilon (i,j) * R(i,j,k,l). \\ \end{gathered} $

Данный пример демонстрирует применение как простых свойств симметрии тензора Римана (1), (2), так и многочленные свойства Бианки (6). При этом мы не использовали никаких специальных методов работы с подобными линейными соотношениями, которые, как правило, используют в других системах компьютерной алгебры. Например, для соотношения Бианки (6) используется следующее представление [22]:

$R(i,j,k,l) = \frac{1}{3}(2R(i,j,k,l) - R(i,l,j,k) + R(i,k,j,l)).$

Главным недостатком такого подхода является то, что для каждого конкретного случая требуется использование своего трюка.

VII. ЗАКЛЮЧЕНИЕ

В работе даны определения канонической формы полиномов с абстрактными индексами, построен оператор приведения к каноническому виду, который связан с результатом усреднения исходного выражения по действию некоторой конечной группы (стабилизатору сигнатуры). Алгоритм позволяет последовательно учесть все виды соотношений между элементарными выражениями с абстрактными индексами, включая линейные соотношения общего вида. Значительное сокращение времени работы достигается за счет использования усреднения по стабилизаторам сигнатур, размер которых достаточно небольшой.

Если количество индексов суммирования невелико, то канонический вид эффективно находится прямым перебором элементов группы переименований. Однако с ростом числа индексов суммирования d вычислительная сложность растет как $d!$ и при d > 7 необходим более тонкий анализ. Такой анализ требует построения автоморфизмов связанного с мономом оснащенного графа и построением его геометрических инвариантов. Подробно данный анализ будет описан в отдельной статье.

Используя приведенное выше определение оператора приведения к каноническому виду, была разработана программа на языке Python, которая реализует данное построение. В практических случаях, например для выражений от тензоров кривизны Римана, предложенные алгоритмы демонстрируют высокую эффективность при количестве сомножителей в мономе порядка десяти и количестве индексов в сомножителях порядка четырех, что было проверено на множестве примеров с полной сверткой произведения 10 тензоров Римана. Заметим, что наличие в мономе индексов не являющихся индексами суммирования и элементов различных типов резко увеличивает эффективность вычислений.

Авторы выражают благодарность В.А. Ильину и С.А. Абрамову за плодотворные обсуждения. Данная работа была выполнена в рамках Государственного задания № 115041410196.

Список литературы

Martin-Garcia J.M., Yllanesa D., Portugal R. The Invar tensor package: Differential invariants of Riemann // Comput. Phys. Commun. 2008. V. 179. P. 597. http:// www.xact.es
Anderson I.M., Torre C.G. New symbolic tools for differential geometry, gravitation, and field theory // J. Math. Phys. 2012. V. 53. P. 013511. http://digitalcommons.usu.edu/dg/
GRTensorII. http://grtensor.phy.queensu.ca/
Atlas 2. http://digi-area.com/Maple/atlas/
xTerior. http://www.xact.es/xTerior/index.html
Gourgoulhon E., Mancini M. Symbolic tensor calculus on manifolds. 2018. https://arxiv.org/abs/1804.07346v1
Абрамов С.А., Боголюбская А.А. Семинар по компьютерной алгебре в 2016–2017 гг. // Программирование. 2018. № 2. С. 3–4. http://www.ccas.ru/sabramov/seminar/doku.php
Королькова А.В., Кулябов Д.С., Севастьянов Л.А. Тензорные расчеты в системах компьютерной алгебры // Программирование. 2013. № 3. С. 47–57.
Toth V. Tensor Manipulation in GPL Maxima. 2008. http://www.vttoth.com/
MAXIMA. http://maxima.sourceforge.net/
Brewin L. A brief introduction to Cadabra: a tool for tensor computations in General Relativity // Comput. Phys. Commun. 2010. V. 181. P. 489–498.
Hearn A.C., Schöpf R. REDUCE User’s Manual, Free Version. https://reduce-algebra.sourceforge.io/manual/manual.html
Poslavsky S., Bolotin D. Redberry: a computer algebra system designed for tensor manipulation. Proceedings International Workshop ACAT 2014, 2015 // J. Phys.: Conf. Ser. V. 608. P. 012060.
Li H., Li Z., Li Y. Riemann Tensor Polynomial Canonicalization by Graph Algebra Extension. Proceedings of the International Symposium on Symbolic and Algebraic Computation (ISSAC). Kaiserslautern, Germany, July 25–28, 2017. P. 269–276.
Rodionov A.Y., Taranov A.Y. Combinatorial aspects of simplification of algebraic expressions. Proceedings European Conference EUROCAL’89 // Lect. Notes Comput. Sci. 1989. V. 378. P. 192–201.
Butler G. Computing normalizers in permutation groups // J. Algorithms. 1993. V. 4. P. 163–175.
Butler G. On Computing Double Coset Representatives in Permutation Groups. Computational Group Theory / Atkinson M.D. Ed. Academic Press, 1984. P. 283.
Butler G. Fundamental Algorithms for Permutation Groups. Berlin: Springer-Verlag, 1991.
Slattery M.C. Computing Double Cosets in Soluble Groups // J. Symbolic Computation. 2001. V. 31. P. 179–192.
Ilyin V.A., Kryukov A.R. ATENSOR – REDUCE program for tensor simplification // Comput. Phys. Commun. 1996. V. 96. P. 36–52.
Martí-García J.M., Portugal R., Manssur L.R.U. The Invar tensor package // Comput. Phys. Commun. 2007. V. 177. P. 640–648.
Bolotin D., Poslavsky S. Introduction to Redberry: a computer algebra system designed for tensor manipulation. 2015. https://arxiv.org/pdf/1302.1219v2

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал