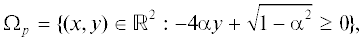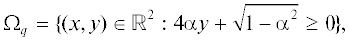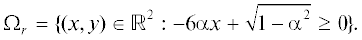Программирование, 2019, № 3, стр. 64-72
ПРИМЕНЕНИЕ КОМПЬЮТЕРНОЙ АЛГЕБРЫ ПРИ РЕКОНСТРУКЦИИ ПОВЕРХНОСТИ ПО ЕЕ ФОТОМЕТРИЧЕСКИМ ОБРАЗАМ
Р. Козера a, b, *, А. Н. Прокопеня a, **, А. Вилинский a, ***
a Варшавский университет естественных наук – SGGW
02-776 Варшава, ул. Новоурсыновска, 159, Польша
b School of Computer Science and Software Engineering, The University of Western Australia
WA 6009 Crawley Perth, Stirling Highway 35
* E-mail: ryszard.kozera@gmail.com
** E-mail: alexander_prokopenya@sggw.pl
*** E-mail: artur_wilinski@sggw.pl
Поступила в редакцию 27.08.2018
После доработки 20.09.2018
Принята к публикации 20.09.2018
Аннотация
Обсуждается проблема реконструкции формы неизвестной ламбертовской поверхности, задаваемой в трехмерном пространстве непрерывно дифференцируемой функцией $z = u(x,y)$, по ее фотометрическим изображениям, получаемым при последовательном освещении поверхности тремя различными удаленными источниками света. Используя методы компьютерной алгебры, показана возможность продолжения единственного решения проблемы, которое существует в области определения всех трех изображений Ω, за пределы этой области на основе решений, получаемых для любой пары из заданных трех изображений. Для устранения неоднозначности решения проблемы реконструкции поверхности по двум ее образам предлагается вычислять соответствующее значение параметра $\varepsilon $ на границе области Ω. Справедливость полученных теоретических результатов подтверждается примерами моделирования фотометрических образов различных поверхностей.
1. ВВЕДЕНИЕ
Получение информации о форме поверхности, заданной в трехмерном пространстве, на основе ее двумерного изображения (или нескольких изображений) является одной из весьма важных проблем, возникающих при разработке систем компьютерного зрения (см. [1]). Предположим, что на поверхность $S = graph(u)$, задаваемую непрерывной функцией двух переменных $u(x,y)$, падает параллельный пучок света от удаленного источника, направление на который определяется единичным вектором $\vec {p}\, = \,({{p}_{1}},{{p}_{2}},{{p}_{3}}),{\text{||}}\vec {p}{\text{||}}\, = \,\sqrt {p_{1}^{2} + p_{2}^{2} + p_{3}^{2}} $ = 1. Фотометрическое изображение фиксирует информацию о интенсивности света ${{E}_{p}}(x,y)$, отраженного от этой поверхности в каждой ее точке $s = (x,y,u(x,y))$. При этом интенсивность ${{E}_{p}}(x,y)$ зависит как от физических свойств поверхности, так и от ее ориентации по отношению к источнику света. В данной работе будем считать, что поверхность $S$ является ламбертовской, т.е. она полностью отражает все падающее на нее излучение и яркость отражаемого от нее света одинакова по всем направлениям. В этом случае функция ${{E}_{p}}(x,y)$ зависит только от косинуса угла между вектором нормали к поверхности $\vec {n}(s) = ({{n}_{1}},{{n}_{2}},{{n}_{3}})$ в точке $s \in S$ и направлением на источник света и определяется выражением (см. [1, 2])
(1.1)
${{E}_{p}}(x,y) = \frac{{\langle \vec {n}{\text{|}}\vec {p}\rangle }}{{{\text{||}}\vec {n}{\text{||}}}} \equiv \frac{{{{n}_{1}}{{p}_{1}} + {{n}_{2}}{{p}_{2}} + {{n}_{3}}{{p}_{3}}}}{{{\text{||}}\vec {n}{\text{||}}}},$где $\langle \cdot \,{\text{|}}\,{\text{s}} \cdot \rangle $ обозначает стандартное скалярное произведение векторов в трехмерном евклидовом пространстве.
Отметим, что функция ${{E}_{p}}(x,y)$ может принимать только неотрицательные значения и определена в области Ωp = 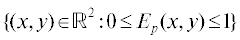 . Свет, отражаемый от поверхности в точке $s$ при заданном положении источника, может быть зафиксирован наблюдателем только в том
случае, когда угол между вектором $\vec {p}$ и нормалью $\vec {n}(s)$ не превышает π/2.
. Свет, отражаемый от поверхности в точке $s$ при заданном положении источника, может быть зафиксирован наблюдателем только в том
случае, когда угол между вектором $\vec {p}$ и нормалью $\vec {n}(s)$ не превышает π/2.
Обычно предполагается, что источник света и наблюдатель располагаются в области отрицательных значений координаты $z$. Поэтому ${{p}_{3}} < 0$, а внешняя нормаль к поверхности $z = u(x,y)$ определяется выражением $\vec {n}(s) = ({{u}_{x}}(x,y),{{u}_{y}}(x,y)$, –1), где ${{u}_{x}} = \partial u{\text{/}}\partial x$, ${{u}_{y}} = \partial u{\text{/}}\partial y$. Тогда выражение (1.1) можно переписать в виде следующего нелинейного дифференциального уравнения в частных производных (см. [1]):
(1.2)
$\frac{{{{p}_{1}}{{u}_{x}} + {{p}_{2}}{{u}_{y}} - {{p}_{3}}}}{{\sqrt {u_{x}^{2} + u_{y}^{2} + 1} }} = {{E}_{p}}(x,y).$Таким образом, проблема реконструкции поверхности S по ее фотометрическому образу ${{E}_{p}}(x,y)$, полученному при заданном направлении на источник света, определяемом вектором $\vec {p}$, сводится к поиску соответствующего решения $u(x,y)$ уравнения (1.2). Обычно решение ищется в классе непрерывно дифференцируемых функций $u \in $ Ck, k = 1, 2, с точностью до произвольной постоянной, поскольку перемещение поверхности вдоль оси Oz не изменяет ее фотометрического образа.
Следует отметить, что проблема реконструкции поверхности S по одному ее изображению ${{E}_{p}}(x,y)$ допускает однозначное решение лишь в специальных случаях (см., например, [1–4]). С другой стороны, при наличии трех изображений ${{E}_{p}}(x,y)$, ${{E}_{q}}(x,y)$, ${{E}_{r}}(x,y)$, получаемых последовательно при освещении поверхности S с трех различных направлений, задаваемых линейно независимыми единичными векторами $\vec {p}$, $\vec {q}$, $\vec {r}$, соответственно, компоненты вектора нормали $\vec {n}\, = \,({{n}_{1}},{{n}_{2}},{{n}_{3}})$ находятся однозначно. Действительно, записывая уравнение (1.1) для каждого из векторов $\vec {p}$, $\vec {q}$, $\vec {r}$ и единичного вектора нормали ${\text{||}}\vec {n}{\text{||}} = 1$, получаем систему из трех линейных уравнений
В силу линейной независимости векторов $\vec {p}$, $\vec {q}$, $\vec {r}$ определитель матрицы системы (1.3), который можно представить в виде Δ = p1(q2r3 – q3r2) + + ${{p}_{2}}({{q}_{3}}{{r}_{1}} - {{q}_{1}}{{r}_{3}}) + {{p}_{3}}({{q}_{1}}{{r}_{2}} - {{q}_{2}}{{r}_{1}}) = \langle \vec {p}|\vec {q} \times \vec {r}\rangle $, не равен нулю. Потому ее решение находится однозначно и имеет вид
Заметим, что области ${{\Omega }_{p}}$, ${{\Omega }_{q}}$, ${{\Omega }_{r}}$ на плоскости $Oxy$, в которых определены изображения ${{E}_{p}}(x,y)$, ${{E}_{q}}(x,y)$, ${{E}_{r}}(x,y)$, соответственно, зависят от формы поверхности и направлений на источники света и в общем случае не совпадают. Потому компоненты вектора нормали (1.4) определяются только в области $\Omega = {{\Omega }_{p}} \cap {{\Omega }_{q}} \cap {{\Omega }_{r}}$, принадлежащей каждой из областей ${{\Omega }_{p}}$, ${{\Omega }_{q}}$, ${{\Omega }_{r}}$. Найденные компоненты ${{n}_{1}},{{n}_{2}},{{n}_{3}}$ позволяют вычислить градиент функции $u(x,y)$ в явном виде
(1.5)
${{u}_{x}} = - \frac{{{{n}_{1}}}}{{{{n}_{3}}}},\quad {{u}_{y}} = - \frac{{{{n}_{2}}}}{{{{n}_{3}}}},$Реконструкция поверхности возможна и при использовании только двух ее изображений [5, 6, 8–15]. При этом требуется дополнительный анализ необходимых и достаточных условий однозначного определения функции $u(x,y)$, связанный с весьма громоздкими символьными вычислениями. В работах [6, 9, 16, 17] такой анализ был выполнен при специальном выборе двух направлений на источники света, что позволило значительно упростить вычисления и исследовать проблему интегрируемости уравнений (1.2). Отметим также, что при реконструкции ламбертовской поверхности второго порядка по двум ее изображениям неоднозначности в определении функции $u(x,y)$ возникают только в специальных случаях (см. [18]).
Поскольку области ${{\Omega }_{p}}$, ${{\Omega }_{q}}$, ${{\Omega }_{r}}$ на плоскости OXY в общем случае не совпадают, естественно ожидать, что область изображения Ω = ${{\Omega }_{p}}\, \cap \,{{\Omega }_{q}}\, \cap \,{{\Omega }_{r}}$, получаемого при освещении поверхности с трех различных направлений, будет меньшей по сравнению со случаем, когда используются только любые два из трех изображений ${{E}_{p}}(x,y)$, ${{E}_{q}}(x,y)$, ${{E}_{r}}(x,y)$. Например, при использовании функций ${{E}_{p}}(x,y)$ и ${{E}_{q}}(x,y)$ соответствующая область определения образа ${{\Omega }_{{pq}}} = {{\Omega }_{p}} \cap {{\Omega }_{q}}$ включает в себя дополнительную подобласть ${{\Omega }_{1}} = {{\Omega }_{{pq}}}{\backslash }\Omega $. При этом в области $\Omega $ градиент функции $u(x,y)$ определяется однозначно на основе трех ее изображений ${{E}_{p}}(x,y)$, ${{E}_{q}}(x,y)$, ${{E}_{r}}(x,y)$ (см. (1.5)), а решение проблемы реконструкции поверхности в области ${{\Omega }_{{pq}}}$ на основе только двух изображений допускает неоднозначности (см. [6, 9, 16–18]). Если функция $u(x,y)$ является непрерывной вместе с первыми производными, то на границе областей $\Omega $ и ${{\Omega }_{1}}$ решения, получаемые на основе трех и двух изображений должны быть одинаковыми. Это условие позволяет устранить все неоднозначности и найти единственное решение проблемы реконструкции поверхности в области ${{\Omega }_{1}}$ на основе двух образов ${{E}_{p}}(x,y)$ и ${{E}_{q}}(x,y)$. Аналогичным образом можно найти однозначное решение проблемы реконструкции поверхности в областях ${{\Omega }_{2}} = {{\Omega }_{{pr}}}{\backslash }\Omega $ и ${{\Omega }_{3}} = {{\Omega }_{{qr}}}{\backslash }\Omega $, где ${{\Omega }_{{pr}}} = {{\Omega }_{p}} \cap {{\Omega }_{r}}$, ${{\Omega }_{{qr}}} = {{\Omega }_{q}} \cap {{\Omega }_{r}}$.
Целью данной работы является исследование проблемы реконструкции поверхности по двум и трем ее фотометрическим образам на границе области $\Omega $ и получение условий однозначного нахождения градиента функции $u(x,y)$ в большей по сравнению с $\Omega $ области ${{\Omega }_{{pq}}} \cup {{\Omega }_{{pr}}} \cup {{\Omega }_{{qr}}}$. Получение соответствующих выражений для градиента и исследование интегрируемости векторных полей связано с довольно громоздкими символьными вычислениями, которые удобно выполнять с помощью систем компьютерной алгебры. В данной работе для выполнения всех расчетов используется система компьютерной алгебры Mathematica [19].
2. РЕКОНСТРУКЦИЯ ПОВЕРХНОСТИ НА ОСНОВЕ ДВУХ ИЗОБРАЖЕНИЙ
Рассмотрим проблему реконструкции поверхности в области ${{\Omega }_{{pq}}} = \Omega \cup {{\Omega }_{1}}$ на основе двух изображений ${{E}_{p}}(x,y)$, и ${{E}_{q}}(x,y)$, предполагая, что в области $\Omega $ имеется также третье ее изображение ${{E}_{r}}(x,y)$. Напомним, что в области $\Omega $ выражения (1.4) и (1.5) однозначно определяют компоненты единичного вектора нормали $\vec {n} = ({{n}_{1}},{{n}_{2}},{{n}_{3}})$ и градиент функции $u(x,y)$.
В области ${{\Omega }_{1}}$, где имеются только два фотометрических образа ${{E}_{p}}(x,y)$ и ${{E}_{q}}(x,y)$, соответствующих двум неколлинеарным единичным векторам $\vec {p}$ и $\vec {q}$, однозначно определяется только составляющая ${{\vec {n}}_{\parallel }}$ вектора нормали, параллельная плоскости, натянутой на векторы $\vec {p}$ и $\vec {q}$. Действительно, выражая из первых двух уравнений системы (1.3) компоненты
(2.1)
${{n}_{2}} = \frac{{ - {{E}_{p}}{{q}_{1}} + {{E}_{q}}{{p}_{1}} + {{n}_{3}}({{p}_{3}}{{q}_{1}} - {{p}_{1}}{{q}_{3}})}}{{{{p}_{1}}{{q}_{2}} - {{p}_{2}}{{q}_{1}}}},$Хотя решение квадратного уравнения (2.2) можно легко выписать, приведение его к компактной форме вида:
(2.3)
$ + \frac{{\varepsilon ({{p}_{1}}{{q}_{2}} - {{p}_{2}}{{q}_{1}})\sqrt \Lambda }}{{1 - \mathop {\left( {\langle \vec {p}|\vec {q}\rangle } \right)}\nolimits^2 }},$(2.4)
$\Lambda = 1 - E_{p}^{2} - E_{q}^{2} - \langle \vec {p}|\vec {q}\rangle (\langle \vec {p}|\vec {q}\rangle - 2{{E}_{p}}{{E}_{q}}),$Подставляя полученное выражение (2.3) в (2.1), находим единичный вектор нормали $\vec {n}(s)$, который можно представить в компактной векторной форме (см. [6, 17, 18]):
(2.5)
$ + \frac{{\varepsilon \left( {\vec {p} \times \vec {q}} \right)\sqrt \Lambda }}{{1 - \mathop {\left( {\langle \vec {p}|\vec {q}\rangle } \right)}\nolimits^2 }}.$Последнее слагаемое в (2.5) определяет составляющую ${{\vec {n}}_{ \bot }}$ вектора нормали, перпендикулярную плоскости, натянутой на векторы $\vec {p}$ и $\vec {q}$. Поскольку $\varepsilon = \pm 1$, при заданных образах ${{E}_{p}}(x,y)$ и ${{E}_{q}}(x,y)$ вектор ${{n}_{ \bot }}$ может иметь два противоположных направления.
С учетом (2.5) уравнения (1.5) можно переписать в виде (см. [6, 8, 9]):
(2.6)
${{u}_{y}}\, = \,\frac{{{{E}_{p}}({{q}_{2}}\langle \vec {p}|\vec {q}\rangle \, - \,{{p}_{2}})\, + \,{{E}_{q}}({{p}_{2}}\langle \vec {p}|\vec {q}\rangle \, - {{q}_{2}})\, + \,c\varepsilon \sqrt \Lambda }}{{{{E}_{p}}({{p}_{3}}\, - \,{{q}_{3}}\langle \vec {p}|\vec {q}\rangle )\, + \,{{E}_{q}}({{q}_{3}}\, - \,{{p}_{3}}\langle \vec {p}|\vec {q}\rangle )\, + \,b\varepsilon \sqrt \Lambda }},$Отметим, что наличие двух знаков $\varepsilon = \pm 1$ в выражениях (2.6) в общем случае приводит к неоднозначному определению градиента функции $u(x,y)$ и, следовательно, к неоднозначному определению искомой функции $u(x,y)$.
Из уравнения (2.5) следует, что выражение (2.4) для $\Lambda $ можно также записать в виде
Поскольку векторное произведение неколлинеарных векторов $\vec {p}$ и $\vec {q}$ не равняется нулю, условие $\Lambda = 0$ выполняется только в том случае, когда вектор нормали перпендикулярен векторному произведению $(\vec {p} \times \vec {q})$. При этом три вектора $\vec {n}$, $\vec {p}$, $\vec {q}$ лежат в одной плоскости, и двух функций ${{E}_{p}}$ и ${{E}_{q}}$, которые равняются проекциям вектора нормали $\vec {n}$ на векторы $\vec {p}$ и $\vec {q}$ соответственно, достаточно для однозначного определения вектора $\vec {n}$.
Если функция $u(x,y)$ принадлежит к классу ${{C}^{1}}$ или ${{C}^{2}}$, в области $\Omega $ может существовать гладкая кривая $\Gamma $, вдоль которой $\Lambda = 0$. Эта кривая делит $\Omega $ на подобласти ${{\Omega }^{{(1)}}}$ и ${{\Omega }^{{(2)}}}$, так что Ω = ${{\Omega }^{{(1)}}} \cup {{\Omega }^{{(2)}}} \cup \Gamma $, ${{\Omega }^{{(1)}}} \cap {{\Omega }^{{(2)}}} = \emptyset $ и $\Lambda > 0$ в каждой из подобластей ${{\Omega }^{{(1,2)}}}$. В точках $(x,y) \in \Gamma $ система (2.6) определяет только одно векторное поле $({{u}_{x}},{{u}_{y}})$, а в каждой из подобластей ${{\Omega }^{{(1,2)}}}$ получаем два векторных поля $(u_{x}^{ \pm },u_{y}^{ \pm })$, отвечающих выбору знака $\varepsilon = 1$ или ε = –1. Если оба этих поля являются интегрируемыми, то задача реконструкции поверхности $S$ может иметь четыре решения, которые получаются при выборе векторных полей $(u_{x}^{ + },u_{y}^{ + })$ или $(u_{x}^{ - },u_{y}^{ - })$ в каждой из подобластей ${{\Omega }^{{(1)}}}$ и ${{\Omega }^{{(2)}}}$ и их склеивании вдоль кривой $\Gamma $ (см. [6, 9]).
Указанные неоднозначности определения векторного поля (2.6) в области $\Omega $ легко устраняются, если имеется третье изображение Er = $\langle \vec {r}|\vec {n}\rangle $. Подставляя вместо вектора $\vec {n}$ выражение (2.5) и разрешая полученное уравнение относительно $\varepsilon $, находим
(2.7)
$\frac{{{{E}_{q}}\left( {\langle \vec {q}|\vec {r}\rangle - \langle \vec {p}|\vec {q}\rangle \langle \vec {p}|\vec {r}\rangle } \right) - {{E}_{r}}(1 - {{{\langle \vec {p}|\vec {q}\rangle }}^{2}})}}{{\langle \vec {r}|\vec {p} \times \vec {q}\rangle \sqrt \Lambda }}.$При $\Lambda \ne 0$ выражение (2.7) позволяет однозначно определить множитель $\varepsilon $ и тем самым решить проблему выбора знака в выражениях (2.6) во всей области ${{\Omega }_{{pq}}}$. Действительно, подставляя (2.7) в (2.1) и (2.3) и выполняя необходимые символьные преобразования с использованием встроенных функций системы $Mathematica$, получаем для вектора нормали выражения (1.4), однозначно определяющие искомое векторное поле (1.5).
Следует отметить также, что кривая $\Gamma $, вдоль которой Λ = 0, может располагаться в области ${{\Omega }_{{pq}}}$ за границами области $\Omega $, так что Ωpq = ${{\Omega }^{{(1)}}} \cup {{\Omega }^{{(2)}}} \cup \Gamma $ и ${{\Omega }^{{(2)}}} \subset {{\Omega }_{1}}$. В этом случае выражения (2.6), (2.7) позволяют однозначно найти искомое векторное поле только в подобласти ${{\Omega }^{{(1)}}}$. В подобласти ${{\Omega }^{{(2)}}}$ выражения (2.6) определяют два векторных поля $u_{x}^{ \pm }$, $u_{y}^{ \pm }$, соответствующих фотометрическим образам ${{E}_{p}}$, ${{E}_{q}}$, и проблему однозначной реконструкции поверхности следует решать на основе анализа интегрируемости векторных полей $u_{x}^{ \pm }$, $u_{y}^{ \pm }$ (см. [6, 9, 16–18]).
В редких случаях кривая $\Gamma $ может совпадать с частью границы области $\Omega $, находящейся в ${{\Omega }_{{pq}}}$. Тогда выполняются условия ${{\Omega }^{{(1)}}} \subset \Omega $ и $\Omega \cap {{\Omega }^{{(2)}}} = \not {0}$, причем Λ = 0 на границе области Ω. Поскольку в области ${{\Omega }^{{(2)}}}$ функция ${{E}_{r}}(x,y)$ не определена, параметр $\varepsilon $ не может быть вычислен и выражения (2.6) определяют два векторных поля $u_{x}^{ \pm }$, $u_{y}^{ \pm }$. Поэтому проблема однозначной реконструкции поверхности в области ${{\Omega }^{{(2)}}}$ требует дополнительного исследования.
Если функция $u(x,y)$ и ее первые производные являются непрерывными функциями координат, т.е. $u \in {{C}^{1}}$, то вектор нормали $\vec {n}(s)$ и интенсивности ${{E}_{p}}(x,y)$, ${{E}_{q}}(x,y)$, ${{E}_{r}}(x,y)$ также непрерывно зависят от координат $x$ и $y$. При этом граница области $\Omega $ определяется из условия, что одна из трех интенсивностей обращается в ноль, поскольку вектор нормали к поверхности перпендикулярен к соответствующему направлению на источник света (см. (1.1)). Часть поверхности S, в точках которой угол между нормалью и направлением на источник превышает π/2, не освещается и, соответственно, она не появляется на фотометрическом изображении. Однако другие два источника могут освещать эту часть поверхности и она присутствует на двух фотометрических образах. Если в этой области выражение (2.7) позволяет определить множитель $\varepsilon $, то векторное поле (2.6) определяется однозначно и поверхность может быть реконструирована.
Предположим, например, что на границе областей $\Omega $ и ${{\Omega }_{1}}$ обращается в ноль интенсивность ${{E}_{r}}(x,y)$, поскольку $\langle \vec {n}|\vec {r}\rangle = 0$. В этом случае на границе области $\Omega $ выражение (2.7) принимает вид
(2.8)
$\frac{{{{E}_{q}}\left( {\langle \vec {q}|\vec {r}\rangle - \langle \vec {p}|\vec {q}\rangle \langle \vec {p}|\vec {r}\rangle } \right)}}{{\langle \vec {p} \times \vec {q}|\vec {r}\rangle \sqrt \Lambda }}.$Вычисляя $\varepsilon $ и подставляя соответствующее выражение в (2.6), получаем искомое векторное поле во всей области ${{\Omega }_{{pq}}}$ при условии, что кривая $\Gamma $ находится в области $\Omega $. Аналогичные рассуждения справедливы также для областей ${{\Omega }_{{pr}}}$, ${{\Omega }_{{qr}}}$.
3. ПРИМЕРЫ
Для демонстрации полученных результатов рассмотрим ламбертовскую поверхность $S$, имеющую форму эллиптического параболоида, определяемого уравнением
Чтобы не усложнять вычисления, три единичных вектора $\vec {p}$, $\vec {q}$, $\vec {r}$, задающих направления на источники света, выберем в виде
где $0 < \alpha < 1$. Легко видеть, что векторы $\vec {p}$ и $\vec {q}$ параллельны плоскости $Oyz$, вектор $\vec {r}$ располагается в перпендикулярной плоскости $Oxz$, а параметр $\alpha $ определяет величину угла между указанными векторами и осью Oz. Соответствующие фотометрические образы определяются уравнением (1.1) и имеют вид(3.3)
${{E}_{q}} = \frac{{4\alpha y + \sqrt {1 - {{\alpha }^{2}}} }}{{1 + 36{{x}^{2}} + 16{{y}^{2}}}},$Из условия $0 \leqslant {{E}_{{p,q,r}}}(x,y) \leqslant 1$ находим области определения этих трех образов (см. Рис. 1)
Рис. 1.
Фотометрические образы ${{E}_{p}}$ ${{E}_{q}}$ и ${{E}_{r}}$ поверхности (3.1), соответствующие векторам (3.2), α = 0.2.

Подставляя (3.2), (3.3) в (1.5) и выполняя необходимые символьные преобразования, убеждаемся в том, что получаемый градиент ${{u}_{x}} = 6x$, uy = $4y$ однозначно определяет функцию (3.1) в области $\Omega = {{\Omega }_{p}} \cap {{\Omega }_{q}} \cap {{\Omega }_{r}}$, которая естественно значительно меньше области $\tilde {\Omega } = {{\Omega }_{{pq}}} \cup {{\Omega }_{{pr}}} \cup {{\Omega }_{{qr}}}$, где ${{\Omega }_{{pq}}}$, ${{\Omega }_{{pr}}}$, ${{\Omega }_{{qr}}}$ обозначают области, в которых можно реконструировать поверхность (3.1), используя соответствующую пару фотометрических образов (3.3).
Чтобы реконструировать поверхность во всей области Ωpq = $\left\{ {(x,y): - \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }} \leqslant y \leqslant \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}} \right\}$, заметим, что ${{E}_{r}} = 0$ на прямой $x = \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{6\alpha }}$. Выполняя необходимые вычисления, получаем для $\Lambda $ следующее выражение:
Легко видеть, что $\Lambda = 0$ только при x = 0, т.е. прямая $\Gamma $ располагается в области $\Omega $, в которой выражения (1.4), (1.5) определяют градиент ${{u}_{x}}$ = 6x, ${{u}_{y}} = 4y$, что позволяет однозначно реконструировать поверхность (3.1). При этом выражения (2.6), определяющие градиент $({{u}_{x}},{{u}_{y}})$ на основе только двух образов ${{E}_{p}}$ и ${{E}_{q}}$, определяют два векторных поля $u_{x}^{ \pm } = 6x\varepsilon $, $u_{y}^{ \pm } = 4y$. Хотя оба векторных поля удовлетворяют уравнению (1.2) и являются интегрируемыми, только при ε = 1 получаем градиент $u_{x}^{ + } = 6x$, $u_{y}^{ + }$ = 4y, соответствующий поверхности (3.1). Отметим, что вычисление параметра $\varepsilon $, определяемого выражением (2.7), дает правильный результат ε = 1. Таким образом, использование выражений (2.6) при ε = 1 позволяет однозначно определить градиент $({{u}_{x}},{{u}_{y}})$ и реконструировать поверхность в области Ω1 = = $\left\{ {(x,y)\,:\,x \geqslant \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{6\alpha }} \wedge - \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}\, \leqslant \,y\, \leqslant \,\frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}} \right\}$, в которой образ ${{E}_{r}}$ не определен, без дополнительного анализа интегрируемости векторных полей $u_{x}^{ \pm }$, $u_{y}^{ \pm }$.
В области Ωpr = $\left\{ {(x,y)\,:\,x\, \leqslant \,\frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{6\alpha }}\, \wedge \,y\, \leqslant \,\frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}} \right\}$ граница с подобластью ${{\Omega }_{2}}$ проходит вдоль прямой $y = - \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}$, которая определяется из условия ${{E}_{q}}$ = 0. Прямая $\alpha + 2(3x + 2y)\sqrt {1 - {{\alpha }^{2}}} = 0$, вдоль которой выполняется условие Λ = 0, частично располагается в области $\Omega $, а вычисление параметра (2.7) на прямой $y = - \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}$ дает ε = 1. Вычисление градиента по формулам (2.5) при ε = 1 дает ожидаемый результат $u_{x}^{ + } = 6x$, $u_{y}^{ + } = 4y$, в то время как при $\varepsilon = - 1$ получаем
Подчеркнем, что исключение этого векторного поля требует дополнительного исследования его интегрируемости, в то время как выбор параметра ε = 1 согласно (2.7) и использование выражений (2.6) позволяет правильно определить градиент $({{u}_{x}},{{u}_{y}})$ во всей области ${{\Omega }_{{pr}}}$, хотя в подобласти ${{\Omega }_{2}}$ образ ${{E}_{q}}$ не определен.
Наконец, в области Ωpr = $\left\{ {(x,y)\,:\,x\, \leqslant \,\frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{6\alpha }}\, \wedge \,y\,} \right.$ ≥ ≥ $\left. { - {\kern 1pt} \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}} \right\}$ граница с подобластью ${{\Omega }_{3}}$ проходит вдоль прямой $y = \frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}$, которая определяется из условия ${{E}_{p}} = 0$. Условие Λ = 0 выполняется на прямой α + $2(3x - 2y)\sqrt {1 - {{\alpha }^{2}}} $ = 0, которая частично располагается в области $\Omega $. Вычисление параметра (2.7) на прямой y = $\frac{{\sqrt {1 - {{\alpha }^{2}}} }}{{4\alpha }}$ дает $\varepsilon = - 1$, что приводит к правильному выражению для градиента $u_{x}^{ - } = 6x$, $u_{y}^{ - } = 4y$. При ε = 1 соответственно получаем
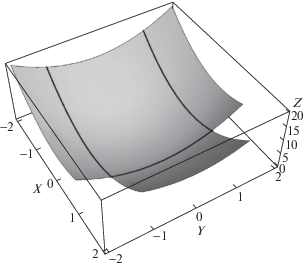
Исследование показывает, что векторное поле $(u_{x}^{ + },u_{y}^{ + })$ является неинтегрируемым и потому задача реконструкции поверхности (3.1) по двум ее фотометрическим образам ${{E}_{q}}$ и ${{E}_{r}}$ в области ${{\Omega }_{{qr}}}$ имеет единственное решение. Однако использование выражений (2.6) с параметром $\varepsilon $, вычисленным по формуле (2.7), позволяет правильно определить градиент $({{u}_{x}},{{u}_{y}})$ во всей области ${{\Omega }_{{qr}}}$ без исследования интегрируемости векторных полей $u_{x}^{ \pm }$, $u_{y}^{{pm}}$. Реконструированная поверхность показана на рис. 2 вместе с границами области $\Omega = {{\Omega }_{p}} \cap {{\Omega }_{q}} \cap {{\Omega }_{r}}$.
В качестве второго примера рассмотрим ламбертовскую поверхность $S$, имеющую форму полусферы, определяемой уравнением
Три единичных вектора $\vec {p}$, $\vec {q}$, $\vec {r}$, задающих направления на источники света, выберем в виде
(3.5)
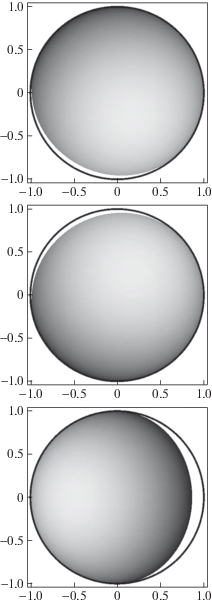
$\vec {q} = \left( {\frac{\alpha }{2},\frac{{\alpha \sqrt 3 }}{2}, - \sqrt {1 - {{\alpha }^{2}}} } \right),$Из условия $0 \leqslant {{E}_{{p,q,r}}}(x,y) \leqslant 1$ находим области определения этих трех образов (см. Рис. 3)
Рис. 3.
Фотометрические образы ${{E}_{p}}$ ${{E}_{q}}$ и ${{E}_{r}}$ поверхности (3.4), соответствующие векторам (3.5), $\alpha = 1{\text{/}}3$, $\beta = 1{\text{/}}2$.
Выполняя необходимые вычисления по формулам (1.4), (1.5) для векторов (3.5) и фотометрических образов (3.6), убеждаемся в том, что получаемый градиент ${{u}_{x}} = x{\text{/}}\sqrt {1 - {{x}^{2}} - {{y}^{2}}} $, uy = $y{\text{/}}\sqrt {1 - {{x}^{2}} - {{y}^{2}}} $ однозначно определяет функцию (3.4) в области $\Omega = {{\Omega }_{p}} \cap {{\Omega }_{q}} \cap {{\Omega }_{r}}$.
Заметим, что в области ${{\Omega }_{{pq}}} = {{\Omega }_{p}} \cap {{\Omega }_{q}}$ существует кривая $\Gamma $, определяемая выражением (2.4):
Легко убедиться в том, что граница области $\Omega $, принадлежащая области ${{\Omega }_{{pq}}}$ и определяемая из условия ${{E}_{r}} = 0$, представляет собой эллипс
При условии
кривая $\Gamma $ располагается в области $\Omega $ и неоднозначность выбора параметра $\varepsilon $ в выражениях (2.6) легко устраняется, поскольку вычисления по формуле (2.7) приводят к результату $\varepsilon = - 1$, что соответствует искомому векторному полю $u_{x}^{ - }$ = $x{\text{/}}\sqrt {1 - {{x}^{2}} - {{y}^{2}}} $, $u_{y}^{ - } = y{\text{/}}\sqrt {1 - {{x}^{2}} - {{y}^{2}}} $. И хотя выбор второго значения $\varepsilon = 1$ приводит к векторному полю4. ЗАКЛЮЧЕНИЕ
В настоящей работе исследуется проблема реконструкции ламбертовской поверхности S = = $graph(u)$ по трем ее фотометрическим изображениям ${{E}_{p}}(x,y)$, ${{E}_{q}}(x,y)$, ${{E}_{r}}(x,y)$, получаемым последовательно при освещении поверхности $S$ с трех различных направлений, задаваемых линейно независимыми единичными векторами $\vec {p}$, $\vec {q}$, $\vec {r}$, соответственно. Поскольку области определения ${{\Omega }_{p}}$, ${{\Omega }_{q}}$, ${{\Omega }_{r}}$ этих изображений на плоскости $OXY$ в общем случае не совпадают, однозначная реконструкция поверхности на основе трех изображений производится в меньшей области Ω = = ${{\Omega }_{p}} \cap {{\Omega }_{q}} \cap {{\Omega }_{r}}$. Однако в случае непрерывно дифференцируемой функции $u(x,y)$ получаемое решение может быть продолжено за границы области $\Omega $, если воспользоваться результатами вычислений градиента функции $u(x,y)$ в областях ${{\Omega }_{{pq}}}$, ${{\Omega }_{{pr}}}$ и ${{\Omega }_{{qr}}}$ на основе только двух соответствующих образов. Возникающие при этом неоднозначности решения устраняются путем определения параметра $\varepsilon $ по результатам вычислений по формулам (2.7), (2.8). Моделирование фотометрических образов различных поверхностей при различных направлениях на источники света показало справедливость полученных теоретических результатов.
Отметим, что хотя выражения (2.6), (2.7) для градиента искомой функции $u(x,y)$ и для параметра $\varepsilon $ удается записать в достаточно компактной форме, получение и анализ этих выражений связаны с весьма громоздкими символьными вычислениями, которые можно эффективно выполнять с помощью систем компьтерной алгебры. В данной работе все вычисления и визуализация результатов выполнены с использованием системы компьютерной алгебры Mathematica.
Список литературы
Horn B.K.P. Robot Vision. MIT Press, Cambridge, Massachusetts, London, England, 2001.
Horn B.K.P., Brooks M.J. Shape from Shading. MIT Press, Cambridge, Massachusetts, London, England, 1989.
Oliensis J. Uniqueness in Shape from Shading. International Journal of Computer Vision. 1991. V. 6 (2). P. 75–104.
Deift P., Sylvester J. Some Remarks on Shape-from-Shading in Computer Vision. Journal of Mathematical Analysis and Applications. 1991. V. 1 (84). P. 235–248.
Woodham R.J. Photometric Stereo: a Reflectance Map Technique for Determining Surface Orientation from Multiple Images. Optical Engineering. 1980. V. 19 (1.1). P. 139–144.
Kozera R. Existence and Uniqueness in Photometric Stereo. Applied Mathematics and Computation. 1991. V. 44 (1). P. 1–104.
Noakes L., Kozera R. Non-linearities and noise reduction in 3-source photometric stereo. Journal of Mathematical Imaging and Vision. 2003. V. 18 (2). P. 119–127.
Onn R., Bruckstein A.M. Integrability disambiguates surface recovery in two-image photometric stereo. International Journal of Computer Vision. 1990. V. 5 (1). P. 105–113.
Kozera R. On shape recovery from two shading patterns. International Journal of Pattern Recognition and Artificial Intelligence, 1992. V. 6 (4). P. 673–698.
Brooks M.J., Chojnacki W., Kozera R. Shading without Shape. Quarterly of Applied Mathematics. 1992. V. 50 (1). P. 27–38.
Kozera R. On Complete Integrals and Uniqueness in Shape from Shading. Applied Mathematics and Computation. 1995. V. 73 (1). P. 1–37.
Kozera R. Uniqueness in Shape from Shading Revisited. International Journal of Mathematical Imaging and Vision. 1997. V. 7. P. 123–138.
Bruss A.R. The Eikonal Equation: Some Results Applicable to Computer Vision. Journal of Mathematical Physics. 1982. V. 5 (23). P. 890–896.
Brooks M.J., Chojnacki W., Kozera R. Circularly Symmetrical Eikonal Equations and Nonuniqueness in Computer Vision. Journal of Mathematical Analysis and Applications. 1992. V. 165 (1). P. 192–215.
Kimmel R., Bruckstein A.M. Tracking Level Sets by Level Sets: a Method of Solving the Shape from Shading Problem. Computer Vision, Graphics and Image Understanding. 1995. V. 62. P. 47–58.
Kozera R., Prokopenya A. Orthogonal Illuminations in Two Light-Source Photometric Stereo. In: Computer Information System and Industrial Management / CISIM’2016, K. Saeed and W. Homenda (Eds.), LNCS 9842. Berlin, Springer-Verlag, 2016. P. 402–415.
Козера Р., Прокопеня А.Н. Применение компьютерной алгебры при реконструкции поверхности по ее фотометрическому стереообразу // Программирование. 2017. Т. 43 (2). С. 45–53.
Козера Р., Прокопеня А.Н. Применение компьютерной алгебры в фотометрическом стерео с двумя источниками света // Программирование. 2018. Т. 44 (2). С. 51–59.
Wolfram S. An elementary introduction to the Wolfram Language. Wolfram Media, Inc., 2016.
Дополнительные материалы отсутствуют.
Инструменты
Программирование