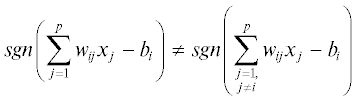Программирование, 2019, № 5, стр. 25-35
УСТРАНЕНИЕ ОТРИЦАТЕЛЬНЫХ ЦИКЛОВ В НЕКОТОРЫХ СТРУКТУРАХ НЕЙРОННЫХ СЕТЕЙ С ЦЕЛЬЮ ДОСТИЖЕНИЯ СТАЦИОНАРНЫХ РЕШЕНИЙ
Ю. Л. Карпов a, *, Л. Е. Карпов b, c, **, Ю. Г. Сметанин d, e, ***
a ООО Люксофт Профешнл
123060 Москва, 1-й Волоколамский проезд, 10, Россия
b Институт системного программирования им. В.П. Иванникова РАН
109004 Москва, ул. Солженицына, 25, Россия
c Московский государственный университет имени М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
d Федеральный исследовательский центр “Информатика и управление” РАН
119333 Москва, ул. Вавилова, д. 44, кор. 2, Россия
e Московский физико-технический институт (технический университет)
141701 Московская область, г. Долгопрудный, Институтский пер., 9, Россия
* E-mail: y.l.karpov@yandex.ru
** E-mail: mak@ispras.ru
*** E-mail: ysmetanin@rambler.ru
Поступила в редакцию 10.04.2019
После доработки 13.05.2019
Принята к публикации 13.05.2019
Аннотация
Рассмотрена задача улучшения структурных свойств искусственных нейронных сетей. Предлагается рассматривать структуру таких сетей как графовую, в которой при определенных обстоятельствах (например, при наличии обратных связей между слоями нейронов в сети) могут возникать циклические подструктуры. Некоторые свойства циклов в графах нейронных сетей могут оказывать существенное влияние как на скорость достижения решения поставленных пользователями сетей задач, так и на саму возможность получения (устойчивого) решения. К таким свойствам относится отрицательность части циклов, выявляемых в графах сетей. Приводится алгоритм, который при соблюдении сформулированных ограничений позволяет устранять отрицательные циклы из графов, способствуя росту шансов на получение решения задач, для которых разрабатывались соответствующие нейронные сети. Приведен иллюстративный пример.
1. ВВЕДЕНИЕ
Этап тестирования нейронных сетей – это очень важная составляющая их жизненного цикла, оказывающая влияние на возможность решения большого круга задач в самых разных прикладных областях. Искусственные нейронные сети используются при решении задач классификации, оптимизации, распознавания речи, машинного перевода, в задачах обработки и анализа изображений, и в других приложениях, причем не только в неспешных лабораторных условиях, но и в режиме реального времени [1–4].
Разнообразие решаемых задач приводит к разнообразию используемых структур нейронных сетей. В различных приложениях можно видеть, что используются многослойные персептроны [5, 6], сети Хопфилда [7], машины Больцмана [8], самоорганизующиеся карты Кохонена [9], рекуррентные [10], сверточные сети [11], нейронные машины Тьюринга [12] и множество других структур, их вариантов и комбинаций.
При создании нейронной сети для решения конкретной задачи программист задает набор пар (вход, выход) и определяет параметры сети с помощью некоторого эвристического правила (характерного для данной нейросетевой модели). Он не определяет конкретные операции нейронной сети и не контролирует их. Таким образом, обрабатывая огромные объемы информации, сами искусственные нейронные сети остаются информационными “черными ящиками”. Тем не менее, искусственная нейронная сеть – это программная система, и ее жизненный цикл подчиняется всем правилам, законам, стандартам, разработанным для программных систем. Конечно, при этом каждый этап жизненного цикла искусственной нейронной сети имеет свои особенности, отличающие его от того, с чем приходится сталкиваться при разработке более традиционно выглядящих программных систем. В частности, тестирование нейронных сетей во многом связано не с проверкой правильности соединения отдельных узлов и/или слоев сети друг с другом, а с исследованием правильности принятых разработчиком сети структурных решений.
Тестирование структурных особенностей искусственных нейронных сетей в некотором смысле даже более важно, чем стандартная проверка правильности кодирования отдельных узлов сети и соединений между ними. Связано это с тем, что операции, выполняемые в узлах сети (нейронах), весьма просты – обычно это действия по сложению, умножению и сравнению вещественных чисел, причем в некоторых случаях операции по вычислению суммы произведений заменяются операциями вычисления максимума (или минимума) группы вещественных чисел [13].
В то же время влияние структурных изменений на способность искусственной нейронной сети решать поставленную задачу огромно. Количество слоев нейронов, начальные значения коэффициентов матриц весов межнейронных связей, методы изменения этих коэффициентов, векторы порогов срабатывания нейронов, метрики, позволяющие сравнивать выходы сети с обучающими выходными образцами, множество обучающих векторов, вид сигмоидальной функции, используемой при формировании выходных векторов на основе матрицы весов и значений входных векторов, методы решения проблемы переобучения сетей – вот далеко не полный перечень объектов, “правильность” которых надо проверять еще до того, как нейронная сеть приступит к решению своей основной задачи, ради которой она разрабатывалась.
В своей предыдущей работе [14] авторы уже обозначали важность тестирования нейронных сетей. Мы обращали внимание и на их программную природу, и на их особенности, отличающие их от традиционных программных продуктов. Программная сущность искусственных нейронных сетей заставляет относиться к ним как к обычному программному обеспечению, жизненный цикл которого подчиняется известным национальным и международным стандартам [15–19]. Структурные особенности нейронных сетей стали объектом исследований на следующем этапе.
Важность тестирования определяется не только получением положительного или отрицательного ответа на вопрос о соответствии результатов работы тестируемой программы на тестовых примерах заранее созданным эталонным ответам. В случае отрицательного ответа у тестировщика появляется обильный материал для последующей коррекции тестировавшейся им программы с целью устранения ошибок и исправления ее неправильного поведения.
Исправлять структуру искусственных нейронных сетей в случае обнаружения их неправильной работы не слишком сложно, поэтому одновременно с тестированием полезно выявлять те ее фрагменты, которые можно исправлять после тестирования. Для выявления мест, подлежащих исправлению, нами была выбрана графовая модель представления структуры искусственной нейронной сети, в которой сама сеть представляется в виде графа, нейроны сети – в виде вершин этого графа, а межнейронные связи – в виде ребер.
Очевидно, что для многослойных сетей с прямым распространением сигналов в качестве базовой модели должен служить ориентированный граф (орграф) со структурой дерева, а моделями рекуррентных нейронных сетей могут быть сложные графы с обратными связями.
Наличие обратных связей в графе нейронной сети дает немалые преимущества, расширяя классы задач, которые могут быть решены с привлечением нейронных сетей, но одновременно порождает множество проблем.
Один из видов неправильной работы рекуррентных нейронных сетей – возникновение зацикливания, при котором сеть не сходится к неподвижной точке. Это зацикливание непосредственно связано со знаками циклов на графе.
Мы предлагаем использовать методику обнаружения циклов и выявления среди прочих тех циклов, которые могут привести к появлению бесконечного зацикливания в нейронной сети, а также методику исправления таких “неправильных” циклов. Метод может эффективно применяться в симметричных рекуррентных нейронных сетях для удаления нестационарных решений и при внедрении дополнительных обратных связей в нейронные сети с прямым распространением для реализации возможностей ассоциативной памяти и снижения чувствительности к ошибкам входов.
Первые разделы статьи будут посвящены рассмотрению задачи выявления в графе всех циклов, приводящих к зацикливанию нейронной сети с топологией, задаваемой этим графом. На вид графов никаких ограничений накладываться при этом не будет.
Во второй части статьи будет предложена процедура исправления таких циклов и описан алгоритм ее работы. При этом будет предполагаться, что все циклы, которые целесообразно устранить, уже найдены, перечень этих циклов сформирует входную информацию этой процедуры, а в результате будет проведена некоторая модификация структуры нейронной сети, при которой нежелательные циклы исчезнут.
2. ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ
Ориентированным графом (орграфом) называется пара G = (V, E), где $V = ({{v}_{1}}, \ldots ,{{v}_{p}})$ – множество вершин, $E \subseteq V \times V = ({{v}_{i}},{{v}_{j}})$ – множество ребер, причем $E = \{ {{e}_{1}} = ({{{v}}_{{{{i}_{1}}}}},{{{v}}_{{{{j}_{1}}}}}), \ldots ,({{{v}}_{{{{i}_{q}}}}},{{{v}}_{{{{j}_{q}}}}})\} $, |E| = q ≤ p2. Ребро, связывающее вершину ${{v}_{i}}$ с вершиной ${{v}_{j}}$, будем также обозначать символом eij, то есть eij = $({{v}_{i}},{{v}_{j}})$.
Если E ⊆ V2 (то есть пары вершин не упорядочены), то орграф называется просто графом или неориентированным графом.
Множество $\Gamma ({{v}_{i}})$ есть множество вершин, из которых выходят ребра, входящие в ${{v}_{i}}$, $({{v}_{j}},{{v}_{i}}) \in E$, аналогично множество ${{\Gamma }^{ + }}({{v}_{i}})$ – это множество вершин, в которые входят ребра, выходящие из ${{v}_{i}}$, $({{v}_{i}},{{v}_{j}}) \in E$.
Путь в орграфе – непустая последовательность C = $({{v}_{0}},{{e}_{{01}}},{{v}_{1}},{{e}_{{12}}},{{v}_{2}}, \ldots ,{{e}_{k}}{{_{{ - 1,}}}_{k}},{{v}_{k}})$ . Путь называется простым, если могут совпадать только ${{v}_{0}}$ и ${{v}_{k}}$, то есть начальная и конечная вершины пути, а все остальные вершины различны. Простой путь, у которого ${{v}_{0}} = {{v}_{k}}$, называется циклом.
Орграф называется связным, если для любой пары вершин ${{v}_{i}}$, ${{v}_{j}}$ есть путь из ${{v}_{i}}$, в ${{v}_{j}}$. Связный граф без циклов называется деревом.
Остовным (покрывающим) деревом S в графе G, называется дерево, в которое входят все вершины графа. Для графа G = (V, E) и его остовного дерева S = (V, E') кографом K называется граф с множеством вершин V и множеством ребер E\E'.
Пусть задана функция w: E → R. Тогда значение w(eij) называется весом ребра eij. Функция w определяет для орграфа матрицу W весов его ребер.
Далее при анализе знаков весов ребер на путях в орграфе будем использовать функцию sgn, определяемую как:
Цикл $C = \left( {{{v}_{0}},{{e}_{{01}}},{{v}_{1}},{{e}_{{12}}},{{v}_{2}}, \ldots ,{{e}_{k}}_{{ - 1}}{{,}_{0}},{{v}_{0}}} \right)$ называется положительным, если число входящих в него ребер с отрицательным весом четно, в противном случае он называется отрицательным. Такой выбор терминологии объясняется тем, что положительность цикла эквивалентно условию
Величину sgnΠ(C) будем называть знаком цикла.
Мы будем рассматривать модель дискретной нейронной сети, определяемую как четверка N = = (G, W, b, sgn), где G – связный орграф, W – матрица весов ребер (межнейронных связей), b – вектор вещественных пороговых значений вершин (нейронов), b = (b1, …, bp), sgn – определенная выше функция.
Значения каждого нейрона xi ∈ { –1, 1}, i = 1, 2, …, p, изменяются в дискретные моменты времени в соответствии с его входами, определяемыми состояниями всех нейронов сети = (x1, …, xp), и изменения эти описываются функцией, зависящей от состояний всех нейронов, xi(t + 1) = fi(x1(t), …, xp(t)). Динамика нейронной сети определяется соотношением
Отметим, что данными определениями допускается наличие отрицательных весов, соответствующих отрицательному влиянию весов друг на друга. Сети, в которых все веса изначально положительны, легко сводятся к этому случаю простым преобразованием переменных.
Следуя работе [20], будем рассматривать нейронные сети, обладающие двумя достаточно естественными дополнительными свойствами: отсутствия нейронов, не меняющих своего значения ни при каких входах, и отсутствия незначащих путей:
● Первое свойство означает, что для любой вершины ${{v}_{i}}$ орграфа существуют два состояния нейронной сети${{\bar {X}}^{{1,2}}}$ такие, что fi(t + 1) = –1 при входе ${{\bar {X}}^{1}}$(t) и fi(t + 1) = +1 при входе ${{\bar {X}}^{2}}$(t). Невыполнение этого условия для некоторой вершины означает, что соответствующий нейрон просто играет роль порога. В работе [20] доказано, что это условие эквивалентно неравенствам
● Второе свойство означает, что удаление любого ребра из орграфа приводит к изменению динамики нейронной сети, то есть для любого $({{v}_{i}},{{v}_{k}})$ существует x ∈ { –1, 1}p такой, что
3. СВЯЗЬ МЕЖДУ ЦИКЛАМИ И НЕПОДВИЖНЫМИ ТОЧКАМИ НЕЙРОННОЙ СЕТИ
В обычно используемых нейросетевых моделях графы, описывающие топологию сетей, как правило, принадлежат к одному из весьма немногочисленных типов, обладающих некоторыми свойствами регулярности. Например, у сети Хопфилда это полный неориентированный граф, у многослойного персептрона – ориентированное дерево, у морфологической сети – граф, у которого каждая вершина связана с вершинами из некоторой окрестности. Обычно выбор модели нейронной сети производится заранее, а обучение нацелено на такую настройку весов межнейронных связей, при которых во время решения поставленной задачи у сети будут предписанные неподвижные точки. Это такие состояния, при попадании в которые сеть, начиная с некоторого момента времени (шага) работы динамической системы, какой является нейронная сеть, навсегда в них остается:
Такой выбор может приводить к тому, что некоторые межнейронные связи оказываются явно избыточными, приводящими только к замедлению сходимости и, возможно, к ложным неподвижным точкам. Наша цель, в идеале – построить минимальную архитектуру, обеспечивающую возможность реализации требуемых неподвижных точек и отсутствие ложных неподвижных точек. С этой целью мы сначала опишем связь между циклами в графе и неподвижными точками.
В работе [20] доказана следующая теорема.
Теорема. Если в нейронной сети с симметричными межнейронными связями все циклы положительны, то существует вектор $\bar {X}$, который является неподвижной точкой этой сети. Если в графе нейронной сети есть сильно связный компонент, все циклы которого отрицательны, то неподвижных точек у нейронной сети нет.
Идея доказательства заключается в следующем. Пусть требуется, чтобы в сети была неподвижная точка (x1, …, xp). Если зафиксировать остовное дерево S и присвоить корню этого дерева значение x1, то весам выходящих из корня ребер e1m надо присвоить знаки sgn(x1xm), а затем проделать ту же процедуру над ребрами, инцидентными этим вершинам m, продолжив процесс до конца. Из условия (*) и требования положительности циклов, получаемых при добавлении к остовному дереву одного ребра, легко вывести, что (x1, …, xp) будет неподвижной точкой. При выделении положительных и отрицательных циклов в следующем разделе также будет использована процедура анализа остовного дерева и добавления к нему одиночных ребер.
Отметим, что оба утверждения в теореме не являются необходимыми и ничего не говорят о графах, в которых есть как положительные, так и отрицательные циклы. Можно только утверждать, что отрицательные циклы способствуют возникновению колебательных режимов в сети, поэтому их удаление полезно.
4. ВЫДЕЛЕНИЕ ВСЕХ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЦИКЛОВ
В кограф G\S входят (|E| – |V| + 1) = (q – p + 1) ребер, то есть G\S = e1, e2, …, eq – p + 1.
Любое ребро ei из кографа G\S, соответствует единственному циклу ci в подграфе (S ∪ ei), а удаление из этого цикла любого ребра, отличного от ei, приводит к образованию нового остовного дерева.
Множество всех циклов С в графе G можно разбить на непересекающиеся подмножества в соответствии с числом ребер, входящих в цикл и не входящих в S (соответствует верхнему индексу):
Множество {C1} получается поочередным добавлением к остовному дереву S по одному ребру из кографа G\S, |C1| = q – p + 1.
Пусть e1 и e2 – ребра из кографа G\S, c1 – цикл в S ∪ e1, c2 – цикл в S ∪ e2. Возможны две ситуации:
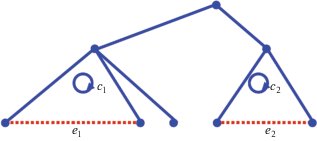
В первом случае циклы c1 и c2 не имеют общих ребер. Тогда добавление к S одновременно e1 и e2 приводит к появлению в графе S ∪ e1 ∪ e2 только тех же циклов c1 и c2 и никаких других (рис. 1).
Рис. 1.
Добавление ребра e1 приводит к появлению цикла с1, добавление ребра e2 – к появлению цикла c2, не пересекающегося с с1.
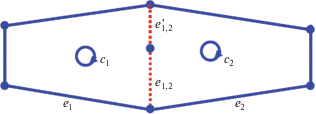
Рассмотрим другой случай, когда оба цикла c1 и c2 имеют общее ребро e1,2 (рис. 2).
Рис. 2.
Добавление ребра e1 приводит к появлению цикла с1, добавление ребра e2 – к появлению цикла c2, имеющего общее ребро e1,2 с циклом с1.
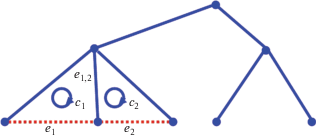
После удаления этого ребра граф S ∪ e1 ∪ e2\e1,2 остается связным графом, в котором число вершин равно числу ребер. Это означает, что в нем есть один цикл c1,2, причем этот цикл
a) не совпадает ни c1, ни с c2, включающими e1,2,
b) включает и e1, и e2, иначе он попал бы в С1.
Отсюда следует, что полученный цикл c1,2 принадлежит множеству C2. Поясним этот вывод на следующем примере (рис. 3). После удаления из графа S ∪ e1 ∪ e2 ребра e1,2 в графе остается единственный цикл. Чтобы такой цикл получить, из графа S ∪ e1 ∪ e2 вычеркиваются все остальные ребра, входящие в оба цикла c1, и c2. На рис. 3 сверху к ребру e1,2 примыкает ребро $e_{{1,2}}^{'}$, которое принадлежит обоим циклам c1 и c2 и не входит в получающийся цикл. Снизу ребра e1,2, как видно на рис. 3, начинается разветвление, и оба ребра e1 и e2 должны быть оставлены в получающемся цикле. Следовательно, для его получения надо добавить к остовному дереву два ребра, и он принадлежит множеству C2.
Теорема о знаках циклов.
Для вычисления П(c) для всех циклов графа достаточно вычислить его для всех таких циклов, которые получаются при добавлении к остовному дереву строго одного ребра из кографа.
Теорема непосредственно следует из следующей леммы.
Лемма о знаках смежных циклов.
Докажем, что sgn Π(с1,2) = sgn (Π(с1)Π(с2)).
Рассмотрим граф G12 = c1 ∪ c2.
Пусть вершины, смежные с e1,2 в G12 – это ${{v}_{{1,2}}}$ и ${{v}_{{2,1}}}$.
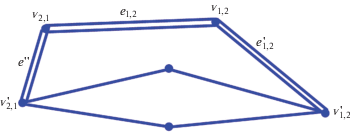
Пометим ребро e1,2. Если в графе G12 есть другое ребро, инцидентное ${{v}_{{1,2}}}$ и принадлежащее обоим графам c1 и c2, то пометим и его и будем продолжать эту процедуру до тех пор, пока не попадем в вершину $v_{{1,2}}^{'}$, которой инцидентны два непомеченных ребра – одно из цикла c1 и одно из цикла c2. После этого аналогичная процедура повторяется в другую сторону, от вершины ${{v}_{{2,1}}}$ до вершины $v_{{2,1}}^{'}$.
Из вершины $v_{{1,2}}^{'}$ выходят два пути по непомеченным ребрам. По построению графа G12 они должны снова сойтись.
Если пути сойдутся в точке отличной от $v_{{2,1}}^{'}$, это будет означать, что из непомеченных ребер получаются два цикла (рис. 4). Эти циклы не имеют общих ребер, что невозможно по предположению.
Рис. 4.
Двойной линией обозначены помечаемые ребра. В показанной ситуации из непомеченных ребер получаются два непересекающихся цикла.
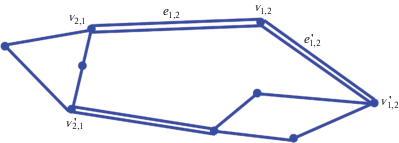
Следовательно, пути сойдутся в $v_{{2,1}}^{'}$, то есть они образуют искомый цикл (на рис. 5 этот цикл состоит из 4 ребер, обозначенных одинарными линиями).
В произведение Π(с1)Π(с2) каждое помеченное ребро входит дважды, то есть дает положительный сомножитель (квадрат вещественного числа), а следовательно, удаление всех этих сомножителей не изменяет знака. Отсюда следует утверждение леммы.
Построение любого цикла в C2 сводится к последовательному выполнению описанной процедуры с разными циклами из C1. Построение циклов из Cj, для j > 2, выполняется полностью аналогично: рассматриваются объединения циклов из Cj – 1 и C1.
Таким образом, для вычисления П(c) для всех циклов графа достаточно вычислить эту величину для циклов, получающихся добавлением к остовному дереву одного ребра. Теорема доказана.
Следствие.
Если E+ – множество ребер, не входящих в S, добавление каждого из которых приводит к положительному циклу, то все циклы остовного подграфа, получающегося добавлением E+ к S, положительны.
5. ИСПРАВЛЕНИЕ ЦИКЛОВ
Нейронные сети представляют собой такие структуры, которые можно относительно легко исправлять в случае обнаружения их неправильной работы, что делает естественным переход от этапа тестирования к этапу отладки.
Опираясь на доказанную теорему о знаках циклов, авторы выполнили разработку алгоритма внесения корректирующих исправлений в структуру графа и для иллюстрации его работы провели экспериментальную проверку.
Суть описанного далее алгоритма состоит в поочередном добавлении ребер из кографа и поиске получающихся при этом циклов. Если среди обнаруженных циклов имеются отрицательные, все они модифицируются вставкой в них дополнительных вершин и ребер, в результате чего циклы меняют знак на положительный (рис. 6 и 7).
Рис. 6.
Отрицательные циклы (1-2-3-1 и 1-2-4-1), получающиеся на остовном дереве некоторого графа (показано сплошными линиями) добавлением к нему ребер из кографа (показаны пунктирными линиями).
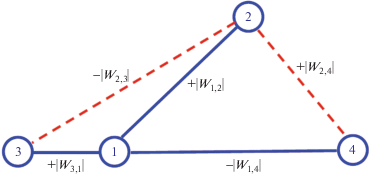
Рис. 7.
Модифицированные положительные циклы, получающиеся на остовном дереве (сплошными линиями показан его фрагмент) добавлением к нему по одному ребра из кографа (показаны линией из точек).
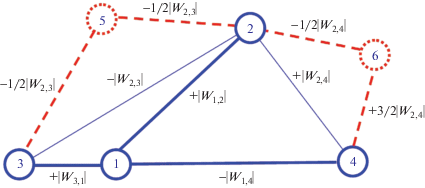
Сумму весов ребер цикла по разным соображениям лучше не менять, поэтому в случае, если вес ребра из кографа, для которого анализируется получающийся цикл, меньше нуля, веса двух новых ребер можно (например) выбирать так, как показано на рис. 7, то есть оба ребра должны получить отрицательные веса, а их абсолютные величины можно установить как некоторые доли от абсолютной величины веса заменяемого ребра. Если вес ребра из кографа больше нуля, одно из двух новых ребер должно получить отрицательный вес, а другое – положительный. Абсолютное значение одного из ребер можно установить, например, в размере 50% от исходного значения, дав весу этого ребра отрицательный знак, а другому новому ребру с положительным весом дать абсолютное значение веса в размере 150% от исходного значения. Разумеется, реальные соотношения весов в наибольшей степени определяются прикладной задачей, которая должна будет решаться с применением соответствующей нейронной сети.
Алгоритм коррекции неориентированного графа для удаления из последнего отрицательных циклов.
Вход: Произвольный неориентированный граф G, несовпадающий с собственным остовным деревом, все вершины которого имеют одновременно и входящие и выходящие ребра.
Выход: Неориентированный граф G', в котором отсутствуют отрицательные циклы (циклы с нечетным количеством ребер, имеющих отрицательные веса).
Шаг 1. Создать граф G', в который включить все ребра и вершины графа G.
Шаг 2. Выбрать произвольную вершину графа G и построить остовное дерево S с корнем в выбранной вершине.
Шаг 3. На основе графа G построить кограф K остовного дерева S.
Шаг 4. Создать граф S', в который включить все ребра и вершины остовного дерева S.
Шаг 5. Для каждого ребра из кографа K выполнять шаги с шага 6 до шага 15.
Шаг 6. Добавить выбранное ребро кографа K к графу S', объявить это ребро текущим.
Шаг 7. Выделить цикл в графе S' и подсчитать его знак, выделенный цикл будет единственным.
Шаг 8. Если выделенный цикл имеет отрицательный знак, выполнить шаги с шага 9 до шага 13, иначе перейти к шагу 14.
Шаг 9. Создать одну новую вершину V и два новых ребра F и T, веса которых рассчитываются на шаге 10.
Шаг 10. Рассчитать веса двух ребер F и T таким образом, чтобы их суммарный вес был равен весу текущего ребра кографа. При этом, если текущее ребро имеет положительный вес, то весам обоих новых ребер дать положительные значения, в противном случае весу одного из новых ребер дать положительное значение, а весу второго – отрицательное.
Шаг 11. Ребро F сделать инцидентным входящей вершине текущего ребра и новой вершине V.
Шаг 12. Ребро T сделать инцидентным новой вершине V и выходящей вершине текущего ребра.
Шаг 13. Включить вершину V, а также ребра F и T в граф G'.
Шаг 14. Удалить текущее ребро из графа S' и из графа G'.
Шаг 15. Если в кографе K есть невыбранные ребра, выбрать из него очередное ребро и перейти к шагу 6, в противном случае объявить граф G' результатом работы алгоритма.
Приведенный алгоритм модифицирует исходный граф таким образом, что, все отрицательные циклы, получающиеся при добавлении к произвольному остовному дереву исходного графа одного из ребер соответствующего кографа, становятся положительными. Ранее доказанная лемма и следствия из нее позволяют утверждать, что преобразованный в соответствии с показанным алгоритмом граф не будет иметь ни одного отрицательного цикла.
Наиболее сложным действием в приведенном алгоритме является построение остовного дерева на шаге 2, для которого алгоритм Прима ([21, 22]) дает оценку времени выполнения как O(|E| + |V|log|V|). Все остальные шаги выполняются не более, чем |E| – |V| + 1 раз, то есть реального вклада в сложность алгоритма не вносят.
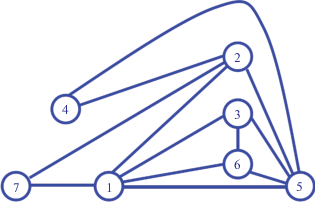
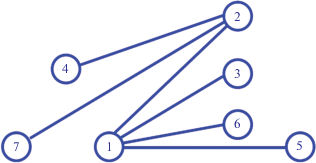
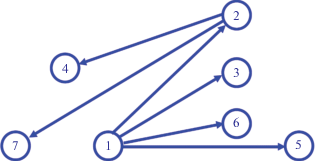
6. ИЛЛЮСТРАТИВНЫЙ ПРИМЕР КОРРЕКЦИИ НЕОРИЕНТИРОВАННОГО ГРАФА
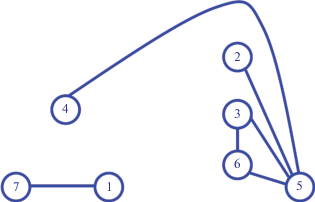
Для иллюстрации работы приведенного здесь алгоритма выберем в качестве тестового примера неориентированный граф G (рис. 8), для которого определены вершины, ребра и их веса (табл. 1). Построим остовное дерево S, имеющее корнем вершину 1 (рис. 9). Для этого дерева построим кограф K (рис. 10). Для каждой вершины этого кографа K будем проводить процедуру, заключающуюся в поочередном их присоединении к остовному дереву S и проверке знаков получающихся циклов. Число таких циклов будет совпадать с числом ребер в кографе K (в данном случае оно будет равно 6). Таблица 2 содержит сведения о получающихся для каждой такой последовательности действий циклов и их знаках. Из приведенных сведений видно, что только три из шести ребер кографа образуют отрицательные циклы. Именно эти циклы и надо корректировать применением показанного алгоритма.
Таблица 1.
Исходно заданные ребра графа G и их веса (жирным шрифтом выделены 6 ребер, входящих в остовное дерево S)
| N | v1 | v2 | W | N | v1 | v2 | W | N | v1 | v2 | W |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 2.1 | 5 | 3 | 6 | 5.5 | 9 | 2 | 4 | –1.7 |
| 2 | 1 | 3 | 2.2 | 6 | 7 | 1 | 2.0 | 10 | 4 | 5 | 1.8 |
| 3 | 1 | 5 | 4.3 | 7 | 3 | 5 | 3.2 | 11 | 2 | 7 | –3.0 |
| 4 | 1 | 6 | 8.4 | 8 | 5 | 2 | –3.6 | 12 | 6 | 5 | 5.0 |
Таблица 2.
Ребра кографа K и циклы, которые возникают в неориентированном графе G, если к остовному дереву S присоединять эти ребра по одному, и знаки этих циклов
| Номер ребра графа G, входящего в кограф K | Номера вершин графа G, соединяемых ребром кографа K(ei) | Цикл на графе S ∪ ei | Знак цикла |
|---|---|---|---|
| 5 | 3-6 | 1-3-6-1 | положительный |
| 6 | 7-1 | 1-2-7-1 | отрицательный |
| 7 | 3-5 | 1-3-5-1 | положительный |
| 8 | 5-2 | 1-2-5-1 | отрицательный |
| 10 | 4-5 | 1-2-4-5-1 | отрицательный |
| 12 | 6-5 | 1-6-5-1 | положительный |
Для проведения экспериментов и построения иллюстраций к доказанной теореме авторами было разработано специальное программное обеспечение, которое включает процедуры
● построения графа по таблице ребер и вершин,
● построения остовного дерева графа,
● построения кографа остовного дерева,
● поиска всех циклов в графе,
● определения знака цикла,
● преобразования отрицательного цикла.
Все показанные далее таблицы с тестовыми примерами построены автоматически с применением разработанного программного обеспечения.
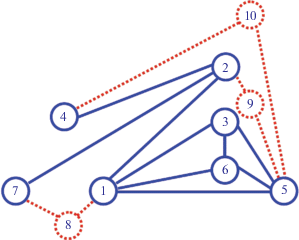
В результате выполнения алгоритма коррекции неориентированного графа G все циклы, образованные поочередным присоединением ребер из кографа K остовного дерева S к этому дереву, становятся положительными. Одновременно возникает новый граф G' (рис. 11, табл. 3), в котором из 29 выявляемых циклов нет ни одного отрицательного. Несложный подсчет показывает, что в исходном графе G тоже можно было выявить 29 циклов (что естественно), но 11 из них имели отрицательный знак.
7. ОСОБЕННОСТИ ОРИЕНТИРОВАННЫХ ГРАФОВ
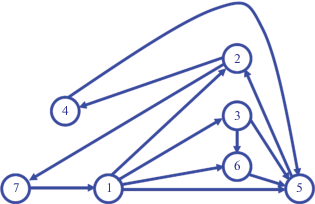
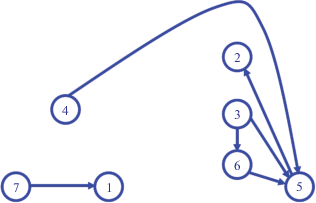
Ориентированные графы также могут быть преобразованы с помощью алгоритма, описанного в разделе 5, однако при их преобразовании можно столкнуться с проблемами, не возникающими для неориентированных графов. Причина, по которой возникают эти проблемы, кроется в том, что некоторые ребра кографов при их добавлении к соответствующим остовным деревьям не образуют циклов. Например, если рассматривать граф G (рис. 8, табл. 1) как ориентированный, он примет вид, показанный на рис. 12. В этом графе можно выявить 6 циклов, только один из которых (1-2-7-1) имеет отрицательный знак. Остовное дерево S'' этого графа, аналогичное остовному дереву S неориентированного графа G, и кограф K'' примут вид, показанный на рис. 13 и рис. 14. При этом окажется, что некоторые ребра кографа K'' при их добавлении к остовному дереву S'' могут создавать положительные циклы, некоторые могут создавать отрицательные циклы, а некоторые не создают циклы вовсе (табл. 4).
Таблица 4.
Ребра кографа K'' и циклы, которые возникают в ориентированном графе G'', если к остовному дереву S'' присоединять эти ребра по одному, и знаки этих циклов
| Номер ребра графа G'', входящего в кограф K'' | Номера вершин графа G'', соединяемых ребром кографа K''(ei) | Цикл на графе S'' ∪ ei | Знак цикла |
|---|---|---|---|
| 5 | 3-6 | – | цикл не создается |
| 6 | 7-1 | 1-2-7-1 | отрицательный |
| 7 | 3-5 | – | цикл не создается |
| 8 | 5-2 | – | цикл не создается |
| 10 | 4-5 | – | цикл не создается |
| 12 | 6-5 | – | цикл не создается |
Возникающая при этом неопределенность не позволяет достичь главной цели, преследовавшейся разработчиками алгоритма – добиться полного устранения отрицательных циклов в графе, а, следовательно, в структуре обратных связей искусственной нейронной сети. Можно надеяться лишь на некоторое уменьшение числа таких “плохих” циклов.
Впрочем, такие надежды могут оказаться призрачными, так как совсем не исключена ситуация, в которой замена лишь части ребер кографа парами новых ребер приведет не к уменьшению, а к увеличению числа отрицательных циклов в результирующем графе. Это означает, что обойтись исследованием множества C1 (см. раздел 4) не удается. Переход к рассмотрению множества С2 и других множеств, более высоких порядков, поможет достижению поставленной цели. Однако это серьезно увеличит количество вариантов и затруднит решение задачи. Тогда опять, как это часто бывает при разработке методики тестирования программных продуктов, придется прибегать к эмпирике. Разработчик структуры нейронной сети с помощью ее графовой модели может попытаться самостоятельно найти те ребра, замена которых на пару других ребер с промежуточной вершиной, исправит ситуацию. Как и все эмпирические методы, такая замена в каждом конкретном случае может привести к успеху, но может обернуться пустой тратой времени и ресурсов.
8. БЛАГОДАРНОСТИ
Авторы выражают благодарность Российскому Фонду Фундаментальных исследований, который поддерживает проекты № 18-07-00697-а, № 18-07-01211-а, № 19-07-00321-а, № 19-07-00493-а.
9. ЗАКЛЮЧЕНИЕ
В работе предложен алгоритм, позволяющий преобразовывать структуры искусственных нейронных сетей с обратными связями, добиваясь устранения в них циклов с отрицательными знаками. Фактически, алгоритм применим к произвольным сетям, даже к тем, в которых весовые коэффициенты изначально положительны: достаточно перейти к логарифмической шкале представления этих коэффициентов.
Целью разработки этого алгоритма было устранение циклических нестационарных решений, которые часто являются препятствием к использованию искусственных нейронных сетей для решения некоторых задач.
Выбранная авторами графовая модель при всей ее очевидности является весьма плодотворной. Применение этой модели позволяет добиться решения одной из главных задач, встающих перед разработчиками нейронных сетей, которые получают возможность выбрать структуру сети, проверить ее основные свойства, провести необходимые структурные преобразования. При этом в руках разработчика и его помощника-тестировщика появляется сам предмет отладки – структурированная сеть, в которой остается провести правильную расстановку весовых коэффициентов.
Известно, что задача реструктуризации сложных сетей достаточно трудоемка, однако, как показано в данной работе, в определенных ограничениях она решается вполне эффективно: в некоторых случаях (в сетях с симметричными межнейронными связями) достаточно проверить только линейное число циклов, в других же (в многослойном персептроне с добавлением небольшого числа обратных связей) этих циклов мало.
Авторы намерены в дальнейшем развивать выбранное ими направление исследований. В область их интересов попали такие задачи, как построение ассоциативной и долговременной памяти на структурах нейронных сетей. При обычно принятом подходе к решению задачи с помощью нейронной сети топология сети выбирается заранее. Предложенный подход к выявлению циклов может оказаться полезным при попытке строить для заданных обучающих примеров сеть с наименьшим числом межнейронных связей, решающую поставленную задачу.
Еще одним возможным направлением является создание нейросетевых архитектур, целью которых является запоминание циклических аттракторов вместо неподвижных точек. Такие архитектуры до сих пор не получили широкого распространения, и одной из причин этого является трудность анализа их динамики.
Список литературы
Cireşan D., Meier U., Masci J., Schmidhuber J. Multi-column deep neural network for traffic sign classification. Neural Networks. Selected. August 2012.
CES 2015: Nvidia Demos a Car Computer Trained with “Deep Learning”, A commercial device uses powerful image and information processing to let cars interpret 360∘ camera views, David Talbot, January 6, 2015, MIT Technology Review; Schmidt.
Roth S. Shrinkage Fields for Effective Image Restoration (PDF). IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2014.
Deng L., Yu D. Deep Learning: Methods and Applications, Foundations and Trends in Signal Processing. 2014. V. 7. № 3–4. P. 1–19.
Rosenblatt F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Spartan Books, Washington DC, 1961.
Rumelhart D.E., McClelland J.L. and the PDP research group. (editors). Parallel distributed processing: Explorations in the microstructure of cognition, Volume 1: Foundation. MIT Press, 1986.
Hopfield J.J. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences of the USA, April 1982. V. 79. № 8. P. 2554–2558.
Ackley D.H., Hinton, G.E., Sejnowski T.J. A Learning Algorithm for Boltzmann Machines. Cognitive Science. 1985. V. 9. № 1. P. 147–169.
Kohonen T. Self-Organized Formation of Topologically Correct Feature Maps. Biological Cybernetics. 1982. V. 43. № 1. P. 59–69.
Elman J.L. Finding structure in time. Cognitive science. 1990. V. 14. № 2. P. 79–211.
Lecun Y., Bottou L., Bengio Y., Haffner P. Gradient-based learning applied to document recognition Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998. V. 86. № 11. P. 2278–2324.
Graves A., Greg W., Ivo D. Neural Turing Machines, 2014, arXiv preprint arXiv.
Ritter G. X., Sussner P. An Introduction to morphological neural networks. Proceedings of 13th International Conference on Pattern Recognition (25–29 Aug. 1996, Vienna, Austria). P. 709–717.
Karpov Yu.L., Karpov, L.E., Smetanin Yu.G. Adaptation of General Concepts of Software Testing to Neural Networks, Programming and Computer Software. 2018. V. 44. № 5. P. 324–334. https://rdcu.be/7skN. Pleiades Publishing, Ltd. (Карпов Ю.Л., Карпов Л.Е., Сметанин Ю.Г. Адаптация общих концепций тестирования программного обеспечения к нейронным сетям. Программирование. 2018, № 5. С. 43–56).
ГОСТ Р 56920-2016, ГОСТ Р 56921–2016, ГОСТ Р 56922–2016. https://allgosts.ru.
ISO/IEC 29119-2013 1-5. Software testing. http://files.stroyinf.ru/Data2/1/4293754// 4293754866.pdf.
ГOCT P 12207-2010, ISO/IEC 12207:2008. http://docs.cntd.ru/document/1200082859.
IEEE 829. Standard for Software Test Documentation. IEEE 1008. Standard for Software Unit Testing. https://www.twirpx.com/file/1615980/.
ISO/МЭК 12119. Пакеты программ. Требования к качеству и тестированию. http://docs.cntd.ru/document/1200025075.
Aracena J., Demongeot J.D., Goles E. Positive and Negative Circuits in Discrete Neural Networks, IEEE Transactions on Neural Networks, Jan. 2004. V. 15. № 1.
Prim R. C. Shortest Connection Networks and Some Generalizations. Bell System Technical Journal. 1957. V. 36. № 6. P. 1389–1401.
Cormen T.H., Charles E., Leiserson C.E., Rivest R.L., Stein C. Introduction to Algorithms. Second Edition, The MIT Press, McGraw-Hill Book Company, 2002. (Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клиффорд. Алгоритмы: построение и анализ, 2-е изд. М.: Вильямс, 2005. 1296 с.).
Дополнительные материалы отсутствуют.
Инструменты
Программирование