Программирование, 2020, № 2, стр. 14-29

БИФУРКАЦИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ СИСТЕМЫ ГАМИЛЬТОНА С ДИСКРЕТНОЙ ГРУППОЙ СИММЕТРИЙ

А. Б. Батхин^a, b, *

^a Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., д. 4, Россия

^b Московский физико-технический институт (государственный университет)
141701 Московской области, г. Долгопрудный, Институтский переулок, д. 9, Россия

^* E-mail: batkhin@gmail.com

Поступила в редакцию 25.08.2019
После доработки 18.09.2019
Принята к публикации 18.09.2019

DOI: 10.31857/S0132347420020041

Полный текст (PDF)

Аннотация

Рассматривается автономная система Гамильтона с двумя степенями свободы, инвариантная относительно четверной группы Клейна линейных канонических автоморфизмов расширенного фазового пространства системы. Строится последовательность симплектических преобразований матрицы монодромии симметричного периодического решения системы. С помощью этих преобразований исследуется структура и перестройка фазового потока в окрестности этого решения. Показано, что перестройки, соответствующие кратному увеличению периода, происходят иначе для решений, обладающих двойной симметрией, чем для решений с одной симметрией. Приведен пример критических периодических решений семейства двояко симметричных орбит плоской круговой задачи Хилла. Большинство трудоемких аналитических выкладок в работе выполнены с использованием пакетов для вычисления базисов Грёбнера и работы с полиномиальными идеалами системы компьютерной алгебры Maple.

1. ВВЕДЕНИЕ

Восходящий к Пуанкаре подход к исследованию фазового потока неинтегрируемой системы обыкновенных дифференциальных уравнений состоит в поиске некоторого “скелета”, состоящего из иерархической структуры инвариантных многообразий различных размерностей. Наиболее простыми компонентами этой структуры являются положения равновесия и семейства периодических решений. Один из способов вычисления периодических решений использует метод регулярных возмущений. Он состоит в том, что в исходной системе неким образом выделяется интегрируемая подсистема, а полная система рассматривается как ее некоторое малое возмущение. Для интегрируемой подсистемы находится множество общих решений, с помощью которых с учетом возмущения вычисляются порождающие решения – предельные положения решений возмущенной задачи при стремлении возмущения к нулю.

Хорошо известно, что интегрируемость системы ОДУ связана с наличием достаточного числа первых интегралов этой системы, что, в силу теоремы Эмми Нётер, означает наличие некоторого количества непрерывных групп симметрий исходных уравнений. В общем случае возмущение интегрируемой системы разрушает часть этих групп инвариантов, превращая полную систему в неинтегрируемую. Однако зачастую в силу специфики возмущения от непрерывной группы симметрий может остаться та или иная дискретная группа. Как следствие, должны существовать решения возмущенной системы уравнений, инвариантные относительно такой группы. Например, рассматривая ограниченную задачу трех тел (ОЗТТ) при значении массового параметра $\mu $ близкого к нулю как возмущение интегрируемой задачи Кеплера вравномерно вращающейся системе координат, имеем ситуацию, при которой возмущение “разрушает” интеграл площадей, индуцированный группой $SO(1)$ поворотов конфигурационного пространства задачи, но, тем не менее, сохраняет дискретную группу порядка 2 линейных канонических преобразований расширенного фазового пространства. В следствие этого ОЗТТ обладает периодическими решениями, орбиты которых симметричны относительно оси OX. Другие примеры систем Гамильтона с различными дискретными группами симметрий см., например, в [1].

Наличие даже дискретной симметрии уравнений ОДУ часто позволяет существенно упростить процедуру поиска периодических решений. В данной работе рассматривается ситуация, когда некоторая автономная система Гамильтона с двумя степенями свободы, обладающая единственным первым интегралом, – интегралом энергии – имеет дополнительно дискретную группу линейных канонических автоморфизмов расширенного фазового пространства системы. Эта группа изоморфна четверной группе Клейна ${{K}_{4}}$, две образующие которой суть обратимые преобразования. Исследуется структура матрицы монодромии невырожденного двояко симметричного периодического решения. В критических решениях семейства рассматриваются различные сценарии ветвления семейства.

Работа состоит из введения, пяти разделов и списка литературы. В разделе 2 приведено описание представлений четверной группы Клейна и классификация решений системы Гамильтона с учетом симметрии уравнений. В разделе 3 рассматриваются особенности структуры матрицы монодромии симметричного периодического решения, а в разделе 4 рассматривается преобразование матрицы монодромии к виду, удобному для ее последующего исследования в критических случаях. Раздел 5 посвящен анализу возможных сценариев ветвления семейства двояко симметричных решений. Наконец, в разделе 6 приводится пример численного исследования семейства f₃ двояко симметричных периодических решений плоской круговой задачи Хилла и его поведения в критических решениях. Отметим, что для численного интегрирования системы Гамильтона и ее уравнений в вариациях используются пакеты TAYLOR [2] и TIDES [3], основанные на алгоритмах автоматического дифференцирования с применением системы компьютерной алгебры Wolfram Mathematica.

В работе интенсивно используются пакеты LinearAlgebra, Groebner и PolynomialIdeals системы компьютерной алгебры Maple [4] для проведения некоторых вычислений, связанных с преобразованиями симплектических матриц. Эти вычисления проводились по следующей схеме:

1) рассматривается матрица M в символьном виде;

2) строится некоторый полиномиальный идеал $\mathcal{J}$, описывающий то или иное условие на элементы матрицы M, например, симплектичность или ортогональность матрицы, существование собственного числа ±1 и т. п.;

3) вычисляется базис Грёбнера $\mathcal{G}\mathcal{B}\mathcal{J}$ этого идеала для соответствующего лексикографического порядка;

4) выполняются полилинейные преобразования матрицы M, после чего полиномиальные элементы новой матрицы приводятся к канонической форме по модулю идеала $\mathcal{G}\mathcal{B}\mathcal{J}$.

Такого рода вычисления можно выполнить в любой системе компьютерной алгебры, позволяющей вычислять базис Грёбнера, например в открытой системе SymPy [5] или проприетарных Maplesoft Maple или Wolfram Mathematica [6].

Предварительные результаты работы докладывались на международных конференциях: Polynomial Computer Algebra’2019, 15–20 апреля в Санкт-Петербурге [7], Computer Algebra, 17–21 июня в Москве [8] и опубликованы в препринте [9].

2. ДИСКРЕТНАЯ ГРУППА АВТОМОРФИЗМОВ СИСТЕМЫ ГАМИЛЬТОНА

Рассмотрим автономную систему Гамильтона с двумя степенями свободы с гамильтонианом $H({\mathbf{z}})$ в случае общего положения, где ${\mathbf{z}} = ({\mathbf{x}},{\mathbf{y}})$ – вектор фазового пространства $\mathbb{M} \equiv {{\mathbb{R}}^{4}}$, т.е. система канонических уравнений

(2.1)

${\mathbf{\dot {z}}} = {\mathbf{J}}H({\mathbf{z}}),\quad {\mathbf{J}} = \left( {\begin{array}{*{20}{c}} 0&{{{{\mathbf{E}}}^{2}}} \\ { - {{{\mathbf{E}}}^{2}}}&0 \end{array}} \right),$

имеет единственный первый интеграл

(2.2)

$H({\mathbf{z}}) = h.$

Положим, что система (2.1) инвариантна относительно конечной группы линейных канонических автоморфизмов расширенного фазового пространства $\tilde {\mathbb{M}} \equiv \mathbb{R} \times \mathbb{M}$, изоморфной четверной группе Клейна V₄.

Четверная группа Клейна V₄ (или диэдральная группа ${{D}_{2}} \cong {{\mathbb{Z}}_{2}} \otimes {{\mathbb{Z}}_{2}}$) – это группа порядка 4, являющаяся наименьшей нециклической абелевой группой, а также 2-примарной абелевой группой. Она задается либо соотношениями

(2.3)

$\langle g_{1}^{2} = g_{2}^{2} = {{({{g}_{1}} \circ {{g}_{2}})}^{2}} = id\rangle ,$

где ${{g}_{{1,2}}}$ – два генератора группы, либо соотношениями

$\langle {{r}^{2}} = {{s}^{2}} = id,{{s}^{{ - 1}}} \circ r \circ s = {{r}^{{ - 1}}}\rangle ,$

где $r$ – поворот, а $s$ – симметрия. Известно, что любую группу диэдра ${{D}_{n}}$ можно представить как группу линейных преобразований плоскости, состоящей из $n$-операторов поворота ${{r}_{k}}$, k = 0, ..., $n - 1$, на угол $2\pi k{\text{/}}n$, и n-операторов симметрии ${{s}_{k}}$, $k = 0, \ldots ,n - 1$, относительно прямой, составляющей угол $\pi k{\text{/}}n$ с осью абсцисс. Для ${{D}_{2}}$ выберем два генератора ${{g}_{1}} \cong {{s}_{0}}$ и ${{g}_{2}} \cong {{s}_{1}}$, тогда g₃ = ${{g}_{1}} \circ {{g}_{2}}$ = = ${{g}_{2}} \circ {{g}_{1}}$ = r₁. Для конфигурационного пространства ${{\mathbb{R}}^{2}}$ автоморфизмы ${{g}_{1}}$ и ${{g}_{2}}$ задаются соответственно матрицами ${{{\mathbf{S}}}_{0}} = \{ 1, - 1\} $ и ${{{\mathbf{S}}}_{1}} = \{ - 1,1\} $. Следовательно, с учетом того, что автоморфизмы ${{g}_{{1,2}}}$ обращают время, в расширенном фазовом пространстве $\mathbb{M}$ они имеют вид

$\begin{gathered} {{g}_{1}}:(t,{\mathbf{z}}) \to ( - t,{{{\mathbf{G}}}_{1}}{\mathbf{z}}),\quad {{{\mathbf{G}}}_{1}} = \{ + 1, - 1, - 1, + 1\} , \\ {{g}_{2}}:(t,{\mathbf{z}}) \to ( - t,{{{\mathbf{G}}}_{2}}{\mathbf{z}}),\quad {{{\mathbf{G}}}_{2}} = \{ - 1, + 1, + 1, - 1\} . \\ \end{gathered} $

Автоморфизм g₃ в этом случае является центральной симметрией фазового пространства $\mathbb{M}$:

${{g}_{3}}:(t,{\mathbf{z}}) \to (t,{{{\mathbf{G}}}_{3}}{\mathbf{z}}),\quad {{{\mathbf{G}}}_{3}} = \{ - 1, - 1, - 1, - 1\} .$

Итак, каждый из автоморфизмов ${{g}_{i}}$, $i = 1,2,3$ в силу соотношений (2.3), является инволюцией, но при этом преобразования ${{g}_{1}}$ и ${{g}_{2}}$, в свою очередь, будут обратимыми, поскольку

$\frac{d}{{dt}}{{g}_{i}}({\mathbf{z}}) = - {\mathbf{J}}{\text{grad}}H({{g}_{i}}({\mathbf{z}})),\quad i = 1,2.$

Инвариантные множества ${{\Sigma }_{{1,2}}} \equiv \{ {\mathbf{z}}{\text{|}}{{g}_{{1,2}}}({\mathbf{z}}) = {\mathbf{z}}\} $ преобразований ${{g}_{{1,2}}}$ являются двумерными координатными плоскостями – плоскостями симметрии преобразований

(2.4)

${{\Sigma }_{1}}:\{ {{x}_{2}} = {{y}_{1}} = 0\} ,\quad {{\Sigma }_{2}}:\{ {{x}_{1}} = {{y}_{2}} = 0\} .$

Инвариантное множество преобразования ${{g}_{3}}$ состоит из одной точки – начала координат.

Определение 1 ([10]). Пусть ${\mathbf{o}}({{{\mathbf{z}}}_{0}})$ – орбита системы (2.1):

${\mathbf{o}}({{{\mathbf{z}}}_{0}}) = \{ z(t,{{z}_{0}}){\text{|}}t \in \mathbb{R}\} .$

Тогда орбита ${\mathbf{o}}({{{\mathbf{z}}}_{0}})$ называется $g$-симметричной, если она является инвариантным множеством преобразования $g$: $g({\mathbf{o}}({{{\mathbf{z}}}_{0}})) = {\mathbf{o}}({{{\mathbf{z}}}_{0}})$.

Теорема 1 ([10]). Пусть ${\mathbf{o}}({{{\mathbf{z}}}_{0}})$ – орбита системы (2.1) с обратимой симметрией g. Тогда

(1) орбита ${\mathbf{o}}({{{\mathbf{z}}}_{0}})$ является g-симметричной тогда и только тогда, когда она пересекает соответствующее инвариантное множество

$\Sigma (g) = \{ {\mathbf{z}}{\text{|}}g({\mathbf{z}}) = {\mathbf{z}}\} .$

При этом орбита пересекает $\Sigma (g)$ не более чем в двух точках и целиком содержится в $\Sigma ({{g}^{2}})$.

(2) орбита ${\mathbf{o}}({{{\mathbf{z}}}_{0}})$ пересекает $\Sigma (g)$ в точности в двух точках тогда и только тогда, когда она – орбита периодического решения (но не положения равновесия) и симметрична относительно автоморфизма g.

Каждое решение ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$ системы (2.1) с начальным условием ${\mathbf{z}}(0) = {{{\mathbf{z}}}_{0}}$ принадлежит к одному из следующих классов в зависимости от типа симметрии.

• Несимметричные решения, фазовые траектории которых неинвариантны относительно любого из преобразований ${{g}_{i}}$, $i = 1,2,3$.

• Однократно симметричные решения, фазовые траектории которых инвариантны лишь относительно какого-либо одного преобразования ${{g}_{i}}$, $i = 1,2,3$.

• Двояко симметричные решения, фазовые траектории которых инвариантны относительно любого из преобразований ${{g}_{i}}$, $i = 1,2,3$.

Заметим, что если решение ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$ симметрично относительно двух обратимых автоморфизмов ${{g}_{1}}$ и ${{g}_{2}}$, то оно симметрично относительно преобразования центральной симметрии ${{g}_{3}}$. Обратное, вообще говоря, неверно, т.е. среди однократно симметричных решений следует выделять обратимо симметричные и центрально симметричные.

Пусть ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$ – периодическое решение с периодом $T > 0$, т.е. решение удовлетворяющее условию периодичности для любого $t$:

${\mathbf{z}}(t + T,{{{\mathbf{z}}}_{0}}) = {\mathbf{z}}(t,{{{\mathbf{z}}}_{0}}).$

Периодические решения автономной системы Гамильтона не являются изолированными, а образуют семейства (см. [11, Lemma 6.4.1]). Размерности этих семейств равны числу независимых первых интегралов системы Гамильтона. Для автономной неинтегрируемой системы Гамильтона семейства периодических решений являются обычно однопараметрическими, где параметром может служить значение, например, величина $h$ интеграла (2.2). Итак, каждое семейство периодических решений описывается парой функций ${{{\mathbf{z}}}_{0}}(\lambda )$ и $T(\lambda )$, где $\lambda $ – параметр семейства. Здесь, следуя [12, п. 2.5], под $T(\lambda {\text{*}})$ понимается не минимальный период конкретного решения, соответствующего значению параметра $\lambda {\text{*}}$ на семействе, а предел минимальных периодов решений семейства при стремлении $\lambda \to \lambda {\text{*}}$. Это позволяет рассматривать функцию $T(\lambda )$ как непрерывную функцию параметра $\lambda $ даже для ситуаций, когда одно семейство пересекает другое с решениями кратных периодов.

Как известно (см., например, [13]), семейства периодических решений могут быть либо замкнутыми, либо натурально ограниченными, когда одна или более количественных характеристик решения – наибольшее расстояние от орбиты до начала координат, значение интеграла $h$ или периода $T$ – неограниченно возрастают. При продолжении семейства по параметру $\lambda $ эти и другие характеристики (например, индекс устойчивости $S$) периодического решения меняются гладко вдоль семейства, в то время как симметрия решения является глобальным инвариантом семейства. Семейство решений может пересекаться с другим семейством, но оно всегда может быть единственным образом продолжено через точку пересечения.

3. ФАЗОВЫЙ ПОТОК СИСТЕМЫ ГАМИЛЬТОНА ВБЛИЗИ ПЕРИОДИЧЕСКОГО РЕШЕНИЯ

3.1. Свойства фазового потока

Динамика фазового потока $\Phi (t)$ в окрестности решения ${\mathbf{z}}(t)$ описывается матрицей ${\mathbf{Z}}(t,{\mathbf{z}})$, которая есть решение задачи Коши уравнения в вариациях Пуанкаре

(3.1)

${\mathbf{\dot {Z}}} = {\mathbf{J}}{\text{Hess}}H({\mathbf{z}}){\mathbf{Z}},\quad {\mathbf{Z}}(0) = {{{\mathbf{Z}}}_{0}},\quad {\text{rang}}{{{\mathbf{Z}}}_{0}} = 4,$

где ${\text{Hess}}H({\mathbf{z}})$ – гессиан функции $H({\mathbf{z}})$, вычисляемый вдоль решения ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$. Решение ${\mathbf{Z}}(t,{{{\mathbf{Z}}}_{0}})$ называется матрицантом и, если матрица ${{{\mathbf{Z}}}_{0}}$ симплектическая, т.е. удовлетворяет матричному тождеству

(3.2)

${\mathbf{Z}}_{0}^{{\text{t}}}{\mathbf{J}}{{{\mathbf{Z}}}_{0}} = {\mathbf{J}},$

то такой же будет и матрицант ${\mathbf{Z}}(t)$ для любого $t$ [14, Гл. II, п. 3.4].

Здесь и далее значок $^{{\text{t}}}$ означает операцию транспонирования матрицы или вектора.

Определение 2. Матрицей монодромии периодического решения $({{{\mathbf{Z}}}_{0}},T)$ называется матрица M = = ${\mathbf{Z}}_{0}^{{ - 1}} \cdot {\mathbf{Z}}(T,{{{\mathbf{Z}}}_{0}})$, а ее собственные числа ${{\rho }_{i}}$, i = $1, \ldots ,4$, называются мультипликаторами.

В дальнейшем, если не оговорено противное, будем считать, что ${{{\mathbf{Z}}}_{0}} \equiv {{{\mathbf{E}}}^{4}}$, т.е. матрица ${\mathbf{Z}}(t,{{{\mathbf{Z}}}_{0}})$ есть нормированная фундаментальная матрица системы в вариациях (3.1).

Приведем здесь основные свойства матрицы монодромии M, которые будут использоваться в дальнейшем.

1) Пусть ${\mathbf{Z}}(t)$ – фундаментальная матрица системы (3.1), тогда

(3.3)

${\mathbf{Z}}(t + T) = {\mathbf{Z}}(t){\mathbf{M}}.$

2) В силу симплектичности матрицы M ее характеристический многочлен ${{P}_{\lambda }}({\mathbf{M}})$ возвратный [15]. Для симплектической матрицы M обратная к ней вычисляется по формуле

(3.4)

${{{\mathbf{M}}}^{{ - 1}}} = {{{\mathbf{J}}}^{{\text{t}}}}{{{\mathbf{M}}}^{{\text{t}}}}{\mathbf{J}} = - {\mathbf{J}}{{{\mathbf{M}}}^{{\text{t}}}}{\mathbf{J}}.$

3) В силу вещественности системы (3.1) и симплектичности M ее мультипликаторы попарно взаимно комплексно-сопряженные и взаимно обратные.

4) Вектор-столбец фазовой скорости v₀≡ ≡ ${\mathbf{J}}{\text{grad}}H({{{\mathbf{z}}}_{0}})$ является правым собственным вектором матрицы M с соответствующим мультипликатором ${{\rho }_{1}} = + 1$ [11, Lemma 6.4.1]. Это следует непосредственно из дифференцирования по t тождества, задающего групповую структуру z(τ, z(t, z₀)) = = ${\mathbf{z}}(\tau + t,{{{\mathbf{z}}}_{0}})$, при подстановке в него значений $\tau = T$ и $t = 0$:

${\mathbf{M}} \cdot {\mathbf{\dot {z}}}(T) = {\mathbf{M}} \cdot {{{\mathbf{v}}}_{0}} = {{{\mathbf{v}}}_{0}}.$

5) Мультипликатор ${{\rho }_{1}} = {{\rho }_{2}} = + 1$ имеет алгебраическую кратность 2.

6) Поскольку система (2.1) автономна и обладает первым интегралом (2.2), то, дифференцируя по ${{{\mathbf{z}}}_{0}}$ тождество $H({\mathbf{z}}(T,{{{\mathbf{z}}}_{0}})) = H({{{\mathbf{z}}}_{0}})$, получим, что вектор-строка ${{{\mathbf{\tilde {v}}}}_{1}} \equiv {\text{grad}}H({{{\mathbf{z}}}_{0}})$ является левым собственным вектором матрицы монодромии ${\mathbf{M}}$ [11, Lemma 6.5.1]:

${\text{grad}}H({{{\mathbf{z}}}_{0}}){\mathbf{M}} = H({{{\mathbf{z}}}_{0}}).$

7) Характеристический многочлен ${{P}_{\lambda }}({\mathbf{M}})$ матрицы монодромии ${\mathbf{M}}$ раскладывается на множители

${{P}_{\lambda }}({\mathbf{M}}) = {{(\lambda - 1)}^{2}}({{\lambda }^{2}} - 2S\lambda + 1),$

где

(3.5)

$S = {\text{Tr}}{\mathbf{M}}{\text{/}}2 - 1$

– индекс устойчивости периодического решения $({{{\mathbf{z}}}_{0}},T)$.

Величина $S$ позволяет определить характер устойчивости периодического решения в линейном приближении. А именно,

• если ${\text{|}}S{\text{|}} > 1$, то ${{\rho }_{{3,4}}} \in \mathbb{R}$, ${{\rho }_{3}} = 1{\text{/}}{{\rho }_{4}}$ и решение ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$ неустойчиво;

• если ${\text{|}}S{\text{|}} < 1$, то ${{\rho }_{3}} = {{\bar {\rho }}_{4}}$, ${\text{|}}{{\rho }_{3}}{\text{|}} = {\text{|}}{{\rho }_{4}}{\text{|}} = 1$ и решение ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$ орбитально устойчиво;

• критический случай |S| = 1 требует дополнительного исследования.

Особо интересен случай, когда индекс устойчивости $S = cos(2\pi p{\text{/}}q)$, где $p,q \in \mathbb{N}$. Его впервые рассмотрел А. Пуанкаре в своем знаменитом трактате Les méthods nouvelles de la méchanique céleste [16, Гл. XXX]. Этот случай соответствует появлению в окрестности исходного периодического решения так называемых периодических решений второго рода по Пуанкаре с периодом $T{\kern 1pt} ' = qT$.

3.2. Вычисление матрицы монодромии

В общем случае вычисление матрицы монодромии ${\mathbf{M}}$ требует одновременного интегрирования двух систем уравнений: исходной системы (2.1), дающей интегральную кривую ${\mathbf{Z}}(t,{{{\mathbf{Z}}}_{0}})$, и системы уравнений в вариациях (3.1) для четырех начальных условий. Как отмечено в [17], подставляя в (3.3) значение $t = - T{\text{/}}2$, получим Z(T/2) = = ${\mathbf{Z}}( - T{\text{/}}2){\mathbf{M}}$, откуда

${\mathbf{M}} = {{{\mathbf{Z}}}^{{ - 1}}}( - T{\text{/}}2){\mathbf{Z}}(T{\text{/}}2) = - {\mathbf{J}}{{{\mathbf{Z}}}^{{\text{t}}}}( - T{\text{/}}2){\mathbf{JZ}}(T{\text{/}}2).$

При этом матрицы ${\mathbf{Z}}( - T{\text{/}}2)$ и ${\mathbf{Z}}(T{\text{/}}2)$ можно вычислять параллельно. Численное интегрирование систем (2.1) и (3.1) на половине периода дает более точные результаты, чем интегрирование на всем периоде, особенно для сильно неустойчивых решений.

Рассмотрим вычисление матрицы монодромии симметричного периодического решения. Если периодическое решение симметрично относительно обратимого преобразования ${{g}_{i}}$, $i = 1,2$, то, согласно теореме 1, начальное условие ${{{\mathbf{z}}}_{0}}$ можно выбрать на инвариантном множестве $\Sigma ({{g}_{i}})$, и тогда через полпериода ${\mathbf{z}}(T{\text{/}}2,{{{\mathbf{z}}}_{0}}) \in \Sigma ({{g}_{i}})$. Инвариантность системы (2.1) относительно ${{g}_{i}}$ означает инвариантность гамильтониана $H({\mathbf{z}})$ и равносильна матричному тождеству

${\text{Hess}}H({\mathbf{z}}( - t)) = {\mathbf{J}}{{{\mathbf{G}}}_{i}}{\mathbf{J}}{\text{Hess}}H({\mathbf{z}}(t)){\mathbf{G}}_{i}^{{ - 1}},\quad i = 1,2.$

Это означает, что для системы (2.1) выполнено условие $t$-инвариантности [14], а матрицы ${\mathbf{Z}}( - t)$ и ${\mathbf{Z}}(t)$ для таких систем связаны соотношением Z(–t) = = ${\mathbf{G}}_{i}^{{ - 1}}{\mathbf{Z}}(t){{{\mathbf{G}}}_{i}}$, в частности, Z(–T/2) = ${\mathbf{G}}_{i}^{{ - 1}}{\mathbf{Z}}(T{\text{/}}2){{{\mathbf{G}}}_{i}}$.

Так как матрица ${\mathbf{Z}}( - T{\text{/}}2)$ симплектическая, то с учетом формулы (3.4) получаем матрицу монодромии ${{{\mathbf{M}}}_{1}}$, вычисленную от точки ${{{\mathbf{z}}}_{0}}$,

(3.6)

${{{\mathbf{M}}}_{1}} = {{{\mathbf{\tilde {G}}}}_{i}}{{{\mathbf{Z}}}^{{\text{t}}}}(T{\text{/}}2){{{\mathbf{\tilde {G}}}}_{i}}{\mathbf{Z}}(T{\text{/}}2),$

где ${{{\mathbf{\tilde {G}}}}_{i}} = {{{\mathbf{G}}}_{i}}{\mathbf{J}}$, ${\mathbf{\tilde {G}}}_{i}^{{ - {\text{1}}}} = {\mathbf{\tilde {G}}}_{i}^{{\text{t}}} = {{{\mathbf{\tilde {G}}}}_{i}}$. Нетрудно получить матрицу монодромии ${{{\mathbf{M}}}_{2}}$, вычисленную от точки ${\mathbf{z}}(T{\text{/}}2)$

(3.7)

${{{\mathbf{M}}}_{2}} = {\mathbf{Z}}(T{\text{/}}2){{{\mathbf{\tilde {G}}}}_{i}}{{{\mathbf{Z}}}^{{\text{t}}}}(T{\text{/}}2){{{\mathbf{\tilde {G}}}}_{i}}.$

Вычисление матриц монодромии ${{{\mathbf{M}}}_{1}},\;{{{\mathbf{M}}}_{2}}$ по формулам (3.6) и (3.7) соответственно предпочтительнее по следующим соображениям. Во-первых, интегрирование системы (3.1) на половине периода требует меньших вычислительных затрат и дает более точные результаты. Во-вторых, в случае бифуркации потери симметрии (см. подраздел 1) требуется информация о структуре матрицы монодромии как в точке z(0), так и в точке ${\mathbf{z}}(T{\text{/}}2)$.

Воспользуемся этими соображениями для выявления свойств матрицы монодромии двояко симметричного периодического решения. Тогда для ее вычисления достаточно знать решение системы (3.1) на четверти периода ${\mathbf{Z}}(T{\text{/}}4)$. Действительно, пусть начальная точка ${{{\mathbf{z}}}_{0}}$ дважды симметричной орбиты расположена на множестве ${{\Sigma }_{1}}$, тогда через четверть периода ${\mathbf{Z}}(T{\text{/}}4) \in {{\Sigma }_{2}}$. Обозначим через ${{{\mathbf{Z}}}_{1}}(T{\text{/}}4)$ решение системы (3.1), соответствующее начальной точке z(0), а через ${{{\mathbf{Z}}}_{2}}(T{\text{/}}4)$ – решение, соответствующее начальной точке ${\mathbf{z}}(T{\text{/}}4)$. Согласно групповому свойству решений имеем ${{{\mathbf{Z}}}_{1}}(T{\text{/}}2) = {{{\mathbf{Z}}}_{2}}(T{\text{/}}4){{{\mathbf{Z}}}_{1}}(T{\text{/}}4)$. С другой стороны, в силу свойства $t$-инвариантности уравнения в вариациях относительно преобразования ${{g}_{2}}$, имеем

$\begin{gathered} {{{\mathbf{Z}}}_{2}}( - T{\text{/}}4) = {\mathbf{G}}_{2}^{{ - 1}}{{{\mathbf{Z}}}_{2}}(T{\text{/}}4){{{\mathbf{G}}}_{2}} \Rightarrow \\ \, \Rightarrow {{{\mathbf{Z}}}_{2}}(T{\text{/}}4) = {{{\mathbf{G}}}_{2}}{{{\mathbf{Z}}}_{2}}( - T{\text{/}}4){\mathbf{G}}_{2}^{{ - 1}}. \\ \end{gathered} $

Используя тот факт, что Z₂(–T/4) = ${\mathbf{Z}}_{1}^{{ - 1}}(T{\text{/}}4)$ = = $ - {\mathbf{JZ}}_{1}^{{\text{t}}}(T{\text{/}}4){\mathbf{J}}$, получаем для ${{{\mathbf{Z}}}_{1}}(T{\text{/}}2)$ выражение

${{{\mathbf{Z}}}_{1}}(T{\text{/}}2) = {{{\mathbf{\tilde {G}}}}_{1}}{\mathbf{Z}}_{1}^{{\text{t}}}(T{\text{/}}4){{{\mathbf{\tilde {G}}}}_{2}}{{{\mathbf{Z}}}_{1}}(T{\text{/}}4).$

Применяя $t$-инвариантность системы (3.1) относительно преобразования ${{g}_{1}}$, в итоге получим формулы для матриц монодромии ${{{\mathbf{M}}}_{1}}$ и ${{{\mathbf{M}}}_{2}}$

(3.8)

$\begin{gathered} {{{\mathbf{M}}}_{1}} = {{[{{{{\mathbf{\tilde {G}}}}}_{1}}{\mathbf{Z}}_{1}^{{\text{t}}}(T{\text{/}}4){{{{\mathbf{\tilde {G}}}}}_{3}}{{{\mathbf{Z}}}_{1}}(T{\text{/}}4)]}^{2}}, \\ {{{\mathbf{M}}}_{2}} = {{[{{{\mathbf{Z}}}_{1}}(T{\text{/}}4){{{{\mathbf{\tilde {G}}}}}_{1}}{\mathbf{Z}}_{1}^{{\text{t}}}(T{\text{/}}4){{{{\mathbf{\tilde {G}}}}}_{2}}]}^{2}}. \\ \end{gathered} $

Непосредственными вычислениями убеждаемся в том, что для двояко симметричного периодического решения матрицы монодромии, вычисленные в точках ${\mathbf{z}}(0)$ и ${\mathbf{z}}(T{\text{/}}2)$, а также в точках ${\mathbf{z}}(T{\text{/}}4)$ и ${\mathbf{z}}(3T{\text{/}}4)$, попарно равны.

Наконец, рассмотрим случай ${{g}_{3}}$-инвариантных периодических решений. Пусть ${{{\mathbf{z}}}_{0}}$ – начальная точка такого решения, тогда нетрудно видеть, что ${{{\mathbf{z}}}_{1}} \equiv {\mathbf{z}}(T{\text{/}}2,{{{\mathbf{z}}}_{0}}) = - {{{\mathbf{z}}}_{0}}$. В силу симметрии векторы фазовой скорости, вычисленные в точках ${{{\mathbf{z}}}_{0}}$ и ${{{\mathbf{z}}}_{1}}$, будут равны по абсолютной величине и противоположны по направлению. Следовательно, вектор ${{{\mathbf{v}}}_{0}}$ является собственным вектором матрицы ${\mathbf{Z}}(T{\text{/}}2$, z₀) и ему соответствует собственное число –1. Матрица монодромии в этом случае есть

(3.9)

${\mathbf{M}} = {{{\mathbf{Z}}}^{2}}(T{\text{/}}2,{{{\mathbf{z}}}_{0}}).$

Этот факт будет использован в дальнейшем при исследовании удвоения периода двояко симметричных периодических решений.

Особая структура матрицы монодромии обратимо-симметричного периодического решения приводит к наличию некоторой внутренней симметрии матрицы $M$:

(3.10)

$\begin{gathered} {{m}_{{33}}} = {{m}_{{11}}},\quad {{m}_{{44}}} = {{m}_{{22}}},\quad {{m}_{{43}}} = - {{m}_{{12}}}, \\ {{m}_{{23}}} = - {{m}_{{14}}},\quad {{m}_{{34}}} = - {{m}_{{21}}},\quad {{m}_{{41}}} = - {{m}_{{32}}}. \\ \end{gathered} $

Заметим, что наличие двух симметрий у периодического решения не добавляет дополнительных связей к равенствам (3.10).

Величина индекса устойчивости $S$ центрально симметричного периодического решения ограничена снизу значением –1. Это следует непосредственно из формул (3.8) или (3.9) и того, что след матрицы ${\mathbf{M}}$ такого решения равен сумме квадратов собственных чисел вещественной матрицы ${\mathbf{Z}}(T{\text{/}}2,{{{\mathbf{z}}}_{0}})$, т.е., является неотрицательной величиной, а значение $S$ вычисляется по формуле (3.5).

4. ПРОДОЛЖЕНИЕ СЕМЕЙСТВА ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

Процедура вычисления семейства периодического решения обычно строится по предикторно-корректорной схеме. Вначале предиктор находит малые поправки $\delta {\mathbf{z}}$ и $\delta T$ к начальным условиям и периоду, а затем корректор уточняет поправки и в случае успеха получает новое периодическое решение семейства.

Пусть известно некоторое невырожденное периодическое решение ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$ семейства с начальным условием и периодом $({{{\mathbf{z}}}_{0}},T)$, тогда вблизи него должно быть периодическое решение z(t) + $\delta {\mathbf{z}}(t)$ с периодом $T + \delta T$. Раскладывая левую часть условия периодичности ${\mathbf{z}}(T + \delta T,{{{\mathbf{z}}}_{0}} + \delta {\mathbf{z}})$ = z₀ + δz в ряд Тейлора, оставляя в разложении члены не выше первого порядка малости по $\delta {\mathbf{z}}$ и $\delta T$, получаем, что малые добавки $\delta {\mathbf{z}}$ и $\delta T$ должны удовлетворять линейной однородной системе

(4.1)

$({\mathbf{M}} - {\mathbf{E}})\delta {\mathbf{z}}(T) + {{{\mathbf{v}}}_{1}}\delta T = 0,$

где ${{{\mathbf{v}}}_{1}} = {\mathbf{J}}{\text{grad}}H({\mathbf{z}}(T,{{{\mathbf{z}}}_{0}}))$. Множество решений этой системы определяется структурой матрицы монодромии ${\mathbf{M}}$.

Для обратимых симметричных периодических решений (которые рассматриваются в данной работе) вместо системы (4.1) удобнее продолжать однопараметрическое семейство по другой схеме – схеме продолжения по длине дуги [18, Гл. 5]. Выбирая начальное приближение симметричного решения на инвариантном множестве ${{\Sigma }_{b}}$, $b = 1,2$, в силу теоремы 1 условие периодичности эквивалентно условию равенства нулю отображения

${\mathbf{g}}:{{\mathbb{R}}^{3}} \to {{\mathbb{R}}^{2}}:\xi \mapsto {\mathbf{g}}(\xi ),$

где $\xi = (z_{0}^{j},z_{0}^{k},\tau )$, ${\mathbf{g}}(\xi ) = {{({{z}_{l}}(\tau ,z_{0}^{j},z_{0}^{k}),{{z}_{m}}(\tau ,z_{0}^{j},z_{0}^{k}))}^{{\text{t}}}}$. Величина $\tau $ равна T/2 для однократно и T/4 для двояко симметричного решения, а индексы j, k, $l,\;m$ выбираются так, чтобы пара $j,\;k$ соответствовала ненулевым компонентам вектора начального условия ${{{\mathbf{z}}}_{0}} \in {{\Sigma }_{b}}$, а пара l, m – нулевым компонентам вектора ${\mathbf{g}} \in {{\Sigma }_{e}}$, $e = 1,2$, согласно формулам (2.4). Тогда решая однородную систему $D{\mathbf{g}}(\xi )\delta \xi $ = 0 по формулам

$\frac{{\delta {{\xi }_{1}}}}{{{{D}_{1}}}} = \frac{{\delta {{\xi }_{2}}}}{{{{D}_{2}}}} = \frac{{\delta {{\xi }_{3}}}}{{{{D}_{3}}}},$

где ${{D}_{i}}$ – определитель матрицы Якоби $D{\mathbf{g}}(\xi )$ с удаленным $i$-м столбцом, взятый со знаком ${{( - 1)}^{i}}$, находим поправки $\delta \xi $ в виде

$\delta {{\xi }_{i}} = {{D}_{i}}\Delta s,\quad {{\tilde {D}}_{i}} = {{D}_{i}}{\text{/}}\sqrt {D_{1}^{2} + D_{2}^{2} + D_{3}^{2}} .$

Шаг смещения $\Delta s$ вдоль семейства выбирается таким образом, чтобы обеспечить сходимость корректора.

Когда найдены поправки $\delta \xi $ первого порядка применяется корректор, который обычно реализуется в виде итерационной процедуры по модифицированной схеме Ньютона. Пусть ${{\xi }^{{(0)}}}$ – вычисленное на шаге предиктора приближенное начальное условие периодического решения, тогда итерационная схема имеет вид

${{\xi }^{{(k + 1)}}} = {{\xi }^{{(k)}}} - {{[D{\mathbf{g}}({{\xi }^{{(k)}}})]}^{ + }}{\mathbf{g}}({{\xi }^{{(k)}}}),$

где знаком $^{ + }$ обозначена псевдообратная матрица [19, Гл. 1, § 5] матрицы Якоби $D{\mathbf{g}}(\xi )$ размера $2 \times 3$, состоящей из соответствующих компонентов матрицанта ${\mathbf{Z}}(\tau )$ и компонентов вектора фазовой скорости ${\mathbf{v}}(\tau )$. Псевдообратная матрица ${{{\mathbf{A}}}^{ + }}$ матрицы ${\mathbf{A}}$ размера $m \times n$, $m > n$, может быть вычислена по формуле

${{{\mathbf{A}}}^{ + }} = {{{\mathbf{A}}}^{{\text{t}}}}{{({\mathbf{A}} \cdot {{{\mathbf{A}}}^{{\text{t}}}})}^{{ - 1}}}$

при условии, что ${\text{rang}}{\mathbf{A}} = n$.

Описанная схема продолжения семейства по длине дуги обладает тем преимуществом, что позволяет проходить “складки”, т.е. когда одна из величин ${{\xi }_{i}}$, $i = 1,2,3$, достигает экстремального значения.

Покажем, что собственному числу +1 матрица монодромии M невырожденного периодического решения $({{{\mathbf{z}}}_{0}},T)$ автономной неинтегрируемой системы Гамильтона соответствует жорданова клетка второго порядка.

Определение 3. Периодическое решение $({{{\mathbf{z}}}_{0}},T)$ автономной неинтегрируемой системы Гамильтона (2.1) называется невырожденным или простым, если ее матрица монодромии ${\mathbf{M}}$ имеет единственный элементарный делитель ${{(\lambda - 1)}^{2}}$, соответствующий мультипликатору ${{\rho }_{{1,2}}} = 1$, а все остальные элементарные делители просты.

Действительно, в случае общего положения, т.е. когда периодическое решение невырождено, согласно [11, Ch. 6. Theorem 6.5.1], оно (решение) лежит на гладкой двумерной цилиндрической поверхности периодических решений, образующая которой параметризуется значением интеграла $H({\mathbf{z}})$. Из этой теоремы следует, что размерность пространства решений системы (4.1) равна двум и, следовательно, ранг матрицы $(\begin{array}{*{20}{c}} {{\mathbf{M}} - {\mathbf{E}}}& \vdots &{{{{\mathbf{v}}}_{0}}} \end{array})$ системы (4.1) должен быть равен трем. Очевидно, что если у некоторой матрицы M размера $n \times n$ собственное число $\lambda $ полупростое и имеет кратность $k$, то ${\text{rang}}({\mathbf{M}} - \lambda {\mathbf{E}}) = n - k$. Следовательно, собственное число +1 кратности 2 не является полупростым и ему соответствует жорданова клетка размера $2 \times 2$. Эти же рассуждения верны и для произвольной автономной системы Гамильтона с $n$ степенями свободы.

Утверждение 1. Матрица монодромии M невырожденного периодического решения автономной неинтегрируемой системы Гамильтона в случае общего положения, т.е. когда имеется единственный первый интеграл $H({\mathbf{z}}) = h$, всегда имеет жорданову клетку второго порядка, соответствующую собственному числу +1 кратности 2.

Анализ решений системы (4.1) удобнее проводить в том базисе, в котором матрица M имеет наиболее простую форму, т.е. нормальную форму. Классификация всех нормальных форм постоянных канонических матриц была дана еще Вильямсоном в1937 году (см. [20, 21, Гл. II]), однако здесь воспользуемся несколько иным подходом. Этот подход основан на идее перехода к некоторому сопутствующему ортонормированному базису, в котором один орт – это касательный вектор к фазовой траектории, а другой – нормаль к изоэнергетической поверхности $H({\mathbf{z}})$ = h.

4.1. Преобразования матрицы монодромии M

Выполним линейное преобразование матрицы M, упрощающее ее структуру и облегчающее ее анализ. Потребуем, чтобы матрица A этого преобразования принадлежала группе Sp(4, $\mathbb{R}) \cap SO(4,\mathbb{R})$, т.е. была одновременно и симплектической и ортогональной. Дополнительным условием должно быть сохранение внутренней симметрии (3.10) для обратимых симметричных периодических решений.

Как указано в [22], задача построения такой матрицы A эквивалентна проблеме построения невырожденного непрерывного касательного векторного поля на сфере ${{S}^{3}}$. Как известно, для ${{S}^{3}}$ это возможно, следовательно, такое преобразование всегда существует.

Условие симплектичности матрицы A выполнено, если ее столбцы ${{{\mathbf{a}}}_{i}}$ удовлетворяют условиям ${{{\mathbf{a}}}_{{i + 2}}} = - {\mathbf{J}}{{{\mathbf{a}}}_{i}}$, $i = 1,2$ и $\left| {{{{\mathbf{a}}}_{j}}} \right| = 1$, $j = 1, \ldots ,4$. Условие ортогональности матрицы ${\mathbf{A}}$ записывается в виде $({{{\mathbf{a}}}_{i}},{{{\mathbf{a}}}_{j}}) = {{\delta }_{{ij}}}$, $i,j = 1, \ldots ,4$, ${{\delta }_{{ij}}}$ – символ Кронекера. Столбцы ${{{\mathbf{a}}}_{1}}$ и ${{{\mathbf{a}}}_{3}}$, как указано выше, определены как нормированные векторы фазовой скорости и градиента первого интеграла соответственно. Остается найти компоненты столбца ${{{\mathbf{a}}}_{2}}$ или ${{{\mathbf{a}}}_{4}}$. Из указанных выше условий составляется полиномиальный идеал. Его размерность оказалась равна 1, т.е. имеется однопараметрическое семейство матриц преобразования A. Условие сохранения внутренней симметрии (3.10) матрицы монодромии M в итоге выделяет из этого семейства только две матрицы, отличающиеся порядком столбцов ${{{\mathbf{a}}}_{2}}$ и ${{{\mathbf{a}}}_{4}}$.

Одна из таких матриц A была предложена Б.Б. Крейсманом при исследовании периодических решений ограниченной задачи трех тел (см., например, [17]). Пусть ${{{\mathbf{a}}}_{3}} = ({{H}_{1}},{{H}_{2}},{{H}_{3}},{{H}_{4}})$ – нормированный вектор ${\text{grad}}H({{{\mathbf{z}}}_{0}})$. Тогда матрица ${\mathbf{A}}$ имеет вид

(4.2)

${\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {{{H}_{3}}}&{ - {{H}_{4}}}&{{{H}_{1}}}&{{{H}_{2}}} \\ {{{H}_{4}}}&{{{H}_{3}}}&{{{H}_{2}}}&{ - {{H}_{1}}} \\ { - {{H}_{1}}}&{ - {{H}_{2}}}&{{{H}_{3}}}&{ - {{H}_{4}}} \\ { - {{H}_{2}}}&{{{H}_{1}}}&{{{H}_{4}}}&{{{H}_{3}}} \end{array}} \right).$

Утверждение 2 ([17]). Пусть симплектическая матрица M имеет собственное значение +1, которому соответствует собственный вектор ${{{\mathbf{v}}}_{0}} = {{{\mathbf{a}}}_{1}}$. Тогда матрица ${\mathbf{N}} = {{{\mathbf{A}}}^{{\text{t}}}}{\mathbf{MA}}$ имеет вид

(4.3)

${\mathbf{N}} = \left( {\begin{array}{*{20}{c}} 1&{{{n}_{{12}}}}&{{{n}_{{13}}}}&{{{n}_{{14}}}} \\ 0&{{{n}_{{22}}}}&{{{n}_{{23}}}}&{{{n}_{{24}}}} \\ 0&0&1&0 \\ 0&{{{n}_{{42}}}}&{{{n}_{{43}}}}&{{{n}_{{44}}}} \end{array}} \right).$

Это утверждение приведено в [17] без доказательства. В данной работе истинность утверждения проверена с использованием системы компьютерной алгебры Maple, хотя такие же преобразования могут быть выполнены в любой системе компьютерной алгебры, позволяющей вычислять базис Грёбнера полиномиального идеала и с его помощью находить каноническое представление произвольного многочлена по модулю идеала. Общая схема проверки такова.

1) Для произвольной 4 × 4 матрицы M с помощью условия симплектичности (3.2) составляется полиномиальный идеал ${{\mathcal{J}}_{1}}$. Для него вычисляется базис Грёбнера $\mathcal{G}\mathcal{B}{{\mathcal{J}}_{1}}$ для чистого лексикографического порядка от элементов ${{m}_{{ij}}}$, $i,j = 1, \ldots ,4$ матрицы ${\mathbf{M}}$.

2) Согласно свойству 4) на стр. 4 матрица M имеет собственное число, равное +1. Поэтому вычисляется характеристический многочлен ${{P}_{\lambda }}({\mathbf{M}})$, его коэффициенты упрощаются по модулю идеала $\mathcal{G}\mathcal{B}{{\mathcal{J}}_{1}}$, и к этому идеалу добавляется полином, равный сумме коэффициентов многочлена ${{P}_{\lambda }}({\mathbf{M}})$. Для нового идеала вычисляется его базис Грёбнера $\mathcal{G}\mathcal{B}{{\mathcal{J}}_{2}}$ с тем же лексикографическим порядком.

3) Записывается в символьной форме собственный вектор ${{{\mathbf{v}}}_{0}}$ матрицы M как решение однородной системы линейных алгебраических уравнений с матрицей ${\mathbf{M}} - {\mathbf{E}}$ в виде

$\frac{{v_{0}^{1}}}{{{{M}_{1}}}} = - \frac{{v_{0}^{2}}}{{{{M}_{2}}}} = \frac{{v_{0}^{3}}}{{{{M}_{3}}}} = - \frac{{v_{0}^{4}}}{{{{M}_{4}}}},$

где ${{M}_{i}}$ – миноры элементов первой строки матрицы ${\mathbf{M}} - {\mathbf{E}}$. Компоненты вектора ${{{\mathbf{v}}}_{0}}$ упрощаются по модулю идеала $\mathcal{G}\mathcal{B}{{\mathcal{J}}_{2}}$.

4) В идеал $\mathcal{G}\mathcal{B}{{\mathcal{J}}_{2}}$ добавляется многочлен ${\mathbf{v}}_{0}^{2} - 1$, обеспечивающий условие нормировки вектора ${{{\mathbf{v}}}_{0}}$, и вычисляется новый базис Грёбнера $\mathcal{G}\mathcal{B}{{\mathcal{J}}_{3}}$. Из компонентов вектора ${{{\mathbf{v}}}_{0}}$ составляется матрица A по формуле (4.2) и с ее помощью выполняется переход к матрице N.

5) После этого каждый элемент матрицы N упрощается по модулю базиса $\mathcal{G}\mathcal{B}{{\mathcal{J}}_{3}}$. Матрица N принимает форму (4.3).

В силу громоздкости получаемых в процессе вычисления выражений они здесь не приводятся, но легко могут быть восстановлены по данному выше описанию с помощью какой-либо системы компьютерной алгебры.

4.2. Общее решение уравнения продолжения для невырожденного периодического решения

Преобразование матрицы монодромии M с помощью матрицы A позволяет, с одной стороны, прояснить структуру решений уравнения продолжения (4.1) для несимметричного периодического решения [17], а с другой стороны, упростить ее анализ в критических случаях (см. далее п. 5).

Отметим, что случай двояко симметричного периодического решения ничем не отличается от случая однократно симметричного, рассмотренного в [17].

Для обратимого симметричного периодического решения ${\mathbf{z}}(t,{{{\mathbf{z}}}_{0}})$ с начальным условием ${{{\mathbf{z}}}_{0}} \in {{\Sigma }_{i}}$ матрица ${{{\mathbf{A}}}_{i}}$ имеет вид

${{{\mathbf{A}}}_{1}} = \left( {\begin{array}{*{20}{c}} 0&{ - {{H}_{4}}}&{{{H}_{1}}}&0 \\ {{{H}_{4}}}&0&0&{ - {{H}_{1}}} \\ { - {{H}_{1}}}&0&0&{ - {{H}_{4}}} \\ 0&{{{H}_{1}}}&{{{H}_{4}}}&0 \end{array}} \right),$

${{{\mathbf{A}}}_{2}} = \left( {\begin{array}{*{20}{c}} {{{H}_{3}}}&0&0&{{{H}_{2}}} \\ 0&{{{H}_{3}}}&{{{H}_{2}}}&0 \\ 0&{ - {{H}_{2}}}&{{{H}_{3}}}&0 \\ { - {{H}_{2}}}&0&0&{{{H}_{3}}} \end{array}} \right).$

Внутренняя симметрия (3.10) матрицы M приводит к следующим соотношениям для преобразованной матрицы N:

${{n}_{{22}}} = {{n}_{{44}}},\quad {{n}_{{23}}} = - {{n}_{{14}}},\quad {{n}_{{43}}} = - {{n}_{{12}}},$

а индекс устойчивости в этом случае $S = {{n}_{{22}}}$.

Вектор ${\mathbf{b}}$ продолжения семейства имеет вид

(4.4)

${\mathbf{b}} = (0,2{{n}_{{23}}},2(1 - {{n}_{{22}}}),0, - ({{n}_{{12}}}{{m}_{2}} + {{n}_{{13}}}{{m}_{3}}){\text{/}}v).$

Его проекция $\widetilde {\mathbf{b}}$ на фазовое пространство $\mathbb{M}$ определяется только вторым и третьим столбцами матрицы A, что, очевидно, подтверждает приведенные выше рассуждения о продолжении обратимого симметричного решения.

Утверждение 3 ([17]). Продолжение невырожденного симметричного периодического решения вдоль семейства сохраняет его симметрию.

5. КРИТИЧЕСКИЕ РЕШЕНИЯ СЕМЕЙСТВА ДВОЯКО СИММЕТРИЧНОГО РЕШЕНИЯ

В предыдущем пункте рассматривалась ситуация, когда периодическое решение невырожденное. Здесь выясним, как симметрия периодического решения влияет на поведение его семейства в критических решениях, т.е. для тех решений, для которых либо у матрицы монодромии M, либо у ее q-й степени ${{{\mathbf{M}}}^{q}}$ соответствующего критического решения появляются дополнительные элементарные делители. Это решение семейства будем называть бифуркационным решением.

Отметим, что соответствующий бифуркационный анализ однократно симметричных периодических решений был проведен ранее. Так, в Главе VIII книги [21] это было сделано с использованием метода нормальной формы. В статье [17] анализ симметричного решения проводился с использованием последовательных симплектических преобразований матрицы M. Фактически эта работа является продолжением методики последней работы на случай двояко симметричных решений.

Мы рассмотрим три типичных критических случая, которые обычно относят к одному из видов бифуркации периодического решения [23, Ch. 11]:

• бифуркация рождения-гибели (седло-узел);

• бифуркация потери симметрии (типа “вилки”);

• бифуркация кратного увеличения периода.

Первые два случая соответствуют значению индекса устойчивости S = 1, последний случай соответствует значению $S = cos(2\pi p{\text{/}}q)$, $p,q \in \mathbb{N}$, $p$ и $q$ взаимно просты. Отдельно рассмотрим важный случай бифуркации удвоения периода при $S = - 1$.

5.1. Случай S = 1

В этом случае ${{n}_{{22}}} = {{n}_{{44}}} = 1$, матрица ${\mathbf{N}}$ принимает вид

${\mathbf{N}} = \left( {\begin{array}{*{20}{c}} 1&{{{n}_{{12}}}}&{{{n}_{{13}}}}&{{{n}_{{14}}}} \\ 0&1&{ - {{n}_{{14}}}}&{{{n}_{{24}}}} \\ 0&0&1&0 \\ 0&{{{n}_{{42}}}}&{ - {{n}_{{12}}}}&1 \end{array}} \right),$

а два компонента ${{m}_{3}},\;{{m}_{4}}$ вектора ${\mathbf{b}}$ согласно (4.4) равны 0. Условие симплектичности матрицы ${\mathbf{N}}$ приводит к условиям

$2{{n}_{{14}}} = {{n}_{{24}}}{{n}_{{12}}},\quad {{n}_{{24}}}{{n}_{{42}}} = 0,\quad {{n}_{{14}}}{{n}_{{42}}} = 0.$

Здесь возможны два случая в зависимости от значения единственного нетривиального компонента ${{m}_{2}}$.

Случай ${{m}_{2}} \ne 0$. Тогда из (4.4) следует, что ${{n}_{{42}}}$ = 0, и матрица ${\mathbf{N}}$ принимает вид

${\mathbf{N}} = \left( {\begin{array}{*{20}{c}} 1&{{{n}_{{12}}}}&{{{n}_{{13}}}}&{\frac{1}{2}{{n}_{{12}}}{{n}_{{24}}}} \\ 0&1&{ - \frac{1}{2}{{n}_{{12}}}{{n}_{{24}}}}&{{{n}_{{24}}}} \\ 0&0&1&0 \\ 0&0&{ - {{n}_{{12}}}}&1 \end{array}} \right) \sim exp({\mathbf{JC}}),$

где матрица ${\mathbf{C}}$ согласно [21, Гл. II, § 1] подобна матрице

$\left( {\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&0&1&0 \\ 0&1&1&0 \\ 0&0&0&0 \end{array}} \right)$

и, следовательно, имеет элементарный делитель ${{(\lambda - 1)}^{4}}$. В этом случае вектор продолжения семейства ${\mathbf{b}} = {{(0, - {{n}_{{12}}},0,0, - {{n}_{{12}}}{{m}_{2}}{\text{/}}v)}^{{\text{t}}}}$, а его проекция $\widetilde {\mathbf{b}}$ ортогональна вектору $H({{{\mathbf{z}}}_{0}})$. Следовательно, первый интеграл $H({\mathbf{z}})$ достигает экстремума на семействе периодических решений, на характеристике семейства в координатах $(h,S)$ имеется складка, а само критическое решение называется бифуркацией рождения-гибели. При прохождении через это решение меняется устойчивость семейства.

Случай ${{m}_{2}} = 0$. Тогда из (4.4) следует, что ${{n}_{{24}}}$ = 0, ${{n}_{{42}}} \ne 0$, и матрица ${\mathbf{N}}$ принимает вид

$N = \left( {\begin{array}{*{20}{c}} 1&{{{n}_{{12}}}}&{{{n}_{{13}}}}&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&{{{n}_{{42}}}}&{ - {{n}_{{12}}}}&1 \end{array}} \right).$

Выполним дополнительное симплектическое преобразование

${\mathbf{\tilde {A}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&{{{n}_{{12}}}{\text{/}}{{n}_{{42}}}} \\ 0&1&{{{n}_{{12}}}{\text{/}}{{n}_{{42}}}}&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right),$

${\mathbf{\tilde {N}}} = \left( {\begin{array}{*{20}{c}} 1&0&{{{n}_{{13}}} + n_{{12}}^{2}{\text{/}}{{n}_{{42}}}}&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&{{{n}_{{42}}}}&0&1 \end{array}} \right).$

Нетрудно видеть, что матрица $\widetilde {\mathbf{N}}$ имеет два элементарных делителя ${{(\lambda - 1)}^{2}}$ и ${{(\lambda - 1)}^{2}}$. Корневой вектор, соответствующий первому элементарному делителю, задает направление главного семейства ${{{\mathbf{b}}}_{1}} = {{(0,0,1,0, - {{\tilde {n}}_{{13}}}{\text{/}}v)}^{{\text{t}}}}$. Собственный вектор b₂ = = $(0,0,0,1,0)$, соответствующий второму элементарному делителю, задает направление нового семейства периодических решений с периодом, равным периоду решения главного семейства. В этом случае новое решение будет обладать только одной из двух симметрий. Поскольку для двояко симметричных периодических решений матрицы монодромии M₁ и M₂, вычисленные от взаимно симметричных точек, отстоящих через полпериода, равны, то в результате получаем два порожденных семейства однократно симметричных решений. Периодические решения этих двух порожденных семейств взаимно симметричны относительно другого автоморфизма ${{g}_{i}}$. Другими словами, если порожденные семейства состоят из ${{g}_{1}}$-симметричных орбит, то эти орбиты взаимно ${{g}_{2}}$-симметричны.

5.2. Случай $S = - 1$

Рассмотрим подробнее критический случай, соответствующий бифуркации удвоения периода. В общем случае компонента ${{m}_{3}} \ne 0$ и можно выполнить дополнительное симплектическое преобразование

(5.1)

$\begin{gathered} {\mathbf{\tilde {A}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&{{{m}_{2}}{\text{/}}{{m}_{3}}} \\ 0&1&{{{m}_{2}}{\text{/}}{{m}_{3}}}&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right), \\ {\mathbf{\tilde {N}}} = \left( {\begin{array}{*{20}{c}} 1&0&{{{{\tilde {n}}}_{{13}}}}&0 \\ 0&{ - 1}&0&{{{n}_{{24}}}} \\ 0&0&1&0 \\ 0&{{{n}_{{42}}}}&0&{ - 1} \end{array}} \right). \\ \end{gathered} $

с дополнительным условием ${{n}_{{24}}}{{n}_{{42}}} = 0$. Здесь ${{\tilde {n}}_{{13}}} = {{n}_{{12}}}{{m}_{2}}{\text{/}}{{m}_{3}}$ + n₁₃.

Для однократно симметричного периодического решения имеем либо ${{n}_{{24}}} = 0$, ${{n}_{{42}}} \ne 0$, либо ${{n}_{{42}}}$ = 0, ${{n}_{{24}}} \ne 0$. Тогда матрица ${\mathbf{\tilde {N}}}$ имеет два элементарных делителя ${{(\lambda - 1)}^{2}}$ и ${{(\lambda + 1)}^{2}}$. Корневой вектор ${{{\mathbf{r}}}_{1}}$, соответствующий первому элементарному делителю, задает направление главного семейства ${{{\mathbf{b}}}_{1}} = {{{\mathbf{r}}}_{1}}$. Для второго элементарного делителя возможны два варианта с собственным вектором ${\mathbf{b}}_{2}^{1} = (0,1,0,0)$ в первом случае и ${\mathbf{b}}_{2}^{2}$ =(0, 0, 0, 1) во втором. Этот вектор задает направление нового семейства периодических решений с периодом, равным периоду решения главного семейства. Анализ, проведенный в [17], показывает, что на порожденном семействе всегда имеет место экстремум $H({\mathbf{z}})$ и оно (семейство) сохраняет тип симметрии порождающего решения.

Рассмотрим случай двояко симметричного решения. В этом случае матрица монодромии ${\mathbf{M}}$, согласно (3.9), является квадратом матрицы решения ${\mathbf{Z}}(T{\text{/}}2,{{{\mathbf{z}}}_{0}})$ уравнения в вариациях (3.1) на половине периода. Но тогда, в силу вещественности, у нее не может быть элементарного делителя ${{(\lambda + 1)}^{2}}$, поскольку вещественного квадратного корня из жордановой клетки второго порядка, соответствующей этому делителю, нет [23, Ch. 3].

Утверждение 4. Матрица монодромии M двояко симметричного периодического решения при $S = - 1$ в случае общего положения имеет три элементарных делителя: ${{(\lambda - 1)}^{2}}$, $(\lambda + 1)$ и $(\lambda + 1)$. Двум последним соответствуют однократно симметричные решения с разными типами симметрии и периодом $T{\text{'}} = 2T$. На каждом из семейств однократно симметричных решений первый интеграл $H({\mathbf{z}})$ достигает экстремума в бифуркационном решении.

Имеется два сценария бифуркации удвоения периода:

1) на обоих новых порожденных семействах интеграл $H({\mathbf{z}})$ имеет один и тот же тип экстремума (максимум или минимум) в критическом решении,

2) на новых порожденных семействах интеграл $H({\mathbf{z}})$ имеет разные типы экстремума (у одной пары минимум, у другой – максимум).

При первом сценарии в результате бифуркации появляется четыре пары периодических решений с удвоенным периодом – две пары с одним типом симметрии, две с другим. В этом случае одна пара семейств двояко периодических решений имеет устойчивые орбиты, а другая неустойчивые.

При втором сценарии в окрестности бифуркационного решения имеется по одной паре периодических решений с удвоенным периодом. Поскольку индекс устойчивости $S$ порождающего семейства всегда больше или равен –1, то порожденные семейства двояко периодических решений всегда имеют только неустойчивые орбиты.

5.3. Случай кратного увеличения периода

Случай бифуркации удвоения периода является частным случаем бифуркации кратного увеличения периода когда $S = cos\varphi $, $\varphi = 2\pi p{\text{/}}q$. Количественный анализ аналогичный тому, что был проведен в [17], показывает, что при $S \ne \pm 1$ компонента ${{m}_{3}}$ вектора b не равна нулю. Тогда произведение матриц ${\mathbf{\tilde {A}}}$ из (5.1) и ${\mathbf{C}} = {\text{diag}}\{ 1,{{c}_{{22}}},1,{{c}_{{44}}}\} $, где ${{c}_{{44}}} = \sqrt {{{n}_{{42}}}{\text{/sin}}\varphi } $, ${{c}_{{22}}} = 1{\text{/}}{{c}_{{44}}}$, дает матрицу симплектического преобразования ${\mathbf{\tilde {A}C}}$, приводящего матрицу монодромии ${\mathbf{\tilde {N}}}$ к виду

(5.2)

${\mathbf{\tilde {M}}} = \left( {\begin{array}{*{20}{c}} 1&0&{{{{\tilde {n}}}_{{13}}}}&0 \\ 0&{cos\varphi }&0&{ - sin\varphi } \\ 0&0&1&0 \\ 0&{sin\varphi }&0&{cos\varphi } \end{array}} \right).$

При этом угол $\varphi $ определяется из условий

$cos\varphi = S,\quad {{n}_{{42}}}sin\varphi \geqslant 0.$

Из (5.2) следует, что для нечетных и взаимно простых чисел p, q матрица ${{{\mathbf{\tilde {M}}}}^{q}}$ имеет структуру элементарных делителей ${{(\lambda - 1)}^{2}}$, $(\lambda - 1)$ и $(\lambda - 1)$. Если же одно из чисел p, q, четно, то у матрицы ${\mathbf{Z}}(qT{\text{/}}2,{{{\mathbf{z}}}_{0}})$ структура элементарных делителей ${{(\lambda - 1)}^{2}}$, $(\lambda + 1)$ и $(\lambda + 1)$, т.е. такая же как в утверждении 4. Как и в предыдущих случаях, корневой вектор жордановой клетки второго порядка с собственным числом +1 дает направление продолжения главного семейства. Собственные векторы, соответствующие простым элементарным делителям, дают направление либо одному двояко симметричному порожденному семейству для нечетных p, q, либо двум парам семейств однократно симметричных периодических решений, когда одно из p, q четно. Качественное объяснение этого эффекта состоит в следующем.

Рассмотрим двояко симметричное периодическое решение, орбита которого последовательно ортогонально пересекает плоскости симметрии ${{\Sigma }_{{1,2}}}$ через четверть периода. Пусть это решение с периодом T является порождающим решением для периодического решения второго рода с периодом qT. Для того чтобы орбита порожденного решения также имела две симметрии, необходимо выполнение указанного выше условия ортогональности. Пусть начальная точка порожденной орбиты лежит на плоскости ${{\Sigma }_{1}}$, тогда через четверть периода следующая ортогональная точка будет лежать на плоскости ${{\Sigma }_{2}}$, при этом точка орбиты должна совершить $(2k - 1){\text{/}}4$ оборота вокруг начала координат, где $k \in \mathbb{N}$. Поэтому за весь период qT точка орбиты совершит $2k - 1$ оборотов, то есть число q всегда нечетное. С другой стороны, орбита, соответствующая резонансу p/q, может быть представлена в фазовом пространстве как замкнутая винтовая линия, лежащая на некотором торе [24], которая делает за один период $q$ оборотов по одной образующей тора и $p$ оборотов по другой образующей. Поэтому для двояко симметричной орбиты число $p$ тоже должно быть нечетным.

Утверждение 5. Пусть двояко симметричное периодическое решение с периодом $T$ имеет значение индекса устойчивости $S$, равное $cos(2\pi p{\text{/}}q)$, где $p,q \in \mathbb{N}$ и взаимно просты.

• Если оба числа $p,\;q$ нечетные, то в окрестности исходного решения имеется одно семейство двояко симметричных решений с периодом $T{\text{'}} = qT$.

• Если одно из чисел $p$ или $q$ четно, то в окрестности исходного решения имеется две пары семейств однократно симметричных решений с различными типами симметрий для каждой пары и с периодами $T{\text{'}} = qT$.

Для всех случаев, кроме случая $p{\text{/}}q = 1{\text{/}}3$, интеграл $H$ достигает экстремума на порожденных семействах (подробнее см. [21, Гл. VIII]).

6. ИССЛЕДОВАНИЕ СЕМЕЙСТВ ДВОЯКО СИММЕТРИЧНЫХ РЕШЕНИЙ ЗАДАЧИ ХИЛЛА

6.1. Задача Хилла и ее свойства

Плоская круговая задача Хилла [25, 26, § 10.4] используется для исследования динамики тела “нулевой” массы (спутника), движущегося в окрестности меньшего из двух тяготеющих тел и остающегося в плоскости их движения. Эта задача является некоторым предельным вариантом известной ограниченной задачи трех тел (ОЗТТ) [26], когда

i) массовый параметр $\mu $ в ОЗТТ стремится к нулю и

ii) большее из двух массивных тел стремится к $ + \infty $ вдоль оси абсцисс в равномерно вращающейся (синодической) системе координат.

Хотя задача Хилла неинтегрируема [27], но ее уравнения движения в отличие от уравнений ОЗТТ не содержат массового параметра $\mu $, что делает их существенно проще уравнений ОЗТТ. Вторым важным отличием уравнений задачи Хилла от уравнений ОЗТТ является наличие у них двух дополнительных симметрий, т.е., уравнения задачи Хилла инвариантны относительно четверной группы Клейна линейных автоморфизмов с двумя образующими, обозначаемыми ${{g}_{1}}$ и ${{g}_{2}}$ (см. раздел 2). Каждое из этих преобразований имеет инвариантное множество в виде двумерной плоскости в расширенном фазовом пространстве задачи.

Единственным первым интегралом системы канонических уравнений задачи Хилла

$\left\{ \begin{gathered} \mathop {\dot {x}}\nolimits_1 = {{y}_{1}} + {{x}_{2}},\mathop {\quad \dot {y}}\nolimits_1 = {{y}_{2}} + 2{{x}_{1}} + \frac{{{{x}_{1}}}}{{{{{\left| {\mathbf{x}} \right|}}^{3}}}}, \hfill \\ \mathop {\dot {x}}\nolimits_2 = {{y}_{2}} - {{x}_{1}},\mathop {\quad \dot {y}}\nolimits_2 = - {{y}_{1}} - {{x}_{2}} + \frac{{{{x}_{2}}}}{{{{{\left| {\mathbf{x}} \right|}}^{3}}}}, \hfill \\ \end{gathered} \right.$

остается интеграл энергии, традиционно записываемый в форме интеграла Якоби

$\mathcal{J} \equiv 3x_{1}^{2} + \frac{2}{{\left| {\mathbf{x}} \right|}} - \dot {x}_{1}^{2} - \dot {x}_{2}^{2} = C,$

где постоянная $C$ удовлетворяет соотношению $C = - 2H({\mathbf{z}})$.

6.2. Семейство ${{{\mathbf{f}}}_{3}}$ двояко симметричных решений

Для плоской круговой задачи Хилла было найдено большое количество семейств периодических решений (см., например, книгу [25] и библиографию в ней, а также [28]). Среди этих семейств можно выделить основные, которые прямо или опосредованно связаны другими семействами через порождающие и/или критические решения [29]. Такими семействами можно считать семейства двояко симметричных прямых и обратных спутниковых орбит ${\mathbf{g}}$ и f соответственно (см. [30, 25 ]).

Семейства ${\mathbf{g}}$ и f не имеют участков, где индекс устойчивости менялся бы на всем интервале устойчивости, поэтому здесь в качестве примера рассмотрим семейство двояко симметричных трехоборотных периодических решений ${{{\mathbf{f}}}_{3}}$. Это семейство найдено М. Эноном в [31] (где названо ${{{\mathbf{g}}}_{3}}$), подробно исследовано в [32, 25 ], где приведены примеры его орбит. В табл. 1 приведены начальные условия на плоскостях симметрии, период, значения константы C и индекса устойчивости $S$ для критических орбит семейства ${{{\mathbf{f}}}_{3}}$.

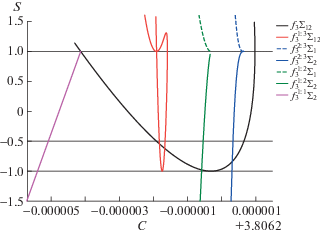
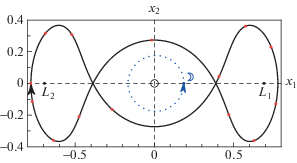
Участок характеристики этого семейства в координатах $(C,S)$, а также других семейств, пересекающихся с ним в критических решениях, показан на рис. 1, а пример орбиты семейства – на рис. 2. Здесь и далее на рис. 3 и 4 показано положение точек либрации ${{L}_{1}}$, ${{L}_{2}}$, а также орбита Луны (пунктир). Точками обозначено положение спутника на орбите с временным интервалом в один месяц.

Рис. 1.

Характеристика семейства f₃ и связанных с ним семейств на плоскости $(C,S)$.

Рис. 2.

Орбита семейства f₃.

Рис. 3.

Орбиты ${{g}_{2}}$-симметричных семейств ${{{\mathbf{f}}}_{3}}{{\Sigma }_{2}}$.

Рис. 4.

Орбиты семейств двояко периодических решений.

Индекс устойчивости $S$ семейства ${{{\mathbf{f}}}_{3}}$ пересекает значение +1 в двух точках (см. рис. 1). В самой правой точке (строка 5 табл. 1) константа C на семействе достигает экстремума и, следовательно, имеет место бифуркация рождения-гибели. В самой левой точке (строка 1 табл. 1) семейство пересекает значение +1 монотонно, здесь происходит появление двух семейств ${{g}_{2}}$-периодических решений ${{{\mathbf{f}}}_{3}}{{\Sigma }_{2}}$. Эти семейства были найдены в [33], где обозначены ${{H}_{k}}$. Более подробно они описаны в [25, п. 4.3.5]. Примеры орбит этих семейств показаны на рис. 3.

Таблица 1.

Параметры критических периодических решений семейства f₃

№	${{x}_{1}}(0)$	${{y}_{2}}(0)$	T	S	${{x}_{2}}(T{\text{/}}4)$	${{y}_{1}}(T{\text{/}}4)$
1	0.7790205	0.0162955	6.6496347	1.0	0.2725126	–2.1521173
2	0.7790055	0.0162955	6.6477869	–0.5	0.2723290	–2.1532489
3	0.7789904	0.0162951	6.6459314	–1.0	0.2721447	–2.1543862
4	0.7789752	0.0162942	6.6440671	–0.5	0.2719594	–2.1555297
5	0.7789601	0.0162930	6.6421949	1.0	0.2717735	–2.1566791

Рассмотрим появление двух семейств двояко периодических однократно симметричных решений, когда индекс устойчивости S главного семейства ${{{\mathbf{f}}}_{3}}$ проходит значение –1 (строка 3 табл. 1). Для этого начального условия вычисляются матрицы ${{{\mathbf{A}}}_{1}}$ и ${{{\mathbf{A}}}_{2}}$ – каждая для точки на соответствующей плоскости симметрии. Вторые столбцы этих матриц дают векторы ${\mathbf{b}}_{2}^{1}$ и ${\mathbf{b}}_{2}^{2}$, в направлении которых ответвляются двукратные периодические решения симметричные относительно преобразований ${{g}_{1}}$ и ${{g}_{2}}$ соответственно. Эти векторы равны

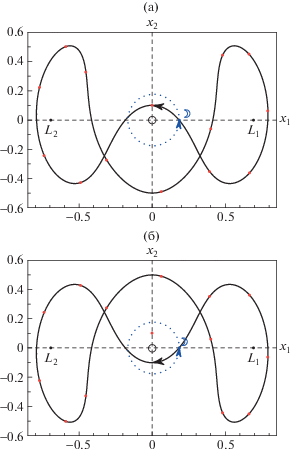
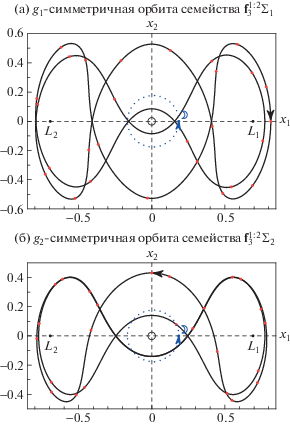
$\begin{gathered} {\mathbf{\tilde {b}}}_{2}^{1} = {{( - 0.9953708,0.0,0.0, - 0.0961093)}^{{\text{t}}}}, \\ {\mathbf{\tilde {b}}}_{2}^{2} = {{(0.0,0.1599010,0.9871331,0.0)}^{{\text{t}}}}. \\ \end{gathered} $

В соответствии с утверждением 4 в этом случае наблюдается появление двух семейств согласно сценарию 1) на стр. 23, поскольку оба семейства имеют максимум по C. Два семейства ${\mathbf{f}}_{3}^{{1:2}}{{\Sigma }_{1}}$ ${{g}_{1}}$-симметричных орбит содержат только неустойчивые решения. Некоторые начальные условия этого семейства даны в табл. 2. Пример орбиты приведен на рис. 4а. Ей соответствует последняя строка таблицы.

Таблица 2.

Начальные условия периодических решений семейства ${\mathbf{f}}_{3}^{{1:2}}{{\Sigma }_{1}}$

№	${{x}_{1}}(0)$	${{y}_{2}}(0)$	T	S	${{x}_{1}}(T{\text{/}}2)$	${{y}_{2}}(T{\text{/}}2)$
1	0.7789945	0.0162954	13.2918621	1.0029942	0.7789862	0.0162946
2	0.7790215	0.0162972	13.2918633	10.189443	0.7789594	0.0162912
3	0.8146104	–0.2266505	13.7419253	3.0 × 10¹¹	0.7734352	–0.2359037

Два семейства ${\mathbf{f}}_{{\mathbf{3}}}^{{{\mathbf{1:2}}}}$Σ₂g₂-симметричных орбит имеют небольшой участок с устойчивыми решениями. Некоторые начальные условия этого семейства даны в таб. 3. Пример орбиты приведен на рис. 4б). Ей соответствует последняя строка таблицы.

Наконец, рассмотрим появление трехкратно периодических порожденных решений. Оно происходит, когда $S = - 1{\text{/}}2$, что возможно в двух ситуациях.

При $p{\text{/}}q = 1{\text{/}}3$. В этой ситуации согласно утверждению 5 появляется одно семейство двояко симметричных решений, которое вблизи порождающего семейства имеет только неустойчивые решения. Однако здесь на семействе при продолжении достигается максимум константы C, что видно по его характеристике на рис. 1. Следовательно, при одном и том же значении интеграла C на сечении Пуанкаре должны наблюдаться два набора неподвижных точек: один набор устойчивых, другой – неустойчивых. Это можно наблюдать на рис. 5.

Рис. 5.

Сечение Пуанкаре плоскостями ${{\Sigma }_{1}}$ (слева) и ${{\Sigma }_{2}}$ (справа) двояко симметричных периодических решений вблизи семейства f₃ для случая $p{\text{/}}q = 1{\text{/}}3$.

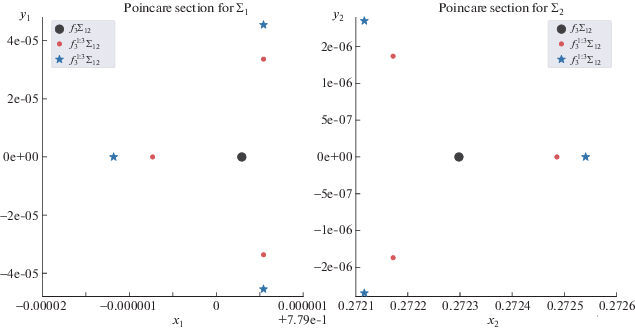
Таблица 3.

Начальные условия периодических решений семейства ${\mathbf{f}}_{3}^{{1:2}}{{\Sigma }_{2}}$

№	${{x}_{2}}(0)$	${{y}_{1}}(0)$	T	S	${{x}_{2}}(T{\text{/}}2)$	${{y}_{1}}(T{\text{/}}2)$
1	0.2722264	–2.1538817	13.2917712	0.9998048	0.2720628	–2.1548915
2	0.2725404	–2.1519454	13.2901165	–1.0088341	0.2717481	–2.1568361
3	0.4308632	–1.4454805	12.1324885	–4.57 × 10⁹	0.1405653	–3.3987653

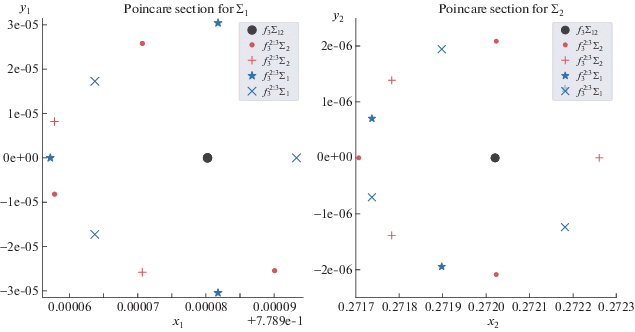
При $p{\text{/}}q = 2{\text{/}}3$. Согласно утверждению 5 появляется четыре семейства однократно симметричных решений – одна пара семейств ${{g}_{1}}$-симметричных неустойчивых решений, другая пара семейств ${{g}_{2}}$-симметричных устойчивых решений. Таким образом, на сечении Пуанкаре при определенных условиях можно наблюдать 12 неподвижных точек: по три точки на периодическое решение каждого из семейств, что видно на рис. 6.

Рис. 6.

Все результаты, полученные в разделе 6, получены путем численного интегрирования системы Гамильтона задачи Хилла и ее уравнений в вариациях с использованием пакетов TAYLOR [2] и TIDES [3].

Список литературы

Barrio R., Blesa F. Systematic search of symmetric periodic orbits in 2DOF Hamiltonian systems // Chaos, Solitons and Fractals. 2009. V. 41. № 2. P. 560–582.
Jorba A., Zou M. A software package for the numerical integration of ODE by means of high order Taylor methods. 2004. P. 32. Preprint.
Algorithm 924: TIDES, a Taylor Series Integrator for Di_erential EquationS / Alberto Abad, Roberto Barrio, Fernando Blesa, Marcos Rodrí guez // ACM Transactions on Mathematical Software. 2012. November. V. 39. № 1. Article No. 5.
Thompson I. Understanding Maple. Cambridge University Press, 2016. 228 p.
SymPy: symbolic computing in Python / Aaron Meurer, Christopher P. Smith, Mateusz Paprocki et al. // PeerJ Computer Science. 2017. V. 3. P. e103. Access mode: https://doi.org/10.7717/peerjcs.103
Wolfram S. The Mathematica Book. Wolfram Media, Inc., 2003. 1488 p.
Batkhin A.B. Some properties of doubly symmetric periodic solutions to Hamiltonian system // International Conference Polynomial Computer Algebra '2019; St. Petersburg, April 15–20, 2019 / Ed. by N.N. Vassiliev; Euler International Mathematical Institute. St. Petersburg, Russia: VVM Publisher, 2019. P. 25–28.
Батхин А.Б. Бифуркации периодических решений системы Гамильтона с дискретными симметриями // Компьютерная алгебра: материалы Международной конференции. Москва, 17–21 июня 2019 г. / Под ред. С.А. Абрамова, Л.А. Севастьянова. М.: РУДН, 2019. С. 90–97.
Батхин А.Б. О структуре фазового потока в окрестности симметричного периодического решения системы Гамильтона // Препринты ИПМ им. М.В. Келдыша. 2019. № 69.
Lamb J.S.W., Roberts J.A.G. Time-reversal symmetry in dynamical systems: A survey // Physica D. 1998. V. 112. P. 1–39.
Meyer K.R. Periodic Solutions of the N-body Problem. Lecture Notes in Mathematics, V. 1719. Berlin, Heidelberg, New York: Springer–Verlag, 1999.
Hénon M. Generating Families in the Restricted Three-Body Problem. Lecture Note in Physics. Monographs no. 52. Berlin, Heidelber, New York: Springer, 1997. 278 p.
Уинтнер А. Аналитические основы небесной механики. М.: Наука, 1967. 523 с.
Якубович В.А., Старжинский В.М. Линейные дифференциальные уравнения с периодическими коэффициентами. М.: Наука, 1972. 720 с.
Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Гл. ред. физ.-мат. литер. изд-ва. Наука., 1978. 352 с.
Пуанкаре А. Новые методы небесной механики. Топология. Теория чисел. М.: Наука, 1972. Т. II. С. 9–356.
Крейсман Б.Б. Семейства периодических решений гамильтоновой системы с двумя степенями свободы. Несимметричные периодические решения плоской ограниченной задачи трех тел // Космические исследования. 2005. Т. 43. № 2. С. 1–23.
Методы анализа нелинейных динамических моделей / М. Холодниок, А. Клич, М. Кубичек, М. Марек. М.: Мир, 1991. 368 с.
Гантмахер Ф.Р. Теория матриц. 4-е изд. изд. М.: Наука, 1988. 552 с.
Williamson J. On the normal forms of linear canonical transformations in dynamics // American Journal of Mathematics. 1937. Jul. V. 59. № 3. P. 599–617.
Брюно А.Д. Ограниченная задача трех тел: Плоские периодические орбиты. М.: Наука, 1990. 296 с.
Каримов С.Р., Сокольский А.Г. Метод продолжения по параметрам естественных семейств периодических движений гамильтоновых систем. 1990. Препринт ИТА АН СССР. № 9.
Meyer K.R., Offin D.C. Introduction to Hamiltonian Dynamical Systems and the N-Body Problem. Applied Mathematical Sciences, V. 90. 3nd edition edition. New York: Springer International Publishing, 2017.
Теория бифуркаций / В.И. Арнольд, В.С. Афраймович, Ю.С. Ильяшенко, Л.П. Шильников. М.: ВИНИТИ АН СССР, 1985. Т. 5 из Современные проблемы математики. Фундаментальные направления.
Батхин А.Б., Батхина Н.В. Задача Хилла. Волгоград: Волгоградское научное издательство, 2009. 200 с.
Себехей В. Теория орбит: ограниченная задача трех тел. М.: Наука, 1982. 656 с.
Morales-Ruiz J., Simó C., Simon S. Algebraic proof of the non–integrability of hill’s problem // Ergodic Theory and Dynamical Systems. 2005. V. 25. № 4. P. 1237–1256.
Батхин А.Б. Симметричные периодические решения задачи Хилла. II // Космические исследования. 2013. Т. 51. № 6. С. 497–510.
Батхин А.Б. Сеть семейств периодических орбит обобщенной задачи хилла // ДАН. 2014. Т. 458. № 2. С. 131–137.
Hénon M. Numerical exploration of the restricted problem. V. Hill’s case: periodic prbits and their stability // Astron. & Astrophys. 1969. V. 1. P. 223–238.
Hénon M. Numerical exploration of the restricted problem. VI. Hill’s case: non-periodic orbits // Astron. & Astr. 1970. no. 9. P. 24–36.
Hénon M. New families of periodic orbits in Hill’s problem of three bodies // Celest. Mech. Dyn. Astr. 2003. V. 85. P. 223–246.
Hénon M. Families of asymmetric periodic orbits in Hill’s problem of three bodies // Celest. Mech. Dyn. Astr. 2005. V. 93. P. 87–100.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал