Программирование, 2020, № 2, стр. 53-59

1. ВВЕДЕНИЕ

Классическая машина Атвуда, первоначально разработанная для демонстрации равноускоренного движения, состоит из двух грузов, соединенных невесомой нерастяжимой нитью, перекинутой через шкив, который может вращаться без трения вокруг горизонтальной оси (см. [1]). Предполагая, что грузы могут перемещаться только вдоль вертикали, а нить не проскальзывает по шкиву, получаем простую механическую систему с одной степенью свободы, уравнение движения которой легко интегрируется. Простейшее обобщение этой системы, когда один из грузов во время движения может совершать колебания в вертикальной плоскости, приводит к появлению дополнительной степени свободы, что существенно усложняет уравнения движения и их общее решение не может быть записано в символьной форме [2]. Однако динамика такой системы была исследована довольно подробно [3]. В частности, было показано, что уравнения движения являются интегрируемыми только в том случае, когда отношение масс грузов равняется 3. При этом система может демонстрировать различные виды движения, например, квазипериодическое и хаотическое движение (см. [4–6]). Радиус шкива также влияет на динамику системы (см. [7]), но его изменение не приводит к каким-либо качественным изменениям движения.

Следует отметить, что именно колебания груза существенно влияют на характер движения системы, особенно при небольшой разнице масс грузов. Исследование движения машины Атвуда с одним колеблющимся грузом показало (см. [8]), что колебания приводят к возрастанию средней силы натяжения нити, причем ее величина зависит от амплитуды колебаний. Если оба груза одинаковой массы (${{m}_{1}} = {{m}_{2}}$) находятся в равновесии и одному из них сообщается горизонтальная начальная скорость, то этот колеблющийся груз начинает движение вниз и тянет второй груз вверх даже в случае малых колебаний. При этом длина отрезка нити r между колеблющимся грузом и шкивом увеличивается, а амплитуда его колебаний и средняя сила натяжения нити убывают. Таким образом, при наличии колебаний одного из двух одинаковых грузов равновесное решение уравнений движения машины Атвуда $r = {\text{const}}$ не существует. Такое решение возможно только в том случае, когда колебания отсутствуют или же оба груза совершают колебания в противофазе с одинаковыми амплитудами и частотами (см. [9]).

С другой стороны, при небольшой разнице масс колебания груза меньшей массы приводят к возможности квазипериодического движения системы (см. [8]). Естественно предположить, что при подходящих начальных условиях система может находиться в состоянии динамического равновесия, когда груз большей массы совершает поступательное движение и колеблется около некоторого равновесного положения, а движение груза меньшей массы представляет собой наложение двух взаимно перпендикулярных колебаний. Соответствующее решение уравнений движения системы должно быть периодическим.

Целью данной работы является построение периодического решения уравнений движения машины Атвуда в виде степенного ряда по малому параметру и определение начальных условий, при которых такое движение может происходить. Отметим, что построение и исследование таких решений обычно связано с выполнением весьма громоздких символьных вычислений, которые удобно выполнять с помощью систем компьютерной алгебры (см., напр., [10–14]). В данной работе для выполнения всех расчетов и визуализации полученных результатов используется система компьютерной алгебры Wolfram Mathematica [15].

2. УРАВНЕНИЯ ДВИЖЕНИЯ

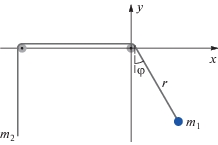
Рассматривается обобщенная модель машины Атвуда, в которой шкив конечного радиуса заменяется двумя отдельными малыми шкивами и один груз может колебаться в вертикальной плоскости (Рис. 1). Такая модификация классической машины Атвуда не изменяет ее физической природы, но позволяет исключить влияние размеров шкива и сосредоточиться на исследовании влияния колебаний на движение системы.

Функция Лагранжа рассматриваемой системы имеет вид

где точка над символом означает полную производную соответствующей функции по времени, $g$ – ускорение свободного падения, r – расстояние между шкивом и грузом ${{m}_{1}}$, а угол $\varphi $ определяет отклонение груза от вертикали (см. рис. 1). Выражение (2.1) записано в предположении, что радиус шкива пренебрежимо мал и изменением длины нити r при колебаниях груза за счет наматывания нити на шкив можно пренебречь.

Уравнения движения, записанные в форме Лагранжа с использованием (2.1), имеют вид

Легко видеть, что при $r = {{R}_{0}} = {\text{const}}$ уравнение (2.3) сводится к уравнению колебаний математического маятника

однократное интегрирование которого приводит к закону сохранения механической энергии где ${{\Phi }_{0}}$ – амплитуда колебаний. При $r = {\text{const}}$ уравнение (2.2) с учетом (2.4) принимает вид

Поскольку ${{\dot {\varphi }}^{2}} \geqslant 0$ и, следовательно, $\left| \varphi \right| \leqslant {{\Phi }_{0}}$, уравнение (2.5) имеет единственное решение $\varphi = {{\Phi }_{0}}$ = 0 только в случае равных масс грузов (m₁ = m₂). Таким образом, система (2.2)–(2.3) имеет равновесное решение $r = {{R}_{0}} = {\text{const}}$, $\varphi = 0$ только при условии ${{m}_{1}} = {{m}_{2}}$.

Далее будем предполагать, что колебания груза m₁ являются малыми (выполняется условие $\left| \varphi \right| \ll 1$), и заменим тригонометрические функции в уравнениях (2.2), (2.3) их разложениями в степенные ряды с точностью до второго порядка включительно. Тогда уравнения движения примут вид

Заметим, что уравнения (2.6), (2.7) являются нелинейными и существование периодических движений грузов, которыми мы интересуемся в данной работе, возможно только вследствие нелинейного взаимодействия между степенями свободы системы. В линейном приближении переменные $r(t)$ и $\varphi (t)$ разделяются и интересные нелинейные эффекты, которые проявляются даже в случае малых колебаний, теряются.

3. ПЕРИОДИЧЕСКОЕ РЕШЕНИЕ

Напомним, что колебания груза m₁ приводят к увеличению средней силы натяжения нити и она становится больше силы тяжести ${{m}_{1}}g$ (см. [8]). Следовательно, можно ожидать, что при небольшой разнице в массах грузов, когда выполняется условие $(\left| {{{m}_{2}} - {{m}_{1}}} \right|{\text{/}}{{m}_{1}} \equiv \varepsilon \ll 1)$, средняя сила натяжения нити может уравновесить силу тяжести ${{m}_{2}}g$ и система будет находиться в состоянии динамического равновесия, при котором обе переменные $r(t)$, $\varphi (t)$ осциллируют около равновесного решения и являются периодическими функциями времени. Поскольку уравнения движения (2.6)–(2.7) являются нелинейными, амплитуда и частота колебаний будут зависеть от амплитуды и, следовательно, от параметра ε. При $\varepsilon \to 0$, когда грузы имеют одинаковые массы, функции $r(t)$, $\varphi (t)$ должны сводится к равновесному решению $r = {{R}_{0}}$, φ = 0.

Для удобства вычислений произведем замену переменных

где $r{\text{*}}$ и $t{\text{*}} = t\sqrt {g{\text{/}}{{R}_{0}}} $ – безразмерные переменные, которые далее будем обозначать обычным образом через r, t. В результате уравнения движения (2.6)–(2.7) принимают вид, удобный для применения теории возмущений:

Решение системы (3.2)–(3.3) можно искать в виде степенных рядов по малому параметру $\varepsilon $:

Поиск неизвестных функций ${{r}_{k}}(t),\;{{\varphi }_{k}}(t)$ в разложениях (3.4)–(3.5) требует выполнения стандартных, но достаточно громоздких символьных вычислений, которые выполняются в данной работе с помощью системы компьютерной алгебры Wolfram Mathematica. Для подстановки решений $r(t),\;\varphi (t)$ в уравнения (3.2)–(3.3) и автоматического вычисления всех производных удобно воспользоваться анонимными функциями (pure functions) и определить правила замены вида

Для разложения правых частей полученных уравнений в ряды по степеням параметра $\varepsilon $ с точностью до второго порядка, например, достаточно к каждому уравнению применить функцию

Затем встроенная функция $Coefficient[eq,\varepsilon ,k]$ позволяет выделить в выражении $eq$ коэффициент при ${{\varepsilon }^{k}},\;k = 0,1,2,...$

Выполняя описанные символьные вычисления и приравнивая коэффициенты при одинаковых степенях параметра $\varepsilon $ в левой и правой части каждого уравнения (3.2)–(3.3), получаем следующую систему линейных дифференциальных уравнений:

Отметим, что линейные дифференциальные уравнения второго порядка (3.6)–(3.11) последовательно решаются с помощью встроенной функции $DSolve$. Без ограничения общности рассуждений можем предположить, что в начальный момент времени груз ${{m}_{1}}$ находится в отклоненном от вертикали положении и начинает движение без начальной скорости. Тогда решение уравнения (3.6) при начальном условии ${{\dot {\varphi }}_{0}}(0) = 0$ можно записать в виде

где ${{C}_{0}}$ – неизвестная постоянная, равная амплитуде колебаний в нулевом приближении по ε, которая находится из условия, что в правой части уравнения (3.7) присутствуют только осциллирующие функции. Подставляя решение (3.12) в (3.7) и выполняя несложные символьные преобразования, получаем:

Отметим, что наличие постоянного слагаемого в правой части уравнения (3.13) приводит к возрастанию или убыванию функции ${{r}_{1}}(t)$. Поскольку нас интересует периодическое решение, не зависящее от времени слагаемое следует приравнять к нулю. В результате находим:

Поскольку груз m₁ начинает движение без начальной скорости, а его начальное положение не известно, дифференциальное уравнение второго порядка (3.13) интегрируем с одним начальным условием ${{\dot {r}}_{1}}(0) = 0$ и с учетом (3.14) получаем:

В решении (3.15) появляется новая неизвестная постоянная ${{B}_{1}}$, которая находится из условия, что в правой части уравнения (3.8) отсутствуют резонансные члены, пропорциональные $\cos t$ и $sint$. Отметим, что появление резонансных членов в правой части (3.8) привело бы к неограниченному возрастанию функции ${{\varphi }_{1}}(t)$, что невозможно в замкнутой консервативной системе (см., напр., [16]).

Подставляя решения (3.12) и (3.15) в уравнение (3.8), получаем:

Условие отсутствия резонансов в (3.16) дает

Интегрируя (3.16) с учетом (3.17) при начальном условии ${{\dot {\varphi }}_{1}}(0) = 0$, находим:

где C₁ – неизвестная постоянная, которая опять находится из условия, что в правой части уравнения (3.9) присутствуют только осциллирующие функции.

Подставляя решения (3.12), (3.15) и (3.18) в уравнение (3.9) и учитывая (3.14), (3.17), получаем:

Из уравнения (3.19) находим

Интегрирование (3.19) с учетом (3.20) при начальном условии ${{\dot {r}}_{2}}(0) = 0$ дает:

где B₂ – неизвестная постоянная, которая находится из условия, что в правой части уравнения (3.10) отсутствуют резонансные члены.

Подставляя решения (3.12), (3.15), (3.18) и (3.21) в уравнение (3.10) и учитывая (3.14), (3.17), (3.20), получаем:

Условие отсутствия резонансов в (3.22) дает

Интегрируя (3.22) с учетом (3.23) при начальном условии ${{\dot {\varphi }}_{2}}(0) = 0$, находим:

где C₂ – неизвестная постоянная, которая опять находится из условия, что в правой части уравнения (3.11) присутствуют только осциллирующие функции.

Подставляя решения (3.12), (3.15), (3.18), (3.21) и (3.24) в уравнение (3.11) и учитывая (3.14), (3.17), (3.20), (3.23), получаем:

Из уравнения (3.25) находим

Интегрирование (3.25) с учетом (3.26) при начальном условии ${{\dot {r}}_{3}}(0) = 0$ дает:

где ${{B}_{2}}$ – неизвестная постоянная, которая находится из условия, что в правой части уравнения для φ₃(t) отсутствуют резонансные члены.

В результате с точностью до второго порядка по $\varepsilon $ получаем решение уравнений движения (3.2)–(3.3) в виде

Легко видеть, что полученное решение является периодическим, причем частота колебаний длины маятника $r(t)$ равняется удвоенной частоте колебаний угловой переменной $\varphi (t)$, т.е. наблюдается резонанс частот $2:1$.

Напомним, что переменные $r(t)$ и $\varphi (t)$ в (3.28), (3.29) являются безразмерными (см. (3.1)). Используя выражения (3.28), (3.29), определяем начальные условия в исходных переменных:

Отметим, что амплитуда колебаний маятника, определяемая выражением (3.30) и равная $\varphi (0)$, зависит от разницы масс грузов. При заданной частоте колебаний, определяемой параметром ${{R}_{0}}$ и равной $\sqrt {g{\text{/}}{{R}_{0}}} $, начальная длина маятника $r(0)$ также зависит от $\varepsilon $ (см. (3.30)).

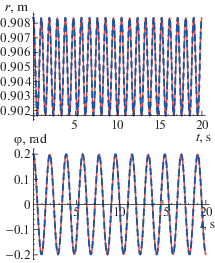
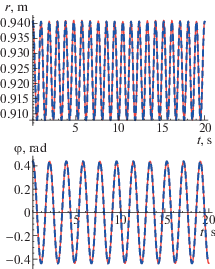
Для демонстрации корректности найденного аналитического решения (3.28), (3.29) выберем некоторые реалистичные значения параметров, например, ${{R}_{0}} = 0.9$ м, $\varepsilon = 0.01$ и g = 9.8 м/с² и найдем численное решение системы (3.2)–(3.3), используя встроенную функцию $NSDolve$ и начальные условия (3.30). Найденному численному решению соответствуют на рис. 2 сплошные линии, а штриховые линии изображают функции (3.28), (3.29). Как видим, обе кривые совпадают. Отметим также, что увеличение разницы масс грузов ($\varepsilon = 0.05$) приводит к изменению начальных значений $r(0)$ и $\varphi (0)$ (см. (3.30)), что означает возрастание амплитуды колебаний и изменение равновесного значения длины маятника r(t) (рис. 3). Очевидно, при дальнейшем возрастании параметра ε амплитуда периодических колебаний системы также должна возрастать, что приведет к нарушению условия малости колебаний и необходимости учета членов более высоких порядков в разложениях тригонометрических функций в уравнениях движения (2.2)–(2.3).

Если предположить, что в начальный момент времени грузу ${{m}_{1}}$, который покоится в положении $\varphi (0) = 0$, сообщают горизонтальную начальную скорость, то уравнение (3.6) следует решать при соответствующем начальном условии, что дает

где C₀ – неизвестная постоянная. Повторяя вычисления с функцией ${{\varphi }_{0}}(t)$, определяемой выражением (3.31), получаем новое решение системы (3.2)–(3.3):

Заметим, что при замене $t \to t + \pi {\text{/}}2$ решение (3.32), (3.33) переходит в полученное ранее решение (3.28), (3.29). Аналогичный результат получается при выборе решения уравнения (3.6) в общем виде

где ${{C}_{0}},\;{{D}_{0}}$ – неизвестные постоянные, и повторения всех вычислений. При этом следует следить за тем, чтобы в дифференциальных уравнениях (3.8), (3.10) для коэффициентов ${{\varphi }_{k}}(t)$ не появились резонансные члены, пропорциональные cost и sint, а в правых частях уравнений (3.7), (3.9), (3.11) сохранялись только осциллирующие члены.

Таким образом, при заданных параметрах ε и ${{R}_{0}}$ существует единственное периодическое решение уравнений движения (3.2), (3.3), представимое в виде степенных рядов (3.4), (3.5). Выполняя вычисления в высших порядках по $\varepsilon $, можно найти искомое периодическое решение с необходимой точностью, хотя вычисления становятся все более громоздкими и для их выполнения требуется применение систем компьютерной алгебры.

4. ЗАКЛЮЧЕНИЕ

В настоящей работе обсуждается проблема построения периодического решения уравнений движения обобщенной машины Атвуда. Показано, что при небольшой разнице масс двух грузов и малых колебаниях груза меньшей массы уравнения движения имеют единственное периодическое решение, представимое в виде степенных рядов по малому параметру ε. Последовательно описаны символьные вычисления, необходимые для определения коэффициентов этих рядов, и найдено соответствующее решение с точностью до второго порядка по ε. Сравнение найденного аналитического решения с численным решением уравнений движения показало справедливость полученных теоретических результатов.

Отметим, что хотя найденные решения (3.28), (3.29) не выглядят слишком громоздкими, их получение с точностью до третьего и более высокоих порядков по ε связаны с большим объемом символьных вычислений, которые можно эффективно выполнять с помощью систем компьтерной алгебры. В данной работе все вычисления и визуализация результатов выполнены с использованием системы компьютерной алгебры Wolfram Mathematica.