1. На главную
  2. Электронные версии
  3. Программирование
  4. № 4, 2020

Программирование, 2020, № 4, стр. 36-45

НЕКОТОРЫЕ НЕДОСТАТКИ ВХОДНОГО СИНТАКСИСА KeYmaera

Т. Баар *

Hochschule für Technik und Wirtschaft (HTW) Berlin, Department of Engineering I
12459 Berlin, Wilhelminenhofstraße 75A, Germany

* E-mail: thomas.baar@htw-berlin.de

Поступила в редакцию 10.02.2020
После доработки 20.02.2020
Принята к публикации 15.03.2020

Полный текст (PDF)

Аннотация

Автоматическое средство доказательства теорем KeYmaera позволяет (1) описать киберфизические системы в виде гибридных программ, (2) специфицировать свойства для определенной системы, и (3) формально верифицировать эти свойства с использованием специальной логики, называемой дифференциальной динамической логикой. Синтаксис гибридных программ достаточно примитивен и охватывает только самые основные операторы, такие как присваивание (assignment), условная инструкция (test), последовательность инструкций (sequential composition), недетерминированный выбор (nondeterministic choice) и итерация (iteration). Решение сохранить синтаксис гибридных программ очень простым имеет различные последствия: преимущество заключается в том, что логическое исчисление для верификации также остается относительно простым; недостатком является то, что даже маленькие программы сложно понимать, и разработчик вынужден программировать, используя метод копирования и вставки, что значительно затрудняет сопровождение. Однако самый существенный недостаток – это отсутствие модуляризации и концепции библиотек, что сильно затрудняет разработку и проверку крупных систем. В данной работе мы выделяем несколько проблем входного синтаксиса KeYmaera и иллюстрируем их на примерах. Для преодоления этих проблем мы сначала создаем метамодель для оригинального синтаксиса. Затем мы предлагаем расширить метамодель с помощью устоявшихся концепций программирования, таких, например, как подпрограмма и внезапное завершение. Мы иллюстрируем наши расширения с помощью нового графического синтаксиса. Примеры из недавно появившегося учебника KeYmaera используются в нашей статьи в качестве иллюстраций.

1. МОТИВАЦИЯ

Киберфизическая система – это система реального мира, которая обычно состоит как из кибер-, так и из физических компонентов. Поведение киберкомпонентов задается (компьютерной) программой, в то время как поведение физического компонента следует законам физики, например, для описания крутящего момента, ускорения, скорости и т.д. Важным подмножеством киберфизических систем являются системы управления, состоящие из датчиков, процессоров и приводов, правильное функционирование которых имеет первостепенное значение и должно быть проверено с использованием методов формальной верификации.

Гибридная система является формальной моделью киберфизической системы. Для определения поведения киберкомпонентов гибридная система должна быть выражена в нотации программ. Поведение физических составляющих моделируется по законам физики, которые формулируются в терминах обыкновенных дифференциальных уравнений. Средство доказательства теорем KeYmaera способно формально верифицировать свойства гибридных систем, выраженных в виде дифференциальной динамической логики [13, 18]. В настоящей статье мы анализируем эту логику, используемую KeYmaera в качестве входного синтаксиса. Мы указываем на некоторые сложности в данном входном синтаксисе и вносим предложения для их устранения.

Одна из главных проблем используемой логики состоит в том, что она представляет собой единственный формализм, который используется для трех разных целей, а именно: i) описать систему, подлежащую анализу (описание системы), ii) формализовать свойства, которые должны быть выполнимыми для системы (спецификация системы) и iii) сформулировать доказательства (верификация системы). Следует обратить внимание на то, что доказательство является деревом формул дифференциальной динамической логики, где каждая связь между узлами дерева доказательств должна быть обоснована одним из правил используемого логического исчисления.

Таким образом, один и тот же формализм служит совершенно разным целям и бывают случаи, когда трудно сказать, каково же назначение данного артефакта на самом деле. Например, пользователь KeYmaera иногда вынужден формулировать описание системы в неинтуитивном виде, просто для того, чтобы свойство этой системы можно было верифицировать. Другими словами, требование к системе, которое нужно доказать, оказывает сильное влияние на то, как описывается сама система! Обратите внимание, что – в идеале – необходимо уметь формулировать описание системы совершенно независимо от таких свойств системы, которые нужно доказать – они определяются, как правило, позже. Как мы проиллюстрируем на примере очень простой модели прыгающего мяча, такая независимость не всегда возможна. Это делает использование KeYmaera скорее искусством, чем инженерией.

Синтаксис KeYmaera достаточно примитивен и заставляет пользователя описывать всю систему как огромный объект (Big Blob), поскольку модуляризация, например, в виде подсистем или подпрограмм, синтаксически просто невозможна. При проведении нашего анализа мы выявили также и другие недостатки, например то, что корректное поведение непрерывных состояний зависит от выполнения правильных инструкций перед входом в состояние, или то, что в разных состояниях, как правило, высокая доля похожести обыкновенных дифференциальных уравнений системы. К сожалению, текущий синтаксис не позволяет непрерывному состоянию “наследоваться” от уже определенного непрерывного состояния, чтобы избежать использования метода копирования-вставки при описании системы.

В дополнение к анализу проблем входного синтаксиса KeYmaera, в настоящей работе мы также делаем предложения по устранению этих проблем. Для того, чтобы описать наши решения на нужном уровне абстракции, мы вместо текстового синтаксиса переходим к абстрактному синтаксису, который мы определяем в виде метамодели. Для того чтобы подчеркнуть независимость наших решений от конкретного синтаксиса, мы также будем использовать графический синтаксис, близкий к абстрактному синтаксическому дереву (AST).

2. ОСНОВНЫЕ ПОНЯТИЯ

Сначала мы рассмотрим логическую основу средства доказательства теорем KeYmaera.

2.1. Динамическая логика

Термин динамическая логика впервые был использован Харелом и др. в работе [7], которая в свою очередь основывается на работах Пратта [16] и Хоара/Флойда [4, 8]. Пратт недавно опубликовал обзор по истории динамической логики в [17].

Динамическая логика (первого порядка) традиционно используется в анализе компьютерных программ и позволяет для программ $\alpha $ сформулировать свойства, описывающие предусловия/постусловия их выполнения. Синтаксически формулы динамической логики строятся на основе арифметических выражений и атомарных формул, таких как $x < 5 + 3$.

Множество формул замкнуто относительно логических операций $\neg ,\; \wedge ,\; \vee ,\; \to ,\; \leftrightarrow $, кванторов $\forall $, $\exists $ и параметризованных модальностей $[\alpha ]$ (box), $\left\langle \alpha \right\rangle $ (diamond), где $\alpha $ – это программа.

Программа синтаксически определяется как дерево операторов. Они включают присваивание (:=), условный оператор ($?$), пустой оператор ($skip$11) как атомарные операторы и недетерминированный выбор ($ \cup $), последовательность операторов ($;$), и итерация ($ * $) как составные операторы. Кроме того, разрешены некоторые производные инструкции (известные как синтаксический сахар). Например, программа

$if\;c\;then\;s1\;else\;s2\;endif$
определяется как синоним для

$(?c;s1) \cup (?\neg c;s2)$

В версии динамической логики, поддерживаемей KeYmaera, все условия (например, 3 + 8), включая переменные, имеют тип Real, поэтому нет поддержки сложной системы типов. Для подробного ознакомления с синтаксисом и семантикой динамической логики, читатель может обратиться к [6].

Семантически, формула в виде $\phi \to [\alpha ]\psi $ декларирует, что программа $\alpha $, при запуске в состоянии, в котором ϕ выполнена, может либо не завершиться либо, в случае фактического завершения, всегда приведет к состоянию, в котором выполнена $\psi $. Другая модальность динамической логики $\langle \,\rangle $ (diamond), имеет следующую семантику: $\left\langle \alpha \right\rangle \psi $ декларирует, что программа $\alpha $ завершается и для хотя бы одного состояния формула $\psi $ выполнена (обратите внимание, что $\alpha $ может вести себя недетерминированно).

В качестве примера рассмотрим формулу

(2.1)
$\begin{gathered} x > 0 \to [if\;x > 0\;then\;x: = x - 1 \\ else\;x: = - 25\;ednif;\;x: = x + 2]x > 1 \\ \end{gathered} $

Программа $\alpha $ внутри []-модальности представляет собой последовательную композицию (оператор $;$) условного выражения и присваивания (оператор $: = $). Требование, сформулированное в (2.1) к программе $\alpha $ читается следующим образом: Всякий раз, когда $\alpha $ начинается в состоянии, в котором x > 0 выполнено, x > 1 также должен выполняться и после завершения $\alpha $ (обратите внимание, что завершаемость $\alpha $ не является частью требования). Формула (2.1) действительно корректна, т.е. во всех случаях формула оценивается как истинная (см. [6] для формального определения корректности).

В неформальной обстановке довольно легко спорить о корректности (2.1): импликация принимает значение false, если его предпосылка оценивается как true, а его следствие – false. Предпосылка здесь – x > 0. Согласно этому, при выполнении программы $\alpha $, then ветвь первого оператора (if) всегда выполняется и уменьшает переменную $x$ на два. Во второй инструкции значение $x$ увеличивается опять на один, так что значение $x$ в постусловии – давайте обозначим его ${{x}_{{post}}}$ – это ${{x}_{{post}}}$ = = xpre – 1 + 2, где ${{x}_{{pre}}}$ обозначает значение переменной $x$ в предусловии. Таким образом, (2.1) может быть сведено к условию корректности ${{x}_{{pre}}}$ – 1 + + 2 > 1, которое никогда не сможет обратиться в false, если мы предположим, что ${{x}_{{pre}}} > 0$. К счастью, нам не нужно полагаться далее на неформальные способы, чтобы показать корректность (2.1), ведь можно использовать средство KeYmaera, которое доказывает (2.1) полностью автоматически.

Обратите внимание, что формулы динамической логики ничего не говорят о времени исполнения программы $\alpha $, а формулируют только свойства по отношениям $\alpha $ к предусловию/постусловию. Можно просто считать, что все операторы в программе $\alpha $ исполняются мгновенно, т.е. их исполнение не занимает никакого времени. Это важное отличие от расширения динамической логики, называемого дифференциальной динамической логикой, которое мы рассмотрим ниже.

2.2. Дифференциальная динамическая логика

Дифференциальная динамическая логика [12] является расширением динамической логики, что означает, что каждая формула динамической логики также является и формулой дифференциальной динамической логики, и она таким же образом задает предположения о программе $\alpha $.

Однако, так как формулы дифференциальной динамической логики в основном используются для описания поведения киберфизических систем, мы говорим, что программа $\alpha $ есть код поведения киберфизической системы, а не $\alpha $ выполняется на машине, как мы делаем для программ $\alpha $ чистых формул динамической логики.

Единственная разница между динамической логикой и дифференциальной динамической логикой состоит в добавлении нового вида операторов, называемым оператор непрерывного состояния ({…}) (или просто оператор эволюции), который допускается в программах α. Когда во время выполнения α достигается оператор эволюции, выполнение этого оператора занимает время и система остается в соответствующем непрерывном состоянии на некоторое время. Обратите внимание, что речь идет о новом семантическом концепте дифференциальной динамической логики, который знаменует собой важнейшее отличие от чистой динамической логики!

Выполнение оператора эволюции для модели киберфизической системы означает для системы оставаться в непрерывном состоянии столько, сколько нужно (время пребывания, как правило, выбирается недетерминированно). Тем не менее, разработчик модели имеет две возможности ограничить период времени, в течение которого система остается в таком состоянии. Первая возможность состоит в том, чтобы добавить так называемое ограничение домена к оператору эволюции, которое является формулой первого порядка и отделено от остальной части утверждения с помощью & (амперсанд). Ограничение домена семантически означает, что система не может оставаться в непрерывном состоянии дольше, чем на период времени, в котором ограничение оценивается как true. Другими словами: как только текущее значение ограничения домена переключается с true на false, система должна покинуть состояние эволюции.

Вторая возможность ограничить период времени – это задать последовательную композицию оператора эволюции с последующей условной инструкцией. Теоретически, машина может выйти из состояния эволюции в любое время, но если последующее условие оценивается как false, тогда эта ветвь выполнения отстраняется от логического анализа поведения системы. Таким образом, оператор эволюции, за которым сразу следует условный оператор, является общей техникой, чтобы заставить систему оставаться в непрерывном состоянии до тех пор, пока условие теста оценивается как false.

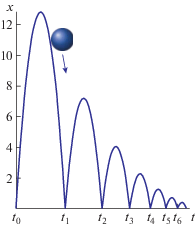
2.2.1. Прыгающий мяч. Мы проиллюстрируем как использование оператора эволюции, так и два упомянутых метода ограничения времени, в течение которого система будет оставаться в непрерывном состоянии, с помощью следующего примера прыгающего мяча:

(2.2)
$\begin{gathered} {{\alpha }_{{BB}}} \equiv (\{ x{\text{'}} = v,v{\text{'}} = - g\& x \geqslant 0\} ; \\ ?x = 0;\;v: = - cv) * \\ \end{gathered} $

Поведение прыгающего мяча описывается с помощью нового типа переменных, называемых непрерывные переменные. Например, переменная x всегда неотрицательна и хранит положение мяча, а переменная ${v}$ – хранит скорость, которая может быть как положительной (мяч поднимается), так и отрицательной (мяч опускается). Константа g является ускорением свободного падения, она больше 0. Константа c – это коэффициент демпфирования, число от 0 до 1.

Структура ${{\alpha }_{{BB}}}$ такова, что эта программа представляет собой оператор итерации (оператор *) над последовательностью (оператор ;), состоящей из оператора эволюции (заключенного в фигурные скобки $\{ \ldots \} $), сопровождаемого проверкой условия (оператор ?), а также присваиванием (оператор :=). Программа ${{\alpha }_{{BB}}}$ читается следующим образом: система запускается в состоянии с заданными значениями для переменных x и $v$ (эти значения пока не указаны, но позже мы заставим начальную позицию x0 быть положительным числом, в то время как начальная скорость ${{v}_{0}}$ может быть положительной, нулевой или отрицательной) и, пока система остается в первом непрерывном состоянии, значения $x,v$ будут изменяться непрерывно с течением времени в соответствии с законами физики. Таким образом, непрерывные переменные $x,v$ представляют собой скорее функции $x(t),v(t)$ от времени t. Соответствующие физические законы для $x,v$ выражаются двумя обыкновенными дифференциальными уравнениями:

$\begin{gathered} x{\text{'}} = v \\ v{\text{'}} = - g \\ \end{gathered} $

Последнее означает, что скорость постоянно уменьшается со временем из-за гравитационной силы Земли. К счастью, это дифференциальное уравнение имеет простое полиноминальное решение, которое значительно облегчает анализ всей системы:

$v(t) = {{v}_{0}} + - g * t$

Аналогично, в зависимости от изменяющейся скорости $v$, положение x прыгающего мяча изменяется как

$x(t) = {{x}_{0}} + {{v}_{0}} * t + \frac{{ - g}}{2} * {{t}^{2}}$

Ограничение домена $x \geqslant 0$, упомянутое в операторе эволюции, позволяет системе оставаться в непрерывном состоянии только до тех пор, пока x неотрицательно. Теоретически, система может в любой момент покинуть это состояние, но следующим оператором является проверка условия $? = 0$. Таким образом, если система выходит из непрерывного состояния с x > 0, то эта вычислительная ветвь будет отбрасываться.

При верификации свойств системы мы можем полагаться на то, что система покидает непрерывное состояние только тогда, когда x = 0, то есть когда мяч касается земли. Следующее присваивание ${v}: = - c{v}$ определяет, что мяч отпрыгивает вверх: отрицательное значение ${v}$ падения мяча мгновенно изменится до положительного значения (умножение на –c), а абсолютное значение ${v}$ уменьшается, поскольку мяч теряет энергию при касании земли и изменении направления движения. На рис. 1 показано, как меняется позиция x прыгающего мяча с течением времени (пример траектории).

Рис. 1.

Пример траектории прыгающего мяча [13, стр. 98].

3. ПРОБЛЕМЫ ВХОДНОГО СИНТАКСИСА KeYmaera

Дифференциальная динамическая логика, представленная выше, поддерживается средством KeYmaera которое позволяет формально верифицировать важные свойства технической системы, что было продемонстрировано в многочисленных тематических исследованиях в разных доменах, например, для самолетов [9, 14], поездов [15] и роботов [11].

Тем не менее, входной синтаксис, используемый для формализации свойств в виде формул дифференциальной динамической логики, страдает от многочисленных проблем, которые описаны ниже. Решения, которые мы предлагаем для преодоления этих проблем, представлены далее в разделе 4.

(1) Инвариантные спецификации не поддерживаются явно. Помимо описания поведения гибридных систем, как показано на примере программы ${{\alpha }_{{BB}}}$ для прыгающего мяча, основное назначение дифференциальной динамической логики – определить также требования для таких систем. Типичными и очень важными на практике требованиями являются так называемые свойства безопасности, сообщающие, что система никогда не попадает в “плохую ситуацию”. Давайте зададим “плохую ситуацию” с помощью $\neg \psi $. Мы можем показать отсутствие $\neg \psi $, доказав, что во всех достижимых состояниях системы формула $\psi $ выполнима, то есть $\psi $ является инвариантом. Если мы допустили, что все операторы, кроме операторов эволюции, выполнены мгновенно, тогда представленный инвариант на самом деле означает, что $\psi $ выполняется в то время, когда система находится в любом из своих непрерывных состояний. Тем не менее, модальные операторы позволяют описать состояние только после того, как программа завершилась. Например, для системы прыгающего мяча ${{\alpha }_{{BB}}}$, определенной в (2.2), мы можем очень легко доказать

(3.1)
$x = 0 \to [{{\alpha }_{{BB}}}]x = 0$

Заметьте, однако, что не было доказано, что x = 0 является инвариантом! Если мы хотим выразить такой инвариант, что позиция $x$ остается все время в интервале $[0,H]$, в то время как H задает начальную позицию системы, и если скорость ${v}$ изначально равна 0, мы должны признать, что формула

(3.2)
$\begin{gathered} H > 0 \wedge {v} = 0 \wedge x = H \\ \wedge \,0 < c \wedge c < 1 \to [{{\alpha }_{{BB}}}]x \leqslant H \\ \end{gathered} $
доказуема, но НЕ определяет $x \leqslant H$ как инвариант, потому что эта формула не говорит ничего о x и H, пока система остается в непрерывном состоянии $\{ x{\text{'}} = v,\;v{\text{'}} = - g\& x \geqslant 0\} $, которое является частью ${{\alpha }_{{BB}}}$. Чтобы доказать, что $x \leqslant H$ является инвариантом, пользователь вынужден переформулировать ${{\alpha }_{{BB}}}$ в

(3.3)
$\begin{gathered} \alpha _{{BB}}^{'} \equiv (\{ x{\text{'}} = v,v{\text{'}} = - g\& x \geqslant 0\} ; \\ (skip \cup (?x = 0;v: = - cv))) * \\ \end{gathered} $

Это, однако, было бы примером описания системы исходя из требования, которое мы хотели бы доказать! Мы считаем это плохим стилем.

(2) Определение оператора эволюции не может быть использовано повторно. Оператор эволюции должен содержать все обыкновенные дифференциальные уравнения, которые выполняются в соответствующих состояниях. Если программа содержит несколько операторов эволюции, то все уравнения, как правило, приходится копировать для всех таких операторов, так как обыкновенное дифференциальное уравнение обычно моделирует физический закон, который выполняется в каждом из непрерывных состояний. В настоящее время, синтаксис KeYmaera не позволяет определить все обыкновенные дифференциальные уравнения один раз и затем повторно использовать эти определения для всех встречающихся операторов эволюции. Этот недостаток повторного использования проявляется в стиле “копирование и вставка” при описании системы. В качестве примера, обратимся к пункту 3a из руководства по KeYmaera [18], стр. 10, уравнение (20):

$\begin{gathered} \left\{ {p{\text{'}} = v,v{\text{'}} = - a\& v \geqslant 0 \wedge p + \frac{{{{v}^{2}}}}{{2B}} \leqslant S} \right\} \cup \\ \, \cup \left\{ {p{\text{'}} = v,v{\text{'}} = - a\& v \geqslant 0 \wedge p + \frac{{{{v}^{2}}}}{{2B}} \geqslant S} \right\} \\ \end{gathered} $

Здесь приведено определение двух эволюционных операторов (в фигурных скобках), которые очень похожи и созданы копированием и вставкой.

(3) Определение непрерывного состояния не инкапсулировано. В руководстве по KeYmaera [12, 18] есть часто применяемый шаблон, чтобы гарантировать, что система остается в непрерывном состоянии $ev \equiv \{ \ldots \& \ldots \} $ не дольше, чем на время ε. Это достигается путем расширения определения $ev$ до $ev{\text{'}} \equiv \{ \ldots ,t{\text{'}} = 1\& \ldots \wedge t \leqslant \varepsilon \} $, где $t$ – свежая непрерывная переменная. Вместе с $t{\text{'}} = 1$ дополнительное доменное ограничение $t \leqslant \varepsilon $ вынуждает систему выходить из $ev{\text{'}}$ не позднее, чем через время $\varepsilon $. Однако это уточненное определение $e{v}$ работает только в том случае, если значение $t$ заранее установлено на 0. Чтобы достичь этого, выражение $e{v}$ обычно заменяется на $t: = 0;ev{\text{'}}$. Хотя этот шаблон на практике обычно и работает, определение $ev{\text{'}}$ не инкапсулируется и мешает целостности программ.

(4) Отсутствие понятия подпрограммы (или вызова функции в целом). Когда примеры из руководства по KeYmaera [12, 18] становятся немного сложнее, они описываются в составном виде, например, пункт 3а из [18, p. 10]: $init \to [(ctrl;plant) * ]req$, где $init \equiv \ldots $, $ctrl \equiv \ldots $, $plant \equiv \ldots $, $req \equiv \ldots $. Представление проблемы в такой декомпозированной форме значительно улучшает читабельность. Тем не менее, использование составной записи невозможно для входного файла KeYmaera. В то время как можно задать новые связанные символы $init,\;req$ и ограничения их интерпретации с помощью подформул $init \leftrightarrow \ldots $, $req \leftrightarrow \ldots $, в настоящее время невозможно определить подпрограммы ctrl и plant и составить результирующую программу из этих подпрограмм.

4. ПОДХОД НА ОСНОВЕ МЕТАМОДЕЛИ ДЛЯ РЕШЕНИЯ ВЫЯВЛЕННЫХ ПРОБЛЕМ

Указанные выше проблемы могут быть преодолены путем включения языковых концепций из объектно-ориентированных языков программирования и диаграмм состояний во входной синтаксис KeYmaera. Для того, чтобы обсудить включение новых языковых концепций на правильном уровне абстракции, мы формулируем наше предложение в виде измененной метамодели для входного синтаксиса KeYmaera. В качестве отправной точки мы представляем метамодель для текущего синтаксиса.

4.1. Метамодель для текущего синтаксиса KeYmaera

Метамоделирование [5] – это широко распространенный метод определения абстрактного синтаксиса языков моделирования и программирования. Одним известным способом определения языка является применение языка унифицированного моделирования (UML) [19].

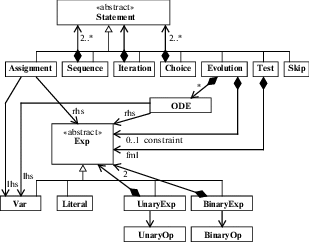
Рисунок 2 показывает скетч метамодели для текущего входного синтаксиса KeYmaera с акцентом на операторы программы. Все метаассоциации с кратностью больше 1 предполагаются упорядоченными. Если кратность метаассоциации отсутствует, тогда 1 является ее значением по умолчанию. Метакласс Exp представляет выражения обоих типов Real (например, 5 + x) и Boolean (например, x $ < $ 10).

Рис. 2.

Метамодель для входного синтаксиса KeYmaera.

Конкретная программа α для KeYmaera может быть представлена экземпляром метамодели. Этот экземпляр эквивалентен результату, полученному при синтаксическом разборе такой программы, т.е. абстрактному синтаксическому дереву (AST).

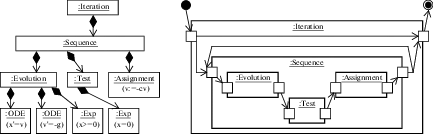
Левая часть рис. 3 показывает метамодель для экземпляра программы прыгающего мяча ${{\alpha }_{{BB}}} \equiv (\{ x{\text{'}}$ = = $v$, $v{\text{'}} = - g\& x \geqslant 0\} $; $?x = 0;v: = - cv) * $, как определено в (2.2). В правой части мы видим выровненное графическое представление абстрактного синтаксическое дерева той же программы. Каждый тип оператора представлен блоком с входными и выходными пинами. Поток управления визуализируется направленными ребрами, соединяющими два пина. Предварительные и заключительное состояния выполнения программы представлены символом начальное/конечное состояние, знакомое из машин состояний UML [19].

Рис. 3.

Экземпляр метамодели (слева) и графический синтаксис, созданный под влиянием потока управления (справа) для программы прыгающего мяча (αBB).

4.2. Решения выявленных проблем

Основываясь на введенных выше графических обозначениях, перейдем к обсуждению решений проблем, перечисленных в разделе 3.

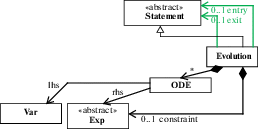
(1) Инвариантные спецификации не поддерживаются явно. Как описано в разделе 3, модальный оператор $[\alpha ]$ всегда относится к пост-состоянию, представленному узлом заключительного состояния на рис. 3, правая часть. Однако для проверки инварианта нам нужна ссылка на состояние после завершения каждого оператора эволюции. Этот момент в решении представлен выходным пином состояния Evolution. То, что требуется в семантике программы – это прямое ребро от каждого выходного пина каждого состояния Evolution до заключительного состояния, как показано на рис. 4, зеленое ребро. Эта концепция известна как внезапное завершение (abrupt termination).

Рис. 4.

Решение проблемы инвариантной спецификации.

Обратите внимание, что внезапное завершение может быть реализовано без каких-либо изменений входного синтаксиса KeYmaera, поскольку оно требует лишь изменения потока управления для существующих операторов.

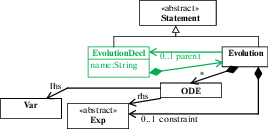
(2) Определение оператора эволюции не может быть использовано повторно. Часто одни и те же обыкновенные дифференциальные уравнения и ограничения появляются в нескольких непрерывных состояниях снова и снова, что ухудшает читабельность. Чтобы предотвратить это, мы предлагаем ввести объявление именованных операторов эволюции, на которые может ссылаться, например, другой оператор эволюции, и наследовать от них дифференциальные уравнения и ограничения. Соответствующее изменение метамодели показано на рис. 5.

Рис. 5.

Решение проблемы повторного использования непрерывных состояний.

Еще одна проблема, которую предстоит обсудить, заключается в том, может ли описание непрерывного состояния производиться в произвольном месте в программе или оно должно быть сделано до программы в качестве глобального описания. Этот вопрос затрагивает важную проблему о том, какую область видимости должен иметь на самом деле идентификатор, введенный таким описанием (см. метаатрибут name). Так как разрешение области действия идентификатора является скорее проблемой при разборе программы, эта проблема выходит за рамки этой статьи.

(3) Определение непрерывного состояния не инкапсулировано. Как было показано при определении проблем, оператор эволюции иногда работает как задумано, только когда переменная была заранее установлена правильным значением. Практически, это означает, что непрерывное состояние EV всегда предшествует присвоению ASGN, поэтому для правильности (ASGN; EV) должен всегда быть определен. Чтобы избавиться от зависимости непрерывного состояния от присваиваний по контексту (который предотвращает простое повторное использование EV в другом контексте), мы предлагаем расширить непрерывное состояние с помощью дополнительных утверждений, которые всегда выполняются при входе или выходе из состояния. Это расширение состояния хорошо известно как входные/выходные действия для машин состояний UML. Соответствующее изменение метамодели показано на рис. 6.

Рис. 6.

Решение проблемы инкапсуляции непрерывного состояния.

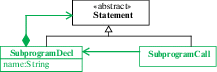
(4) Отсутствие понятия подпрограммы. Одно из основополагающих понятий в программировании – это возможность инкапсулировать инструкции с данным именем и повторно использовать эти инструкции в различных местах программы. Эта концепция обычно называется подпрограмма, процедура или метод; в зависимости от того, используются ли параметры или нет. В целом, это очень старая, проверенная и хорошо понятная концепция, так что мы представляем в настоящем предложении решения только самый простой вариант (см. рис. 7).

Рис. 7.

Решение проблемы с отсутствующими подпрограммами.

5. НА ПУТИ К РЕАЛИЗАЦИИ ПРЕДЛОЖЕНИЙ ПО РЕШЕНИЮ

В этом разделе мы рассмотрим возможные варианты реализации предложенного решения и дадим рекомендации по одному из вариантов реализации.

5.1. Реализация путем расширения средства доказательства теорем KeYmaera

Средство доказательства KeYmaera состоит в основном из синтаксического анализатора для входного синтаксиса и исчисления в форме правил доказательств, которые даже могут быть изменены пользователем. Кроме того, существуют некоторые технические компоненты, такие как (i) движок для применения правил доказательств для создания формального доказательства, (ii) адаптеры для подключения внешних систем доказательств, такие как Z3 или Mathematica, и (iii) графический интерфейс для контроля процесса редактирования доказательства. Однако все эти технические компоненты выходят за рамки этой статьи.

Чтобы понять наши предложения, необходимо отличать чисто синтаксические изменения от тех, которые влияют на логическое исчисление, используемое KeYmaera. К последним относятся поддержка внезапного завершения (проблема (1)) и возможность вызова подпрограмм (проблема (4)). Эти изменения потребуют значительного расширения исчисления KeYmaera. Хотя такое расширение требует глубокого знания основного механизма доказательств, тем не менее, оно возможно, как демонстрирует средство доказательства KeY [1]22. KeY – это интерактивный инструмент формальной верификации программ, реализованных на языке Java, и его исчисление охватывает все тонкости реального языка программирования, включая вызов функции, стек вызовов, область видимости переменных, внезапное завершение, выбрасывание исключения, анализ кучи и т.д.

Чисто синтаксические изменения среди наших предложений, то есть решение проблем (2), (3), могут быть реализованы в KeYmaera просто путем расширения синтаксического парсера. Обратите внимание, что создание альтернативного входного синтаксиса также является и темой текущего проекта под названием Sphinx [10], осуществляемого авторами KeYmaera. Sphinx преследует цель добавить средству доказательства графический интерфейс и позволит пользователю создавать программу в чисто графическом синтаксисе (аналогично нашей графической нотации, предложенной на рис. 3, правая часть).

Общая проблема, при любых глубоких изменениях средства доказательства KeYmaera заключается в необходимости технических знаний. Кроме того, существуют веские причины для сохранения версии KeYmaera с оригинальным синтаксисом из-за его простоты, благодаря которой KeYmaera гораздо проще использовать для обучения, чем, например, его предшественника KeY. Новую версию KeYmaera с глубокими изменениями сложно поддерживать, так как оригинальная KeYmaera может в будущем также развиваться. По этим причинам глубокие изменения могут сделать только первоначальные авторы KeYmaera сами, и вряд ли кто-то другой.

5.2. Реализация путем создания DSL-фронтэнда

Альтернативным и гибким подходом является разработка DSL-фронтэнда (внешнего интерфейса в виде проблемно-ориентированного языка) с целью включения новых концепций языка, представленных в разделе 4.2. Основная идея заключается в разработке нового предметно-ориентированного языка в соответствии с данной метамоделью. Обратите внимание, что метамодель охватывает только абстрактный синтаксис и сохраняет некоторую гибкость для конкретного синтаксиса. Современные фреймворки для создания DSL языков, такие как Xtext и Sirius, даже позволяют иметь для одного DSL несколько представлений (т.е. конкретных синтаксисов), поддерживаемых соответствующими редакторами, например, для текстового и графического синтаксиса.

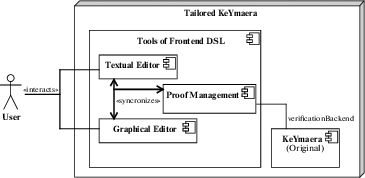
Рисунок 8 показывает общую архитектуру такого инструмента. Следует обратить внимание, что новый инструмент позволит пользователю для создания модели синхронно работать и с текстовым, и с графическим представлением. Однако, такие модели нельзя просто преобразовать во входные файлы для KeYmaera, потому что новый синтаксис поддерживает некоторые семантически-новые понятия, такие как внезапное завершение или стек вызова подпрограммы. Задача компонента ProofManagement – разделить задачи, например, для доказательства инварианта – на меньшие условия корректности, которые могут быть сформулированы как формулы дифференциальной динамической логики, и передать эти условия оригинальному средству KeYmaera в виде проверочного бэкэнда. Как инвариантная задача может быть разбита на небольшие условия корректности, показано на конкретном примере в [2].

Рис. 8.

Архитектура решения с использованием DSL-фронтэнда.

6. ОБЗОР ЛИТЕРАТУРЫ ПО ТЕМЕ ИССЛЕДОВАНИЯ

Разработка DSL может быть проведена с помощью многочисленных технологий, например Xtext, Spoofax, Metaedit, MPS. Для реализации DSL как с текстовым, так и с графическим конкретным синтаксисом, очень интересно сочетание Xtext и Sirius.

Расширение средства доказательства KeYmaera графическим синтаксисом для программ дифференциальной динамической логики (DDL) проделано в проекте Sphinx [10]. Архитектура этого инструмента очень похожа на наше предложение, представленное на рис. 8, но акцент – в отличии от нашего подхода – лежит не на улучшении читабельности и модульности, делая входной синтаксис более богатым, а чтобы позволить пользователю графически построить программу для DDL.

Обогащение простого императивного языка понятиями из объектно-ориентированного программирования – не редкость в истории компьютерной науки (например, переход от C к C++ или от Modula к Oberon), однако это все еще считается вызовом. В [3] указан отличный учебник Bettini на тему, как включить в простой последовательный язык на основе простых выражений дополнительные понятия из объектно-ориентированного программирования (например, класс, поле, метод, область видимости). Полученный язык называется в этом учебнике SmallJava и иллюстрирует почти все технические трудности при реализации Java-подобного языка программирования на основе DSL.

7. ЗАКЛЮЧЕНИЕ И ДАЛЬНЕЙШАЯ РАБОТА

Синтаксис программ дифференциальной динамической логики, поддерживаемый средством доказательства теорем KeYmaera, очень прост и низкоуровнен. Преимущество этого решения заключается в том, что даже логическое исчисление для доказательства правильности таких программ является относительно простым, доказательства могут быть легко построены и поняты. С другой стороны, как только примеры становятся немного сложнее – программы становится трудно читать, они плохо структурированы, и их невозможно использовать повторно в другом контексте.

В данной статье мы определили четыре общие проблемы при применении текущего синтаксиса программ на практике. Кроме того, мы внесли предложения по преодолению выявленных проблем путем включения во входной синтаксис KeYmaera проверенных концепций из языков программирования и машин состояний UML. Эти концепции могут сделать программы масштабируемыми и более понятны, так как они способствуют удобочитаемости и модульности.

Наши предложения были сформулированы в форме измененной метамодели, представляющей абстрактный синтаксис программ. Ее преимущество для формулирования предложений заключается в их высокой точности, при этом вопрос, как на самом деле должны быть реализованы изменения в данном конкретном синтаксисе, остается открытым. В настоящее время реализация DSL-фронтэнда, основной составляющей набора инструментов адаптированной KeYmaera, находится в стадии разработки, которая еще не завершена.

Список литературы

  1. Ahrendt W., Beckert B., Bubel R., Hähnle R., Schmitt P.H., Ulbrich M. (eds.): Deductive Software Verification – The KeY Book – From Theory to Practice, Lecture Notes in Computer Science, vol. 10001. Springer, 2016.

  2. Baar T., Staroletov S. A control flow graph based approach to make the verification of cyber-physical systems using KeYmaera easier. Modeling and Analysis of Information Systems. 2018. V. 25 (5). P. 465–480.

  3. Bettini L. Implementing Domain-Specific Languages with Xtext and Xtend. Packt Publisher, 2nd edn. 2016.

  4. Floyd R.W. Assigning meanings to programs. In: Schwartz J.T. (ed.) Proceedings of Symposium on Applied Mathematics. pp. 19–32. Mathematical Aspects of Computer Science, American Mathematical Society, 1967.

  5. Gonzalez-Perez C., Henderson-Sellers B. Metamodelling for software engineering. Wiley, 2008.

  6. Harel D., Kozen D., Tiuryn J. Dynamic Logic. Foundation of Computing, MIT Press, 2000.

  7. Harel D., Meyer A.R., Pratt V.R. Computability and completeness in logics of programs (preliminary report). In: Hopcroft J.E., Friedman E.P., Harrison M.A. (eds.) Proceedings of the 9th Annual ACM Symposium on Theory of Computing, May 4-6, 1977, Boulder, Colorado, USA. pp. 261–268. ACM (1977).

  8. Hoare C.A.R. An axiomatic basis for computer programming. Commun. ACM 12(10), 576–580 (1969).

  9. Jeannin J., Ghorbal K., Kouskoulas Y., Gardner R., Schmidt A., Zawadzki E., Platzer A. A formally verified hybrid system for the nextgeneration airborne collision avoidance system. In: Baier C., Tinelli C. (eds.) Tools and Algorithms for the Construction and Analysis of Systems – 21st International Conference, TACAS 2015. LNCS, vol. 9035, pp. 21–36. Springer, 2015.

  10. Mitsch S. Modeling and Analyzing Hybrid Systems with Sphinx – A User Manual. Carnegie Mellon University and Johannes Kepler University (2013), available from: http://www.cs.cmu.edu/afs/cs/Web/People/smitsch/pdf/userdoc.pdf.

  11. Mitsch S., Ghorbal K., Platzer A. On provably safe obstacle avoidance for autonomous robotic ground vehicles. In: Newman P., Fox D., Hsu D. (eds.) Robotics: Science and Systems IX, Technische Universität Berlin, Berlin, Germany, June 24–June 28, 2013.

  12. Platzer A. Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics. Springer, Heidelberg, 2010.

  13. Platzer A. Logical Foundations of Cyber-Physical Systems. Springer, 2018.

  14. Platzer A., Clarke E.M. Formal verification of curved flight collision avoidance maneuvers: A case study. In: Cavalcanti A., Dams D. (eds.) FM 2009: Formal Methods, Second World Congress, Eindhoven, The Netherlands, November 2–6, 2009. Proceedings. Lecture Notes in Computer Science, vol. 5850, pp. 547–562. Springer, 2009.

  15. Platzer A., Quesel J. European train control system: A case study in formal verification. In: Breitman K.K., Cavalcanti A. (eds.) Formal Methods and Software Engineering, 11th International Conference on Formal Engineering Methods, ICFEM 2009, Rio de Janeiro, Brazil, December 9–12, 2009. Proceedings. Lecture Notes in Computer Science, vol. 5885, pp. 246–265. Springer, 2009.

  16. Pratt V.R. Semantical considerations on Floyd-Hoare logic. In: 17th Annual Symposium on Foundations of Computer Science, Houston, Texas, USA, 25–27 October 1976. pp. 109–121. IEEE Computer Society, 1976.

  17. Pratt V.R. Dynamic logic: A personal perspective. In: Madeira A., Benevides M.R.F. (eds.) Dynamic Logic. New Trends and Applications – First International Workshop, DALI 2017, Brasilia, Brazil, September 23–24, 2017, Proceedings. Lecture Notes in Computer Science, vol. 10669, pp. 153–170. Springer, 2017.

  18. Quesel J.D., Mitsch S., Loos S., Arêchiga N., Platzer A. How to model and prove hybrid systems with KeYmaera: A tutorial on safety. STTT. 2016. V. 18 (1). P. 67–91.

  19. Rumbaugh J.E., Jacobson I., Booch G. The unified modeling language reference manual – covers UML 2.0, Second Edition. Addison Wesley object technology series, Addison-Wesley, 2005.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал