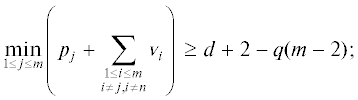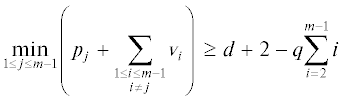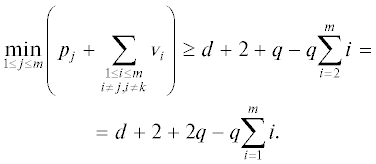Программирование, 2021, № 1, стр. 45-55
ПОСТРОЕНИЕ ЧАСТИЧНЫХ ЛОРАНОВЫХ РЕШЕНИЙ УСЕЧЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ
a Факультет вычислительной математики и кибернетики МГУ им. М.В. Ломоносова
119991 Москва, Воробьевы горы, Россия
b Федеральный исследовательский центр “Информатика и управление” РАН
119333 Москва, ул. Вавилова, 40, Россия
* E-mail: ast.a_s@mail.ru
Поступила в редакцию 01.08.2020
После доработки 26.08.2020
Принята к публикации 14.09.2020
Аннотация
Рассматривается задача построения начальных членов формальных лорановых рядов, являющихся решениями для заданной компоненты yk ($1 \leqslant k \leqslant m$) вектора неизвестных y дифференциальной системы $y{\kern 1pt} ' = Ay$, где $y = {{({{y}_{1}}, \ldots ,{{y}_{m}})}^{T}}$, A – m × m-матрица, элементами которой являются d-усечения формальных лорановых рядов, т.е. их начальные члены до степени $d \geqslant 0$ включительно. Предлагается алгоритм решения задачи с использованием алгоритма TSLS (Truncated Series Laurent Solution). Строящиеся предлагаемым алгоритмом первые члены формальных лорановых решений для yk являются инвариантными относительно возможных продолжений элементов матрицы исходной системы.
1. ВВЕДЕНИЕ
Дифференциальные системы вида
где A – матрица размера m × m, а $y = {{({{y}_{1}}, \ldots ,{{y}_{m}})}^{T}}$ – вектор неизвестных, которые часто называют нормальными дифференциальными системами, находят широкое применение в различных областях математики. Под решением системы (1) понимается вектор y из m компонент. К настоящему времени известно много алгоритмов построения решений дифференциальных систем разного вида, многие из которых реализованы и доступны в современных системах компьютерной алгебры. В некоторых прикладных задачах интерес могут представлять не все компоненты вектора неизвестных, а только их часть. В этом случае целесообразна постановка задачи частичного решения системы, т.е. построение некоторых заранее выбранных компонент вектора решений. Методы построения частичных решений также известны (см., например, [1]).Отдельный интерес представляют системы, коэффициентами которых являются формальные ряды (степенные или лорановы). Поскольку ряды являются потенциально бесконечными объектами, их использование вызывает ряд трудностей при реализации в компьютерных системах символьных вычислений. При этом некоторые задачи оказываются алгоритмически неразрешимыми (см. [2, 3]). Тем не менее, методы для построения решений дифференциальных систем, коэффициентами которых являются ряды, существуют ([4]).
Ряды, использующиеся в качестве коэффициентов систем, могут быть заданы в приближенном виде, а именно в виде так называемых усечений – начальных отрезков рядов. Задачи, связанные с дифференциальными уравнениями, коэффициенты которых являются усеченными рядами, рассматриваются в некоторых работах ([3, 5]).
В настоящей работе также будут рассматриваться дифференциальные системы вида (1), коэффициентами которых являются усечения формальных лорановых рядов. Нас будет интересовать задача построения частичного решения, т.е. построение некоторой заранее заданной компоненты решения yk ($1 \leqslant k \leqslant m$), в виде такого усечения лоранового ряда, которое не зависит от возможных продолжений коэффициентов системы.
В разделе 2 приводятся обозначения и определения основных понятий, используемых в работе. В разделе 3 приводится постановка задачи и общая схема решения. Описание предлагаемого алгоритма решения поставленной задачи приведено в подразделе 4.4, некоторые детали его реализации в системе Maple – в подразделе 4.5.
2. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Пусть K – поле характеристики 0, под которым будет пониматься некоторое числовое поле, например, поле рациональных чисел $\mathbb{Q}$. Также будем использовать стандартное обозначение K[x] для кольца многочленов переменной $x$ с коэффициентами из K: если p – ненулевой многочлен из K[x], то $p = {{a}_{0}} + {{a}_{1}}x + \ldots + {{a}_{n}}{{x}^{n}} = \sum\nolimits_{i = 0}^n \,{{a}_{i}}{{x}^{i}}$, где ${{a}_{i}} \in K$ (i = = 0, 1, ..., n), ${{a}_{n}} \ne 0$, $degp = n$ – степень многочлена p; при этом $deg0 = - \infty $.
Наряду с обычными многочленами из K[x], будем также рассматривать многочлены Лорана (лорановы многочлены) из кольца $K[x,{{x}^{{ - 1}}}]$: если p – ненулевой многочлен Лорана, то $p = \sum\nolimits_{i = m}^n \,{{a}_{i}}{{x}^{i}}$, где $m,n \in Z$, $m \leqslant n$, ${{a}_{i}} \in K$ ($m \leqslant i \leqslant n$), ${{a}_{m}} \ne 0$, ${{a}_{n}} \ne 0$, $degp = n$.
Кольца K[x] и $K[x,{{x}^{{ - 1}}}]$ будем рассматривать как дифференциальные кольца с обычным дифференцированием ${\kern 1pt} ' = \tfrac{d}{{dx}}$, для которых K будет являться полем констант.
Для кольца квадратных матриц размера m × m над кольцом R будем использовать стандартное обозначение ${\text{Ma}}{{{\text{t}}}_{m}}(R)$. Пусть A = $({{a}_{{ij}}}) \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x$, x–1]), тогда $degA = ma{{x}_{{1 \leqslant i,j \leqslant m}}}deg{{a}_{{ij}}}$.
Для кольца формальных степенных рядов и для кольца формальных лорановых рядов с коэффициентами из K будем использовать стандартные обозначения $K[[x]]$ и $K((x))$ соответственно. Для ненулевого элемента $a = \sum {{{a}_{i}}{{x}^{i}}} \in K((x))$ его валюация valα определяется как $min\{ i\,{\text{|}}\,{{a}_{i}} \ne 0\} $, при этом ${\text{val}}0 = \infty $. Пусть $A = ({{a}_{{ij}}}) \in {\text{Ma}}{{{\text{t}}}_{m}}(K((x)))$, тогда ${\text{val}}A = mi{{n}_{{1 \leqslant i,j \leqslant m}}}{\text{val}}{{a}_{{ij}}}$.
Пусть $a \in K((x))$, $d \in \mathbb{Z} \cup \{ - \infty \} $, тогда d-усечение ${{a}^{{\langle d\rangle }}}$ получается отбрасыванием всех членов a степени большей, чем d; если $d = - \infty $, то ${{a}^{{\langle d\rangle }}} = 0$. Пусть $B = ({{b}_{{ij}}}) \in {\text{Ma}}{{{\text{t}}}_{m}}(K((x)))$, тогда d-усечением матрицы B назовем такую матрицу A = = $({{a}_{{ij}}}) \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x$, x–1]), элементы которой являются d-усечениями соответствующих элементов матрицы $B$: ${{a}_{{ij}}} = b_{{ij}}^{{\langle d\rangle }}$; d-усечение матрицы B будем обозначать ${{B}^{{\langle d\rangle }}}$.
Пусть $A = ({{a}_{{ij}}}) = {{B}^{{\langle d\rangle }}}$ для некоторой матрицы $B \in {\text{Ma}}{{{\text{t}}}_{m}}(K((x)))$. Матрицу $\tilde {A}\, = \,({{\tilde {a}}_{{ij}}})\, \in \,{\text{Ma}}{{{\text{t}}}_{m}}(K((x)))$ будем называть продолжением матрицы A, если для всех $1 \leqslant i,$ $j \leqslant m$ выполняется ${{a}_{{ij}}} - {{\tilde {a}}_{{ij}}} = O({{x}^{{d + 1}}})$, т.е. ${\text{val}}({{a}_{{ij}}} - {{\tilde {a}}_{{ij}}}) > d$.
Дифференциальным модулем M называется m-мерное линейное пространство над K, на котором определено аддитивное отображение $\Delta {\kern 1pt} :\;M \to M$, удовлетворяющее следующему свойству (см. [6]): $\Delta (fv) = f{\kern 1pt} 'v + f\Delta v$ для всех $f \in K$ и $v \in M$. Отображение $\Delta $ будем называть дифференцированием в M.
3. ПОСТАНОВКА ЗАДАЧИ
Будем рассматривать систему (1), ненулевая матрица A которой является d-усечением некоторой неизвестной матрицы $B \in {\text{Ma}}{{{\text{t}}}_{m}}(K((x)))$: $A = {{B}^{{\langle d\rangle }}}$. Нас будут интересовать частичные лорановы решения системы (1), т.е. решения в виде лорановых рядов для некоторых заранее фиксированных компонент вектора неизвестных. При этом нас не будет интересовать вопрос построения всех коэффициентов таких решений (если они есть), а возможность определения максимального количества начальных членов лорановых рядов, которые являются инвариантными относительно возможных продолжений A, а также вычисление коэффициентов этих членов.
Для простоты задачу частичного решения будем рассматривать в постановке определения одной компоненты решений yk ($1 \leqslant k \leqslant m$). Таким образом задача сводится к определению, существуют ли решения исходной системы (1), k-я компонента которых может быть представлена в виде лоранового ряда вне зависимости от продолжения коэффициентов системы, и если ответ положительный, то требуется определить максимальное число первых членов такого ряда, не зависящих от возможных продолжений элементов матрицы A.
Для решения поставленной задачи сведем ее к задаче построения лорановых решений скалярных линейных дифференциальных уравнений с коэффициентами в виде усеченных степенных рядов, которая подробно рассмотрена в работе [5]. Там же предложен алгоритм, который для краткости будем называть TSLS (Truncated Series Laurent Solution). Для решения задачи с использованием TSLS алгоритма потребуется:
1. для заданной компоненты yk исходной системы (1) построить скалярное дифференциальное уравнение, позволяющее строить решения k‑й компоненты исходной усеченной системы;
2. представить коэффициенты построенного скалярного уравнения в виде усеченных степенных рядов, приняв во внимание усеченность коэффициентов исходной системы;
3. применить алгоритм TSLS для построения начальных элементов лорановых решений для компоненты yk исходной системы.
3.1. Алгоритм TSLS
В работе [5] авторами подробно рассмотрена задача построения лорановых решений скалярных дифференциальных уравнений вида
где ${{a}_{i}} \in K[x]$, неотрицательные целые ${{t}_{i}} \geqslant deg{{a}_{i}}$, $\theta = x\tfrac{d}{{dx}}$. Числа ti являются степенями усечения коэффициентов: ${{a}_{i}} = b_{i}^{{\langle {{t}_{i}}\rangle }}$ для некоторого ${{b}_{i}} \in K[[x]]$.Алгоритм TSLS (подробности см. [5]) по уравнению (2) строит индуцированное рекуррентное уравнение
такое, что уравнение (2) имеет лораново решение $y(x) = {{c}_{{v}}}{{x}^{{v}}} + {{c}_{{{v} + 1}}}{{x}^{{{v} + 1}}} + \ldots $ тогда и только тогда, когда двусторонняя последовательность удовлетворяет уравнению (3), т.е.4. ЧАСТИЧНЫЕ ЛОРАНОВЫ РЕШЕНИЯ
Для применения алгоритма TSLS необходимо по исходной системе (1) построить скалярное уравнение вида (2), позволяющее строить решения для компоненты yk. Также потребуется определить степени усечения коэффициентов построенного скалярного уравнения, чтобы учесть степени усечения коэффициентов исходной системы.
4.1. Построение скалярного уравнения
Задача решения нормальных дифференциальных систем относительно части неизвестных подробно рассмотрена в [1], где приводится алгоритм (AB-алгоритм), который в частности позволяет построить по заданной системе для фиксированной неизвестной yk ($1 \leqslant k \leqslant m$) скалярное дифференциальное уравнение, все решения которого и только они являются первыми компонентами всех решений исходной системы (см. [1, предл. 2]). Будем использовать метод, основанный на AB-алгоритме.
Чтобы скалярное дифференциальное уравнение, строящееся AB-алгоритмом, использовало в качестве дифференцирования θ, будет удобно перейти от системы (1) к системе
где матрица системы $\hat {A} = xA$. Рассмотрим дифференциальный модуль $K{{[x]}^{m}}$ с дифференцированием ΔxA : $v \to \theta v + x{{A}^{T}}v$. Определим матрицу $[{{\Delta }_{{xA}}}v] \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x$, x–1]), столбцы которой ${{[{{\Delta }_{{xA}}}v]}_{{*,i}}}$ = = $\Delta _{{xA}}^{{i - 1}}v$, $1 \leqslant i \leqslant m$, считая $\Delta _{{xA}}^{0}v = v$.Возьмем вектор ${{e}_{k}} = {{(0, \ldots ,0,1,0, \ldots ,0)}^{T}} \in {{K}^{m}}$, в котором “1” стоит в k-й позиции. Пусть $det[{{\Delta }_{{xA}}}{{e}_{k}}]$ ≠ ≠ 0, тогда коэффициенты скалярного уравнения
(4)
${{a}_{m}}{{\theta }^{m}}{{y}_{k}} + {{a}_{{m - 1}}}{{\theta }^{{m - 1}}}{{y}_{k}} + \ldots + {{a}_{0}}{{y}_{k}} = 0,$(5)
$\begin{gathered} {{a}_{m}} = det[{{\Delta }_{{xA}}}{{e}_{k}}], \\ {{a}_{{i - 1}}} = - det({{[{{\Delta }_{{xA}}}{{e}_{k}}]}_{{(i)}}}),\quad i = 1,2, \ldots ,m. \\ \end{gathered} $Здесь [ΔxAek](i) – матрица, получающаяся из [ΔxAek] заменой i-го столбца вектором $\Delta _{{xA}}^{m}$ek.
Корректность формул (5) следует непосредственно из корректности AB-алгоритма (см. [1]). Решениями уравнения (4) являются k-е компоненты решений системы (1) в произвольном дифференциальном расширении основного поля.
Поскольку элементами матрицы A являются многочлены Лорана, в случае ${\text{val}}A < - 1$ коэффициенты ai ($i = 0,1, \ldots ,m$), вычисляемые по формулам (5), в общем случае являются многочленами Лорана. Чтобы гарантировано получить скалярное уравнение, коэффициенты которого являются многочленами, в случае ${\text{val}}A < - 1$ домножим каждый из коэффициентов на ${{x}^{{qm(m + 1)/2}}}$, где $q = - {\text{val}}A - 1$:
(6)
$\begin{gathered} {{a}_{m}} = {{x}^{{qm(m + 1)/2}}}det[{{\Delta }_{{xA}}}{{e}_{k}}], \\ {{a}_{{i - 1}}} = - {{x}^{{qm(m + 1)/2}}}det({{[{{\Delta }_{{xA}}}{{e}_{k}}]}_{{(i)}}}),\quad i = 1,2, \ldots ,m. \\ \end{gathered} $Замечание 1. При вычислении коэффициентов скалярного уравнения по формулам (5) или (6) возможно появление общих множителей. Для дальнейшего будет важно, что сокращение на общие множители не производится.
4.2. Оценки коэффициентов скалярного уравнения
Поскольку коэффициенты системы (1) являются усечениями лорановых рядов, мы не обладаем всей полнотой информации о системе. Различные продолжения коэффициентов системы могут влиять на строящиеся решения. Строящиеся коэффициенты скалярного уравнения для компоненты yk, являющиеся многочленами, также нужно рассматривать как усечения рядов. На следующем этапе необходимо установить соответствие степеней усечения коэффициентов скалярного уравнения со степенями усечения коэффициентов исходной системы.
Определим ${{A}^{{({{i}_{0}},{{j}_{0}})}}}$ – как матрицу, полученную продолжением $({{i}_{0}},{{j}_{0}})$-го элемента A, тогда ее (i, j)-й элемент будет выражаться следующим образом:
Поскольку формулы вычисления коэффициентов скалярного дифференциального уравнения для неизвестной yk различаются в зависимости от значения $q = - {\text{val}}(xA) = - {\text{val}}A - 1$, рассмотрим случаи $q \leqslant 0$ и $q > 0$ отдельно.
Предложение 1. Пусть $1 \leqslant k \leqslant m$, $A \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x$, x–1]), такая, что $det[{{\Delta }_{{xA}}}{{e}_{k}}] \ne 0$, d = degA, q = = $ - {\text{val}}A - 1 \leqslant 0$, ${{a}_{i}}$ ($0 \leqslant i \leqslant m$) – коэффициенты скалярного дифференциального уравнения, вычисленные по формулам (5). Пусть $\tilde {A} = A + {{x}^{{d + 1}}}B$, где $B \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x])$ – произвольная матрица такая, что $det[{{\Delta }_{{x\tilde {A}}}}{{e}_{k}}] \ne 0$, и $\mathop {\tilde {a}}\nolimits_i $ ($0 \leqslant i \leqslant m$) – коэффициенты скалярного дифференциального уравнения, вычисленные по формулам (5) для матрицы $\tilde {A}$.
Тогда:
1) для $1 < i \leqslant m$: ${{a}_{i}} - {{\tilde {a}}_{i}} = O({{x}^{{{{r}_{1}}}}})$, где ${{r}_{1}} = d + 2$ – – q(m – 2);
2) ${{a}_{0}} - {{\tilde {a}}_{0}} = O({{x}^{{{{r}_{2}}}}})$, где ${{r}_{2}} = d + 2 - q(m - 1)$.
Доказательство. Достаточно рассмотреть одноэлементное продолжение ${{A}^{{({{i}_{0}},{{j}_{0}})}}}$. Обозначим pj ($j = 0,1, \ldots ,m$) – минимальную степень x среди элементов вектора $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{k}{{e}_{k}}$, в коэффициенте при которой появляется символьный коэффициент α; если α вообще не появляется ни в одном из элементов вектора $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{j}{{e}_{k}}$, то положим ${{p}_{j}} = \infty $. Через ${{{v}}_{j}}$ ($j = 0,1, \ldots ,m$) обозначим минимальную валюацию элементов вектора $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{j}{{e}_{k}}$. Для pj и ${{{v}}_{j}}$ верны следующие оценки, непосредственно следующие из определения ${{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}$: ${{p}_{0}} = {{{v}}_{0}} = 0$; для $j \geqslant 1$
(7)
$\begin{array}{*{20}{c}} {{{p}_{j}} \geqslant d + 2,} \\ {{{{v}}_{j}} \geqslant - q.} \end{array}$Символьный коэффициент α будет присутствовать в определителях, участвующих в формулах (5), в качестве коэффициента при минимальной степени x, если оценки (7) обратятся в равенства.
1) Поскольку $[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$ состоит из векторов $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{j}{{e}_{k}}$ ($j = 0,1, \ldots ,m - 1$), то минимальная степень x, в коэффициенте при которой возможно появление символьного коэффициента α в $det[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$, определяется как
Для $1 \leqslant n < m$ в коэффициентах an участвуют матрицы ${{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(n + 1)}}}$, отличающиеся от $[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$ одним (n + 1)-м столбцом, вместо которого подставляется вектор $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{m}{{e}_{k}}$. Минимальная степень x, в коэффициенте при которой возможно появление символьного коэффициента α в $det({{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(n)}}})$, определяется как
2) ${{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(1)}}}$ отличается от $[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$ первым столбцом, в качестве которого используется вектор $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{m}{{e}_{k}}$. Поэтому минимальная степень x, в коэффициенте при которой возможно появление символьного коэффициента α в $det({{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(1)}}})$, определяется как
Предложение 2. Пусть $1 \leqslant k \leqslant m$, $A \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x$, x–1]), такая, что $det[{{\Delta }_{{xA}}}{{e}_{k}}] \ne 0$, d = degA, q = = $ - {\text{val}}A - 1$ > 0, ai ($0 \leqslant i \leqslant m$) – коэффициенты скалярного дифференциального уравнения, вычисленные по формулам (6). Пусть $\tilde {A} = A + {{x}^{{d + 1}}}B$, где $B \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x])$ – произвольная матрица такая, что $det[{{\Delta }_{{x\tilde {A}}}}{{e}_{k}}] \ne 0$, и ${{\tilde {a}}_{i}}$ ($0 \leqslant i \leqslant m$) – коэффициенты скалярного дифференциального уравнения, вычисленные по формулам (6) для матрицы $\tilde {A}$.
Тогда:
1) ${{a}_{m}} - {{\tilde {a}}_{m}} = O({{x}^{{{{r}_{1}}}}})$, где ${{r}_{1}} = d + 2 + q(m + 1)$;
2) для $1 < i < m$: ${{a}_{i}} - {{\tilde {a}}_{i}}\, = \,O({{x}^{{{{r}_{2}}}}})$, где ${{r}_{2}} = d + 2$ + 2q;
3) ${{a}_{0}} - \mathop {\tilde {a}}\nolimits_0 = O({{x}^{{{{r}_{2}}}}})$, где ${{r}_{2}} = d + 2 + q$.
Доказательство отличается от доказательства предложения 1 оценками величин pj, ${{{v}}_{j}}$. В случае q > 0 для $j \geqslant 1$ будут справедливы следующие неравенства:
1) Поскольку $[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$ состоит из векторов $\Delta _{{{{A}^{{({{i}_{0}},{{j}_{0}})}}}}}^{i}{{e}_{1}}$ ($i = 0,1, \ldots ,m - 1$), то минимальная степень x, в коэффициенте при которой возможно появление символьного коэффициента α в $det[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$, определяется как
Учитывая множитель ${{x}^{{qm(m + 1)/2}}}$ в (6), получаем ${{r}_{1}} = d + 1 - q\sum\nolimits_{i = 2}^{m - 1} \,i$ + $q\sum\nolimits_{i = 1}^m \,i = d + 1 + q(m + 1);$
2) Для $1 \leqslant n < m$ в коэффициентах an участвуют матрицы ${{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(n + 1)}}}$, отличающиеся от $[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$ одним (n + 1)-м столбцом, вместо которого подставляется вектор $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{m}{{e}_{k}}$. Минимальная степень x, в коэффициенте при которой возможно появление символьного коэффициента α в $det({{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(n)}}})$, определяется как
Учитывая множитель ${{x}^{{qm(m + 1)/2}}}$ в (6), получаем ${{r}_{2}} = d + 2 + 2q - q\sum\nolimits_{i = 1}^m \,i$ + $q\sum\nolimits_{i = 1}^m \,i = d + 2 + 2q$;
3) ${{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(1)}}}$ отличается от $[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]$ первым столбцом, в качестве которого используется вектор $\Delta _{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}^{m}{{e}_{k}}$. Поэтому минимальная степень x, в коэффициенте при которой возможно появление символьного коэффициента α в $det({{[{{\Delta }_{{{{{(xA)}}^{{({{i}_{0}},{{j}_{0}})}}}}}}{{e}_{k}}]}_{{(1)}}})$, определяется как
Учитывая множитель ${{x}^{{qm(m + 1)/2}}}$ в (6), получаем ${{r}_{3}} = d + 2 + q - q\sum\nolimits_{i = 1}^m \,i$ + $q\sum\nolimits_{i = 1}^m \,i = d + 2 + q$. ◻
Пример 1. Рассмотрим усеченную систему $y{\kern 1pt} ' = Ay$, где
$y = {{({{y}_{1}},{{y}_{2}})}^{T}}$ и степень усечения коэффициентов d = 1. Построим начальный отрезок лоранового решения для компоненты y1, не зависящий от продолжений коэффициентов системы. Коэффициенты скалярного дифференциального уравнения для y1 вычисляются по формулам (5), само уравнение будет иметь вид:(8)
${{x}^{2}}{{\theta }^{2}}{{y}_{1}} + ( - 2{{x}^{3}} - 2{{x}^{2}})\theta {{y}_{1}} + ({{x}^{6}} + {{x}^{4}} + {{x}^{3}}){{y}_{1}} = 0.$Не все слагаемые в коэффициентах уравнения (8) являются инвариантными относительно возможных продолжений коэффициентов исходной системы. Применяя оценки из предложения 1, уравнение (8) можно переписать в виде
(9)
$\begin{gathered} (1 + O(x)){{\theta }^{2}}{{y}_{1}} + ( - 2 + O(x))\theta {{y}_{1}} + \\ \, + (x + O({{x}^{2}})){{y}_{1}} = 0. \\ \end{gathered} $Алгоритм TSLS, примененный к уравнению (9), построит определяющий многочлен ${{u}_{0}}(n) = {{n}^{2}} - 2n$, откуда получаем множество возможных валюации решений {0, 2}. Далее будет построено решение с валюацией 2: ${{y}_{1}} = {{c}_{2}}{{x}^{2}} + O({{x}^{3}})$, где c2 – произвольная постоянная. При этом решение с валюацией 0 построено не будет, поскольку не при всех продолжениях коэффициентов уравнения (9) оно будет иметь лораново решение с валюацией 0. В то же время valA = 0 и, согласно [7, Theorem 13.1], эта система должна иметь два линейно независимых решения в виде степенных рядов. Поскольку $det[{{\Delta }_{{xA}}}{{e}_{1}}] \ne 0$, два линейно независимых решения в виде степенных рядов должна иметь компонентна y1.
Продолжения коэффициентов построенного скалярного дифференциального уравнения (9) не являются произвольными и зависят от продолжений коэффициентов исходной системы. Чтобы учесть это, применим метод наращивания коэффициентов, заключающийся в следующем: добавим к коэффициентам исходной системы символьные коэффициенты до xn (n > d) включительно, построив матрицу A[n], элементы которой $A_{{ij}}^{{[n]}} = {{A}_{{ij}}} + \sum\nolimits_{l = d + 1}^n \,{{\alpha }_{{ijl}}}{{x}^{l}}$, где ${{\alpha }_{{ijl}}}$ – символьные коэффициенты. Добавленные коэффициенты считаются известными, поэтому они будут использованы алгоритмом TSLS в строящихся решениях. Будем последовательно наращивать коэффициенты, пока в каждое из решений, строящихся алгоритмом TSLS, не попадут добавленные символьные коэффициенты. После этого усечем полученные решения так, чтобы в них не осталось символьных коэффициентов. Так построенные решения будут содержать максимальное число начальных членов лорановых рядов, не зависящих от возможных продолжений коэффициентов исходной усеченной системы.
Для рассматриваемого примера матрица A[2] будет иметь вид:
Скалярное уравнение для неизвестной y1 системы с матрицей A [2], коэффициенты которого вычислены по формулам (5) и усечены, используя оценки предложения 1, будет иметь вид (x2 + x3α122 + + $O({{x}^{4}})){{\theta }^{2}}{{y}_{1}}$ + $( - 2{{x}^{2}} + ( - 3{{\alpha }_{{122}}} - 2){{x}^{3}} + O({{x}^{4}}))\theta {{y}_{1}}$ + + $({{x}^{3}} + (2{{\alpha }_{{122}}} + 1){{x}^{4}} + O({{x}^{5}})){{y}_{1}}$ = 0, применение алгоритма TSLS к этому уравнению даст два линейно независимых решения ${{c}_{1}} + {{c}_{1}}x + {{c}_{2}}{{x}^{2}} + O({{x}^{3}})$ и ${{c}_{2}}{{x}^{2}} + \left( {{{c}_{2}} + \frac{2}{3}{{c}_{2}}{{\alpha }_{{122}}}} \right){{x}^{3}}$ + O(x4) с валюациями 0 и 2 соответственно. Поскольку в первое решение не вошли элементы с добавленными символьными коэффициентами α, нет гарантии, что первое решение содержит максимальное число слагаемых, не зависящих от возможных продолжений коэффициентов исходной системы, и нужно добавить символьные коэффициенты с x3, т.е. рассмотреть систему с матрицей
Применение TSLS алгоритма к скалярному дифференциальному уравнению с усеченными коэффициентами, строящемуся по системе с матрицей A [3] относительно y1, дает два линейно независимых решения ${{c}_{1}} + {{c}_{1}}x + {{c}_{2}}{{x}^{2}} + \left( {\frac{1}{3}{{c}_{1}}{{\alpha }_{{112}}}} \right.$ – $\frac{1}{3}{{c}_{1}}{{\alpha }_{{122}}}$ + $\frac{2}{3}{{c}_{2}}{{\alpha }_{{122}}}$ – – $\left. {\frac{1}{3}{{c}_{1}} + {{c}_{2}}} \right){{x}^{3}}$ + O(x4) и c2x2 + $\left( {\frac{2}{3}{{c}_{2}}{{\alpha }_{{122}}} + {{c}_{2}}} \right){{x}^{3}}$ + + $\left( {\frac{2}{3}{{c}_{2}}{{\alpha }_{{122}}} + \frac{1}{2}{{c}_{2}} + \frac{1}{2}{{c}_{2}}{{\alpha }_{{123}}}} \right){{x}^{4}}$ + O(x5). Отбрасывая элементы, начиная с которых в коэффициенты входят добавленные символьные коэффициенты α, окончательно получаем два линейно независимых решения с максимальным числом элементов, инвариантных относительно возможных продолжений коэффициентов исходной системы: ${{c}_{1}} + {{c}_{1}}x + {{c}_{2}}{{x}^{2}}$ + + O(x3) и ${{c}_{2}}{{x}^{2}} + O({{x}^{3}})$. Заметим, что второе решение является частным случаем первого решения при c1 = 0.
4.3. Вполне определенные системы
Не всегда наращивание коэффициентов позволяет решить поставленную задачу. Рассмотрим следующий пример.
Пример 2. Пусть матрица усеченной дифференциальной системы (1) с вектором неизвестных $y = {{({{y}_{1}},{{y}_{2}},{{y}_{3}})}^{T}}$ имеет вид
(10)
$A = \left[ {\begin{array}{*{20}{c}} { - x - {{x}^{2}} + {{x}^{3}}}&{ - 1}&0 \\ { - 1}&{1 + x}&{{{x}^{3}}} \\ x&1&1 \end{array}} \right].$Будем интересоваться лорановыми решениями для компоненты y1. Скалярное уравнение для y1 после усечения коэффициентов будет иметь вид
Алгоритм TSLS не применим к уравнениям такого вида, поскольку в коэффициентах содержится слишком мало информации, из-за чего не возможно построить определяющий многочлен ${{u}_{0}}(n)$ для определения возможных валюаций решений. Добавление символьных коэффициентов к элементам A до степени x4 дает A [4] с элементами
Скалярное уравнение для ${{y}_{1}}$, построенное по A[4], после усечения коэффициентов будет иметь вид $(( - 4{{\alpha }_{{134}}} + 1){{x}^{6}} + O({{x}^{7}})){{\theta }^{3}}{{y}_{1}}$ + ((24α134 – 6)x6 + + $O({{x}^{7}})){{\theta }^{2}}{{y}_{1}}$ + $(( - 20{{\alpha }_{{134}}}\, + \,5){{x}^{6}}\, + \,O({{x}^{7}}))\theta {{y}_{1}}\, + \,O({{x}^{8}}){{y}_{1}}$ = = 0. Определяющий многочлен, строящийся алгоритмом TSLS, будет иметь вид u0(n) = = $( - 4{{\alpha }_{{134}}} + 1){{n}^{3}}$ + $(24{{\alpha }_{{134}}} - 6){{n}^{2}}$ + $( - 20{{\alpha }_{{134}}} + 5)n$ = = $n(n - 1)(n - 5)(1 - 4{{\alpha }_{{134}}})$, т.е. будет зависеть от значения добавленного символьного коэффициента α134. Добавление символьных коэффициентов с большими степенями не изменит определяющий многочлен. И в этом случае без дополнительных исследований алгоритм TSLS оказывается неприменим.
Определение 1. Пусть $A \in {\text{Ma}}{{{\text{t}}}_{m}}(K[x,{{x}^{{ - 1}}}])$ – матрица системы (1), $d = degA$, $q = - {\text{val}}(xA)$ = –valA – 1, $1 \leqslant k \leqslant m$. Пусть $q \leqslant 0$ ($q > 0$), ai ($0 \leqslant i \leqslant m$) – коэффициенты, вычисленные по формулам (5) (по формулам (6)), $v = mi{{n}_{{0 \leqslant i \leqslant m}}}{\text{val}}{{a}_{i}}$, $R = d + 2 - q(m - 2)$ ($R = d + 2 + q$). Систему (1) будем называть вполне определенной относительно неизвестной yk, если $v < R$.
Алгоритм TSLS для построения частичных решений для неизвестной yk может быть гарантированно применен только к вполне определенным относительно yk системам. В этом случае определяющий многочлен, строящийся алгоритмом TSLS, гарантированно не зависит от возможных продолжений коэффициентов исходной системы. Возможность использования алгоритма TSLS для систем, не являющихся вполне определенными относительно yk, требует дополнительного исследования, которое в настоящей работе не проводится.
Система с матрицей (10) из предыдущего примера не является вполне определенной относительно y1: в этом случае d = 3, $q = - 1$, R = 6, ${v} = 6$ и условие $v < R$ не выполняется. Также система из примера 3 не является вполне определенной относительно y2, но в то же время она является вполне определенной относительно неизвестной y3.
4.4. Алгоритм
Предлагаемый алгоритм построения частичных решений усеченной дифференциальной системы (1) принимает на вход матрицу A системы, являющейся d-усечением некоторой неизвестной матрицы $B \in {\text{Ma}}{{{\text{t}}}_{m}}(K((x)))$ и номер $1 \leqslant k \leqslant m$ неизвестной, для которой необходимо построить лораново решение.
Алгоритм состоит из следующих шагов:
1. $p: = d$; $q: = - {\text{val}}A - 1$;
2. $p: = p + 1$;
3. построить матрицу ${{A}^{{[p]}}}$, добавив к элементам A члены до степени xp с символьными коэффициентами: $A_{{ij}}^{{[p]}} = {{A}_{{ij}}} + \sum\nolimits_{l = d + 1}^p \,{{\alpha }_{{ijl}}}{{x}^{l}}$ ($1 \leqslant i,j \leqslant m$);
4. построить скалярное дифференциальное уравнение для компоненты yk, используя для коэффициентов формулы (5), если $q \leqslant 0$, или формулы (6), если $q > 0$;
5. усечь коэффициенты скалярного дифференциального уравнения, используя оценки предложения 1 (при $q \leqslant 0$) или предложения 2 (при q > 0);
6. применить к полученному скалярному дифференциальному уравнению с усеченными коэффициентами алгоритм TSLS;
7. если результатом алгоритма TSLS является пустое множество, то закончить выполнение алгоритма, лорановых решений нет;
8. если хотя бы в одно из решений, выданных алгоритмом TSLS, не входят добавленные символьные коэффициенты α, то вернуться к шагу 2;
9. усечь полученные решения так, чтобы в них остались только члены, в коэффициенты которых не входят α, и выдать их в качестве результата работы.
Предложение 3. Пусть усеченная дифференциальная система (1) является вполне определенной относительно неизвестной yk ($1 \leqslant k \leqslant m$). Тогда предложенный алгоритм построит максимальное число начальных членов лоранового решения k-й компоненты решений системы (1), независящих от продолжений коэффициентов системы, либо установит, что таких решений не существует.
Доказательство. Поскольку заданная усеченная система (1) является вполне определенной относительно неизвестной yk, определяющий многочлен, строящийся алгоритмом TSLS по скалярному дифференциальному уравнению для yk, не зависит от возможных продолжений коэффициентов системы и позволяет определить все возможные валюации лорановых решений для компоненты yk или установить, что лорановых решений нет. Докажем, что алгоритм всегда завершает свою работу, т.е. что процесс наращивания коэффициентов системы (шаги 2 и 3) обязательно приводит к тому, что все полученные алгоритмом TSLS решения будут зависеть от символьных коэффициентов α. Для этого покажем, что для достаточно больших значений p условие шага 8 не выполняется и возврата к шагу 2 не происходит.
Пусть $q = - {\text{val}}A - 1$. Рассмотрим отдельно случаи $q \leqslant 0$ и $q > 0$.
1) Пусть $q \leqslant 0$, тогда коэффициенты скалярного уравнения для yk вычисляются по формулам (5) и усекаются, используя оценки предложения 1. Поскольку степень усечения коэффициента am не больше степени усечения других коэффициентов скалярного уравнения, достаточно, чтобы символьные коэффициенты α остались после усечения в коэффициенте am. Пусть $p > d = degA$, обозначим $a_{m}^{{[p]}} = det[{{\Delta }_{{x{{A}^{{[p]}}}}}}{{e}_{k}}]$ – старший коэффициент скалярного уравнения, построенного для неизвестной ${{y}_{k}}$ дифференциальной системы (1) с матрицей A[p]. Не трудно видеть, что $dega_{m}^{{[p]}}$ = m(m – – 1)(p + 1)/2, причем старший коэффициент, т.е. коэффициент при ${{x}^{{dega_{m}^{{[p]}}}}}$ в $a_{m}^{{[p]}}$, вычисляется только через ${{\alpha }_{{ijp}}}$ ($1 \leqslant i,j \leqslant m$). После наращивания коэффициентов получаем $dega_{m}^{{[p + 1]}} > dega_{m}^{{[p]}}$, причем коэффициент при ${{x}^{{dega_{m}^{{[p]}}}}}$ в $a_{m}^{{[p + 1]}}$ отличается от коэффициента при той же степени x в $a_{m}^{{[p]}}$ слагаемыми, в каждое из которых множителем входят добавленные коэффициенты ${{\alpha }_{{i,j,p + 1}}}$, подстановка нулей вместо которых необходимо приводит к коэффициенту при ${{x}^{{dega_{m}^{{[p]}}}}}$ в $a_{m}^{{[p]}}$. Таким образом, коэффициент при ${{x}^{{dega_{m}^{{[d + 1]}}}}}$ обязательно будет содержать символьные коэффициенты α при $p \geqslant d + 1$. Чтобы член с ${{x}^{{dega_{m}^{{[d + 1]}}}}}$ остался после усечения в коэффициенте $a_{m}^{{[p]}}$, должно выполняться условие p + 2 – $q(m - 2)$ > $dega_{m}^{{[d + 1]}}$. Чтобы коэффициент при ${{x}^{{dega_{m}^{{[d + 1]}}}}}$ участвовал в построении решений (см. [3, Prop. 1]), дополнительно требуется выполнение условия $p + 2 - q(m - 2)$ – $mi{{n}_{{0 \leqslant i \leqslant m}}}{\text{val}}{{a}_{i}} > e{\kern 1pt} * - {{e}_{*}}$, где ai ($0 \leqslant i \leqslant m$) – коэффициенты скалярного дифференциального уравнения для yk, вычисленные по формулам (5), $e{\kern 1pt} *,\;{{e}_{*}}$ – соответственно наибольший и наименьший целые корни определяющего многочлена, строящегося алгоритмом TSLS. Окончательно получаем, что для
(11)
$\begin{gathered} {{p}_{{max}}} \leqslant \\ \, \leqslant max\left( {\frac{{m(m - 1)(d + 2)}}{2},e{\kern 1pt} * - \;{{e}_{*}} + \mathop {min}\limits_{0 \leqslant i \leqslant m} {\text{val}}{{a}_{i}}} \right) + \\ \, + q(m - 2) - 1. \\ \end{gathered} $2) Пусть q > 0, коэффициенты скалярного уравнения для yk вычисляются по формулам (6) и усекаются, используя оценки предложения 2. Поскольку наименьшая из оценок усечения соответствует коэффициенту a0, рассуждения аналогичны п. 1, но относительно коэффициента a0. Пусть $p > d$ = degA, обозначим $a_{0}^{{[p]}}$ = $ - {{x}^{{qm(m + 1)/2}}}det{{[{{\Delta }_{{x{{A}^{{[p]}}}}}}{{e}_{k}}]}_{{(1)}}}$ – младший коэффициент скалярного уравнения, построенного для неизвестной yk дифференциальной системы (1) с матрицей A[p]. Тогда $dega_{0}^{{[p]}}$ = = $qm(m + 1){\text{/}}2\, + \,deg{{[{{\Delta }_{{x{{A}^{{[p]}}}}}}{{e}_{k}}]}_{{(1)}}}$ = m(m – 1)(p + q + 1)/2, поскольку, как нетрудно показать, $deg{{[{{\Delta }_{{x{{A}^{{[p]}}}}}}{{e}_{k}}]}_{{(1)}}}$ = = $m(m + 1)(p + 1){\text{/}}2$. Чтобы член с ${{x}^{{dega_{0}^{{[d + 1]}}}}}$ остался после усечения в коэффициенте $a_{0}^{{[p]}}$, должно выполняться условие $p + 2 + q > dega_{0}^{{[d + 1]}}$, и чтобы коэффициент при ${{x}^{{dega_{0}^{{[d + 1]}}}}}$ участвовал в построении решений (см. [3, Prop. 1]), дополнительно требуется выполнение условия $p + 2 + q - mi{{n}_{{0 \leqslant i \leqslant m}}}{\text{val}}{{a}_{i}}$ > > $e{\kern 1pt} * - \;{{e}_{*}}$, где ai ($0 \leqslant i \leqslant m$) – коэффициенты скалярного дифференциального уравнения для yk, вычисленные по формулам (6), $e{\kern 1pt} *,\;{{e}_{*}}$ – соответственно наибольший и наименьший целые корни определяющего многочлена, строящегося алгоритмом TSLS. Окончательно получаем, что для
(12)
$\begin{gathered} {{p}_{{\max }}} \leqslant \max \left( {\frac{{m(m + 1)(d + q + 2)}}{2},} \right. \\ \left. {_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}e{\text{*}} - {{e}_{*}} + \mathop {\min }\limits_{0 \leqslant i \leqslant m} {\text{val}}{{a}_{i}}} \right) - q - 1. \\ \end{gathered} $□
Пример 3. Рассмотрим работу алгоритма на примере усеченной системы $y{\kern 1pt} ' = Ay$, где $y = {{({{y}_{1}},{{y}_{2}})}^{T}}$,
Данная система является вполне определенной относительно y1. Найдем лорановы решения для компоненты y1, используя предложенный алгоритм.
Для заданной системы степень усечения d = 0. На шаге 1 устанавливаем $p: = 0$, $q: = - {\text{val}}A - 1 = 1$. На шаге 2, являющимся началом цикла, увеличиваем p до 1. На шаге 3 строим матрицу
На шаге 4 получаем скалярное дифференциальное уравнение для неизвестной y1, которое, после усечения коэффициентов на шаге 5, примет вид $({{x}^{3}}\, + \,{{\alpha }_{{121}}}{{x}^{5}}\, + \,O({{x}^{6}})){{\theta }^{2}}{{y}_{1}}$ + $( - {{x}^{2}} + {{x}^{3}} + ( - {{\alpha }_{{121}}} + 1){{x}^{4}}$ + + O(x5))θy1 + $({{x}^{2}} - {{x}^{3}} + O({{x}^{4}})){{y}_{1}}$ = 0. Лораново решение, строящееся для этого скалярного уравнения с помощью алгоритма TSLS на шаге 6, имеет вид ${{y}_{1}} = {{c}_{1}}x + {{c}_{1}}{{x}^{2}} + O({{x}^{3}})$. Поскольку построенное решение не содержит добавленных символьных коэффициентов α, возвращаемся к шагу 2 и увеличиваем p до 2. На шаге 3 строим матрицу A [2], которая примет вид
Скалярное дифференциальное уравнение, строящееся по ${{A}^{{[2]}}}$, после усечения коэффициентов на шаге 5, будет иметь вид: $({{x}^{3}} + {{\alpha }_{{121}}}{{x}^{5}} + {{\alpha }_{{122}}}{{x}^{6}}$ + O(x7))θ2y1 + + $( - {{x}^{2}} + {{x}^{3}} + ( - {{\alpha }_{{121}}} + 1){{x}^{4}}$ + $( - {{\alpha }_{{111}}} - {{\alpha }_{{121}}}$ – α122 – ‒ α221)x5 + O(x6))θ2y1 + $({{x}^{2}} - {{x}^{3}} + (4{{\alpha }_{{121}}} + {{\alpha }_{{221}}}){{x}^{4}}$ + + $O({{x}^{5}})){{y}_{1}}$ = 0. Применение к нему алгоритма TSLS дает в результате решение ${{y}_{1}} = {{c}_{1}}x + {{c}_{1}}{{x}^{2}}$ + + $\left( {\frac{3}{2}{{\alpha }_{{121}}} + \frac{1}{2}{{\alpha }_{{221}}} + 3} \right){{c}_{1}}{{x}^{3}} + O({{x}^{4}})$. Отбрасывая члены, начиная со степени x3, поскольку в коэффициент перед ней вошли добавленные ${{\alpha }_{{121}}},{{\alpha }_{{221}}}$, окончательно получаем ${{y}_{1}} = {{c}_{1}}x + {{c}_{1}}{{x}^{2}} + O({{x}^{3}})$.
Замечание 2. Оценки (11) и (12) степени наращивания коэффициентов системы зачастую оказываются завышенными. Для системы из примера 2, используя оценку (12), можно получить условие ${{p}_{{max}}} \leqslant max(9,2) - 2 = 7$ хотя алгоритм завершил работу уже при p = 2. Последовательное наращивание коэффициентов зачастую позволяет избежать лишних вычислений.
4.5. Реализация
Предложенный алгоритм реализован в системе компьютерной алгебры Maple в виде процедуры LaurentPartialSolution(A,k,d), принимающей в качестве параметров матрицу A системы (1), элементами которой являются многочлены или многочлены Лорана, порядковый номер k компоненты вектора неизвестных, для которой будут строиться частичные решения, и необязательный параметр d, задающий степень усечения коэффициентов системы. Если параметр d не указан, в качестве степени усечения берется максимальная степень элементов матрицы A.
Процедура LaurentPartialSolution использует для работы ряд вспомогательных процедур: MinimalEquationTheta, MinimalTruncatedEquationTheta, ReduceSolutions.
Процедура MinimalEquationTheta(A,k) предназначена для построения скалярного дифференциального уравнения, записанного с помощью оператора $\theta = x\frac{d}{{dx}}$, для компоненты решений yk дифференциальной системы (1) с матрицей A. Для этого используются формулы (5) или (6) в зависимости от вычисляемого значения q = = –valA – 1.
Процедура MinimalTruncatedEquationTheta(A,k) строит скалярное дифференциальное уравнение с помощью процедуры MinimalEquationTheta и усекает его коэффициенты с помощью оценок предложений 1 или 2 в зависимости от значения q = –valA – 1.
Процедура ReduceSolutions(L), которой передается список L лорановых решений, строящихся алгоритмом TSLS, сокращает его, убирая решения с большими валюациями, являющиеся частными случаями решений с меньшими валюациями при занулении свободных постоянных.
Результатом работы процедуры LaurentPartialSolution является список найденных лорановых решений (начальные члены, инвариантные относительно продолжения коэффициентов системы) для компоненты yk дифференциальной системы (1), либо сообщение об ошибке, если система не является вполне определенной относительно неизвестной yk. Строящийся список решений в частности может быть пустым, если для k-й компоненты нетривиальных лорановых решений не существует.
В своей работе процедура LaurentPartialSolution обращается к реализации алгоритма TSLS, разработанной авторами [5] и доступной по адресу http://www.ccas.ru/ca/truncatedseries. Исходный код процедуры LaurentPartialSolution и всех вспомогательных процедур доступен по адресу http://www.ccas.ru/ca/_media/ tslps.mpl.
Пример 4. Продемонстрируем работу процедур на примере дифференциальной системы (1) с матрицей
> A:=Matrix([[1, x], [-x, 1]] )
> MinimalEquationTheta(A,1)
> MinimalTruncatedEquationTheta(A,1)
> LaurentPartialSolution(A,1)
Список литературы
Абрамов С.А., Бронштейн М. Решение линейных дифференциальных и разностных систем по отношению к части неизвестных // Журнал вычисл. матем. и матем. физ. 2006. № 2. С. 229–241.
Abramov S.A., Barkatou M.A., Khmelnov D.E. On full rank differential systems with power series coefficients // Journal of Symbolic Computation. 2015. V. 68. P. 120–137.
Abramov S., Barkatou M., Pflügel E. Higher-order linear differential systems with truncated coefficients // Proc. of CASC’2011. Lecture Notes in Computer Science. 2011. V. 6885. P. 10–24.
Абрамов С.А., Рябенко А.А., Хмельнов Д.Е. Процедуры поиска локальных решений линейных дифференциальных систем с бесконечными степенными рядами в роли коэффициентов // Программирование. 2016. № 2. С. 75–86.
Абрамов С.А., Рябенко А.А., Хмельнов Д.Е. Линейные обыкновенные дифференциальные уравнения и усеченные ряды // Журнал вычисл. матем. и матем. физ. 2019. Т. 59. № 10. С. 1706–1717.
van der Put M., Singer M.F. Galois Theory of Linear Differential Equations. Grundlehren der mathematischen Wissenschaften, 328, Springer, Heidelberg, 2003.
Hartman P. Ordinary differential equations. – John Wiley and Sons, Inc., New York, 1964.
Дополнительные материалы отсутствуют.
Инструменты
Программирование