Программирование, 2021, № 1, стр. 56-64

1. ВВЕДЕНИЕ

Классическая машина Атвуда (см. [1]), в которой один из грузов может колебаться в вертикальной плоскости под действием силы тяжести, представляет собой консервативную механическую систему с двумя степенями свободы, которая была предметом исследования многих работ (см. [2–7]). Следует отметить, что учет колебаний груза приводит к значительному усложнению уравнений движения системы и их общее решение не может быть записано в символьной форме. Численное исследование уравнений движения показывает, что машина Атвуда с одним колеблющимся грузом демонстрирует весьма интересное поведение и может совершать различные виды движения, например, квазипериодическое и хаотическое движение (см. [3, 5, 7]).

Заметим, что колебания груза приводят к возрастанию средней силы натяжения нити, причем ее величина оределяется амплитудой колебаний (см. [8]). Поэтому при небольшой разнице масс и соответствующей амплитуде колеблющийся груз меньшей массы может тянуть более тяжелый груз вверх, что невозможно в отсутствие колебаний. С другой стороны, при заданной разнице масс можно выбрать такие начальные условия, при которых система будет находиться в состоянии динамического равновесия, когда груз большей массы уравновешивается колеблющимся грузом меньшей массы. В таком случае более тяжелый груз совершает поступательное движение и также колеблется около некоторого равновесного положения, а груз меньшей массы ведет себя как маятник, длина которого совершает малые колебания. При этом наблюдается резонанс частот вида 2 : 1, т.е. частота колебаний длины маятника в два раза превышает частоту колебаний угловой переменной. Соответствующее равновесное состояние системы описывается периодическим решением уравнений движения, построенным в [9].

Если оба груза имеют одинаковые массы (m₁ = m₂), то в отсутствие колебаний система может находиться в равновесии при любом положении грузов. Если же один из грузов совершает колебания, то равновесное состояние машины Атвуда не существует, поскольку колеблющийся груз будет двигаться вниз и тянуть второй груз вверх даже при малой амплитуде колебаний. Однако можно ожидать, что рассматриваемая система может находиться в состоянии динамического равновесия, когда второй груз также совершает колебания. Численное решение уравнений движения машины Атвуда с двумя колеблющимися грузами показало, что такое состояние системы существует, если оба груза совершают синфазные колебания или колеблются в противофазе с одинаковыми амплитудами и частотами (см. [10]).

Целью данной работы является поиск решений уравнений движения машины Атвуда с двумя колеблющимися грузами одинаковой массы, определяющих состояния динамического равновесия системы, когда длина маятника r совершает малые колебания около некоторого равновесного значения, а также определение условий, при которых такие решения существуют. Поскольку уравнения движения системы существенно нелинейны и записать их точное решение не представляется возможным, будем искать приближенные решения в виде степенных рядов. Отметим, что построение и исследование таких решений обычно связано с выполнением весьма громоздких символьных вычислений, которые удобно выполнять с помощью систем компьютерной алгебры (см., напр., [11–15]). В данной работе для выполнения всех расчетов и визуализации полученных результатов используется система компьютерной алгебры Wolfram Mathematica [16].

2. УРАВНЕНИЯ ДВИЖЕНИЯ

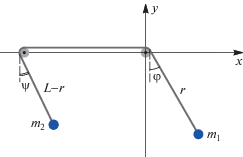
Рассматривается машина Атвуда, в которой шкив конечного радиуса заменяется двумя отдельными малыми шкивами и оба груза могут колебаться в вертикальной плоскости (рис. 1). Такая модификация классической машины Атвуда (см. [1]) не изменяет ее физической природы, но позволяет исключить влияние размеров шкива и сосредоточиться на исследовании влияния колебаний на движение системы.

Рассматриваемая система имеет три степени свободы, а ее функция Лагранжа имеет вид

где точка над символом означает полную производную соответствующей функции по времени, g – ускорение свободного падения, r и $(L - r)$ – расстояния между шкивами и грузами ${{m}_{1}}$ и ${{m}_{2}}$ соответственно, а углы $\varphi $ и $\psi $ определяют отклонения грузов от вертикали (см. рис. 1). Выражение (2.1) записано в предположении, что радиусы шкивов пренебрежимо малы и изменением длины нити r и $(L - r)$ при колебаниях грузов за счет наматывании нити на шкив можно пренебречь.

Используя функцию Лагранжа (2.1) и выполняя дифференцирование с помощью встроенной функции D системы Mathematica (см. [16]), получаем уравнения движения в виде

Для удобства дальнейших вычислений введем безразмерные переменные

где R₀ – длина нити $r$ в положении равновесия $\varphi = 0,$ $\psi = 0$ в отсутствие колебаний при ${{m}_{1}} = {{m}_{2}}$. Далее безразмерные переменные $r{\kern 1pt} *,\;t{\kern 1pt} *$ будем обозначать обычным образом через r, t. Тогда уравнения движения (2.2)–(2.4) принимают вид где учтено равенство масс тел и введен параметр $k = L{\text{/}}{{R}_{0}} > 1$.

Легко видеть, что при $r = {\text{const}}$ уравнения (2.6), (2.7) сводятся к двум независимым уравнениям колебаний математических маятников длиной r и $k - r$ соответственно:

Уравнения (2.9) имеют равновесные решения $\varphi = 0,$ $\psi = 0$, подстановка которых в уравнение (2.8) обращает его в тождество при $r = {\text{const}}$. Это ожидаемый результат, поскольку в отсутствие колебаний система может находиться в равновесии при любом значении $r = {\text{const}}$. Кроме того, уравнение (2.8) имеет решение $r = {\text{const}}$ и в случае ненулевых решений уравнений (2.9), которые выражаются через эллиптические функции (см., например, [17]), если выполняется условие $\varphi (t) = \pm \psi (t)$. Это возможно при k = 2r, когда оба маятника совершают нелинейные колебания одинаковой частоты и амплитуды (см. [10]), а их фазы совпадают $(\varphi (t) = \psi (t))$ или противоположны $(\varphi (t) = - \psi (t))$.

Однако система (2.6)–(2.8) может иметь и другие решения, которые описывают связанные колебания двух математических маятников переменной длины. Целью данной работы является поиск решений системы (2.6)–(2.8), описывающих состояния динамического равновесия, когда оба маятника совершают нелинейные колебания, а функция r(t) совершает малые квазипериодические колебания около некоторого равновесного значения.

Отметим, что уравнения (2.6)–(2.8) являются нелинейными и существование квазипериодических движений грузов в окрестности состояний динамического равновесия, которыми мы интересуемся в данной работе, возможно только вследствие нелинейного взаимодействия между степенями свободы системы.

3. РЕШЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ

Напомним, что колебания математического маятника приводят к увеличению средней силы натяжения нити, причем ее величина определяется амплитудой колебаний (см. [8]). Поскольку мы рассматриваем машину Атвуда с двумя колеблющимися грузами одинаковой массы, можно ожидать, что при одинаковых амплитудах колебаний система будет находиться в состоянии динамического равновесия, при котором переменные $r(t)$, $\varphi (t)$, $\psi (t)$ совершают малые колебания около некоторых равновесных значений и являются квазипериодическими функциями времени. Поскольку уравнения движения (2.6)–(2.8) являются нелинейными, частоты колебаний маятников будут зависеть от амплитуд (см., например, [18]). Далее будем считать, что амплитуды колебаний грузов определяются параметром ε, который предполагается малым, но конечным. При $\varepsilon \to 0$, функции $r(t)$, $\varphi (t)$, $\psi (t)$ должны сводиться к равновесному решению $r = 1$, $\varphi = 0$, $\psi = 0$.

Для удобства вычислений произведем замену переменных

и будем предполагать, что $r(t)$, $\varphi (t)$, $\psi (t)$ являются ограниченными осциллирующими функциями. Подставляя (3.1) в (2.6)–(2.8) и заменяя тригонометрические функции их разложениями в степенные ряды с точностью до пятого порядка включительно, перепишем уравнения движения в виде, удобном для применения теории возмущений (см. [18, 19]):

Решение системы (3.2)–(3.4) будем искать в виде степенных рядов по малому параметру ε:

Функции ${{\varphi }_{0}}(t)$, ${{\psi }_{0}}(t)$ в разложениях (3.5), (3.6) представляют собой решения уравнений (3.2), (3.3) при $\varepsilon = 0$ и без ограничения общности рассуждений могут быть представлены в виде

где начальная фаза переменной ${{\varphi }_{0}}(t)$ равна нулю, а постоянная α определяет разность фаз колебаний маятников в момент времени $t = 0$. Амплитуды колебаний в (3.8) одинаковы, что обеспечивает равенство нулю постоянной составляющей функции в правой части уравнения (3.4) и не приводит к появлению линейной или квадратичной зависимости от времени функции ${{r}_{0}}(t)$ в (3.7), которая является решением уравнения (3.4) при ε = 0. Напомним, что интересующее нас решение (3.7) описывает малые колебания длины $r(t)$ около равновесного значения r = 1, а амплитуды колебаний переменных $\varphi (t)$ и $\psi (t)$ определяются параметром ε (см. (3.1)).

Частоты колебаний ${{\omega }_{1}}$, ${{\omega }_{2}}$ также можем представить в виде степенных рядов по ε:

где частоты гармонических колебаний ${{\omega }_{{10}}} = 1$, ω₂₀ = = $1{\text{/}}\sqrt {k - 1} $ определяются уравнениями (3.2), (3.3) при ε = 0. Коэффициенты ${{\omega }_{{11}}},{{\omega }_{{21}}},{{\omega }_{{12}}},{{\omega }_{{22}}},...$ в разложениях (3.9) будут определяться из условия, что в правой части уравнений (3.2) и (3.3) отсутствуют резонансные члены, пропорциональные $cos({{\omega }_{1}}t)$, $sin({{\omega }_{1}}t)$ и $cos({{\omega }_{2}}t)$, $sin({{\omega }_{2}}t)$ соответственно, которые приводят к неограниченному возрастанию амплитуды колебаний (см. [17, 18]). Поскольку левые стороны уравнений (3.2), (3.3) должны обращаться строго в нуль при подстановке в них функций вида (3.8) с точными значениями частот (3.9), эти уравнения перепишем в эквивалентном виде

Полученная в результате система уравнений (3.4), (3.10), (3.11) записана в форме, удобной для вычисления неизвестных функций ${{r}_{k}}(t),\;{{\varphi }_{k}}(t),\;{{\psi }_{k}}(t)$ в разложениях (3.5)–(3.7). Соответствующий алгоритм символьных вычислений в данной работе реализуется с помощью системы компьютерной алгебры Wolfram Mathematica [16]. Сначала определяем правила замены вида

и выполняем подстановку выражений (3.5)–(3.7) в уравнения (3.4), (3.10), (3.11). Отметим, что использование анонимных функций (pure functions) в правилах замены приводит к автоматическому вычислению всех производных в уравнениях движения. Кроме того, в правой части каждого уравнения выполняем подстановку

Далее в каждом из полученных уравнений разлагаем левую и правую части в степенные ряды по параметру ε с помощью функции $Series$. Для выполнения разложений с точностью до второго порядка, например, достаточно к каждому уравнению применить функцию

Встроенная функция $Coefficient[eq,\varepsilon ,k]$ позволяет выделить в выражении eq коэффициент при ε^k, $k = 0,1,2,...$

Выполняя описанные выше символьные вычисления и приравнивая коэффициенты при одинаковых степенях параметра ε в левой и правой части каждого уравнения (3.4), (3.10), (3.11), получаем следующую систему дифференциальных уравнений:

Далее предполагаем, что функции ${{\varphi }_{k}}(t)$, k = 1, 2, ... удовлетворяют нулевым начальным условиям ${{\varphi }_{k}}(0) = 0,$ ${{\dot {\varphi }}_{k}}(0) = 0$, и будем искать такие решения уравнений (3.14)–(3.20), которые описывают малые колебания функций ${{\varphi }_{k}}(t),\;{{\psi }_{k}}(t),\;{{r}_{k}}(t)$.

Очевидно, функции (3.8) являются решениями уравнений (3.12), (3.13), а их подстановка в (3.14) и замена произведений тригонометрических функций на сумму тригонометрических функций от кратных аргументов с помощью встроенной функции $TrigReduce$ системы $Mathematica$ приводит к дифференциальному уравнению

Отметим, что выбор одинаковых амплитуд переменных ${{\varphi }_{0}}(t)$, ${{\psi }_{0}}(t)$ в (3.8) обеспечивает обнуление постоянной составляющей функции в правой части (3.21) и позволяет найти частное решение дифференциального уравнения (3.21) в виде осциллирующих функций. Для получения такого решения достаточно дважды проинтегрировать правую часть уравнения (3.21) с помощью встроенной функции $Integrate[\# ,t,t]\& $. В результате находим

Далее подставляем решение (3.22) в уравнение (3.15) и, преобразуя его правую часть в линейную комбинацию тригонометрических функций с помощью функции $TrigReduce$, получаем

Аналогичным образом приводим уравнение (3.16) к виду

Дифференциальные уравнения (3.23), (3.24) описывают вынужденные колебания переменных ${{\varphi }_{1}}(t)$, ${{\psi }_{1}}(t)$ и их решения будут ограниченными осциллирующими функциями только при условии, что правые части этих уравнений не содержат резонансных членов (см. [17–19]).

Далее рассмотрим специальный случай одинаковых частот ${{\omega }_{1}} = {{\omega }_{2}}$, что возможно при условии $L = 2{{R}_{0}}$ или k = 2, и выделим резонансные члены в правой части (3.23):

Легко видеть, что существуют только четыре значения начальной фазы α, при которых сумма двух колебаний одинаковой частоты обращается в нуль. Если α = 0 или $\alpha = \pi $, то резонансные члены исчезают при ${{\omega }_{{11}}} = - \tfrac{1}{{16}}$. В этом случае уравнение (3.23) принимает вид

а его решение, удовлетворяющее начальным условиям ${{\varphi }_{1}}(0) = {{\dot {\varphi }}_{1}}(0) = 0$, легко вычисляется с помощью встроенной функции $DSolve$

Если же $\alpha = \pm \pi {\text{/}}2$, то условие обнуления резонансных членов в (3.23) дает ${{\omega }_{{11}}} = \frac{5}{{64}}$, а соответствующее решение уравнения (3.23) имеет вид

Условие обнуления резонансных членов в уравнении (3.24) приводит к таким же результатам ${{\omega }_{{21}}} = - \tfrac{1}{{16}} = {{\omega }_{{11}}}$ или ${{\omega }_{{21}}} = \tfrac{5}{{64}} = {{\omega }_{{11}}}$, что естественно ожидать, так как частоты колебаний предполагаются одинаковыми (${{\omega }_{1}} = {{\omega }_{2}}$). При α = 0 решения уравнений (3.23) и (3.24) совпадают и имеют вид (3.26), а при $\alpha = \pi $ знак функции ${{\psi }_{1}}(t)$ изменяется на противоположный (${{\psi }_{1}}(t) = - {{\varphi }_{1}}(t)$). Заметим, что при ${{\omega }_{1}} = {{\omega }_{2}}$ функции ${{\varphi }_{0}}(t)$ и ${{\psi }_{0}}(t)$ в (3.8) также совпадают при α = 0 и имеют противоположные знаки при $\alpha = \pi $. В обоих случаях подстановка найденных функций ${{\varphi }_{1}}(t)$ и ${{\psi }_{1}}(t)$ в (3.17) с учетом (3.8) приводит к обнулению правой части, что дает решение ${{r}_{1}}(t) = 0$. Поскольку ${{r}_{0}}(t) = 0$ при ${{\omega }_{1}} = {{\omega }_{2}}$ (см. (3.22)), то можно утверждать, что с точностью до членов порядка $O({{\varepsilon }^{2}})$ включительно длина обоих маятников остается постоянной $r(t) = 1$, а сами маятники совершают колебания с одинаковыми частотами и амплитудами синфазно $(\varphi (t) = \psi (t))$ или в противофазе $(\varphi (t) = - \psi (t))$.

При ${{\omega }_{{11}}} = {{\omega }_{{21}}} = \frac{5}{{64}}$ решение уравнения (3.23) имеет вид (3.27) при обоих значениях начальной фазы $\alpha = \pm \pi {\text{/}}2$, а решения уравнения (3.24), удовлетворяющие начальному условию ${{\psi }_{1}}(0) = 0$, запишем в виде

Поскольку при решении уравнения (3.24) начальное значение производной $\mathop {\dot {\psi }}\nolimits_1 (0)$ не задано, решение (3.28) содержит постоянную C₁, которая далее будет найдена при решении уравнения (3.17).

Действительно, при подстановке функций (3.27), (3.28) в уравнение (3.17) получаем

При условии ${{C}_{1}} = \mp 47{\text{/}}768$ постоянная составляющая функции в правой части (3.29) обнуляется, что приводит к осциллирующему частому решению

Вычисления в более высоких порядках по ε выполняются аналоничным образом с примененим встроенных функций системы $Mathematica$, таких как $Expand$, $TrigExpand$, $Collect$, $Coefficient$, D, $Integrate$, $Series$, $Normal$, $DSolve$. Так, подстановка найденных выше функций в (3.18) при α = 0 приводит к уравнению

Условие отсутствия резонансных членов, пропорциональных $cos({{\omega }_{1}}t)$, дает ${{\omega }_{{12}}} = 1{\text{/}}3072$, а решение уравнения (3.31), удовлетворяющее начальным условиям ${{\varphi }_{2}}(0) = {{\dot {\varphi }}_{2}}(0) = 0$, получается в виде

Анализ уравнения (3.19) дает ${{\omega }_{{22}}} = 1{\text{/}}3072$ = ω₁₂, а вычисление функции ${{\psi }_{2}}(t)$ приводит к результату ${{\psi }_{2}}(t) = {{\varphi }_{2}}(t)$ при $\alpha = 0$ и ${{\psi }_{2}}(t) = - {{\varphi }_{2}}(t)$ при α = π. Далее из уравнения (3.20) находим ${{r}_{2}}(t) = 0$.

Описанный процесс последовательного решения дифференциальных уравнений, которые получаются путем приравнивания коэффициентов при одинаковых степенях параметра ε в левой и правой части каждого из уравнений (3.4), (3.10), (3.11), можно продолжить и вычислить решения (3.5)–(3.7) и частоты (3.9) с требуемой точностью, хотя в более высоких порядках такие вычисления становятся все более громоздкими. Например, с точностью до третьего порядка по $\varepsilon $ находим

При этом длины маятников одинаковы и не изменяются $r(t) = 1 = k - r(t)$, а колебания маятников происходят синфазно $(\psi (t) = \varphi (t))$ или в противофазе $(\psi (t) = - \varphi (t))$.

Следует отметить, что при $\psi (t) = \varphi (t)$ или ψ(t) = = $ - \varphi (t)$ правая часть точного уравнения движения (2.8) обращается в нуль и при начальных условиях $r(0) = 1$, $\dot {r}(0) = 0$ его точным решением есть постоянная функция $r(t) = 1$. При этом уравнения (2.6), (2.7) являются независимыми и сводятся к (2.9). Таким образом, выражение (3.33) определяет приближенное решение нелинейного дифференциального уравнения колебаний математического маятника (2.9). Соответственно, разложение (3.34) дает приближенное выражение для частоты нелинейных колебаний маятника, которая является функцией амплитуды колебаний, и совпадает с соответствующим разложением точного выражения, выраженного через эллиптические функции Якоби (см. [17]).

Выбор начальной фазы $\alpha = \pi {\text{/}}2$ приводит к появлению зависимости функции $r(t)$ от времени, хотя вычисления функций ${{\varphi }_{k}}(t),\;{{\psi }_{k}}(t),\;{{r}_{k}}(t)$ во втором и более высоких порядках по ε производятся подобно случаю α = 0. Так, подстановка выражений (3.8), (3.22), (3.27), (3.28), (3.30) в уравнения (3.18), (3.19) дает

Из условия обнуления резонансных членов в правых частях уравнений (3.35), (3.36) получаем

Решения уравнений (3.35), (3.36), удовлетворяющие начальным условиям ${{\varphi }_{2}}(0) = {{\dot {\varphi }}_{2}}(0) = 0$, ${{\psi }_{2}}(0)$ = 0, легко вычисляются с помощью встроенной функции $DSolve$:

Неизвестная постоянная C₂ в выражении (3.39) может быть найдена из уравнения (3.20). Действительно, подставляя полученные выше решения в уравнение (3.20), получаем

Условие обнуления постоянной составляющей функции в правой части уравнения (3.40) дает

Интегрируя дважды правую часть уравнения (3.40) с учетом (3.41), получаем

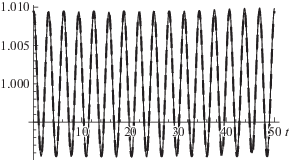
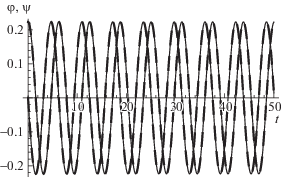
Описанные вычисления можно продолжить и получить функции (3.5)–(3.7) с необходимой точностью, хотя вычисления становятся все более громозкими и для их выполнения требуется применение систем компьютерной алгебры. Используя найденные решения, можно вычислить начальные значения функций $\varphi (0)$, $\psi (0)$, $r(0)$ и их производных $\dot {\varphi }(0)$, $\dot {\psi }(0)$, $\dot {r}(0)$ при выбранном значении параметра ε, а затем найти соответствующие численные решения уравнений движения (3.2)–(3.4) с помощью встроенной функции $NDSolve$. Визуализация найденных аналитических решений при $\varepsilon = 0.05$ (штриховые линии на рис. 2 и 3) демонстрирует хорошее совпадение с численными решениями (сплошные тонкие линии на рис. 2 и 3).

4. ЗАКЛЮЧЕНИЕ

В настоящей работе обсуждается проблема построения решений уравнений движения машины Атвуда с двумя колеблющимися грузами одинаковой массы, которые описывают состояние динамического равновесия системы. Показано, что при одинаковых амплитудах и частотах колебаний система может находиться в равновесии, если оба маятника имеют одинаковую длину $r(t) = 1$ и совершают синфазные колебания или колеблются в противофазе. Существование такого равновесного состояния соответствует нашим ожиданиям, так как система обладает симметрией и оба груза в каждый момент времени действуют на нить с одинаковыми силами. Эта симметрия нарушается при сдвиге фаз $\alpha = \pm \pi {\text{/}}2$ и, хотя в среднем действия обоих грузов на нить уравновешиваются, в каждый момент времени действие на нить одного из грузов оказывается большим. В результате длина каждого из маятников совершает малые колебания около равновесного значения r = 1, причем частота этих колебаний равняется удвоенной частоте колебаний угловых переменных $\varphi (t)$ и $\psi (t)$ и зависит от амплитуды. Соответствующие решения уравнений движения найдены в виде степенных рядов по малому параметру ε, который определяет амплитуды колебаний. Последовательно описаны символьные вычисления, необходимые для определения коэффициентов этих рядов, а сами функции найдены с точностью до второго порядка по ε включительно. Сравнение найденного аналитического решения с численным решением уравнений движения показало справедливость полученных теоретических результатов.

Отметим также, что в данной работе все вычисления и визуализация результатов выполнены с использованием системы компьютерной алгебры Wolfram Mathematica.