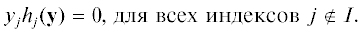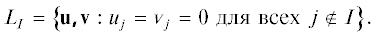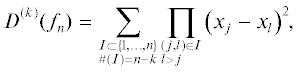Программирование, 2021, № 2, стр. 5-14
ИНВАРИАНТНЫЕ КООРДИНАТНЫЕ ПОДПРОСТРАНСТВА НОРМАЛЬНОЙ ФОРМЫ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
a Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., д. 4, Россия
* E-mail: batkhin@gmail.com
Поступила в редакцию 15.07.2020
После доработки 20.08.2020
Принята к публикации 02.09.2020
Аннотация
Для систем обыкновенных дифференциальных уравнений (ОДУ) с невырожденной линейной частью в общем и гамильтоновом случаях ставится задача отыскания инвариантных координатных подпространств в координатах ее нормальной формы, вычисленной вблизи положения равновесия. Приведены условия существования таких инвариантных подпространств в терминах резонансных соотношений между собственными числами линейной части системы. Дан алгоритм поиска резонансных соотношений между собственными числами без их явного вычисления, который существенно использует методы компьютерной алгебры и q-аналог субрезультантов многочлена. Обсуждается его реализация в трех распространенных системах компьютерной алгебры – Mathematica, Maple и SymPy. Приведены содержательные модельные примеры.
1. ВВЕДЕНИЕ
Подход А. Пуанкаре к исследованию систем нелинейных обыкновенных дифференциальных уравнений (ОДУ) заключался в том, чтобы посредством аналитических обратимых преобразований максимально упростить правые части системы. Этот подход привел к теории нормальных-форм систем ОДУ, разработанной в работах А. Дюляка и А.Д. Брюно для общих систем (подробнее см. [1]) и в работах Дж. Биркгофа, Т.М. Черри, Ф.Г. Густавсона, К.Л. Зигеля, Ю. Мозера, А.Д. Брюно и других для систем Гамильтона (подробнее см. [2, Гл. I, II]).
Хотя нормальная форма системы ОДУ в окрестности инвариантного многообразия (положения равновесия, периодического решения, k-мерного тора) является формальным объектом, т.е. переход к нормальной форме обычно является расходящимся преобразованием, она может быть эффективно использована для исследования устойчивости соответствующего инвариантного многообразия [3], [4, Part II], локальной интегрируемости системы в его окрестности [5], поиска периодических решений, первых интегралов [6, 7], а также асимптотического интегрирования исходной системы [8].
Цель настоящей работы состоит в изучении инвариантных координатных подпространств в нормальной форме общей системы ОДУ в случае, когда линейная часть этой системы невырождена, т.е. имеет хотя бы одно ненулевое собственное число. Существование координатного инвариантного подпространства позволяет изучать динамику фазового потока исходной системы на пространстве меньшей размерности и в некоторых случаях дает информацию о периодических решениях полной системы.
Работа состоит из введения, четырех разделов и двух списков – литературы и условных обозначений. В разделе 2 дается определение нормальной формы общей системы ОДУ и формулируется условие существования инвариантного координатного подпространства. В разделе 3 рассматривается нормальная форма системы Гамильтона и формулируется условие существования инвариантного координатного подпространства в этом случае. Раздел 4 содержит три модельных примера, демонстрирующих типичные ситуации с собственными числами линейной части системы ОДУ. Наконец, в заключительном разделе 5 приведена методика применения q-аналогов таких классических объектов, как субдискриминант многочлена и его производная, для анализа резонансных соотношений между собственными числами линейной части системы ОДУ в ситуации, когда эти собственные числа попарно рационально соизмеримы. Описанные алгоритмы могут быть реализованы в различных системах компьютерной алгебры, таких как Wolfram Mathematica [9], Maplesoft Maple [10], SymPy [11]. Приведен пример определения резонансных соотношений для модельной колебательной системы с шестью степенями свободы.
Замечания об обозначениях
• Символы, набранные полужирным шрифтом $x$, $y$, $u$, $v$, обозначают векторы-столбцы в n-мерном вещественном ${{\mathbb{R}}^{n}}$ или комплексном ${{\mathbb{C}}^{n}}$ пространствах.
• Символы, набранные полужирным шрифтом $p$, $q$, обозначают векторы в n-мерной целочисленной решетке ${{\mathbb{Z}}^{n}}$.
• $\left| p \right| = \sum\limits_{j = 1}^n {\left| {{{p}_{j}}} \right|} $.
• Для $x = \mathop {({{x}_{1}}, \ldots ,{{x}_{n}})}\nolimits^{\text{т}} $ и $p = {{\left( {{{p}_{1}}, \ldots ,{{p}_{n}}} \right)}^{{\text{т}}}} \in {{\mathbb{Z}}^{n}}$ величина ${{x}^{p}}\, \equiv \,\prod\nolimits_{j = 1}^n {x_{j}^{{{{p}_{j}}}}} $, а величина $\langle p,x\rangle \, \equiv \,\sum\nolimits_{j = 1}^n {{{p}_{j}}{{x}_{j}}} $ – скалярное произведение.
2. ИНВАРИАНТЫЕ КООРДИНАТНЫЕ ПОДПРОСТРАНСТВА ОБЩЕЙ СИСТЕМЫ ОДУ
Рассмотрим аналитическую систему ОДУ
вблизи ее положения равновесия совпадающего с началом координат.Пусть линейная часть
(2.2)
$\dot {x} = Ax,\quad A = \mathop {\left. {\frac{{\partial f}}{{\partial x}}} \right|}\nolimits_{x = 0} ,$Согласно теореме I из [1] существует формальное обратимое преобразование $g:x \to y$
представленное в виде степенных рядов, которое приводит исходную систему (2.1) к ее нормальной форме.Определение 1 ([1]). Нормальная форма исходной системы (2.1) это система ОДУ в виде
правые части ${{y}_{j}}{{h}_{j}}(y)$ которой суть степенные ряды(2.4)
${{y}_{j}}{{h}_{j}}(y) = {{y}_{j}}\sum\limits_q {{{h}_{{jq}}}} {{y}^{q}},\quad {{h}_{{j0}}} = {{\lambda }_{j}},\quad j = 1,\; \ldots ,\;n,$Здесь ${{h}_{{jq}}}$ суть постоянные коэффициенты, при этом в слагаемых ${{y}_{j}}{{h}_{j}}(y)$ целочисленные координаты ${{q}_{j}} \geqslant - 1$, но другие координаты ${{q}_{k}} \geqslant 0$.
Введем кортеж $I = {\text{\{ }}{{i}_{1}},\; \ldots ,\;{{i}_{k}}{\text{\} }}$ возрастающих индексов $1 \leqslant {{i}_{1}}$, ${{i}_{k}} \leqslant n$, $k \leqslant n$. Обозначим через KI координатное подпространство
Все ненулевые координаты ${{y}_{j}}$, j ∈ I, подпространства KI назовем внутренними координатами и обозначим их для краткости ${{y}_{I}}$. Остальные координаты назовем внешними.
Аналогично, собственные числа ${{\lambda }_{j}}$, j ∈ I, соответствующие внутренним координатам ${{y}_{I}}$, назовем внутренними собственными числами и обозначим их ${{\lambda }_{I}}$. Остальные собственные числа ${{\lambda }_{j}}$,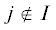 
, назовем внешними.
Рассмотрим следующую задачу.
Задача 1. Какие координатные подпространства KI инвариантны в нормальной форме (2.3), (2.4), (2.5)?
Решение задачи 1 дает следующая теорема.
Теорема 1. Координатное подпространство KI размерности k инвариантно в нормальной форме (2.3)–(2.5), если каждое внешнее собственное число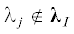 
удовлетворяет условию
Доказательство. Из условия (2.6) следует, что каждый ряд ${{h}_{j}}(y)$ для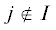 
не содержит ни одного слагаемого ${{h}_{{jq}}}{{y}^{q}}$, чьи индексы ${{q}_{j}}$ = –1, ${{q}_{i}} \geqslant 0$, 
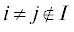. Поскольку внешние переменные ${{y}_{j}}$, $j \notin I$, равны нулю на подпространстве KI, то из этого следует, что для $y \in {{K}_{I}}$
Таким образом, подпространство KI инвариантно в нормальной форме (2.3)–(2.5).
3. ИНВАРИАНТНЫЕ КООРДИНАТНЫЕ ПОДПРОСТРАНСТВА СИСТЕМЫ ГАМИЛЬТОНА
Рассмотрим аналитическую систему Гамильтона
с n степенями свободы вблизи положения равновесияФункция Гамильтона $H(x,y)$ раскладывается в сходящийся степенной ряд
с постоянными коэффициентами ${{H}_{{pq}}}$, $p,q \geqslant 0$, $\left| p \right| + \left| q \right| \geqslant 2$. Каноническое преобразование координат x, yсохраняет гамильтонову структуру исходной системы (3.1).Введем фазовый вектор $z = (x,y) \in {{\mathbb{R}}^{{2n}}}({{\mathbb{C}}^{{2n}}})$. Тогда линейная часть системы (3.1) может быть записана в виде
(3.4)
$\dot {z} = Bz,\quad B = \frac{1}{2}\mathop {\left. {\left( {\begin{array}{*{20}{c}} {\frac{{{{\partial }^{2}}H}}{{\partial y\partial x}}}&{\frac{{{{\partial }^{2}}H}}{{\partial y\partial y}}} \\ { - \frac{{{{\partial }^{2}}H}}{{\partial x\partial x}}}&{ - \frac{{{{\partial }^{2}}H}}{{\partial x\partial y}}} \end{array}} \right)} \right|}\nolimits_{x = y = 0} .$Пусть ${{\lambda }_{1}},\; \ldots ,\;{{\lambda }_{{2n}}}$ – собственные числа матрицы B, которые могут быть переупорядочены следующим образом ${{\lambda }_{{j + n}}} = - {{\lambda }_{j}}$, $j = 1,\; \ldots ,\;n$. Обозначим через вектор $\lambda = ({{\lambda }_{1}},\; \ldots ,\;{{\lambda }_{n}})$ набор базовых собственных чисел системы (3.4).
Согласно теореме 12 из [12, § 12] существует каноническое формальное преобразование (3.3), где все функции f и g суть степенные ряды, которое приводит гамильтонову систему (3.1) к ее нормальной форме
задаваемой нормализованным Гамильтонианом $h({\mathbf{u}},{\mathbf{v}})$(3.6)
$h(u,v) = \sum\limits_{j = 1}^n {{{\lambda }_{j}}} {{u}_{j}}{{{v}}_{j}} + \sum {{{h}_{{pq}}}} {{u}^{p}}{{v}^{q}},$Здесь $0 \leqslant p$, $q \in {{\mathbb{Z}}^{n}}$, $\left| p \right| + \left| q \right| \geqslant 2$, а коэффициенты ${{h}_{{pq}}}$ – постоянные величины.
Резонансное уравнение (3.7) имеет два вида решений, которым соответствуют два вида резонансных членов в нормальной форме (3.6):
1) вековые члены вида ${{h}_{{pp}}}{{u}^{p}}{{v}^{p}}$, которые всегда присутствуют в гамильтоновой нормальной форме из-за особой структуры матрицы B линеаризованной системы (3.8);
2) чисто резонансные члены, которые соответствуют нетривиальным целочисленным решениям уравнения
Следуя [2, Гл. I, § 3] определим кратность резонанса $\mathfrak{k}$ как число линейно независимых решений $p \in {{\mathbb{Z}}^{n}}$ уравнения (3.8), а порядок резонанса $\mathfrak{q} = min\left| p \right|$ по $p \in {{\mathbb{Z}}^{n}}$, $p \ne 0$, $\left\langle {p,\lambda } \right\rangle = 0$.
Главным отличием нормальной формы системы Гамильтона (3.1) от нормальной формы общей системы ОДУ (2.1) является то, что первая всегда содержит вековые члены, даже при отсутствии нетривиальных решений уравнения (3.8). В этом случае имеем так называемую нормальную форму Биркгофа [13].
Пусть, как и в разделе 2, $I = {\text{\{ }}{{i}_{1}},\; \ldots ,\;{{i}_{k}}{\text{\} }}$ – кортеж возрастающих индексов $1 \leqslant {{i}_{1}}$, ${{i}_{k}} \leqslant n$, $k \leqslant n$. Обозначим через ${{L}_{I}}$ координатное подпространство
Все ненулевые координаты ${{w}_{j}} = ({{u}_{j}},{{{v}}_{j}})$, $j \in I$, подпространства LI назовем внутренними координатами и обозначим их для краткости ${{w}_{I}}$, остальные назовем внешними. Собственные числа ${{\lambda }_{j}}$, $j \in I$, соответствующие внутренним координатам wI назовем внутренними собственными числами и обозначим их ${{\lambda }_{I}}$. Остальные собственные числа λj,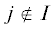 
, назовем внешними собственными числами.
Задача 2. Какие координатные подпространства LI инвариантны в нормальной форме (3.5), (3.6), (3.7)?
Теорема 2. Координатное подпространство LI размерности $2k$ инвариантно в нормальной форме (3.5)–(3.7), если каждое внешнее собственное число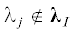 
удовлетворяет следующему условию
Доказательство. Непосредственно следует из теоремы 1.
Замечание 1. Принципиальной разницей между условием (2.6) теоремы 1 и условием (3.9) теоремы 2 является то, что в гамильтоновом случае выбирается ненулевой вектор p из решетки ${{\mathbb{Z}}^{k}}$, а в общем случае выбирается уже неотрицательный вектор $0 \leqslant p \in {{\mathbb{Z}}^{k}}$.
4. ПРИМЕРЫ
Рассмотрим некоторые модельные примеры существования инвариантных координатных подпространств в общем и гамильтоновом случаях.
Пример 1. Пусть собственные числа линейной части общей системы ОДУ равны ${{\lambda }_{1}} = 1$, ${{\lambda }_{2}} = \sqrt 2 $, ${{\lambda }_{3}} = 1 + \sqrt 2 $.
Имеется три одномерных инвариантных координатных подпространства Kj, $j = 1,\;2,\;3$, соответствующих каждому из собственных чисел λj, ибо ни одно из соотношений ${{\lambda }_{i}}{\text{/}}{{\lambda }_{j}}$ при $i \ne j$ не является натуральным числом.
Из трех двумерных координатных подпространств инвариантными являются подпространства K13 и K23, но K12 неинвариантно, поскольку между собственными числами имеется соотношение ${{\lambda }_{3}} = {{\lambda }_{1}} + {{\lambda }_{2}}$, но при этом ни для каких векторов $p \geqslant 0$, $p \in {{\mathbb{Z}}^{2}}$ не выполняются соотношения ${{\lambda }_{1}} = {{p}_{1}}{{\lambda }_{2}} + {{p}_{2}}{{\lambda }_{3}}$ и ${{\lambda }_{2}} = {{p}_{1}}{{\lambda }_{1}} + {{p}_{2}}{{\lambda }_{3}}$.
Пример 2. Пусть собственные числа ${{\lambda }_{j}}$, $j = 1$, ..., n, таковы, что отношения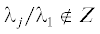 
, $j = 2$, ..., n. Тогда нормальная форма имеет двумерное инвариантное координатное подпространство
L1 = = 
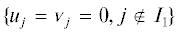, где кортеж ${{I}_{1}} = {\text{\{ }}1{\text{\} }}$. На подпространстве ${{L}_{1}}$ нормальная форма (3.6) индуцирует гамильтонову нормальную форму с одной степенью
свободы. В этом случае условие А выполнено (см [12, § 12]) и нормализующее преобразование
сходится.
Если ${{\lambda }_{1}} \ne 0$ и чисто мнимое, тогда для вещественной системы Гамильтона (3.1) вещественное подпространство L1 является семейством периодических решений. Этот факт впервые был обнаружен А.М. Ляпуновым [14] и описан К. Зигелем в книге [15, §§16, 17] с применением гамильтонова формализма.
Пример 3. Пусть имеется единственная пара собственных чисел ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, удовлетворяющая условию
где $r,s \in \mathbb{Z}$, $s \ne 0$, $(r,s) = 1$, т.е. кратность $\mathfrak{k}$ резонанса равна 1, а порядок резонанса равен $\mathfrak{q} = \left| r \right|$ + |s|. Тогда уравнение (3.8) имеет однопараметрическое семейство решений $p = (lr, - ls,0,\; \ldots )$, $l \in \mathbb{Z}{\backslash \{ }0{\text{\} }}$, а нормальная форма помимо вековых членов содержит чисто резонансные члены. Эти члены наименьшего порядка при l = 1 имеют вид ${{h}_{{12}}}u_{1}^{r}{v}_{2}^{s}$ и ${{h}_{{21}}}{v}_{1}^{r}u_{2}^{s}$.Пусть, например, знаменатель s в (4.1) равен единице. Тогда нормальная форма содержит чисто резонансные члены $u_{1}^{r}{{{v}}_{2}}$ и ${v}_{1}^{r}{{u}_{2}}$. Это значит, что координатное подпространство L1 не может быть инвариантным, поскольку правые части уравнений для внешних переменных ${{u}_{2}}$, ${{{v}}_{2}}$ содержат слагаемые, зависящие от внутренних переменных ${{u}_{1}}$, ${{{v}}_{1}}$ и, тем самым, эти правые части не могут быть всегда равны нулю когда ${{u}_{2}} = {{{v}}_{2}} = 0$. В то же самое время координтаное подпространство L2 является инвариантным.
Пример 4. Пусть матрица B линейной части системы Гамильтона с четырьмя степенями свободы имеет четыре пары собственных чисел: одна пара вещественных ±1, вторая пара чисто мнимых ±i, третья и четвертая пары – комплексных $ \pm 1 \pm i$. Переупорядочим эти собственные числа так, что вектор $\lambda $ имеет следующий вид:
Очевидно, что имеется четыре двумерных инвариантных координатных подпространства L1, L2, L3, L4, соответствующих каждому из собственных чисел ${{\lambda }_{j}}$, $j = 1,\;2,\;3,\;4$, ибо все отношения ${{\lambda }_{i}}{\text{/}}{{\lambda }_{j}}$, $i \ne j$, не являются целыми числами.
Из шести координатных подпространств размерности четыре имеем:
• ${{L}_{{12}}}$ не является инвариантным, поскольку ${{\lambda }_{3}} = {{\lambda }_{1}}$ + λ2.
• ${{L}_{{13}}}$ не является инвариантным, поскольку ${{\lambda }_{2}} = {{\lambda }_{3}}$ – λ1.
• ${{L}_{{14}}}$ не является инвариантным, поскольку ${{\lambda }_{2}} = {{\lambda }_{1}}$ – λ4.
• ${{L}_{{23}}}$ не является инвариантным, поскольку ${{\lambda }_{1}} = {{\lambda }_{3}}$ – λ2.
• ${{L}_{{24}}}$ не является инвариантным, поскольку ${{\lambda }_{1}} = {{\lambda }_{2}}$ + λ4.
• ${{L}_{{34}}}$ инвариантно, поскольку ни ${{\lambda }_{1}}$ ни ${{\lambda }_{2}}$ не могут быть получены как линейная комбинация ${{\lambda }_{3}}$ и ${{\lambda }_{4}}$ с целыми коэффициентами. Тем самым условие (3.9) теоремы 2 выполнено.
Наконец, не существует ни одного инвариантного координатного подпространства размерности шесть.
5. ПРИМЕНЕНИЕ q-СУБДИСКРИМИНАНТОВ ДЛЯ ПОИСКА РЕЗОНАНСОВ
Как следует из рассуждений пп. 2 и 3, вид резонансных членов нормальной формы общей (2.1) или гамильтоновой (3.1) систем определяется исключительно собственными значениями $\lambda $ матрицы A или B соответственно. Это значит, что для выяснения вопроса существования инвариантных подпространств в нормальной форме (2.3)–(2.5) или (3.5)–(3.7) достаточно определить структуру собственных чисел матриц A или B, а именно, выполняются или нет соответствующие условия (2.6) или (3.9). Частично ответ на этот вопрос может быть получен с использованием техники q-субдискриминантов характеристического многочлена $f(\lambda )$ матрицы A или B.
В дальнейшем ограничимся важным с точки зрения приложений случаем, когда вектор собственных чисел $\lambda $ матриц A или B состоит только из вещественных и/или чисто мнимых величин. Дополнительно предположим, что если собственные числа $\lambda $ удовлетворяют резонансному уравнению (2.5) или (3.8), то все ${{\lambda }_{j}}$, входящие в эти уравнения попарно рационально соизмеримы. Другими словами, нет такой ситуации с собственными числами как в примерах 1 и 4.
5.1. q-Субдискриминанты многочлена и их свойства
Применение q-субдискриминантов $D_{q}^{{(k)}}(f)$ характеристического многочлена позволяет не только выяснить наличие у него соизмеримых корней, но и, при определенных условиях, найти эти корни, не прибегая к вычислению всех собственных чисел. Если правые части систем (2.1) или (3.1) зависят от параметров, то и q-субдискриминанты являются функциями этих параметров, что позволяет определить, при каких значениях последних имеет место быть резонанс соответствующей кратности и порядка.
Вначале кратко напомним определение субдискриминанта k-го порядка произвольного приведенного многочлена степени $n$ (подробнее, см. [16, 17]).
Определение 2. Пусть
(5.1)
${{f}_{n}}(x) = {{x}^{n}} + {{a}_{1}}{{x}^{{n - 1}}} + \; \ldots \; + {{a}_{{n - 1}}}x + {{a}_{n}}$
Составим последовательность субдискриминантов многочлена ${{f}_{n}}(x)$
Пусть $P(S)$ есть число знакопостоянств в последовательности $S$, а $V(S)$ – число знакоперемен этой последовательности.
Утверждение 1 ([17, Theorem 4.33]). Число вещественных корней многочлена fn(x) равно величине
Для проверки условия, что все корни многочлена вещественные и/или чисто мнимые, следует
перейти к вспомогательному многочлену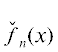 
, все корни которого суть квадраты корней исходного многочлена (2). Это легко сделать
применив преобразование Чирнгауза [18, § 136]: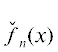 
= Resz(fn(z), x – z2). Используя последовательность субдискриминантов 
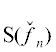и утверждение 1, легко получить следующее.
Утверждение 2. Многочлен (5.1) имеет только вещественные и/или чисто мнимые корни, если все субдискриминанты
вспомогательного многочлена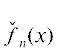 
неотрицательны.
Вычисление субдискриминанта многочлена осуществляется либо с помощью одного из матричных методов с использованием матрицы Безу, Сильвестра, ганкелевой матрицы ньютоновых сумм, либо с использованием алгоритма псевдоделения Якоби (см., например, [16, 19, 20]).
Отметим, что многие указанные выше методы реализованы в различных системах компьютерной алгебры. Например, в системе Wolfram Mathematica [9] функции Subresultants[f1,f2,x] и SubresultantPolynomials[f1,f2,x] позволяют находить соответственно скалярные и полиномиальные субрезультанты пары многочленов f1, f2 относительно переменной x. Фрагмент соответствующего кода приведен в листинге 1.
Листинг 1
coefflst = Reverse [Join [{1}, Array [a, 3]]];
f3 = Total [coefflst x^(Range [4] = 1)]
Df3 = D[f3 , x]
x^3 + x^2 a [1] + x a [2] + a [3]
Subresultants [f3, Df3 , x]
{-a [1]^2 a [2]^2 + 4 a [2]^3 + 4 a [1]^3 a [3]
- 18 a [1] a [2] a [3] + 27 a [3]^2,
Система компьютерной алгебры Maple [10] предлагает набор процедур (SubresultantChain, SubresultantOfIndex, LastSubresultant) из пакета RegularChains[ChainTools], позволяющих вычислять структуру данных, хранящуюполиномиальные субрезультанты пары многочленов от нескольких переменных. Непосредственные вычисления также могут быть произведены с использованием процедур BezoutMatrix, SylvesterMatrix и HankelMatrix из пакета LinearAlgebra (см. [20]).
Наконец, пакет SymPy [11] для языка программирования Python также содержит ряд функций, позволяющих вычислять полиномиальные субрезультанты пары многочленов в символьном виде. Пример вычисления дискриминанта квартики f4(x) дан в листинге 2.
Листинг 2
from sympy import *
nord = 4
x = var (“x”)
c f l s t = symbols (“a1 : { }”.format (nord))
f 4 = Poly (x** nord+sum([c f l s t [nord=1=i] * x** i\
for i in range (nord)]), x)
Df4 = f 4.d i f f (x)
SubDf4 = s u b r e s u l t a n t s (f4, Df4)
print (SubDf4 [=1])
$\begin{gathered} - 27a_{1}^{4}a_{4}^{2} + 18a_{1}^{3}{{a}_{2}}{{a}_{3}}{{a}_{4}} - 4a_{1}^{3}a_{3}^{3} - 4a_{1}^{2}a_{2}^{3}{{a}_{4}} + a_{1}^{2}a_{2}^{2}a_{3}^{2} + 144a_{1}^{2}{{a}_{2}}a_{4}^{2} - 6a_{1}^{2}a_{3}^{2}{{a}_{4}} - 80{{a}_{1}}a_{2}^{2}{{a}_{3}}{{a}_{4}} + 18{{a}_{1}}{{a}_{2}}a_{3}^{3} - \\ 192{{a}_{1}}{{a}_{3}}a_{4}^{2} + 16a_{2}^{4}{{a}_{4}} - 4a_{2}^{3}a_{3}^{2} - 128a_{2}^{2}a_{4}^{2} + 144{{a}_{2}}a_{3}^{2}{{a}_{4}} - 27a_{3}^{4} + 256a_{4}^{3} \\ \end{gathered} $
Для определения рациональной соизмеримости корней многочлена воспользуемся q-аналогами классических производной и субдискриминанта.
Напомним основные q-объекты (см., например, [21–23]), используемые далее.
Определение 3. Определим следующие объекты:
• q-скобка числа a: ${{[a]}_{q}} = \tfrac{{{{q}^{a}} - 1}}{{q - 1}}$, $a \in \mathbb{R}{\backslash \{ }0{\text{\} }}$,
• сдвинутый q-факториал (q-символ Похгаммера): ${{(a;q)}_{n}} = \prod\nolimits_{k = 0}^{n - 1} {(1 - a{{q}^{k}})} $, ${{(a;q)}_{0}} = 1$,
• q-факториал ${{[n]}_{q}}! = \prod\nolimits_{k = 1}^n {{{{[k]}}_{q}}} = \tfrac{{{{{(q;q)}}_{n}}}}{{{{{(1 - q)}}^{n}}}}$, $q \ne 1$,
• q-биномиальные (гауссовы) коэффициенты
$\mathop {\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)}\nolimits_q = \frac{{{{{[n]}}_{q}}!}}{{{{{[n - k]}}_{q}}!{{{[k]}}_{q}}!}} = \prod\limits_{i = 1}^k {\frac{{{{q}^{{n - i + 1}}} - 1}}{{{{q}^{i}} - 1}}} ,$
• q-бином:
${{{\text{\{ }}x;a{\text{\} }}}_{{n;q}}}\mathop = \limits^{{\text{def}}} \prod\limits_{i = 0}^{n - 1} {(x - a{{q}^{i}})} ,\quad {{{\text{\{ }}x;t{\text{\} }}}_{{0;q}}} = 1.$
• При $q \to 1$ все определенные выше объекты становятся классическими.
Отметим, что коэффициенты q-бинома суть гауссовы коэффициенты.
Производная Джексона (q-производная, q-дифференциальный оператор Джексона) есть
Она обладает всеми свойствами обычной производной. Исключением является правило дифференцирования сложной функции, которое отсутствует в случае q-производной.
Утверждение 3. Пусть f и $h$ – два многочлена, тогда
1. $({{\mathcal{A}}_{q}}f)(x) \equiv 0 \Leftrightarrow f(x) \equiv {\text{const;}}$
2. $({{\mathcal{A}}_{q}}(fh))(x) = ({{\mathcal{A}}_{q}}f)(x)h(x) + f(qx)({{\mathcal{A}}_{q}}h)(x);$
3. $\left( {{{\mathcal{A}}_{q}}\frac{f}{h}} \right)(x) = \tfrac{{({{\mathcal{A}}_{q}}f)(x)h(x) - f(x)({{\mathcal{A}}_{q}}h)(x)}}{{h(x)h(qx)}};$
4. $f(qx) = f(x) + (q - 1)x({{\mathcal{A}}_{q}}f)(x).$
Помимо указанных выше свойств отметим, что q-производная функции xn равна ${{\left[ n \right]}_{q}}{{x}^{{n - 1}}}$, а применение q-производной к q-биному степени $n$ снова дает q-бином степени $n - 1$, умноженный на ${{[n]}_{q}}$.
С помощью q-производной теперь определяется q-аналог классического дискриминанта многочлена.
Определение 4. Определим q-дискриминант ${{D}_{q}}({{f}_{n}})$ многочлена ${{f}_{n}}(x)$ как результант пары многочленов ${{f}_{n}}(x)$ и $({{\mathcal{A}}_{q}}{{f}_{n}})(x)$:
Равенство нулю q-дискриминанта многочлена ${{f}_{n}}(x)$ при фиксированном q является признаком существования по крайней мере одной пары q-соизмеримых корней, однако подробную структуру всех соизмеримых корней можно получить с использованием последовательности q-субдискриминантов различных порядков многочлена ${{f}_{n}}(x)$
(5.2)
${{S}_{q}}({{f}_{n}})\mathop = \limits^{{\text{def}}} (D_{q}^{{(0)}}({{f}_{n}}),D_{q}^{{(1)}}({{f}_{n}}),\; \ldots ,\;D_{q}^{{(n - 1)}}({{f}_{n}})).$Частным случаем результата, доказанного для оператора Хана, обобщающего q-производную, в [22, 24], является следующая теорема.
Теорема 3. Многочлен ${{f}_{n}}(x)$ имеет ровно $n - d$ различных последовательностей q-соизмеримых корней, тогда и только тогда, когда в последовательности (5.2) $k$ – х q-субдискриминантов $D_{q}^{{(k)}}({{f}_{n}})$, криминант многочлена fn, $k = 0,\; \ldots ,\;n - 2$, первым отличным от нуля является q-субдискриминант $D_{q}^{{(d)}}({{f}_{n}})$ с номером d.
Все соизмеримые корни многочлена ${{f}_{n}}(x)$ являются корнями наибольшего общего делителя многочлена ${{f}_{n}}(x)$ и его q-производной $({{\mathcal{A}}_{q}}{{f}_{n}})(x)$:
Теорема 3 утверждает, что степень многочлена ${{\tilde {f}}_{q}}(x)$ равна номеру d первого ненулевого q-субдискриминанта в последовательности ${{S}_{q}}({{f}_{n}})$.
Отметим, что q-субдискриминанты вычисляются с помощью любого из матричных методов вычисления классических субрезультантов пары многочленов ${{f}_{n}}(x)$ и $({{\mathcal{A}}_{q}}{{f}_{n}})(x)$. Например, если составить из коэффициентов указанных выше многочленов матрицу Сильвестра ${\mathbf{Syl}}{{{\mathbf{v}}}_{q}}({{f}_{n}})$ размера $(2n - 1) \times (2n - 1)$ в форме Сильвестра–Хабихта, то $k$-й q-субдискриминант $D_{q}^{{(k)}}({{f}_{n}})$ равен определителю k-го иннора [25, Гл. I] этой матрицы.
Пусть в условиях теоремы 3 первый отличный от нуля q-дискриминант имеет номер d, $0 < d$ < n – 1. Обозначим через ${\mathbf{M}}_{d}^{{(i)}}$, $i = 1, \ldots ,d$, d-й иннор модифицированной q-матрицы Сильвестра ${\mathbf{Syl}}{{{\mathbf{v}}}_{q}}({{f}_{n}})$, в которой столбец с номером $2n - 1 - d$ заменен ее столбцом с номером $2n - 1 - d + i$, а через $M_{d}^{{(i)}}$ – определитель этого иннора. Тогда, как показано в [22] имеет место быть утверждение.
Утверждение 4. Если в последовательности q-субдискриминантов $D_{q}^{{(i)}}({{f}_{n}})$, $i = 0,\; \ldots ,\;n - 2$, первым отличным от нуля является q-субдискриминант с номером d, то
(5.3)
${{\tilde {f}}_{q}}(x) \equiv D_{q}^{{(d)}}{{x}^{d}} + M_{d}^{{(1)}}{{x}^{{d - 1}}} + \; \ldots \; + M_{d}^{{(i)}}.$Укажем здесь некоторые важные свойства q-субдистриминантов приведенного многочлена (5.1).
I. k-й q-субдискриминант $D_{q}^{{(k)}}({{f}_{n}})$ представляет собой квазиоднородный многочлен от переменных ${{a}_{1}}, \ldots ,{{a}_{n}}$, такой, что
При этом k-й субдискриминант зависит не более чем от $m$ первых коэффициентов многочлена (5.1), где $m = min(2(n - k - 1),n)$.
II. k-й q-субдискриминант $D_{q}^{{(k)}}({{f}_{n}})$ представляет собой возвратный многочлен четного порядка от переменной q. Возвратность следует из того, что соизмеримость корней ${{\lambda }_{i}}{\text{/}}{{\lambda }_{j}} = q$, $i \ne j$, влечет соизмеримость ${{\lambda }_{j}}{\text{/}}{{\lambda }_{i}} = 1{\text{/}}q$. Это свойство позволяет, с одной стороны, понизить вдвое степень q-субдискриминанта, как многочлена от q с помощью подстановки
а с другой стороны избежать двойной проверки соизмеримости пары корней q и 1/q. В силу вышесказанного, степень ${{D}_{q}}({{f}_{n}})$ как многочлена от q равна $n(n - 1)$.5.2. Алгоритм поиска резонансов
Рассмотрим алгоритм исследования линейной части (2.2) общей системы ОДУ для поиска резонансов. Алгоритм представлен в виде последовательности шагов.
Шаг 1. Для матрицы A системы (3) вычисляем характеристический многочлен ${{f}_{n}}(\lambda )$ и проверяем наличие у него только вещественных и/или чисто мнимых корней с использованием утверждения 2.
Шаг 2. По многочлену ${{f}_{n}}(\lambda )$ вычисляем последовательность ${{S}_{q}}(f)$ (5.2) q-субдискриминантов порядков от 0 до $n - 2$. На этом этапе их степени как многочленов от q можно понизить вдвое, как указано в свойстве II.
Дальнейшие действия зависят от того, насколько легко удается найти рациональные корни q-дискриминанта ${{D}_{q}}({{f}_{n}})$ как многочлена от q.
Шаг 3а. Пусть ${{D}_{q}}({{f}_{n}})$ является многочленом из кольца $\mathbb{Z}[q]$. Тогда его следует попытаться факторизовать с использованием различных алгоритмов (например, Кантора–Цассенхауза или Берлекемпа, см. [26, Гл. 6]). В случае успеха, получаем все (или часть) значений q, для которых имеет место соизмеримость корней многочлена (5.1).
Шаг 3б. Если менение предыдущего шага невозможно, то применим некоторый вариант перебора. Ограничимся определенным максимальным порядком $m$ резонанса. Составим упорядоченный кортеж ${{\mathcal{P}}_{m}}$ всевозможных натуральных пар $(r,s)$ таких, что $r,s \in \mathbb{N}$, ${\text{НОД}}(r,s) = 1$, $r \geqslant s$, $r + s \leqslant m$. Теперь, последовательно перебирая элементы кортежа ${{\mathcal{P}}_{m}}$, для каждой пары $(r,s)$ проверяем равенство нулю q-дискриминанта ${{D}_{q}}(f)$ для значения $q = r{\text{/}}s$.
Шаг 4. Пусть для некоторого рационального $q_{1}^{ * }$ выполнено условие ${{D}_{q}}({{f}_{n}}) = 0$. Тогда вычисляем по последовательности (5.2) степень многочлена ${{\tilde {f}}_{{q_{1}^{ * }}}}(x)$, по формуле (5.3) сам этот многочлен и определяем структуру его корней. Если степень этого многочлена мала, то соизмеримые корни могут быть найдены по соответствующим формулам, а исходный многочлен ${{f}_{n}}(\lambda )$ можно представить в виде ${{f}_{n}}(\lambda ) = u(\lambda ){v}(\lambda )$, где $u(\lambda )$ – множитель с уже известными корнями, а ${v}(\lambda )$ – с еще неизвестными, но среди которых нет $q_{1}^{ * }$-соизмеримых корней.
Шаг 5. Последующие действия сводятся к исследованию, имеют ли множители $u(x)$ и ${v}(x)$ q-соизмеримые корни или нет, а также, имеет ли множитель ${v}(x)$ q-соизмеримые корни для $q \ne q_{1}^{ * }$.
Замечание 2. При исследовании линейной части (3.4) системы Гамильтона следует учитывать, что характеристический многочлен ${{f}_{{2n}}}(\lambda )$ матрицы $B$ является многочленом только четных степеней λ. Следовательно, можно понизить его порядок вдвое и исследовать многочлен, названный в [27] полухарактеристическим, ${{\hat {f}}_{n}}(u) = {{f}_{{2n}}}(\lambda )$, где $\mu = {{\lambda }^{2}}$. В этом случае кортеж ${{\mathcal{P}}_{m}}$ составляется из пар $({{r}^{2}},{{s}^{2}})$ натуральных взаимно простых чисел $r$ и $s$.
Отметим, что в случае когда удается явно выразить собственные числа матрицы B, квадратичную часть гамильтониана (3.2) можно привести к нормальной форме одним из методов, описанным в книгах [8, 28].
Замечание 3. Описанный выше метод обладает двумя недостатками. Во-первых, при наличии резонанса кратности $\mathfrak{k} > 1$ может возникнуть ситуация, когда попарная соизмеримость собственных чисел задается большими значениями q, но сам резонанс может иметь малый порядок. Например, если три собственных числа ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, ${{\lambda }_{3}}$ относятся как натуральные числа $2k - 1$, $2k$, $2k + 1$, $k \in \mathbb{N}$, т.е. ${{\lambda }_{1}}:{{\lambda }_{2}}:{{\lambda }_{3}} = (2k - 1):2k:(2k + 1)$, то наименьший порядок попарной соизмеримости равен $4k - 1$. Однако, в то же самое время, имеет место быть резонансное соотношение ${{\lambda }_{3}} = 2{{\lambda }_{2}}$ – λ1, имеющее порядок 4. Во-вторых, метод неспособен находить такие резонансы, которые задействуют три и более собственных чисел, но при этом эти числа не являются попарно соизмеримыми.
Замечание 4. Описанные в этом разделе методы исследования характеристического многочлена $f(\lambda )$ линейной части ОДУ легко алгоритмизируются и могут быть реализованы во многих системах компьютерной алгебры. Автором были написаны библиотеки процедур в системах компьютерной алгебры Maple и SymPy, предназначенные для вычисления q-субдискриминантов многочлена и исследования резонансных соотношений между корнями последнего без их явных вычислений. Ниже дан пример таких вычислений.
5.3. Модельный пример
Рассмотрим шесть симпатических математических маятников (т.е. одинаковой массы $m$ и длины l), точки подвеса которых расположены на равных расстояниях d на горизонтальной прямой. Пусть маятники соединены между собой невесомыми линейно упругими пружинами жесткости k длиной d в недеформированном состоянии. Точки прикрепления пружин расположены на расстоянии $b \leqslant d$ от точек подвеса маятников. Следуя работе [29], в которой рассмотрена пара таких маятников, несложно получить квадратичную часть ${{\Pi }_{2}}$ потенциальной энергии в окрестности положения равновесия, когда все углы ${{\varphi }_{i}}$, $i = 1, \ldots ,6$, отклонения маятников от вертикали равны нулю. Переходя к каноническим переменным и масштабируя время $\tau = \sqrt {\tfrac{g}{l}} t$ можно получить полухарактеристический многочлен (вековое уравнение) в виде
(5.5)
$\begin{gathered} {{{\hat {f}}}_{6}}(\mu ) = {{\mu }^{6}} - 2\left( {5\beta + 3} \right){{\mu }^{5}} + (36{{\beta }^{2}} + 50\beta + 15){{\mu }^{4}} - \\ - \;2(28{{\beta }^{3}} + 72{{\beta }^{2}} + 50\beta + 10){{\mu }^{3}} + \\ + \;(35{{\beta }^{4}} + 168{{\beta }^{3}} + 216{{\beta }^{2}} + 100\beta + 15){{\mu }^{2}} - \\ - \;2(3{{\beta }^{5}} + 35{{\beta }^{4}} + 84{{\beta }^{3}} + 72{{\beta }^{2}} + 25\beta + 3)\mu + \\ + \;(2\beta + 1)(3\beta + 1)(\beta + 1)({{\beta }^{2}} + 4\beta + 1), \\ \end{gathered} $Следуя шагу 2 Алгоритма вычислим первый q-субдискриминант ${{D}_{q}}({{\hat {f}}_{6}})$ и используя подстановку (5.4) упростим его. В результате получим многочлен относительно переменной Q степени 15. Здесь его явное выражение не приводится в силу его громоздкости. В системе Maplesoft Maple этот многочлен удалось разложить на линейные и квадратные множители, что позволило легко найти все соизмеримости между корнями многочлена (5.5). Таким образом, выполнен шаг 3а Алгоритма и имеется возможность найти все корни многочлена, а следовательно проверить выполнение резонансных соотношений между ними.
В системе SymPy разложить q-дискриминант ${{D}_{q}}({{\hat {f}}_{6}})$ на множители не удалось, поэтому применим шаги 3б и далее Алгоритма для некоторого фиксированного значения параметра $\beta = 48{\text{/}}25$. Выберем максимальный порядок резонанса m = 20 и, согласно замечанию 2, составим кортеж ${{\mathcal{P}}_{{20}}}$ всевозможных пар $({{r}^{2}},{{s}^{2}})$ таких, что ${\text{НОД}}(r,s) = 1$ и $r + s \leqslant 20$, $r,s \in \mathbb{N}$. Перебирая все такие пары из ${{\mathcal{P}}_{{20}}}$ найдем, что при $q_{1}^{ * } = 121{\text{/}}25$ и $q_{2}^{ * } = 169{\text{/}}25$ $q$-дискриминант обращается в нуль, а остальные q-субдискриминанты нет. При этом многочлены ${{\tilde {f}}_{{{{q}_{1}}}}}(\mu )$ и ${{\tilde {f}}_{{{{q}_{2}}}}}(\mu )$, вычисленные по формуле (5.3) имеют один и тот же корень ${{\mu }_{1}}$ = 1. Следовательно, должно быть еще одно значение $q_{3}^{ * } = q_{2}^{ * }{\text{/}}q_{1}^{ * } = 169{\text{/}}121$, при котором обнуляется q-дискриминант. Таким образом, найдены три корня многочлена (5.5): ${{\mu }_{1}}$ = 1, ${{\mu }_{2}}\, = \,q_{1}^{ * }$, ${{\mu }_{3}}\, = \,q_{2}^{ * }$, и, следовательно, f6(μ) = (μ – 1)(μ – ‒ $q_{1}^{ * })(\mu - q_{2}^{ * }){{{v}}_{3}}(\mu )$. Остальные иррациональные корни ${{\mu }_{k}}$, $k = 4,5,6$, кубического многочлена ${{{v}}_{3}}(\mu )$ легко находятся с помощью тригонометрической формулы Виета [18, § 119].
Итак, имеется резонансное соотношение (3.8)
между частотами ${{\lambda }_{1}} = 1$, ${{\lambda }_{2}} = 11{\text{/}}5$, ${{\lambda }_{3}} = 13{\text{/}}5$. Соотношение (5.6) имеет три целочисленных решения ${{p}_{1}} = (1,\; - {\kern 1pt} 4,\;3)$, ${{p}_{2}} = (3,\;1,\; - {\kern 1pt} 2)$ и ${{p}_{3}} = (4,\; - {\kern 1pt} 3,\;1)$, из которых следует, что условие (3.9) теоремы 2 не выполнено. Таким образом, имеется инвариантное координатное подпространство LI, $I = {\text{\{ }}1,2,3{\text{\} }}$, размерности шесть в нормальной форме, соответствующее трем собственным числам ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, ${{\lambda }_{3}}$. Каждому из оставшихся собственных чисел ${{\lambda }_{i}}$, $i = 4,5,6$, соответствует двумерное инвариантное координатное подпространство Li. В силу того, что порядки целочисленных векторов ${{p}_{1}}$, ${{p}_{2}}$, ${{p}_{3}}$ равны соответственно, 4, 3, 4, то исследование динамики исходной системы на подпространстве LI возможно лишь выполнив нелинейную нормализацию исходной системы по крайней мере до 6-го порядка включительно.Список литературы
Брюно А.Д. Аналитическая форма дифференциальных уравнений (I) // Тр. ММО. 1971. Т. 25. С. 119–262.
Брюно А.Д. Ограниченная задача трех тел: Плоские периодические орбиты. М.: Наука, 1990. 296 с.
Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Гл. ред. физ.-мат. литер. изд-ва “Наука”, 1978. 352 с.
Bruno A.D. Local Methods in Nonlinear Differential Equations. Berlin–Heidelberg–New York–London–Paris–Tokyo: Springer–Verlag, 1989. 350 p.
Bruno A.D., Enderal V.F., Romanovski V.G. On new integrals of the Algaba-Gamero-Garcia system // Computer Algebra in Scientific Computing / Ed. by V.P. Gerdt, W. Koepf, E.W. Mayr, E.V. Vorozhtsov. Berlin Heidelberg: Springer, 2017. V. 10490 of Lecture Notes in Computer Science. P. 40–50.
Брюно А.Д. Нормальная форма системы Гамильтона с периодическим возмущением // ЖВММФ. 2020. Т. 60. № 1. С. 36–52.
Брюно А.Д. Нормализация периодической системы Гамильтона // Программирование. 2020. Т. 46. № 2. С. 76–83.
Журавлев В.Ф., Петров А.Г., Шундерюк М.М. Избранные задачи гамильтоновой механики. М.: ЛЕНАНД, 2015. 304 с.
Wolfram S. The Mathematica Book. Wolfram Media, Inc., 2003. 1488 p.
Thompson I. Understanding Maple. Cambridge University Press, 2016. 228 p.
SymPy: symbolic computing in Python / Aaron Meurer, Christopher P. Smith, Mateusz Paprocki et al. // Peer J. Computer Science. 2017. V. 3. P. e103. https://doi.org/10.7717/peerjcs.103
Брюно А.Д. Аналитическая форма дифференциальных уравнений (II) // Тр. ММО. 1972. Т. 26. С. 199–239.
Биркгоф Д.Д. Динамические системы. Ижевск: Изд. дом “Удмуртский университет”, 1999. 408 с.
Lyapunov A.M. Problme gnral de la stabilit du monvement // Ann. Fac. Sci. Toulouse Math. 1892. V. 9 (1907). № 2. P. 204474. Ann Math. Studies (1947). Stability of Motion. New York, London: Academic Press, 1966 (English).
Зигель К., Мозер Ю. Лекции по небесной механике. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001. 384 с.
Калинина Е.А., Утешев А.Ю. Теория исключения: Учеб. пособие. СПб.: Изд-во НИИ химии СПбГУ, 2002. 72 с.
Basu S., Pollack R., Roy M.-F. Algorithms in Real Algebraic Geometry. Algorithms and Computations in Mathematics 10. Berlin Heidelberg New York: Springer-Verlag, 2006. ix+662 p.
Сушкевич А.К. Основы высшей алгебры. 4-е изд. М.-Л.: ОГИЗ ГИТТЛ, 1941. 460 с.
Gathen J. von zur, Leking T. Subresultants revisited // Theoretical Computer Science. 2003. V. 297. P. 199–239.
Батхин А.Б. Параметризация дискриминантного множества вещественного многочлена // Программирование. 2016. Т. 42. № 2. С. 8–21.
Кац В.Г., Чен П. Квантовый анализ. М.: МЦНМО, 2005. 128 с.
Батхин А.Б. Параметризация множества, определяемого обобщенным дискриминантом многочлена // Программирование. 2018. № 2. С. 5–17.
Батхин А.Б. Вычисление резонансного множества многочлена при ограничениях на коэффициенты // Программирование. 2019. № 2. С. 6–15.
Батхин А.Б. Вычисление обобщенного дискриминанта вещественного многочлена // Препринты ИПМ им. М.В. Келдыша. 2017. № 88. 40 с. http://www.keldysh.ru/papers/2016/prep2017_88.pdf.
Джури Э. Инноры и устойчивость динамических систем. М., 1979. 304 с.
Акритас А.Г. Основы компьютерной алгебры с приложениями. М.: Мир, 1994. 544 с.
Батхин А.Б., Брюно А.Д., Варин В.П. Множества устойчивости многопараметрических гамильтоновых систем // Прикл. мат. мех. 2012. Т. 76. № 1. С. 80–133.
Маркеев А.П. Линейные гамильтоновы системы и некоторые задачи об устойчивости движения спутника относительно центра масс. М.-Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2009. 396 с.
Маркеев А.П. Нелинейные колебания симпатических маятников // Нелинейная динамика. 2010. Т. 6. № 3. С. 605–621.
Дополнительные материалы отсутствуют.
Инструменты
Программирование
Пн.-пт.: 10.00-19.00