Программирование, 2021, № 2, стр. 44-50
КОМПЬЮТЕРНАЯ АЛГЕБРА НА JULIA
Д. С. Кулябов a, b, *, А. В. Королькова a, **
a Кафедра прикладной информатики и теории вероятностей, Российский университет дружбы народов
117198 Москва, ул. Миклухо-Маклая, д. 6, Россия
b Лаборатория информационных технологий, Объединенный институт ядерных исследований
141980 Московская область, Дубна, ул. Жолио-Кюри 6, Россия
* E-mail: kulyabov-ds@rudn.ru
** E-mail: korolkova-av@rudn.ru
Поступила в редакцию 03.08.2020
После доработки 05.09.2020
Принята к публикации 05.09.2020
Аннотация
В последнее время на место основного языка научных и инженерных расчетов выдвигается язык Julia. У ряда пользователей возникает желание работать полностью внутри “экосистемы” Julia, подобно тому, как происходит работа в “экосистеме” Python. Для Julia существуют библиотеки, покрывающие большинство потребностей научно-инженерных расчетов. Перед авторами возникла необходимость использовать символьные вычисления для задач математического моделирования. Поскольку основным языком реализации численных алгоритмов мы выбрали язык Julia, то и задачи компьютерной алгебры хотелось бы решать на этом же языке. Авторы выделили основные функциональные области, задающие разные варианты применения систем компьютерной алгебры. В каждой из областей нами выделены наиболее характерные представители систем компьютерной алгебры на Julia. В результате авторы делают вывод, что в рамках “экосистемы” Julia возможно (и даже удобно) использовать системы компьютерной алгебры.
1. ВВЕДЕНИЕ
Для задач математического моделирования мы ориентированы на использование языка Julia [1–4].
Язык Julia является проблемно-ориентированным языком для научных и инженерных расчетов. Язык имеет простой синтаксис. Для облегчения перехода научно-инженерных работников, Julia использует удачные языковые конструкции, заимствованные из языков MATLAB, R, Python, FORTRAN [5, 6]. Для поддержки интерактивной разработки и оптимизации времени исполнения Julia использует JIT-компиляцию. Внутри Julia является LISP-подобным языком, поэтому она органично использует функциональные конструкции. Julia поддерживает библиотеки, написанные на других языках программирования.
Одной из причин выбора Julia является последовательная реализация принципа одного языка. Дело в том, что в своем развитии языки программирования для научных и инженерных задач разошлись по двум направлениям: языки для создания высокопроизводительных программ (FORTRAN, C, C++) и языки для быстрого прототипирования и использования непрограммистами (Matlab, R, Python). Julia старается решить проблему двух языков11. Однако задачи компьютерной алгебры выпадают из основного направления развития языка Julia.
С учетом различного характера возникающих при этом задач, выделим следующие области применения систем компьютерной алгебры:
• Пользовательские системы компьютерной алгебры. Данные системы предлагают пользователю широкий спектр возможностей, не требуя от него глубоких знаний в программировании. Примеры: SymPy, Maxima, Axiom, Reduce.
• Языки компьютерной алгебры. С помощью них можно писать нетривиальные программы символьных вычислений. Примеры: Wolfram, R-Lisp.
• Предметно-ориентированные системы компьютерной алгебры.
В работе рассмотрены системы компьютерной алгебры, реализованные на языке Julia, с точки зрения этих областей применимости.
1.1. Структура статьи
В разделе 2 рассматривается пользовательская системa компьютерной алгебры, использующая библиотеку SymPy. В разделе 3 рассматривается язык компьютерной алгебры, реализованный на основе идеологии языка Wolfram. В разделе 4 рассмотрен проблемно-ориентированный язык символьных вычислений для задач непрерывного моделирования динамических систем.
2. SymPy.lj – ИНТЕРФЕЙС К СИСТЕМЕ КОМПЬЮТЕРНОЙ АЛГЕБРЫ НА ЯЗЫКЕ PYTHON
Одной из ключевых основ идеологии языка Julia (как и у языка Python) является возможность использования сторонних библиотек. Например, Julia может подключать библиотеки, написанные на языках C, FORTRAN. Сходной идеологией обладает и язык Python (что и послужило основой его популярности). Поэтому было бы непредусмотрительно не использовать это богатство. Julia использует для вызова библиотек языка Python пакет PyCall.
Пакет SymPy (http://sympy.org/) является библиотекой Python для символьной математики. Фактически, это один из наиболее мощных свободных пакетов символьных вычислений. Естественно, что с ним можно работать из Julia.
Рассмотрим для примера, как мы можем использовать функционал SymPy из среды Julia. Установим пакет PyCall, загрузим его, а затем импортируем библиотеку SymPy.
import Pkg
Pkg.add (“PyCall”)
using PyCall
sympy = pyimport (“sympy”)
Дальнейшие операции похожи на работу в SymPy. Определим символьную переменную x и возьмем синус от этой переменной.
x = sympy.Symbol (“x”)
y = sympy.sin(x)
Вычислим теперь sin(π):
y.subs(x, pi)
Результат будет иметь тип PyObject. Чтобы его использовать в дальнейшем, следует привести его к какому-либо числовому типу. Например, следующим образом:
y.subs(x, pi) |> float
Это пример, кроме всего прочего, демонстрирует функциональную природу Julia. В данном выражении оператор |> задает действие функции справа (по аналогии с конвейером в оболочке Unix). То есть записи f(x) и x |> f эквивалентны.
Однако, вышеприведенная запись выглядит несколько тяжеловесной. Для простейших операций требуется писать много дополнительного кода, не несущего никакого содержания. К счастью, можно использовать стандартные возможности Julia для расширений языка. Для того, чтобы операции SymPy не выделялись на фоне остальных вычислений Julia, вызов питоновской библиотеки производится с помощью пакета SymPy.lj [7]:
import Pkg
Pkg.add(“SymPy”)
using SymPy
Тогда вышерассмотренный пример примет следующий вид:
x = Sym(“x”)
y = sin(x)
subs(y, x, pi) |> float
Для объектов SymPy используется тип Sym.
В принципе, на этом можно и завершить. Если читатель имел опыт работы с SymPy в Python, он сможет работать и с SymPy.lj в Julia.
Язык Julia создавался таким образом, чтобы на нем легко могли писать программы люди, перешедшие с других языков программирования с научной и инженерной спецификой (таких, как Matlab, R, FORTRAN). По этой причине Julia содержит много синтаксического сахара, в частности одну и ту же операцию можно выполнить несколькими путями. Так, символьную переменную можно задать с помощью конструктора:
x = Sym(“x”)
Также можно задать с помощью макроса:
syms x y z
Также можно задать с помощью функции, имитирующей работу в SymPy из Python:
x, y = symbols(“x y”, commutative=false)
Здесь, кроме всего, кроме объявления символических переменных указываются и их свойства.
Следует заметить, что обязательное явное задание типа несколько противоречит динамической природе Julia. Однако, в данном случае мы используем внешнюю библиотеку, поэтому играем по чужим правилам. Здесь можно провести аналогию с Python, который, при работе с внешними библиотеками, использует соглашения этой библиотеки, а не подменяет ее синтаксис своим.
SymPy.lj дает пользователю Julia возможность манипулировать символьными выражениями, предлагает для этого удобный интерфейс. Правда (учитывая производительность современных компьютеров) никакой оптимизации по скорости выполнения не производится.
Приведем несколько примеров работы с SymPy.lj.
При операциях с алгебраическими выражениями весьма полезны операции факторизации (factor) и расширения (expand).
x, y = symbols(“x, y”)
factor(x^2 - 2x + 1)
expand((x –1)*(x+1))
В символьных выражениях можно применять конструкции Julia, например включения22:
expand(prod([x–i for i in 1:5]))
Это происходит от того, что SymPy.lj представляет символьные матрицы как массивы с элементами типа Sym, например, как Array{Sym}33.
Зададим символьную матрицу.
x, y = symbols(“x y”)
m = [x 1; 1 x]
Тогда с матрицами можно производить стандартные операции, например умножать:
m * m
m .* m
Также большинство стандартных операций с матрицами расширены для работы с символьными значениями. Это, кстати, один из примеров реализации множественной диспетчеризации.
Упомянутые выше функции factor и expand производят некоторое (необходимое нам) упрощение исходного выражения. В SymPy есть много функций для выполнения различного рода упрощений. Например, существует общая функция называемая simplify, которая пытается получить простейшую форму выражения, используя для этого разнообразные эвристики: simplify:
a = (x + x^2)/(x*sin(y)^2 + x*cos(y)^2) simplify(a)
Для решения уравнений и систем уравнений можно использовать функцию solve. Например, решим уравнение
относительно x:
x = symbols(“x”)
solve(x^2 + 3*x + 2, x))
Для систем уравнений можно использовать векторную нотацию:
x, y = symbols(“x y”)
eq1 = x + y – 1
eq2 = x – y – 2
solve([eq1, eq2], [x, y])
DictAny,Any with 2 entries:
y => –1/2
x => 3/2
И наконец, дифференцирование и интегрирование.
Функция diff используется для вычисления производной символьных выражений. Можно вычислить частные производные и производные высшего порядка. Зададим, например, функции:
x, y = symbols(“x y”)
f(x) = exp(–x) * sin(x)
g(x, y) = x^2 + 17*x*y^2
Вычислим производную $\frac{{{\text{d}}f(x)}}{{{\text{d}}x}}$:
diff(f(x))
Мы здесь опустили аргумент, по которому ведется дифференцирование. Впрочем, его можно и обозначать:
diff(f(x), x)
Также можем получить производную более высокого порядка $\frac{{{{{\text{d}}}^{3}}f(x)}}{{{\text{d}}{{x}^{3}}}}$
diff(f(x), x, 3)
Можно взять и частную производную $\frac{{\partial g(x,y)}}{{\partial x}}$
diff(g(x,y), x)
Аналогично можно проводить символьное интегрирование. Вычислим $\int {({{x}^{2}} + x + 2){\text{d}}x} $:
x, y = symbols(“x y”)
integrate(x^2 + x + 2)
Или двойной интеграл $\int {{\text{d}}y} \int {{\text{d}}xxy} $:
integrate(x*y, (x, y))
Можно вычислить и определенный интеграл $\int_0^1 {x{\text{d}}x} $:
integrate(x^2, (x, 0, 1))
Таким образом мы имеем очень богатую систему компьютерной алгебры. И работать с ней можно прямо из среды Julia.
3. SYMATA – ЯЗЫК КОМПЬЮТЕРНОЙ АЛГЕБРЫ ДЛЯ JULIA
При том, что SymPy является великолепной системой компьютерной алгебры, у нее есть небольшой недостаток. Это готовая система, “работающая из коробки”. Она предоставляет “пользовательский слой” для символьных вычислений, но не “слой разработчика”, позволяющий писать программный код. Для разработки можно использовать язык программирования для задач символьной математики Symata [8]44. Язык Symata реализован на языке Julia. В качестве основы для дизайна языка Symata принят язык Wolfram [9].
Для использования данной системы необходимо установить пакет Symata:
import Pkg
Pkg.add(“Symata”)
Загружается Symata стандартным образом:
using Symata;
Следует обратить внимание на следующее свойство Symata. Если SymPy.lj проектировался таким образом, чтобы его можно было использовать напрямую из среды программирования Julia, бесшовно, то Symata является предметно-ориентированным языком, написанным на Julia. Он достаточно сильно отличается от языка Julia. Поэтому необходимо явно переключаться между этими языками. Переключение в режим языка Julia осуществляется с помощью следующей функции
Julia()
Обратно в режим Symata можно переключиться с помощью функции
isymata()
Вычисления в Symata похожи на работу в системе Mathematica. Приведем пример. Пусть нам надо вычислить значение косинуса:
expr = cos(pi * x)
Зададим значение переменной x:
x = 1/3
Теперь собственно можно получить значение выражения expr:
expr
Изменим значение переменной x:
x = 1/6
Тогда изменится и значение вычисляемого выражения:
expr
Сбросим значение переменной x. Тогда искомое выражение перестанет вычисляться:
Clear(x)
expr
Фактически средствами Julia реализован язык Wolfram. Так что, наверное, нет необходимости более подробно освещать здесь синтаксис системы Symata. Впрочем, стоит остановиться на некоторых отличиях языка Symata от языка Wolfram. Большинство этих отличий проистекает из того желания, чтобы Symata наследовала синтаксис Julia. Например, комментарий задается символом #, в то время как в языке Wolfram комментарий выглядит следующим образом:
(* comment *)
Для задания списка используются не фигурные скобки {}, а квадратные:
[a, b, c]
Элементы списка могут разделяться как запятыми, так и переходом на новую строку:
[
a
c + d
Expand((x+y)^2)
]
Аргумент функции задается не в квадратных скобках, как в Wolfram, а в круглых, как в Julia:
f(x)
Подобно функциям в Julia, некоторые функции приобрели инфиксную нотацию.
Функция Map(f, list) приобретает инфиксную форму
f % list
Функция Apply(x, y):
x .% y
Более подробно можно посмотреть в документации к Symata.
Можно сделать вывод, что на основе Julia (с использованием ее мощных возможностей по созданию предметно-ориентированных языков) реализован исключительно удобный язык для компьютерной алгебры. При этом интересно отметить, что для многих аналитических вычислений в языке Symata используется библиотека SymPy.
4. КОМПЬЮТЕРНАЯ АЛГЕБРА В JULIA ДЛЯ ЗАДАЧ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
В предыдущих разделах мы рассмотрели реализацию систем компьютерной алгебры общего назначения на языке Julia. Но также большой интерес вызывают специализированные, предметно-ориентированные применения компьютерной алгебры.
Пакет ModelingToolkit.jl [10] предлагает специализированный язык компьютерной алгебры для задач математического моделирования. Для этого он использует возможности метапрограммирования [11] языка Julia. Отметим, что основным режимом работы для ModelingToolkit.jl является не интерактивный режим, а пакетный.
Для задания символьных переменных служит макрос @variables:
@variables x y
После этого данные символьные переменные можно использовать в символьных выражениях (сохраняя синтаксис Julia):
z = x^2 + y
Для моделирования непрерывных динамических систем необходимо использовать производные. В пакете ModelingToolkit.jl дифференциальные операторы строятся с помощью макроса @derivatives:
@variables t
@derivatives D’ ~t
Здесь задан дифференциальный оператор D = $\frac{{\text{d}}}{{{\text{d}}t}}$. Количество штрихов ' указывает на порядок дифференциального оператора. Можно записать выражение:
z = t + t^2
D(z)
Оператор дифференцирования не вычисляет ничего непосредственно в этот момент, поскольку является “ленивым” оператором. Впрочем, мы можем получить результат сразу, применив функцию expand_derivatives:
expand_derivatives(D(z))
1 + 2t
Поскольку в Julia функции являются объектами первого порядка, то объявленные символьные переменные являются, фактически, функциями. Можно при объявлении переменных явно указать зависимости:
@variables t x(t) y(t)
Эта зависимость учитывается при дифференцировании:
z = x + y*t
expand_derivatives(D(z))
Последнее выражение будет раскрыто как
derivative(x(t), t) + y(t) +
↪ derivative(y(t), t) * t
В качестве примера посмотрим, как решается классическая задача типа “хищник–жертва” [12, 13]:
(1)
$\left\{ \begin{gathered} \frac{{{\text{d}}x}}{{{\text{d}}t}} = ax - byx, \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}t}} = cxy - dy, \hfill \\ \end{gathered} \right.$Сначала загрузим необходимые пакеты (при необходимости):
import Pkg
Pkg.add(“ModelingToolkit”)
Pkg.add(“OrdinaryDiffEq”)
Также загрузим пакет для поддержки построения графиков:
Pkg.add(“Plots”)
Теперь подключим необходимые пакеты:
using ModelingToolkit
using OrdinaryDiffEq
using Plots
Собственно, теперь можно решать нашу задачу. Определим переменные и операторы дифференцирования. Часть переменных определим как параметры.
@parameters t a b c d
@variables x(t) y(t)
@derivatives D’ ~t
Теперь просто перепишем исследуемую систему (1), используя синтаксис Julia:
eqs = [D(x) ~ a *x – b*x*y,
D(y) ~ c*x*y – d*y]
Теперь применим символьные преобразования и приведем нашу систему к виду, необходимому для пакета OrdinaryDiffEq.lj [14]:
sys = ODESystem(eqs)
Дальнейшие манипуляции проводятся в рамках пакета OrdinaryDiffEq.lj. Зададим начальные значения переменных:
u0 = [x => 1.0
y => 1.0]
Также зададим параметры задачи:
p = [a => 1.1
b => 0.4
c => 0.1
d => 0.4]
Будем решать задачу на следующем временном промежутке:
tspan = (0.0, 100.0)
Создадим структуру, содержащую всю нашу задачу:
prob = ODEProblem(sys, u0, tspan, p;
↪ jac=true)
Дополнительный параметр jac=true указывает системе символически сгенерировать оптимизированную функцию Якоби для улучшения работы решателей дифференциальных уравнений.
И, наконец, применим решатель из пакета OrdinaryDiffEq.lj:
sol = solve(prob)
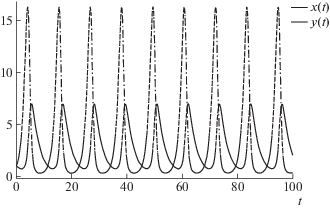
Нарисуем график, представленный на рис. 1:
plot(sol)
Рассмотренный подход очень хорошо вписывается в идеологию специализированного языка для научных и инженерных расчетов. При данном подходе для символьных вычислений используется не специальный универсальный язык, а для каждого направления исследований создается свой проблемно-ориентированный язык символьных расчетов. Этот язык должен бесшовно стыковаться с базовым языком, в нашем случае, с Julia.
5. ЗАКЛЮЧЕНИЕ
Наш обзор (далеко не полный) систем компьютерной алгебры для языка Julia показал, что и сам язык, и его инфраструктура являются достаточно зрелыми. При этом системы компьютерной алгебры языка Julia охватывают широкий спектр применения: пользовательские системы компьютерной алгебры (SymPy.lj), мощные языки компьютерной алгебры (Symata.lj), проблемно-ориентированные языки компьютерной алгебры (ModelingToolkit.jl). Все это позволяет надеяться, что популярность языка Julia будет возрастать не только в области численных, но и символьных расчетов.
Список литературы
Bezanson J., Edelman A., Karpinski S., Shah V.B. Julia: A fresh approach to numerical computing // SIAM Review. 2017. 1. V. 59. № 1. P. 65–98. arXiv: 1411.1607.
Joshi A., Lakhanpal R. Learning Julia. Packt Publishing, 2017. 316 p. ISBN: 9781785883279.
Tate B.A., Daoud F., Dees I., Moffitt J. Seven More Languages in Seven Weeks. 2015. 318 p. ISBN: 9781941222157.
Bezanson J., Karpinski S., Shah V.B., Edelman A. Julia: A Fast Dynamic Language for Technical Computing. 2012. P. 1–27. arXiv: 1209.5145.
Bezanson J., Chen J., Chung B. et al. Julia: dynamism and performance reconciled by design // Proceedings of the ACM on Programming Languages. 2018. 10. V. 2. № OOPSLA. P. 1–23. URL: https://doir.org.https://doi.org/10.1145/3276490https://dl.acm.org/doi/10.1145/3276490.
A Comparison of Programming Languages in Economics Research; Executor: S. Boraan Aruoba, Jesús Fernández-Villaverde. Cambridge, MA: 2014. 6 p. URL: http://www.nber.org/papers/w20263.pdf.
Julia interface to SymPy via PyCall. URL: https://github.com/JuliaPy/SymPy.jl.
Symata.jl. Symbolic mathematics language. URL: https://github.com/jlapeyre/Symata.jl.
Wolfram S. An Elementary Introduction to the Wolfram Language. 2015. 313 p. ISBN: 978.1-1944183-01-1. URL: http://www.wolfram.com/language/elementary-inroduction/.
ModelingToolkit.jl. URL: https://github.com/SciML/ModelingToolkit.jl.
Lämmel R. Software Languages. Syntax, Semantics, and Metaprogramming. Cham: Springer International Publishing, 2018. XXX, 424 p. ISBN: 978-3-319-90798-7. URL: http://link.springer.com/10.1007/978-3-319-90800-7.
Lotka A.J. Elements of Physical Biology. Baltimore: Williams and Wilking Company, 1925. 435 p. URL: https://archive.org/details/elementsofphysic017171mbp.
Kulyabov D.S., Korolkova A.V., Sevastianov L.A. Two Formalism of Stochastication of One-Step Models // Physics of Atomic Nuclei. 2018. V. 81. № 6. P. 916–922. arXiv: 1908.04294.
Rackauckas C., Nie Q. DifferentialEquations.jl – A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia // Journal of Open Research Software. 2017. V. 5.
Дополнительные материалы отсутствуют.
Инструменты
Программирование