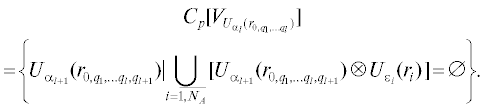Программирование, 2021, № 4, стр. 3-13

1. ВВЕДЕНИЕ

В ряде задач, например таких как исследования энергетических состояний кристаллической структуры (которая определяется электромагнитным взаимодействием ядер и электронов составляющих ее атомов) [1], энергетических ландшафтов движения мешкообразных структур везикул, которые перемещают гормоны и нейротрансмиттеры (например, инсулин и серотонин) по клеткам и телу [2], ландшафта потенциальной энергии состояния белковой молекулы [3], энергетического ландшафта скалярного поля вакуума [4] и других задач необходимо моделирование энергетических ландшафтов. Данные ландшафты представляются в виде скалярных полей, где каждой точке пространства (как правило, это пространство Rⁿ, где R множество действительных чисел), ставится в соответствие скалярная величина, например значения энергии в данной точке пространства, то есть, чаще всего задается скалярная функция $\nu ( \cdot ){\text{:}}\,{{R}^{n}} \to R$.

Для практического моделирования сложных энергетических ландшафтов был предложен эффективный подход на основе формализации расположения энергетических бассейнов [5]. При этом множество состояний описывалось набором квазиравновесных состояний (локальных минимумов), которые при помощи эквипотенциальных сечений объединялись в “бассейны” минимумов, иерархически вложенных друг в друга. Иерархия сечений множества квазиравновесных состояний, разделенных энергетическими барьерами на ландшафте, задает иерархическую структуру бассейнов [6]. В этом случае целесообразно, чтобы область определения функции скалярного поля учитывала потенциальную иерархическую структуру поля.

Для описания межбассейновой динамики энергетический ландшафт считается фиксированным на время исследования. Однако, сам энергетический ландшафт может изменяться. Для описания динамики изменения энергетического ландшафта необходимо иметь возможность на ландшафте выделить произвольное подмножество, которое может изменить свой энергетический уровень. Следовательно, должна быть возможность формально задать данное подмножество учитывая потенциальную иерархическую структуру энергетического ландшафта. Для учета наложения ряда изменений ландшафта необходимо иметь возможность выполнения логических операций над такими подмножествами, которые образуют соответствующую алгебру подмножеств.

2. ПОСТАНОВКА ЗАДАЧИ

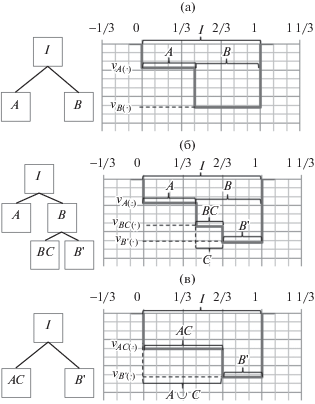
Пример 1. Рассмотрим ландшафт в виде простейшего одномерного скалярного поля, заданного на интервале $I = [0,1] \subset R$ с двумя энергетическими бассейнами (рис. 1а), где ${{\nu }_{A}}( \cdot ),{{\nu }_{B}}( \cdot )$ – скалярные величины энергий бассейнов $A,B \subseteq I$, соответственно. Данный ландшафт представляется в виде графа [5], изображенного на данном рисунке. Изменение ландшафта происходит под воздействием внешних факторов. Пусть в первый момент изменения происходят на подмножестве $C \subseteq I$ с энергией ${{\nu }_{C}}( \cdot )$. В результате в области $BC = C \cap B$ возникает новый бассейн с энергией ${{\nu }_{{BC}}}( \cdot ) = F({{\nu }_{C}}( \cdot ),{{\nu }_{B}}( \cdot ))$ (рис. 1б), где $F( \cdot )$ некоторая агрегирующая функция. При этом соответствующий граф ландшафта изменится. Во второй момент, допустим, что внешние факторы, действующие в области $A \cup C$ приводят к единому бассейну AC с энергией ${{\nu }_{{AC}}}( \cdot ) = F\left( {{{\nu }_{C}}( \cdot ),{{\nu }_{A}}( \cdot )} \right)$ и соответственно изменению графа ландшафта (рис. 1в). Из данного простейшего примера можно сделать три замечания. Во-первых, для определения нового распределения скалярного поля $\nu ( \cdot )$ необходимо иметь возможность определения всех образовавшихся подмножеств (бассейнов) интервала I, которые формируются на основе алгебры подмножеств. Во-вторых, бассейны образуют иерархические структуры, которые можно представить соответствующим графом, и это необходимо учитывать при изменении скалярного поля ландшафта, “выделении” и “поглощении” отдельных бассейнов. В-третьих, при описании ландшафта, используя иерархическую структуру расположения бассейнов, можно регулировать уровень его детализации.

Как было показано в [8] координаты точек b в которых реально может быть измерено скалярное поле принадлежат множеству рациональных чисел Q. Для нашего примера $b \in X \subset Q$, где X ограничено отрезком $[0,1] \subset R$, $R$ множество вещественных чисел со стандартной метрикой. Для каждого $b \in X$ справедливо разложение b = ${{p}^{k}} \cdot \frac{m}{n}$, где p – выбранное простое число, k, m, $n \in Z$, а $\frac{m}{n}$ – несократимая дробь, где m и n не делятся на p [7]. Согласно теореме Островского [8], описывающей все возможные нормы, поле рациональных чисел может быть пополнено либо по евклидовой норме, либо по неархимедовой р-адической норме вида ${{\left| b \right|}_{p}} = {{p}^{{ - k}}}$, которая удовлетворяет условию сильного неравенства треугольника:

Пополнение Q по р-адической норме ${{\left| b \right|}_{p}}$ приводит к полю р-адических чисел Q_p, которое естественным образом может отражать иерархическую структуру [9]. Любое р-адическое число $r \in {{Q}_{p}}$ отличное от нуля имеет вид [10]:

Каноническая запись p-адического числа будет $r = {{( \ldots {{q}_{l}}{{q}_{{l - 1}}} \ldots {{q}_{1}},{{q}_{0}}{{q}_{{ - 1}}} \ldots {{q}_{{ - m}}})}_{p}}$, то есть бесконечная влево и конечная вправо последовательность целых чисел ${{q}_{l}} = 0, \ldots ,p - 1$. р-адические числа с нормой ${{\left| r \right|}_{p}} \leqslant 1$, для которых $m \geqslant 0$ образуют кольцо целых р-адических чисел Z_p [11]. Их каноническая запись имеет вид бесконечной влево последовательности $r = {{\left( { \ldots {{q}_{l}}{{q}_{{l - 1}}} \ldots {{q}_{1}}{{q}_{0}}} \right)}_{p}}$ целых чисел q_l. Иногда для записи канонической формы целых р-адических чисел для удобства используют бесконечную вправо последовательность целых чисел q_l в виде $r = {{\left( {{{q}_{0}}{{q}_{1}} \ldots {{q}_{l}} \ldots } \right)}_{p}}$ [12], которую мы в дальнейшем будем использовать.

Для множества р-адических чисел Q_p существует непрерывное отображение вида $\theta (r):{{Q}_{p}} \to $ R₊, где R₊ – множество неотрицательных действительных чисел [11]:

Отображение θ(r) сюръективно, взаимно однозначно почти всюду, то есть сохраняет меру (переводит р-адическую меру Хаара в меру Лебега на полупрямой), непрерывно и гёльдерово с показателем 1 [13]. При этом непересекающиеся шары отображаются на интервалы, которые не пересекаются или имеют пересечение нулевой меры. Образ целого р-адического числа $r \in {{Z}_{p}}$ в единичном интервале вещественных чисел будет определяться соотношением вида [14]:

Таким образом, каждая точка $x \in I \subset R$ в которой задано одномерное скалярное поле может рассматриваться как образ р-адической координаты $r \in {{Z}_{p}}$, а произвольное подмножество $A \subseteq I$ как объединение образов р-адических шаров. В этом случае, например одномерное скалярное поле (см. Пример 1), представляющее ландшафт, может быть рассмотрено как отображение вида $\nu \left( \cdot \right){\text{:}}\,{{Z}_{p}} \to R$. Тогда для описания изменения скалярного поля ландшафта с бассейнами необходимо иметь возможность описать произвольное подмножество $A \subseteq I$ в виде множества р-адических шаров, объединение образов которых определяют данное подмножество, а также определяет операции объединения, пересечения и отрицания на множествах р-адических шаров с учетом иерархической структуры их расположения для определения изменения поля.

3. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Представление подмножества ограниченного числового множества в виде образа множества р‑адических шаров. Поле р-адических чисел Q_p с р-адической нормой ${{\left| \cdot \right|}_{p}}$ является полным метрическим пространством с ультраметрикой $\forall {{r}_{i}},{{r}_{j}} \in {{Q}_{p}}$, $\rho ({{r}_{i}},{{r}_{j}}) = {\text{|}}{{r}_{i}} - {{r}_{j}}{{{\text{|}}}_{p}}$, удовлетворяющей условию:

Для р-адических чисел Q_p ультраметрика $\rho ({{r}_{i}},{{r}_{j}})$ может быть определена как обобщенная метрика Кантора [15]: $\rho \left( {{{r}_{i}},{{r}_{j}}} \right) = {{\left( {\frac{1}{p}} \right)}^{{LCP\left( {{{r}_{i}},{{r}_{j}}} \right)}}}$, $LCP\left( {{{r}_{i}},{{r}_{j}}} \right)$ – длина общего префикса последовательностей для канонического представления р-адических чисел r_i, ${{r}_{j}} \in {{Q}_{p}}$. В частности, для ${{r}_{i}},{{r}_{j}} \in {{Z}_{p}}$ величина $LCP({{r}_{i}}$, r_j) определяется из условия:

$\forall {{r}_{i}},{{r}_{j}}$, где ${{r}_{i}} = {{({{q}_{0}},{{q}_{1}}, \ldots {{q}_{l}} \ldots )}_{p}}$, r_j = ${{({{a}_{0}},{{a}_{1}}, \ldots {{a}_{l}} \ldots )}_{p}}$, $LCP\left( {{{r}_{i}},{{r}_{j}}} \right) = k$, если выполняется q_l = a_l, $l = \overline {0,k} $, ${{q}_{{k + 1}}} \ne {{a}_{{k + 1}}}$.

р-Адический шар с центром a ∈ I и радиусом $\varepsilon \in ~$ R₊ задается выражением:

Известно (см. например, [10]), что p-адические шары имеют следующие свойства:

1. Пусть U и V два р-адических шара в X. Тогда мы имеем только два случая:

1a. шары упорядочены по включению (или $U \subset V$, или $V \subset U$);

1b. не пересекаются ($U \cap V = \emptyset $).

2. Каждая точка шара является его центром.

3. Каждый шар в X одновременно открыт и замкнут.

Для однозначного задания р-адического шара необходимо задать его центр и радиус. Центры р‑адических шаров, объединение образов которых определяет подмножество $A \subseteq I$ находится на основе алгоритма.

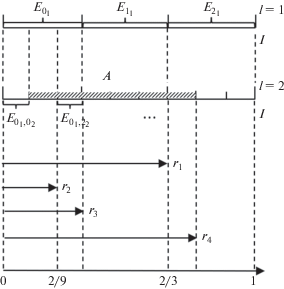
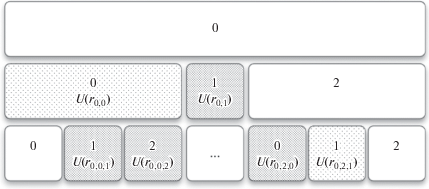
1. Рассматриваем ограниченное числовое множество $I \subset R$ и в нем подмножество $A \subseteq I$. Фиксируем простое число p (например, p = 3, рис. 2). Определяем максимальную детализацию разбиения множества I на подмножества как максимальное количество уровней иерархии L.

2. Выполняем последовательное разбиение множества I на подмножества ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}}$, q_l = 0, ..., p – 1, $l = \overline {1,L} $, q₀ = 0 так, чтобы выполнялись условия:

3. Задаем l = 0, фиксируем начальный индекс q₀ = 0 для формируемых последовательностей индексов.

4. Определяем $l = l + 1$ и выполняем проверку не пустоты пересечения подмножеств ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}}$ с подмножеством $A \subseteq I$ для формирования последовательностей из чисел ${{q}_{l}} = 0, \ldots ,p - 1$. При этом:

4a. если ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \cap A = \emptyset $, то подмножество ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}}$ не рассматривается и последовательность не формируется;

4b. если ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \cap A \ne \emptyset ,{{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \varsubsetneq A$, то в последовательности фиксируем q_l;

4c. если ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \subseteq A$, то фиксируем q_l и принимаем $\forall i = 1, \ldots , + \infty ,{{q}_{{l + i}}} = p - 1$. Формирование последовательности “останавливается”.

5. Для каждого случая b) повторяем выполнение пункта 4 и формируем последовательности $\left( {{{q}_{0}}{{q}_{1}} \ldots {{q}_{l}}{{q}_{{l + 1}}}} \right)$.

6. Пункты 4 и 5 выполняются до момента, пока формирование всех последовательностей не будет “остановлено” или пока не выполнится l = L. Для всех “неостановленных” последовательностей при l = L принимаем $\forall i = 1, \ldots , + \infty ,{{q}_{{L + i}}}$ = p – 1.

Полученные с использованием приведенного алгоритма последовательности при разбиении на p подмножеств, где p – простое число, на каждом уровне иерархии задают положительные целые р‑адические числа $r \in {{Z}_{p}}$ в канонической форме.

Пример 2. Применение описанного алгоритма для подмножества $A \subseteq I$ (рис. 2) формирует четыре последовательности вида $\left( {{{q}_{0}}{{q}_{1}} \ldots {{q}_{l}}} \right)$. Данные последовательности задают целые р-адические числа:

В соответствии с приведенным алгоритмом последовательность индексов подмножества ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \subseteq A \subseteq I$ однозначно определяет р-адическое число r. Это р-адическое число имеет единственный образ $\varphi \left( r \right)$ во множестве I. Прообразом интервала ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \subseteq I$ во множестве Q_p будет р‑адический шар [13] ${{U}_{\varepsilon }}\left( r \right)$ с центром $r \in I$ и радиусом $\varepsilon \in {{R}_{ + }}$ для которого:

a. Координата центра р-адического шара для подмножества ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \subseteq A$ задается р-адическим числом $r = {{\left( {{{q}_{0}} \ldots {{q}_{l}}\left( {p - 1} \right) \ldots } \right)}_{p}}$, которое получено на основании описанного выше алгоритма.

b. Радиус шара определяется по условию включения в шар всех р-адических чисел, имеющих образ в подмножестве ${{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}} \subseteq A$ и равен ε = ρ $({{r}_{i}},{{r}_{j}})$ = p^–l, где ${{r}_{i}},{{r}_{j}} \in {{Q}_{p}}$ любые р-адические числа, для которых $\varphi \left( {{{r}_{i}}} \right),\varphi \left( {{{r}_{j}}} \right) \in {{E}_{{{{q}_{0}}, \ldots ,{{q}_{l}}}}}$.

Пример 3. Для Примера 2, где p = 3, р-адическое расстояние заданное метрикой Кантора для ${{r}_{1}},{{r}_{2}} \in {{Z}_{p}}$ и ${{r}_{2}},{{r}_{3}} \in {{Z}_{p}}$ будет: $\rho \left( {{{r}_{1}},{{r}_{2}}} \right) = {{\left( {\frac{1}{p}} \right)}^{1}} = \frac{1}{3}$, $\rho \left( {{{r}_{2}},{{r}_{3}}} \right) = {{\left( {\frac{1}{p}} \right)}^{2}} = \frac{1}{9}$.

Образы непересекающихся р-адических шаров отображаются на интервалы вещественных чисел, которые не пересекаются или имеют пересечение нулевой меры. Тогда произвольное подмножество $A \subseteq I$ будет определяться объединением образов р-адических шаров с указанными выше центрами и радиусами.

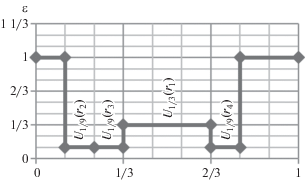
Пример 4. Для примера на рис. 2 подмножество $A \subseteq I$ будет объединением образов р-адических шаров (рис. 3) из множества шаров:

Далее будем говорить, что множество шаров U(A) = $\{ {{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})\left| {i = \overline {1,{{N}_{A}}} } \right.\} $, описывает подмножество $A \subseteq I$. Множество U(A) целесообразно упорядочить по убыванию величины радиуса ${{\varepsilon }_{i}}$, а для одинаковых радиусов упорядочить по возрастанию значения $\varphi \left( {{{r}_{i}}} \right)$. Исходя из свойств р-адических шаров, выполняется условие: $\forall a,b \in {{Q}_{p}}$, $a \in {{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})$, $b \in {{U}_{{{{\varepsilon }_{j}}}}}({{r}_{j}})$, ρ(a, b) = const.

р-адическое приближение и покрытие множества шаров.

Определение 1. Для множества шаров U(A) = = $\{ {{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})\left| {i = \overline {1,{{N}_{A}}} } \right.\} $, описывающих $A \subseteq I$, подмножество шаров ${{U}_{{{{\varepsilon }_{{apr}}}}}}(A) \subseteq U(A)$, с радиусами ${{\varepsilon }_{i}}\, \geqslant \,{{\varepsilon }_{{apr}}}$, называется р-адическим приближением подмножества A с погрешностью до ${{\varepsilon }_{{apr}}} \in \left[ {0,1} \right]$.

Пример 5. Р-адическим приближением подмножества A (Пример 4) с точностью ${{\varepsilon }_{{apr}}} = \frac{1}{3}$ будет подмножество ${{A}_{{\frac{1}{3}}}} = {{E}_{{{{0}_{0}},{{1}_{1}}}}}$, описывающееся шаром ${{U}_{{\frac{1}{3}}}}\left( {{{r}_{1}}} \right)$.

Определение 2. Покрывающим шаром или покрытием множества шаров $\mathcal{U}$ = $\{ {{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}}),\left| {i = \overline {1,N} } \right.\} $ называется шар U_α(r), для которого $\forall i,{{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}}) \subseteq {{U}_{\alpha }}(r)$. В этом случае будем записывать ${{U}_{\alpha }}(r) = Co{{v}_{\alpha }}$($\mathcal{U}$).

Центром покрывающего шара ${{U}_{\alpha }}(r)$ будем считать точку с координатой r = $({{q}_{0}}{{q}_{1}} \ldots {{q}_{l}}(p - 1)$(p – – 1)...)_p, где $\left( {{{q}_{0}}{{q}_{1}} \ldots {{q}_{l}}} \right)$ – общий префикс для последовательностей канонического представления р-адических чисел координат всех центров шаров множества $\mathcal{U}$, $l \leqslant {{l}_{{{\text{max}}}}}$, ${{l}_{{{\text{max}}}}} = \mathop {{\text{min}}}\limits_{i,j = \overline {1,N} } LCP\left( {{{r}_{i}},{{r}_{j}}} \right)$ – длина максимального общего префикса р-адических чисел всех центров. Радиусом покрывающего шара ${{U}_{\alpha }}\left( r \right)$ будет величина $\alpha = \frac{1}{{{{p}^{l}}}}$. Множество всех покрытий для множества $\mathcal{U}$ будет CS($\mathcal{U}$) = = {$Co{{v}_{{{{\rho }^{{ - l}}}}}}$($\mathcal{U}$)|$l \leqslant {{l}_{{{\text{max}}}}}$}. Любое подмножество CB($\mathcal{U}$) ⊆ $~ \subseteq CB$($\mathcal{U}$) задает покрывающее тело множества шаров $\mathcal{U}$.

Покрывающий шар ${{U}_{{{{\alpha }_{{min}}}}}}\left( r \right)$, для которого $l = {{l}_{{{\text{max}}}}}$, будет минимальным покрытием множества $\mathcal{U}$. Для него радиус будет соответственно ${{\alpha }_{{{\text{min}}}}} = {{p}^{{ - {{l}_{{{\text{max}}}}}}}}$. При этом для множества шаров $\mathcal{U}$ выполняется условие $\forall i,\rho \left( {{{r}_{i}},r} \right) \leqslant {{\alpha }_{{min}}}$. Центр минимального покрывающего шара будет удовлетворять условию $r = \mathop {{\text{max}}}\limits_{i = \overline {1,N} } {{r}_{i}}$. Минимальное покрытие для множества из одного шара ${{U}_{{{{\varepsilon }_{i}}}}}\left( {{{r}_{i}}} \right)$ будет совпадать с данным шаром. Максимальным покрытием ${{U}_{1}}\left( 1 \right)$ любого множества $\mathcal{U}$ является шар, для которого множество I является его образом. Шар ${{U}_{1}}\left( 1 \right)$ имеет центр $r = {{(0(p - 1)(p - 1) \ldots )}_{p}}$ и радиус α = 1.

Пример 6. Для примера рис. 2 покрытиями для множества шаров $\mathcal{U}$ = $\left\{ {{{U}_{{\frac{1}{9}}}}\left( {{{r}_{2}}} \right),{{U}_{{\frac{1}{9}}}}\left( {{{r}_{3}}} \right)} \right\}$ будут шары ${{U}_{{{{\alpha }_{1}}}}}\left( {{{r}_{{{{\alpha }_{1}}}}}} \right)$ с центром ${{r}_{{{{\alpha }_{1}}}}} = {{\left( {00222 \ldots } \right)}_{3}}$ и радиусом ${{\alpha }_{1}} = \frac{1}{3}$ и ${{U}_{{{{\alpha }_{2}}}}}\left( {{{r}_{{{{\alpha }_{2}}}}}} \right)$ с центром ${{r}_{{{{\alpha }_{1}}}}} = {{\left( {02222 \ldots } \right)}_{3}}$ и радиусом ${{\alpha }_{1}} = 1$. При этом шар ${{U}_{{{{\alpha }_{1}}}}}\left( {{{r}_{{{{\alpha }_{1}}}}}} \right)$ будет минимальным покрытием множества шаров $\mathcal{U}$.

Определение 3. Два шара ${{U}_{{{{\varepsilon }_{i}}}}}\left( {{{r}_{i}}} \right)$ и ${{U}_{{{{\varepsilon }_{j}}}}}({{r}_{j}})$ называются сходными по покрытию ${{U}_{\alpha }}(r)$, если шар ${{U}_{\alpha }}(r)$ является их покрывающим шаром. Если шары ${{U}_{{{{\varepsilon }_{i}}}}}\left( {{{r}_{i}}} \right)$ и ${{U}_{{{{\varepsilon }_{j}}}}}\left( {{{r}_{j}}} \right)$ имеют радиусы ${{\varepsilon }_{i}} = {{\varepsilon }_{j}} = {{p}^{{ - l}}}$ и сходны по минимальному покрытию ${{U}_{\alpha }}\left( r \right)$ с радиусом $\alpha \leqslant {{p}^{{1 - l}}}$, то они называются равными по покрытию. Условие равенства шаров по покрытию будем записывать как:

В частности, для Примера 3 будем иметь ${{U}_{{\frac{1}{9}}}}\left( {{{r}_{2}}} \right) \equiv {{U}_{{\frac{1}{9}}}}\left( {{{r}_{3}}} \right)\left\{ {Cov\left| {{{U}_{{\frac{1}{3}}}}\left( {{{r}_{{{{\alpha }_{1}}}}}} \right)} \right.} \right\}$.

Определим во множестве шаров $\mathcal{U}$ = $\{ {{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})$, ${\text{|}}i = \overline {1,N} \} $ шар наименьшего радиуса ${{U}_{{\varepsilon '}}}(r') \in ~$ $\mathcal{U}$, $\varepsilon {\kern 1pt} ' = \mathop {{\text{min}}}\limits_i {{\varepsilon }_{i}} = {{p}^{{ - l'}}}$. Пусть ${{U}_{\alpha }}\left( r \right),\alpha = {{p}^{{ - {{l}_{\alpha }}}}}$ – покрывающий шар для данного множества шаров.

Определение 4. Высотой покрытия ${{U}_{\alpha }}\left( r \right)$ для множества шаров $\mathcal{U}$ называется величина, определяемая соотношением: $hg{{t}_{U}}({{U}_{\alpha }}(r)) = l{\kern 1pt} '\, - {{l}_{\alpha }}$. Если ${{U}_{\alpha }}\left( r \right)$ является минимальным покрытием, то $hg{{t}_{U}}\left( {{{U}_{\alpha }}\left( r \right)} \right)$ называется минимальной высотой покрытия ${{U}_{\alpha }}\left( r \right)$ для множества шаров $\mathcal{U}$.

Высота покрытия шара ${{U}_{{{{\varepsilon }_{i}}}}}\left( {{{r}_{i}}} \right)$ будет $hg{{t}_{{{{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})}}}({{U}_{\alpha }}(r))$ = l_i – l_α, где ${{l}_{i}} = - lo{{g}_{p}}{{\varepsilon }_{i}}$. Тогда для одного шара минимальная высота покрытия равна нулю.

Пример 7. Для Примера 2 наименьший радиус шара будет $\varepsilon {\kern 1pt} ' = \mathop {{\text{min}}}\limits_i {{\varepsilon }_{i}} = {{p}^{{ - 2}}} = \frac{1}{9}$, l' = 2. Минимальный покрывающий шар совпадает с множеством I. Следовательно, $\alpha = {{p}^{0}} = 1$, ${{l}_{\alpha }}$ = 0. Тогда минимальная высота покрытия для множества шаров U(A), будет определяться значением $hg{{t}_{{U(A)}}}({{U}_{\alpha }}(r))$ = l' – l_α = 2 – 0 = 2.

p-Адическая плотность подмножества. p-Адические шары из множества U(A) = $\{ {{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})\left| {i = \overline {1,{{N}_{A}}} } \right.\} $ не пересекаются. Мощность подмножества A будет определяться в виде $Card\left( A \right) = \mathop \sum \limits_{i = 1}^{{{N}_{A}}} {{\varepsilon }_{i}}$. Для описания внутренней структуры подмножества $A \subseteq I$ определим степень его р-адической плотности. В общем случае множество плотно, если между двумя произвольными элементами множества всегда возможно найти третий элемент этого множества [16]. Если множество не плотно, то оно считается разряженным. Свойствами р-адических шаров является то, что они одновременно и открыты, и замкнуты. Поэтому использование классического определения плотности множества затруднено. Однако, интуитивно понятно, что для более плотного подмножества $A \subseteq X$ размеры “пустот” между шарами, описывающими его, должны быть минимальными.

Определение 5: Степенью р-адической плотности подмножества A называется величина, которая определяется соотношением:

где $\left\{ {{{U}_{{{{\varepsilon }_{i}}}}}\left( {{{r}_{i}}} \right)\left| {i = \overline {1,{{N}_{A}}} } \right.} \right\} = U\left( A \right)$ множество шаров, представляющих подмножество $A \subseteq I$, U_α(r) – минимальный покрывающий р-адический шар для U(A).

Степень р-адической плотности показывает, насколько множество A заполнено шарами на всех уровнях разбиения множества I. Если $\delta (A) \to 1$, то множество будем считать р-адически плотным, а при $\delta \left( A \right) \to 0$ – р-адически разряженным. Очевидно, что р-адическая плотность будет $\delta \left( A \right) = 1$, если множество U(A) описывается единственным шаром, равным минимальному покрытию.

Утверждение 1. р-Адическая плотность множества A будет стремиться к единице $\delta (A) \to 1$, если его мощность Card(A) стремится к величине радиуса минимального покрывающего шара ${{U}_{\alpha }}(r)$.

Доказательство. Радиус минимального покрывающего р-адического шара U_α(r) определяется величиной $\alpha = {{p}^{{ - {{l}_{\alpha }}}}}$. Пусть U(A) = $\{ {{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})\left| {i = \overline {1,{{N}_{A}}} } \right.\} $, где $\forall i,{{\varepsilon }_{i}} = {{p}^{{ - {{l}_{i}}}}}$. Подставим данные значения в формулу для р-адической плотности. Тогда имеем:

Тогда $\delta \left( A \right) \to 1$, если $Card\left( A \right) \to \alpha $. ■

Утверждение 2. Для множества A р-адическая плотность $\delta \left( A \right) \to 0$, когда минимальный покрывающий р-адический шар U_α(r) имеет радиус $\alpha \ne 0$, а р-адическое приближение данного множества с погрешностью ${{\varepsilon }_{{apr}}} \to 0$ является пустым множеством.

Доказательство. Исходя из условия, радиус покрывающего шара U_α(r) будет иметь значение α = = ${{p}^{{ - {{l}_{\alpha }}}}} \ne 0$ и, следовательно ${{l}_{\alpha }} \ne + \infty $. Пусть подмножество A описывается шарами с радиусами ε_i = ${{p}^{{ - {{l}_{i}}}}},i = \overline {1,{{N}_{A}}} $. По условию утверждения р-адическое приближение при ${{\varepsilon }_{{apr}}} \ne 0$ будет ${{U}_{{{{\varepsilon }_{{apr}}}}}}(A) = \emptyset $. Следовательно, $\forall i,{{\varepsilon }_{i}} < {{\varepsilon }_{{apr}}}$. Но ${{\varepsilon }_{{apr}}} \to 0$, тогда все ${{\varepsilon }_{i}} \to 0$, что равносильно ${{l}_{i}} \to + \infty $. В этом случае $\forall i,hg{{t}_{{{{U}_{{{{\varepsilon }_{i}}}}}\left( {{{r}_{i}}} \right)}}}\left( {{{U}_{\alpha }}\left( r \right)} \right) = {{l}_{i}} - {{l}_{\alpha }} \to + \infty $. Тогда:

Таким образом, р-адическая плотность подмножества позволяет учесть его внутреннюю структуру. Плотность будет максимальной при совпадении подмножества A с его минимальным покрытием. Минимальная плотность будет, когда шары, описывающие подмножество, имеют минимальные радиусы и максимально “разбросаны” на множестве I.

Пример 8. Рассмотрим подмножество $A \subseteq I$, представленное на рис. 2. Оно описывается множеством шаров U(A) = $\left\{ {{{U}_{{\frac{1}{3}}}}({{r}_{1}}),{{U}_{{\frac{1}{9}}}}({{r}_{2}}),{{U}_{{\frac{1}{9}}}}({{r}_{3}}),{{U}_{{\frac{1}{9}}}}({{r}_{4}})} \right\}$. Для данного множества шаров имеем ${{l}_{{i = 1}}} = 1$, ${{l}_{{i = \overline {2,4} }}}$ = 2. Минимальное покрытие U_α(r) будет иметь параметры ${{r}_{\alpha }} = {{\left( {02222 \ldots } \right)}_{3}}$ и $\alpha = {{p}^{{ - {{l}_{\alpha }}}}} = 1$. Следовательно, ${{l}_{\alpha }} = 0$. Высота покрытия ${{U}_{\alpha }}\left( r \right)$ для шаров из множества U(A) будет: $hg{{t}_{{{{U}_{{{{\varepsilon }_{1}}}}}({{r}_{1}})}}}({{U}_{\alpha }}(r))$ = l₁ – l_α = 1 и $i = \overline {2,4} $, $hg{{t}_{{{{U}_{{{{\varepsilon }_{i}}}}}({{r}_{i}})}}}({{U}_{\alpha }}(r)) = {{l}_{i}} - {{l}_{\alpha }} = 2$. Тогда степень р-адической плотности подмножества $A \subseteq I$ будет:

Операции над множествами, представленными р-адическими шарами. Теоретико-множественные операции над множествами, представленными р-адическими шарами должны учитывать свойства взаимодействия шаров. В частности учитывать, что два шара могут либо не пересекаться, либо шар с меньшим радиусом поглощается шаром с большим радиусом. Рассмотрим два шара $U_{\alpha }^{A}\left( {{{r}_{A}}} \right)$ и $U_{\beta }^{B}\left( {{{r}_{B}}} \right)$, которые относятся к множествам A и B соответственно. Шар $U_{\alpha }^{A}\left( {{{r}_{A}}} \right)$ будет вложенным в шар $U_{\beta }^{B}\left( {{{r}_{B}}} \right)$ если $\alpha < \beta $ и $\rho ({{r}_{A}},{{r}_{B}}) \leqslant \varepsilon {\text{*}}$ = = max(α, β).

Утверждение 3. Шары $U_{\alpha }^{A}\left( {{{r}_{A}}} \right)$ и $U_{\beta }^{B}\left( {{{r}_{B}}} \right)$ не пересекаются, если $\sigma \left( {\varepsilon {\text{*}}} \right) = {{p}^{{{{l}_{{\varepsilon *}}} - l}}} > 1$, где l_ε* = = $\mathop {{\text{min}}}\limits_{i,j} LCP({{r}_{i}},{{r}_{j}}),\forall {{r}_{i}},{{r}_{j}} \in {{U}_{{\varepsilon *}}}(r{\text{*}}) = \left\{ {\begin{array}{*{20}{c}} {U_{\alpha }^{A}({{r}_{A}}),\alpha \geqslant \beta ,} \\ {U_{\beta }^{B}({{r}_{B}}),\alpha < \beta ,} \end{array}} \right.$ и $l = LCP\left( {{{r}_{A}},{{r}_{B}}} \right)$.

Доказательство. Расстояние между центрами шаров $U_{\alpha }^{A}\left( {{{r}_{A}}} \right)$ и $U_{\beta }^{B}\left( {{{r}_{B}}} \right)$ определяется метрикой $\rho \left( {{{r}_{A}},{{r}_{B}}} \right) = {{\left( {\frac{1}{p}} \right)}^{l}}$. Величина ${{l}_{{\varepsilon {\text{*}}}}}$ задает радиус наибольшего шара $\varepsilon * = {{\left( {\frac{1}{p}} \right)}^{{{{l}_{{\varepsilon *}}}}}}$. Для того, чтобы шары не пересекались должно выполняться условие $\rho \left( {{{r}_{A}},{{r}_{B}}} \right) - \varepsilon * > 0$. После подстановки значений получим условие:

Так как рассматриваются не пустые шары, то ${{p}^{{{{l}_{{\varepsilon *}}}}}} > 0$. Отсюда следует, что шары не будут пересекаться, если ${{p}^{{{{l}_{{\varepsilon *}}} - l}}} = \sigma \left( {\varepsilon {\text{*}}} \right) > 1$.■

В том случае, когда шары упорядочены по включению будет выполняться условие $\sigma \left( {\varepsilon {\text{*}}} \right) \leqslant 1$. В зависимости от значения ε* будет определяться поглощаемый шар. Если $\varepsilon {\text{*}} = \alpha $, то поглощается шар $U_{\beta }^{B}\left( {{{r}_{B}}} \right)$, и наоборот. С учетом свойства функции $\sigma \left( {\varepsilon {\text{*}}} \right)$ введем в рассмотрение операции поглощения и выделения р-адических шаров.

Определение 6. Операциями выделения $ \otimes $ и поглощения $ \oplus $ р-адических шаров называются операции, заданные бинарными функциями вида:

где $\sigma \left( {\varepsilon {\text{*}}} \right) = {{p}^{{{{l}_{{\varepsilon {\text{*}}}}} - l}}},\varepsilon {\text{*}} = {\text{max}}\left( {\alpha ,\beta } \right)$.

Результатом операции выделения для двух шаров является либо шар с меньшим радиусом, либо пустое множество, а результатом операции поглощения – либо шар с большим радиусом, либо объединение сравниваемых шаров. Если функция $\sigma \left( {\varepsilon {\text{*}}} \right) = 1$, то $U_{\alpha }^{A}\left( {{{r}_{A}}} \right) = U_{\beta }^{B}\left( {{{r}_{B}}} \right)$. В этом случае выполняется условие:

Пример 9. Пусть имеем три шара A, B и C с характеристиками (рис. 4):

Определим результат операции выделения для шаров A и B. В этом случае имеем ${{l}_{{{{\varepsilon }^{*}}}}} = 1,l \to + \infty $. Тогда функция $\sigma \left( {\varepsilon {\text{*}}} \right) < 1$. Следовательно, шары упорядочены по включению. Так как ${{\varepsilon }_{B}} > {{\varepsilon }_{A}}$, то $U_{{{{\varepsilon }_{A}}}}^{A}({{r}_{A}}) \otimes U_{{{{\varepsilon }_{B}}}}^{B}({{r}_{B}}) = U_{{{{\varepsilon }_{A}}}}^{A}({{r}_{A}})$, то есть шар A выделяется на фоне шара B. Для шаров A и C рассуждения аналогичны. В этом случае ${{l}_{{\varepsilon *}}} = 2,l = 0$, $\sigma (\varepsilon {\text{*}})$ = 9 > 1. Тогда $U_{{{{\varepsilon }_{A}}}}^{A}({{r}_{A}}) \otimes U_{{{{\varepsilon }_{C}}}}^{C}({{r}_{C}}) = \not {0}$, то есть шары A и C не пересекаются. Аналогично приведенным рассуждениям операция поглощения для шаров A, B и C даст следующие результаты: $U_{{{{\varepsilon }_{A}}}}^{A}({{r}_{A}}) \oplus U_{{{{\varepsilon }_{B}}}}^{B}({{r}_{B}})$ = = $U_{{{{\varepsilon }_{B}}}}^{B}({{r}_{B}})$, $U_{{{{\varepsilon }_{A}}}}^{A}\left( {{{r}_{A}}} \right) \oplus U_{{{{\varepsilon }_{C}}}}^{C}\left( {{{r}_{C}}} \right) = U_{{{{\varepsilon }_{A}}}}^{A}\left( {{{r}_{A}}} \right) \cup U_{{{{\varepsilon }_{C}}}}^{C}\left( {{{r}_{C}}} \right)$.

Операции выделения и поглощения позволяют определить операции р-адического пересечения и объединения множеств $A,B \subseteq I$, представленных множествами р-адических шаров.

Операция р-адического пересечение множеств. Рассмотрим подмножества $A,B \subseteq I$, которые описываются соответственно множествами шаров $U(A) = \{ U_{{{{\alpha }_{i}}}}^{A}({{r}_{i}})\left| {i = \overline {1,{{N}_{A}}} } \right.\} $, U(B) = $\{ U_{{{{\beta }_{j}}}}^{B}({{r}_{j}})\left| {j = \overline {1,{{N}_{B}}} } \right.\} $. Их можно представить векторами размерности ${{N}_{A}},{{N}_{B}}$. Компонентами векторов будут соответствующие шары. Используя операцию выделения шаров, р-адическое пересечение множеств $A,B \subseteq X$ может быть представлено в виде:

где операция объединения рассматривается в классическом теоретико-множественном смысле [17]. В общем случае операции ${{ \cap }_{p}}$ и $ \cap $ не совпадают, так как упорядоченные по включению шары для классической операции пересечения рассматриваются как различные элементы множеств. Операция р-адического пересечения множеств шаров U(A) и U(B) определяет множество всех наименьших шаров, которые были выделены. Если во множествах U(A) и U(B) нет упорядоченных по включению шаров, то $U(A){{ \cap }_{p}}U(B)$ = = $U(A) \cap U(B)$.

Операция р-адического объединения множеств. Рассмотрим подмножества $A,B \subseteq I$, представленные множествами шаров: $U(A) = \{ U_{{{{\alpha }_{i}}}}^{A}\left( {{{r}_{i}}} \right)\left| {i = \overline {1,{{N}_{A}}} } \right.\} $, $U\left( B \right) = \left\{ {U_{{{{\beta }_{j}}}}^{B}\left( {{{r}_{j}}} \right)\left| {j = \overline {1,{{N}_{B}}} } \right.} \right\}$. На основе операции поглощения р-адических шаров строится матрица с элементами $\{ U_{{{{\alpha }_{i}}}}^{A}\left( {{{r}_{i}}} \right) \oplus U_{{{{\beta }_{j}}}}^{B}\left( {{{r}_{j}}} \right)\} $. Тогда соотношения ${{\Delta }_{B}}(U(A)) = {\text{|}}i(j\{ U_{{{{\alpha }_{i}}}}^{A}({{r}_{i}}) \oplus U_{{{{\beta }_{j}}}}^{B}({{r}_{j}})\} )$ и ${{\Delta }_{A}}(U(B))$ = = ${\text{|}}j(i\{ U_{{{{\alpha }_{i}}}}^{A}({{r}_{i}}) \oplus U_{{{{\beta }_{j}}}}^{B}({{r}_{j}})\} )$ задают множества шаров из множеств U(A) и U(B), которые не были поглощены. В этом случае операция р-адического объединения множеств $A,B \subseteq X$, представленных р-адическими шарами, будет определяться соотношением:

Результатом данной операции будет множество всех не поглощенных шаров, входящих хотя бы в одно из множеств U(A) или U(B). Если нет поглощаемых шаров, то $U(A){{ \cup }_{p}}U(B)$ = $U(A) \cup U(B)$.

Операция р-адического дополнения. Операция р-адического дополнения должна учитывать свойства р-адических шаров. Обозначим через ${{U}_{{{{\alpha }_{l}}}}}\left( {{{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}}} \right)$ покрывающий шар на уровне l. Радиус данного шара будет ${{\alpha }_{l}} = \frac{1}{{{{p}^{l}}}}$. Центр этого шара определяется р-адической координатой ${{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}}$ = = ${{(0{{q}_{1}} \ldots ,{{q}_{l}}(p - 1)(p - 1) \ldots )}_{p}}$, ${{q}_{j}} \in \{ 0,(p - 1)\} $ = QP, $j = \overline {1,l} $. Пусть ${{V}_{{{{U}_{{{{\alpha }_{l}}}}}({{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}})}}}$ = $\left\{ {{{U}_{{{{\alpha }_{{l + 1}}}}}}\left( {{{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}},{{q}_{{l + 1}}}}}}} \right)} \right\}$ множество всех равных по покрытию ${{U}_{{{{\alpha }_{l}}}}}\left( {{{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}}} \right)$ шаров, то есть:

В этом случае $\forall l = \overline {0, + \infty } ,Card({{V}_{{{{U}_{{{{\alpha }_{l}}}}}\left( {{{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}}} \right)}}}) = p$.

Пусть множество $A \subseteq I$ представляется множеством шаров $U\left( A \right) = \left\{ {{{U}_{{{{\varepsilon }_{i}}}}}\left( {{{r}_{i}}} \right)\left| {i = \overline {1,{{N}_{A}}} } \right.} \right\}$. p-адическое дополнение к множеству U(A) во множестве ${{V}_{{{{U}_{{{{\alpha }_{l}}}}}\left( {{{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}}} \right)}}}$ будет определяться соотношением:

Множество ${{C}_{p}}[{{V}_{{{{U}_{{{{\alpha }_{l}}}}}\left( {{{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}}} \right)}}}]$ содержит шары из множества ${{V}_{{{{U}_{{{{\alpha }_{l}}}}}\left( {{{r}_{{0,{{q}_{1}}, \ldots ,{{q}_{l}}}}}} \right)}}}$, которые не выделяются и не поглощаются шарами из множества U(A). Тогда на уровне $l = \overline {1,L} $ все множество дополнений будет определяться выражением:

Рассмотрение ${{C}_{p}}[{{U}^{l}}\left( A \right)]$ целесообразно до уровня покрытий минимальных шаров из U(A), то есть до $L = - {{\log }_{p}}(\mathop {{\text{min}}}\limits_i {{\varepsilon }_{i}}) - 1$. На уровне l = 0 будем иметь ${{C}_{p}}[{{U}^{0}}\left( A \right)] = {{C}_{p}}[{{V}_{{{{U}_{{{{\alpha }_{0}}}}}\left( {{{r}_{0}}} \right)}}}]$. Тогда p-адическое дополнение множества $A \subseteq X$, представленного множеством шаров U(A), будет определяться соотношением:

p-Адическое дополнением является множество шаров, не входящих во множество U(A) и не поглощенных шарами из множества U(A). Подмножество $C_{p}^{{apr}}\left[ {U\left( A \right)} \right] \subseteq {{C}_{p}}\left[ {U\left( A \right)} \right]$ р-адического дополнения множества шаров U(A) с радиусами $\varepsilon \geqslant {{\varepsilon }_{{apr}}} \in \left[ {0,1} \right]$ будет р-адическим приближением дополнения U(A) с погрешностью до ${{\varepsilon }_{{apr}}}$. В общем случае $C_{p}^{{apr}}\left[ {U\left( A \right)} \right] \cup {{U}_{{{{\varepsilon }_{{apr}}}}}}\left( A \right) \subset I$. Однако максимальный шар ${{U}_{1}}\left( 1 \right)$ является минимальным покрытием (${{\alpha }_{{{\text{min}}}}} = 1$) объединения р-адических приближений множества шаров U(A) и его дополнения:

Пример 10. Рассмотрим пример выполнения операций р-адического пересечения, объединения и дополнения для двух множеств $A,B \subseteq I$, представленных множествами: U(A) = $\left\{ {{{U}_{{\frac{1}{3}}}}({{r}_{{0,1}}})} \right.$, $\left. {{{U}_{{\frac{1}{9}}}}({{r}_{{0,0,1}}}),{{U}_{{\frac{1}{9}}}}({{r}_{{0,0,2}}}),{{U}_{{\frac{1}{9}}}}({{r}_{{0,2,0}}})} \right\}$ и U(B) = $\left\{ {{{U}_{{\frac{1}{3}}}}({{r}_{{0,0}}})} \right.$, $\left. {{{U}_{{\frac{1}{9}}}}({{r}_{{0,2,1}}})} \right\}$, где: ${{r}_{{0,1}}} = {{\left( {0122 \ldots } \right)}_{3}}$, ${{r}_{{0,0,1}}}\, = {{(0012 \ldots )}_{3}}$, r_{0, 0, 2} = = ${{(0022 \ldots )}_{3}}$, ${{r}_{{0,2,0}}}\, = \,{{(0202 \ldots )}_{3}}$, ${{r}_{{0,0}}} = {{\left( {0022 \ldots } \right)}_{3}}$, r_{0, 2, 1} = = ${{(0212 \ldots )}_{3}}$.

p-Адическое пересечение множеств U(A) и U(B), на основании операции выделения будет определяться соотношением:

Для определения р-адического объединения множеств U(A) и U(B), на основании операции поглощения мы сформируем матрицу вида:

Тогда ${{\Delta }_{B}}\left( {U\left( A \right)} \right) = \left\{ {{{U}_{{\frac{1}{3}}}}\left( {{{r}_{{0,1}}}} \right),\not {0},\not {0},{{U}_{{\frac{1}{9}}}}\left( {{{r}_{{0,2,0}}}} \right)} \right\}$ и ${{\Delta }_{A}}\left( {U\left( B \right)} \right) = \left\{ {{{U}_{{\frac{1}{3}}}}\left( {{{r}_{{0,0}}}} \right),{{U}_{{\frac{1}{9}}}}\left( {{{r}_{{0,2,1}}}} \right)} \right\}$. Отсюда имеем: $U(A){{ \cup }_{p}}U(B) = \left\{ {{{U}_{{\frac{1}{3}}}}({{r}_{{0,0}}}),{{U}_{{\frac{1}{3}}}}({{r}_{{0,1}}}),{{U}_{{\frac{1}{9}}}}({{r}_{{0,2,0}}}),{{U}_{{\frac{1}{9}}}}({{r}_{{0,2,1}}})} \right\}$.

Для р-адического дополнения множества $A \subseteq I$ определим вспомогательные множества шаров на каждом уровне $l = \overline {0,L} $. Максимальный уровень определяется выражением L = $ - {{\log }_{p}}(\mathop {{\text{min}}}\limits_i {{\varepsilon }_{i}})$ – – 1. Тогда $L = - {\text{lo}}{{{\text{g}}}_{3}}\left( {\mathop {{\text{min}}}\limits_i \left\{ {\frac{1}{3},\frac{1}{9},\frac{1}{9},\frac{1}{9}} \right\}} \right)$ – 1 = 1, то есть $l \in \left\{ {0,1} \right\}$.

На уровне l = 0 покрытие рассматривается для шаров с радиусом ${{\alpha }_{1}} = \frac{1}{3}$. Дополнение на данном уровне будет ${{C}_{p}}[{{U}^{0}}\left( A \right)] = {{C}_{p}}[{{V}_{{{{U}_{{{{\alpha }_{0}}}}}\left( {{{r}_{0}}} \right)}}}]$, где

Для уровня l = 1 покрытия рассматриваются для шаров с радиусом ${{\alpha }_{2}} = \frac{1}{9}$. В этом случае будем иметь: ${{C}_{p}}[{{V}_{{{{U}_{{{{\alpha }_{1}}}}}\left( {{{r}_{{0,0}}}} \right)}}}] = \left\{ {{{U}_{{\frac{1}{9}}}}\left( {{{r}_{{0,0,0}}}} \right)} \right\}$, ${{C}_{p}}[{{V}_{{{{U}_{{{{\alpha }_{1}}}}}\left( {{{r}_{{0,1}}}} \right)}}}] = \{ \not {0}\} $, ${{C}_{p}}[{{V}_{{{{U}_{{{{\alpha }_{1}}}}}\left( {{{r}_{{0,2}}}} \right)}}}]$ = $\left\{ {{{U}_{{\frac{1}{9}}}}\left( {{{r}_{{0,2,1}}}} \right),{{U}_{{\frac{1}{9}}}}\left( {{{r}_{{0,2,2}}}} \right)} \right\}$. Следовательно:

Тогда р-адическое дополнение множества $A \subseteq I$, представленное множеством U(A), будет определяться множеством шаров:

4. ВЫВОДЫ

Приведенный подход позволяет представить произвольные подмножества ограниченного числового множества I в виде объединения образов множества р-адических шаров. В этом случае все множество I может быть представлено как прообраз множества целых р-адических чисел Z_p. Предложен алгоритм определения центров р-адических шаров, которые определяются во множестве Z_p. Полученные р-адические операции пересечения, объединения и дополнения над множествами шаров учитывают ультраметрические свойства поля р-адических чисел. На основе данных операций может быть сформирована соответствующая алгебра множеств р-адических шаров. Максимальным элементом алгебры будет шар U₁(1), имеющий образом все множество I. Минимальным элементом алгебры будет пустое множество шаров. Представление подмножеств ограниченного числового множества I в виде подмножества р-адических шаров позволяет моделировать логику изменения нестационарных скалярных полей. Это является желательным при исследовании различных нестационарных энергетических ландшафтов. При этом множество шаров, представляющих множество $A \subseteq I$, будет определять множество нижних точек такого ландшафта, а р‑адическое тело данного множества будет задавать профиль энергетического ландшафта.