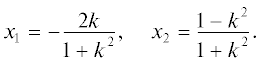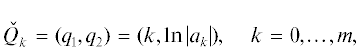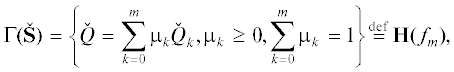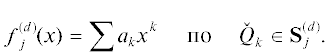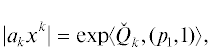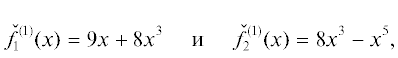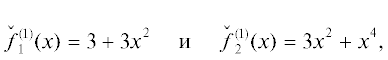Программирование, 2021, № 5, стр. 22-43
АЛГОРИТМЫ И ПРОГРАММЫ ВЫЧИСЛЕНИЯ КОРНЕЙ МНОГОЧЛЕНА ОТ ОДНОЙ ИЛИ ДВУХ НЕИЗВЕСТНЫХ
А. Д. Брюно a, *, А. Б. Батхин a, b, **
a Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., д. 4, Россия
b Московский физико-технический институт (государственный университет)
141701 Долгопрудный, Институтский переулок, д. 9, Россия
* E-mail: abruno@keldysh.ru
** E-mail: batkhin@gmail.com
Поступила в редакцию 10.03.2021
После доработки 15.03.2021
Принята к публикации 19.03.2021
Аннотация
Здесь дается описание алгоритмов и программного обеспечения для двух новых методов решения полиномиальных уравнений, основанных на построении выпуклого многоугольника. Первый метод позволяет находить приближенные корни многочлена с помощью многоугольника Адамара. Второй метод позволяет находить ветви алгебраической кривой вблизи ее особой точки и вблизи бесконечности с помощью многоугольника Ньютона и строить эскизы вещественных алгебраических кривых на плоскости. Указаны соответствующие геометрии и алгоритмы компьютерной алгебры, которые позволяют анализировать любые сложные случаи.
1. ВВЕДЕНИЕ
Здесь излагается два новых метода решения полиномиальных уравнений, основанных на построении выпуклого многоугольника по полиному. Первый метод позволяет находить приближенные корни многочлена с помощью многоугольника Адамара (раздел 4). Второй метод позволяет находить ветви алгебраической кривой вблизи ее особой точки и вблизи бесконечности с помощью многоугольника Ньютона (раздел 5). Он также позволяет строить эскизы вещественных алгебраических кривых на плоскости. Эти методы обобщаются на большие размерности [1]. Описанию методов предшествуют подготовительные разделы 2 и 3. В разделе 2 дается обзор методов решения полиномиального уравнения разных геометрий: евклидовой, аффинной, проективной, алгебраической и указано место новой степенной геометрии [2], которая является основной в дальнейшем исследовании. В разделе 3 напоминаются определения и свойства выпуклых многогранников и многоугольников. Все алгоритмы снабжены описанием их программной реализации в различных системах компьютерной алгебры. Изложение сопровождается примерами.
Укажем новые моменты данной работы:
• активно используется понятие конуса задачи;
• дано применение многоугольника Ньютона для отыскания ветвей кривой вблизи бесконечности;
• приведена теория метода ломаной Адамара;
• программное обеспечение всех алгоритмов.
Обозначения
Транспонированную матрицу $A$ обозначаем звездочкой: При этом $\mathop {\left( {AB} \right){\text{*}}}\nolimits^ = B{\text{*}}A{\text{*}}$. Вектор – это матрица-строка $X = ({{x}_{1}}, \ldots ,{{x}_{n}})$, тогда
это матрица-столбец. Для матриц используем начальные буквы латинского алфавита, а для векторов – конечные.Скалярное произведение
При этом2. ГЕОМЕТРИИ
Геометрия изучает строение различных тел, фигур и их взаимное расположение. Интуитивно каждый понимает, что это такое. Но впервые определение геометрии дал Ф. Клейн в 1872 г. в Эрлангенской программе [3]:
“Геометрия – это совокупность двух объектов: пространства и группы его преобразований”.
Преобразования образуют группу, если вместе с каждым преобразованием координат A имеется его обратное преобразование A–1, такое, что $A \cdot {{A}^{{ - 1}}}$ – это тождественное преобразование, которое ничего не меняет. При разных пространствах и разных группах получаются разные геометрии. Ниже рассмотрим некоторую последовательность геометрий, из которых каждая следующая включает предыдущую. А именно: евклидову, аффинную, проективную, алгебраическую и степенную. При этом пространство будет одно и то же – вещественное n-мерное пространство ${{\mathbb{R}}^{n}}$, но группы преобразований будут расширяться.
2.1. Евклидова геометрия [4, 5]
Здесь имеется длина вектора
а группа преобразований $X* = AY{\text{*}}$ ее сохраняет:Матрицы с этим свойством называются ортогональными. Они образуют группу невырожденных квадратных матриц $O(n)$ над полем $\mathbb{R}$. В группу преобразований включается и параллельный перенос
где X0 – фиксированный вектор. Эти преобразования сохраняют углы и вообще форму, включая площади и объемы.2.2. Аффинная геометрия [4, 5]
Здесь имеются два пространства: основное ${{\mathbb{R}}^{n}}$ = = {X} и сопряженное (т.е. двойственное) $\mathbb{R}_{ * }^{n}$ = {Y}, а преобразования
сохраняют скалярные произведения векторов сопряженных (двойственных) пространств:Следовательно,
т.е.Множество взаимно однозначных аффинных отображений пространства ${{\mathbb{R}}^{n}}$ в себя образует группу, обозначаемую Aff ${{\mathbb{R}}^{n}}$. Эта группа отображается на полную линейную группу $GL(n,\mathbb{R})$, состоящую из квадратных невырожденных матриц размера n × n. В группу аффинных преобразований также входят параллельные переносы (2.1).
В этой геометрии прямые, плоскости и любые линейные многообразия переходят в прямые, плоскости и линейные многообразия соответственно. При этом углы не сохраняются, но сохраняется ортогональность между векторами прямого и двойственного пространств:
Кроме скалярного (или внутреннего) произведения двух векторов имеется внешнее произведение $n - 1$ вектора ${{X}_{1}},\; \ldots ,\;{{X}_{{n - 1}}} \in {{\mathbb{R}}^{n}}$:
2.3. Проективная Геометрия [5, 6]
Рассмотрим такую задачу:
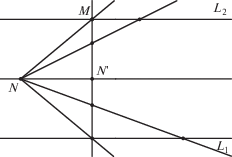
Пример 1. На плоскости заданы параллельные прямые L1 и L2, ортогональная к ним прямая $M$ и точка наблюдения $N$. Требуется спроектировать на прямую $M$ из точки $N$ части прямых L1 и L2 при $x \to \infty $ (см. рис. 1, на котором показано изображение перспективы на картине).
Получим, что все проекции прямых ${{L}_{i}}$ на прямую $M$ заканчиваются в одной точке $N{\text{'}} \in M$, по которой пересекается с M прямая ${{L}_{0}}$, проходящая через точку наблюдения $N$ и параллельная прямым L1, L2. Такая задача возникает при рисовании на картине прямых, уходящих вдаль. Здесь прямые L1 и L2 – это пол и потолок соответственно, а точка $N$ – это глаз художника (или фотоаппарат), $M$ – это полотно картины. Такое свойство возникает при плоском изображении протяженных пространственных объектов. При этом на картине возникает одна точка (центр), соответствующая бесконечности. Но многие картины выдающихся художников имеют по несколько центров для большей выразительности.
Свойства, сохраняющиеся при прямолинейных проектированиях, описываются проективной геометрией. Для нее группой преобразований служит так называемая проективная группа $P({{\mathbb{R}}^{n}})$.
В ней вводятся однородные координаты u0, ${{u}_{1}}, \ldots ,{{u}_{n}}$:
и делаются линейные преобразования где $V = ({{{v}}_{0}}, \ldots ,{{{v}}_{n}})$, $B$ – квадратная матрица размера $n + 1$, $detB \ne 0$. ЗдесьПроективная геометрия позволяет упрощать полиномиальные уравнения малых степеней.
2.4. Алгебраическая геометрия [7]
Алгебраическая геометрия [7] Она изучает алгебраические многообразия, заданные в ${{\mathbb{R}}^{n}}$ системой алгебраических (т.е. полиномиальных) уравнений ${{f}_{i}}(X) = 0$, $i = 1,\; \ldots ,\;m$, где ${{f}_{i}}$ – многочлены. При этом рассматриваются бирациональные преобразования
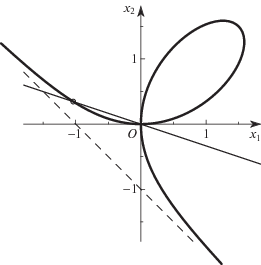
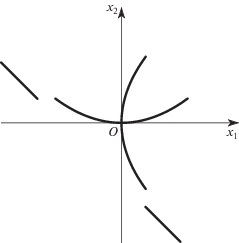
Пример 2. Рассмотрим кривую “Декартов лист”, заданную уравнением
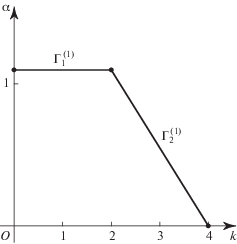
и попробуем ее параметризовать одной переменной. Кривая на плоскости ${{x}_{1}},{{x}_{2}}$ имеет вид, показанный на рис. 2. На нем изображены лист Декарта, секущая прямая и асимптота. Точка ${{x}_{1}} = {{x}_{2}}$ = 0 является ее двойной точкой. Положим ${{x}_{2}} = k{{x}_{1}}$ и подставим это в уравнение кривой. После сокращения на $x_{1}^{2}$ получаем
т.е.Каждой точке кривой (2.2) при $({{x}_{1}},{{x}_{2}}) \ne 0$ соответствует одна определенная прямая ${{x}_{2}} = k{{x}_{1}}$ с наклоном k, который является искомым параметром.
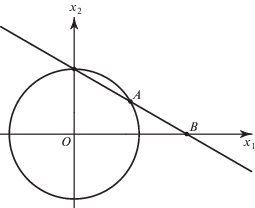
Пример 3. Найдем параметризацию окружности $x_{1}^{2} + x_{2}^{2} = 1$, начиная с ее точки ${{x}_{1}} = 0$, ${{x}_{2}} = 1$, чтобы каждой точке окружности соответствовала одна прямая ${{x}_{2}} - 1 = k{{x}_{1}}$ и одна точка оси ${{x}_{1}}$, по которой эти прямые пересекаются.
Через точку ${{x}_{1}} = 0$, ${{x}_{2}} = 1$, лежащую на нашей окружности, проведем прямую с наклоном k. Ее уравнение есть
т.е. ${{x}_{2}} = 1 + k{{x}_{1}}$. Подставляем его в уравнение окружности $x_{1}^{2} + x_{2}^{2} - 1 = 0$ и получаем уравнениеВместе с уравнением (2.3) оно имеет два решения
${\text{и}}$Замена (2.5) дает преобразование $k \to ({{x}_{1}},{{x}_{2}})$, а формула (2.3) – обратное преобразование (x1, ${{x}_{2}}) \to k$:
Получаем бирациональное преобразование. Здесь параметром является наклон k прямой или точка $B = ( - 1{\text{/}}k,0)$. Рисунок 3 показывает параметризацию точками $B$ точек окружности $A$.
В алгебраической геометрии имеется
Теорема 1. Алгебраическое многообразие $f(X)$ = 0 с ${\text{ord}}f \leqslant n$ всегда бирационально эквивалентно пространству ${{\mathbb{R}}^{{n - 1}}}$.
В этой геометрии возможно раздутие точки в прямую или плоскость и к пространству ${{\mathbb{R}}^{n}}$ добавлена бесконечно удаленная гиперплоскость $\tilde {\mathbb{R}}_{\infty }^{{n - 1}}$. Алгоритмы алгебраической геометрии позволяют решать некоторые системы алгебраических уравнений, но они недостаточны для решения таких систем в сложных случаях.
2.5. Степенная геометрия [2, 8]
Пусть $X = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$, $Q = ({{q}_{1}},\; \ldots ,\;{{q}_{n}})$, XQ = = $x_{1}^{{{{q}_{1}}}}\; \cdots x_{n}^{{{{q}_{n}}}} = exp\left\langle {lnX,Q} \right\rangle $, где lnX = $(ln{{x}_{1}}, \ldots ,ln{{x}_{n}})$. Преобразование
переводит XQ в ${{Y}^{{Q{{A}^{ * }}}}}$, ибоРассмотрим сумму
В результате преобразования (2.6) она перейдет в сумму
Если все ${{Q}_{i}}$ лежат в одной гиперплоскости L, т.е. $\left\langle {{{Q}_{i}},N} \right\rangle = c = {\text{const}}$, тогда линейное преобразование
может перевести гиперплоскость L в гиперплоскость ${{p}_{n}} = c = {\text{const}}$. Тогда сумма (2.7) содержит ${{y}_{n}}$ только в степени $c$, множитель $y_{n}^{c}$ можно вынести за скобку и после сокращения на $y_{n}^{c}$ останется многочлен только от переменных ${{y}_{1}},\; \ldots ,\;{{y}_{{n - 1}}}$. Здесь для векторных показателей $Q \in {{\mathbb{R}}^{n}}$ получается аффинная геометрия. При этом векторы lnX, lnY лежат в сопряженном пространстве $\mathbb{R}_{ * }^{n}$. Преобразования степенной геометрии включают параллельный перенос (2.1), линейные замены $X = YA$ и степенные преобразования (2.6). Алгоритмы алгебраической и степенной геометрий позволяют решать алгебраические уравнения любой сложности при использовании соответствующего программного обеспечения [9].В принципе, степенная геометрия пригодна и для упрощения более сложных уравнений – обыкновенных дифференциальных и в частных производных [2, 10–13].
2.6. Другие геометрии
В качестве основного пространства можно рассматривать многообразия. Имеются еше дифференциальная геометрия, неевклидовы геометрии и, наконец, топология, в которой преобразования – это любые непрерывные трансформации.
Более подробное изложение евклидовой, аффинной и проективной геометрий см. в [14].
3. МНОГОГРАННИК И НОРМАЛЬНЫЕ КОНУСЫ
3.1. Теория
При первом чтении здесь можно полагать, что n = 2. Тогда многогранник становится многоугольником и все объекты легко изображаются рисунками на двух плоскостях: основной ${{\mathbb{R}}^{2}}$ и двойственной $\mathbb{R}_{ * }^{2}$ (см. [8, Гл. 1]).
Пусть в ${{\mathbb{R}}^{n}}$ задано несколько точек $\{ {{Q}_{1}}, \ldots ,{{Q}_{k}}\} $ = S. Их выпуклая оболочка
При этом вектор P лежит в пространстве $\mathbb{R}_{ * }^{n}$, двойственном пространству ${{\mathbb{R}}^{n}}$. Вообще, здесь мы находимся в ситуации аффинной геометрии.
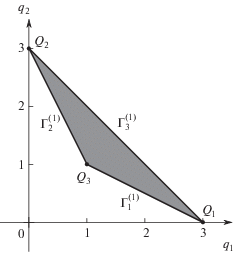
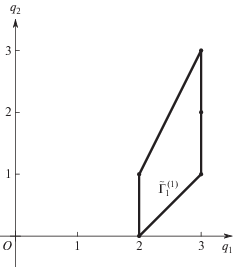
Пример 4. Пусть n = 2 и множество S состоит из трех точек ${{Q}_{1}} = (3,\;0)$, ${{Q}_{2}} = (0,\;3)$, ${{Q}_{3}} = (1,\;1)$. Их выпуклая оболочка $\Gamma $ – это треугольник с этими вершинами $\Gamma _{j}^{{(0)}} = {{Q}_{j}}$, $j = 1,2,3$ и тремя ребрами $\Gamma _{j}^{{(1)}}$ на плоскости ${{\mathbb{R}}^{2}}$. На рис. 4 изображены носитель и многоугольник $\Gamma $ примера 4.
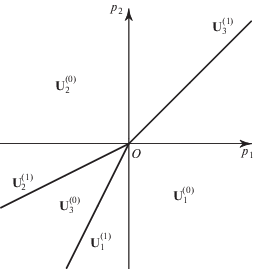
Ребро $\Gamma _{1}^{{(1)}} = [{{Q}_{1}},{{Q}_{3}}]$, его направляющий вектор ${{R}_{1}}\, = \,{{Q}_{3}}\, - \,{{Q}_{1}}\, = \,(2, - {\kern 1pt} 1)$. Нормальный вектор ${{N}_{1}}$ = (1, 2). Но этот вектор ${{N}_{1}}$ направлен от ребра $\Gamma _{1}^{{(1)}}$ внутрь треугольника $\Gamma $. Поэтому внешняя нормаль ${{\tilde {N}}_{1}} = ( - {\kern 1pt} 1$, –2). Натянутый на него луч $\lambda {{\tilde {N}}_{1}} = ( - \lambda $, ‒2λ) с $\lambda > 0$ является нормальным конусом ${\mathbf{U}}_{1}^{{(1)}}$. Аналогично находим ${\mathbf{U}}_{2}^{{(1)}} = \lambda $(–2, –1) и ${\mathbf{U}}_{3}^{{(1)}}$ = λ(1, 1) с $\lambda > 0$. Нормальный конус вершины $\Gamma _{1}^{{(0)}} = {{Q}_{1}}$ есть
Аналогично находим нормальные конусы
Нормальные конусы ${\mathbf{U}}_{j}^{{(d)}}$ граней $\Gamma _{j}^{{(d)}}$ многоугольника $\Gamma $ рис. 4 показаны на рис. 5.
Итак, на сопряженной плоскости $\mathbb{R}_{ * }^{2}$ лучи, нормальные к ребрам $\Gamma _{j}^{{(1)}}$ и направленные наружу треугольника $\Gamma $, образуют нормальные конусы ${\mathbf{U}}_{j}^{{(1)}}$ ребер $\Gamma _{j}^{{(1)}}$ (рис. 5). Секторы между ними – это нормальные конусы ${\mathbf{U}}_{j}^{{(0)}}$ вершин $\Gamma _{j}^{{(0)}}$.
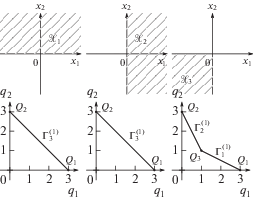
Пусть в силу исходной задачи нас интересует не вся граница $\partial \Gamma $, а только ее часть, соответствующая некоторому множеству $\mathcal{K}$ направлений $P$. Тогда множество $\mathcal{K}$ назовем конусом задачи. Он не обязательно выпуклый. Через $\partial \Gamma (\mathcal{K})$ обозначим ту часть границы $\partial \Gamma $, для элементов которой $\Gamma _{j}^{{(d)}}$ их нормальные конусы ${\mathbf{U}}_{j}^{{(d)}}$ пересекаются с конусом задачи $\mathcal{K}$. Назовем $\partial \Gamma (\mathcal{K})$ – границей задачи.
Пример 5. Пусть n = 2 и ${{\mathcal{K}}_{1}}$ – это верхняя полуплоскость ${{\mathcal{K}}_{1}} = {\text{\{ }}P = ({{p}_{1}},{{p}_{2}}):{{p}_{2}} > 0{\text{\} }}$, ${{\mathcal{K}}_{2}}$ – это правая полуплоскость ${{\mathcal{K}}_{2}} = \left\{ {P = ({{p}_{1}},{{p}_{2}}):{{p}_{1}} > 0} \right\}$, и ${{\mathcal{K}}_{3}}$ – это третий квадрант ${{\mathcal{K}}_{3}} = \left\{ {P = ({{p}_{1}},{{p}_{2}}) < 0} \right\}$, тогда $\partial \Gamma ({{\mathcal{K}}_{1}})$ – это верхняя часть границы $\partial \Gamma $, $\partial \Gamma ({{\mathcal{K}}_{2}})$ – это правая часть границы $\partial \Gamma $ и $\partial \Gamma ({{\mathcal{K}}_{3}})$ – это пересечение левой и нижней частей границы $\partial \Gamma $.
Для многоугольника $\Gamma $ примера 4 границы задач таковы:
Конусы этих задач и границы задач примеров 4 и 5 показаны на рис. 6.
Все векторы нормального конуса ${\mathbf{U}}_{j}^{{(d)}}$ ортогональны грани $\Gamma _{j}^{{(d)}}$.
3.2. Программное обеспечение
Для работы с выпуклыми множествами имеется различное программное обеспечение. Здесь кратко опишем только те программы, которые могут быть использованы как для вычисления выпуклых оболочек, так и для вычисления их нормальных конусов.
Пакет Qhull [15] используется во многих пакетах прикладных программ, как коммерческих, так и свободных, программный интерфейс с пакетом Qhull имеют системы для научных расчетов Matlab, GNU Octave, системы компьютерной алгебры Mathematica и Maple, библиотеки SciPy и geometry для языков программирования Python и R соответственно.
Применение этого пакета совместно с системой компьютерной алгебры Maple для исследования алгебраических сингулярностей описано в работе авторов [16].
Основной особенностью пакета является то, что вычисления производятся с использованием вещественных чисел, а не в поле рациональных чисел, что удобно при работе с многогранником Адамара. При вычислениях многогранника Ньютона требуются дополнительные действия для приведения результатов вычислений к рациональным значениям.
Пакет PolyhedralSets системы Maple [17]. Начиная с версии 2015 года система компьютерной алгебры Maple включает в себя пакет PolyhedralSets. Он позволяет, в частности, вычислять выпуклую оболочку множества, давать ее $H$‑ или $V$-представления, т.е. либо в виде уравнений гиперплоскостей границы, либо в виде набора крайних точек и лучей, линейная комбинация которых дает неограниченную выпуклую оболочку. В этом пакете все вычисления производятся в поле рациональных чисел, что несколько упрощает его использование для исследования многогранников Ньютона, но делает бесполезным при работе с многогранником Адамара. Отметим, что пакет PolyhedralSets по сравнению с пакетом Qhull имеет крайне низкую производительность. Ниже приведен листинг 1 программы вычисления нормальных конусов выпуклого многоугольника листа Декарта (пример 4) в системе Maple.
Листинг 1: Maple
># Загрузка библиотеки
>with(PolyhedralSets):
>SuppFolium := [ [3, 0], [0, 3], [1, 1]]:
>ConvSuppFolium:=
ConvexHull (PolyhedralSet ( SuppFolium)):
>Relations (ConvSuppFolium);
$\left[ { - {{x}_{1}} - 2{{x}_{2}} \leqslant - 3,\; - {{x}_{1}} - \tfrac{{{{x}_{2}}}}{2} \leqslant - \tfrac{3}{2},\;{{x}_{2}} + {{x}_{1}} \leqslant 3} \right]$
Результат вычислений дает H-представление выпуклой оболочки, из которой уже легко получить внешние нормальные векторы (–1, –2), $( - 1, - 1{\text{/}}2)$, (1, 1), найденные в примере 4.
Другие пакеты. Большой выбор библиотек для исследования в области вычислительной геометрии предоставляет свободно распространяемая система компьютерной алгебры Sage [18]. Она позволяет работать с библиотеками: cdd [19], PPL (Parma Polyhedral Library) [20], polymake, Qhull и другими. Пример вычисления выпуклой оболочки и нормальных конусов листа Декарта с использованием Qhull и SymPy [21] на языке Python приведен в листинге 2.
Листинг 2: SymPy
# Загрузка библиотек
from scipy.spatial import ConvexHull
import sympy as sym
import sympy.printing as printing
import numpy as np
# Уравнение листа Декарта
x, y = sym.var (“x y”)
Folium=sym.Poly (x**3+y**3=3*x*y, [x, y])
print (printing.latex (Folium))
${\text{Poly}}({{x}^{3}} - 3xy + {{y}^{3}},x,y,domain = \mathbb{Z})$
# Вычисление носителя и выпуклой оболочки
support=np.array ([[x, y] for x, y in\
Folium.monoms ( ) ] )
CH=ConvexHull (support)
# Вычисление нормальных конусов к граням
CH_ncoeffs=CH. equations [: , : 2]
mincoeffs=np.min(np.abs (CH_ncoeffs), axis=1)
CH_NC=np.array (CH_ncoeffs/mincoeffs [ :, None], \
dtype=np.int)
printing.latex (CH_NC)
[[1, 1] [−2 −1] [−1 −2]]
4. КОРНИ МНОГОЧЛЕНА ОТ ОДНОЙ НЕИЗВЕСТНОЙ
4.1. Алгоритм
Для многочлена
с вещественными или комплексными коэффициентами ak его корни всегда выражаются в радикалах, если $m \leqslant 4$ (формулы Кардано и Феррари – XVI век).Согласно Абелю и Галуа (1830) общее уравнение ${{f}_{m}}(x) = 0$ с $m > 4$ неразрешимо в радикалах от его коэффициентов. Для уравнения пятой степени Эрмит, Кронекер и Бриоски (1858) показали, что его корни могут быть выражены через тета-функции Якоби [22]. При $m > 6$ известно, в каких сложных функциях от коэффициентов ak оно разрешается [23], но явных формул, пригодных для вычисления, пока нет. Имеются различные способы определения числа вещественных корней на заданном интервале $x \in [a,b]$ и их приближенных значений.
Опишем новый способ вычисления приближенных значений корней многочлена (4.1). Для этого на вещественную плоскость ${{q}_{1}},{{q}_{2}}$ наносятся точки
образующие суперноситель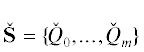 , и строится их выпуклая оболочка
которая называется многоугольник Адамара [24] (Hadamard, 1893). Граница $\partial {\mathbf{H}}$ является ломаной линией. Каждому ребру $\Gamma _{j}^{{(1)}}$ и вершине $\Gamma _{j}^{{(0)}}$ этой границы $\partial {\mathbf{H}}$ соответствует граничное подмножество ${\mathbf{S}}_{j}^{{(d)}}$ точек
, и строится их выпуклая оболочка
которая называется многоугольник Адамара [24] (Hadamard, 1893). Граница $\partial {\mathbf{H}}$ является ломаной линией. Каждому ребру $\Gamma _{j}^{{(1)}}$ и вершине $\Gamma _{j}^{{(0)}}$ этой границы $\partial {\mathbf{H}}$ соответствует граничное подмножество ${\mathbf{S}}_{j}^{{(d)}}$ точек 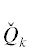 , лежащих на $\Gamma _{j}^{{(d)}}$, и укороченный многочлен
, лежащих на $\Gamma _{j}^{{(d)}}$, и укороченный многочлен
В укороченный многочлен входят те и только те слагаемые ${{a}_{k}}{{x}^{k}}$, у которых модуль ${\text{|}}{{a}_{k}}{{x}^{k}}{\text{|}}$ наибольший при фиксированном $\left| x \right|:ln\left| x \right| = {{p}_{1}}$, ибо тогда
а экспонента – монотонная функция.Если $\Gamma _{j}^{{(d)}}$ – вершина, то укороченный многочлен (4.2) является мономом, который не имеет ненулевого корня. Если же $\Gamma _{j}^{{(d)}}$ – ребро, то укороченный многочлен (4.2) имеет ненулевые корни, которые дают приближенные значения для корней полного многочлена (4.1). Кроме исключительных случаев, укороченные многочлены (4.2) существенно проще исходного многочлена (4.1), и их корни вычисляются легче.
Поскольку вектор $({{p}_{1}},1)$ лежит в верхней полуплоскости двойственной плоскости $\mathbb{R}_{ * }^{2}$, то конус задачи здесь $\mathcal{K} = \left\{ {P = ({{p}_{1}},{{p}_{2}}):{{p}_{2}} > 0} \right\}$, т.е. – это верхняя полуплоскость. Поэтому согласно примеру 5 раздела 3 соответствующая часть $\partial {\mathbf{H}}(\mathcal{K})$ границы $\partial {\mathbf{H}}$ – это ее верхняя часть. Ее назовем ломаной Адамара и обозначим $\tilde {H}$ [24], [8, гл. IV, § 2, п. 2.1].
Пример 6. В этом примере метод ломанной Адамара дает хорошие начальные приближения как для вещественных, так и для комплексных корней.
Рассмотрим многочлен
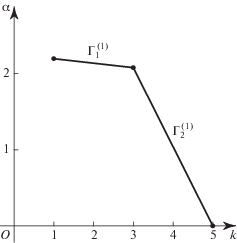
с корнями $x_{k}^{0} = 0, \pm i, \pm 3$. Его ломаная Адамара натянута на три вершины $(1,\;ln9)$, $(3,\;ln8)$, (5, 0) и показана на рис. 7. Она имеет два ребра $\Gamma _{1}^{{(1)}}$ и $\Gamma _{2}^{{(2)}}$.Ребрам $\Gamma _{1}^{{(1)}}$ и $\Gamma _{2}^{{(2)}}$ соответствуют укороченные многочлены
корни которых ${{x}_{1}} = 0$, ${{x}_{{2,3}}} = \pm \sqrt {9{\text{/}}8} i \approx \pm 1.060660i$ и ${{x}_{{4,5}}} = \pm \sqrt 8 \approx \pm 2.828427$ дают приближенные значения ненулевых корней полного многочлена $f(x)$. Для их уточнения можно использовать метод Ньютона, т.е. искать разложение корня ${{x}^{0}} = x + {{\varepsilon }_{1}} + {{\varepsilon }_{2}} + \; \ldots $ Для первых добавок ${{\varepsilon }_{1}}$ из уравнения $f(x) + {{\varepsilon }_{1}}f{\kern 1pt} {\text{'}}(x) = 0$ получаем значение ${{\varepsilon }_{1}} = - f(x){\text{/}}f{\kern 1pt} {\text{'}}(x)$. Значения приближенных корней xk, добавок ${{\varepsilon }_{1}}$ в ${{x}_{k}}$, $k = 2,\; \ldots ,\;5$, и уточненных значений ${{x}_{k}} + {{\varepsilon }_{1}}$ показаны в табл. 1. В ее нижней строке указаны значения точных корней $x_{k}^{0}$ многочлена (4.3). Дальнейшие вычисления показывают, что достаточно еще 4-х итераций, чтобы получить приближенные значения корней с точностью до 10-го знака после запятой.Таблица 1
| $k$ | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| ${{x}_{k}}$ | 1.06066i | –1.06066i | 2.828427 | –2.828427 |
| ${{\varepsilon }_{1}}$ | –0.05518i | 0.05518i | 0.2139 | –0.2139 |
| ${{x}_{k}} + {{\varepsilon }_{1}}$ | 1.00548i | –1.00548i | 3.042342 | –3.042342 |
| $x_{k}^{0}$ | i | i | 3 | –3 |
Из примера 6 можно сделать вывод, что укороченные уравнения изначально дают хорошие начальные приближения, которые заведомо сходятся к точным решениям исходного уравнения. Следующий пример демонстрирует, что это не всегда так.
Пример 7. С помощью ломаной Адамара найдем приближенные значения корней многочлена
с корнями $x_{k}^{0}\, = \, \pm \frac{1}{2}\sqrt { - 6\, \pm \,2i\sqrt 3 } \, \approx \, \pm 0.340625$ ± 1.271230i. Его ломаная Адамара натянута на три вершины $(0,\;ln3)$, $(2,\;ln3)$, $(4,\;0)$ и показана на рис. 8.Она имеет два ребра $\Gamma _{1}^{{(1)}}$ и $\Gamma _{2}^{{(2)}}$, которым соответствуют укороченные многочлены
с соответствующими корнями ${{x}_{{1,2}}} = \pm i$ и x3, 4 = = $ \pm \sqrt 3 i \approx \pm 1.732051i$.Итерации этих корней по методу Ньютона не сходятся к точным значениям корней. Для ${{x}_{{1,2}}}$ получаем периодическую последовательность значений с периодом 2 вблизи $ \pm 1.042i$. Итерации корней ${{x}_{{3,4}}}$ вообще демонстрируют хаотическое поведение.
В целом метод ломаной Адамара состоит в том, что исходный многочлен заменяется набором более простых многочленов, корни которых вычисляются просто и дают такие приближения корней исходного многочлена, которые достаточно хороши для численного уточнения по методу Ньютона. В конце раздела 6 объясняются случаи, когда уточнения не сходятся к точному значению.
4.2. Программное обеспечение
Отметим, что имеются многочисленные программы, позволяющие численно находить с любой точностью корни любого многочлена. Любая система компьютерной алгебры позволяет делать это численно. Так, например,
• в системе Mathematica это делает функция NRoots;
• в Python имеется пакет высокоточной арифметики mpmath, где вычисление корней осуществляет функция polyroots;
• в системе Maple имеется специальный пакет RootFinding, содержащий функции для изолирования вещественных и комплексных корней с произвольной точностью.
Ниже приведен пример вычисления корней многочлена 7-й степени пример 3 из статьи [1] в системе Maple с помощью пакета RootFinding (см. листинг 3).
Листинг 3: Maple
with( RootFinding):
>f7 :=–4320–9336*x–4972*x^2–3754*x^3–1426*x^4+104*x^5+51*x
^6+3*x^7:
>Analytic (f7, x , r e =–10. .10 , im=–10. .10 , digits = 25);
[ –0.5818662859936160237203075,
–2.098451028439695378650494,
5.255155425603335889745440,
–9.839354523877774394108640 – 0.9310465789411591695975430*
I,
–9.839354523877774394108643 + 0.9310465789411591695975413*
I,
0.05193546829276215042132425 – 1.514851641026718679226917*
I,
0.05193546829276215042132410 + 1.514851641026718679226917*
I]
Замечание 1. Общие корни $(x_{1}^{0},x_{2}^{0})$ двух многочленов $f({{x}_{1}},{{x}_{2}})$ и $g({{x}_{1}},{{x}_{2}})$ можно найти с помощью метода исключения [25, 26], который позволяет исключить одну из неизвестных (скажем ${{x}_{1}}$) и получить их результант, как многочлен $h({{x}_{2}})$ от другой неизвестной (здесь ${{x}_{2}}$). Найдя корни $x_{2}^{0}$ многочлена $h({{x}_{2}})$ и подставив их значения в многочлены f и $g$, получаем два алгебраических уравнения от одной неизвестной ${{x}_{1}}$. Из них находим общие корни.
Замечание 2. Имеется большое число способов вычисления результанта двух многочленов, самым популярным, но далеко не самым эффективным из которых является метод Сильвестра [25, 26]. Все системы компьютерной алгебры имеют встроенные функции для вычисления результанта, используя при этом метод псевдоделения, предложенный Якоби (см., подробнее, [27, 28]). В системе Maple для пары многочленов замечания 1 достаточно просто вызвать команду resultant(f,g,x2).
5. ПЛОСКАЯ АЛГЕБРАИЧЕСКАЯ КРИВАЯ
Пусть $f({{x}_{1}},{{x}_{2}})$ – многочлен с вещественными или комплексными коэффициентами. Множество решений ${{x}_{1}}$, ${{x}_{2}}$ уравнения
в $X = ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}$ или ${{\mathbb{C}}^{2}}$ называется плоской алгебраической кривой $\mathcal{F}$.Точка X = X0, $f({{X}^{0}}) = 0$ называется простой точкой кривой $\mathcal{F}$, если в ней вектор ($\partial f{\text{/}}\partial {{x}_{1}}$, $\partial f{\text{/}}\partial {{x}_{2}}$) ненулевой. В противном случае точка X0 называется особой. Сдвигом перенесем точку X0 в начало координат.
5.1. Локальный анализ простой точки
Теорема 2. (Коши [2]). Если при ${{X}^{0}} = 0$ производная $\partial f{\text{/}}\partial {{x}_{i}} \ne 0$, то все решения уравнения (6.1) вблизи точки ${{X}^{0}} = 0$ содержатся в разложении
где ${{b}_{k}}$ – постоянные, а $j = 3 - i$.5.2. Локальный анализ особой точки ${{X}^{0}} = 0$ и точек $(0,\infty )$, $(\infty ,0)$, $(\infty ,\infty )$ [8, гл. 1, § 2], [2, гл. 2]
Запишем многочлен $f(X)$ в виде
(5.3)
$f(X) = \sum {{{f}_{Q}}} {{X}^{Q}}\quad {\text{по}}\quad Q \geqslant 0,\quad Q \in {{\mathbb{Z}}^{2}},$Каждой обобщенной грани $\Gamma _{j}^{{(d)}}$ соответствуют: ее граничное подмножество ${\mathbf{S}}_{j}^{{(d)}} = {\mathbf{S}} \cap \Gamma _{j}^{{(d)}}$, ее укороченный многочлен
Пусть ${{x}_{1}} \in \mathbb{C}$, ${{x}_{1}} \to 0$ или $\infty ,$ а $o(1)$ – функция от ${{x}_{1}}$, которая при этом стремится к нулю. На кривой
где $b = {\text{const}} \in \mathbb{C}$, $p \in \mathbb{R}$, моном где $Q = ({{q}_{1}},{{q}_{2}})$, ${{X}^{Q}} = x_{1}^{{{{q}_{1}}}}x_{2}^{{{{q}_{2}}}}$, ${{f}_{Q}} = {\text{const}} \in \mathbb{C}$, $X\, \in \,{{\mathbb{C}}^{2}}$, принимает значенияПри этом $P = (1,p)$,
Это означает, что при заданных P и $\omega $ наибольшие модули имеют те мономы (5.4) суммы (5.3), на которых величина
достигает максимума.Если ${{x}_{1}} \to 0,$ то $\omega = - 1$ и вектор $\omega P = ( - 1, - p).$ Следовательно, здесь конус задачи $\mathcal{K}$ – это левая полуплоскость плоскости $\mathbb{R}_{ * }^{2}$ и точки Q с максимальными значениями произведения (5.5) лежат на левой части границы $\partial {\mathbf{N}}.$
Если ${{x}_{1}} \to \infty ,$ то ω = 1 и вектор $\omega P = (1,p).$ Следовательно, здесь конус задачи $\mathcal{K}$ – это правая полуплоскость плоскости $\mathbb{R}_{ * }^{2}$ и точки $Q$ с наибольшими значениями произведения (5.5) лежат на правой части границы $\partial {\mathbf{N}}.$
Будем искать решения уравнения
(5.6)
$f(X)\mathop = \limits^{{\text{def}}} \sum\limits_{Q \in {\mathbf{S}}} {{{f}_{Q}}} {{X}^{Q}} = 0$(5.7)
${{x}_{2}} = {{b}_{1}}x_{1}^{{{{p}_{1}}}} + {{b}_{2}}x_{1}^{{{{p}_{2}}}} + {{b}_{3}}x_{1}^{{{{p}_{3}}}} + \; \cdots ,$В этих разложениях показатели степени pk возрастают вместе с k, если ${{x}_{1}} \to 0$, и убывают, если ${{x}_{1}} \to \infty $.
Итак, доказана
Теорема 3. Для решений (5.7) уравнения (5.6) укороченное решение
является решением укороченного уравнениясоответствующего элементу границы $\Gamma _{j}^{{(d)}}$ с внешним нормальным вектором $\omega (1,{{p}_{1}}).$Теперь заметим, что левая часть укороченного уравнения (5.6), соответствующего вершине, состоит из одного монома (5.4). Такое укороченное уравнение имеет только нулевой корень и не дает первое приближение (5.8). Поэтому теорема 3 относится только к укороченным уравнениям (5.9), соответствующим ребрам, т.е. d = 1.
Пример 8. Пусть
Носитель состоит из трех точек ${{Q}_{1}} = (3,\;0)$, ${{Q}_{2}} = (0,\;3)$, ${{Q}_{3}} = (1,\;1)$ (пример 4 раздела 3). Их выпуклая оболочка – это треугольник $\Gamma = {\mathbf{N}}$ с этими вершинами (рис. 4 раздела 3). Он имеет три ребра $\Gamma _{1}^{{(1)}}$, $\Gamma _{2}^{{(1)}}$ и $\Gamma _{3}^{{(1)}}$ с внешними нормалями $ - (2,\;1)$, –(1, 2), (1, 1) соответственно. Ребру $\Gamma _{1}^{{(1)}}$ соответствует укороченное уравнение $\tilde {f}_{1}^{{(1)}} = x_{1}^{3} - 3{{x}_{1}}{{x}_{2}} = 0$. Оно имеет решение
Ребру $\Gamma _{2}^{{(1)}}$ соответствует укороченное уравнение $\tilde {f}_{2}^{{(1)}} = x_{2}^{3} - 3{{x}_{1}}{{x}_{2}} = 0$. Оно имеет решение
Ветви (5.11) и (5.12) относятся к окрестности нуля ${{x}_{1}} = {{x}_{2}} = 0,$ поскольку внешние нормали соответствующих ребер $\Gamma _{1}^{{(1)}}$ и $\Gamma _{2}^{{(1)}}$ имеют обе координаты отрицательными. Наконец, ребру $\Gamma _{3}^{{(1)}}$ соответствует укороченное уравнение $\tilde {f}_{3}^{{(1)}} = x_{1}^{3} + x_{2}^{3}$ = $({{x}_{1}} + {{x}_{2}})(x_{1}^{2} - {{x}_{1}}{{x}_{2}} + x_{2}^{2}) = 0$. Оно имеет только одно вещественное решение
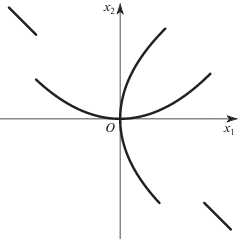
Оно относится к окрестности бесконечности ${{x}_{1}} = {{x}_{2}} = \infty $, ибо у внешней нормали к ребру $\Gamma _{3}^{{(1)}}$ обе координаты положительны. Куски (5.11)–(5.13) кривой (5.10) вблизи нуля и бесконечности показаны на рис. 9.
По укороченному уравнению (5.9) однозначно определяется знак $\omega $ и показатель степени ${{p}_{1}}.$ Если в сумме (5.3) все векторные показатели степени $Q = ({{q}_{1}},{{q}_{2}})$ имеют рациональные компоненты ${{q}_{1}}$ и ${{q}_{2}}$, то показатель ${{p}_{1}}$ – рационален. Для коэффициента ${{b}_{1}}$ получаем алгебраическое уравнение
Будем различать 2 случая:
а) ${{b}_{1}}$ – простой корень уравнения (5.14), тогда
б) ${{b}_{1}}$ – кратный корень уравнения (5.14), тогда
Для вычисления второго члена ${{b}_{2}}x_{1}^{{{{p}_{2}}}}$ разложения (5.7) решения уравнения (5.6) делаем замену
Тогда уравнение (5.6) принимает вид
В случае б) после замены (6.15) надо снова строить многоугольник Ньютона для уравнения
находить его ребра и т.д. Если на некотором шаге k мы приходим к простому корню ${{b}_{k}}$ укороченного уравнения вида (5.14), то по теореме 2 получаем степенное разложение (5.7) решения исходного уравнения (5.6).Если на каждом шаге получаем только кратные решения ${{b}_{k}}$, то многочлен $f(X)$ надо разложить на неприводимые полиномиальные множители ${{f}_{l}}(X)$:
используя алгоритмы разложения на множители [25, § 53], [29, Часть III, п. 6] имеющиеся в любой системе компьютерной алгебры. В каждом множителе ${{f}_{l}}(X)$ все ветви простые и имеют вид (5.7). Иначе многочлены ${{f}_{l}}(X)$ и $\partial {{f}_{l}}(X){\text{/}}\partial {{x}_{2}}$ имели бы общий полиномиальный множитель. Итак, доказанаТеорема 4. Для полиномиального уравнения (5.6) все решения ${{x}_{2}}({{x}_{1}})$ разлагаются в ряды вида (5.7), где все показатели степени pk суть рациональные числа с общим знаменателем.
Для окрестности точки X = 0 теорема 4 – это теорема В. Пюизё, 1850 г. [30], т.е. для конуса задачи $\mathcal{K} = \{ P = ({{p}_{1}},{{p}_{2}}):{{p}_{1}}$, p2 < 0}. Соответствующая часть (левая нижняя) границы $\partial {\mathbf{N}}$ называется ломаной Ньютона. Разложения теоремы 2 сходятся (см. [31], § 184), поэтому сходятся и все разложения (5.7) для решений полиномиальных уравнений (5.6).
Пример 9 (продолжение примера 8). В случае ребра $\Gamma _{1}^{{(1)}}$ после подстановки ${{x}_{2}} = x_{1}^{2}\left( {\frac{1}{3} + {{y}_{2}}} \right)$ получаем
(5.17)
$\begin{gathered} f = x_{1}^{3} + x_{1}^{6}{{\left( {\frac{1}{3} + {{y}_{2}}} \right)}^{3}} - 3x_{1}^{3}\left( {\frac{1}{3} + {{y}_{2}}} \right) = \\ = \;x_{1}^{3}\left( { - 3{{y}_{2}} + \frac{1}{{27}}x_{1}^{3} + \ldots } \right). \\ \end{gathered} $В случае ребра $\Gamma _{2}^{{(1)}}$ после подстановки x2 = = $\sqrt {{{x}_{1}}} ( \pm \sqrt 3 + {{y}_{2}})$ получаем
Укороченное уравнение для многочлена в скобках – это $x_{1}^{{3/2}} + 6{{y}_{2}} = 0,$ т.е. ${{y}_{2}} = - x_{1}^{{3/2}}{\text{/}}6$. Итак,
Наконец, для ребра $\Gamma _{3}^{{(1)}}$ для укороченного решения (5.13) после подстановки ${{x}_{2}} = {{x}_{1}}( - 1 + {{y}_{2}})$ в (5.10) получаем
(5.20)
$\begin{gathered} f = x_{1}^{3} + x_{1}^{3}{{( - 1 + {{y}_{2}})}^{3}} - 3x_{1}^{2}( - 1 + {{y}_{2}}) = \\ = \;x_{1}^{3}(3{{y}_{2}} - 3y_{2}^{2} + y_{2}^{3}) + 3x_{1}^{2} - 3x_{1}^{2}{{y}_{2}}. \\ \end{gathered} $Носитель и многоугольник Ньютона этого многочлена показаны на рис. 10. Здесь ${{x}_{1}} \to \infty $, ${{y}_{2}}\, \to \,0$, поэтому конус задачи $\mathcal{K}\, = \,{\text{\{ }}P\,:\,{{p}_{1}}\, > \,0$, p2 < 0}, т.е. надо рассмотреть правую нижнюю часть границы многоугольника. Там есть только одно ребро $\tilde {\Gamma }_{1}^{{(1)}}$ с укороченным уравнением
Его решение ${{y}_{2}} = - \tfrac{1}{{{{x}_{1}}}}$. Итак, здесь
и разложение идет по убывающим степеням ${{x}_{1}}$. Прямая – это асимптота ветвей, уходящих в бесконечность.Здесь во всех случаях первые приближения имели простые корни, и им соответствовало по одной ветви кривой.
Уточненные куски (5.18), (5.19), (5.21) листа Декарта (2.2), (5.10) вблизи нуля и бесконечности показаны на рис. 11.
5.3. Вещественная кривая
Если у многочлена (5.1) все коэффициенты ${{f}_{Q}}$ вещественны, то уравнение (5.3) при $x \in \mathbb{R}$ определяет вещественную кривую F на плоскости ${{x}_{1}},{{x}_{2}}$. Для нее в разложении (5.2) теоремы 2 все коэффициенты bk вещественны, а из разложений (5.7) теоремы 4 имеют смысл только те, в которых все коэффициенты bk вещественны. Поскольку они вычисляются последовательно, то на каждом шаге надо оставлять только вещественные коэффициенты bk, а комплексные отбрасывать.
В особой точке $X = 0$ разложение (5.2) начинается с квадратичных членов
(6.23)
$\begin{gathered} f = {{g}_{{20}}}x_{1}^{2} + {{g}_{{11}}}{{x}_{1}}{{x}_{2}} + \\ + \;{{g}_{{02}}}x_{2}^{2} + \; \ldots \mathop = \limits^{{\text{def}}} {{g}_{2}}({{x}_{1}},{{x}_{2}}) + \; \ldots \\ \end{gathered} $Теорема 5. Если $\Delta < 0$, то кривая $F$ не имеет вещественных ветвей, проходящих через критическую точку $X = 0$.
Пусть имеются два многочлена степени 2 и 3 соответственно:
Их результант (т.е. результат исключения переменной x из них) – это многочлен от их коэффициентов
(5.24)
$\begin{gathered} \Omega = R(g,h) = h_{3}^{2}g_{0}^{3} - {{h}_{2}}{{h}_{3}}g_{0}^{2}{{g}_{1}} + \\ + \,( - 2{{h}_{1}}{{h}_{3}} + h_{2}^{2})g_{0}^{2}{{g}_{2}} + {{h}_{1}}{{h}_{3}}{{g}_{0}}g_{1}^{2} + \\ + \,(3{{h}_{0}}{{h}_{3}} - {{h}_{1}}{{h}_{2}}){{g}_{0}}{{g}_{1}}{{g}_{2}} + \\ + \;( - 2{{h}_{0}}{{h}_{2}} + h_{1}^{2}){{g}_{0}}g_{2}^{2} - {{h}_{0}}{{h}_{3}}g_{1}^{3} + {{h}_{0}}{{h}_{2}}g_{1}^{2}{{g}_{2}} - \\ - \;{{h}_{0}}{{h}_{1}}{{g}_{1}}g_{2}^{2} + h_{0}^{2}g_{2}^{3}. \\ \end{gathered} $Если многочлены $g$ и $h$ имеют общий корень, то результант $\Omega $ тождественно равен нулю.
Теорема 6. Пусть в особой точке $X = 0$
где ${{f}_{k}}(X)$ – это однородные формы степени k по ${{x}_{1}}$, ${{x}_{2}}$, форма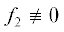 и ее дискриминант $\Delta = 0$, а результант $\Omega $ форм ${{f}_{2}}$ и ${{f}_{3}}$ отличен от нуля. Тогда вблизи точки $X = 0$ кривая $F$ – это полукубическая парабола видагде $\alpha $ – это кратный корень многочлена ${{f}_{2}}(1,\alpha )$.
и ее дискриминант $\Delta = 0$, а результант $\Omega $ форм ${{f}_{2}}$ и ${{f}_{3}}$ отличен от нуля. Тогда вблизи точки $X = 0$ кривая $F$ – это полукубическая парабола видагде $\alpha $ – это кратный корень многочлена ${{f}_{2}}(1,\alpha )$.
5.4. Эскиз вещественной кривой
Пусть у многочлена $f(X)$ все коэффициенты вещественны, тогда на вещественной плоскости $X \in {{\mathbb{R}}^{2}}$ можно нарисовать все ее ветви, используя локальный анализ, описанный выше. Разобьем эту процедуру на несколько шагов.
Шаг 1. Разлагаем многочлен $f(X)$ на полиномиальные множители (5.16), используя указанные выше алгоритмы. Далее строим эскизы кривых для каждого неразложимого множителя ${{f}_{l}}(X)$ отдельно.
Шаг 2. Находим все вещественные конечные особые точки ${{X}^{0}}$ кривой f = 0, в которых
Шаг 3. Вблизи каждой особой точки ${{X}^{0}}$ находим все вещественные ветви вида (5.7), перенося ее в начало координат и используя методы разделов 3, 5.2 и 5.3.
Шаг 4. Находим точки пересечения кривой с осями ${{x}_{1}} = 0$ и ${{x}_{2}} = 0$, как решения уравнений $f(0,{{x}_{2}}) = 0$ и $f({{x}_{1}},0) = 0$, используя методы раздела 4 и уточняя их по теореме 2.
Шаг 5. Находим конечные точки пересечения кривой с бесконечностями ${{x}_{1}} = \infty $ и ${{x}_{2}} = \infty $ по укороченным уравнениям с $P = (1,\;0)$ и $P = (0,\;1).$ Для каждой из них вычисляем начальные члены разложений типа (5.7).
Шаг 6. Находим ветви кривой при ${{x}_{1}} \to 0$, ${{x}_{2}} \to \infty $, используя часть границы $\partial {\mathbf{N}}$ с конусом задачи ${{\mathcal{K}}_{1}} = \left\{ {P:{{p}_{1}} < 0,{{p}_{2}} > 0} \right\}$. Аналогично при ${{x}_{1}} \to \infty $, ${{x}_{2}} \to 0$ – с конусом задачи ${{\mathcal{K}}_{2}} = \left\{ {P:{{p}_{1}} > 0,{{p}_{2}} < 0} \right\}$.
Шаг 7. Находим ветви кривой при ${{x}_{1}},{{x}_{2}} \to \infty $, используя часть границы $\partial {\mathbf{N}}$ с конусом задачи ${{\mathcal{K}}_{3}} = \left\{ {P:{{p}_{1}} > 0,{{p}_{2}} > 0} \right\}$.
Шаг 8. Соединяем найденные куски ветвей кривой, учитывая, что вне особых точек X0 ветви кривой не пересекаются.
Пример 10 (продолжение примеров 8 и 9). Здесь применение наших шагов к многочлену (5.10) дает следующее.
1. Многочлен неразложим.
2. У него только одна особая точка ${{X}^{0}} = 0$.
3. Вблизи этой точки мы нашли две ветви (5.18) и (5.19).
4. Кривая пересекается с осями только в точке $X = 0$.
5. С бесконечностями ${{x}_{1}} = \infty $ и ${{x}_{2}} = \infty $ кривая не пересекается, так как им соответствуют вершины ${{Q}_{1}}$ и ${{Q}_{2}}$.
6. С конусами задач ${{\mathcal{K}}_{1}}$ и ${{\mathcal{K}}_{2}}$ пересекаются только нормальные конусы ${\mathbf{U}}_{2}^{{(0)}}$ и ${\mathbf{U}}_{1}^{{(0)}}$ вершин ${{Q}_{2}}$ и ${{Q}_{1}}$ соответственно (рис. 5 раздела 3). Поэтому нет ветвей с ${{x}_{1}} \to 0$, ${{x}_{2}} \to \infty $ и ${{x}_{1}} \to \infty $, ${{x}_{2}} \to 0$.
7. Конусу задачи ${{\mathcal{K}}_{3}}$ соответствует ребро $\Gamma _{3}^{{(1)}}$, которое дало в бесконечности ветвь (5.21).
8. Соединяя найденные куски кривой из рис. 9, получаем рис. 2, на котором пунктирная прямая – это асимптота (5.22).
5.5. Программное обеспечение
В системе Maple имеется замечательный пакет algcurves, который позволяет исследовать плоские алгебраические кривые: строить их эскизы с высокой точностью, вычислять их род, находить особые точки, для кривых рода 0 находить рациональную параметризацию по методу [32], для эллиптических кривых приводить к нормальной форме Вейерштрасса. Пакет позволяет строить эскиз кривой $f(x,y) = 0$ путем численного интегрирования дифференциального уравнения $f_{x}^{'}\, + \,f_{y}^{'}y{\text{'}}$ = 0 для некоторого набора начальных условий, определяемых точками, в которых хотя бы одна из частных производных функции $f(x,y)$ равна нулю. Использование данного пакета для исследования набора кривых с разными порядками особенностей показало, что в случае особенностей высоких порядков качество эскиза получается не слишком высоким.
Рассмотрим пример исследования листа Декарта с помощью этого пакета. Вначале найдем особые точки кривой, вычислим ее род и рациональную параметризацию, а затем построим разложение ветвей в окрестности нуля и бесконечности. Последовательность вычислений в системе компьютерной алгебры Maple приведена в листинге 4.
Листинг 4. Maple
>with(algcurves):
>Folium:=x^3+y^3=3*x*y:
# Особые точки
>singularities (Folium, x, y);
[[0, 0, 1], 2, 1, 2]
# Род
>genus (Folium, x, y);
0
# Параметризация
>Param_Folium:=zip (‘= ‘, [x, y], parametrization (Folium, x, y, t))
$\left[ {x = \tfrac{{3{{t}^{2}}}}{{{{t}^{3}} + 1}},y = \tfrac{{3t}}{{{{t}^{3}} + 1}}} \right]$
# Ветви вблизи нуля
>branch1 := sort (puiseux (Folium, x = 0, y, 9) [1], x, ascending);
>branch2 := sort (puiseux (Folium, x = 0, y, 5) [2], x, ascending);
$\tfrac{{{{x}^{2}}}}{3} + \tfrac{{{{x}^{5}}}}{{81}} + \tfrac{{{{x}^{8}}}}{{729}}$
$\sqrt 3 \sqrt x - \tfrac{{{{x}^{2}}}}{6} - \tfrac{{\sqrt 3 }}{{72}}{{x}^{{\tfrac{7}{2}}}}$
# Ветвь вблизи бесконечности
>branch_inf := expand (puiseux (Folium, x = infinity, y , 4) [1]);
$ - 1 - \tfrac{1}{{3{{x}^{3}}}} + \tfrac{1}{{3{{x}^{2}}}} - x$
Начиная с версии 12 система компьютерной алгебры Wolfram Mathematica [33] включает процедуру AsymptoticSolve, реализующую асимптотическое представление решений уравнений или систем уравнений (не обязательно алгебраических) в виде либо рядов Тейлора, либо рядов Лорана, либо рядов Пьюизе в окрестности конечной или бесконечной точек. Если точка особая, то процедура пытается вычислить асимптотические разложения всех ветвей. В этом случае можно указать, что следует ограничиться только вещественными разложениями. Листинг 5 демонстрирует такое вычисление разложения ветвей листа Декарта в окрестности особой точки и бесконечности.
Листинг 5: Mathematica
Folium = x^3+y^3 – 3 x y == 0
${{x}^{3}} - 3xy + {{y}^{3}}$
AsymptoticSolve [Folium, {y, 0}, {x , 0, 5}, Reals, Direction –> "
FromAbove"]
$\left\{ {\left\{ {y \to \tfrac{{{{x}^{2}}}}{3} + \tfrac{{{{x}^{5}}}}{{81}}} \right\}} \right.,\left\{ {x \to - \sqrt 3 \sqrt x - \tfrac{{{{x}^{2}}}}{6} + \tfrac{{{{x}^{{7/2}}}}}{{24\sqrt 3 }} - \tfrac{{{{x}^{5}}}}{{162}}} \right\},$
$\left. {\left\{ {x \to \sqrt 3 \sqrt x - \tfrac{{{{x}^{2}}}}{6} - \tfrac{{{{x}^{{7/2}}}}}{{24\sqrt 3 }} - \tfrac{{{{x}^{5}}}}{{162}}} \right\}} \right\}$
AsymptoticSolve [Folium==0, y, x–>Infinity, Reals,
SeriesTermGoal–>5]
$\left\{ {\left\{ {y \to - 1 - \tfrac{1}{{3{{x}^{3}}}} + \tfrac{1}{{3{{x}^{2}}}} - x} \right\}} \right\}$
5.6. Большой пример
Пример 11. Рассмотрим пример исследования некоторой нетривиальной кривой, имеющей несколько особых точек. Все дальнейшие вычисления выполнялись в системе компьютерной алгебры Maple с использованием описанных выше пакетов. Такие же вычисления несложно реализуются в других системах компьютерной алгебры, таких как Mathematica и SymPy.
В работах [9, 16] рассматривалась устойчивость в линейном приближении одной многопараметрической системы Гамильтона. В процессе исследования возникла необходимость изучить нули некоторого многочлена $g(x,y,z)$ 6-го порядка от трех переменных $x$, $y$, $z$ (см. формулу (3.7) в [16]). Здесь исследуем алгебраическую кривую $f(y,z)\mathop = \limits^{{\text{def}}} \mathop {\left. {g(x,y,z)} \right|}\nolimits_{x = 0} = 0$ в соответствии со схемой подпункта 5.4, где
(6.25)
$\begin{gathered} + \;37928{{y}^{3}}{{z}^{2}} + 67608{{y}^{3}}z + 46656{{y}^{3}} + \\ + \;14848{{y}^{2}}{{z}^{4}} - 14976{{y}^{2}}{{z}^{3}} - 35496{{y}^{2}}{{z}^{2}} - \\ \end{gathered} $Шаг 1. Многочлен (5.25) факторизуется на два множителя: линейный $3z - 2y$ и полином пятой степени
(5.26)
$\begin{gathered} h(y,z) = 2500{{y}^{4}}z - 6750{{y}^{4}} - 5600{{y}^{3}}{{z}^{2}} + \\ + 10540{{y}^{3}}z\, + \,12609{{y}^{3}}\, + \,4736{{y}^{2}}{{z}^{3}}\, - \,5616{{y}^{2}}{{z}^{2}} - \\ - \;14130{{y}^{2}}z\, - \,15552{{y}^{2}}\, - \,1792y{{z}^{4}}\, + \,1248y{{z}^{3}} + \\ + \;2412y{{z}^{2}} + 20736yz + 256{{z}^{5}} - \\ - \;128{{z}^{4}} + 936{{z}^{3}} - 6912{{z}^{2}}. \\ \end{gathered} $Далее рассматриваем только кривую $\mathcal{F}:h(y,z)$ = = 0.
Шаг 2. Находим особые точки кривой, решая систему $h = \partial h{\text{/}}\partial y = \partial h{\text{/}}\partial z = 0$. Для этого вычислим базис Грёбнера $\mathcal{G}\mathcal{B}\mathcal{J}$ данной системы, выбрав чисто лексикографический порядок переменных (см. [34, Гл. 2]). Полученный идеал является нульмерным, т.е. исходная система имеет конечное число особых точек. Их координаты легко определить, если вычислить два базиса Грёбнера для порядков $y > z$ и $z > y$ соответственно и выписать первые полиномы получившихся базисов:
(5.27)
$\begin{gathered} {{y}^{4}}\left( {y - 14} \right) \times \\ \times \;\mathop {(8000{{y}^{3}} - 50832{{y}^{2}} + 111321y - 84672)}\nolimits^2 , \\ \end{gathered} $(5.28)
$\begin{gathered} {{z}^{4}}\left( {z - 27} \right) \times \\ \times \;\mathop {(2560{{z}^{3}} - 22176{{z}^{2}} + 63909z - 61344)}\nolimits^2 . \\ \end{gathered} $Кубические полиномы в (5.27) и (5.28) имеют по одному вещественному корню ${{y}_{3}}$, ${{z}_{3}}$ соответственно, следовательно, особых точек три: $({{y}_{1}},{{z}_{1}}) = (0,0)$, $({{y}_{2}},{{z}_{2}}) = (14,27)$ и $({{y}_{3}},{{z}_{3}})$.
Шаг 3. Найдем все вещественные ветви в окрестности каждой из особых точек $({{y}_{i}},{{z}_{i}})$, $i = 1,2,3$.
а) Разложение в точке $({{y}_{1}},{{z}_{1}}) = (0,\;0)$. Здесь конус задачи есть ${{\mathcal{K}}_{3}} = \left\{ {P = ({{p}_{1}},{{p}_{2}}) < 0} \right\}$. Непосредственные вычисления показывают, что квадратичная форма ${{h}_{2}}$ ряда Тейлора многочлена h есть полный квадрат $ - 1728{{(3y - 2z)}^{2}}$ и имеет общий множитель с кубичной формой ${{h}_{3}}$. Таким образом, теоремы 5 и 6 неприменимы, и здесь необходимо применить технику подраздела 5.2.
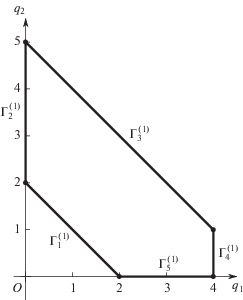
Вычисляем выпуклую оболочку носителя многочлена (5.26) с использованием пакета PolyhedralSets. Многоугольник Ньютона и его ребра показаны на рис. 12.
Ребру $\Gamma _{1}^{{(1)}}$ соответствует укороченный многочлен $h_{1}^{{(1)}} = - 1728{{(3y - 2z)}^{2}}$. Выполним подстановку $3y - 2z = t$ и получим многочлен $\tilde {h}$ в переменных $y$, $t$:
Единственному ребру $\tilde {\Gamma }_{1}^{{(1)}}$ выпуклой оболочки носителя ${\mathbf{S}}(\tilde {h})$, попадающему в конус задачи ${{\mathcal{K}}_{3}}$, соответствует укороченный многочлен $\tilde {h}_{1}^{{(1)}}$ = –12(12t – – y2)2. Следовательно, здесь требуется еще одна подстановка $t = u + {{y}^{2}}{\text{/}}12$. Она приводит к многочлену $\tilde {\tilde {h}}_{1}^{{(1)}}$ от переменных y, $u$. Его носитель имеет единственное ребро из конуса задачи ${{\mathcal{K}}_{3}}$, которому соответствует многочлен $\tilde {\tilde {h}}_{1}^{{(1)}} = - 1728{{u}^{2}}$ + 4y5/3. Таким образом, получаем два решения u1, 2 = = $ \pm {{y}^{{5/2}}}{\text{/}}36$. Выполняя обратную подстановку, в итоге получаем разложения двух ветвей
которые в особой точке (0, 0) имеют касание второго порядка. Вычисления с использованием функции puisex из пакета algcurves системы Maple или с использованием функции AsymptoticSolve системы Mathematica приводят к таким же результатам.б) Разложение в точке $({{y}_{2}},{{z}_{2}}) = (14,\;27)$. Вычисляем (с точностью до постоянного множителя) квадратичную форму ${{h}_{2}}$ в особой точке $({{y}_{2}},{{z}_{2}})$:
Ее дискриминант $\Delta = - 560$, следовательно, по теореме 5 вещественных ветвей нет, а особая точка является точкой пересечения комплексных ветвей, в которой обнуляются их мнимые части.
в) Разложение в точке $({{y}_{3}},{{z}_{3}}) \approx (2.34274429915$, $3.2427747207226)$. Как было указано выше, координаты $({{y}_{3}},{{z}_{3}})$ этой точки являются корнями кубических многочленов
(5.30)
$\begin{gathered} 8000{{y}^{3}} - 50832{{y}^{2}} + 111321y - 84672, \\ 2560{{z}^{3}} - 22176{{z}^{2}} + 63909z - 61344. \\ \end{gathered} $Эти многочлены имеют по одному вещественному и по паре комплексно-сопряженных корней, значения которых могут быть записаны в кубических радикалах. Однако в таком виде проводить символьные вычисления крайне неудобно из-за громоздкости получающихся выражений. Можно предложить три способа вычисления асимптотических разложений ветвей в этом случае.
Способ 1. Каждый корень многочленов (5.30) заменяется своим приближенным числовым значением, вычисленным с достаточной точностью. При подстановке этих значений в исходный многочлен появляются “паразитные” мономы с малыми коэффициентами. Для избавления от них следует сделать оценку абсолютной величины их коэффициентов и на каждом шаге вычислений удалять те мономы, коэффициенты которых не превышают полученной оценки. В силу приближенного характера коэффициентов применение теорем 5 и 6 потребует другого способа работы с дискриминантами и результантами.
Способ 2. Можно проводить все вычисления с полиномами в расширении поля рациональных чисел $\mathbb{Q}$ алгебраическими числами $\gamma $, $\delta $ – корнями многочленов (5.30). В этом случае на каждом шаге вычислений следует выполнять упрощение коэффициентов получающихся многочленов. Многие системы компьютерной алгебры позволяют проводить такого рода расчеты. Например, пакет Algebraic системы Maple содержит различные процедуры для работы с многочленами, коэффициенты которых суть алгебраические числа. Функция AlgebraicNumber системы Mathematica позволяет работать с корнями алгебраического уравнения как с обычными числами. Результат вычислений асимптотических разложений ветвей представляет собой ряд с коэффициентами, зависящими от алгебраических чисел $\gamma $, $\delta $. Заменяя их соответствующими числовыми значениями, получим ряды с приближенными коэффициентами. Основной недостаток этого способа заключается в том, что далеко не всегда удается упростить получающиеся выражения до соответствующих тривиальных значений, что в итоге приводит к громоздким выражениям и, как следствие, к трудоемким вычислениям.
Способ 3. По-видимому, самым общим способом аналитического вычисления асимптотических разложений ветвей кривой является способ вычисления по модулю иделал $\mathcal{J}$, определяющему особую точку. Все вычисления выполняются с использованием базиса Гребнера этого идеала с априорно заданным лексикографическим порядком переменных. В нашем случае используем пакет Groebner системы Maple и процедуры Basis и NormalForm из него.
Сделаем замену переменных $y = {{y}_{3}} + \eta $, $z = {{z}_{3}}$ + + ζ. Нульмерный идеал $\mathcal{J}$, определяющий особую точку $({{y}_{3}},{{z}_{3}})$, состоит из многочленов (5.30) и производных $h_{y}^{'}$, $h_{z}^{'}$. Его базис Гребнера $\mathcal{G}\mathcal{B}\mathcal{J}$ с лексикографическим порядком ${{y}_{3}} < {{z}_{3}}$ имеет вид
Для особой точки $({{y}_{3}},{{z}_{3}})$ первой невырожденной формой является квадратичная форма h2 вблизи точки $({{y}_{3}},{{z}_{3}})$ ряда Тейлора:
(5.31)
$\begin{gathered} {{h}_{2}}({{y}_{3}} + \eta ,{{z}_{3}} + \zeta ) = \\ = \;\left( {\frac{{775125y_{3}^{2}}}{{472}} - \frac{{26927775{{y}_{3}}}}{{3776}} + \frac{{496125}}{{59}}} \right){{\eta }^{2}} + \\ + \;\left( { - \frac{{119565y_{3}^{2}}}{{59}} + \frac{{3588165{{y}_{3}}}}{{472}} - \frac{{476280}}{{59}}} \right)\eta \zeta + \\ + \;\left( {\frac{{327213y_{3}^{2}}}{{295}} - \frac{{10769787{{y}_{3}}}}{{2360}} + \frac{{1555848}}{{295}}} \right){{\zeta }^{2}}. \\ \end{gathered} $Ее дискриминант по модулю идеала равен нулю.
Вычисляем кубичную форму h3 вблизи точки $({{y}_{3}},{{z}_{3}})$:
(5.32)
$\begin{gathered} {{h}_{3}}({{y}_{3}} + \eta ,{{z}_{3}} + \zeta ) = \\ = \;\left( {\frac{{605211}}{{59}} - \frac{{1196255{{y}_{3}}}}{{118}} + \frac{{455000y_{3}^{2}}}{{177}}} \right){{\eta }^{3}} + \\ + \;\left( {\frac{{195000y_{3}^{2}}}{{59}} - \frac{{767820{{y}_{3}}}}{{59}} + \frac{{728442}}{{59}}} \right){{\eta }^{2}}\zeta + \\ + \;\left( { - \frac{{321600y_{3}^{2}}}{{59}} + \frac{{1238940{{y}_{3}}}}{{59}} - \frac{{1205532}}{{59}}} \right)\eta {{\zeta }^{2}} + \\ + \;\left( {\frac{{267872y_{3}^{2}}}{{177}} - \frac{{327988{{y}_{3}}}}{{59}} + \frac{{317112}}{{59}}} \right){{\zeta }^{3}} \\ \end{gathered} $Вычисления по модулю идеала $\mathcal{G}\mathcal{B}\mathcal{J}$ приводят к следующим результатам:
Поскольку $c < 0$, то $\eta < 0$ и разложение в переменных $y$, $z$ принимает вид
Шаг 4. Ребрам $\Gamma _{2}^{{(1)}}$ и $\Gamma _{5}^{{(1)}}$ соответствуют укороченные многочлены
Их нули дают координаты пересечения кривой $\mathcal{F}$ с осями $Oz$ и $Oy$ соответственно. Многочлен $\hat {h}_{2}^{{(1)}}$ имеет два вещественных корня: 0 и $2.747016946$, а многочлен $\hat {h}_{5}^{{(1)}}$ – только корень 0.
Шаг 5. Ребру $\Gamma _{4}^{{(1)}}$ соответствует укороченный многочлен $\hat {h}_{4}^{{(1)}} = 250{{y}^{4}}(10z - 27)$. Значит при $y \to \infty $ имеем $z \to 27{\text{/}}10$. Применяя технику пункта 5.3, находим разложение ветви кривой на бесконечности:
Итак, кривая $\mathcal{F}$ имеет горизонтальную асимптоту.
Стремящейся к $\infty $ координате z в многоугольнике Γ соответствует верхняя вершина, т.е. при $z = \infty $ нет точек кривой $\mathcal{F}$.
Шаг 6. Конусам задач ${{\mathcal{K}}_{1}}$ и ${{\mathcal{K}}_{2}}$ соответствуют только вершины многоугольника Ньютона рис. 12.
Шаг 7. Ребру $\Gamma _{3}^{{(1)}}$ соответствует укороченный многочлен
Шаг 8. Теперь имеется достаточно информации для построения эскиза кривой, который приведен на рис. 13. На нем показан график кривой $\mathcal{F}$ кроме точки $({{y}_{2}},{{z}_{2}}) = (14,\;27)$. Вблизи особых точек $({{y}_{1}},{{z}_{1}})$ и $({{y}_{3}},{{z}_{3}})$ пунктиром показаны ветви, вычисленные приближенно, и асимптота z = 2.7.
Рассмотрим другой способ вычисления особых точек кривой $\mathcal{F}$ и ее разложения в их окрестностях. Этот способ существенно использует систему компьютерной алгебры Maple и, в частности, пакет algcurves из нее. Особенность пакета algcurves состоит в том, что все вычисления по умолчанию производятся в поле комплексных чисел $\mathbb{C}$, что требует дополнительных усилий при исследовании вещественных кривых.
Функция genus из указанного выше пакета позволяет вычислить род кривой $\mathcal{F}$ с помощью команды genus(F,y,z). Ее род оказывается равным 0, т.е. эта кривая допускает рациональную параметризацию. Функция parametrization пакета algcurves позволяет вычислить эту рациональную параметризацию. Однако ее непосредственное применение приводит к очень громоздкому результату (здесь он не приводится), слабо пригодному для дальнейших вычислений. Последующие упрощения полученного в результате выражения приводят к параметризации кривой $\mathcal{F}$ в виде
(5.33)
$\begin{gathered} y = \frac{{3({{s}^{3}} + 36{{s}^{2}} + 54s + 216){{s}^{2}}}}{{2{{{(5{{s}^{2}} + 6s + 18)}}^{2}}}}, \\ z = \frac{{27(5{{s}^{2}} + 9s + 36){{s}^{2}}}}{{2{{{(5{{s}^{2}} + 6s + 18)}}^{2}}}}. \\ \end{gathered} $Кривая $\mathcal{F}$ на рис. 13 построена с использованием этих формул.
Особые точки кривой могут быть вычислены с использованием функции singularities(F,y,z), но в нашем случае часть из них представляется в виде алгебраических чисел. Покажем, как найти такие точки используя только вычисленную выше параметризацию (5.33) кривой $\mathcal{F}$.
Особые точки кривой – это точки,
1. в которых либо обе производные одновременно обращаются в нуль: $y{\text{'}}(s) = z{\text{'}}(s) = 0$,
2. либо это изолированные точки, в которой обнуляются мнимые части ее комплексных ветвей.
В случае 1 вычисления приводят к уравнению
которое имеет два вещественных корня ${{s}_{1}} = 0$, ${{s}_{3}} \approx - 85.62562644$. Эти значения параметра s определяют особые точки $({{y}_{1}},{{z}_{1}})$ и $({{y}_{3}},{{z}_{3}})$ соответственно.В случае 2 выполняем подстановку $s = u + i{v}$ в (5.33) и решаем систему ${\text{Im}}y(u\, + \,i{v}) = {\text{Im}}z(u\, + \,i{v})$ = 0, ${v} \ne 0$. Ее решения суть ${{s}_{2}} = - 1{\text{/}}3 \pm i\sqrt {35} {\text{/}}3$ и ${{s}_{4}} = - 3{\text{/}}5 \pm i9{\text{/}}5$. Значению s2 соответствует особая точка $({{y}_{2}},{{z}_{2}})$, а значению ${{s}_{4}}$ – бесконечно-удаленная точка $( \pm \infty ,0)$.
Наконец, зная координаты особых точек и параметризацию (5.33), можно вычислить разложение ветвей кривой $\mathcal{F}$ в их окрестности с использованием команды series. Так, например, для точки $({{y}_{1}},{{z}_{1}})$ это разложение имеет вид
В заключение отметим, что непосредственное применение процедуры puisex из пакета algcurves приводит к результатам, где разложения кривой представлены в виде громоздких выражений от алгебраических чисел – корней соответствующего уравнения третьей степени, задающего особые точки. В такой форме использовать полученные ряды для визуализации кривой и численных расчетов фактически невозможно.
6. ТЕОРИЯ МЕТОДА ЛОМАНОЙ АДАМАРА
Здесь выявим причину удаленности точных корней $x_{i}^{0}$ многочлена
и приближенных корней xi, полученных методом ломаной Адамара (см. раздел 4). ПоложимПри $y \to \infty $ ветви кривой $\mathcal{F}$ приближаются решениями укороченных уравнений
соответствующих ребрам $\tilde {\Gamma }_{l}^{{(1)}}$ ломаной Адамара ${\mathbf{\tilde {H}}}$ многочлена (6.1). Если в интервале эти ветви не пересекаются и не сливаются, то приближенные корни xi полученные с помощью ломаной Адамара, близки к точным корням $x_{i}^{0}$ многочлена (6.1). Но если в интервале (6.4) эти ветви пересекаются или сливаются, то при $y = e$ их взаимное расположение отличается от предельного расположения при $y \to \infty $. Но пересекаться или сливаться ветви кривой (7.3) могут только в точках $({{x}^{0}},{{y}^{0}})$: т.е. там, где дискриминант $\Delta $ многочлена $g$ от $x$ равен нулю.Поэтому, если кривая (7.3) не имеет точек
в интервале (6.4), то приближенные корни ${{x}_{i}}$ близки к точным корням $x_{i}^{0}$ многочлена (6.1). Но если кривая (6.3) имеет в интервале (6.4) точки (6.5), то приближенные корни ${{x}_{i}}$ могут быть далеки от точных корней $x_{i}^{0}$ многочлена (6.1). Для близости вещественных корней ${{x}_{i}}$ и $x_{i}^{0}$ достаточно отсутствия вещественных не изолированных точек (6.5) в интервале (6.4).Пример 12 (продолжение примера 6). Здесь сумма (6.2) для многочлена (4.3) есть
где ${{\alpha }_{1}} = ln9 \approx 2.197$, ${{\alpha }_{3}} = ln8 \approx 2.0794$. Положим $z = {{x}^{2}}$ и $h = g{\text{/}}x$, тогда получим суммуЕе дискриминант $\Delta = {{y}^{{2{{\alpha }_{3}}}}} + 4{{y}^{{{{\alpha }_{1}}}}}$. Он равен нулю только при y = 0, заведомо меньшем e.
Итак, в интервале (6.4) нет нулевых точек дискриминанта. Поэтому ветви кривой (6.3) при $y \to + \infty $ расположены также, как их пересечения с горизонталью y = e.
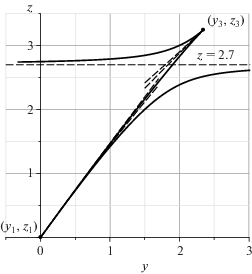
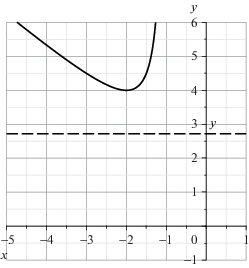
Пример 13. Пусть
Тогда
Дискриминант этого многочлена по $x$ равен $\Delta \, = \,{{y}^{2}}\, - \,4y$. Он обращается в ноль при y = 0 и y = 4. Поскольку y = 4 лежит в интервале (6.4), то вещественные приближенные корни ${{x}_{1}} = - e$ и ${{x}_{2}} = - 1$ при уточнении по методу Ньютона не сходятся к точным комплексным корням
многочлена $f(x)$. Итерации приближенных корней ${{x}_{1}}$ и ${{x}_{2}}$ показаны в табл. 2, где в верхней строке приведен номер $k$ итерации по алгоритму Ньютона. График ветви кривой g = 0 для $y > 0$ показан на рис. 14. Из рисунка видно, что два приближенных корня, соответствующих каждой из ветвей кривой, при стремлении $y \to 4$ сливаются и до значения $y = e$ уже не доходят.Таблица 2
| $k$ | 0 | 1 | 2 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| ${{x}_{1}}$ | –1.000 | –2.392 | –1.454 | 3.179 | 0.8141 | –0.4729 | –1.407 |
| ${{x}_{2}}$ | –2.718 | –1.718 | –0.3261 | –1.264 | –5.898 | –3.532 | –2.245 |
Отметим, что школьница Ирина Зобова [35] освоила оба метода, описанные в разделах 4 и 5:
1. вычисление приближенных корней многочлена и их уточнение;
2. нахождение ветвей алгебраической кривой.
Список литературы
Брюно А.Д. Алгоритмы решения одного алгебраического уравнения // Программирование. 2019. Т. 45. № 1. С. 59–72.
Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М. : ФИЗМАТЛИТ, 1998. 288 с.
Клейн Ф. Лекции о развитии математики в XIX столетии: В 2-х томах / Под ред. Постников М.М. М.: Наука, 1989. Т. 1. 456 с.
Ефимов Н.В. Высшая геометрия. 7-е изд. М.: ФИЗМАТЛИТ, 2004. 584 с.
Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. 2-е изд. М.: Наука, 1986. 304 с.
Юнг Д.В. Проективная геометрия. М.: ИЛ, 1949. 186 с.
Шафаревич И.Р. Основы алгебраической геометрии. М.: МЦНМО, 2007. 590 с.
Брюно А.Д. Локальный метод нелинейного анализа дифференциальных уравнений. М.: Наука, 1979. 252 с.
Брюно А.Д., Батхин А.Б. Разрешение алгебраической сингулярности алгоритмами степенной геометрии // Программирование. 2012. № 2. С. 12–30.
Брюно А.Д. Асимптотики и разложения решений обыкновенного дифференциального уравнения // УМН. 2004. Т. 57. № 3 (357). С. 31–80.
Брюно А.Д., Шадрина Т.В. Осесимметричный пограничный слой на игле // Труды ММО. 2007. Т. 68. С. 224–287.
Брюно А.Д., Горючкина И.В. Асимптотические разложения решений шестого уравнения Пенлеве // Труды ММО. 2010. Т. 71. С. 6–118.
Брюно А.Д. Разложение решений обыкновенного дифференциального уравнения в трансряды // ДАН. 2019. Т. 484. № 3. С. 36–39.
Gallier J. Geometric Methods and Applications. For Computer Science and Engineering. New York, Dordrecht, Heidelberg, London: Springer, 2011.
Barber C.B., Dobkin D.P., Huhdanpaa H.T. The Quickhull algorithm for convex hulls // ACM Trans. on Mathematical Software. 1996. V. 22. № 4. P. 469–483.
Батхин А.Б., Брюно А.Д., Варин В.П. Множества устойчивости многопараметрических гамильтоновых систем // Прикл. мат. мех. 2012. Т. 76. № 1. С. 80–133.
Thompson I. Understanding Maple. Cambridge University Press, 2016. 228 p.
The Sage Developers. SageMath, the Sage Mathematics Software System (Version 9.1.1), 2020. https://www.sagemath.org.
Fukuda K. cdd, cddplus and cddlib homepage. McGill University, Montreal, Canada, 2002. Access mode: http://www.cs.mcgill.ca/~fukuda/software/cdd_home/cdd.html
Bagnara R., Hill P.M., Zaffanella E. The Parma Polyhedra Library: Toward a Complete Set of Numerical Abstractions for the Analysis and Verification of Hardware and Software Systems // Science of Computer Programming. 2008. V. 72. № 1–2. P. 3–21.
Aaron Meurer, Christopher P. Smith, Mateusz Paprocki et al. SymPy: symbolic computing in Python // PeerJ Computer Science. 2017. V. 3. P. e103. Access mode: https://doi.org/10.7717/peerjcs.103
Bruce King R. Beyond the quartic equation. Boston: Birkhäser, 1996. 149 p.
Умемура Х. Решение алгебраических уравнений с помощью тэта-констант / В кн. Мамфорд, Д. Лекции о тэта-функциях. Пер. с англ. М.: Наука, 1988. С. 362–370.
Hadamard J. Etude sur les propriétés des fonctions entières et en particulier d’une fonction considéro par Riemann // Journal de mathématiques pures et appliquos ${{4}^{e}}$ série. 1893. V. 9. P. 171–216.
Курош А.Г. Курс высшей алгебры. М.: Наука, 1956. 431
Калинина Е.А., Утешев А.Ю. Теория исключения: Учеб. пособие. СПб.: Изд-во НИИ химии СПбГУ, 2002. 72 с.
Gathen J. von zur, Lücking T. Subresultants revisited // Theoretical Computer Science. 2003. V. 297. P. 199–239.
Батхин А.Б. Параметризация дискриминантного множества вещественного многочлена // Программирование. 2016. Т. 42. № 2. С. 8–21.
Акритас А.Г. Основы компьютерной алгебры с приложениями. М.: Мир, 1994. 544 с.
Puiseux V. Recherches sur les fonctions algлriques // Journal de mathématiques pures et appliquos ${{1}^{{re}}}$ série. 1850. V. 15. P. 365–480.
Гурса Э. Курс математического анализа. М.-Л.: ГТТИ, 1933. Т. 1. 235 с.
Hoeij M. Rational parametrizations of algebraic curves using a canonical divisor // J. Symbolic Computation. 1997. V. 23. P. 209–227.
Wolfram S. The Mathematica Book. Wolfram Media, Inc. 2003. 1488 p.
Кокс Д., Литтл Д., О’Ши Д. Идеалы, многообразия и алгоритмы. Введение в вычислительные аспекты алгебраической геометрии и коммутативной алгебры. М.: Мир, 2000. 687 с.
Зобова И. Геометрические методы решения полиномиальных уравнений // Материалы XIX Международной научной конференции школьников “Колмогоровские чтения”, 5–8 мая 2019, МАТЕМАТИКА. М.: Специализированный учебно-научный центр (факультет) – школа-интернат имени А.Н. Колмогорова МГУ. 2019. С. 15–16.
Дополнительные материалы отсутствуют.
Инструменты
Программирование