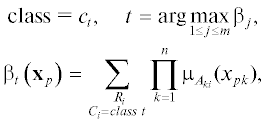1. На главную
  2. Электронные версии
  3. Программирование
  4. № 5, 2021

Программирование, 2021, № 5, стр. 44-59

Методы бинаризации алгоритма стаи ласточек для решения задачи отбора признаков

А. О. Слезкин a, *, И. А. Ходашинский a, **, А. А. Шелупанов a, ***

a Томский государственный университет систем управления и радиоэлектроники
634050 Томск, проспект Ленина, д. 40, Россия

* E-mail: saotom724@gmail.com
** E-mail: hodashn@rambler.ru
*** E-mail: saa@tusur.ru

Поступила в редакцию 05.02.2021
После доработки 16.03.2021
Принята к публикации 12.05.2021

Полный текст (PDF)

Аннотация

Предложены шесть методов бинаризации алгоритма стаи ласточек для решения задачи отбора признаков по методу обертки. Эффективность выбранных подмножеств признаков оценивается двумя классификаторами: нечетким классификатором и классификатором на основе k-ближайших соседей. При поиске оптимального подмножества признаков учитывались количество признаков и точность классификации. Разработанные алгоритмы протестированы на наборах данных из репозитория KEEL. Для статистической оценки методов бинаризации использовался двухфакторный дисперсионный анализ Фридмана для связных выборок. Лучшие способности к отбору признаков показал гибридный метод, основанный на методе модифицированных алгебраических операций и введенной нами операции MERGE. Лучшая точность классификации получена с использованием метода V-образной функции трансформации.

1. ВВЕДЕНИЕ

Отбор признаков – одна из важнейших тем исследований в области интеллектуального анализа данных и машинного обучения. Удаление нерелевантных и избыточных признаков позволяет уменьшить размерность исходных данных, ускорить процесс обучения, упростить разрабатываемую модель, повысить ее эффективность и обобщающие возможности, уменьшить риск переобучения.

Основная цель отбора признаков – исключить из набора данных признаки, которые слабо или даже негативно влияют на определение метки класса классификатором. Избавление от таких признаков, позволит как снизить сложность получаемой модели, так и, возможно, повысить точность классификации. Таким образом, отбор признаков можно рассматривать как двухкритериальную задачу. Однако часто указанная двухкритериальная задача сводится к однокритериальной задаче введением единой целевой функции, в которой с помощью весовых коэффициентов учтены ошибка классификации и отобранное число признаков.

Методы отбора признаков разделяются на три группы: фильтры, обертки и встроенные методы. Фильтры используют только сами данные, не требуя построения классификатора. Преимущество этой группы методов состоит в низкой вычислительной сложности. Обертки требуют построения классификатора и включения его в процесс отбора признаков. По этой причине, получаемые результаты по качеству часто превосходят результаты, полученные методами фильтра, однако при этом возрастает и вычислительная сложность [1]. Встраиваемые методы интегрируются в процесс построения классификатора и производят отбор признаков в процессе его обучения.

В статье [2] авторы формулируют и доказывают теорему о NP-трудности проблемы отбора признаков, сводя эту проблему к задаче максимального покрытия, которая является NP-трудной. Таким образом, нахождение оптимального решения проблемы отбора признаков может быть гарантировано только полным перебором. Однако в современных наборах данных размер признакового пространства может достигать нескольких сотен, тысяч и даже больше [3]. Полный перебор средствами современных вычислительных средств является затратной или даже невыполнимой задачей. Для решения этой проблемы можно использовать метаэвристики, которые позволяют найти оптимальное либо субоптимальное решение за приемлемое время.

Кратко остановимся на понятии “метаэвристика”, но сначала дадим рабочее определение понятию эвристика – это способ нахождения “достаточно хороших” решений без доказательства оптимальности найденных решений. Качество или эффективность решения могут быть выражены через точность, стабильность, экономию памяти или времени. Термин “мета” указывает на обобщенность и “методологию верхнего уровня”. Как правило, эвристики предназначены для решения конкретных задач, в то время как метаэвристики независимы от решаемых проблем. По мнению Шона Люка [4], метаэвристика – общее, но неудачное название стохастического алгоритма оптимизации, который применяется в качестве последней надежды на пути к решению задачи оптимизации. Применяются метаэвристики в том случае, когда 1) неизвестен способ поиска оптимального решения; 2) недостаточно имеющейся априорной информации; 3) невозможен полный перебор; 4) можно проверить качество решения, т.е. неизвестна аналитическая форма целевой функции, но ее значение может быть вычислено для конкретного решения.

Метаэвристики не используют вычисление производных целевой функции, однако, в отличие от детерминированных методов оптимизации, метаэвристики позволяют находить за приемлемое время удовлетворительные решения задач большой размерности. Широкому применению метаэвристик способствует увеличение вычислительной мощности компьютеров и развитие параллельных архитектур [5].

Отбор признаков ведется в бинарном пространстве поиска, когда возможны два состояния – признак используется или не используется в классификаторе. Большинство метаэвристических алгоритмов изначально разрабатывалось для работы в непрерывном пространстве поиска, которое задается множеством действительных чисел на определенном интервале для каждого признака; бинарное пространство поиска задается только двумя возможными значениями для каждого признака – 0 или 1. Поэтому для решения задачи отбора признаков алгоритмы, работающие в непрерывном пространстве поиска, необходимо адаптировать для работы в бинарном пространстве и разработать систему кодирования решения, сохранив при этом изначальную идею алгоритма. В процессе адаптации возникает ряд трудностей: пространственная разобщенность, возникающая, когда близкие решения, генерируемые метаэвристикой в непрерывном пространстве, не преобразуются в близкие решения в дискретном пространстве; параметры по умолчанию, найденные для непрерывной метаэвристики, не всегда оптимальны для бинарной метаэвристики [6].

Предметом нашего исследования является метаэвристический алгоритм стаи ласточек (АСЛ). Алгоритм основан на поведенческих особенностях стаи ласточек. Он имеет некоторые общие черты с алгоритмом роящихся частиц (АРЧ) [7], но есть и отличия. В АСЛ популяция делится на субпопуляции, в которых есть свои частицы-лидеры или лучшие решения. Скорость частиц обновляется, как в АРЧ, но в обновлении учитывается позиция частицы-лидеры субпопуляции. Существенным отличием является наличие в АСЛ случайно сгенерированных решений, что позволяет АСЛ успешно осуществлять процесс диверсификации и успешнее преодолевать локальные оптимумы. Еще одним преимуществом АСЛ является тот факт, что во время одной итерации не изменяют свое положение частицы-лидеры. По этой причине снижается вычислительная сложность алгоритма, по сравнению с другими метаэвристиками, во время итерации которых изменяется положение всех частиц, как например АРЧ.

АСЛ доказал свою высокую эффективность при поиске оптимума мультимодальных функций. Алгоритм был протестирован на 19 функциях, показав высокую скорость сходимости, редкое застревание в точках локальных экстремумов и быстрое перемещение на участках со слабым изменением целевой функции. Результаты сравнивались со стандартным АРЧ, алгоритмом рыб и десятью различными модификациями АРЧ [8].

Адаптированная дискретная версия АСЛ использовалась авторами [9, 10] для решения задач комбинаторной оптимизации и по утверждению авторов оказалась более эффективной по сравнению с другими протестированными алгоритмами. В [11] описана бинарная версия АСЛ, выполненная с помощью разработанной авторами операции MERGE. Результаты экспериментов, выполненные на 30 наборах данных, показали перспективность предлагаемого метода для отбора признаков.

Метод на основе обертки ищет оптимальное подмножество признаков, адаптированное к конкретному классификатору и набору данных. В нашем исследовании используются два различных метода классификации: метрический – k-NN [12] и основанный на правилах – нечеткий классификатор [13, 14]. Эти классификаторы были выбраны потому, что они широко используются в машинном обучении, и, самое главное, решение каждого из них может быть интерпретируемо. В k-NN выбор решения обосновывается через прецеденты, в нечетком классификаторе – посредством лингвистического правила, нечеткие термы которого можно интерпретировать как нечеткие величины, например, очень маленькие, маленькие, средние, большие, очень большие [15, 16].

Основная цель этой статьи – исследовать методы бинаризации метаэвристического алгоритма стаи ласточек для решения задач отбора признаков по методу обертки.

Метод обертки включает в себя два основных компонента: собственно метод отбора признаков и классификатор, который оценивает эффективность отобранных признаков. Предметом исследования в нашей статье является метод бинаризации АСЛ, классификатор в нашем исследовании играет вспомогательную роль и не является предметом исследования.

2. БЛИЗКИЕ РАБОТЫ

Принято выделять две основные группы методов бинаризации. Первая группа получила название “поэтапная бинаризация”. Методы этой группы позволяют работать с непрерывными метаэвристиками без модификации их операторов; здесь на каждой итерации вещественные векторы решений преобразуются в двоичные значения, используя заданные правила бинаризации. Вторая группа методов основана на введении оператора, выполняющая преобразование из непрерывного пространства поиска в бинарное пространство.

2.1. Поэтапная бинаризация

Метод ближайшего целого – простейшая одноэтапная процедура бинаризации, которая состоит в присвоении каждому элементу бинарного решения b ближайшего целого числа (0 или 1), полученного путем округления элемента непрерывного решения x по формуле:

$b = \left\lfloor {\left| {x\bmod 2} \right|} \right\rfloor .$

Авторы [17] использовали этот метод для бинаризации алгоритма дифференциальной эволюции. В работе [18] указанный метод применялся для бинаризации непрерывного алгоритма светлячков.

В двухэтапном методе бинаризация выполняется в два этапа, на этапе нормализации непрерывное решение ${{\Re }^{N}}$ трансформируется в решение [0, 1]N, на втором этапе по заранее определенному правилу выполняется преобразование решения [0, 1]N в двоичное представление {0, 1}N [19]. В рамках этого метода рассмотрим метод трансформационных функций и метод угловой модуляции.

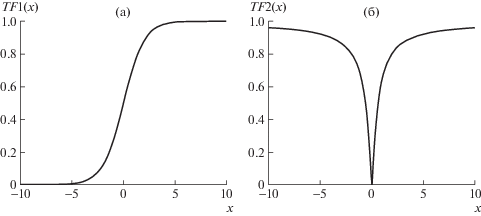
Метод трансформационных функций основывается на идее преобразования непрерывного решения к бинарному виду с помощью некоторой трансформационной функции, которая определяет вероятность изменения отдельной позиции решения и формирует промежуточное решение [0, 1]N. Различают два типа трансформационных функций: S-образные и V-образные. На рисунке 1 представлены графики типичных представителей этих функций, S-образная функция описана формулой:

$TF1(x) = \frac{1}{{1 + {{e}^{{ - x}}}}},$
V-образная функция задается выражением:

$TF2(x) = \left| {\frac{2}{\pi }\arctan \left( {\frac{\pi }{2}x} \right)} \right|.$
Рис. 1.

Трансформационные функции: (a) S-образная, (б) V-образная.

В [20] предложена линейная функция:

$L(x) = \frac{{x - {{R}_{{\min }}}}}{{{{R}_{{\max }}} - {{R}_{{\min }}}}},$
где [Rmin, Rmax] – диапазон изменения действительной переменной x.

На втором этапе промежуточное решение, полученное на предыдущем этапе, по заданному правилу преобразуется в бинарное решение. В [22] для S-образной функции приведено правило бинаризации следующего вида:

$b = \left\{ \begin{gathered} 1\quad {\text{если}}\quad rand{\text{ }} < TF1(x) \hfill \\ 0\quad {\text{иначе}} \hfill \\ \end{gathered} \right..$

Для линейной функции авторы [7] вводят аналогичное правило:

$b = \left\{ \begin{gathered} 1\quad {\text{если}}\quad rand{\text{ }} < L(x) \hfill \\ 0\quad {\text{иначе}} \hfill \\ \end{gathered} \right..$

Авторы [23] вместо случайно сгенерированного числа rand используют константу:

$\begin{gathered} b = \left\{ \begin{gathered} 1\quad {\text{если}}\quad L(x) > 0.5 \hfill \\ 0\quad {\text{иначе}} \hfill \\ \end{gathered} \right.. \hfill \\ \hfill \\ \end{gathered} $

В [23, 24] для V-образной функции предложено правило:

$b(t + 1)\, = \,\left\{ \begin{gathered} not(b(t))\quad {\text{если}}\quad rand\, < \,TF2(x(t + 1)) \hfill \\ b(t)\quad {\text{если}}\quad rand{\text{ }} \geqslant TF2(x(t + 1)) \hfill \\ \end{gathered} \right..$
S-образные и V-образные функции трансформации были успешно применены для бинаризации метаэвристических алгоритмов серого волка [25], летучей мыши [26], стрекозы [27, 28], бабочки [29], дрозофилы [30], роящихся частиц [31, 32], гравитационного поиска [23, 24, 33].

Метод угловой модуляции на первом этапе использует тригонометрическую функцию с четырьмя параметрами [22, 34]:

$g(x) = \sin \left( {2\pi \left( {x - {{a}_{1}}} \right){{a}_{2}}\cos \left( {2\pi \left( {x - {{a}_{1}}} \right){{a}_{3}}} \right)} \right) + {{a}_{4}}.$

Правило бинаризации имеет вид:

$b = \left\{ \begin{gathered} 1\quad {\text{если }}g(x) > 0 \hfill \\ 0\quad {\text{иначе}} \hfill \\ \end{gathered} \right..$

Метод угловой модуляции применялся для бинаризации алгоритма искусственной пчелиной колонии [35], роящихся частиц [36], опыления цветов [34], дифференциальной эволюции [37].

В [22] отмечается, что эффективность трансформационных и тригонометрических функций все еще неясна и не изучена, предстоит понять, зависит ли эффективность этих функций от используемого алгоритма и решаемой проблемы.

2.2. Переопределение исходных операторов метаэвристики

Метод модифицированных алгебраических операций. В этом методе арифметические операции заменяют на их логические аналоги. Вместо сложения используют логическое “или” (OR), вместо умножения – логическое “и” (AND), а вместо вычитания – исключающее “или” (XOR). Таким образом, пространство поиска изменяется на бинарное, однако исходная идея алгоритма, формально, сохраняется.

Данный метод имеет несколько недостатков, из-за которых он не может быть применен к некоторым метаэвристическим алгоритмам. Первый недостаток заключается в невозможности применения этого метода к алгоритмам, которые используют какие-либо операции кроме сложения, вычитания, умножения и деления. Второй недостаток связан с тем, что многие метаэвристические алгоритмы используют вещественные коэффициенты. При переходе к бинарным векторам, эти коэффициенты должны быть тоже некоторым образом преобразованы или исключены из алгоритма. Так, в [38] при модификации алгоритма PSO, авторы отказались от использования коэффициента инерции, а вместо коэффициентов скорости использовали случайные бинарные вектора.

Метод модифицированных алгебраических операций был применен для бинаризации метаэвристических алгоритмов кошек [39], пчел [40], паукообразных обезьян [41, 42].

Квантовый подход. Двоичная природа принципов квантовых вычислений позволяет применять их для решения проблемы бинаризации. Наименьшая информация, которую можно сохранить в Q-бите, представлена следующим образом:

$\left[ {\begin{array}{*{20}{c}} \alpha \\ \beta \end{array}} \right];\quad \forall \alpha ,\beta \in \left[ {0,\;1} \right],$
${{\left| \alpha \right|}^{2}} + {{\left| \beta \right|}^{2}} = 1.$

В приведенном выше уравнении |α|2 и |β|2 означают вероятности перехода Q-бита в состояние “0” и “1” соответственно. Большее значение |α|2 определяет вероятность того, что Q-бит окажется в состоянии “0”, |β|2 – в состоянии “1”. Таким образом, Q-бит подчиняется принципу линейной суперпозиции:

$\left| \varphi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle .$

Строка из NQ-битов задается следующим образом:

$\left[ {\left. {\begin{array}{*{20}{c}} {{{\alpha }_{1}}} \\ {{{\beta }_{1}}} \end{array}} \right|\left. {\begin{array}{*{20}{c}} {{{\alpha }_{2}}} \\ {{{\beta }_{2}}} \end{array}} \right|\begin{array}{*{20}{c}} \ldots \\ \ldots \end{array}\left| {\begin{array}{*{20}{c}} {{{\alpha }_{N}}} \\ {{{\beta }_{N}}} \end{array}} \right.} \right],$
${{\left| {{{\alpha }_{i}}} \right|}^{2}} + {{\left| {{{\beta }_{i}}} \right|}^{2}} = 1,\quad i = 1,\;2,\; \ldots ,\;N.$
Q-бит имеет равные шансы принять состояние “0” или “1” при α = β = $1{\text{/}}\sqrt 2 $. В этом случае, принцип линейной суперпозиции приводит к
$\left| \varphi \right\rangle = \sum\limits_{k = 1}^{{{2}^{N}}} {\frac{1}{{\sqrt {{{2}^{N}}} }}\left| {{{X}_{k}}} \right\rangle } ,$
где Xk описывает состояние k двоичной строкой (x1, x2, …, xN) [43].

Итоговое бинарное решение формируется следующим образом: для каждой j-й позиции генерируется случайное число rand в диапазоне [0, 1] и сравнивается с βj; если rand < βj, то xj = 1, в противном случае xj = 0.

Состояние Q-бита может быть изменено квантовым вентилем (Q-вентилем). Q-вентиль является обратимым и может быть представлен как унитарный оператор U, работающий на базисных Q-битных состояниях и удовлетворяющий условию U+U = UU+, где U+ эрмитово сопряжение U. Существует несколько Q-вентилей, таких как NOT-вентиль, управляемый NOT-вентиль, вентиль вращения, вентиль Адамара. Система из N Q-битов может содержать информацию о 2N состояниях. Однако процесс измерения приведет к мгновенному выбору одного из этих состояний. Такое явление определяется волновой функцией ψ. Коэффициенты ci называются амплитудами вероятности, а |ci|2 задает вероятность перехода $\left| \psi \right\rangle $ в состояние $\left| \varphi \right\rangle $, если будет проведено измерение, причем $\sum\nolimits_i {{{{\left| {{{c}_{i}}} \right|}}^{2}}} = 1$ [44].

В [45] проблемы выбора и оптимизации параметров для нейронных сетей были решены с использованием метода оптимизации роя квантовых частиц (PSO), при этом функции были представлены в виде квантовых битов (Q-битов). Принципы квантовой суперпозиции и квантовой вероятности использовались для ускорения поиска оптимального набора признаков.

Исследователи в [46] предложили гибридный алгоритм интеллекта роя, основанный на квантовых вычислениях и комбинации алгоритма светлячков и PSO для выбора признаков. Квантовые вычисления обеспечили хороший компромисс между интенсификацией и диверсификацией поиска, в то время как комбинация алгоритма светлячка и PSO позволила эффективно исследовать сгенерированные подмножества признаков. Чтобы оценить актуальность этих подмножеств, была использована теория приблизительных множеств.

Хан и Ким в [47] описали квантовый эволюционный алгоритм, основанный на концепции и принципах квантовых вычислений. Алгоритм представляет решение в виде Q-битовой хромосомы и использует квантовый оператор для его обновления, этот оператор является модифицированной версией оператора логического вращения.

В [48] для решения задач бинарной оптимизации был разработан алгоритм квантового гравитационного поиска путем добавления в базовую структуру процедуры гравитационного поиска следующих элементов квантовых вычислений: квантовый бит, квантовые измерения, суперпозиция и модифицированные операторы квантового вращения.

3. ПОСТАНОВКА ЗАДАЧИ

В основе классификации лежит таблица наблюдений:

$T = \{ {{t}_{1}},{{t}_{2}}, \ldots ,{{t}_{M}}\} ,$
где tk = (xk, ck) – k-й помеченный экземпляр таблицы наблюдений, xk = (x1, x2, …, xn) – вектор значений входных переменных, ck – метка класса, M – число наблюдений, n – число входных переменных.

Задача классификации – сопоставить каждому новому непомеченному экземпляру наиболее подходящий класс из множества классов c = {c1, c2, …, cK}, K – количество классов.

Задача отбора признаков формулируется следующим образом: на заданном множестве признаков найти такое подмножество, которое не вызывает значительного снижения точности классификации или даже увеличивает ее при уменьшении количества признаков. Решение представлено в виде вектора s = (s1, s2, …, sn), где si = 0 означает, что i-й признак исключен из классификации, а si = 1 означает, что i-й признак используется классификатором. Эффективность отобранных признаков оценивается по ошибке классификации. Ошибка классификации – это количество неправильно классифицированных экземпляров по отношению к общему количеству экземпляров.

Задача алгоритма бинарной оптимизации – поиск подмножества признаков, на которых ошибка классификации будет минимальной.

4. КЛАССИФИКАТОРЫ

4.1. Классификатор на основе k-ближайших соседей

Алгоритм на основе k-ближайших соседей является одним из простых и наиболее часто используемых классификаторов. У алгоритма есть только один параметр k, который указывает количество соседей, используемых для определения метки класса для нового экземпляра данных. Алгоритм не требует этапа обучения и настройки параметров.

Пошаговое определение алгоритма приведено ниже.

1. Определить значение k.

2. Сохранить таблицу наблюдений T.

3. Для каждого нового экземпляра данных x:

3.1. Рассчитать расстояния от x до каждого экземпляра T.

3.2. Выбрать k ближайших экземпляров.

3.3. Определить наиболее часто встречаемую метку класса c среди выбранных экземпляров.

3.4. Присвоить метку c экземпляру x.

В нашей статье значение k выбрано равным 5.

4.2. Нечеткий классификатор

На основе таблицы наблюдений на области определения каждой входной переменной формируются нечеткие термы. Исходя из разбиения переменных на нечеткие термы, формируется база правил нечеткого классификатора. Правило нечеткого классификатора имеет вид [33, 42, 49]:

$\begin{gathered} {{R}_{i}}:{\text{IF}}{{s}_{1}} \wedge \,{{x}_{1}} = {{A}_{{1i}}}\,{\text{AND}}\,{{s}_{2}}~ \wedge \,{{x}_{2}} = \\ = {{A}_{{2i}}}\,{\text{AND }} \ldots {\text{ AND }}{{s}_{n}} \wedge \,~{{x}_{n}} = {{A}_{{ni}}}\,{\text{ТО}}\,\,{\text{class}} = {{c}_{j}}, \\ j = {\text{ }}1, \ldots ,R, \\ \end{gathered} $
где Aki – нечеткий терм, характеризующий k-й признак в i-м правиле (k = 1, …, n), R – число правил.

На заданной таблице наблюдений метка класса определяется следующим образом:

где ${{\mu }_{{{{A}_{k}}_{i}}}}({{x}_{{pk}}})$ – значение функции принадлежности нечеткого терма Aki в точке xk.

Мера точности классификации задается как отношение количества правильно определенных меток классов к общему количеству экземпляров:

$Acc({\mathbf{\theta }},{\mathbf{S}}) = \frac{{\sum\limits_{p = 1}^Z {\left\{ \begin{gathered} 1,\quad {\text{if}}\quad {{c}_{p}} = \arg \mathop {\max }\limits_{1 \leqslant j \leqslant m} {{f}_{j}}\left( {{{{\mathbf{x}}}_{p}};{\mathbf{\theta }},S} \right) \hfill \\ {\text{0,}}\quad {\text{otherwise}} \hfill \\ \end{gathered} \right.} }}{Z}$

Ошибка классификации определяется как:

$Error = 1 - Acc\left( {{\mathbf{\theta }},{\mathbf{S}}} \right).$

5. БИНАРИЗАЦИЯ АЛГОРИТМА СТАИ ЛАСТОЧЕК

5.1. Алгоритм стаи ласточек для непрерывного пространства поиска

Алгоритм стаи ласточек основан на поведении стаи ласточек при длительных перелетах и поиске пищи [8]. Основная идея алгоритма состоит в разделении всех частиц на три вида: частицы-лидеры, частицы-исследователи, бесцельные частицы. Роль каждой частицы зависит от ее положения в пространстве.

Частицы-лидеры делятся на глобального лидера и локальных лидеров. Глобальным лидером является частица с самым лучшим положением в исследуемом пространстве. Локальные лидеры – это l следующих за глобальным лидером частиц. Бесцельные частицы – это k худших частиц популяции. Остальные частицы – исследователи.

Во время выполнения очередной итерации перемещаются только исследователи и бесцельные частицы. После каждой итерации роли частиц перераспределяются в зависимости от их нового положения. Таким образом, бесцельные частицы и исследователи могут становиться лидерами, а лидеры могут становятся исследователями или бесцельными частицами.

Перемещение исследователя определяют положение глобального лидера, положение ближайшего локального лидера и лучшее положение этой частицы за все время оптимизации. Формулы движения исследователя приведены ниже:

${{{\mathbf{\theta }}}_{{{{e}_{{i + 1}}}}}} = {{{\mathbf{\theta }}}_{{{{e}_{i}}}}} + {{{\mathbf{V}}}_{{i + 1}}},$
${{{\mathbf{V}}}_{{i + 1}}} = {\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}} + {\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}},$
$\begin{gathered} {\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{rand}}(0;\;1) \times ({{{\mathbf{\theta }}}_{{{{e}_{{best}}}}}} - {{{\mathbf{\theta }}}_{{{{e}_{i}}}}}) + \\ + \;{\text{rand}}(0;\;1) \times ({\mathbf{HL}} - {{{\mathbf{\theta }}}_{{{{e}_{i}}}}}), \\ \end{gathered} $
$\begin{gathered} {\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{rand}}(0;\;1) \times ({{{\mathbf{\theta }}}_{{{{e}_{{best}}}}}} - {{{\mathbf{\theta }}}_{{{{e}_{i}}}}}) + \\ + \;{\text{rand}}(0;\;1) \times ({\mathbf{L}}{{{\mathbf{L}}}_{i}} - {{{\mathbf{\theta }}}_{{{{e}_{i}}}}}), \\ \end{gathered} $
где ${{{\mathbf{\theta }}}_{{{{e}_{i}}}}}$ – положение i-й частицы-исследователя, HL – положение глобального лидера, ${\mathbf{L}}{{{\mathbf{L}}}_{i}}$ – положение локального лидера, наименее удаленного от i-й частицы исследователя, ${{{\mathbf{\theta }}}_{{{{e}_{{best}}}}}}$ – лучшее положение i-й частицы-исследователя, V вектор скорости частицы, VHL – вектор скорости движения частицы к глобальному лидеру, VLL – вектор скорости движения частицы к ближайшему локальному лидеру, rand(0; 1) – случайное число из диапазона [0, 1].

Бесцельные частицы перемещаются случайным образом в пространстве поиска. Для этого используются формулы:

${{{\mathbf{\theta }}}_{{{{o}_{{i + 1}}}}}} = {\text{rand}}(0.5;\;2) \times {\mathbf{VSS}},$
${\mathbf{VSS}} = \frac{{\sum\limits_{i = 1}^{N - k} {{{{\mathbf{\theta }}}_{i}}} }}{{N - k}},$
где ${{{\mathbf{\theta }}}_{{{{o}_{i}}}}}$– положение i-й бесцельной частицы, ${{{\mathbf{\theta }}}_{i}}$ – положение i-й частицы популяции, N – количество всех частиц в популяции, k – количество бесцельных частиц.

5.2. Метод модифицированных алгебраических операций

Обозначим логические операции следующим образом: $ \vee $ – логическое “или”, $ \wedge $ – логическое “и”, $ \oplus $ – исключающее “или”. После модификации АСЛ, формулы перемещения частицы исследователя будут выглядеть следующим образом:

${{{\mathbf{S}}}_{{{{e}_{{i + 1}}}}}} = {{{\mathbf{S}}}_{{{{e}_{i}}}}} \vee {{{\mathbf{V}}}_{{i + 1}}},$
${{{\mathbf{V}}}_{{i + 1}}} = {\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}} \vee {\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}},$
$\begin{gathered} {\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{randbinvector}} \wedge ({{{\mathbf{S}}}_{{{{e}_{{best}}}}}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}}) \vee \\ \vee \;{\text{randbinvector}} \wedge ({\mathbf{HL}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}}), \\ \end{gathered} $
$\begin{gathered} {\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{randbinvector}} \wedge ({{{\mathbf{S}}}_{{{{e}_{{best}}}}}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}}) \vee \\ \vee \;{\text{randbinvector}} \wedge ({\mathbf{L}}{{{\mathbf{L}}}_{i}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}}), \\ \end{gathered} $
где ${{{\mathbf{S}}}_{{{{e}_{i}}}}}$ – положение i-й частицы-исследователя, HL – положение глобального лидера, ${\mathbf{L}}{{{\mathbf{L}}}_{i}}$ – положение ближайшего до ${{{\mathbf{S}}}_{{{{e}_{i}}}}}$ локального лидера, ${{{\mathbf{S}}}_{{{{e}_{{best}}}}}}$ – лучшее положение ${{{\mathbf{S}}}_{{{{e}_{i}}}}}$, ${{{\mathbf{V}}}_{i}}$ – вектор скорости ${{{\mathbf{S}}}_{{{{e}_{i}}}}}$, VHL – вектор скорости частицы относительно HL, VLL – вектор скорости частицы относительно LL, randbinvector – случайный бинарный вектор.

Изменение положения бесцельной частицы будет выглядеть следующим образом:

${{{\mathbf{S}}}_{{{{o}_{{i + 1}}}}}} = {\text{randbinvector}}$

5.3. Метод бинаризации, основанный на операции MERGE

Для решения проблемы отбора признаков нами введена авторская операция MERGE, объединяющая два бинарных вектора, путем сохранения совпадающих элементов и случайного выбора из несовпадающих элементов [10]. Определение значения Ci результирующего вектора C из соответствующих элементов векторов A и B может быть представлено следующим образом:

$\begin{gathered} {\text{MERGE(}}{{A}_{i}},{{B}_{i}}{\text{,}}{{С}_{i}}{\text{) = }} \\ {\text{ = }}\;\left\{ \begin{gathered} {{С}_{i}} = {{A}_{i}} = {{B}_{i}},\quad {\text{если }}{{A}_{i}} = {{B}_{i}} \hfill \\ {{С}_{i}} = {{A}_{i}},\quad {\text{если}}\quad {{A}_{i}} \ne {{B}_{i}}\quad {\text{и}}\quad rand(0;1) \leqslant 0.5 \hfill \\ {{С}_{i}} = {{B}_{i}},\quad {\text{если}}\quad {{A}_{i}} \ne {{B}_{i}}\quad {\text{и}}\quad rand(0;1) > 0.5 \hfill \\ \end{gathered} \right., \\ \end{gathered} $
где Ai – i-й элемент вектора A, Bi – i-й элемент вектора B, Ci – i-й элемент вектора C, rand(0; 1) – случайное число из диапазона [0, 1].

Метод бинаризации, основанный на операции MERGE, очень похож на метод модифицированных алгебраических операций, отличие состоит только в том, что все оригинальные арифметические операции необходимо заменить на операцию MERGE. Также, этот метод накладывает те же ограничения, что и метод модифицированных алгебраических операций.

После модификации АСЛ, формулы перемещения частицы исследователя будут выглядеть следующим образом:

${{{\mathbf{S}}}_{{{{e}_{{i + 1}}}}}} = {\text{merge}}({{{\mathbf{S}}}_{{{{e}_{i}}}}},{{{\mathbf{V}}}_{{i + 1}}}),$
${{{\mathbf{V}}}_{{i + 1}}} = {\text{merge}}({\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}},{\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}}),$
$\begin{gathered} {\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{merge}}({\text{merge}}({\text{randbinvector}}, \\ {\text{merge}}({{{\mathbf{S}}}_{{{{e}_{{best}}}}}},{{{\mathbf{S}}}_{{{{e}_{i}}}}}),{\text{merge}}({\text{randbinvector}}, \\ {\text{merge}}({\mathbf{HL}},{{{\mathbf{S}}}_{{{{e}_{i}}}}}))), \\ \end{gathered} $
$\begin{gathered} {\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{merge}}({\text{merge}}({\text{randbinvector}}, \\ {\text{merge}}({{{\mathbf{S}}}_{{{{e}_{{best}}}}}},{{{\mathbf{S}}}_{{{{e}_{i}}}}}), \\ {\text{merge}}({\text{randbinvector}},{\text{merge}}({\mathbf{L}}{{{\mathbf{L}}}_{i}},{{{\mathbf{S}}}_{{{{e}_{i}}}}}))). \\ \end{gathered} $

Изменение положения бесцельной частицы будет выглядеть следующим образом:

${{{\mathbf{S}}}_{{{{o}_{{i + 1}}}}}} = {\text{randbinvector}}$

5.4. Гибридный метод бинаризации, основанный на методе модифицированных алгебраических операций и операции MERGE

Это авторский метод, он похож на метод модифицированных алгебраических операций, отличие состоит только в том, что операцию сложения нужно заменить на операцию MERGE. Также, этот метод накладывает те же ограничения, что и метод модифицированных алгебраических операций.

После модификации АСЛ, формулы перемещения частицы исследователя будут выглядеть следующим образом:

${{{\mathbf{S}}}_{{{{e}_{{i + 1}}}}}} = {\text{merge}}({{{\mathbf{S}}}_{{{{e}_{i}}}}},{{{\mathbf{V}}}_{{i + 1}}}),$
${{{\mathbf{V}}}_{{i + 1}}} = {\text{merge}}({\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}},{\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}}),$
$\begin{gathered} {\mathbf{VH}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{merge}}({\text{randbinvector}} \wedge \\ \wedge \;({{{\mathbf{S}}}_{{{{e}_{{best}}}}}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}}),{\text{randbinvector}} \wedge ({\mathbf{HL}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}})), \\ \end{gathered} $
$\begin{gathered} {\mathbf{VL}}{{{\mathbf{L}}}_{{i + 1}}} = {\text{merge}}({\text{randbinvector}} \wedge \\ \wedge \;({{{\mathbf{S}}}_{{{{e}_{{best}}}}}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}}),{\text{randbinvector}} \wedge ({\mathbf{L}}{{{\mathbf{L}}}_{i}} \oplus {{{\mathbf{S}}}_{{{{e}_{i}}}}})). \\ \end{gathered} $

Изменение положения бесцельной частицы будет выглядеть следующим образом:

${{{\mathbf{S}}}_{{{{o}_{{i + 1}}}}}} = {\text{randbinvector}}$

5.5. Метод трансформационных функций

Для бинаризации использованы три функции трансформации. Одна S-образная, которая описывается следующим образом:

${{F}_{S}}({{{v}}_{{ij}}}) = \frac{1}{{(1 + {{e}^{{ - {{{v}}_{{ij}}}}}})}}$
а также две V-образные:

${{F}_{{V1}}}({{{v}}_{{ij}}}) = \left| {\tanh ({{{v}}_{{ij}}})} \right|,$
${{F}_{{{\text{V}}2}}}({{{v}}_{{ij}}}) = \left| {\frac{{{{{v}}_{{ij}}}}}{{\sqrt {{\text{1 + }}\,{v}_{{ij}}^{2}} }}} \right|.$

Для трансформации вещественного значения в бинарное будет использоваться следующее правило:

$\begin{gathered} {\text{IF}}\,{\text{rand(0;}}\;{\text{1)}} < F{\text{(}}{{{v}}_{{ij}}}{\text{),}} \\ {\text{THEN}}\,{{{\text{s}}}_{{ij}}}{\text{ = 1,}}\quad {\text{ELSE}}\,{{{\text{s}}}_{{ij}}} = {\text{0}}{\text{.}} \\ \end{gathered} $

6. ОПИСАНИЕ ЭКСПЕРИМЕНТА

Вычислительный эксперимент проведен на наборах данных из репозитория KEEL (https:// sci2s.ugr.es/keel/datasets.php). Информация о наборах данных представлена в табл. 1.

Таблица 1.

Описание наборов данных

Набор данных Количество признаков Количество классов Количество экземпляров
australian 14 2 890
balance 4 3 625
banana 2 2 5300
bands 19 2 365
bupa 6 2 345
cleveland 13 5 297
coil2000 85 2 9822
contraceptive 9 3 1473
dermatology 34 6 358
ecoli 7 8 336
glass 9 7 214
haberman 3 2 306
heart 13 2 270
hepatitis 19 2 80
ionosphere 33 2 351
iris 4 3 150
magic 10 2 19 020
newthyroid 5 3 215
optdigits 64 10 5620
page-blocks 10 5 5472
penbased 16 10 10 992
phoneme 5 2 5404
pima 8 2 768
ring 20 2 7400
satimage 36 7 6435
segment 19 7 2310
sonar 60 2 208
spambase 57 2 4597
spectfheart 44 2 267
tae 5 3 151
texture 40 11 5500
thyroid 21 3 7200
titanic 3 2 2201
twonorm 20 2 7400
vehicle 18 4 846
wdbc 30 2 569
wine 13 3 178
wisconsin 9 2 683

Все наборы данных были разделены с помощью десятикратной кросс-валидации. В качестве классификаторов использовались нечеткий классификатор и классификатор kNN с 5 соседями (5NN). В качестве алгоритма отбора признаков использовался АСЛ, бинаризованный шестью различными способами, представленными в табл. 2.

Таблица 2.

Обозначение методов бинаризации

Метод Обозначение
Без отбора признаков NoSelect
Метод, основанный на операции MERGE Operations
Метод модифицированных алгебраических операций Merge
Гибридный метод, основанный на методе модифицированных алгебраических операций и операции MERGE OpMerge
Метод трансформационных функций с функцией трансформации ${{F}_{S}}$ Sigm
Метод трансформационных функций с функцией трансформации ${{F}_{{{{V}_{1}}}}}$ Tanh
Метод трансформационных функций с функцией трансформации ${{F}_{{{{V}_{2}}}}}$ VShaped

Параметры алгоритма всегда были следующие: количество всех частиц популяции – 40, количество локальных лидеров – 3, количество бесцельных частиц – 6, количество итераций – 300. Для каждого набора данных эксперимент повторялся 30 раз, после чего результаты усреднялись.

При проведении эксперимента оценивалось два параметра – точность классификации на тестовых данных и количество признаков, оставленных алгоритмом. Программный код эксперимента и инструкции по воспроизведению тестов опубликованы на платформе GitLab [50].

Результаты эксперимента для нечеткого классификатора представлены в табл. П1 и П2, для классификатора 5NN – в табл. П3 и П4.

Таблица 3.

Ранги методов бинаризации для ошибки классификации

  NoSelect Operations Merge OpMerge Sigm Tanh VShaped
Нечеткий классификатор 6.08 4.26 4.04 3.34 3.57 3.54 3.16
5NN 6.82 5.03 4.24 3.32 2.78 3.07 2.76
Таблица 4.

Ранги методов бинаризации для количества признаков

  Operations Merge OpMerge Sigm Tanh VShaped
Нечеткий классификатор 3.82 4.71 2.49 3.28 3.41 3.30
5NN 3.87 4.74 2.35 2.87 3.75 3.42

Для статистической оценки предложенных методов бинаризации использовался двухфакторный дисперсионный анализ Фридмана для связных выборок (уровень значимости равен 0.05). В табл. 3 и 4 приведены ранги каждого из методов бинаризации для каждого классификатора, а в табл. 5 соответствующие им p-значения.

Таблица 5.

p-значения

  Ошибка классификации Количество признаков
Нечеткий классификатор 4.66e-11 1.4e-06
5NN 1.49e-27 4.82e-8

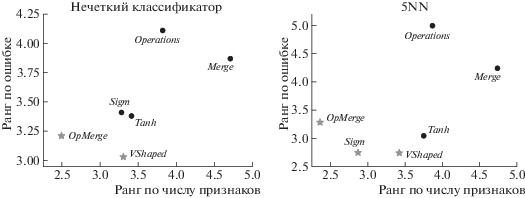
Все p-значения меньше уровня значимости 0.05, значит результаты являются статистически значимыми и отвергаются нулевые гипотезы о равенстве ошибок классификации и числа отобранных признаков для исследуемых методов бинаризации. На основе полученных результатов были построены графики в координатах ошибка-число_признаков и определен Парето-фронт.

На рис. 2 звездочками отмечены элементы, входящие в Парето-множество. Используя один из принципов оптимальности, а именно, принцип идеальной точки можно определить лучшее решение из Парето-множества. Координаты идеальной точки соответствуют минимальным рангам и равны (1, 1). Лучшей является альтернатива, максимально приближенная к идеальной точке. В качестве меры близости можно использовать евклидово расстояние. Для нечеткого классификатора и метода бинаризации OpMerge расстояние до идеальной точки равно:

$\sqrt {{{{\left( {3.21 - 1} \right)}}^{2}} + {{{\left( {2.49 - 1} \right)}}^{2}}} = 2.67,$
Рис. 2.

Графическое представление результатов бинаризации.

a для нечеткого классификатора и метода бинаризации VShaped расстояние равно:

$\sqrt {{{{(3.03 - 1)}}^{2}} + {{{(3.30 - 1)}}^{2}}} = 3.07.$

В этом случае лучшей является альтернатива OpMerge.

Для классификатора 5NN и метода бинаризации OpMerge расстояние до идеальной точки равно 2.64, для метода бинаризации VShaped – 2.98, для метода бинаризации Sigm – 2.56. В случае классификатора 5NN альтернатива OpMerge лишь немного уступает альтернативе Sigm.

Если рассматривать ошибку классификации и число отобранных признаков как отдельные критерии, то гибридный метод OpMerge позволил найти минимальное подмножество признаков для обоих классификаторов, однако лучшие результаты по точности классификации показал метод VShaped.

7. ЗАКЛЮЧЕНИЕ

В данной работе было рассмотрено шесть подходов к бинаризации алгоритма стаи ласточек для решения задачи отбора признаков при классификации 38 наборов данных. Лучшие способности к отбору признаков показал гибридный метод, основанный на методе модифицированных алгебраических операций и введенной нами операции MERGE. Данный метод бинаризации рекомендуется к использованию, если приоритетной задачей является максимальное упрощение получаемой модели. Наибольшую точность классификации показал метод с использованием V-образной функции трансформации. Этот метод рекомендуется к использованию, если приоритетом является точность классификации.

В дальнейших исследованиях предполагается проверить предложенные методы бинаризации на других классификаторах, а также использовать квантовые методы бинаризации и другие трансформационные функции с другими правилами бинаризации.

Список литературы

  1. Bolon-Canedo V., Sanchez-Marono N., Alonso-Betanzos A. Feature Selection for High-Dimensional Data. Heidelberg: Springer, 2015. 163 p.

  2. Qi Z., Wang H., He T., Li J., Gao H. FRIEND: Feature selection on inconsistent data // Neurocomputing. 2020. V. 391. P. 52–64.

  3. Sha Z.-C., Liu1 Z.-M., Ma C., Chen J. Feature selection for multi-label classification by maximizing full-dimensional conditional mutual information // Applied Intelligence. 2021. V. 51. P. 326–340.

  4. Luke S. Essentials of Metaheuristics [Электронный ресурс]. Режим доступа: https://cs.gmu.edu/~sean/book/metaheuristics/

  5. Boussaid I., Lepagnot J., Siarry P. A Survey on Optimization Metaheuristics // Inf. Sci. 2013. V. 237. P. 82–117.

  6. Garcia J., Crawford B., Soto R., Astorga G. A clustering algorithm applied to the binarization of Swarm intelligence continuous metaheuristics // Swarm and Evolutionary Computation. 2019. V. 44. P. 646–664.

  7. Poli R., Kennedy J., Blackwell T. Particle swarm optimization // Swarm Intelligence. 2007. V. 1. P. 33–57.

  8. Neshat M., Sepidnam G., Sargolzaei M. Swallow swarm optimization algorithm: a new method to optimization // Neural Computing and Application. 2013. V. 23. P. 429–454.

  9. Bouzidi S., Riffi M.E., Bouzidi M., Moucouf M. The Discrete Swallow Swarm Optimization for Flow-Shop Scheduling Problem // Advances in Intelligent Systems and Computing. 2019. V. 915. P. 228–236.

  10. Bouzidi S., Riffi M.E. Discrete Swallow Swarm Optimization algorithm for Travelling Salesman Problem // Proceedings of the 2017 International Conference on Smart Digital Environment. 2017. P. 80–84.

  11. Hodashinsky I., Sarin K., Shelupanov A., Slezkin A. Feature selection based on swallow swarm optimization for fuzzy classification // Symmetry. 2019. V. 11. № 11. P. 1423.

  12. Cover T., Hart P. Nearest neighbor pattern classification // IEEE Transactions on Information Theory. 1967. V. 13. P. 21–27.

  13. Roh S.-Be., Pedrycz W., Ahn T.-C. A design of granular fuzzy classifier // Expert Systems with Applications. 2014. V. 41. P. 6786–6795.

  14. Mekh M.A., Hodashinsky I.A. Comparative analysis of differential evolution methods to optimize parameters of fuzzy classifiers // Journal of Computer and Systems Sciences International. 2017. V. 56. P. 616–626.

  15. Evsukoff A.G., Galichet S., de Lima B.S.L.P., Ebecken N.F.F. Design of interpretable fuzzy rule-based classifiers using spectral analysis with structure and parameters optimization // Fuzzy Sets and Systems. 2009. V. 160. P. 857–881.

  16. Hodashinsky I.A., Gorbunov I.V. Algorithms of the tradeoff between accuracy and complexity in the design of fuzzy approximators // Optoelectronics, Instrumentation and Data Processing. 2013. V. 49. P. 569–577.

  17. Jiang D., Peng C., Fan Z., Chen Y. Modified binary differential evolution for solving wind farm layout optimization problems // Proceedings of the IEEE Symposium on Computational Intelligence for Engineering Solutions (CIES). 2013. P. 23–28.

  18. Costa M.F.P., Rocha A.M.A.C., Francisco R.B., Fernandes E.M.G.P. Heuristic-based firefly algorithm for bound constrained nonlinear binary optimization // Advances in Operations Research. 2014. Article ID 215182.

  19. Crawford B. et al. Putting continuous metaheuristics to work in binary search spaces // Complexity. 2017. Article ID 8404231.

  20. Wang L., Wang X., Zhen F.J., Zhen L. A novel probability binary particle swarm optimization algorithm and its application // Journal of Software. 2008. V. 3. № 9. P. 28–35.

  21. Kennedy J., Eberhart R. A discrete binary version of the particle swarm algorithm // Proceedings of the IEEE International Conference on Computational Cybernetics and Simulation. 1997. P. 4104–4108.

  22. Dahi Z.A.E.M., Mezioud C., Draa A. Binary Bat Algorithm: On the Efficiency of Mapping Functions When Handling Binary Problems Using Continuous-variable-based Metaheuristics // IFIP Advances in Information and Communication Technology. V. 456. Cham: Springer, 2015. P. 3–14.

  23. Rashedi E., Nezamabadi-pour H., Saryazdi S. BGSA: binary gravitational search algorithm // Natural Computing. 2009. V. 9. № 3. P. 727–745.

  24. Mirhosseini M., Nezamabadi-pour H. BICA: a binary imperialist competitive algorithm and its application in CBIR systems // International Journal of Machine Learning and Cybernetics. 2018. V. 9. P. 2043–2057.

  25. Emary E., Zawbaa H.M., Hassanien A.E. Binary grey wolf optimization approaches for feature selection // Neurocomputing. 2016. V. 172. P. 371–381.

  26. Qasim O.S., Algamal Z.Y. Feature selection using different transfer functions for binary bat algorithm // International Journal of Mathematical, Engineering and Management Sciences. 2020. V. 5. № 4. P. 697–706.

  27. Sayed G.I., Tharwat A., Hassanien A.E. Chaotic dragonfly algorithm: an improved metaheuristic algorithm for feature selection // Applied Intelligence. 2019. V. 49. P. 188–205.

  28. Too J., Mirjalili S. A Hyper Learning Binary Dragonfly Algorithm for Feature Selection: A COVID-19 Case Study // Knowledge-Based Systems. 2021. V. 212. 106553.

  29. Arora S., Anand P. Binary Butterfly Optimization Approaches for Feature Selection // Expert Systems with Application. 2019. V. 116. P. 147–160.

  30. Zhang X. et al. Gaussian mutational chaotic fruit fly-built optimization and feature selection // Expert Systems with Application. 2020. V. 141. P. 112976.

  31. Ji B. et al. Bio-inspired feature selection: An improved binary particle swarm optimization approach // IEEE Access. 2020. V. 8. P. 85989–86002.

  32. Mirjalili S., Lewis A. S-shaped versus V-shaped transfer functions for binary Particle Swarm Optimization // Swarm and Evolutionary Computation. 2013. V. 9. P. 1–14.

  33. Bardamova M., Konev A., Hodashinsky I., Shelupanov A. A fuzzy classifier with feature selection based on the gravitational search algorithm // Symmetry. 2018. V. 10. № 11. P. 609.

  34. Dahi Z.A.E.M., Mezioud C., Draa A. On the efficiency of the binary flower pollination algorithm: Application on the antenna positioning problem // Applied Soft Computing. 2016. V. 47. P. 395–414.

  35. Yavuz G., Aydin D. Angle Modulated Artificial Bee Colony Algorithms for Feature Selection // Applied Computational Intelligence and Soft Computing. 2016. Article ID 9569161.

  36. Pampara G., Franken N., Engelbrecht A. Combining particle swarm optimisation with angle modulation to solve binary problems // Proceedings of the IEEE Congress on Evolutionary Computation, vol. 1. IEEE Press, Piscataway, NJ, 2005, P. 89–96.

  37. Pampara G., Engelbrecht A.P., Franken N. Binary differential evolution // Proceedings of the IEEE Congress on Evolutionary Computation (CEC’06). IEEE, 2006. P. 1873–1879.

  38. Yuan X., Nie H., Su A., Wang L., Yuan Y. An Improved Binary Particle Swarm Optimization for Unit Commitment Problem // Expert Systems with Application. 2009. V. 36. P. 8049–8055.

  39. Siqueira H., Figueiredo E., Macedo M., Santana C.J., Bastos-868 Filho C.J., Gokhale A.A. Boolean binary cat swarm optimization algorithm // 2018 IEEE Latin American Conference on 870 Computational Intelligence (LA-CCI). IEEE, 2018. P. 1–6.

  40. Kiran M.S., Gunduz M. XOR-Based Artificial Bee Colony Algorithm for Binary Optimization // Turkish Journal of Electrical Engineering and Computer Sciences. 2013. V. 21. P. 2307–2328.

  41. Singh U., Salgotra R., Rattan M. A Novel Binary Spider Monkey Optimization Algorithm for Thinning of Concentric Circular Antenna Arrays // IETE Journal of Research. 2016. V. 62. P. 736–744.

  42. Hodashinsky I.A., Nemirovich-Danchenko M.M., Samsonov S.S. Feature selection for fuzzy classifier using the spider monkey algorithm // Business Informatics. 2019. V. 13. № 2. P. 29–42.

  43. Srikanth K. et al. Meta-heuristic framework: Quantum inspired binary grey wolf optimizer for unit commitment problem // Computers and Electrical Engineering. 2018. V. 70. P. 243–260.

  44. Manju A., Nigam M.J. Applications of quantum inspired computational intelligence: a survey // Artificial Intelligence Review. 2014. V. 42. P. 79–156.

  45. Hamed H.N.A., Kasabov N.K., Shamsuddin S.M. Quantum inspired particle swarm optimization for feature selection and parameter optimization in evolving spiking neural networks for classification tasks // Evolutionary algorithms. IntechOpen, 2011. P. 133–148.

  46. Zouache D., Abdelaziz F.B. A cooperative swarm intelligence algorithm based on quantum-inspired and rough sets for feature selection // Computers and Industrial Engineering. 2018. V. 115. P. 26–36.

  47. Han K.-H., Kim J.-H. Quantum-Inspired Evolutionary Algorithms with a New Termination Criterion, He Gate, and Two-Phase Scheme // IEEE Transactions on Evolutionary Computation. 2004. V. 8. P. 164–171.

  48. Nezamabadi-pour H. A quantum-inspired gravitational search algorithm for binary encoded optimization problems // Engineering Applications of Artificial Intelligence. 2015. V. 40. P. 62–75.

  49. Ходашинский И.А., Мех М.А. Построение нечеткого классификатора на основе методов гармонического поиска // Программирование. 2017. № 1. С. 54–65.

  50. Программный код и инструкции [Электронный ресурс]. Режим доступа: https://gitlab.com/core_developers/fuzzy_core/-/tree/master/experiments/binarization_methods

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал