Программирование, 2021, № 5, стр. 60-74

1. ВВЕДЕНИЕ

Безопасность функционирования современных информационно-компьютерных систем становится критически важной, поскольку их отказ может привести к серьезным потерям, разрушениям и даже человеческим жертвам. Для верификации поведения таких систем необходимо использовать формализмы, позволяющие описывать и анализировать как функциональные (качественные), так и реально-временные (количественные) свойства систем.

В теории сетей Петри (СП) известны разнообразные реально-временные расширения, в которых временные характеристики сопоставляются различным элементам (местам, переходам, дугам, фишкам) сетевых моделей [1]. Наибольшую популярность получили расширения сетей Петри, где с их переходами (действиями моделируемых систем) связываются временные задержки, а модельные часы измеряют ход времени в состояниях сети (системы). В литературе рассматриваются два подхода – дискретно-временные СП (ДВСП) [2] и непрерывно-временные СП (НВСП) [3]. В ДВСП имеются глобальные часы и каждому переходу сопоставляется целочисленное значение – длительность срабатывания перехода, тогда как в НВСП с каждым переходом связываются локальные часы и статический интервал действительных чисел – временных задержек срабатывания перехода (при этом срабатывание перехода считается мгновенным). Известно, что НВСП равномощны машинам Тьюринга и включают класс ДВСП, поэтому именно модели НВСП вызывают наибольший интерес у исследователей. Чтобы обеспечить разрешимость проблем анализа поведенческих свойств, как правило, в литературе рассматриваются $n$-ограниченные НВСП, в местах которых не накапливается бесконечное количество фишек (ресурсов моделируемой системы), а их количество ограничено некоторым натуральным числом $n$. Как было показано в работе [4], выразительные мощности $n$-ограниченных и 1-ограниченных (безопасных) НВСП эквивалентны относительно временной бисимуляции.

НВСП имеют следующую операционную семантику (поведение). Состояние НВСП содержит текущую разметку (распределение фишек по местам сети) и показания часов разрешенных переходов (т.е. переходов, все входные места которых имеют достаточное количество фишек при данной разметке). Переход может сработать в состоянии только в том случае, если переход разрешен в этой разметке и его часы достигли момента времени, который находится в пределах временного интервала данного перехода. Изменения состояний НВСП происходят двумя способами: ходом времени (часы разрешенных переходов идут вперед) и/или срабатыванием перехода (текущая разметка меняется на новую (в которой фишки потреблены из входных мест и произведены в выходные места срабатывающего перехода), а часы переходов, которые становятся разрешенными в новой разметке (вновь разрешенные переходы), переустанавливаются).

В литературе были предложены различные представления операционной семантики НВСП, которые классифицируются в соответствии с дихотомиями относительно: определения временной информации в состояниях сети (единичное/интервальное значение часов в состоянии), стратегии по ходу времени (сильная/слабая), стратегии контроля памяти (промежуточная/атомарная), а также представления срабатываний параллельных переходов НВСП (интерливинг/‘истинный параллелизм’).

Единичное/интервальное значение часов в состоянии. В синтаксисе НВСП с каждым переходом связан статический временной интервал срабатывания данного перехода. При функционировании НВСП показания часов разрешенных переходов в состоянии – это либо действительные числа (единичные значения), либо интервалы действительных чисел (интервальные значения).

Если показания часов в состоянии НВСП представлены действительными числами (см., например, [5]), то часы вновь разрешенных переходов устанавливаются в 0 и затем значения увеличиваются синхронно с ходом времени в НВСП до тех пор, пока эти переходы не сработают или станут неразрешенными за счет срабатывания конфликтных переходов¹¹. При этом разрешенные переходы могут сработать в состоянии, только если показания их часов принадлежат их статическим интервалам.

В случае, когда показания часов в состоянии НВСП – интервалы действительных чисел (см., например, [6]), то показания часов вновь разрешенных переходов – это их статические интервалы срабатываний. При функционировании НВСП границы динамических интервалов уменьшаются синхронно с ходом времени в НВСП до тех пор, пока переходы не сработают или станут неразрешенными. Разрешенный переход может сработать в состоянии не раньше, чем нижняя граница его динамического интервала установится в ноль, и не позднее, чем верхняя граница его интервала достигнет ноля. В статье [7] была показана эквивалентность подходов относительно временной бисимуляции для некоторых семантик НВСП. В литературе предпочтение отдают первому подходу, который, как правило, упрощает изложение материала.

Сильная/слабая временная стратегия. Различают две стратегии хода времени в состоянии НВСП. В сильной семантике запрещен ход времени, приводящий к выходу за границы временного интервала хотя бы одного из разрешенных переходов, такой переход должен сработать в состоянии, когда время не может идти дальше. Напротив, в слабой семантике допускается любой ход времени, срабатывание переходов не форсируется и, как следствие, они, вообще, могут не сработать. В [1] авторами было доказано, что эти две семантики являются несравнимыми относительно слабой временной бисимуляции.

Промежуточная/атомарная пространственная стратегия. В литературе представлены промежуточная, атомарная и устойчиво атомарная стратегии, которые определяют, когда сбрасываются (переустанавливаются) часы разрешенных переходов. Классическая, названная промежуточной, стратегия учитывает промежуточную разметку, которая получается после потребления фишек и перед производством фишек при срабатывании перехода $t$. Часы перехода $t{\text{'}}$ сбрасываются, если он не являлся разрешенным в промежуточной разметке и стал разрешенным в разметке, полученной после производства фишек в результате срабатывания перехода $t$. При атомарной стратегии часы перехода $t{\text{'}}$ сбрасываются, если он не являлся разрешенным до срабатывания $t$ и стал разрешенным после срабатывания $t$. Если срабатывающий переход $t$ снова становится разрешенным после своего срабатывания, то его часы сбрасываются в промежуточной и атомарной стратегиях, но этого не происходит в устойчиво атомарной. Пространственные стратегии были изучены для сильной временной стратегии в статье [8], где было установлено, что все три стратегии совпадают в случае ограниченных НВСП с замкнутыми справа статическими интервалами и устойчиво атомарная стратегия более выразительна в других случаях, и для слабой временной стратегии в работе [9], где было показано, что атомарная стратегия строго менее выразительна, чем устойчиво атомарная, а промежуточная стратегия не является более выразительной, чем атомарная. В обеих этих статьях утверждается, что устойчиво атомарная стратегия является более предпочтительной для моделирования реальных систем, чем промежуточная и атомарная.

Интерливинг/‘истинный параллелизм’. Классическая интерливинговая семантика НВСП представляется в виде пробега – последовательности смены ее состояний посредством хода времени и срабатываний одиночных переходов. Эта семантика позволяет анализировать свойства безопасности и живости моделируемых систем, однако информация о параллелизме переходов НВСП полностью утрачивается. Чтобы исправить ситуацию, была предложена ‘истинно параллельная’ семантика, названная шаговой, при которой в пробеге НВСП при смене состояний одновременно срабатывает множество параллельных переходов (шаг). В другой ‘истинно параллельной’ семантике используется отношение частичного порядка для представления причинной зависимости между событиями моделируемых систем, отсутствие частичного порядка говорит о параллелизме событий. Для НВСП невозможно напрямую определить частичный порядок, так как графы НВСП могут содержать циклы. Поэтому, чтобы построить частично-упорядоченную семантику для НВСП, используют понятие временных процессов, состоящих из ациклических конструкций – временных причинно-следственных сетей (ВПСС), состоящих из событий и условий, связанных частичным порядком, – и отображений (гомоморфизмов) из ВПСС в НВСП. ‘Истинно параллельные’ семантики НВСП полезны при формальной верификации поведения моделируемых систем, так как число анализируемых состояний сокращается, поскольку не требуется рассмотрение всех вариантов интерливинговых последовательностей. В работе [10] для НВСП с сильной временной и промежуточной пространственной стратегиями предложена частично упорядоченная семантика, где с событиями ВПСС связаны временные характеристики, представляющие времена срабатываний соответствующих переходов. Этот подход был обобщен на шаговую семантику и использован для определения и изучения поведенческих эквивалентностей НВСП с такими же стратегиями поведения в [11, 12]. Метод, аналогичный предложенному в [10], используется в статье [13] для ограниченного по структуре класса НВСП (где интервалы срабатываний конфликтных переходов становятся несущественными) с некоторым подобием слабой временной стратегии, т.е. ход времени вперед неограничен, как в слабой стратегии, но возможен ход времени вспять, чтобы переходы срабатывали с учетом их временных интервалов, как в сильной стратегии. В работе [14] для НВСП со слабой временной и промежуточной пространственной стратегиями показана корректность частично-упорядоченной семантики, при построении которой использовалось преобразование целочисленных значений хода времени в специальные tick-события ВПСС. Однако такой метод приводит к значительному увеличению количества элементов ВПСС.

В данной работе изучается влияние слабой временной и устойчиво атомарной пространственной²² стратегий на построение семантики частичного порядка НВСП. В частности, предлагается метод, основанный на сопоставлении ‘разметкам’ (сечениям) ВПСС временных характеристик, соответствующих ходу времени в состояниях НВСП, тогда как выполнения событий ВСПП, представляющие срабатывания переходов, мгновенны, что адекватно отражает особенности поведения изучаемого класса НВСП, и показывается корректность такого подхода относительно интерливинговой и шаговой семантик.

Статья построена следующим образом. В разделе 2 рассматриваются определения синтаксиса НВСП и их интерливинговой и шаговой семантик в терминах пробега – последовательности смены состояний посредством хода времени и срабатываний одного перехода или шага параллельных переходов соответственно. В разделе 3 определяется ВПСС и интерливинговый/шаговый график ее выполнения, изучаются свойства временного процесса НВСП, состоящего из ВПСС и ее гомоморфизма в НВСП. В следующем разделе устанавливается существование биективного отображения между интерливинговым/шаговым графиком временного процесса НВСП и интерливинговым/шаговым пробегом НВСП. Раздел 5 завершает статью. Доказательства лемм можно найти по адресу: https://www.iis.nsk.su/files/proofs2021.pdf.

2. НЕПРЕРЫВНО-ВРЕМЕННЫЕ СЕТИ ПЕТРИ

В этом разделе рассматриваются определения, относящиеся к модели сетей Петри с временными интервалами, представляющими временные задержки срабатываний переходов. Сначала напомним синтаксис и семантику сетей Петри.

Сеть Петри (СП) состоит из двух разных множеств элементов – мест и переходов; отношения инцидентности между элементами и начальной разметки – распределения фишек по местам сети. Состояние СП задается разметкой – подмножеством мест, которые содержат фишки при функционировании сети. Переход СП разрешен в разметке, если все его входные места содержат фишки. Множество переходов, входные и выходные места которых не пересекаются, образуют шаг параллельных переходов. Шаг разрешен в разметке, если каждый переход шага разрешен в этой разметке. Срабатывание разрешенного в разметке шага приводит к новой разметке, в которой фишки удалены из входных мест и добавлены в выходные места переходов этого шага. Последовательность смены разметок посредством срабатываний переходов называется пробегом СП.

Определение 1. Сеть Петри (СП) – это набор $\mathcal{N}\, = \,(P,T,F,{{M}_{0}})$, где P – конечное множество мест и $T$ – конечное множество переходов такие, что $P \cap T = \not {0}$ и $P \cup T \ne \not {0}$; $F \subseteq (P \times T) \cup (T \times P)$ – отношение инцидентности; $\not {0} \ne {{M}_{0}} \subseteq P$ – начальная разметка. Для элемента $x \in P \cup T$ определим множество $^{ \bullet }x = {\text{\{ }}y|(y,x) \in F{\text{\} }}$ входных и множество ${{x}^{ \bullet }}\, = \,{\text{\{ }}y|(x,y)\, \in \,F{\text{\} }}$ выходных элементов, которые для подмножества элементов $X\, \subseteq \,P\, \cup \,T$ обобщаются соответственно до множеств $^{ \bullet }X\, = \,\bigcup\nolimits_{x \in X} {^{ \bullet }x} $ и ${{X}^{ \bullet }} = \bigcup\nolimits_{x \in X} {{{x}^{ \bullet }}} $.

• Разметка M СП $\mathcal{N}$ – это любое подмножество множества $P$. Переход $t \in T$ разрешен в разметке M, если $^{ \bullet }t \subseteq M$.

Непустое подмножество $U \subseteq T$ называется шагом, если ${{(}^{ \bullet }}t \cup {{t}^{ \bullet }}) \cap {{(}^{ \bullet }}t{\text{'}} \cup t{{{\text{'}}}^{ \bullet }}) = \not {0}$ для всех $t \ne t{\text{'}} \in U$. Шаг U разрешен в разметке M, если каждый переход $t \in U$ разрешен в разметке M, т.е. $^{ \bullet }U \subseteq M$. Обозначим через $En(M)$ множество всех шагов, разрешенных в разметке M. Если ${\text{\{ }}t{\text{\} }} \in En(M)$, то будем писать $t \in En(M)$.

Срабатывание шага, разрешенного в разметке M, приводит к новой разметке $M{\text{'}}$ (обозначается $M\xrightarrow{U}M{\text{'}}$), где $M{\text{'}} = (M{{{{\backslash }}}^{ \bullet }}U) \cup {{U}^{ \bullet }}$. Будем писать $M\xrightarrow{\vartheta }M{\text{'}}$, если $\vartheta = {{U}_{1}}\; \ldots \;{{U}_{n}}$ и M = = ${{M}^{0}}\xrightarrow{{{{U}_{1}}}}{{M}^{1}}\; \ldots \;{{M}^{{n - 1}}}\xrightarrow{{{{U}_{n}}}}{{M}^{n}} = M{\text{'}}$ ($n \geqslant 0$). В этом случае $\vartheta $ – пробег из M (в $M{\text{'}}$), а $M{\text{'}}$ – достижимая из $M$ разметка в $\mathcal{N}$.

СП $\mathcal{N}$ называется бесконтактной, если для любой достижимой из M₀ разметки $M$ и любого шага U, разрешенного в M, верно, что $(M{{{{\backslash }}}^{ \bullet }}U) \cap {{U}^{ \bullet }} = \not {0}$; $T$-закрытой, если $^{ \bullet }t \ne \not {0}$ и ${{t}^{ \bullet }} \ne \not {0}$ для всех переходов сети.

Непрерывно-временная сеть Петри (НВСП) состоит из базовой сети Петри и статической временной функции, отображающей каждый переход во временной интервал с неотрицательными рациональными границами. Подразумевается, что у каждого перехода есть собственные часы, которые отсчитывают время, прошедшее с момента, когда переход стал разрешенным. Одной разметки недостаточно, чтобы задавать состояние НВСП, поэтому к разметке добавлена динамическая временная функция, показывающая значения часов переходов, разрешенных в этой разметке. Начальное состояние НВСП состоит из начальной разметки и динамической временной функции с нулевыми значениями часов всех разрешенных переходов. При функционировании НВСП смена состояний осуществляется либо ходом времени, либо срабатыванием шага. Поскольку рассматривается слабая временная стратегия НВСП, то ход времени может быть представлен любым действительным числом, которое добавляется к значению часов разрешенных переходов при смене текущего состояния на новое. Шаг может сработать в состоянии, только если он разрешен в разметке и значения часов всех переходов из шага принадлежат их временным интервалам. Срабатывание шага приводит к новому состоянию, т.е. новой разметке и новым значениям динамической временной функции. Устойчиво атомарная пространственная стратегия НВСП определяет предикат $ \uparrow enabled(t,M,U)$, который указывает, нужно ли сбрасывать часы перехода $t$ после срабатывания шага $U$ в разметке M. Данный предикат принимает истинное значение, если $t$ не являлся переходом, разрешенным в разметке $M$ и становится разрешенным в новой разметке, полученной после срабатывания шага $U$ в M. Последовательность смены состояний посредством хода времени и срабатываний шагов называется пробегом НВСП.

Пусть ${{\mathbb{Q}}_{{ \geqslant 0}}}$ – множество неотрицательных рациональных чисел и Interv = ${\text{\{ }}[a,b],[a,b)|a \in {{\mathbb{Q}}_{{ \geqslant 0}}}$, $b \in ({{\mathbb{Q}}_{{ \geqslant 0}}} \cup {\text{\{ }}\infty {\text{\} }}),a \leqslant b{\text{\} }}$.

Определение 2.

• Непрерывно-временная сеть Петри (НВСП) – это пара $\mathcal{T}N = (\mathcal{N},D)$, где $\mathcal{N} = (P,T,F,{{M}_{0}})$ – базовая сеть Петри и $D:T \to Interv$ – статическая временная функция, сопоставляющая каждому переходу из $T$ временной интервал из $Interv$. Для перехода $t$ границы интервала $D(t)$ называются соответственно ранним ($Eft$) и поздним (Lft) временем срабатывания этого перехода.

• Состояние НВСП $\mathcal{T}\mathcal{N}$ – это пара $S = (M,I)$, где M – разметка и $I:En(M) \to {{\mathbb{R}}_{{ \geqslant 0}}}$ – динамическая временная функция. Начальное состояние $\mathcal{T}\mathcal{N}$ – это пара ${{S}_{0}} = ({{M}_{0}},{{I}_{0}})$, где ${{M}_{0}}$ – начальная разметка и ${{I}_{0}}(t) = 0$ для всех $t \in En({{M}_{0}})$. Шаг U, разрешенный в разметке M, может сработать в состоянии $S = (M,I)$, если $Eft(t) \leqslant I(t) \leqslant Lft(t)$ для всех $t \in U$. Обозначим через $Fi(S)$ множество всех шагов, которые могут сработать в состоянии $S$. Если ${\text{\{ }}t{\text{\} }} \in Fi(S)$, то будем писать $t \in Fi(S)$.

Для НВСП возможны два способа изменения состояния: ход времени и срабатывание шага.

Ход времени $\tau \in {{\mathbb{R}}_{{ \geqslant 0}}}$ в состоянии $S = (M,I)$ приводит к новому состоянию $S{\text{'}} = (M{\text{'}},I{\text{'}})$ (обозначается $S\xrightarrow{\tau }S{\text{'}}$), где $M{\text{'}} = M$ и $I{\text{'}}(t) = I(t) + \tau $ для всех $t \in En(M{\text{'}})$.

Срабатывание шага $U \in Fi(S = (M,I))$ приводит к новому состоянию $S{\kern 1pt} {\text{'}} = (M{\kern 1pt} {\text{'}},I{\kern 1pt} {\text{'}})$ (обозначается $S\xrightarrow{U}S{\kern 1pt} {\text{'}}$) такому, что верно:

где предикат $ \uparrow enabled(t,M,U)$ = $t \notin En(M)$ ∧ ∧ $t \in En(M{\text{'}})$³³ указывает на необходимость сброса часов перехода t, который не был разрешенным в разметке M и стал разрешенным в разметке $M{\text{'}}$ после срабатывания шага $U$.

Будем писать $S\xrightarrow{\sigma }S{\kern 1pt} {\text{'}}$, если σ = x₁ ... ${{x}_{n}} \in {{(\mathcal{P}(T) \cup {{\mathbb{R}}_{{ \geqslant 0}}})}^{n}}$ и $S = {{S}^{0}}$ $\xrightarrow{{{{x}_{1}}}}$ ${{S}^{1}}$ ... ${{S}^{{n - 1}}}\xrightarrow{{{{x}_{n}}}}{{S}^{n}} = S{\kern 1pt} {\text{'}}$ ($n \geqslant 0$). В этом случае $\sigma $ – (шаговый) пробег $\mathcal{T}\mathcal{N}$ из состояния $S$ (в состояние $S{\text{'}}$). Пусть $\mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ – множество всех пробегов из ${{S}_{0}}$ в $\mathcal{T}\mathcal{N}$. Обозначим через $Untimed(\sigma )$ проекцию пробега $\sigma $ на множество $\mathcal{P}(T)$, т.е. безвременную часть пробега $\sigma $. Будем называть $\sigma $ интерливинговым пробегом, если $\left| {{{x}_{i}}} \right| = 1$ для всех ${{x}_{i}}$ из $Untimed(\sigma )$.

НВСП $\mathcal{T}\mathcal{N}$ называется бесконтактной (T-закрытой), если базовая сеть является бесконтактной (T-закрытой). В дальнейшем будем рассматривать только бесконтактные и T-закрытые НВСП.

Для НВСП $\mathcal{T}\mathcal{N}$ обозначим через $\widehat {\mathcal{F}\mathcal{S}}(\mathcal{T}\mathcal{N})$ множество всех шаговых пробегов из $\mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ следующего вида: $\hat {\sigma } = {{\theta }_{0}}{{U}_{1}}{{\theta }_{1}}\; \ldots \;{{U}_{n}}{{\theta }_{n}}$, где ${{\theta }_{i}} \in {{\mathbb{R}}_{{ \geqslant 0}}}$ ($0 \leqslant i \leqslant n$) и ${{U}_{j}} \in \mathcal{P}(T)$ ($1 \leqslant j \leqslant n$), т.е. ход времени и срабатывания шагов чередуются в пробеге из $\widehat {\mathcal{F}\mathcal{S}}(\mathcal{T}\mathcal{N})$. Тогда в $\mathcal{T}\mathcal{N}$ для пробега $\hat {\sigma } \in \widehat {\mathcal{F}\mathcal{S}}(\mathcal{T}\mathcal{N})$ будут иметь место следующие изменения состояний: $({{M}_{0}},{{I}_{0}})$ $\xrightarrow{{{{\theta }_{0}}}}$ (M₀, $I_{0}^{'})$ $\xrightarrow{{{{U}_{1}}}}$ $({{M}_{1}},I_{1}^{{}})$ $\xrightarrow{{{{\theta }_{1}}}}$ → $({{M}_{1}},I_{1}^{'})$ ... $({{M}_{{n - 1}}},{{I}_{{n - 1}}})$ $\xrightarrow{{{{\theta }_{{n - 1}}}}}$ $({{M}_{{n - 1}}},I_{{n - 1}}^{'})$ $\xrightarrow{{{{U}_{n}}}}$ → $({{M}_{n}},{{I}_{n}})$ $\xrightarrow{{{{\theta }_{n}}}}$ $({{M}_{n}},I_{n}^{'})$.

Оказалось, что любой пробег из $\mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ может быть преобразован в представленную выше форму. Справедливость этого факта непосредственно следует из определения хода времени в состоянии НВСП.

Лемма 1. Пусть $\mathcal{T}\mathcal{N}$ – НВСП и $\sigma \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$. Тогда существует $\hat {\sigma } \in \widehat {\mathcal{F}\mathcal{S}}(\mathcal{T}\mathcal{N})$ такой, что $Untimed(\sigma ) = Untimed(\hat {\sigma })$.

Для простоты изложения материала далее будем рассматривать только пробеги с чередованием хода времени и срабатываний шагов.

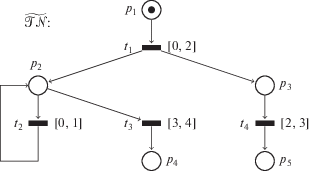
Пример 1. На рис. 1 показана НВСП $\widetilde {\mathcal{T}\mathcal{N}}$, в которой места представлены окружностями, а переходы – барьерами. Рядом с элементами указаны их имена. Между элементами, входящими в отношение инцидентности, изображены направленные дуги. Каждое место, принадлежащее начальной разметке, отмечено наличием в нем фишки (жирной точки). Значения статической временной функции указаны рядом с переходами.

Покажем, что $\sigma = 0$ {t₁} 1 ${\text{\{ }}{{t}_{2}}{\text{\} }}$ 2 ${\text{\{ }}{{t}_{3}},{{t}_{4}}{\text{\} }}$ $3 \in \widehat {\mathcal{F}\mathcal{S}}(\widetilde {\mathcal{T}\mathcal{N}})$, т.е. ${{S}_{0}}\, = \,({{M}_{0}},{{I}_{0}})$ $\xrightarrow{0}$ $S_{0}^{'} = ({{M}_{0}},I_{0}^{'})$ $\xrightarrow{{\{ {{t}_{1}}\} }}$ ${{S}_{1}} = ({{M}_{1}},{{I}_{1}})$ $\xrightarrow{1}$ $S_{1}^{'} = ({{M}_{1}},I_{1}^{'})$ $\xrightarrow{{\{ {{t}_{2}}\} }}$ → ${{S}_{2}} = ({{M}_{2}},{{I}_{2}})$ $\xrightarrow{2}$ $S_{2}^{'} = ({{M}_{2}},I_{2}^{'})$ $\xrightarrow{{\{ {{t}_{3}},{{t}_{4}}\} }}$ → ${{S}_{3}} = ({{M}_{3}},{{I}_{3}})$ $\xrightarrow{3}$ $S_{3}^{'} = ({{M}_{3}},I_{3}^{'})$.

Изначально имеем, что ${{S}_{0}} = ({{M}_{0}},{{I}_{0}})$, где M₀ = ${\text{\{ }}{{p}_{1}}{\text{\} }}$ и ${{I}_{0}}({{t}_{1}}) = 0$, поскольку $En({{M}_{0}}) = {\text{\{ }}{{t}_{1}}{\text{\} }}$. Тогда S₀ = (M₀, ${{I}_{0}})$ $\xrightarrow{0}$ $S_{0}^{'} = ({{M}_{0}},I_{0}^{'})$, где $I_{0}^{'}({{t}_{1}}) = 0$, по определению хода времени. Поскольку ${{t}_{1}} \in En({{M}_{0}})$ и Eft(t₁) = = $0 \leqslant I_{0}^{'}({{t}_{1}}) \leqslant Lft({{t}_{1}})$ = 2, т.е. ${{t}_{1}} \in Fi(S_{0}^{'})$, то, по определению срабатывания шага, получаем, что $S_{0}^{'}\xrightarrow{{\{ {{t}_{1}}\} }}{{S}_{1}} = ({{M}_{1}},{{I}_{1}})$, где M₁ = $({{M}_{0}}{{{{\backslash }}}^{ \bullet }}{\text{\{ }}{{t}_{1}}{\text{\} }}) \cup {{{\text{\{ }}{{t}_{1}}{\text{\} }}}^{ \bullet }}$ = = {p₂, p₃} и для всех $t\, \in \,{\text{\{ }}{{t}_{2}},{{t}_{3}},{{t}_{4}}{\text{\} }}$ верно, что ${{I}_{1}}(t)\, = \,0$, так как 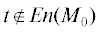и $t\, \in \,En({{M}_{1}})$, т.е. $ \uparrow enabled(t,{{M}_{0}},{\text{\{ }}{{t}_{1}}{\text{\} }})$ = = true.

Далее, согласно определению хода времени, имеем, что ${{S}_{1}} = ({{M}_{1}},{{I}_{1}})$ $\xrightarrow{1}$ $S_{1}^{'} = ({{M}_{1}},I_{1}^{'})$, где $I_{1}^{'}(t) = {{I}_{1}}(t)$ + 1 = 1 для $t \in {\text{\{ }}{{t}_{2}},{{t}_{3}},{{t}_{4}}{\text{\} }}$, так как $t \in En({{M}_{1}})$. Поскольку ${{t}_{2}} \in En({{M}_{1}})$ и Eft(t₂) = = $0 \leqslant I_{1}^{'}({{t}_{2}}) \leqslant Lft({{t}_{2}})$ = 1, т.е. ${{t}_{2}} \in Fi(S_{1}^{'})$, то, по определению срабатывания шага, получаем, что $S_{1}^{'}\,\xrightarrow{{\{ {{t}_{2}}\} }}\,{{S}_{2}}\, = \,({{M}_{2}},{{I}_{2}})$, где ${{M}_{2}} = ({{M}_{1}}{{{{\backslash }}}^{ \bullet }}{\text{\{ }}{{t}_{2}}{\text{\} }}) \cup {{{\text{\{ }}{{t}_{2}}{\text{\} }}}^{ \bullet }}$ = = {p₂, p₃} и для всех $t \in {\text{\{ }}{{t}_{2}},{{t}_{3}},{{t}_{4}}{\text{\} }}$ верно, что I₂(t) = = $I_{1}^{'}(t) = 1$, так как $t \in En({{M}_{1}})$ и $t \in En({{M}_{2}})$, т.е. $ \uparrow enabled(t,{{M}_{2}},{\text{\{ }}{{t}_{2}}{\text{\} }})$ = false. Хотя переход ${{t}_{2}}$ сработал в $S_{1}^{'} = ({{M}_{1}},I_{1}^{'})$, его часы не сбросились, как было бы при промежуточной и атомарной пространственных стратегиях. Тогда как после срабатывания перехода ${{t}_{2}}$ часы перехода ${{t}_{3}}$ сбросились бы при промежуточной стратегии, но не сбросились бы при атомарной, а часы перехода ${{t}_{4}}$ не сбрасываются ни при какой стратегии.

Теперь, по определению хода времени, получаем, что ${{S}_{2}} = ({{M}_{2}},{{I}_{2}})$ $\xrightarrow{2}$ $S_{2}^{'} = ({{M}_{2}},I_{2}^{'})$, где $I_{2}^{'}(t)$ = = I₂(t) + 2 = 3 для всех $t \in {\text{\{ }}{{t}_{2}},{{t}_{3}},{{t}_{4}}{\text{\} }}$, так как $t \in En({{M}_{2}})$. Видим, что $I_{2}^{'}({{t}_{2}}) = 3 > Lft({{t}_{2}}) = 1$, т.е. 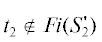. Благодаря слабой временной стратегии, стало возможным не форсировать срабатывание перехода ${{t}_{2}}$ до того, как время на его часах перейдет верхнюю границу его временного интервала. Исходя из того, что ${{(}^{ \bullet }}{{t}_{3}} \cup t_{3}^{ \bullet }) \cap {{(}^{ \bullet }}{{t}_{4}} \cup t_{4}^{ \bullet }) = \not {0}$, ${\text{\{ }}{{t}_{3}},{{t}_{4}}{\text{\} }}$ – шаг в НВСП $\widetilde {\mathcal{T}\mathcal{N}}$. Кроме, того ${\text{\{ }}{{t}_{3}},{{t}_{4}}{\text{\} }} \in En({{M}_{2}})$ и Eft(t₃) = = $3 \leqslant I_{2}^{'}({{t}_{3}})$ = $3 \leqslant Lft({{t}_{3}})$ = 4, Eft(t₄) = = $2 \leqslant I_{2}^{'}({{t}_{4}}) = 3 \leqslant Lft({{t}_{4}})$ = 3, т.е. ${\text{\{ }}{{t}_{3}},{{t}_{4}}{\text{\} }} \in Fi(S_{2}^{'})$. Следовательно, $S_{2}^{'}\xrightarrow{{\{ {{t}_{3}},{{t}_{4}}\} }}{{S}_{3}} = ({{M}_{3}},{{I}_{3}})$, где M₃ = = $({{M}_{2}}{{{{\backslash }}}^{ \bullet }}{\text{\{ }}{{t}_{3}},{{t}_{4}}{\text{\} }}) \cup {{{\text{\{ }}{{t}_{3}},{{t}_{4}}{\text{\} }}}^{ \bullet }} = {\text{\{ }}{{p}_{4}},{{p}_{5}}{\text{\} }}$ и ${{I}_{3}}$ неопределено, так как $En({{M}_{3}}) = \not {0}$.

И наконец, по определению хода времени, имеем, что ${{S}_{3}} = ({{M}_{3}},{{I}_{3}})$ $\xrightarrow{3}$ $S_{3}^{'} = ({{M}_{3}},I_{3}^{'})$, где $I_{3}^{'}$ неопределено, так как $En({{M}_{3}}) = \not {0}$.

Таким образом, получили, что $\sigma = 0$ ${\text{\{ }}{{t}_{1}}{\text{\} }}$ 1 ${\text{\{ }}{{t}_{2}}{\text{\} }}$ 2 ${\text{\{ }}{{t}_{3}},{{t}_{4}}{\text{\} }}$ $3 \in \widehat {\mathcal{F}\mathcal{S}}(\widetilde {\mathcal{T}\mathcal{N}})$.

3. ВРЕМЕННЫЕ ПРОЦЕССЫ НВСП

В данном разделе вводится и изучается концепция временных процессов в контексте НВСП со слабой временной и устойчиво атомарной пространственной стратегиями. Сначала определим причинно-следственную сеть, которая состоит из событий и условий, связанных отношениями причины и параллелизма.

Определение 3. Причинно-следственная сеть (ПСС) – это конечная ацикличная сеть N = = $(B,E,G)$, где $B$ – множество условий; $E$ – множество событий; $G \subseteq (B \times E)$ ∪ $(E \times B)$ – отношение инцидентности такое, что $\left| {{{b}^{ \bullet }}} \right| \leqslant 1$ и $\left| {^{ \bullet }b} \right| \leqslant 1$ для всех $b \in B$ и $E = {{\,}^{ \bullet }}B = {{B}^{ \bullet }}$.

Для ПСС $N = (B,E,G)$ введем дополнительные понятия и обозначения:

– $^{ \bullet }N = {\text{\{ }}b \in B|{{\,}^{ \bullet }}b = \not {0}{\text{\} }}$, ${{N}^{ \bullet }} = {\text{\{ }}b \in B|{{b}^{ \bullet }} = \not {0}{\text{\} }}$;

– $x \prec x{\text{'}} \Leftrightarrow x{{G}^{ + }}x{\text{'}}$ и $x \preccurlyeq x{\text{'}} \Leftrightarrow xG{\text{*}}x{\text{'}}$, где x, $x{\text{'}} \in B \cup E$ (отношение причины);

– x ( x' $ \Leftrightarrow \neg ((x \preccurlyeq x{\text{'}}) \vee (x{\text{'}} \preccurlyeq x))$, где x, $x{\text{'}} \in B \cup E$ (отношение параллелизма);

– непустое подмножество $E{\text{'}} \subseteq E$ называется шагом в ПСС N, если $e$ ( e' для всех $e \ne e{\text{'}} \in E{\text{'}}$;

– непустое подмножество $B{\text{'}} \subseteq B$ называется (-множеством в N, если $b$ ( b' для всех $b \ne b{\text{'}} \in B{\text{'}}$. Сечение C в N – это максимальное по включению (-множество. Обозначим через $\mathcal{C}\mathcal{U}\mathcal{T}(N)$ множество всех сечений в ПСС N. Для $C \in \mathcal{C}\mathcal{U}\mathcal{T}(N)$ пусть $ \downarrow C = {\text{\{ }}e \in E|e \preccurlyeq (e{\text{'}} \in {{\,}^{ \bullet }}C){\text{\} }}$ (множество событий, предшествующих сечению C). Неформально говоря, сечение – это ‘разметка’ ПСС N, которая достигается после того, как предшествующие сечению события произошли. Заметим, что $^{ \bullet }N,{{N}^{ \bullet }} \in \mathcal{C}\mathcal{U}\mathcal{T}(N)$ и $ \downarrow {{N}^{ \bullet }} = E$, если $B \ne \not {0}$.

Для сечений $C,C{\text{'}} \in \mathcal{C}\mathcal{U}\mathcal{T}(N)$ определим следующие понятия:

• событие $e \in E$ разрешено в сечении C, если $^{ \bullet }e \subseteq C$; шаг $V$ разрешен в C, если каждое событие $e \in V$ разрешено в C, т.е. $^{ \bullet }V \subseteq C$. Через $En(C)$ обозначим множество шагов, разрешенных в сечении C. Если ${\text{\{ }}e{\text{\} }} \in En(C)$, то будем писать $e \in En(C)$;

• $C\xrightarrow{V}C{\text{'}}$ $ \Leftrightarrow $ $V \in En(C)$ и $C{\text{'}} = (C{{{{\backslash }}}^{ \bullet }}V) \cup {{V}^{ \bullet }}$. Заметим, что для любого шага V  и любого сечения $C\, \in \,\mathcal{C}\mathcal{U}\mathcal{T}(N)$ таких, что $V\, \in \,En(C)$ верно $((C{{{{\backslash }}}^{ \bullet }}V) \cup {{V}^{ \bullet }})$ ∈ $\mathcal{C}\mathcal{U}\mathcal{T}(N)$⁴⁴. Будем писать $C{{\xrightarrow{e}}_{i}}C{\text{'}}$, если $V = {\text{\{ }}e{\text{\} }}$. Если шаг V не существенен, то будем опускать его. Тогда $ \preccurlyeq \, = {{( \to )}^{ \star }}$ (отношение причины на сечениях). Заметим, что $C \preccurlyeq C{\text{'}} \Leftrightarrow \, \downarrow C \subseteq \, \downarrow C{\text{'}}$;

• C ( $C{\text{'}} \Leftrightarrow \neg ((C \preccurlyeq C{\text{'}}) \vee (C{\text{'}} \preccurlyeq C))$ (отношение параллелизма на сечениях). Пусть Cut(C) = = ${\text{\{ }}C{\text{'}}\, \in \,\mathcal{C}\mathcal{U}\mathcal{T}(N)|C$ ( C  '} (множество сечений, параллельных сечению C). Ясно, что C ( $C{\text{'}}\, \Leftrightarrow \,\neg ( \downarrow C\, \subseteq \, \downarrow C{\text{'}})$ и $\neg ( \downarrow C{\text{'}} \subseteq \downarrow C)$.

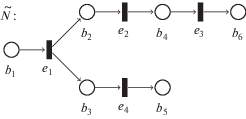
Пример 2. На рис. 2 представлена ПСС $\tilde {N} = (B,E,G)$, где $B = {\text{\{ }}{{b}_{1}},\; \ldots ,\;{{b}_{6}}{\text{\} }}$, $E = {\text{\{ }}{{e}_{1}},\; \ldots ,\;{{e}_{4}}{\text{\} }}$, $G = {\text{\{ }}({{b}_{1}},{{e}_{1}}),$ $({{e}_{1}},{{b}_{2}}),$ $({{e}_{1}},{{b}_{3}}),$ $({{b}_{2}},{{e}_{2}}),$ $({{b}_{3}},{{e}_{4}}),$ $({{e}_{2}},{{b}_{4}}),$ $({{e}_{4}},{{b}_{5}}),$ $({{b}_{4}},{{e}_{3}}),$ $({{e}_{3}},{{b}_{6}}){\text{\} }}$. Легко видеть, что ${\text{|}}{{b}^{ \bullet }}{\text{|}} \leqslant 1$ и ${{{\text{|}}}^{ \bullet }}b{\text{|}} \leqslant 1$ для любого $b \in B$ и $E\, = {{\,}^{ \bullet }}B\, = \,{{B}^{ \bullet }}$. Так как e₂ ( ${{e}_{4}}$ (e₃ ( ${{e}_{4}}$), то ${\text{\{ }}{{e}_{2}},{{e}_{4}}{\text{\} }}$ (${\text{\{ }}{{e}_{3}},{{e}_{4}}{\text{\} }}$) – шаг в $\tilde {N}$. Понятно, что каждое событие является шагом в $\tilde {N}$. Поскольку ${{b}_{2}} \cup {{b}_{3}}$ (${{b}_{3}} \cup {{b}_{4}}$) и не существует $b \in B{{\backslash \{ }}{{b}_{2}},{{b}_{3}}{\text{\} }}$ ($b \in B{{\backslash \{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}$) такого, что b ( ${{b}_{2}}$ и b ( ${{b}_{3}}$ (b ( ${{b}_{3}}$ и b ( ${{b}_{4}}$), то ${\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }}$ (${\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}$) – сечение в $\tilde {N}$. Нетрудно проверить, что множества ${\text{\{ }}{{b}_{1}}{\text{\} }} = {{\,}^{ \bullet }}\tilde {N}$, ${\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}$, ${\text{\{ }}{{b}_{3}},{{b}_{6}}{\text{\} }}$, ${\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}$, ${\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }} = {{\tilde {N}}^{ \bullet }}$ также являются сечениями в $\tilde {N}$. Исходя из того, что $^{ \bullet }{\text{\{ }}{{e}_{2}},{{e}_{4}}{\text{\} }} \subseteq {\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }}$ ($^{ \bullet }{\text{\{ }}{{e}_{3}},{{e}_{4}}{\text{\} }} \subseteq {\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}$), то ${\text{\{ }}{{e}_{2}},{{e}_{4}}{\text{\} }}$ ({e₃, e₄}) – шаг, разрешенный в ${\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }}$ (${\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}$). Тогда {b₂, b₃} $\xrightarrow{{{\text{\{ }}{{e}_{2}},{{e}_{4}}{\text{\} }}}}$ → {b₄, b₅} (${\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}\xrightarrow{{{\text{\{ }}{{e}_{3}},{{e}_{4}}{\text{\} }}}}{\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }}$), потому что 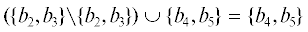(({b₃, b₄}\{b₃, b₄}) ∪ ∪ ${\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }}\, = \,{\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }}$). Далее, постороим множества предшественников сечений: $ \downarrow {\text{\{ }}{{b}_{1}}{\text{\} }} = \not {0}$, $ \downarrow {\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }}$ = = {e₁}, $ \downarrow {\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}\, = \,{\text{\{ }}{{e}_{1}}$, ${{e}_{2}}{\text{\} }}$, $ \downarrow {\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}$ = {e₁, ${{e}_{4}}{\text{\} }}$, $ \downarrow {\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}$ = = {e₁, ${{e}_{2}}$, ${{e}_{4}}{\text{\} }}$, $ \downarrow {\text{\{ }}{{b}_{3}},{{b}_{6}}{\text{\} }} = {\text{\{ }}{{e}_{1}}$, ${{e}_{2}}$, ${{e}_{3}}{\text{\} }}$, $ \downarrow {\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }}$ = = ${\text{\{ }}{{e}_{1}},{{e}_{2}},{{e}_{3}},{{e}_{4}}{\text{\} }}$. Тогда имеем, что Cut({b₁}) = = $Cut({\text{\{ }}{{b}_{2}}$, ${{b}_{3}}{\text{\} }}) = Cut({\text{\{ }}{{b}_{5}}$, ${{b}_{6}}{\text{\} }}) = \not {0}$ и $Cut({\text{\{ }}{{b}_{4}}$, ${{b}_{5}}{\text{\} }}) = {\text{\{ \{ }}{{b}_{3}}$, ${{b}_{6}}{\text{\} \} }}$, $Cut({\text{\{ }}{{b}_{2}}$, ${{b}_{5}}{\text{\} }}) = {\text{\{ \{ }}{{b}_{3}}$, ${{b}_{4}}{\text{\} }}$, ${\text{\{ }}{{b}_{3}}$, ${{b}_{6}}{\text{\} \} }}$.

Введем временное расширение ПСС за счет сопоставления их сечениям временных характеристик, которые, как будет показано далее, соответствуют ходу времени в состояниях НВСП.

Определение 4. Временная ПСС (ВПСС) – это пара $TN = (N,\tau )$, где N – ПСС и $\tau :\mathcal{C}\mathcal{U}\mathcal{T}(N) \to {{\mathbb{R}}_{{ \geqslant 0}}} \cup \{ \bot \} $ – временная функция такая, что для всех $C \in \mathcal{C}\mathcal{U}\mathcal{T}(N)$ верно: τ(C) = = $ \bot \Leftrightarrow \exists C{\text{'}} \in Cut(C):\tau (C{\kern 1pt} {\text{'}})$ > 0. Пусть $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ = = ${\text{\{ }}C \in \mathcal{C}\mathcal{U}\mathcal{T}(N)|\tau (C) \in {{\mathbb{R}}_{{ \geqslant 0}}}{\text{\} }}$.

Пример 3. Рассмотрим ПСС $\tilde {N}$ из примера 2. Определим функцию $\tau :\mathcal{C}\mathcal{U}\mathcal{T}(\tilde {N})$ → ${{\mathbb{R}}_{{ \geqslant 0}}} \cup {\text{\{ }} \bot {\text{\} }}$ следующим образом: $\tau ({\text{\{ }}{{b}_{1}}{\text{\} }}) = 0$, $\tau ({\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }}) = 1$, $\tau ({\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}) = 2$, $\tau ({\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }}) = 3$, $\tau ({\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}) = \tau ({\text{\{ }}{{b}_{3}},{{b}_{6}}{\text{\} }}) = 0$, $\tau (\{ {{b}_{2}},{{b}_{5}}\} ) = \, \bot $. Покажем, что $\tau $ является временной функцией. Для сечения $C \in {\text{\{ \{ }}{{b}_{1}}{\text{\} }},{\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }},{\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} \} }}$ имеем, что $\tau (C) \ne \bot $, так как $Cut(C) = \not {0}$. Сечение ${\text{\{ }}{{b}_{3}},{{b}_{6}}{\text{\} }}$ параллельно сечениям ${\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}$ и ${\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}$, однако $\tau ({\text{\{ }}{{b}_{3}},{{b}_{6}}{\text{\} }}) \ne \, \bot $, потому что $\tau ({\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}) = \, \bot $ и $\tau ({\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}) = 0$. Для сечения ${\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}$ имеем, что $\tau ({\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}) \ne \, \bot $, поскольку хотя ${\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }}$ и параллельно ${\text{\{ }}{{b}_{3}},{{b}_{6}}{\text{\} }}$, но $\tau ({\text{\{ }}{{b}_{3}},{{b}_{6}}{\text{\} }}) = 0$. Сечение ${\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}$ параллельно сечению ${\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}$, однако $\tau ({\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}) \ne \, \bot $, потому что $\tau ({\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}) = \, \bot $. Наконец, для сечения ${\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}$ имеем, что $\tau ({\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}) = \, \bot $, потому что ${\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}$ параллельно ${\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}$ и $\tau ({\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}) = 2 > 0$. Значит, для любого $C \in \mathcal{C}\mathcal{U}\mathcal{T}(\tilde {N})$ верно, что $\tau (C) = \, \bot $, если и только если существует $C{\text{'}} \in Cut(C)$ такое, что $\tau (C{\text{'}}) > 0$. Следовательно, $\tau $ – временная функция. Таким образом, $\widetilde {TN} = (\tilde {N},\tau )$ – ВПСС.

Для сечения $C \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ определим следующие понятия:

• событие $e \in E$ может произойти в C, если $e\, \in \,En(C)$ и $C{\text{'}}\, = \,((C{{{{\backslash }}}^{ \bullet }}e)\, \cup \,{{e}^{ \bullet }})\, \in \,\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$. Шаг V может произойти в C, если каждое событие $e \in V$ может произойти в C и C ' = $((C{{{{\backslash }}}^{ \bullet }}V) \cup {{V}^{ \bullet }})$ ∈ ∈ $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$⁵⁵. Через $Fi(C)$ обозначим множество шагов, которые могут произойти в C. Если ${\text{\{ }}e{\text{\} }} \in Fi(C)$, то будем писать $e \in Fi(C)$.

• $C\mathop \Rightarrow \limits^V C{\text{'}} \Leftrightarrow $ $V \in Fi(C)$ и $C{\text{'}} = (C{{{{\backslash }}}^{ \bullet }}V) \cup {{V}^{ \bullet }}$. Будем писать $C{{\mathop \Rightarrow \limits^e }_{i}}C{\text{'}}$, если $V = {\text{\{ }}e{\text{\} }}$. Если шаг $V$ не существенен, то будем опускать его. Тогда $ \sqsubseteq \, = {{( \Rightarrow )}^{ \star }}$ (отношение причины на временных сечениях);

• $RCut(C) = Cut(C) \cap \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN).$

Для сечений из множества $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ установим ряд свойств, которые следуют из вышеприведенных определений.

Лемма 2. Для сечений $C,C{\text{'}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ верно:

(а) $C \preccurlyeq C'$ $ \Rightarrow $ $C \sqsubseteq C'$;

(б) $\tau (C) = \tau (C{\text{''}}) = 0$ для любого $C{\text{''}} \in RCut(C);$

(в) для любого $e \in Fi(C) \cap Fi(C{\text{'}})$ существует $C{\text{''}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ такой, что $e \in Fi(C{\text{''}})$, $C{\text{''}} \preccurlyeq C$ и $C{\text{''}} \preccurlyeq C{\text{'}}$.

Рассмотрим поведение ВПСС в терминах понятия графика.

Определение 5. Пусть $TN = (N,\tau )$ – ВПСС. Последовательность сечений из $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ и шагов вида $\omega = {{C}_{0}}$ ${{V}_{1}}$ ${{C}_{1}}$ ... ${{V}_{n}}$ ${{C}_{n}}$ ($n \geqslant 0$) называется (шаговым) графиком ВПСС $TN$, если верно: ${{C}_{0}} = {{\,}^{ \bullet }}N$, ${{C}_{n}} = {{N}^{ \bullet }}$ и ${{C}_{{i - 1}}}\mathop \Rightarrow \limits^{{{V}_{i}}} {{C}_{i}}$ для всех $1 \leqslant i \leqslant n$. Если ${{C}_{{i - 1}}}{{\mathop \Rightarrow \limits^e }_{i}}{{C}_{i}}$ для всех $1 \leqslant i \leqslant n$, то ω называется интерливинговым графиком ВПСС TN. Будем писать $\omega = {{C}_{0}}\; \ldots \;{{C}_{n}}$, если шаги не существенны для изложения материала. Для графика $\omega = {{C}_{0}}\; \ldots \;{{C}_{n}}$ определим $\left| \omega \right| = n$ и префикс ${{\omega }_{i}} = {{C}_{0}}\; \ldots \;{{C}_{i}}$ для некоторого $0 \leqslant i \leqslant n$. Пусть $Graph(TN)$ обозначает множество графиков ВПСС $TN$.

Пример 4. Пусть $\widetilde {TN} = (\tilde {N},\tau )$ – ВПСС из примера 3. Рассмотрим последовательность $\omega = {{C}_{0}}$ ${{V}_{1}}$ ${{C}_{1}}$ ${{V}_{2}}$ ${{C}_{2}}$ ${{V}_{3}}$ ${{C}_{3}}$, где ${{C}_{0}} = {\text{\{ }}{{b}_{1}}{\text{\} }}$, ${{V}_{1}} = {\text{\{ }}{{e}_{1}}{\text{\} }}$, ${{C}_{1}} = {\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }}$, ${{V}_{2}} = {\text{\{ }}{{e}_{2}}{\text{\} }}$, ${{C}_{2}}\, = \,{\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }}$, ${{V}_{3}}\, = \,{\text{\{ }}{{e}_{3}},{{e}_{4}}{\text{\} }}$ и ${{C}_{3}}\, = \,{\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }}$. Из примера 2 известно следующее: ${{C}_{0}}\, = \,{\text{\{ }}{{b}_{1}}{\text{\} }}\,{{ = }^{ \bullet }}\tilde {N}$, C₃ = = {b₅, b₆} = ${{\tilde {N}}^{ \bullet }}$, ${{V}_{i}}$ – шаг и C_i = $({{C}_{{i - 1}}}{{{{\backslash }}}^{ \bullet }}{{V}_{i}})\, \cup \,V_{i}^{ \bullet }$ ∈ ∈ $\mathcal{C}\mathcal{U}\mathcal{T}(\tilde {N})$ для всех $1 \leqslant i \leqslant 3$. А из примера 3 знаем, что $\tau ({{C}_{0}}\, = \,{\text{\{ }}{{b}_{1}}{\text{\} }})$ = 0, $\tau ({{C}_{1}}\, = \,{\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }})$ = 1, $\tau ({{C}_{2}}\, = \,{\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }})$ = 2, $\tau ({{C}_{3}} = {\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }})$ = 3, $\tau ({\text{\{ }}{{b}_{2}},{{b}_{5}}{\text{\} }}) = \, \bot $ и $\tau ({\text{\{ }}{{b}_{4}},{{b}_{5}}{\text{\} }})$ = τ({b₃, b₆}) = 0. Тогда ${{C}_{0}}$, ${{C}_{1}}$, ${{C}_{2}}$, ${{C}_{3}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$. Покажем, что ${{V}_{i}} \in Fi({{C}_{{i - 1}}})$, т.е. V_i может произойти в ${{C}_{{i - 1}}}$, для любого $1 \leqslant i \leqslant 3$.

i = 1. $^{ \bullet }{{e}_{1}} \subseteq {{C}_{0}}$, т.е. ${{e}_{1}} \in En({{C}_{0}})$, и $\tau (C{\text{'}} = ({{C}_{0}}{{{{\backslash }}}^{ \bullet }}{{e}_{1}}) \cup e_{1}^{ \bullet } = {\text{\{ }}{{b}_{2}},{{b}_{3}}{\text{\} }})$ = τ(C₁) = 1, т.е. $C{\text{'}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$. Тогда событие ${{e}_{1}}$ может произойти в ${{C}_{0}}$, т.е. ${{V}_{1}} = {\text{\{ }}{{e}_{1}}{\text{\} }} \in Fi({{C}_{0}})$.

i = 2. $^{ \bullet }{{e}_{2}} \subseteq {{C}_{1}}$, т.е. ${{e}_{2}} \in En({{C}_{1}})$, и $\tau (C{\text{'}} = ({{C}_{1}}{{{{\backslash }}}^{ \bullet }}{{e}_{2}}) \cup e_{2}^{ \bullet } = {\text{\{ }}{{b}_{3}},{{b}_{4}}{\text{\} }})$ = τ(C₂) = 2, т.е. $C{\text{'}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$. Значит, событие ${{e}_{2}}$ может произойти в ${{C}_{1}}$, т.е. ${{V}_{2}} = {\text{\{ }}{{e}_{2}}{\text{\} }} \in Fi({{C}_{1}})$.

i = 3. $^{ \bullet }{{e}_{3}} \subseteq {{C}_{2}}$, т.е. ${{e}_{3}} \in En({{C}_{2}})$, и τ(C ' = = $({{C}_{2}}{{{{\backslash }}}^{ \bullet }}{{e}_{3}}) \cup e_{3}^{ \bullet }$ = {b₃, b₆}) = 0, т.е. $C{\text{'}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$. Тогда событие ${{e}_{3}}$ может произойти в ${{C}_{2}}$. Далее, $^{ \bullet }{{e}_{4}} \subseteq {{C}_{2}}$, т.е. ${{e}_{4}} \in En({{C}_{2}})$, и $\tau (C{\text{''}} = ({{C}_{2}}{{{{\backslash }}}^{ \bullet }}{{e}_{4}}) \cup e_{4}^{ \bullet }$ = = {b₄, b₅}) = 0, т.е. $C{\text{''}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$. Значит, событие ${{e}_{4}}$ тоже может произойти в ${{C}_{2}}$. Кроме того, имеем, что τ(C ''' = $({{C}_{2}}{{{{\backslash }}}^{ \bullet }}{\text{\{ }}{{e}_{3}},{{e}_{4}}{\text{\} }})\, \cup \,{{{\text{\{ }}{{e}_{3}},{{e}_{4}}{\text{\} }}}^{ \bullet }}\, = \,{\text{\{ }}{{b}_{5}},{{b}_{6}}{\text{\} }})$ = = τ(C₃) = 0, т.е. $C{\text{'''}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$. Следовательно, получаем, что ${{V}_{3}} = {\text{\{ }}{{e}_{3}},{{e}_{4}}{\text{\} }} \in Fi({{C}_{2}})$.

Значит, ${{C}_{{i - 1}}}\mathop \Rightarrow \limits^{{{V}_{i}}} {{C}_{i}}$ для всех ($1 \leqslant i \leqslant 3$). Таким образом, последовательность $\omega $ – график ВПСС $\widetilde {TN}$.

Сформулируем и докажем свойства графиков ВПСС TN.

Утверждение 1. Для графика $\omega = {{C}_{0}}$ ${{V}_{1}}$ ${{C}_{1}}$ $ \ldots $ ${{V}_{n}}$ ${{C}_{n}} \in Graph(TN)$ верно:

(а) $\bigcap\limits_{1 \leqslant i \leqslant n} {{{V}_{i}}} = \not {0}$ и $\bigcup\limits_{1 \leqslant i \leqslant n} {{{V}_{i}}} = E$;

(б) $\tau (C{\text{'}}) = 0$ для любого $C{\text{'}} \in (\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$\(C₀, C₁, ..., C_n});

(в) если $C \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$, то существует график $\omega {\text{'}} \in Graph(TN)$ такой, что $\omega _{i}^{'} = {{C}_{0}}\; \ldots \;C_{i}^{'}$ = C, где $0 \leqslant i \leqslant \left| {\omega {\text{'}}} \right|$.

Доказательство. Поскольку $\omega \in Graph(TN)$, то $\omega \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}{{(TN)}^{ \star }}$, ${{C}_{0}} = {{\,}^{ \bullet }}N$, ${{C}_{n}} = {{N}^{ \bullet }}$ и ${{C}_{{i - 1}}}\mathop \Rightarrow \limits^{{{V}_{i}}} {{C}_{i}}$ для всех $1 \leqslant i \leqslant n$. Благодаря определению 3, имеем, что $ \downarrow {{\,}^{ \bullet }}N = \not {0}$ и $ \downarrow {{N}^{ \bullet }}$ = E. Исходя из того, что $\not {0} \subseteq \downarrow C \subseteq E$, получаем ${{C}_{0}} \preccurlyeq C \preccurlyeq {{C}_{n}}$ для всех $C \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$. Так как ${{C}_{{i - 1}}}\mathop \Rightarrow \limits^{{{V}_{i}}} {{C}_{i}}$, то верно, что ${{V}_{i}}\, \in \,Fi({{C}_{{i - 1}}})$. Значит, ${{V}_{i}}\, \cap \, \downarrow {{C}_{{i - 1}}}\, = \,\not {0}$ и C_i = = $({{C}_{{i - 1}}}{{{{\backslash }}}^{ \bullet }}{{V}_{i}}) \cup V_{i}^{ \bullet }$, т.е. ${{V}_{i}} \subseteq \downarrow {{C}_{i}}$ для всех $1 \leqslant i \leqslant n$.

(а) Покажем, что $\bigcap\nolimits_{1 \leqslant i \leqslant n} {{{V}_{i}}} = \not {0}$. Предположим обратное, т.е. существует $e \in {{V}_{k}} \cap {{V}_{l}}$ для некоторых $1 \leqslant k < l \leqslant n$. Так как $k < l$, то ${{C}_{k}} \preccurlyeq {{C}_{{l - 1}}}$, т.е. $ \downarrow {\kern 1pt} {{C}_{k}}\, \subseteq \, \downarrow {\kern 1pt} {{C}_{{l - 1}}}$, что противоречит $e\, \in \,{{V}_{k}}\, \subseteq \, \downarrow {\kern 1pt} {{C}_{k}}\, \subseteq \, \downarrow {\kern 1pt} {{C}_{{l - 1}}}$ и ${{V}_{l}} \cap \downarrow {{C}_{{l - 1}}} = \not {0}$.

Поскольку $ \downarrow {{C}_{0}} = \not {0}$, $ \downarrow {{C}_{i}} = \, \downarrow {{C}_{{i - 1}}} \cup {{V}_{i}}$ для всех $1 \leqslant i \leqslant n$ и $ \downarrow {{C}_{n}} = E$, то $\bigcup\nolimits_{1 \leqslant i \leqslant n} {{{V}_{i}}} $ = E.

(б) Возьмем произвольное C ∈ ∈ $(\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$\{C₀, C₁, ..., C_n}). Тогда ${{C}_{0}} \prec C \prec {{C}_{n}}$. Предположим обратное, т.е. $\tau (C) > 0$. По определению 4, имеем, что $C \notin Cut({{C}_{i}})$. Тогда либо $C\, \prec \,{{C}_{i}}$, т.е. $ \downarrow {\kern 1pt} C\, \subset \, \downarrow {\kern 1pt} {{C}_{i}}$, либо ${{C}_{i}} \prec C$, т.е. $ \downarrow {\kern 1pt} {{C}_{i}}\, \subset \, \downarrow {\kern 1pt} C$, для любого $0 \leqslant i \leqslant n$. Поскольку $ \downarrow {{C}_{n}}$ = E, то найдется $1 \leqslant k \leqslant n$ такой, что $ \downarrow {\kern 1pt} {{C}_{{k - 1}}}\, \subset \, \downarrow {\kern 1pt} C\, \subset \, \downarrow {\kern 1pt} {{C}_{k}}$, так как ${{C}_{{k - 1}}}\,\not {z}\,C\,\not {z}\,{{C}_{k}}$. Исходя из того, что $e\, \in \, \downarrow {\kern 1pt} {{C}_{k}}{{\backslash }}{\kern 1pt} \downarrow {\kern 1pt} C$ ⊂ ⊂ V_k ∈ Fi(C_{k – 1}), то верно, что $e \in Fi({{C}_{{k - 1}}})$. Значит, получаем, что ${{C}_{{k - 1}}}{{\mathop \Rightarrow \limits^e }_{i}}C{\kern 1pt} {\text{'}}$ ∈ $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$. Следовательно, $\tau (C{\text{'}}) \ne \bot $ и $C \in Cut(C{\text{'}})$. Пришли к противоречию с тем, что $\tau (C) > 0$, по определению 4.

(в) Поскольку $^{ \bullet }N = C_{0}^{'} \preccurlyeq C \preccurlyeq C_{m}^{'} = {{N}^{ \bullet }}$ и $C_{0}^{'},C,C_{m}^{'} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$, то получаем, что $C_{0}^{'} \sqsubseteq C \sqsubseteq C_{m}^{'}$, по лемме 2(а). Следовательно, существует график $\omega {\text{'}} = C_{0}^{'}$ ... $C_{i}^{'} = C$ ... $C_{m}^{'}$ с префиксом $\omega _{i}^{'} = C_{0}^{'}$ ... $C$, где $m = \left| {\omega {\text{'}}} \right|$ и $0 \leqslant i \leqslant m$. ◻

Определим отображение из ВПСС $TN$ в НВСП $\mathcal{T}\mathcal{N}$.

Определение 6. Пусть $\mathcal{T}\mathcal{N} = (\mathcal{N} = (P$, $T$, $F$, ${{M}_{0}})$, $D)$ – НВСП и $TN = (N = (B$, $E$, $G),\tau )$ – ВПСС. Гомоморфизмом из TN в $\mathcal{T}\mathcal{N}$ называется отображение $\varphi :(B \cup E) \to (P \cup T)$ такое, что верно:

• $\varphi (B) \subseteq P$ и $\varphi (E) \subseteq T$;

• сужение $\varphi $ на подмножество $^{ \bullet }e$ – биекция между $^{ \bullet }e$ и $^{ \bullet }\varphi (e)$ для всех $e \in E$;

• сужение $\varphi $ на подмножество ${{e}^{ \bullet }}$ – биекция между ${{e}^{ \bullet }}$ и $\varphi {{(e)}^{ \bullet }}$ для всех $e \in E$;

• сужение $\varphi $ на подмножество $^{ \bullet }N$ – биекция между $^{ \bullet }N$ и M₀.

В этом случае пара $\pi = (TN,\varphi )$ называется временным процессом НВСП $\mathcal{T}\mathcal{N}$.

Пример 5. Рассмотрим НВСП $\widetilde {\mathcal{T}\mathcal{N}}$, представленную на рис. 1, ВПСС $\widetilde {TN}$ из примера 3 и отображение $\varphi $, определенное следующим образом: $\varphi ({{b}_{i}}) = {{p}_{i}}$ для $i \in \{ 1,2,3,5\} $, $\varphi ({{b}_{4}}) = {{p}_{2}}$, $\varphi ({{b}_{6}}) = {{p}_{4}}$ и $\varphi ({{e}_{i}}) = {{t}_{i}}$ для $1 \leqslant i \leqslant 4$. Тогда имеем, что $\varphi (B) \subseteq P$, $\varphi (E) \subseteq T$ и сужение $\varphi $ на подмножество $^{ \bullet }\widetilde N\, = \,\{ {{b}_{1}}\} $ – биекция между $^{ \bullet }\tilde {N}$ и ${{M}_{0}} = \{ {{p}_{1}}\} $. Кроме того, для всех $e \in \{ {{e}_{1}},\; \ldots ,\;{{e}_{4}}\} $ верно, что сужение $\varphi $ на подмножество $^{ \bullet }e$ (${{e}^{ \bullet }}$) – биекция между $^{ \bullet }e$ (${{e}^{ \bullet }}$) и $^{ \bullet }\varphi (e)$ ($\varphi {{(e)}^{ \bullet }}$). Следовательно, $\varphi $ – гомоморфизм из $\widetilde {TN}$ в $\widetilde {\mathcal{T}\mathcal{N}}$ и $\pi = (\widetilde {TN},\varphi )$ – временной процесс НВСП $\widetilde {\mathcal{T}\mathcal{N}}$.

Два временных процесса π = (TN = (N = = $(B,E,G),\tau ),\varphi )$ и $\pi {\text{'}} = (TN{\text{'}} = (N{\text{'}} = (B{\text{'}},E{\text{'}},G{\text{'}}),\tau {\text{'}}),\varphi {\text{'}})$ являются изоморфными (обозначается $\pi \simeq \pi {\text{'}}$), если существует биективное отображение $\gamma \,:\,B\, \cup \,E\, \to \,B{\text{'}} \cup \,E{\text{'}}$ такое, что верно:

• $\gamma (B) = B{\text{'}}$ и $\gamma (E) = E{\text{'}}$;

• $xGy \Leftrightarrow \gamma (x)G{\text{'}}\gamma (y)$ для любых $x,y \in B \cup E$;

• $\tau (C) = \tau {\text{'}}(\gamma (C))$ для любого $C \in \mathcal{C}\mathcal{U}\mathcal{T}(N)$;

• $\varphi (x) = \varphi {\text{'}}(\gamma (x))$ для любого $x \in B \cup E$.

Рассмотрим свойства гомоморфизма и шага временного процесса НВСП $\mathcal{T}\mathcal{N}$, которые следуют из определений ПСС и гомоморфизма.

Лемма 3. Пусть $\pi = (TN,\varphi )$ – временной процесс НВСП $\mathcal{T}\mathcal{N}$, $C \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ и сужение $\varphi $ на C – биекция между C и $\varphi (C)$. Тогда для любого $V \in En(C)$ верно:

(а) сужение $\varphi $ на множество $^{ \bullet }V$ – биекция между $^{ \bullet }V$ и $^{ \bullet }\varphi (V)$;

(б) сужение $\varphi $ на V – биекция между V и $\varphi (V)$;

(в) если $\varphi (V)$ – шаг НВСП, то сужение $\varphi $ на множество ${{V}^{ \bullet }}$ – биекция между ${{V}^{ \bullet }}$ и $\varphi {{(V)}^{ \bullet }}$.

Пусть $\pi = (TN,\varphi )$ – временной процесс НВСП $\mathcal{T}\mathcal{N}$ и $\omega = {{C}_{0}}\; \ldots \;{{C}_{n}} \in Graph(TN)$. Для префикса ${{\omega }_{i}} = {{C}_{0}} \ldots {{C}_{i}}$ графика $\omega $ и перехода t ∈ T таких, что $t \in En(\varphi ({{C}_{i}}))$ определим функцию

Значение данной функции соответствует времени, прошедшему с момента, когда переход $t$ стал разрешенным в разметке $\varphi ({{C}_{{k + 1}}})$, и до момента, когда этот переход все еще остается разрешенным в разметке $\varphi ({{C}_{i}})$.

Установим полезный факт, который следует из определений временной функции и графика ВПСС TN.

Лемма 4. Пусть $\pi = (TN,\varphi )$ – временной процесс НВСП $\mathcal{T}\mathcal{N}$, ${{\omega }_{l}} = {{C}_{0}}\; \ldots \;{{C}_{l}}$ и $\omega _{m}^{'} = C_{0}^{'}\; \ldots \;C_{m}^{'}$ – префиксы графиков $\omega $ и $\omega {\text{'}}$ из $Graph(TN)$ соответственно и переход $t \in T$ такие, что ${{C}_{l}} = C_{m}^{'}$ и $t \in En(\varphi ({{C}_{l}} = C_{m}^{'}))$. Тогда

Используя эту лемму и тот факт, что для каждого сечения C из $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ существует график, префикс которого заканчивается этим сечением, можем в качестве параметров функции ${\mathbf{Clock}}$ взять сечение $C$ и переход $t$, разрешенный в $\varphi (C)$.

Введем понятие допустимого временного процесса НВСП.

Определение 7. Временной процесс π = (TN = = (N = $(B,E,G)),\varphi )$ НВСП $\mathcal{T}\mathcal{N}$ называется допустимым, если для каждого события $e \in E$ и каждого сечения $C \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ таких, что $e \in Fi(C)$, выполняется:

Пусть $Proc(\mathcal{T}\mathcal{N})$ обозначает множество допустимых процессов НВСП $\mathcal{T}\mathcal{N}$.

Пример 6. Рассмотрим НВСП $\widetilde {\mathcal{T}\mathcal{N}}$ из примера 1 и временной процесс $\pi = (\widetilde {TN},\varphi )$ из примера 5. Покажем, что $\pi \in Proc(\widetilde {\mathcal{T}\mathcal{N}})$.

Перечислим все сечения из $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$ из примера 3: $\tau ({{C}_{0}} = \{ {{b}_{1}}\} ) = 0$, $\tau ({{C}_{1}} = \{ {{b}_{2}},{{b}_{3}}\} ) = 1$, $\tau ({{C}_{2}} = \{ {{b}_{3}},{{b}_{4}}\} ) = 2$, $\tau ({{C}_{3}} = \{ {{b}_{5}},{{b}_{6}}\} ) = 3$ и $\tau (C_{3}^{'}$ = {b₃, b₆}) = $\tau (С_{3}^{{''}} = \{ {{b}_{4}},{{b}_{5}}\} )$ = 0. Легко убедиться в том, что $\omega {\text{'}} = {{C}_{0}}$ $\{ {{e}_{1}}\} $ ${{C}_{1}}$ $\{ {{e}_{2}}\} $ ${{C}_{2}}$ $\{ {{e}_{3}}\} $ $C_{3}^{'}$ $\{ {{e}_{4}}\} $ ${{C}_{3}}$ и $\omega {\text{''}} = {{C}_{0}}$ $\{ {{e}_{1}}\} $ ${{C}_{1}}$ $\{ {{e}_{2}}\} $ ${{C}_{2}}$ $\{ {{e}_{4}}\} $ $C_{3}^{{''}}$ $\{ {{e}_{3}}\} $ C₃ – графики ВПСС $TN$. Кроме того, имеем, что $Fi({{C}_{0}}) = \{ {{e}_{1}}\} $, $Fi({{C}_{1}})$ = {e₂}, $Fi({{C}_{2}}) = \{ {{e}_{3}},{{e}_{4}},\{ {{e}_{3}},{{e}_{4}}\} \} $, $Fi(C_{3}^{'}) = \{ {{e}_{4}}\} $, $Fi(C_{3}^{{''}}) = \{ {{e}_{3}}\} $ и $Fi({{C}_{3}}) = \not {0}$. Заметим, что каждое сечение из $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(\widetilde {TN})$ и каждое событие, которое может произойти в каком-нибудь из этих сечений, присутствуют хотя бы в одном из графиков $\omega {\text{'}}$ и $\omega {\text{''}}$.

Вычислим значение функции ${\mathbf{Clock}}$:

• ${\mathbf{Clock}}({{C}_{0}},\varphi ({{e}_{1}})) = \tau ({{C}_{0}}) = 0$;

• ${\mathbf{Clock}}({{C}_{1}},\varphi ({{e}_{2}})) = \tau ({{C}_{1}}) = 1$;

• ${\mathbf{Clock}}({{C}_{2}},\varphi ({{e}_{3}})) = \tau ({{C}_{1}}) + \tau ({{C}_{2}}) = 3$;

• ${\mathbf{Clock}}({{C}_{2}},\varphi ({{e}_{4}})) = \tau ({{C}_{1}}) + \tau ({{C}_{2}}) = 3$.

• ${\mathbf{Clock}}(С_{3}^{'},\varphi ({{e}_{4}})) = \tau ({{C}_{1}}) + \tau ({{C}_{2}}) + \tau (С_{3}^{'}) = 3$.

• ${\mathbf{Clock}}(С_{3}^{{''}},\varphi ({{e}_{3}})) = \tau ({{C}_{1}}) + \tau ({{C}_{2}}) + \tau (С_{3}^{{''}}) = 3$.

Тогда получаем:

• $Eft({{t}_{1}}) = 0 \leqslant {\mathbf{Clock}}({{C}_{0}},\varphi ({{e}_{1}})) = 0 \leqslant Lft({{t}_{1}}) = 2$;

• $Eft({{t}_{2}}) = 0 \leqslant {\mathbf{Clock}}({{C}_{1}},\varphi ({{e}_{2}})) = 1 \leqslant Lft({{t}_{2}}) = 1$;

• $Eft({{t}_{3}}) = 3 \leqslant {\mathbf{Clock}}({{C}_{2}},\varphi ({{e}_{3}})) = 3 \leqslant Lft({{t}_{3}}) = 4$;

• $Eft({{t}_{4}}) = 2 \leqslant {\mathbf{Clock}}({{C}_{2}},\varphi ({{e}_{4}})) = 3 \leqslant Lft({{t}_{4}}) = 3$.

• $Eft({{t}_{4}}) = 2 \leqslant {\mathbf{Clock}}(С_{3}^{'},\varphi ({{e}_{4}})) = 3 \leqslant Lft({{t}_{4}}) = 3$,

• $Eft({{t}_{3}}) = 3 \leqslant {\mathbf{Clock}}(С_{3}^{{''}},\varphi ({{e}_{3}})) = 3 \leqslant Lft({{t}_{3}}) = 4$.

Следовательно, $\pi $ является допустимым временным процессом НВСП $\widetilde {\mathcal{T}\mathcal{N}}$.

4. ВЗАИМОСВЯЗИ ГРАФИКОВ ВРЕМЕННЫХ ПРОЦЕССОВ И ПРОБЕГОВ НВСП

В этом разделе изучаются связи пробегов НВСП и графиков допустимых временных процессов НВСП.

Пусть $\pi = (TN,\varphi )$ – допустимый временной процесс НВСП $\mathcal{T}\mathcal{N}$ и $\omega = {{C}_{0}}$ ${{V}_{1}}$ ${{C}_{1}}$ ... ${{V}_{n}}$ ${{C}_{n}}$ – график ВПСС TN. Определим отображение FS графика $\omega $ ВПСС TN в последовательность временных задержек и шагов в НВСП $\mathcal{T}\mathcal{N}$ следующим образом: $FS(\omega ) = \tau ({{C}_{0}})$ $\varphi ({{V}_{1}})$ $\tau ({{C}_{1}})$ ... $\varphi ({{V}_{n}})$ $\tau ({{C}_{n}})$.

Покажем, что если FS отображает префикс ${{\omega }_{m}}$ ($0 \leqslant m \leqslant n$) графика ω в пробег из начального состояния $({{M}_{0}},{{I}_{0}})$ в состояние $({{M}_{m}},I_{m}^{'})$ в НВСП $\mathcal{T}\mathcal{N}$, то φ отображает C_m в M_m и значение динамической временной функции $I_{m}^{'}(t)$ равно ${\mathbf{Clock}}({{C}_{m}}$, t) для любого перехода t, разрешенного в M_m.

Утверждение 2. Пусть $\pi = (TN = (N,\tau ),\varphi )$ – допустимый временной процесс НВСП $\mathcal{T}\mathcal{N}$ и ω = C₀${{V}_{1}}$ ${{C}_{1}}$ … V_n C_n – график ВПСС $TN$. Если $FS({{\omega }_{m}})\, \in \,\widehat {\mathcal{I}\mathcal{S}}(\mathcal{T}\mathcal{N})$ ($0 \leqslant m \leqslant n$), т.е. (M₀, I₀) $\xrightarrow{{\tau ({{C}_{0}})}}$ → (M₀, $I_{0}^{'})$ $\xrightarrow{{\varphi ({{V}_{1}})}}$ (M₁, I₁) $\xrightarrow{{\varphi ({{C}_{1}})}}$ $({{M}_{1}},I_{1}^{'})$ … $({{M}_{{m - 1}}},I_{{m - 1}}^{'})$ $\xrightarrow{{\varphi ({{V}_{m}})}}$ (M_m, I_m) $\xrightarrow{{\tau ({{C}_{m}})}}$ $({{M}_{m}},I_{m}^{'})$, то для каждого $0 \leqslant i \leqslant m$ верно:

(а) сужение функции $\varphi $ на C_i – биекция между C_i и M_i;

(б) $I_{i}^{'}(t) = {\mathbf{Clock}}({{C}_{i}},t)$ для всех $t \in En({{M}_{i}})$.

Доказательство. Будем доказывать индукцией по $0 \leqslant i \leqslant m$.

$i = 0$. Тогда ${{C}_{0}} = {{\,}^{ \bullet }}N$ и $\tau ({{C}_{0}}) \in {{\mathbb{R}}_{{ \geqslant 0}}}$, по определению 5.

(а) Сужение функции $\varphi $ на C₀ – биекция между C₀ и M₀, согласно определению 6.

(б) Возьмем произвольное $t \in En({{M}_{0}})$. Так как не существует k < 0 такого, что $t \notin En(\varphi ({{C}_{k}}))$, то ${\mathbf{Clock}}({{C}_{0}},t) = \tau ({{C}_{0}})$. В силу определения 2, имеем, что $I_{0}^{'}(t)\, = \,({{I}_{0}}(t)\, = \,0)\, + \,\tau ({{C}_{0}})$. Следовательно, Clock(C₀, t) = = $I_{0}^{'}(t)$.

i > 0. По предположению индукции, сужение функции φ на ${{C}_{{i - 1}}}$ – биекция между ${{C}_{{i - 1}}}$ и ${{M}_{{i - 1}}}$ и $I_{{i - 1}}^{'}(t) = {\mathbf{Clock}}({{C}_{{i - 1}}},t)$ для всех $t\, \in \,En({{M}_{{i - 1}}}\, = \,\varphi ({{C}_{{i - 1}}}))$.

(а) Согласно условию утверждения, имеем, что $\varphi ({{V}_{i}})$ – шаг НВСП и $\varphi ({{V}_{i}}) \in Fi({{M}_{{i - 1}}},I_{{i - 1}}^{'})$. Используя определение 2, построим M_i = $({{M}_{{i - 1}}}{{{{\backslash }}}^{ \bullet }}\varphi ({{V}_{i}})) \cup \varphi {{({{V}_{i}})}^{ \bullet }}$. Благодаря лемме 3(в), получаем, что M_i = = $(\varphi ({{C}_{{i - 1}}}){{{{\backslash }}}^{ \bullet }}\varphi ({{V}_{i}})) \cup \varphi {{({{V}_{i}})}^{ \bullet }}$ = $\varphi (({{C}_{{i - 1}}}{{{{\backslash }}}^{ \bullet }}{{V}_{i}})\, \cup \,V_{i}^{ \bullet })$ = φ(C_i). Так как $\mathcal{T}\mathcal{N}$ – бесконтактная НВСП, то верно, что $(\varphi ({{C}_{{i - 1}}}){{{{\backslash }}}^{ \bullet }}\varphi ({{V}_{i}})) \cap \varphi {{({{V}_{i}})}^{ \bullet }} = \not {0}$. Следовательно, сужение функции φ на C_i – биекция между C_i и M_i.

(б) Возьмем произвольный переход $t \in En({{M}_{i}})$. Предположим, что $ \uparrow enabled(t$, ${{M}_{{i - 1}}}$, $\varphi ({{V}_{i}}))$ – истина. По определению 2, имеем, что $t \notin En({{M}_{{i - 1}}}$ = = φ(C_{i – 1})), t ∈ $En({{M}_{i}} = \varphi ({{C}_{i}}))$, ${{I}_{i}}(t) = 0$ и $I_{i}^{'}(t)\, = \,\tau ({{C}_{i}})$. Тогда ${\mathbf{Clock}}({{C}_{i}},t) = \tau ({{C}_{i}})\, = \,I_{i}^{'}(t)$. Теперь предположим, что $ \uparrow enabled(t$, M_{i – 1}, $\varphi ({{V}_{i}}))$ – ложь. По определению 2, получаем, что $t\, \in \,En({{M}_{{i - 1}}}$ = φ(C_{i – 1})), I_i(t) = = ${{I}_{{i - 1}}}(t)$ и $I_{i}^{'}(t) = {{I}_{{i - 1}}}(t)$ + τ(C_i). Так как $t \in En({{M}_{{i - 1}}})$ и $t \in En({{M}_{i}})$, то Clock(C_i, t) = ${\mathbf{Clock}}({{C}_{{i - 1}}},t) + \tau ({{C}_{i}})$. Следовательно, верно, что ${\mathbf{Clock}}({{C}_{i}},t) = I_{i}^{'}(t)$. ◻

Покажем, что функция FS отображает любой график допустимого временного процесса в некоторый пробег в контексте НВСП $\mathcal{T}\mathcal{N}$.

Теорема 1. Пусть π = (TN = (N, τ), $\varphi ) \in Proc(\mathcal{T}\mathcal{N})$ и $\omega = {{C}_{0}}{{V}_{1}}{{C}_{1}}\; \ldots \;{{V}_{n}}{{C}_{n}} \in Graph(TN)$. Тогда FS(ω) = $\tau ({{C}_{0}})$ $\varphi ({{V}_{1}})$ $\tau ({{C}_{1}})$ … $\varphi ({{V}_{n}})$ $\tau ({{C}_{n}}){\kern 1pt} \, \in \,\widehat {\mathcal{I}\mathcal{S}}(\mathcal{T}\mathcal{N})$.

Доказательство. Будем доказывать индукцией по $0 \leqslant i \leqslant n$.

i = 0. Очевидно, что $FS({{\omega }_{0}}) = \tau ({{C}_{0}}) \in \widehat {\mathcal{I}\mathcal{S}}(\mathcal{T}\mathcal{N})$.

i > 0. По предположению индукции, имеем, что $FS({{\omega }_{{i - 1}}}) \in \widehat {\mathcal{I}\mathcal{S}}(\mathcal{T}\mathcal{N})$. Из леммы 3(а) и утверждения 2(а) следует, что $\varphi ({{V}_{i}})$ – шаг НВСП. Так как $\omega \in Graph(TN)$, то ${{C}_{{i - 1}}}\mathop \Rightarrow \limits^{{{V}_{i}}} {{C}_{i}}$. Значит, верно, что ${{V}_{i}} \in Fi({{C}_{{i - 1}}})$. Тогда ${{V}_{i}} \in En({{C}_{{i - 1}}})$, т.е. $^{ \bullet }{{V}_{i}} \subseteq {{C}_{{i - 1}}}$. Кроме того, в силу утверждения 2(а), получаем, что $^{ \bullet }\varphi ({{V}_{i}}) \subseteq \varphi ({{C}_{{i - 1}}}) = {{M}_{{i - 1}}}$, т.е. $\varphi ({{V}_{i}}) \in En({{M}_{{i - 1}}})$. Так как ${{V}_{i}} \in Fi({{C}_{{i - 1}}})$, то ${{e}_{i}} \in Fi({{C}_{{i - 1}}})$ для всех e_i ∈ V_i. Тогда, по определению 7, имеем, что $Eft(\varphi ({{e}_{i}})) \leqslant {\mathbf{Clock}}({{C}_{{i - 1}}}$, $\varphi ({{e}_{i}})) \leqslant Lft(\varphi ({{e}_{i}}))$ для всех e_i ∈ V_i. Согласно утверждению 2(б), верно, что $Eft(\varphi ({{e}_{i}})) \leqslant I_{{i - 1}}^{'}(\varphi ({{e}_{i}})) \leqslant Lft(\varphi ({{e}_{i}}))$ для всех $\varphi ({{e}_{i}}) \in \varphi ({{V}_{i}})$. Значит, $\varphi ({{V}_{i}})$ может сработать в состоянии $({{M}_{{i - 1}}},I_{{i - 1}}^{'})$. Используя определение 2, построим M_i, I_i и $I_{i}^{'}$. Тогда имеем ${{M}_{i}} = ({{M}_{{i - 1}}}{{\backslash }}$$^{ \bullet }\varphi ({{V}_{i}}))$ $ \cup $ $ \cup $ $\varphi {{({{V}_{i}})}^{ \bullet }}$. Кроме того, для всех $t \in En({{M}_{i}})$ положим: ${{I}_{i}}(t) = \left\{ \begin{gathered} 0,\,{\text{если}}\, \uparrow enabled(t,{{M}_{{i - 1}}},\varphi ({{V}_{i}})), \hfill \\ I_{{i - 1}}^{'}(t),\,{\text{иначе}}. \hfill \\ \end{gathered} \right.$ Поскольку $\tau ({{C}_{i}}) \in {{\mathbb{R}}_{{ \geqslant 0}}}$, то ход времени $\tau ({{C}_{i}})$ приводит к новому состоянию $({{M}_{i}},I_{i}^{'})$, где $I_{i}^{'}(t) = {{I}_{i}}(t) + \tau ({{C}_{i}})$ для всех $t \in En({{M}_{i}})$. Следовательно, имеем, что $FS({{\omega }_{i}}) \in \widehat {\mathcal{I}\mathcal{S}}(\mathcal{T}\mathcal{N})$. ◻

Покажем, что FS – сюръекция, т.е. для произвольного заданного пробега НВСП $\mathcal{T}\mathcal{N}$ существует ее допустимый временной процесс с некоторым графиком, применение к которому функции FS дает заданный пробег.

Теорема 2. Пусть $\mathcal{T}\mathcal{N} = ((P,T,F,{{M}_{0}}),D)$ – НВСП и $\hat {\sigma } = {{\theta }_{0}}$ ${{U}_{1}}$ ${{\theta }_{1}}$ … U_n ${{\theta }_{n}} \in \widehat {\mathcal{I}\mathcal{S}}(\mathcal{T}\mathcal{N})$. Существует допустимый временной процесс π* НВСП $\mathcal{T}\mathcal{N}$ с графиком ω* таким, что $\hat {\sigma } = FS(\omega *)$.

Доказательство. Сначала построим конструкцию $N* = (B*,E*,G*)$ следующим образом:

Легко видеть, что $N* = (B*,E*,G*)$ – ПСС, поскольку $\mathcal{T}\mathcal{N}$ – T-закрытая НВСП.

Построим шаги $V_{i}^{ * } = {\text{\{ }}e_{{i,t}}^{ * } \in E{\text{*}}|t \in {{U}_{i}}{\text{\} }}$ для всех $1 \leqslant i \leqslant n$ и сечения $C_{0}^{ * }\, = {{\,}^{ \bullet }}N{\text{*}}$ и $C_{i}^{ * }$ = $(C_{{i - 1}}^{ * }{{{{\backslash }}}^{ \bullet }}V_{i}^{ * }) \cup V{{_{i}^{ * }}^{ \bullet }}$ для всех $1 \leqslant i \leqslant n$.

Определим функцию τ* : $\mathcal{C}\mathcal{U}\mathcal{T}(N*)\, \to \,{{\mathbb{R}}_{{ \geqslant 0}}}\, \cup \,{\text{\{ }}{\kern 1pt} \bot {\kern 1pt} {\text{\} }}$ так:

Ясно, что $TN* = (N*,\tau *)$ – ВПСС. Тогда $\omega * = C_{0}^{ * }$ $V_{1}^{ * }$ $C_{1}^{ * }$ ... $V_{n}^{ * }$ $C_{n}^{ * }$ – график $TN{\text{*}}$, по построению и лемме 2(б).

Осталось определить функцию φ так: $\varphi {\text{*}}(b_{{i,p}}^{ * })$ = p для всех $b_{{i,p}}^{ * } \in B{\text{*}}$ и $\varphi {\text{*}}(e_{{i,t}}^{ * }) = t$ для всех $e_{{i,t}}^{ * } \in E{\text{*}}$, которая, как следует из построения TN*, является гомоморфизмом.

Таким образом, $\pi * = (TN*,\varphi *)$ – временной процесс $\mathcal{T}\mathcal{N}$. Понятно, что $FS(\omega *) = \hat {\sigma }$.

Докажем, что $\pi * \in Proc(\mathcal{T}\mathcal{N})$. Рассмотрим произвольное событие $e \in E{\text{*}}$ и произвольное сечение $C \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN*)$ такие, что $e \in Fi(C)$. По построению, существует шаг $V_{i}^{ * }$ ($1 \leqslant i \leqslant n$) такой, что $e\, \in \,V_{i}^{ * }$. Так как $\omega {\text{*}}\, \in \,Graph(TN*)$, то $V_{i}^{ * }\, \in \,Fi(C{\text{'}}\, = \,C_{{i - 1}}^{ * })$ и $C{\text{'}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN*)$. Тогда $e \in Fi(C{\text{'}})$. Поскольку $FS(\omega *) = \hat {\sigma }$, из определения 2 следует, что шаг $\varphi (V_{i}^{ * })$ может сработать в (M_{i – 1}, $I_{{i - 1}}^{'})$, т.е. φ(e) ∈ ∈ $En({{M}_{{i - 1}}})$ и $Eft(\varphi (e))$ ≤ $I_{{i - 1}}^{'}(\varphi (e)) \leqslant Lft(\varphi (e))$. Более того, $I_{{i - 1}}^{'}(\varphi (e))$ =  ${\mathbf{Clock}}(C{\text{'}},\varphi (e))$, согласно утверждению 2(б). Значит, $Eft(\varphi (e)) \leqslant {\mathbf{Clock}}(C{\kern 1pt} {\text{'}}$, φ(e)) ≤ ≤ $Lft(\varphi (e))$.

Покажем, что ${\mathbf{Clock}}(C,\varphi (e)) = {\mathbf{Clock}}(C{\text{'}},\varphi (e))$. Так как $e \in Fi(C) \cap Fi(C{\text{'}})$, то существует C'' ∈ ∈ $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ такое, что $C{\text{''}} \preccurlyeq C$, $C{\text{''}} \preccurlyeq C{\text{'}}$ и $e \in Fi(C{\text{''}})$, по лемме 2(в).

Рассмотрим случай, когда $C{\text{''}} \preccurlyeq C$. Если $C{\text{''}} = C$, то ${\mathbf{Clock}}(C,\varphi (e)) = {\mathbf{Clock}}(C{\text{''}},\varphi (e))$. Пусть $C{\text{''}} \prec C$. Согласно лемме 2(а), $C{\text{''}} \sqsubset C$, т.е. существует график $\omega \in Graph(TN)$ такой, что ${{\omega }_{{l + m}}} = {{C}_{0}}$ … ${{C}_{l}} = C{\text{''}}$ ${{C}_{{l + 1}}}$ … ${{C}_{{l + m}}} = C$, где $0 \leqslant l < \left| \omega \right|$, $m \geqslant 1$ и $0 \leqslant l + m \leqslant \left| \omega \right|$. Рассмотрим произвольное сечение ${{C}_{{l + j}}}$ ($1 \leqslant j \leqslant m$). Так как $\omega \in Graph(TN)$, то ${{C}_{{l + j}}} \in \mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$ и $ \downarrow C{\text{''}} \subset \downarrow {{C}_{{l + j}}} \subseteq \downarrow C$. Поскольку $e \in Fi(C{\text{''}}) \cap Fi(C)$, то $^{ \bullet }e \subseteq C{\text{''}} \cap C$ и C''' = = $((C{\text{''}}{{{{\backslash }}}^{ \bullet }}e) \cup {{e}^{ \bullet }})$ ∈ $\mathcal{R}\mathcal{C}\mathcal{U}\mathcal{T}(TN)$. Кроме того, $^{ \bullet }e \subseteq {{C}_{{l + j}}}$, т.е. $e \notin \downarrow {{C}_{{l + j}}}$. Так как $ \downarrow C{\text{'''}} = \, \downarrow C{\text{''}} \cup {\text{\{ }}e{\text{\} }}$, то $\neg ( \downarrow C{\text{'''}} \subseteq \downarrow {{C}_{{l + j}}})$ и $\neg ( \downarrow {{C}_{{l + j}}} \subseteq \, \downarrow C{\text{'''}})$, т.е. $C{\text{'''}}\,z\,{{C}_{{l + j}}}$. Согласно лемме 2(б), получаем, что $\tau ({{C}_{{l + j}}})$ = 0. По определению 6, $\varphi {{(}^{ \bullet }}e)$ = $^{ \bullet }\varphi (e) \subseteq \varphi ({{C}_{{l + j}}})$, т.е. φ(e) ∈ ∈ $En(\varphi ({{C}_{{l + j}}}))$. В силу произвольности выбора $1 \leqslant j \leqslant m$, имеем Clock(C, φ(e)) = Clock(C'', φ(e)) + $\sum\limits_{1 \leqslant j \leqslant m} \tau ({{C}_{{l + j}}})$. Так как $\sum\limits_{1 \leqslant j \leqslant m} \tau ({{C}_{{l + j}}})$ = 0, то Clock(C, φ(e)) = ${\mathbf{Clock}}(C{\text{''}},\varphi (e))$.

Рассуждая аналогично в случае, когда $C{\text{''}} \preccurlyeq C$, получаем, что ${\mathbf{Clock}}(C{\text{'}},\varphi (e))$ = ${\mathbf{Clock}}(C{\text{''}},\varphi (e))$.

Следовательно, ${\mathbf{Clock}}(C,\varphi (e))\, = \,{\mathbf{Clock}}(C{\text{'}},\varphi (e))$. ◻

Пример 7. Поясним конструкцию допустимого временного процесса π* из доказательства теоремы 2 с использованием НВСП $\widetilde {\mathcal{T}\mathcal{N}}$, представленной на рис. 1, и пробега $\hat {\sigma } = {{\theta }_{0}}$ ${{U}_{1}}$ ${{\theta }_{1}}$ ${{U}_{2}}$ ${{\theta }_{2}}$ ${{U}_{3}}$ ${{\theta }_{3}} = 0$ $\{ {{t}_{1}}\} $ 1 $\{ {{t}_{2}}\} $ 2 $\{ {{t}_{3}},{{t}_{4}}\} $ $3 \in \widehat {\mathcal{I}\mathcal{S}}(\widetilde {\mathcal{T}\mathcal{N}})$ из примера 1.

Сначала построим $N* = (B*,E*,G*)$ следующим образом.

•B* = $\{ b_{{0,p}}^{ * }|p\, \in \,{{M}_{0}}{\text{\} }}\, \cup \,{\text{\{ }}b_{{i,p}}^{ * }|p\, \in \,U_{i}^{ \bullet },1\, \leqslant \,i\, \leqslant \,3{\text{\} }}$ = ${\text{\{ }}b_{{0,{{p}_{1}}}}^{ * },$ $b_{{1,{{p}_{2}}}}^{ * },$ $b_{{1,{{p}_{3}}}}^{ * }$, $b_{{2,{{p}_{2}}}}^{ * }$, $b_{{3,{{p}_{4}}}}^{ * }$, $b_{{3,{{p}_{5}}}}^{ * }{\text{\} }}$, так как ${{M}_{0}} = \{ {{p}_{1}}\} $, $U_{1}^{ \bullet }$ = {p₂, p₃}, $U_{2}^{ \bullet } = \{ {{p}_{2}}\} $, $U_{3}^{ \bullet } = \{ {{p}_{4}},{{p}_{5}}\} $;

• $E* = {\text{\{ }}e_{{i,t}}^{ * }|t \in {{U}_{i}},1 \leqslant i \leqslant 3{\text{\} \{ }}e_{{1,{{t}_{1}}}}^{ * },e_{{2,{{t}_{2}}}}^{ * },e_{{3,{{t}_{3}}}}^{ * },e_{{3,{{t}_{4}}}}^{ * }{\text{\} }}$;

• $G* = {\text{\{ }}(e_{{i,t}}^{ * },b_{{i,p}}^{ * }) \in E{\text{*}} \times B{\text{*}}|p \in {{t}^{ \bullet }}$, $1 \leqslant i \leqslant 3\} $ ∪ ∪ ${\text{\{ }}(b_{{j,p}}^{ * },e_{{i,t}}^{ * })\, \in \,B{\text{*}}\, \times \,E*|p\, \in {{\,}^{ \bullet }}t$, $j\, = \,{\text{max\{ }}k\, < \,i|b_{{k,p}}^{ * }\, \in \,{{B}^{ * }}{\text{\} }}$, $1 \leqslant i \leqslant 3\} = $ ${\text{\{ }}(e_{{1,{{t}_{1}}}}^{ * }$, $b_{{1,{{p}_{2}}}}^{ * })$, $(e_{{1,{{t}_{1}}}}^{ * }$, $b_{{1,{{p}_{3}}}}^{ * })$, $(e_{{2,{{t}_{2}}}}^{ * }$, $b_{{2,{{p}_{2}}}}^{ * })$, $(e_{{3,{{t}_{3}}}}^{ * }$, $b_{{3,{{p}_{4}}}}^{ * })$, $(e_{{3,{{t}_{4}}}}^{ * }$, $b_{{3,{{p}_{5}}}}^{ * }){\text{\} }}$ $ \cup $ ${\text{\{ }}(b_{{0,{{p}_{1}}}}^{ * }$, $e_{{1,{{t}_{1}}}}^{ * })$, $(b_{{1,{{p}_{2}}}}^{ * }$, $e_{{2,{{t}_{2}}}}^{ * })$, $(b_{{2,{{p}_{2}}}}^{ * }$, $e_{{3,{{t}_{3}}}}^{ * })$, $(b_{{1,{{p}_{3}}}}^{ * }$, $e_{{3,{{t}_{4}}}}^{ * }){\text{\} }}$.

Видим, что получили ПСС, представленную на рис. 2, с точностью до переименования условий и событий.

Сейчас можем построить шаги $V_{1}^{ * } = {\text{\{ }}e_{{1,{{t}_{1}}}}^{ * }{\text{\} }}$, $V_{2}^{ * }\, = \,{\text{\{ }}e_{{2,{{t}_{2}}}}^{ * }{\text{\} }}$ и $V_{3}^{ * }\, = \,{\text{\{ }}e_{{3,{{t}_{3}}}}^{ * }$, $e_{{3,{{t}_{4}}}}^{ * }{\text{\} }}$, поскольку $V_{i}^{ * }$ = = ${\text{\{ }}e_{{i,t}}^{ * }\, \in \,E*|t\, \in \,{{U}_{i}}{\text{\} }}$ для всех $1 \leqslant i \leqslant 3$. Тогда получаем:

• $C_{0}^{ * } = {{\,}^{ \bullet }}N* = {\text{\{ }}b \in B{\text{*}}|{{\,}^{ \bullet }}b = \not {0}{\text{\} }} = {\text{\{ }}b_{{0,{{p}_{1}}}}^{ * }{\text{\} }}$;

• $C_{1}^{ * } = (C_{0}^{ * }{{{{\backslash }}}^{ \bullet }}V_{1}^{ * }) \cup V{{_{1}^{ * }}^{ \bullet }}$ = 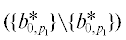∪ ∪ ${\text{\{ }}b_{{1,{{p}_{2}}}}^{ * },b_{{1,{{p}_{3}}}}^{ * }{\text{\} }} = {\text{\{ }}b_{{1,{{p}_{2}}}}^{ * },b_{{1,{{p}_{3}}}}^{ * }{\text{\} }}$;

• $C_{2}^{ * } = (C_{1}^{ * }{{{{\backslash }}}^{ \bullet }}V_{2}^{ * }) \cup V{{_{2}^{ * }}^{ \bullet }}$ = $(\{ b_{{1,{{p}_{2}}}}^{ * },b_{{1,{{p}_{3}}}}^{ * }\} {{\backslash }}\{ b_{{1,{{p}_{2}}}}^{ * }\} )$ ∪ ∪ $\{ b_{{2,{{p}_{2}}}}^{ * }\} = \{ b_{{1,{{p}_{3}}}}^{ * },b_{{2,{{p}_{2}}}}^{ * }\} $;

• $C_{3}^{ * }\, = \,(C_{2}^{ * }{{{{\backslash }}}^{ \bullet }}V_{3}^{ * })\, \cup \,V{{_{3}^{ * }}^{ \bullet }}$ = $({\text{\{ }}b_{{1,{{p}_{3}}}}^{ * }$, 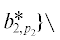$\{ b_{{1,{{p}_{3}}}}^{ * },b_{{2,{{p}_{2}}}}^{ * }\} )$ ∪ ∪ $\{ b_{{3,{{p}_{4}}}}^{ * },b_{{3,{{p}_{5}}}}^{ * }\} = \{ b_{{3,{{p}_{4}}}}^{ * },b_{{3,{{p}_{5}}}}^{ * }\} $.

Легко проверить, что $\mathcal{C}\mathcal{U}\mathcal{T}(N*)$ = ${\text{\{ }}C_{0}^{ * },C_{1}^{ * },C_{2}^{ * },C_{3}^{ * },$ $\{ b_{{1,{{p}_{2}}}}^{ * },b_{{3,{{p}_{5}}}}^{ * }\} ,$ ${\text{\{ }}b_{{1,{{p}_{3}}}}^{ * },b_{{3,{{p}_{4}}}}^{ * }{\text{\} }},$ $\{ b_{{2,{{p}_{2}}}}^{ * },b_{{3,{{p}_{5}}}}^{ * }\} \} $.

Теперь можем построить $TN* = (N*,\tau *)$, где

• $\tau (C_{0}^{ * }) = {{\theta }_{0}} = 0$, $\tau (C_{1}^{ * }) = {{\theta }_{1}} = 1$, $\tau (C_{2}^{ * }) = {{\theta }_{2}} = 2$, $\tau (C_{3}^{ * }) = {{\theta }_{3}} = 3$;

• $\tau (\{ b_{{1,{{p}_{2}}}}^{ * },b_{{3,{{p}_{5}}}}^{ * }\} ) = \, \bot $, так как $\{ b_{{1,{{p}_{2}}}}^{ * },b_{{3,{{p}_{5}}}}^{ * }\} \in Cut(C_{2}^{ * })$ и ${{\theta }_{2}} > 0$;

• $\tau (\{ b_{{1,{{p}_{3}}}}^{ * },b_{{3,{{p}_{4}}}}^{ * }\} ) = \tau (\{ b_{{2,{{p}_{2}}}}^{ * },b_{{3,{{p}_{5}}}}^{ * }\} ) = 0$.

Наконец, определим $\varphi *:(B{\text{*}} \cup E*) \to (P \cup T)$ так: $\varphi (b_{{i,p}}^{ * }) = p$ для всех $b_{{i,p}}^{ * } \in B{\text{*}}$ и $\varphi (e_{{i,t}}^{ * }) = t$ для всех $e_{{i,t}}^{ * } \in E{\text{*}}$.

Таким образом, получили временной процесс $\pi * = (TN*,\varphi *)$ НВСП $\widetilde {\mathcal{T}\mathcal{N}}$. Заметим, что π* является изоморфным допустимому временному процессу из примера 5.

Далее установим, что FS – инъекция, т.е. конструкция допустимого временного процесса НВСП $\mathcal{T}\mathcal{N}$ в доказательстве теоремы 2 единственная с точностью до изоморфизма.

Теорема 3. Пусть $\mathcal{T}\mathcal{N}$ – НВСП и $\hat {\sigma } = {{\theta }_{0}}$ ${{U}_{1}}$ ${{\theta }_{1}}$ ... ${{U}_{n}}$ ${{\theta }_{n}} \in \widehat {\mathcal{I}\mathcal{S}}(\mathcal{T}\mathcal{N})$. Допустимый временной процесс π* НВСП $\mathcal{T}\mathcal{N}$ с графиком $\omega {\text{*}}$ таким, что $\hat {\sigma }$ = = FS(ω*), является единственным с точностью до изоморфизма.

Доказательство. Пусть π = (TN = (N = = $(B,E,G),\tau ),\varphi )$ – произвольный допустимый временной процесс НВСП $\mathcal{T}\mathcal{N}$ и $\omega = {{C}_{0}}$ ${{V}_{1}}$ ${{C}_{1}}$ ... ${{V}_{n}}$ ${{C}_{n}}$ – график ВПСС $TN$ такой, что FS(ω) = = $\hat {\sigma } = \tau ({{C}_{0}})$ $\varphi ({{V}_{1}})$ $\tau ({{C}_{1}})$ ... $\varphi ({{V}_{n}})$ $\tau ({{C}_{n}})$.

Рассмотрим множество $E$. Согласно утверждению 1(а), верно, что $\bigcap\nolimits_{1 \leqslant i \leqslant n} {{{V}_{i}}} = \not {0}$ и $\bigcup\nolimits_{1 \leqslant i \leqslant n} {{{V}_{i}}} = E$. По лемме 3(б), имеем, что сужение $\varphi $ на множество V_i – биекция между V_i и $\varphi ({{V}_{i}}) = {{U}_{i}}$ ($1 \leqslant i \leqslant n$). Тогда без потери общности полагаем, что E = = $\{ {{e}_{{i,t}}} \in {{V}_{i}}|t \in {{U}_{i}}$, $1 \leqslant i \leqslant n\} $ и $\varphi ({{e}_{{i,t}}}) = t$ для каждого ${{e}_{{i,t}}} \in E$.

Рассмотрим множество $B$. Из определения 3 имеем, что $\left| {^{ \bullet }b} \right| \leqslant 1$ для любого b ∈ B и $E{{ = }^{ \bullet }}B$. Тогда $^{ \bullet }b = \not {0}$, если $b{{ \in }^{ \bullet }}N$, и существует единственное событие e ∈ E такое, что ${\text{\{ }}e{\text{\} }} = {{\,}^{ \bullet }}b$, т.е. $b \in {{e}^{ \bullet }}$, если $b \in B{{{{\backslash }}}^{ \bullet }}N$. По утверждению 1(а), верно, что $\bigcap\nolimits_{1 \leqslant i \leqslant n} {{{V}_{i}}} = \not {0}$ и $\bigcup\nolimits_{1 \leqslant i \leqslant n} {{{V}_{i}}} = E$. Значит, для любого условия $b \in B{{{{\backslash }}}^{ \bullet }}N$ существует единственный шаг ${{V}_{i}}$ ($1 \leqslant i \leqslant n$) с единственным событием $e \in {{V}_{i}}$ таким, что $b \in {{e}^{ \bullet }}$, и для любого события e ∈ E существует $b\, \in \,B{{{{\backslash }}}^{ \bullet }}N$ такое, что $b\, \in \,{{e}^{ \bullet }}$, поскольку $E = {{\,}^{ \bullet }}B$. Следовательно, получаем, что $\bigcap\nolimits_{1 \leqslant i \leqslant n} {V_{i}^{ \bullet }} = \not {0}$ и $\bigcup\nolimits_{1 \leqslant i \leqslant n} {V_{i}^{ \bullet }} = B{{{{\backslash }}}^{ \bullet }}N$. В силу определения 6, сужение $\varphi $ на $^{ \bullet }N$ – биекция между $^{ \bullet }N$ и M₀. Кроме того, так как $\varphi ({{V}_{i}})$ $(1 \leqslant i \leqslant n)$ – шаг в НВСП $\mathcal{T}\mathcal{N}$, то из леммы 3(в) следует, что сужение φ на множество $V_{i}^{ \bullet }$ – биекция между $V_{i}^{ \bullet }$ и $\varphi {{({{V}_{i}})}^{ \bullet }} = U_{i}^{ \bullet }$ $(1 \leqslant i \leqslant n)$. Тогда без потери общности полагаем, что $B\, = \,{\text{\{ }}{{b}_{{0,p}}}\,{{ \in }^{ \bullet }}N|p\, \in {{M}_{0}}{\text{\} }}$ ∪ ${\text{\{ }}{{b}_{{i,p}}}\, \in \,V_{i}^{ \bullet }|p\, \in \,U_{i}^{ \bullet }$, $1 \leqslant i \leqslant n{\text{\} }}$ и $\varphi ({{b}_{{j,p}}}) = p$ для каждого ${{b}_{{j,p}}} \in B$.

Рассмотрим множество G. Возьмем произвольное ${{e}_{{i,t}}} \in E$. Согласно конструкциям B и E имеем, что $e_{{i,t}}^{ \bullet } = {\text{\{ }}{{b}_{{i,p}}} \in B|p \in {{t}^{ \bullet }}{\text{\} }}$. Из определения 5 следует, что $^{ \bullet }{{e}_{{i,t}}}{{ \subseteq }^{ \bullet }}{{V}_{i}} \subseteq {{C}_{{i - 1}}}$. В силу утверждения 2(а), сужение функции φ на C_{i – 1} – биекция между C_{i – 1} и M_{i – 1}. Кроме того, из определения 6 имеем, что $\varphi {{(}^{ \bullet }}{{e}_{{i,t}}}) = {{\,}^{ \bullet }}\varphi ({{e}_{{i,t}}}){{ = }^{ \bullet }}t$. Тогда $^{ \bullet }{{e}_{{i,t}}}$ = {b_{j, p} ∈ ∈ $B|p\,{{ \in }^{ \bullet }}t$, ${{b}_{{j,p}}}\, \in \,{{C}_{{i - 1}}}{\text{\} }}$. Значит, $^{ \bullet }{{e}_{{i,t}}}$ = ${\text{\{ }}{{b}_{{j,p}}}\, \in \,B|p\, \in {{\,}^{ \bullet }}t$, $j = {\text{max\{ }}k < i|{{b}_{{k,p}}} \in B{\text{\} \} }}$, поскольку ${{C}_{0}}{{ = }^{ \bullet }}N$ и C_k = $({{C}_{{k - 1}}}{{{{\backslash }}}^{ \bullet }}{{V}_{k}}) \cup V_{k}^{ \bullet }$ ($1 \leqslant k \leqslant n$). Следовательно, G = {(e_i,t, ${{b}_{{i,p}}}) \in E \times B|p \in {{t}^{ \bullet }},$ $1 \leqslant i \leqslant n{\text{\} }}$ ∪ {(b_j,p, ${{e}_{{i,t}}})\, \in \,B\, \times \,E|p\, \in {{\,}^{ \bullet }}t,j$ = max{k < $i|{{b}_{{k,p}}} \in B{\text{\} }},$ $1 \leqslant i \leqslant n{\text{\} }}$.

Так как $FS(\omega ) = \hat {\sigma }$, то, используя определение 4 и утверждение 1(б), для каждого $C \in \mathcal{C}\mathcal{U}\mathcal{T}(N)$ получаем:

Сравним допустимый временной процесс π НВСП $\mathcal{T}\mathcal{N}$ и график ω ВПСС TN c допустимым временным процессом π* НВСП $\mathcal{T}\mathcal{N}$ и графиком ω* ВПСС TN* из доказательства теоремы 2. Так как $FS(\omega ) = FS(\omega {\text{*}}) = \hat {\sigma }$, то эти графики имеют одинаковую длину. Тогда, из построений π и π* получаем, что $\pi \simeq \pi {\text{*}}$. ◻

Итак, было показано, что FS – биективное отображение между графиками временных процессов и пробегами из начального состояния в контексте НВСП $\mathcal{T}\mathcal{N}$.

5. ЗАКЛЮЧЕНИЕ

В статье для НВСП со стратегиями слабого хода времени и устойчиво атомарного сброса часов были определены и изучены интерливинговая и две ‘истинно параллельные’ (шаговая и частично-упорядоченная) семантики. При слабой временной стратегии ход времени в состояниях НВСП произволен, так как неограничен необходимостью срабатывания переходов в соответствии с их временными интервалами. Поэтому при смене состояний НВСП ход времени не может быть совмещен со срабатыванием переходов. В интерливинговом пробеге таких НВСП смена одного состояния на другое осуществляется за счет либо хода времени, либо срабатывания перехода. В шаговом пробеге срабатывает не один переход, а множество параллельных переходов. Частично-упорядоченная семантика представляется в виде множества временных процессов, состоящих из ВПСС и их гомоморфизмов в НВСП. При этом во временных процессах срабатываниям переходов НВСП сопоставляются события ВПСС, а ходу времени в НВСП – временные характеристики сечений ВПСС. Было введено и изучено понятие шагового (интерливингового) графика ВПСС – последовательности смены сечений посредством выполнения параллельных событий (одоного события). Также, было доказано, что при отображении гомоморфизмом графика ВПСС в пробег НВСП разметки в состояниях НВСП соответствуют сечениям графика, а значение динамической временной функции для разрешенных переходов в состояниях НВСП – значениям специально разработанной функции Clock, которая находит ближайшее сечение, в соответствующей разметке которого переход не был разрешен, и суммирует значения временных характеристик сечений, соответствующих разметкам, в которых переход стал и продолжает быть разрешенным. Таким образом, в функции Clock естественным образом отражена устойчиво атомарная пространственная стратегия НВСП. Для того, чтобы во временном процессе учитывались временные задержки срабатываний переходов, заданные в синтаксисе НВСП, определены условия его корректности (допустимости), которые вычисляются на основе границ временных интервалов разрешенных переходов и значений функции Clock. Основным результатом данной работы является установление биективного соответствия между интерливинговыми/шаговыми пробегами НВСП и интерливинговыми/шаговыми графиками ВПСС во временных процессах НВСП. На основе вышесказанного можно сделать вывод, что разработан метод построения адекватного и корректного частично-упорядоченного представления в виде временных процессов поведения НВСП со слабой временной и устойчиво атомарной стратегиями. Насколько нам известно, аналогов этому методу нет в литературе, а также мы не встречали работы, посвященные ‘истинно параллельной’ семантике таких НВСП.

Отметим, что предложенный в [10] метод построения временных процессов для НВСП основывается на сильной временной и промежуточной пространственной стратегиях и поэтому не может быть использован для рассматриваемых в этой статье стратегий поведения НВСП. В сильной временной стратегии ход времени в состоянии НВСП ограничен срабатыванием разрешенного перехода, показания часов которого достигли значений его временного интервала. Поэтому смену состояний в НВСП возможно осуществлять посредством объединенных в единое действие хода времени и срабатывания перехода. В этом случае временные процессы НВСП могут быть построены за счет сопоставления событиям ВПСС временных характеристик, соответствующих временам срабатываний переходов. Кроме того, особенности сильной временной и промежуточной пространственной стратегий отражены в условиях корректности временных процессов, определяемых с учетом границ временных интервалов разрешенных переходов и значений функции TOE, вычисляемых на основе временных характеристик событий ВПСС моменты времени, когда фишки появляются во всех входных местах разрешенных переходов.

В качестве дальнейшей работы планируется использовать разработанные в этой статье семантики для определения и изучения поведенческих эквивалентностей НВСП со слабой временной и различными пространственными стратегиями в дихотомиях интерливинг – частичный порядок и линейное – ‘ветвящееся’ время.