Программирование, 2022, № 1, стр. 34-39

1. ВВЕДЕНИЕ

Целью данной работы является исследование асимптотических разложений решений второго члена четвертой иерархии Пенлеве [1], [2]. Функции Пенлеве используются в статистической физике, квантовой теории поля, геометрии минимальных поверхностей, теории чисел и других областях.

2. МЕТОДЫ СТЕПЕННОЙ ГЕОМЕТРИИ

Для построения асимптотических разложений используются методы степенной геометрии [3]. Выпишем часть шагов этих методов.

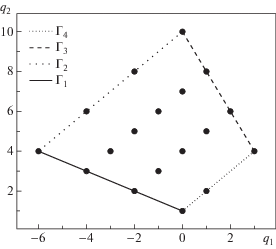
Рассматривается дифференциальное уравнение, которое имеет вид дифференциальной суммы, т.е. его левая часть является многочленом от независимой переменной, зависимой переменной и ее производных – суммой дифференциальных мономов. Для такого уравнения строится многоугольник Ньютона на координатной плоскости (${{q}_{1}}$, ${{q}_{2}}$) – выпуклая оболочка имеющихся точек. В итоге каждой точке полученного многоугольника Ньютона соответствует один или несколько мономов. Последовательно рассматриваются все обобщенные грани многоугольника (вершины и ребра). Суммируются мономы, которые соответствуют обобщенной грани, получают функцию укороченной суммы $\hat {f}_{j}^{{(d)}}(X)$ = $\sum {{{a}_{i}}(X)} $ по $Q({{a}_{i}}) \in S_{j}^{{(d)}}$.

Для каждого ребра строим внешние нормали, общий вид координат которых $\lambda \omega (1,r)$, где $\lambda > 0$. Если $x \to 0$, то $\omega < 0$, если $x \to \infty $, то $\omega > 0$. Координаты нормалей определяют степень первого члена асимптотического разложения решения уравнения, для которого вычисляется асимптотика y(x): для ребра с внешней нормалью $\omega (1,r)$ общий вид асимптотики решения уравнения имеет вид $y = c{{x}^{r}}$. Для вершин также определяются нормальные конусы: как части плоскости, лежащие между лучами, натянутыми на векторы внешних нормалей к ребрам, примыкающим к вершинам.

3. ПОСТРОЕНИЕ МНОГОУГОЛЬНИКА НЬЮТОНА ДЛЯ ВТОРОГО ЧЛЕНА ЧЕТВЕРТОЙ ИЕРАРХИИ ПЕНЛЕВЕ

Запишем второй член четвертой иерархии Пен-леве [3]. Заметим, что это уравнение сразу представлено в виде дифференциальной суммы:

Здесь x – независимая, y – зависимая комплексные переменные, β, δ – комплексные параметры. Далее считаем, что оба параметра уравнения ненулевые.

Дифференциальным мономам, участвующим в уравнении (3.1), соответствуют следующие 18 показателей степени: $( - 4;\;3)$, $( - 6;\;4)$, $( - 3;\;4)$, (–4; 6), $( - 2;\;5)$, $( - 2;\;2)$, $( - 1;\;6)$, $( - 2;\;8)$, (–1; 3), $(0;\;10)$, (1; 8), $(0;\;7)$, $(2;\;6)$, $( - 1;\;5)$, $(0;\;4)$, $(3;\;4)$, $(1;\;2)$, $(0;\;1)$.

Отображаем их на координатную плоскость (${{q}_{1}}$, ${{q}_{2}}$) и строим многоугольник Ньютона как их выпуклую оболочку на рис. 1.

Данный многоугольник можем построить с помощью кода из Листинга 1 (в команду Expand вместо многоточия подставляется левая часть уравнения (3.1)).

(*Исходное уравнение *)

equation = Expand [ . . . ] ;

order = 4 ; v a r i a b l e = x ;

function = y [ x ] ;

(*Вычисление векторных степеней мономов *)

d = Coefficient Rules [equation,

  Join [{variable, function},

  Table [D[function, {variable, i}],

  {i, 1, order}]]]/.Rule => List

vectorDegree [degrees_ ] :=

  {degrees [[1]], degrees[[2]]} +

  Total [Table[{=( i = 2), 1}

  degrees [[i]], {i, 3,

  Length [degrees]}]]

points = Sort [DeleteDuplicates [Map[

vectorDegree, (#[[1]]) & /@d]]]

(*Построение многоугольника Ньютона *)

convexHull = ConvexHullMesh [points,

  PlotTheme => “Detailed”];

convexHull Points =

  MeshCoordinates [convexHull];

Show[convexHull, ListPlot [points,

  PlotStyle => {Red,

  PointSize [Large]}]]

Листинг 1: Построение многоугольника Ньютона

Каждому ребру и вершине многоугольника Ньютона, изображённого на рис. 1, сопоставим принадлежащие ему точки Q_i и составим укороченные суммы. Это можно сделать с помощью программы символьных вычислений, которая приведена в Листинге 2.

(*Точки вершин многоугольника Ньютона *)

gamma0 = (#[[1]]) & /@

  Rationalize [ MeshPrimitives[

Region ‘Mesh‘ MergeCells [convexHull], 0]]

lines = Rationalize [ MeshPrimitives [

Region ‘Mesh‘ MergeCells [convexHull], 1]];

(*Точки сторон многоугольника Ньютона *)

gamma1 = Table [Select [points,

  RegionMember[lines[[i]], #] &], {i,

  1, Length [lines]}]

(*Укороченные уравнения для вершин *)

f0 = Table [FromCoefficientRules [Map[

Rule [#[[1]], #[[2]]]&, Select [d,

vectorDegree [#[[1]]] == gamma0 [[i]]

&]], Join[{variable, function},

Table [D[function, {variable, i}],

{ i, 1, order}]]], {i, 1,

Length [gamma0]}]

(*Укороченные уравнения для сторон *)

f1 = Table [FromCoefficientRules [Map[

Rule [#[[1]], #[[2]]] &,

  Flatten [Table [Select[d,

  vectorDegree [#[[1]]] ==

  gamma1 [[i]] [[j]] &], {j, 1,

  Length [gamma1 [[i]]]}], 1]],

  Join [{variable, function},

  Table [D[function, {variable, i}],

  {i, 1, order}]]], {i, 1,

  Length [gamma1]}]

Листинг 2: Вычисление укороченных уравнений

Теперь последовательно рассмотрим ребра получившегося многоугольника, а затем его вершины и найдём отвечающие им асимптотики и асимптотические разложения.

4. РЕБРО ${{\Gamma }_{1}}$

Ребру ${{\Gamma }_{1}}$ отвечает внешняя нормаль ${{N}_{1}}$ = (–1; –2) и укороченное уравнение

Этому ребру соответствует асимптотика $y = c{{x}^{2}}$ при $x \to 0$. Значения c находим из уравнения

ненулевыми корнями которого являются ${{c}_{1}}$ = –0.1β (некратный) и ${{c}_{2}} = 0.5\beta $ (кратности два).

Проверим, есть ли критические числа, получим линейный оператор

При подстановке $y = - \tfrac{\beta }{{10}}{{x}^{2}}$ в выражение (4.2) получим оператор

Применим оператор $\varkappa $ к ${{x}^{k}}$ и сократим результат на ${{x}^{k}}{{\beta }^{3}}$, получим характеристический многочлен

с корнями ${{k}_{1}} = - 3$, ${{k}_{2}} = 1$, ${{k}_{3}} = 4$, ${{k}_{4}} = 6$. Учитывая подходящие значения k, а именно, k = 4 и $k = 6$, выпишем множество степеней, участвующих в разложении, продолжающем рассматриваемую асимптотику, и сразу приведем соответствующее семейство степенных разложений решений при $x \to 0$: где ${{c}_{4}},{{c}_{6}} \in \mathbb{C}$ – произвольные константы, остальные коэффициенты c_k, где $k > 6,$ однозначно выражаются через них.

При подстановке $y = \tfrac{\beta }{2}{{x}^{2}}$ получим нулевой оператор, так как соответствующий корень был кратным. Делаем замену $y = \tfrac{\beta }{2}{{x}^{2}} + w$ в уравнении (3.1) и проводим вычисления для уравнения, получившегося после замены. Получаем два варианта для следующего члена разложения: w_{1, 2} = $\left( {\tfrac{\beta }{{20}} \pm \tfrac{{3\beta \sqrt {2\delta } }}{{250}}} \right){{x}^{5}}$. Применяя первую вариацию укороченного уравнения, соответствующего ребру многоугольника Ньютона уравнения с зависимой переменной $w$ (вычисленную на решениях ${{w}_{{1,2}}}$), к x^k, получаем характеристический многочлен, корнями которого являются ${{k}_{1}} = 0$, ${{k}_{2}} = 1$, ${{k}_{3}} = 4$, ${{k}_{4}} = 6$. Нам опять подходят только значения 4 и 6. Итак, продолжая асимптотику $y = \tfrac{\beta }{2}{{x}^{2}}$ в виде степенных асимптотических разложений, получаем 2 семейства разложений решений при $x \to 0$:

где ${{c}_{4}},{{c}_{6}} \in \mathbb{C}$ – произвольные константы, c_k, где $k > 6,$ однозначно выражаются через них.

5. РЕБРО ${{\Gamma }_{2}}$

Данному ребру отвечает внешняя нормаль ${{N}_{2}}$ = = (–1; 1) и укороченное уравнение

что дает соответствие асимптотики вида $y = \tfrac{c}{x}$ при $x \to 0$. Значения c находим из уравнения ненулевые корни которого – это ${{c}_{1}} = 2$, ${{c}_{2}} = - 2$ (некратные), ${{c}_{3}} = 1$, ${{c}_{4}} = - 1$ (каждый – кратности два).

Для корней $c = \pm 2$ получаем, что корни k характеристического многочлена таковы, что $k \in \{ - 3$, ‒2, 3, 4}, что влияет на структруру степеней, участвующих в степенном разложении. Для продолжений этих асимтотик при $x \to 0$ имеем такие семейства разложения:

здесь ${{c}_{3}},{{c}_{4}} \in \mathbb{C}$ – произвольные константы, остальные коэффициенты c_k, $k > 4$ однозначно определяются через них.

Для исследования разложений, соответствующих кратным корням $c = \pm 1$ делаем в уравнении (5.1) замену $y = \pm \tfrac{1}{x} + w$, проводя процесс поиска следующего члена асимптотики для нового уравнения и его многоугольника Ньютона. Так, следующее слагаемое асимптотики имеет вид w_{6, 7} = = $ \pm \tfrac{{\sqrt {9\delta - 8 - 8\beta - 2{{\beta }^{2}}} }}{{4\sqrt 2 }}{{x}^{2}}$ для $y = \tfrac{1}{x}$ и w_{8, 9} = = $ \pm \tfrac{{\sqrt { - 9\delta + 8 - 8\beta + 2{{\beta }^{2}}} }}{{4\sqrt 2 }}{{x}^{2}}$ для $y = - \tfrac{1}{x}$ (здесь нумерацию приводим в соответствии с нумерацией соответствующих разложений). Далее находим характеристический многочлен. Его корни – это ${{k}_{1}} = - 2$, ${{k}_{2}} = 0$, ${{k}_{3}} = 3$, ${{k}_{4}} = 4$. Критическими числами являются ${{k}_{3}}$ и ${{k}_{4}}$, так как для них $\operatorname{Re} {{k}_{i}} > 2$. Имеем следующие четыре семейства асимптотических разложений решений при $x \to 0$:

вновь ${{c}_{3}},{{c}_{4}} \in \mathbb{C}$ – произвольные константы, остальные постоянные ${{c}_{k}},$ $k > 4$ однозначно определяются через них.

6. РЕБРО ${{\Gamma }_{3}}$

Ребру ${{\Gamma }_{3}}$ соответствует внешняя нормаль ${{N}_{3}}$ = = (1; 1/2) и укороченное уравнение

Сразу отметим, что укороченное уравнение (6.1) алгебраическое, критических чисел нет. Исходя из вида внешней нормали, ищем степенную асимптотику соответствующего решения в виде y = cx^1/2, подставляя это выражение в уравнение (6.1). Получаем соотношение

откуда выражаем ненулевые значения c: ${{c}_{{1,2}}} = \pm i$ кратности 2, ${{c}_{{3,4}}} = \pm i\sqrt {\tfrac{2}{5}} $ – некратные корни. Продолжая асимптотики вида $y = {{c}_{k}}{{x}^{{1/2}}}$ в виде степенных асимптотических разложений, получаем 6 разложений решений при $x \to \infty $:

7. РЕБРО ${{\Gamma }_{4}}$

Укороченное уравнение для ребра ${{\Gamma }_{4}}$ имеет вид

а внешняя нормаль – это ${{N}_{4}} = (1;\; - 1)$, ребру опять соответствуют асимптотики решений при $x \to \infty $, это асимптотики вида $y = c{{x}^{{ - 1}}}$. Укороченное уравнение вновь является алгебраическим, не дает критических чисел. Для нахождения значений $c$ имеем уравнение откуда выражаем ненулевые значения c: ${{c}_{1}} = \beta $ кратности 1, ${{c}_{2}} = - \tfrac{\beta }{2}$ – кратности 2. Продолжаем асимптотики вида $y = {{c}_{k}}{{x}^{{1/2}}}$ в виде степенных асимптотических разложений, имеем ещё 3 разложения решений при $x \to \infty $:

8. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ РЕШЕНИЙ ДЛЯ ВЕРШИН

Рассмотрим укороченные уравнения, соответствующие вершинам.

Вершинам (0, 1), (3, 4) и (0, 10) соответствуют алгебраические мономы $1{\text{/}}3{{\beta }^{3}}y$, $ - 4{\text{/}}3{{x}^{3}}{{y}^{4}}$, $ - 10{\text{/}}3{{y}^{{10}}}$, они не дают асимптотик решений уравнений, согласно [1]. Вершине $( - 6,\;4)$ соответствует нормальный конус ${\text{\{ }}({{p}_{1}},{{p}_{2}}):({{p}_{1}},{{p}_{2}})$ = λ₁(–1; –2) + + ${{\lambda }_{2}}( - 1;\,\,1),$ ${{\lambda }_{1}},{{\lambda }_{2}} \in \mathbb{R},$ ${{\lambda }_{1}} > 0,{{\lambda }_{2}} > 0{\text{\} }}$, что дает ограничения на показатель степени: {r : –1 < Rer < 2, $r \ne - 1,\;r \ne 2{\text{\} }}$. Также данной вершине отвечает укороченное уравнение

Подставим в него $y = c{{x}^{r}}$, приравняем полученное выражение к нулю и решим уравнение относительно r; получим возможные значения $r$: $r = - 3,$ $r = 0,$ $r = 1,$ $r = 4$.

Только r = 0, $r = 1$ лежат в нормальном конусе, соответствующем данной вершине, откуда легко вычисляются дополнительные однопараметрические семейства асимптотик решений второго члена четвертой иерархии Пенлеве при $x \to 0$, а именно, имеются асимптотики вида $y = c$ и $y = cx$, где $c \in \mathbb{C}{{\backslash \{ }}0{\text{\} }}$ – произвольная постоянная. В данной работе продолжим только вторую асимптотику как асимптотическое разложение.

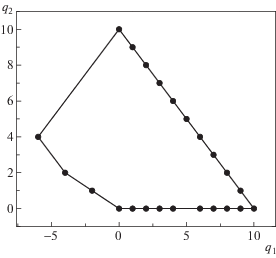
Стандартный метод вычисления структуры разложения сразу не приводит нас к результату: линеаризация укороченного уравнения, соответствующего вершине (–6, 4), на решении $y = cx$, дает нулевой оператор. Поэтому мы продолжаем вычисления, делая сдвиг $y = cx + w$. Для нового уравнения получаем следующий многоугольник Ньютона (рис. 2).

Нас интересуют только те его вершины и ребра, нормальные конусы к которым могут дать асимпотики, соответствующие конусу задачи $\mathcal{K} = {\text{\{ }}k:\operatorname{Re} k \geqslant 1,k \ne 1{\text{\} }}$. Этому условию соответствуют лишь вершины (0, 0) и (–4, 2) и соединяющее их ребро. Последовательно рассмотим их.

Вершине (0, 0) соответствует алгебраическое укороченное уравнение, которое не дает асимптотик.

Вершине (–4, 2) отвечает уравнение

подставим в него $w = {{c}_{1}}{{x}^{{{{r}_{1}}}}}$, видим, что ${{r}_{1}} = 3$ или ${{r}_{1}} = 5$. Ни одно из значений показателей степени не подходит, поскольку вектор $( - 1, - {{r}_{1}})$ не принадлежит нормальному конусу вершины.

Ребру, соединяющему указанные вершины, ставится в соответствие укороченное уравнение

а также внешняя нормаль (–1, –2), поэтому решение данного уравнения ищем в виде $w = A{{x}^{2}}$. После подстановки получили: откуда $A = \tfrac{\beta }{2}$ – корень кратности 2. И поэтому мы продолжаем вычисления, делая сдвиг y = cx + $\frac{\beta }{2}{{x}^{2}}$ + + y₂, добиваясь ненулевых значений линеаризации укороченного уравнения на решении. После подстановки получаем уравнение с многоугольником Ньютона, у которого подходящими являются вершина (–4, 2), дающая следующий член асимптотики вида ${{c}_{3}}{{x}^{3}}$ и критическое число 4, и ребро, соединяющее вершины (–4, 2) и (0, 4) данного многоугольника (критическое число 5).

В итоге получаем следующие семейства степенных асимптотических разложений, продолжающих асимптотику решения $y = cx$ при $x \to 0$:

где c, ${{c}_{3}} \in \mathbb{C}{{\backslash \{ }}0{\text{\} }}$, ${{c}_{4}},$ ${{c}_{5}} \in \mathbb{C}$ – произвольные постоянные, коэффициенты a_k, b_k однозначно через них выражаются.