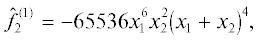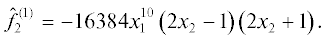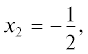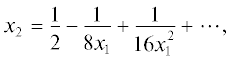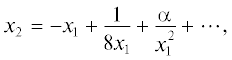Программирование, 2022, № 1, стр. 23-33

1. ВВЕДЕНИЕ

Пусть $X = ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}$. Рассмотрим вещественный многочлен $f(X)$. При постоянной $c \in \mathbb{R}$ кривая на плоскости ${{\mathbb{R}}^{2}}$

является линией уровня многочлена $f(X)$.

Наша задача – описать все типы линий уровня многочлена $f(X)$ на вещественной плоскости $X \in {{\mathbb{R}}^{2}}$. Пусть ${{C}_{ * }} = inff(X)$ и $C* = supf(X)$ по $X \in {{\mathbb{R}}^{2}}$. Основной результат:

Теорема 1. Имеется конечное множество критических значений c:

которым соответствуют критические линии уровняа для значений $c$ из каждого из $m + 1$ интервалалинии уровня топологически эквивалентны. Если ${{C}_{ * }}$ = = $c_{1}^{ * }$ или $C* = c_{m}^{ * }$, то интервалы I₀или I_m отсутствуют.

Поэтому для выявления расположения всех типов линий уровня многочлена $f(X)$ надо найти все критические значения $c_{j}^{ * }$, изобразить m критических линий уровня (1.3) и по одной линии уровня для произвольного значения c из $m + 1$ интервала (1.4). Способ вычисления этих линий уровня описан в [1] и отчасти в [2, гл. 1, § 2] с помощью степенной геометрии. Более традиционный подход см. в [3, гл. 1] или [4]. Локальное строение линий уровня многочлена рассматривалось в [2, гл. 1, § 3]. Здесь некоторые результаты из [2] дополнены.

2. КРИТИЧЕСКИЕ ТОЧКИ И КРИТИЧЕСКИЕ КРИВЫЕ

Точка $X = {{X}^{0}}$ называется простой для многочлена $f(X)$, если в ней отлична от нуля хотя бы одна из частных производных $\partial f{\text{/}}\partial {{x}_{1}}$, $\partial f{\text{/}}\partial {{x}_{2}}$.

Определение 1. Точка $X = {{X}^{0}}$ для многочлена $f(X)$ называется критической порядка $k$, если в точке $X = {{X}^{0}}$ равны нулю все частные производные от $f(X)$ до порядка k, т.е. все

и отлична от нуля хотя бы одна частная производная порядка $k + 1$.

Определение 2. Кривая

называется критической для многочлена $f(X)$, если

1. Она лежит на какой-то линии уровня (1.1) и

2. На ней $\partial f{\text{/}}\partial {{x}_{1}} \equiv 0$, или $\partial f{\text{/}}\partial {{x}_{2}} \equiv 0$.

Значения постоянной $c = f(X)$ в критических точках $X = {{X}^{0}}$ и на критических кривых (2.1) назовем критическими и обозначим $c_{j}^{ * }$ согласно (1.2).

3. ЛОКАЛЬНЫЙ АНАЛИЗ ЛИНИЙ УРОВНЯ

В дальнейшем вблизи точки $X = {{X}^{0}}$ будем рассматривать аналитические обратимые замены координат

где ${{\varphi }_{i}}$ – аналитические функции от $X - {{X}^{0}}$.

Лемма 1. ([2, гл. 1, § 3]). Если точка ${{X}^{0}}$ простая и в ней $\partial f{\text{/}}\partial {{x}_{2}} \ne 0$, то существует замена (3.1), приводящая уравнение (1.1) к виду

Она следует из теоремы о неявной функции.

Линии уровня (3.2) – это прямые, параллельные оси ${{y}_{1}}$.

Рассмотрим решения уравнения (1.1) вблизи критической точки ${{X}^{0}} = 0$ порядка 1. Тогда

Дискриминант $\Delta $ выписанной квадратичной формы есть $\Delta = {{b}^{2}} - 4ac$.

Лемма 2. ([2, гл. 1, § 3]). Если в критической точке первого порядка ${{X}^{0}} = 0$ дискриминант $\Delta \ne 0$, то существует замена (6), приводящая уравнение (1.1) к виду

где σ = 1 (если $\Delta < 0$) или $\sigma = - 1$ (если $\Delta > 0$).

Это двумерный вариант известной леммы Морса [5, гл. 1, § 2].

Лемма 3. Если в критической точке первого порядка ${{X}^{0}} = 0$ дискриминант $\Delta = 0$, то существует замена (3.1), приводящая уравнение (1.1) к виду

где целое $n > 2$ и число $\tau \in {\text{\{ }}{\kern 1pt} - {\kern 1pt} 1,0, + {\kern 1pt} 1{\text{\} }}$.

Доказательство. Сначала невырожденным линейным преобразованием $X = ZB$ приводим квадратичную часть к $z_{2}^{2}$. Разложение многочлена $f(X)$ в ряд по Z имеет вид

Согласно теореме о неявной функции уравнение

имеет аналитическое решение

Теперь сделаем замену

Тогда $\tilde {f}(Z) = \tilde {\tilde {f}}$ и $\partial{ \tilde {\tilde {f}}}{\text{/}}\partial {{w}_{2}} \equiv 0$ при ${{w}_{2}} = 0$. Следовательно,

где ${{\varphi }_{0}}({{w}_{1}}) = \sum\limits_{k \geqslant 3} {{{\alpha }_{k}}} w_{1}^{k}$ и ${{h}^{{(2)}}}(W)$ – степенной ряд от W без свободного члена. При этом возможны два случая:

1. ,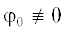

2. ${{\varphi }_{0}} \equiv 0$.

В первом случае пусть n – это младшая степень w₁ в ряду ${{\varphi }_{0}}({{w}_{1}}) = {{a}_{n}}w_{1}^{n} + \; \cdots $ Тогда после замены

получаем формулу (3.4) с $\tau = \pm 1 = sign{{a}_{n}}$.

Во втором случае формулу (3.4) с $\tau = 0$ получаем после замены

Доказательство окончено. ◻

Выражения (3.3) и (3.4) – это нормальные формы многочлена $f(X)$ вблизи его критической точки первого порядка ${{X}^{0}} = 0$.

Пусть теперь критическая точка ${{X}^{0}} = 0$ имеет порядок k > 1. Согласно [1, раздел 5] соответствующая ей линия уровня либо не имеет ветвей, входящих в критическую точку ${{X}^{0}} = 0$, либо имеет несколько таких ветвей.

В первом случае критическая линия уровня состоит из этой точки ${{X}^{0}} = 0$, а остальные линии уровня являются замкнутыми кривыми вокруг нее и соответствуют одному знаку разности $c - f({{X}^{0}})$.

Во втором случае критическая линия уровня состоит из конечного числа ветвей разных кратностей, входящих в критическую точку ${{X}^{0}} = 0$. Они разбивают окрестность этой критической точки на криволинейные секторы. Остальные линии уровня заполняют эти секторы, оставаясь на некотором расстоянии от критической точки ${{X}^{0}}$ = 0. При этом в соседних секторах они соответствуют разным знакам разности $c - f({{X}^{0}})$, если разделяющая их ветвь имеет нечетную кратность, и одному знаку этой разности, если разделяющая их ветвь имеет четную кратность.

4. ГЛОБАЛЬНЫЙ АНАЛИЗ ЛИНИЙ УРОВНЯ

Определение 3. Пусть ребро $\Gamma _{j}^{{(1)}}$ многоугольника Ньютона $\Gamma (f)$ многочлена $f(X)$ имеет внешнюю нормаль с одной или двумя положительными координатами и соответствует укороченному многочлену $f_{j}^{{(1)}}(X)$. Тогда пересечение корня X = $T{{t}^{\alpha }}$, $T$, α = = const, $t \to \pm \infty $, укороченного многочлена $f_{j}^{{(1)}}(X)$ с бесконечностью ${{x}_{i}} = \pm \infty $ назовем бесконечной точкой пересечения. Кратность корня – это кратность этой точки. Только в этих точках линии уровня достигают бесконечности.

У каждого многочлена имеется лишь конечное множество бесконечных точек пересечения и все они с конечными кратностями. Можно исследовать характер линий уровня вблизи бесконечных точек пересечения в зависимости от их кратности. Здесь нет места для такого исследования. Вблизи однократной бесконечной точки пересечения они устроены просто (пример 1). Вблизи двукратной бесконечной точки пересечения они устроены сложнее, как показано в примере 2. Трехкратная точка бесконечного пересечения разобрана в примере 3, а четырехкратная имеется в примере 4.

Лемма 4. Для всех значений постоянной c из одного из m + 1 интервалов (4) линии уровня (1.1) топологически эквивалентны.

Доказательство леммы основано на анализе линий уровня вблизи бесконечных точек пересечения, и здесь его не приводим. Оно будет опубликовано в отдельной статье.

Теорема, сформулированная во введении, следует из лемм 1–4 и описанных выше свойств линий уровня вблизи критической точки ${{X}^{0}} = 0$ порядка k > 1.

5. ВЫЧИСЛЕНИЕ КРИТИЧЕСКИХ ЗНАЧЕНИЙ, ТОЧЕК И КРИВЫХ

В общем случае вычисление критических значений $c_{j}^{ * }$ и соответствующих им критических точек и кривых удобно проводить с использованием алгоритмов компьютерной алгебры, в первую очередь, с помощью базисов Грёбнера [6], [7, Гл. 2, 3].

Идеал, определяющий критические точки и кривые, состоит из следующих полиномов:

Согласно теореме 1 число критических значений $c$ конечно. Тогда базис Грёбнера $\mathcal{G}\mathcal{B}\mathcal{J}$ идеала (5.1) для чистого лексикографического порядка ${{x}_{1}} \prec {{x}_{2}} \prec c$ содержит полином $h(c)$, зависящий только от переменной c. Среди вещественных корней этого полинома следует искать критические значения $c_{j}^{ * }$, для которых имеются вещественные критические линии уровня.

Как следует из раздела 2, аффинное многообразие, определяемое идеалом $\mathcal{G}\mathcal{B}\mathcal{J}$, имеет размерность либо 0, либо 1. В первом случае критических кривых нет, ибо идеал $\mathcal{G}\mathcal{B}\mathcal{J}$ нульмерен. Во втором случае некоторым критическим значениям $c_{j}^{ * }$ соответствуют критические кривые. В обоих случаях, согласно теореме о примарном разложении [7, Гл. 4] или [8, Гл. 4], идеал $\mathcal{G}\mathcal{B}\mathcal{J}$ состоит из конечного числа примарных идеалов, каждый из которых задает либо критическую точку, либо критическую кривую. Определение размерности идеала легко выполняется с помощью вычисленного ранее базиса Грёбнера $\mathcal{G}\mathcal{B}\mathcal{J}$.

В большинстве систем компьютерной алгебры имеются процедуры построения базисов Грёбнера для различных лексикографических порядков, а также некоторые дополнительные процедуры для проверки нульмерности идеала, вычисления его размерности и др. Подробнее рассмотрим как могут быть реализованы подобные вычисления в системе Maple. Можно воспользоваться пакетами Groebner и PolynomialIdeals, а также входящими в него процедурами: Basis – для вычисления базиса Гребнера, HilbertDimension – для вычисления размерности идеала, IsZeroDimensional – для проверки нульмерности идеала, PrimaryDecomposition – для примарного разложения идеала, EquidimensionalDecomposition – для декомпозиции идеала на идеалы различных размерностей.

Предлагаем следующий порядок вычислений.

1. Составляется идеал $\mathcal{J}$ и для него вычисляется базис Грёбнера $\mathcal{G}\mathcal{B}\mathcal{J}$ с чисто лексикографическим порядком ${{x}_{1}} \prec {{x}_{2}} \prec c$ с использованием процедуры Basis пакета Groebner.

2. Базис $\mathcal{G}\mathcal{B}\mathcal{J}$ позволяет найти все критические значения $c_{j}^{ * }$ с помощью полинома h(c) в виде алгебраических чисел. Такой полином автоматически определяется для указанного выше лексикографического порядка, либо с помощью процедуры UnivariatePolynomial.

3. Среди критических значений $c_{j}^{ * }$ нужно отобрать те, которым соответствуют вещественные критические точки и критические кривые. Это можно сделать, например, выполнив примарную декомпозицию базиса $\mathcal{G}\mathcal{B}\mathcal{J}$, а затем определить нули полученных идеалов в поле $\mathbb{R}$.

4. Перед примарной декомпозицией идеала $\mathcal{G}\mathcal{B}\mathcal{J}$ можно вычислить его размерность с помощью процедуры HilbertDimension. Если она не равна нулю, то вначале с использованием процедуры EquidimensionalDecomposition вычисляется последовательность идеалов с размерностями 0 и 1 соответственно, а затем уже выполняется их декомпозиция. Идеалы с размерностью 0 дадут критические точки, а с размерностью 1 – критические кривые (а также вещественные критические точки).

5. Теперь для каждого примарного идеала следует найти его множество вещественных нулей. Если критическое значение $c_{j}^{ * }$ принадлежит $\mathbb{Q}$, то все вычисления выполняются точно. Если же оно есть алгебраическое число, то можно поступить так, как описано в [9, п. 5.6], т.е. проводить все вычисления по модулю идеала, определяющего критическое значение и критическую точку.

6. Теперь характер каждой критической точки определяется с использованием дискриминанта $\Delta $ квадратичной формы разложения функции $f(X)$ вблизи нее согласно леммам 2 и 3.

Выполненные вычисления позволяют перейти к построению эскизов линий уровня.

6. ПОСТРОЕНИЕ ЭСКИЗОВ ЛИНИЙ УРОВНЯ

Для построения эскиза линии уровня можно воспользоваться какой-либо системой компьютерной алгебры, имеющей программы построения изолиний (изоповерхностей) для двумерных или трехмерных скалярных полей. Эти программы используют различные вычислительные алгоритмы, основанные на применении конечных элементов, которые триангулируют (покрывают) некоторую часть плоскости (обычно используются треугольные или квадратные конечные элементы) [10]. Затем вычисляют значения функции (1.1) в вершинах сетки и они интерполируются на весь конечный элемент. Такие алгоритмы хорошо справляются с ситуацией, когда у линии уровня нет особенностей. Наличие особенностей заставляет существенно уменьшать шаг разбиения и, соответственно, увеличивать объем вычислений. В примерах раздела 7 все рисунки линий уровня построены с использованием процедуры contour пакета matplotlib [11] для языка программирования Python.

В ряде случаев удается улучшить качество эскиза линии уровня, если для определенного значения $c$ уравнение (1.1) может быть разложено на множители, а нули этих множителей (или часть их) задают алгебраическую кривую рода $0$. В этом случае можно вычислить рациональную параметризацию такой кривой [12], а по ней построить эскиз с любой точностью. С такой задачей неплохо справляется пакет algcurves системы Maple. Этот пакет, в частности, позволяет исследовать плоские алгебраические кривые. С его помощью можно изобразить эскиз кривой $f({{x}_{1}},{{x}_{2}}) = 0$ путем численного интегрирования соответствующего дифференциального уравнения $\tfrac{{\partial f}}{{\partial {{x}_{1}}}} + \tfrac{{\partial f}}{{\partial {{x}_{2}}}} \cdot \tfrac{{d{{x}_{2}}}}{{d{{x}_{1}}}}$ = 0  для некоторого набора начальных условий, определяемых точками, в которых хотя бы одна из частных производных функции $f({{x}_{1}},{{x}_{2}})$ равна нулю. Использование данного пакета для исследования набора кривых с разными порядками особенностей показало, что в случае особенностей высоких порядков качество эскиза получается не слишком высоким.

7. ПРИМЕРЫ

Пример 1. Рассмотрим многочлен

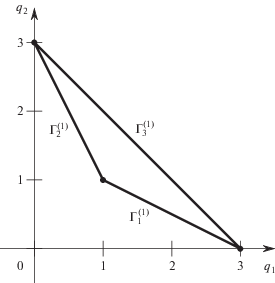
Уравнение ${{f}_{1}}(X) = 0$ определяет алгебраическую кривую, которую называют “Декартов лист”. Многоугольник Ньютона $\Gamma (f)$ показан на рис. 1.

Он содержит три ребра, но только ребро $\Gamma _{3}^{{(1)}}$ имеет внешнюю нормаль ${{N}_{3}} = (1,\;1)$ с положительной координатой. Соответствующий укороченный многочлен

имеет однократный корень

Согласно схеме вычислений раздела 5 вычисляем базис Грёбнера $\mathcal{G}\mathcal{B}\mathcal{J}$ идеала (5.1) и определяем его многочлен $h(c) = c(c + 1)$. Идеал имеет нулевую размерность, его примарная декомпозиция дает три идеала:

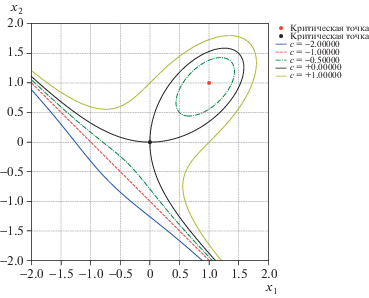
Идеал (7.3) дает критическую точку ${{X}_{1}} = (1,\;1)$ с критическим значением $c_{1}^{ * } = - 1$ и дискриминантом ${{\Delta }_{1}} = - 27 < 0$ (изолированная точка), идеал (7.2) – критическую точку X₂ = 0 с критическим значением $c_{2}^{ * } = 0$ и дискриминантом ${{\Delta }_{2}} = 9 > 0$ (в ней пересекаются две ветви). Идеал (7.4) не имеет вещественных нулей. Линии уровня показаны на рис. 2.

При ${{x}_{1}} \to \pm \infty $ линии уровня стремятся к ${{x}_{2}} \to \mp \infty $, накапливаясь у прямой (7.1) или у линии уровня с $c_{2}^{ * } = 0$.

Заметим, что для $c \notin {\text{\{ }} - 1,\;0{\text{\} }}$ кривая ${{f}_{1}}(X)$ – c = 0 имеет род 1, т.е. является эллиптической кривой, уравнение которой может быть приведено к нормальной форме Вейерштрасса

с помощью преобразования

Параметризация нормальной формы (7.5) задается с помощью функции Вейерштрасса $\wp (z,{{g}_{2}},{{g}_{3}})$

инварианты ${{g}_{2}}$, ${{g}_{3}}$ которой суть коэффициенты, взятые со знаком минус, правой части уравнения (7.5) при степенях 1 и 0 переменной ${{y}_{1}}$ соответственно. Эта параметризация может быть использована для визуализации линий уровня, однако требует подготовительной работы – вычисления периодов и определения множества вещественности функции $\wp (z,{{g}_{2}},{{g}_{3}})$. Авторы не считают возможным уделить здесь достаточно внимания этим вопросам и рекомендуют обратиться к соответствующим источниками, например, к книге [13].

Критические значения $c_{1}^{ * } = - 1$ и $c_{2}^{ * } = 0$ как раз соответствуют ситуации, когда кривая ${{f}_{1}}(X)$ – c = 0 имеет род 0 и допускает рациональную параметризацию. При $c = c_{1}^{ * }$ уравнение линии уровня факторизуется на линейный и квадратичный множители:

нуль последнего есть критическая точка ${{X}_{1}}$ = (1, 1). При $c = c_{2}^{ * }$ имеем рациональную параметризацию Декартового листа

Пример 2. Рассмотрим многочлен

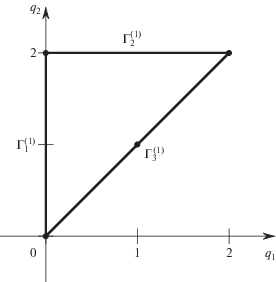
Его многоугольник Ньютона показан на рис. 3.

Он состоит из трех ребер, но только двум из них соответствуют внешние нормали с положительной координатой – это ребра $\Gamma _{2}^{{(1)}}$ и $\Gamma _{3}^{{(1)}}$. Ребру $\Gamma _{2}^{{(1)}}$ соответствует укороченный многочлен

Он не имеет вещественного корня, уходящего в бесконечность.

Ребру $\Gamma _{3}^{{(1)}}$ соответствует укороченный многочлен

имеющий двукратный корень уходящий в точки ${{x}_{1}} = \pm \infty $, ${{x}_{2}} = 0$. Линии уровня многочлена (7.6) показаны на рис. 4.

Базис Гребнера $\mathcal{G}\mathcal{B}\mathcal{J}$ идеала (5.1) для многочлена (7.6) имеет вид ${\text{\{ }}c - 1,{{x}_{1}},{{x}_{2}}{\text{\} }}$, и, следовательно, здесь имеется одна критическая точка ${{x}_{1}} = {{x}_{2}} = 0$ с критическим значением $c_{1}^{ * } = 1$. Линия уровня ${{f}_{2}}(X) = 1$ состоит из прямой ${{x}_{2}} = 0$ и рациональной кривой ${{x}_{2}} = 2{{x}_{1}}{\text{/}}(x_{1}^{2} + 1)$, ее пересекающей. Справа между этой кривой и осью ${{x}_{1}}$ находятся линии уровня с $c \in (0,\;1)$, но нет критической точки. При $c \to 0$ эти линии расположены все правее и как бы сложены. Таково поведение линий уровня вблизи бесконечной точки пересечения ${{x}_{1}} = \infty $, ${{x}_{2}} = 0$ кратности 2. Вблизи бесконечной точки пересечения ${{x}_{1}} = - \infty $, ${{x}_{2}} = 0$ кратности 2 расположение линий уровня симметрично относительно начала координат.

Кстати, здесь ${{C}_{ * }} = inff(X) = 0$, ибо на кривой ${{x}_{2}} = 1{\text{/}}{{x}_{1}}$ значения $f(X) = x_{2}^{2} = 1{\text{/}}x_{1}^{2}$, они стремятся к нулю при ${{x}_{1}} \to + \infty $. При этом $C{\text{*}} = + \infty $, что видно при ${{x}_{1}} = 0$.

Заметим, что поскольку многочлен ${{f}_{2}}$ является суммой квадратов, то для любого $c > 0$, $c \ne 1$, легко построить рациональную параметризацию кривой ${{f}_{2}}(X) - c = 0$, используя известную рациональную параметризацию окружности. Для этой кривой она имеет вид

При $\tau \in ( - 1,\;1)$ получаем линию уровня в верхней полуплоскости, при 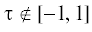– в нижней.

Пример 3. Рассмотрим вычисление линий уровня многочлена

Здесь ${{C}_{ * }} = - \infty $, $C* = + \infty $. Они достигаются при ${{x}_{1}} = 0$.

Базис Грёбнера $\mathcal{G}\mathcal{B}\mathcal{J}$ идеала (5.1) здесь не приводим в силу его громоздкости, а многочлен $h(c)$ вычисленного базиса имеет вид

Среди его корней отбираем те критические значения $c_{j}^{ * }$, для которых соответствующие значения будут вещественными. Можно поочередно к ранее вычисленному идеалу $\mathcal{G}\mathcal{B}\mathcal{J}$ добавлять по одному множителю многочлена (7.8) и вычислять базис Гребнера с лексикографическим порядком $c \prec {{x}_{1}} \prec {{x}_{2}}$. Только для множителя c + 1 получаем идеал $\{ 3x_{2}^{2} + 3{{x}_{2}} + 1,{{x}_{1}} + {{x}_{2}} + 1,c + 1\} $, который не имеет вещественных нулей. Таким образом, критическими значениями будут:

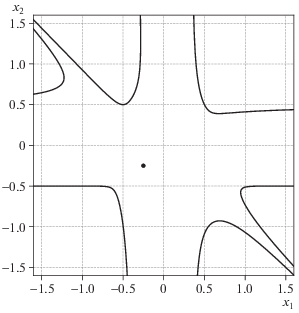
Значению $c_{1}^{ * } \approx - 17.1478$ соответствует критическая точка ${{X}_{1}}:(x_{1}^{{(1)}} = x_{2}^{{(1)}} = (3 + \sqrt {69} ){\text{/}}10)$. В ней дискриминант $\Delta \approx - 14221.2 < 0$, и она является изолированной.

Значению $c_{2}^{ * } \approx - 1.0077$ соответствует критическая точка ${{X}_{2}}:(x_{1}^{{(2)}} = x_{2}^{{(2)}} = (3 - \sqrt {69} {\text{/}}10)$. В ней дискриминант $\Delta \approx 1.3415 > 0$ и через нее проходят две ветви. Критическим значениям $c_{{1,2}}^{ * }$ соответствуют случаи леммы (2).

Значению $c_{3}^{ * } = 0$ соответствует критическая точка ${{X}_{3}}:(x_{1}^{{(1)}} = x_{2}^{{(1)}} = 0)$. В ней дискриминант $\Delta \approx 144 > 0$, и через нее проходят две ветви.

Наконец, при $c_{3}^{ * } = 0$ имеется критическая прямая ${{x}_{1}} + {{x}_{2}} + 2 = 0$.

Заметим, что многочлен (7.7) раскладывается на два множителя: $x_{1}^{3} + x_{2}^{3} - 3{{x}_{1}}{{x}_{2}}$ и ${{({{x}_{1}} + {{x}_{2}} + 2)}^{2}}$. Нулям первого соответствует лист Декарта, нулям второго – пара совпадающих прямых. Используя это разложение многочлена $f(X)$ на множители, можно легко вычислить все три указанные критические точки и критическую прямую ${{x}_{1}} + {{x}_{2}} + 2 = 0$. На ней тождественно аннулируются обе частные производные $\partial {{f}_{1}}{\text{/}}\partial {{x}_{1}}$ и $\partial {{f}_{1}}{\text{/}}\partial {{x}_{2}}$.

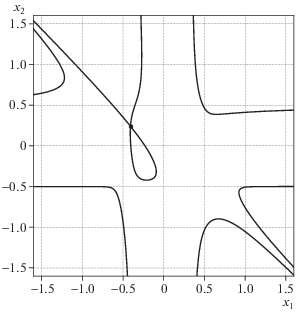
Критические линии уровня для многочлена (7.7) показаны на рис. 5 и 6 в разных масштабах. Критические точки ${{X}_{1}}$, ${{X}_{2}}$ и ${{X}_{3}} = 0$ и критическая прямая ${{x}_{1}} + {{x}_{2}} + 2 = 0$ показаны полужирными.

Линия уровня для критического значения $c_{1}^{ * } \approx - 17.14$ изображена пунктирной. На рис. 5 она состоит из точки ${{X}^{{(1)}}}$ и кривой в левом нижнем углу. На рис. 6 она имеет еще две ветви в левом верхнем и правом нижнем углах.

Линия уровня для критического значения $c_{2}^{ * } \approx - 1$ показана штрих-пунктирной. Она имеет 3 компоненты: овал в первом квадранте, две пересекающиеся ветви выше критической линии и одну кривую ниже нее.

Линия уровня для критического значения $c_{3}^{ * }$ = 0 показана сплошной. Она состоит из двух компонент: критической прямой и листа Декарта.

Четыре типа некритических линий уровня легко восстанавливаются, как лежащие целиком между соседними критическими.

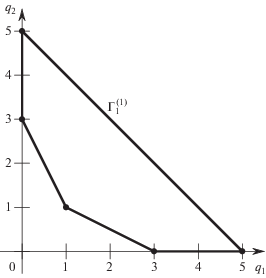
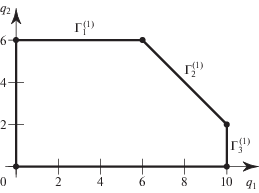
Многоугольник Ньютона многочлена (7.7) показан на рис. 7.

У него только одно ребро $\Gamma _{1}^{{(1)}}$ соответствует бесконечности. Ему соответствует укороченный многочлен

Он имеет трехкратный корень ${{x}_{2}} = - {{x}_{1}}$.

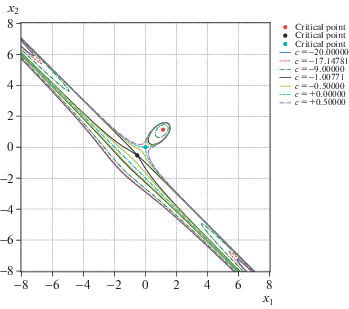
При ${{x}_{1}} \to + \infty $ имеются четыре критических линии: две для $c = c_{3}^{ * } = 0$ (включая критическую прямую ${{x}_{1}} + {{x}_{2}} + 2 = 0$) и две ветви для $c = c_{2}^{ * }$, к которым скапливаются остальные линии уровня. Некоторые из них имеют складку. Аналогичная картина имеет место при ${{x}_{1}} \to - \infty $. Характер этих линий уровня можно видеть на рис. 6.

Пример 4. В работах авторов [14–16] рассматривалась одна вещественная поверхность в ${{\mathbb{R}}^{3}}$, соответствующая особым точкам инвариантных метрик Эйнштейна. На плоскости в ${{\mathbb{R}}^{3}}$, где многочлен имеет кратный корень, сечение поверхности задается нулями многочлена

Здесь, как и в примере 1, ${{C}_{ * }} = - \infty $, $C* = + \infty $.

Базис Гребнера $\mathcal{G}\mathcal{B}\mathcal{J}$ идеала (5.1), составленный для многочлена (7.9), здесь не приводим в силу его громоздкости, а соответствующий многочлен $h(c)$ вычисленного базиса имеет вид

Многочлен четвертой степени имеет два вещественных корня, и, следовательно, множество критических значений $c_{j}^{ * }$ состоит из значений

Перестройка линий уровня происходит при этих четырех значениях.

Размерность идеала $\mathcal{G}\mathcal{B}\mathcal{J}$ равна единице, поэтому здесь вначале находится его декомпозиция на два идеала размерностей 0 и 1 соответственно, а затем уже выполняется их примарное разложение. Для критического значения $c_{3}^{ * } = 0$ структура критических точек и кривых, а также линий уровня была описана в цитируемых выше работах и будет дана ниже. Поэтому рассмотрим структуру примарных идеалов, соответствующих другим критическим значениям параметра $c$.

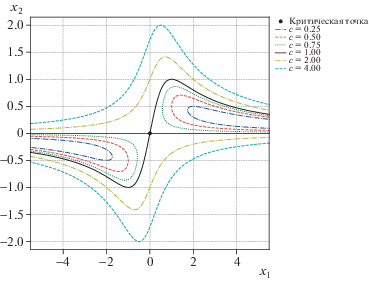
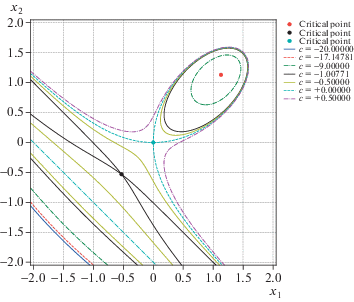
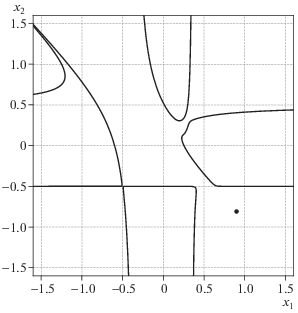
Значению $c_{1}^{ * } = - 16$ соответствует критическая точка $x_{1}^{{(1)}} = x_{2}^{{(1)}} = - 1{\text{/}}4$. В ней дискриминант Δ₁ = = $ - 204800$ < 0 и она является изолированной. Линии уровня для значения $c = c_{1}^{ * }$ показаны на рис. 8.

Критические значения $c_{2}^{ * } \approx - 9.89108$ и $c_{4}^{ * } \approx 0.000228$ являются корнями многочлена 4-й степени, т.е. они алгебраические числа. Вычисления показывают, что при $c = c_{2}^{ * }$ имеется особая точка ${{X}_{2}} \approx ( - 0.4021306894,0.2360338414)$, в которой дискриминант ${{\Delta }_{2}} \approx 63676.18108$ > 0 и, следовательно, в ней происходит пересечение линий уровня (см. рис. 9).

При $c = {{c}_{4}}$ имеется особая точка X₄ ≈ ≈ $(0.8995846960$, –0.8095257544), в которой дискриминант ${{\Delta }_{4}} \approx - 0.01855315801 < 0$, т.е. она изолированная (см. рис. 10).

Наконец, как следует из (7.9), при $c = c_{3}^{ * } = 0$ многочлен ${{f}_{4}}(X)$ раскладывается на множители.

В этом случае имеются критические точки

которые суть точки пересечения рациональных кривых ${{\mathcal{Z}}_{j}}$, $j = 1,\;2,\;3$, задаваемых нулями соответствующих множителей формулы (7.9), а также критическая кривая ${{\mathcal{Z}}_{3}}$ (см. рис. 11). Критической кривой ${{\mathcal{Z}}_{3}}$ (показана сплошной линией на рис. 11) соответствует тройной корень. Здесь сохранены обозначения, используемые в указанных выше работах авторов.

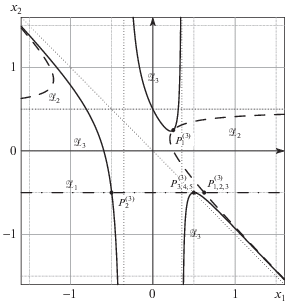
Для анализа критических линий на бесконечности построим многоугольник Ньютона многочлена (7.9) (см. рис. 12) и выделим укороченные многочлены, соответствующие ребрам, чьи нормали имеют хотя бы одну положительную координату.

Подходящие ребра многоугольника обозначены $\Gamma _{1}^{{(1)}}$, $\Gamma _{2}^{{(1)}}$, $\Gamma _{3}^{{(1)}}$ на рис. 12, а соответствующие им укороченные многочлены суть

Следовательно, из разложения многочлена (7.10) следует, что на бесконечности имеются трехкратные корни $X = ( \pm 1{\text{/}}\sqrt 8 ,\infty )$. Из разложения многочлена (7.11) следует наличие четырехкратного корня ${{x}_{2}} = - {{x}_{1}}$ при ${{x}_{1}} \to \pm \infty $. Наконец, из разложения многочлена (7.12) следует наличие простых корней $X = ( \pm \infty ,\; \pm 1{\text{/}}2)$. Эти корни легко отслеживаются в виде вертикальных, наклонных и горизонтальных асимптот на рис. 8–11, причем на последнем рисунке они показаны точечными линиями.

Напоследок опишем перестройку линий уровня многочлена (7.9) при изменении c от $c_{3}^{ * }$ к $c_{4}^{ * }$ и далее. При $c > c_{3}^{ * }$ ветви кривых ${{\mathcal{Z}}_{2}}$ и ${{\mathcal{Z}}_{3}}$, идущие от критических точек $P_{{1,2,3}}^{{(1)}}$ и $P_{{3,4,5}}^{{(3)}}$ соответственно в правый нижний угол рис. 12, соединяются и образуют замкнутую кривую. Эта кривая, по мере приближения c к значению $c_{4}^{ * }$ снизу, стягивается к изолированной критической точке X₄.

В левом верхнем углу рис. 11 ветви кривых ${{\mathcal{Z}}_{2}}$ и ${{\mathcal{Z}}_{3}}$, идущие вдоль асимптоты ${{x}_{2}} = - {{x}_{1}}$, также соединяются. Таким образом, при $c > c_{4}^{ * }$ не остается линий уровня, уходящих на бесконечность вдоль асимптоты ${{x}_{2}} = - {{x}_{1}}$. В этом можно убедиться, если построить разложение ${{f}_{4}}(X) - c$ в ряд Пюизе при ${{x}_{1}} \to \infty $, например, используя процедуру puisex из пакета algcurves системы Maple. Это разложение имеет три ветви:

где $\alpha $ есть корень многочлена

Разложение (7.13) соответствует прямой ${{\mathcal{Z}}_{1}}$, разложение (7.14) соответствует ветви кривой ${{\mathcal{Z}}_{2}}$ при ${{x}_{1}} \to \infty $, ${{x}_{2}} \to 1{\text{/}}2$. Несложно показать либо с использованием последовательности Штурма, либо с помощью теоремы Якоби–Борхарда (см., например, [17, Гл. XVI, § 2]), либо вычисляя последовательность субдискриминантов многочлена (7.16) [18] и применяя теорему 4.33 из [19], что при c > 0 многочлен (7.16) имеет только комплексные корни. Следовательно, разложение (7.15) не соответствует никакой вещественной кривой.