Программирование, 2022, № 1, стр. 40-53
АЛГОРИТМЫ ПРОВЕРКИ НЕКОТОРЫХ СВОЙСТВ N-КВАЗИГРУПП
А. В. Галатенко a, *, А. Е. Панкратьев a, **, В. М. Староверов a, ***
a Московский государственный университет имени М.В. Ломоносова,
ГСП-1
119991 Москва, Ленинские горы, д. 1, Россия
* E-mail: agalat@msu.ru
** E-mail: apankrat@intsys.msu.ru
*** E-mail: staroverovvl@imscs.msu.ru
Поступила в редакцию 23.07.2021
После доработки 05.08.2021
Принята к публикации 15.09.2021
- EDN: RSDMHJ
- DOI: 10.31857/S0132347422010046
Аннотация
В работе описываются эффективные алгоритмы для проверки некоторых существенных с криптографической точки зрения свойств n-квазигрупп: полиномиальной полноты (которая сводится к проверке простоты и неаффинности) и существования $n$-подквазигрупп. Доказываются теоремы об оценках времени работы предложенных алгоритмов и их пространственной сложности, а также приводятся результаты численных экспериментов для оценки практической эффективности программной реализации.
1. ВВЕДЕНИЕ
Конечные квазигруппы являются популярной платформой для реализации различных криптографических примитивов. Шеннон доказал, что табличное гаммирование по латинскому квадрату (т.е. по таблице Кэли конечной квазигруппы) является совершенным шифром [1]. Широкий спектр различных криптографических примитивов на основе квазигрупп представлен в обзорных работах [2, 3]. В последних конкурсах NIST по выбору новых криптографических стандартов регулярно участвуют квазигрупповые алгоритмы-кандидаты (в качестве примерa приведем хэш-функцию EDON-R' [4]). Растет интерес и к структурам более высокой размерности – латинским кубам (таблицам Кэли 3-квазигрупп) и латинским гиперкубам (таблицам Кэли n-квази групп при $n \geqslant 4$). Возникают новые алгоритмы (см., например, [5, 6]), ведутся исследования криптографически важных свойств [7–9].
Наша работа посвящена задаче алгоритмической проверки двух важных свойств n-квазигрупп: полиномиальной полноты и наличия собственных n-подквазигрупп. Важность полиномиальной полноты в криптографических приложениях была отмечена В.А. Артамоновым [10]; она обусловлена тем, что распознавание разрешимости уравнений над полиномиально полными алгебрами является NP-полной задачей [11], что обеспечивает защиту от атак методом решения уравнений на биты ключа. Наличие собственных n-подквазигрупп может привести к вырождению операции на n-подквази группу, что облегчит, например, атаку методом “грубой силы”. При этом в ряде случаев n-подквази группы порядка 1 считаются допустимыми. Задача построения и обоснования эффективных алгоритмов для распознавания упомянутых свойств относится к числу классических проблем компьютерной алгебры.
В случае n = 2 для проверки обоих свойств предложены достаточно эффективные алгоритмы (время работы которых является кубическим от размера квазигруппы k для проверки полиномиальной полноты [12–14], имеет порядок ${{k}^{{7/3}}}\, \cdot \,{{(logk)}^{{2/3}}}$ для проверки наличия собственных подквазигрупп и порядок ${{k}^{3}}logk$ для проверки наличия собственных подквазигрупп из не менее чем двух элементов [15]). В нашей работе приводится обобщение алгоритмов [14, 15] на случай $n$-квазигрупп для $n \geqslant 3$. Проверка полиномиальной полноты сводится к проверке одновременной простоты (сложность $O({{k}^{{n + 1}}})$) и неаффинности (сложность $O({{k}^{n}})$ при $n \geqslant 3$). Результаты были анонсированы в работе [8] и частично представлены на семинаре “Компьютерная алгебра” [16]. Алгоритмы проверки существования собственных $n$-подквази групп и собственных n-подквазигрупп порядка $ \geqslant 2$ были анонсированы в работе [9]; их сложность составляет $O\left( {{{k}^{{\frac{{{{n}^{2}} + n + 1}}{{n + 1}}}}}{\text{lo}}{{{\text{g}}}^{{\frac{n}{{n + 1}}}}}k} \right)$ и $O\left( {{{k}^{{\frac{{{{n}^{2}} + 2n + 4}}{{n + 2}}}}}{\text{lo}}{{{\text{g}}}^{{\frac{n}{{n + 2}}}}}k} \right)$ соответственно. Заметим, что при $n = 2$ полученные оценки уточняют результат работы [15] для случая подквазигрупп порядка $ \geqslant 2$. Помимо доказательства корректности и оценки сложности мы приводим результаты практических экспериментов, полученные при применении распараллеленных реализаций алгоритмов к семейству тестовых примеров.
Дальнейшее изложение имеет следующую структуру. В разделе 2 приводятся необходимые определения. Раздел 3 посвящен проверке простоты, раздел 4 – проверке неаффинности. В разделе 5 суммируются результаты для задачи определения полиномиальной полноты. В разделе 6 изучаются задачи проверки существования собственных $n$-подквазигрупп и собственных $n$-подквазигрупп порядка $ \geqslant 2$. Наконец, раздел 6 является заключением.
При работе над статьей авторы имели счастливую возможность обсуждать материал с В.А. Артамоновым.
Работа выполнена при финансовой поддержке DRDO (Индия), проект “Quasigroup Based Cryptography: Security Analysis and Development of Crypto-Primitives and Algorithms (QGSEC)”, номер гранта SAG/4600/TCID/Prog/QGSEC.
2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Определение 1. Конечной $n$-квазигруппой называется пара (Q, f), где $Q = {\text{\{ }}{{q}_{1}},\; \ldots ,\;{{q}_{k}}{\text{\} }}$ – конечное множество, а $f{\text{:}}\;{{Q}^{n}} \to Q$ такова, что при произвольной фиксации любых $n - 1$ переменных результат является биекцией, то есть перестановкой на множестве $Q$. При этом операция $f$ называется $n$-квазигрупповой.
В дальнейшем все структуры будут конечными, поэтому для краткости слово “конечный” будет опускаться.
Таблица Кэли $n$-квазигрупповой операции является $n$-мерным латинским гиперкубом, то есть $n$-мерной матрицей размера $\left| Q \right| \times \; \ldots \; \times \left| Q \right|$, такой что каждая одномерная “строка” задает перестановку на множестве $Q$. Обратно, произвольный $n$-мерный латинский гиперкуб задает $n$-квазигрупповую операцию с соответствующим универсумом.
Без ограничения общности в дальнейшем мы будем считать, что $Q = {{E}_{k}} = {\text{\{ }}0,\;1, \ldots ,\;k - 1{\text{\} }}$, а $n$-квазигрупповая операция является $n$-арной функцией $k$-значной логики. Пусть ${{P}_{k}}$ – множество всех функций $k$-значной логики, $P_{k}^{0}$ – множество всех констант. Пусть $F \subseteq {{P}_{k}}$. Через $[F]$ обозначим замыкание множества $F$ относительно операции суперпозиции (см., например, [17]).
Определение 2. $n$-квазигруппа $(Q,f)$ называется полиномиально полной, если
При этом "функция (операция)” f также называется полиномиально полной.
Другими словами, полиномиальная полнота означает, что произвольная функция $k$-значной логики может быть получена суперпозициями из функции f и констант. Для описания характеристического свойства полиномиально полных $n$-квазигрупп нам потребуется ввести два вспомогательных понятия.
Пусть ~ является нетривиальным отношением эквивалентности на ${{E}_{k}}$, $g \in {{P}_{k}}$ – функция арности m.
Определение 3. Функция $g$ сохраняет отношение эквивалентности ~, если для любой пары входных наборов $a = ({{a}_{1}},\; \ldots ,\;{{a}_{m}})$ и $b = ({{b}_{1}},\; \ldots ,\;{{b}_{m}})$, таких что ${{a}_{i}} \sim {{b}_{i}}$, $i = 1, \ldots ,m$, выполнено отношение $g(a)$ ~ ~ g(b).
Определение очевидным образом обобщается на случай множества функций.
Определение 4. Множество функций $G \subseteq {{P}_{k}}$ сохраняет отношение эквивалентности $ \sim $, если каждая функция $g \in G$ сохраняет $ \sim $.
Легко увидеть, что $n$-квазигрупповые операции могут сохранять только отношения эквивалентности, все классы которых являются равномощными.
Определение 5. $n$-квазигруппа $(Q,f)$ называется простой, если не существует нетривиального отношения эквивалентности на ${{E}_{k}}$, сохраняемого функцией f.
Определение 6. $n$-квазигруппа $(Q,f)$ называется аффинной, если существует абелева группа $(Q, + )$, автоморфизмы ${{\alpha }_{1}},\; \ldots ,\;{{\alpha }_{n}}$ группы $(Q,f)$ и константа $c \in Q$, такие что выполнено тождество
(2.1)
$f({{x}_{1}},\; \ldots ,\;{{x}_{n}}) \equiv {{\alpha }_{1}}({{x}_{1}}) + \; \ldots \; + {{\alpha }_{n}}({{x}_{n}}) + c.$В противном случае $n$-квазигруппа $(Q,f)$ называется неаффинной.
Известно (см., например, [18]), что $n$-квази группа является полиномиально полной тогда и только тогда, когда она проста и неаффинна.
Пусть $Q{\text{'}} \subseteq Q$. Через $f(Q{\text{'}})$ обозначим замыкание множества $Q{\text{'}}$ относительно операции f, то есть множество всех констант, выразимых через f и элементы $Q{\text{'}}$. Очевидно, что замыкание обладает свойством монотонности: из вложения $Q{\text{'}} \subseteq Q{\text{''}}$ следует вложение $f(Q{\text{'}}) \subseteq f(Q{\text{''}})$.
Определение 7. Множество $Q{\text{'}} \subseteq Q$ называется полным, если $f(Q{\text{'}}) = Q$.
В силу монотонности из полноты $Q{\text{'}}$ следует полнота всех его надмножеств.
Определение 8. Пусть $Q{\text{'}} \subset Q$, $1 \leqslant \left| {Q{\text{'}}} \right| < \left| Q \right|$. Если $f(Q{\text{'}}) = Q{\text{'}}$, то говорим, что $n$-квазигруппа $(Q,f)$ содержит собственную $n$-подквазигруппу $(Q{\text{'}},f{\kern 1pt} {\text{'}})$, где $f{\kern 1pt} {\text{'}}$ – ограничение операции $f$ на $\mathop {\left( {Q{\text{'}}} \right)}\nolimits^n $.
Заметим, что очевидным образом для любого $Q{\text{'}} \subseteq Q$ выполнено равенство $f(f(Q{\text{'}})) = f(Q{\text{'}})$, поэтому если $Q{\text{'}} \ne \not {0}$ и $f(Q{\text{'}}) \ne Q$, то $f(Q{\text{'}})$ является собственной $n$-подквазигруппой.
В дальнейшем для краткости мы будем отождествлять $n$-подквазигруппу $(Q{\text{'}},f{\text{'}})$ с множеством $Q{\text{'}}$.
Определение 9. Пусть $Q{\text{'}}$ – собственная $n$-под-квазигруппа $n$-квазигруппы $(Q,f)$. Если дополнительно выполнено условие $\left| {Q{\text{'}}} \right| > 1$, то подквазигруппа называется нетривиальной.
Для алгоритма проверки существования собственных $n$-подквазигрупп нам потребуется понятие системы представителей.
Определение 10. Пусть M, $\left| M \right| < \infty $ – некоторое множество, $t \in \mathbb{N}$, ${{M}_{1}},\; \ldots ,\;{{M}_{t}}$ – подмножества M. Множество ${{M}_{0}} \subseteq M$ называется системой представителей для ${{M}_{1}},\; \ldots ,\;{{M}_{t}}$, если для всех i от 1 до $t$ найдется элемент ${{m}_{i}} \in {{M}_{0}}$, такой что ${{m}_{i}} \in {{M}_{i}}$.
Элемент ${{m}_{i}} \in {{M}_{0}}$, такой что ${{m}_{i}} \in {{M}_{i}}$, называется представителем множества ${{M}_{i}}$. Заметим, что представители для различных $i$ могут совпадать.
В дальнейшем мы будем считать, что $n$-квазигруппы заданы таблицами Кэли. Случай функционального задания является предметом будущих исследований. Элементарными операциями считаются вычисление $n$-квазигрупповой операции (в нашем случае это просто чтение из памяти), а также арифметические операции в ${{\mathbb{Z}}_{k}}$ (если элементы квазигруппы не помещаются в базовые типы данных, то таблица Кэли не помещается в оперативную память, поэтому допущение является разумным). Основание всех логарифмов в дальнейшем равно 2.
3. АЛГОРИТМ ПРОВЕРКИ ПРОСТОТЫ
Проверка простоты $n$-квазигруппы $(Q,f)$ может быть сведена к поиску нетривиального отношения эквивалентности, сохраняемого множеством всех одноместных функций, порожденных f. Корректность перехода обосновывается следующим утверждением, являющимся аналогом леммы 1 из работы [13]. Обозначим через ${{F}_{1}}$ множество всех одноместных функций, полученных произвольной фиксацией произвольных $(n - 1)$ переменных функции $f$. Мощность множества ${{F}_{1}}$ очевидным образом равна $n \cdot {{k}^{{n - 1}}}$.
Лемма 1. Пусть $(Q,f)$ – $n$-квазигруппа. Oтношение эквивалентности $ \sim $ сохраняется функцией f тогда и только тогда, когда $ \sim $ сохраняется множеством ${{F}_{1}}$.
Доказательство. Сперва докажем необходимость. Пусть $g({{x}_{i}})$ – произвольная функция из ${{F}_{1}}$, полученная из f фиксацией
Рассмотрим произвольную пару эквивалентных элементов $a{\text{'}}$, $a{\text{''}}$. Заметим, что g(a') = f(a1, ..., ai – 1, $a{\text{'}},{{a}_{{i + 1}}}, \ldots ,{{a}_{n}})$, g(a'') = f(a1, ..., ${{a}_{{i - 1}}},a{\text{''}},{{a}_{{i + 1}}}, \ldots ,{{a}_{n}})$. Так как наборы в правых частях являются покомпонентно эквивалентными, а функция f сохраняет отношение эквивалентности, имеем $g(a{\text{'}}) \sim g(a{\text{''}})$. В силу произвольности функции $g$ и пары $a{\text{'}}$, $a{\text{''}}$ необходимость доказана.
Докажем достаточность. Предположим, что отношение $ \sim $ не сохраняется функцией f. По определению существует пара покомпонентно эквивалентных наборов $a = ({{a}_{1}},\; \ldots ,\;{{a}_{n}})$ и b = (b1, ..., bn), таких что 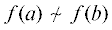 . Рассмотрим наборы ${{c}^{0}} = a$, ${{c}^{1}} = ({{b}_{1}},{{a}_{2}}, \ldots ,\;{{a}_{n}})$, ..., ${{c}^{{n - 1}}} = ({{b}_{1}},\; \ldots ,\;{{b}_{{n - 1}}},{{a}_{n}})$, ${{c}^{n}} = ({{b}_{1}},\; \ldots ,\;{{b}_{n}})$. Заметим, что для любого $i$ от 1 до $n$ наборы ${{c}^{{i - 1}}}$ и ci отличаются ровно в одной компоненте. Кроме того, по предположению
. Рассмотрим наборы ${{c}^{0}} = a$, ${{c}^{1}} = ({{b}_{1}},{{a}_{2}}, \ldots ,\;{{a}_{n}})$, ..., ${{c}^{{n - 1}}} = ({{b}_{1}},\; \ldots ,\;{{b}_{{n - 1}}},{{a}_{n}})$, ${{c}^{n}} = ({{b}_{1}},\; \ldots ,\;{{b}_{n}})$. Заметим, что для любого $i$ от 1 до $n$ наборы ${{c}^{{i - 1}}}$ и ci отличаются ровно в одной компоненте. Кроме того, по предположению 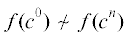 . Следовательно, найдется значение индекса $i$, для которого
. Следовательно, найдется значение индекса $i$, для которого 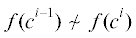 . Рассмотрим функцию $g({{x}_{i}})$, полученную из $f$ фиксацией x1 = b1, ..., ${{x}_{{i - 1}}} = {{b}_{{i - 1}}},{{x}_{{i + 1}}} = {{a}_{i}}, \ldots ,{{x}_{n}} = {{a}_{n}}$. Заметим, что ${{a}_{i}} \sim {{b}_{i}}$, но
. Рассмотрим функцию $g({{x}_{i}})$, полученную из $f$ фиксацией x1 = b1, ..., ${{x}_{{i - 1}}} = {{b}_{{i - 1}}},{{x}_{{i + 1}}} = {{a}_{i}}, \ldots ,{{x}_{n}} = {{a}_{n}}$. Заметим, что ${{a}_{i}} \sim {{b}_{i}}$, но 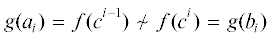 , то есть множество ${{F}_{1}}$ не сохраняет отношение $ \sim $. Достаточность доказана. ◻
, то есть множество ${{F}_{1}}$ не сохраняет отношение $ \sim $. Достаточность доказана. ◻
Рассмотрим следующую процедуру Check($i$), принимающую на вход таблицу Кэли $n$-квази группы и параметр i, $1 \leqslant i \leqslant k - 1$, и вычисляющую транзитивное замыкание отношения $0 \sim i$ под действием множества ${{F}_{1}}$.
1. пометить пару {0, i} как эквивалентную
2. инициализировать очередь пар на проверку
3. добавить пару {0, i} в очередь
4. пока очередь непуста
5. извлечь первую пару из очереди
(пусть это пара {s, t})
6. для каждой функции g из F1
вычислить g(s) и g(t)
7. если пара {g(s), g(t)} не помечена как эквивалентная
8. пометить пару как эквивалентную
9. добавить пару в очередь
10. объединить классы эквивалентности,
соответствующие g(s) и g(t),
и пометить новые
эквивалентные пары
11. добавить новые эквивалентные пары в очередь
12. конец если
13. конец цикла
14. конец цикла
15. если все элементы эквивалентны
16. вернуть “отношение не найдено”
17. иначе
18. вернуть “отношение найдено”
Следующее утверждение обобщает лемму 2 из работы [13].
Лемма 2. Процедура Check($i$) возвращает “отношение найдено” тогда и только тогда, когда существует нетривиальное отношение эквивалентности $ \sim $, сохраняемое ${{F}_{1}}$ и такое, что $0 \sim i$.
Доказательство. Предположим, что процедура вернула “отношение найдено”. Значит, на выходе возникло разбиение множества ${{E}_{k}}$ на непересекающиеся классы, то есть отношение эквивалентности. Обозначим это отношение через $ \sim $. Заметим, что по построению для каждой функции $g \in {{F}_{1}}$ и для каждой пары элементов $a,b \in {{E}_{k}}$, лежащих в одном классе эквивалентности, в процессе выполнения процедуры установлено отношение $g(a)$ ~ g(b). Значит, отношение ~ сохраняется множеством ${{F}_{1}}$.
Обратно, предположим, что процедура вернула “отношение не найдено”, однако множество
${{F}_{1}}$ сохраняет некоторое отношение эквивалентности $ \sim $, для которого $0 \sim i$. Рассмотрим пару ${\text{\{ }}a,b{\text{\} }}$, такую что 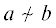 , и для любой пары $\left\{ {a{\text{'}},b{\text{'}}} \right\}$, эквивалентность которой была установлена процедурой до эквивалентности a и b, выполнено $a{\text{'}} \sim b{\text{'}}$. Такая пара очевидным образом существует по предположению. Возможны следующие случаи.
, и для любой пары $\left\{ {a{\text{'}},b{\text{'}}} \right\}$, эквивалентность которой была установлена процедурой до эквивалентности a и b, выполнено $a{\text{'}} \sim b{\text{'}}$. Такая пара очевидным образом существует по предположению. Возможны следующие случаи.
1. Эквивалентность a и b была установлена процедурой на строке 7, то есть для некоторых $g \in {{F}_{1}}$ и $a{\text{'}},b{\text{'}} \in {{E}_{k}}$, $a{\text{'}} \sim b{\text{'}}$, выполнено $g(a{\text{'}}) = a$, $g(b{\text{'}}) = b$. Так как 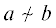 , получаем противоречие с предположением.
, получаем противоречие с предположением.
2. Эквивалентность a и b установлена на строке 10. В этом случае существуют $a{\text{'}},b{\text{'}} \in {{E}_{k}}$, $a{\text{'}} \sim b{\text{'}}$, такие что $a{\text{'}} \sim a$, $b{\text{'}} \sim b$, что противоречит транзитивности отношения эквивалентности $ \sim $. ◻
Применим к процедуре Check($i$) два оптимизирующих преобразования, аналогичные оптимизациям из [14]: не будем добавлять в очередь на проверку пары, возникающие при слиянии классов, а также прекратим работу, если размер хотя бы одного класса станет строго больше, чем $k{\text{/}}2$. Получим следующую процедуру OptimizedCheck($i$), отличающуюся от Check($i$) только в строке 11.
1. пометить пару {0, i} как эквивалентную
2. инициализировать очередь пар на проверку
3. добавить пару {0, i} в очередь
4. пока очередь непуста
5. извлечь первую пару из очереди
(пусть это пара {s, t})
6. для каждой функции g из F1
вычислить g(s) и g(t)
7. если пара {g(s), g(t)} не помечена
как эквивалентная
8. пометить пару как эквивалентную
9. добавить пару в очередь
10. объединить классы эквивалентности,
соответствующие g(s) и g(t)
и пометить новые
эквивалентные пары
11. если размер класса больше k/2
вернуть “отношение не найдено”
12. конец если
13. конец цикла
14. конец цикла
15.если все элементы эквивалентны
16. вернуть “отношение не найдено”
17. иначе
18. вернуть “отношение найдено”
Лемма 3. Процедура OptimizedCheck($i$) возвращает “отношение не найдено” тогда и только тогда, когда процедура Check($i$) возвращает “отношение не найдено”.
Доказательство. Достаточно установить справедливость следующих фактов: не существует нетривиальных отношений эквивалентности, сохраняемых множеством ${{F}_{1}}$, у которых найдется класс, размер которого превышает k/2; если пара была добавлена на проверку в процедуре Check($i$) на строке 11, то при рассмотрении этой пары новых эквивалентностей не будет найдено. Первый факт следует из того, что $n$-квазигрупповые операции могут сохранять только отношения эквивалентности, для которых все классы эквивалентности равномощны (то есть отношение нетривиально, только если размер всех классов $ \leqslant k{\text{/}}2$). Для доказательства второго факта рассмотрим произвольную пару ${\text{\{ }}a,b{\text{\} }}$, добавленную в процедуре Check($i$) на строке 11. Заметим, что перед парой ${\text{\{ }}a,b{\text{\} }}$ на строке 9 в очередь была помещена пара ${\text{\{ }}a{\text{'}},b{\text{'\} }}$, такая что $a{\text{'}} \sim a$, $b{\text{'}} \sim b$. Значит, к моменту начала обработки пары ${\text{\{ }}a,b{\text{\} }}$ будут обработаны пары ${\text{\{ }}a{\text{'}},a{\text{\} }}$, ${\text{\{ }}b{\text{'}},b{\text{\} }}$ и ${\text{\{ }}a{\text{'}},b{\text{'\} }}$. Рассмотрим произвольную функцию $g \in {{F}_{1}}$. Легко увидеть, что g(a) ~ ~ g(a') ~ $g(b{\text{'}}) \sim g(b)$. В силу транзитивности эквивалентность $g(a) \sim g(b)$ уже установлена.
Лемма 4. Сложность процедуры OptimizedCheck($i$) составляет $O({{k}^{n}})$ для $n$-квазигрупп порядка $k$ при фиксированном $n \geqslant 3$ и $k \to \infty $. ◻
Доказательство. Сперва оценим сложность, связанную с объединением классов эквивалентности. Заметим, что в первый момент классов $k - 1$, а в конце процедуры классов не меньше одного. Таким образом, процедура слияния происходит не более $k - 2$ раз. Отсюда, в частности, следует, что число пар, попавших в очередь, не превосходит $k - 1$. Слияние классов легко реализовать со сложностью, линейной по k (например, с помощью массива, сопоставляющего каждому элементу ${{E}_{k}}$ номер класса; для слияния достаточно изменить метки меньшего по мощности из объединяемых классов). Кроме того, общее число эквивалентных пар не более, чем квадратично зависит от k. Таким образом, суммарная сложность шага 10 составляет $O({{k}^{2}})$, то есть $o({{k}^{n}})$ (с учетом неравенства $n \geqslant 3$).
Оставшиеся операции являются элементарными и оцениваются числом итераций цикла. Внешний цикл, как показано выше, выполнится не более $k - 1$ раза. Внутренний цикл будет выполнен столько раз, сколько функций содержится в множестве ${{F}_{1}}$, то есть $n \cdot {{k}^{{n - 1}}} = O({{k}^{{n - 1}}})$ при фиксированном $n$, и итоговая сложность составит $O({{k}^{n}})$. ◻
Рассмотрим следующий алгоритм проверки простоты.
1. цикл по i от 1 до k – 1
2. выполнить OptimizedCheck(i)
3. если результат “отношение найдено”
4. вернуть “непростая”
5. конец цикла
6. вернуть “простая”
Теорема 1. Предложенный алгоритм возвращает “простая” тогда и только тогда, когда $n$-квазигруппа является простой. Сложность алгоритма составляет $O({{k}^{{n + 1}}})$ при фиксированном $n$ и порядке $n$-квазигруппы $k$, стремящемся к бесконечности.
Доказательство. Корректность алгоритма следует из лемм 1, 2 и 3 с учетом равномощности классов эквивалентности (из равномощности вытекает, что в любом нетривиальном отношении эквивалентности ~, сохраняемом $n$-квазигрупповой операцией, есть пара $0 \sim i$ для некоторого $i \in {\text{\{ }}1,\; \ldots ,\;k - 1{\text{\} }}$); оценка сложности непосредственно вытекает из леммы 4. ◻
3.1. Оценка практической эффективности
Алгоритм проверки простоты для 3-квази групп был программно реализован с поддержкой OpenMP-распараллеливания. Программа была протестирована на рабочей станции с 8-ядерным процессором i7–3770 CPU @3.40GHz и 32 гигабайтами памяти на 3-квазигруппах, аналогичных тестовым примерам из [14]. Здесь и далее для контроля корректности написанного кода использовались инструменты AddressSanitizer, LeakSanitizer, ThreadSanitizer (см., например, [19]) и сравнение оптимизированной реализации с референсной. Время работы представлено в табл. 1. В левом столбце приведены порядки 3-квазигрупп, в столбцах со второго по пятый содержатся максимальные времена работы в секундах на соответствующем числе ядер.
Таблица 1.
Время проверки простоты 3-квазигрупп
| $k$ | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| 32 | 0 | 0 | 0 | 0 |
| 64 | 0 | 0 | 0 | 0 |
| 128 | 2 | 1 | 1 | 1 |
| 256 | 75 | 47 | 30 | 17 |
| 512 | 1332 | 733 | 456 | 426 |
Легко увидеть, что результаты численного эксперимента по проверке простоты согласуются с теоретической асимптотикой времени работы алгоритма в зависимости от порядка 3-квазигрупп. Полученные результаты подтверждают возможность проверки простоты 3-квазигрупп за приемлемое время до порядка 512 включительно.
4. АЛГОРИТМ ПРОВЕРКИ НЕАФФИННОСТИ
Алгоритм проверки неаффинности $n$-квази групп при $n \geqslant 3$ является естественным обобщением алгоритма проверки неаффинности квази групп, предложенного в работе [13]. Следующее утверждение является переносом леммы 3 из [13] на случай $n$-квазигрупп.
Лемма 5. Пусть $(Q,f)$ – $n$-квазигруппа, аффинная над абелевой группой $(Q, + )$. Тогда для любого $d \in Q$ существует абелева группа $(Q, + {\text{'}})$, для которой элемент $d$ является нейтральным, и $(Q,f)$ аффинна над $(Q, + {\text{'}})$.
Доказательство. Определим операцию $ + {\text{'}}$ по правилу $x + {\kern 1pt} {\text{'}}\,y = x + y - d$. Пусть $e$ – нейтральный элемент группы $(Q, + )$. Рассмотрим отображение $\varphi :Q \to Q$, заданное соотношением $\varphi (x) = x + d$. Заметим, что $\varphi (x + y) = x + y + d$ = (x + d) + + $(y + d) - d$ = $\varphi (x) + {\text{'}}\varphi (y)$. Таким образом, $(Q, + {\text{'}})$ – абелева группа, изоморфная $(Q, + )$ и имеющая нейтральный элемент $\varphi (e) = e + d = d$. По определению аффинной $n$-квазигруппы справедливо тождество (2.1):
Наконец, преобразуем тождество (2.1) следующим образом:
В дальнейшем мы будем считать, что таблица Кэли операций индексирована естественным образом (то есть набором $(0,\;1,\; \ldots ,\;k - 1)$).
Рассмотрим введенную в [13] процедуру GetGroup, принимающую на вход таблицу Кэли $C$ квазигруппы (в нашем случае достаточно рассмотреть произвольную фиксацию переменных ${{x}_{3}},\; \ldots ,\;{{x}_{n}}$) и возвращающую таблицу Кэли абелевой группы, над которой эта квазигруппа может быть аффинной, или “неаффинна”, если такой группы не существует.
1. рассмотреть первую строку C
как перестановку s
2. вычислить перестановку t, обратную s
3. рассмотреть строки C как перестановки и умножить каждую строку на t справа
4. обозначить результат через C1
5. переупорядочить строки C1 так,
что первый столбец и первая строка
совпадают
6. обозначить результат через C2
7. проверить, что матрица C2 симметрична
8. если C2 несимметрична
9. вернуть “неаффинна”
10. проверить, что C2 задает
ассоциативную операцию
11.если нет,
12. вернуть “неаффинна”
13.иначе
14. вернуть C2
Легко увидеть, что в случае, если процедура возвращает C2, нейтральным элементом операции является $0$.
Лемма 6. Сложность процедуры составляет $O({{k}^{3}})$ при $k \to \infty $.
Доказательство. Первые две строки легко реализовать со сложностью порядка $klogk$; третья, пятая и седьмая строки имеют квадратичную сложность. Наконец, строка 10 реализуется кубической по сложности проверкой тождества $C2[a,C2[b,c]] \equiv C2[C2[a,b],c]$. Оставшиеся строки имеют константную сложность. ◻
В работе [14] предлагается ряд методов оптимизации проверки ассоциативности.
Пусть процедура GetGroup вернула абелеву группу с таблицей Кэли $C2$. Для удобства обозначим соответствующую операцию через $ + $. Заметим, что при произвольной фиксации любых $n - 2$ переменных функции f будет получаться квазигрупповая операция, в таблице Кэли которой найдутся строка и столбец, начинающиеся с $0$ (это следует из того, что первая строка и первый столбец являются перестановками и содержат все элементы, включая $0$). Пусть найденная таким образом строка или столбец соответствуют вариации $i$-й переменной функции f. Тогда соответствующая перестановка обозначается через ${{\alpha }_{i}}$. Поиск ${{\alpha }_{i}}$ несложно реализовать с линейной сложностью. Дополнительно проверим, что ${{\alpha }_{i}}$ является автоморфизмом относительно операции $ + $ (это можно сделать, проверив справедливость тождества ${{\alpha }_{i}}(a + b) \equiv {{\alpha }_{i}}(a) + {{\alpha }_{i}}(b)$; непосредственная проверка имеет сложность $O({{k}^{2}})$). Рассмотрим процедуру поиска автоморфизмов GetAut($i$), вычисляющую описанным выше способом ${{\alpha }_{i}}$ и проверяющую, что это автоморфизм. В случае, если ${{\alpha }_{i}}$ автоморфизмом не является, процедура возвращает “неаффинна”. Оформим приведенные рассуждения о сложности в виде утверждения.
Лемма 7. Сложность процедуры GetAut($i$) составляет $O({{k}^{2}})$ при $k \to \infty $.
Рассмотрим следующий алгоритм проверки неаффинности.
1. C2 = GetGroup
2. если C2 равно “неаффинна”
3. вернуть “неаффинна”
4. цикл по i от 1 до n
5. alpha_i равно GetAut(i)
6. если alpha_i равно “неаффинна”
7. вернуть “неаффинна”
8. конец цикла
9. c = f (0, …, 0)
10. проверить тождество f(x1, …, xn) =
= alpha_1 (x1) + |… +
+ alpha_n (xn) + c
11. если тождество выполнено
12. вернуть “аффинна”
13. иначе
14. вернуть “неаффинна”
Лемма 8. Пусть алгоритм вернул “аффинна” для $n$-квазигруппы $(Q,f)$. Тогда эта $n$-квазигруппа аффинна.
Доказательство. Утверждение является следствием определения аффинности, так как тождество, справедливость которого установлено на строке 10, есть тождество (2.1), выписанное для абелевой операции $ + $ и автоморфизмов ${{\alpha }_{1}},\; \ldots ,\;{{\alpha }_{n}}$. ◻
Лемма 9. Пусть $n$-квазигруппа $(Q,f)$ аффинна. Тогда алгоритм вернет “аффинна”.
Доказательство. Пусть выполнено тождество (2.1). В силу леммы 5 без ограничения общности можно считать, что нейтральным элементом операции + является 0. Первая строка матрицы $C$ в процедуре GetGroup, то есть перестановка s, имеет вид $\alpha (x) + {v}$, где $\alpha $ – автоморфизм группы $(Q, + )$, ${v} \in Q$, а оставшиеся строки с номерами $i = 2,\; \ldots ,\;k$ имеют вид $\alpha (x) + {{{v}}_{i}}$, ${{{v}}_{i}} \in Q$. После умножения справа на $t = {{s}^{{ - 1}}}$ первая строка станет тождественной перестановкой, а оставшиеся примут вид $x + {v}_{i}^{'}$. Следовательно, получившаяся после переупорядочения матрица $C2$ задает операцию x + y, являющуюся коммутативной и ассоциативной, и процедура GetGroup не вернет “неаффинна”.
Перестановка ${{\alpha }_{i}}$ в процедуре GetAut($i$) получается фиксацией оставшихся переменных, такой что ${{\alpha }_{i}}(0) = 0$. По предположению об аффинности, ${{\alpha }_{i}}$ совпадает с соответствующим автоморфизмом в представлении (2.1), и ни одна из процедур GetAut($i$) не вернет “неаффинна”.
Так как все автоморфизмы сохраняют 0, значение $f(0,\; \ldots ,\;0)$ в точности равно константе $c$ в представлении (2.1), поэтому проверка справедливости тождества на строке 10 закончится успехом, и процедура вернет “аффинна”.
Теорема 2. Предложенный алгоритм возвращает “неаффинна” тогда и только тогда, когда $n$-квази группа является неаффинной. Сложность проверки составляет $O({{k}^{n}})$ при фиксированном $n \geqslant 3$ и порядке $n$-квазигруппы $k$, стремящемся к бесконечности.
Доказательство. Корректность алгоритма следует из лемм 8 и 9. Оценим сложность. По лемме 6 сложность восстановления операции $ + $ на строке 1 есть $O({{k}^{3}})$. По лемме 7 сложность цикла оценивается как $O(n \cdot {{k}^{2}}) = o({{k}^{3}})$. Сложность проверки справедливости тождества на строке 10 составляет $O({{k}^{n}})$ (с константной сложностью проверяется справедливость равенства для каждого из ${{k}^{n}}$ входных наборов). Оставшиеся строки выполняются с константной сложностью. Так как $n \geqslant 3$, общая сложность составляет $O({{k}^{n}})$. ◻
Интересно, что при переходе от $n = 2$ к $n = 3$ порядок сложности не увеличивается.
4.1. Оценка практической эффективности
Алгоритм проверки неафинности для 3-квазигрупп был программно реализован с поддержкой OpenMP-распараллеливания. Программа была протестирована на рабочей станции с 8-ядерным процессором i7–3770 CPU @3.40GHz и 32 гигабайтами памяти на 3-квазигруппах, аналогичных тестовым примерам из [14]. Время работы представлено в табл. 2. В левом столбце приведен порядок 3-квазигрупп, в столбцах со второго по пятый содержатся максимальные времена работы в секундах на соответствующем числе ядер для неаффинных/аффинных $3$-квазигрупп.
Таблица 2.
Время проверки неаффинности 3-квазигрупп
| $k$ | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| 512 | 1/1 | 1/1 | 1/1 | 1/1 |
| 1024 | 4/5 | 4/4 | 3/3 | 2/3 |
| 2048 | 79/83 | 56/61 | 42/46 | 32/32 |
Полученные результаты подтверждают возможность проверки неафинности 3-квазигрупп за приемлемое время до порядка 2048 включительно. Заметим, что $k = 2048$ является максимально возможным порядком вида ${{2}^{m}}$, $m \in \mathbb{N}$, при котором 3-квазигруппы допускают табличное задание при 32 гигабайтах оперативной памяти.
5. ПРОВЕРКА ПОЛИНОМИАЛЬНОЙ ПОЛНОТЫ
Так как полиномиальная полнота эквивалентна одновременной простоте и неаффинности, из теорем 1 и 2 вытекает следующий факт.
Следствие 1. Предложенные алгоритмы осуществляют проверку полиномиальной полноты $n$-квазигруппы порядка $k$ со сложностью $O({{k}^{{n + 1}}})$ при фиксированном $n$ и $k \to \infty $.
В ряде случаев одну из проверок можно не проводить. В силу равномощности классов эквивалентности все $n$-квазигруппы простого порядка простые, и в этом случае полиномиальная полнота эквивалентна неаффинности. Полностью аналогично [20, Предложение 3.2] можно показать, что аффинная $n$-квазигруппа может быть простой, только если $k = {{p}^{m}}$ для некоторого простого числа p и $m \in \mathbb{N}$, а абелева группа $(Q, + )$ изоморфна $\mathbb{Z}_{p}^{m}$. Поэтому в случае, когда порядок группы не является степенью простого числа, неаффинность непосредственно следует из простоты.
6. ПРОВЕРКА НАЛИЧИЯ $N$-ПОДКВАЗИГРУПП
В работе П.И. Собянина [21] был предложен алгоритм проверки наличия подквазигрупп, который может быть легко переформулирован для случая проверки наличия собственных $n$-подквазигрупп порядка $ \geqslant d$ (наиболее интересными являются значения $d = 1,\;2$) следующим образом. Для каждого d-элементного подмножества $G \subset Q$ вычисляется замыкание $f(G)$. Легко увидеть, что $n$-подквазигруппа порядка $ \geqslant d$ существует тогда и только тогда, когда хотя бы одно из замыканий $f(G)$ отлично от $Q$. Вычисление одного замыкания несложно реализовать со сложностью $O({{k}^{n}})$, число $d$-элементных подмножеств составляет $O({{k}^{d}})$; таким образом, общая сложность есть $O({{k}^{{n + d}}})$. Понизим сложность этого алгоритма, используя метод, введенный в работе [15] для случая проверки наличия подквазигрупп порядка $ \geqslant d$. Основная идея заключается в следующем. Выбирается параметр $K = K(k)$, $d \leqslant K < k$. Для каждого $d$-элементного подмножества $G$ вычисляется “частичное” замыкание, либо пока не будет найдена $n$-подквазигруппа (и тогда задача решена), либо пока размер частичного замыкания не станет равным $K$. Предположим, что на этом этапе $n$-подквазигруппа не найдена. Тогда для каждого из частичных замыканий $G{\text{'}}$ рассматривается множество всех $d$‑элементных подмножеств $G{\text{'}}$ (обозначим его через $G{\text{''}}$). Для совокупности всех $G{\text{''}}$ строится система представителей. На последнем шаге для каждого представителя (это $d$-элементное подмножество $Q$) вычисляется полное замыкание; $n$‑квазигруппа не содержит собственных подквазигрупп порядка $ \geqslant d$ тогда и только тогда, когда все эти замыкания совпадают с $Q$. Дадим подробное описание алгоритма, докажем его корректность и оценим сложность.
Сперва рассмотрим процедуру GetClosure($G$, $K$), принимающую на вход таблицу Кэли $n$-квази группы $(Q,f)$, подмножество $G \subseteq Q$ и число $K$, $\left| G \right| \leqslant K \leqslant k$, и возвращающую “$n$-подквазигруппа найдена”, если существует собственная $n$-подквазигруппа $Q{\text{'}}$, такая что $G \subseteq Q{\text{'}}$ и $\left| {Q{\text{'}}} \right| \leqslant K$, и частичное замыкание $f(G)$, такое что $\left| {f(G)} \right| = K$, в противном случае. Заметим, что при $K = k$ алгоритм вернул бы полное замыкание.
1. добавить в очередь НаПроверку элементы G
2. создать множество Кандидаты = G
3. пока очередь НаПроверку непуста
4. извлечь элемент из очереди
(пусть это элемент x)
5. для каждого набора s (|s|=n) элементов
из Кандидаты и x,
содержащего хотя бы один x
6. вычислить f(s)
7. если f(s) не лежит в Кандидаты
8. добавить f(s) в очередь
9. если |Кандидаты| = K
10. выйти из циклов
11. добавить f(s) в Кандидаты
12. конец если
13. конец цикла для каждого…
14. конец цикла пока…
15. если очередь НаПроверку пуста
16. вернуть “n-подквазигруппа найдена”
17. иначе
18. вернуть Кандидаты
По построению множество кандидатов является подмножеством $f(G)$. Выход из циклов на строке 10 означает, что размер полного замыкания $f(G) > K$, при этом число кандидатов в точности равно $K$. Наконец, штатное завершение циклов означает, что число кандидатов не превысило $K$, причем подстановка произвольного набора кандидатов (легко увидеть, что каждый такой набор возникнет на строке 5 ровно один раз) в функцию f дает на выходе элемент множества кандидатов, то есть в множестве кандидатов хранится $n$-подквазигруппа. Таким образом, процедура корректна. Оценим сложность. Все операции внутри циклов могут быть реализованы с константной сложностью, поэтому общее время работы “циклической” части по порядку оценивается числом итераций. Общее число итераций оценивается сверху общим числом наборов из рассмотренных элементов очереди, то есть ${{K}^{n}}$. Оставшиеся операции могут быть реализованы с линейной сложностью. Таким образом, верно следующее утверждение.
Лемма 10. Для произвольной $n$-квазигруппы $(Q,f)$ процедура GetClosure($G$, $K$) возвращает “$n$‑подквазигруппа найдена” тогда и только тогда, когда существует $n$-подквазигруппа $Q{\text{'}}$, такая что $G \subseteq Q{\text{'}}$ и $\left| {Q{\text{'}}} \right| \leqslant K$. В противном случае возвращается множество $G{\kern 1pt} {\text{'}} \subseteq f(G)$, такое что $\left| {G{\kern 1pt} {\text{'}}} \right| = K$. Сложность процедуры составляет $O({{K}^{n}})$ при фиксированном $n$ и $K \to \infty $.
Заметим, что если $Q{\text{'}}$ – нетривиальная $n$-подквазигруппа, то очевидным образом выполнено неравенство $\left| {Q{\text{'}}} \right| \leqslant \left| Q \right|{\text{/}}2$, поэтому при практической реализации как только размер множества кандидатов превысит $k{\text{/}}2$, дальнейшие вычисления можно либо не проводить (если интересует только факт нетривиальности замыкания), либо произвольным образом дополнить множество кандидатов до нужного размера.
Пусть для каждого $G$ процедура GetClosure($G$, $K$) вернула множество $G{\kern 1pt} {\text{'}}$, то есть $n$-подквази группа порядка $ \geqslant d$ пока не найдена. Перейдем от множеств $G{\kern 1pt} {\text{'}}$ к множествам $G{\kern 1pt} {\kern 1pt} {\text{''}}$, состоящим из всех $d$-элементных подмножеств соответствующего $G{\kern 1pt} {\text{'}}$. В частности, при $d = 1$ $G{\text{'}}$ и $G{\kern 1pt} {\kern 1pt} {\text{''}}$ совпадают, при d = 2 множество $G{\kern 1pt} {\kern 1pt} {\text{''}}$ состоит из всех неупорядоченных пар элементов соответствующего множества $G{\kern 1pt} {\text{'}}$. Аналогично лемме 1 из [15] построим систему представителей для множеств $G{\kern 1pt} {\kern 1pt} {\text{''}}$ с помощью жадной процедуры GetRepresentatives. Процедура принимает на вход множества ${{M}_{1}}, \ldots ,{{M}_{D}}$, ${{M}_{1}}, \ldots ,{{M}_{D}} \subseteq M$, $\left| {{{M}_{1}}} \right| = \; \ldots \; = \left| {{{M}_{D}}} \right| = T$, $\left| M \right| = S$, и выдает на выход систему представителей ${{M}_{0}}$. На высоком уровне она устроена следующим образом.
1. сделать M0 пустым множеством
2. объявить все Mi непокрытыми
3. пока имеются непокрытые Mi
4. выбрать m – наиболее частый элемент
в непокрытых Mi
5. добавить m в M0
6. объявить покрытыми все непокрытые Mi,
содержащие m
7. конец цикла
8. вернуть M0
То, что ${{M}_{0}}$ является системой представителей, непосредственно следует из построения. В лемме 1 работы [15] доказано, что число итераций цикла (равное размеру системы представителей) удовлетворяет соотношению
Рассмотрим реализацию процедуры в случаях $d = 1$ и $d = 2$ и оценим сложность.
При $d = 1$ имеем $D = S = k$, $T = K$. Сперва создадим массив $V$ размера $k$, в котором для каждого $i$, $0 \leqslant i \leqslant k - 1$, будем хранить число множеств $G{\text{''}}$, в которых встречается элемент $i$. Для заполнения этого массива достаточно пройти по всем множествам $G{\text{''}}$ ровно один раз, то есть сложность пропорциональна $K \cdot k$. Также создадим $k$ списков ${{L}_{j}}$, хранящих идентификаторы множеств $G{\text{''}}$, содержащих элемент $j$. Для этого потребуется число операций и объем памяти, пропорциональные $k \cdot K$. На каждой итерации цикла будем выбирать максимальный элемент массива $V$ (это потребует линейной по $k$ сложности), добавлять этот элемент в множество ${{M}_{0}}$, затем уменьшать значения счетчиков в массиве $V$, соответствующих покрытым на этом шаге множествам. Так как для каждого элемента каждого множества $G{\text{''}}$ вычитание будет произведено ровно один раз, общая сложность этого шага пропорциональна $k \cdot K$, а итоговая сложность есть O(k · K) + + $O(k \cdot (k{\text{/}}K + 1) \cdot (logk + 2))$, то есть O(k · K) + + $O({{k}^{2}} \cdot logk{\text{/}}K)$. Заметим, что дополнительная память по порядку не превосходит объема таблицы Кэли исходной $n$-квазигруппы.
При $d = 2$ имеем $D = S = C_{k}^{2} = k \cdot (k - 1){\text{/}}2$, T = = $C_{K}^{2} = K \cdot (K - 1){\text{/}}2$. Заметим, что в этом случае мы будем пользоваться частичными замыканиями пар элементов множества Q (на что потребуется $O({{k}^{2}} \cdot K)$ памяти) и не будем явно создавать массивы пар элементов. Создадим матрицу $V$ размера $k \times k$, в которой для каждой пары $(i,j)$, $0 \leqslant i < j \leqslant k - 1$, будем хранить число множеств $G{\kern 1pt} {\text{''}}$, в которых встречается пара элементов ${\text{\{ }}i,j{\text{\} }}$. Для заполнения этого массива достаточно пройти по всем парам элементов множеств $G{\kern 1pt} {\text{''}}$ ровно один раз, то есть сложность пропорциональна ${{K}^{2}} \cdot {{k}^{2}}$. Также создадим $k \cdot (k - 1){\text{/}}2$ списков ${{L}_{{i,j}}}$, хранящих идентификаторы множеств $G{\kern 1pt} {\text{''}}$, содержащих пары элементов i, j, $0 \leqslant i < j \leqslant k - 1$. Для этого потребуется число операций, пропорциональное ${{k}^{2}} \cdot {{K}^{2}}$, и объем памяти, пропорциональный ${{k}^{2}} \cdot K$. На каждой итерации цикла будем выбирать максимальный элемент матрицы V (это потребует квадратичной по $k$ сложности), добавлять индексы этого элемента в множество M0 (это множество состоит из пар элементов $Q$), затем уменьшать значения счетчиков в массиве V, соответствующих покрытым на этом шаге множествам. Так как для каждой пары элементов каждого множества $G{\kern 1pt} {\text{''}}$ вычитание будет произведено ровно один раз, общая сложность этого шага пропорциональна ${{k}^{2}} \cdot {{K}^{2}}$, а итоговая сложность есть O(k2 · K2) + + $O({{k}^{2}} \cdot ({{k}^{2}}{\text{/}}{{K}^{2}}) \cdot logk)$. Объем дополнительной памяти равен $O({{k}^{2}} \cdot K)$. Заметим, что при $n \geqslant 3$ в силу неравенства $K \leqslant k$ дополнительная память по порядку заведомо не превосходит объема таблицы Кэли исходной квазигруппы.
Оформим результат в виде леммы.
Лемма 11. Процедура GetRepresentatives корректно строит систему представителей множеств $G{\text{''}}$. В случае $d = 1$ мощность множества представителей не превосходит (k/K + 1) · $(logk + 2)$, временная сложность процедуры составляет $O(k \cdot K)$ + + $O({{k}^{2}} \cdot logk{\text{/}}K)$, при этом используется дополнительная память, объем которой есть $O(k \cdot K)$. В случае $d = 2$ мощность множества представителей не превосходит $(k(k - 1){\text{/}}(K(K - 1))$ + 1) ⋅ $(log(k(k$ – ‒ 1)/2) + 2), временная сложность процедуры составляет O(k2 · K2) + $O(({{k}^{4}}{\text{/}}{{K}^{2}}) \cdot logk)$, при этом используется дополнительная память, объем которой есть $O({{k}^{2}} \cdot K)$.
Наконец, сформулируем итоговый алгоритм.
1. для каждого
d-элементного подмножества G
2. вычислить GetClosure (G, K)
3. если результат
“n-подквазигруппа найдена”
4. вернуть “есть n-подквазигруппы
порядка >= d”
5. конец цикла
6. GetRepresentatives
7. для каждого представителя m
8. вычислить GetClosure (m, k)
9. если результат
“n-подквазигруппа найдена”
10. вернуть “есть n-подквазигруппы
порядка >= d”
11.конец цикла
12.вернуть “n-подквазигруппы
порядка >= d отсутствуют”
Для обоснования корректности нам потребуется два вспомогательных утверждения, аналогичных леммам 2 и 3 из работы [15].
Лемма 12. Пусть $(Q,f)$ – $n$-квазигруппа, $d \in \mathbb{N}$, ${{G}_{1}},\; \ldots ,\;{{G}_{t}} \subset Q$, $\left| {{{G}_{1}}} \right| = \, \ldots \, = \left| {{{G}_{t}}} \right|$ = d, ${{M}_{i}} \subseteq f({{G}_{i}})$, $\left| {{{M}_{i}}} \right| \geqslant d$, $i = 1,\; \ldots ,\;t$, $M_{i}^{'}$ – множество всех d-элементных подмножеств ${{M}_{i}}$, ${{M}_{0}}$ – система представителей множеств $M_{i}^{'}$. Тогда из полноты всех ${{m}_{0}} \in {{M}_{0}}$ следует полнота всех ${{G}_{i}}$.
Доказательство. Предположим противное: найдется ${{G}_{i}}$, не являющееся полным. По условию существует ${{m}_{0}} \in {{M}_{0}}$, такое что ${{m}_{0}} \subseteq f({{G}_{i}})$. В силу монотонности замыкания
что противоречит условию. ◻Лемма 13. Пусть выполнены все условия леммы 12 и дополнительно множества ${{S}_{i}}$ представляют собой все d-элементные подмножества $Q$. Тогда $n$-квазигруппа $(Q,f)$ имеет собственные $n$-подквазигруппы порядка $ \geqslant d$ если и только если существует представитель ${{m}_{0}} \in {{M}_{0}}$, не являющийся полным.
Доказательство. Достаточность очевидна (примером искомой $n$-подквазигруппы является $f({{m}_{0}})$). Необходимость является следствием леммы 12 и того, что все d-элементные подмножества входят в ${\text{\{ }}{{G}_{i}}{\text{\} }}$, $i = 1,\; \ldots ,\;t$. ◻
Наконец, сформулируем основное утверждение раздела. Для доказательства потребуется выбрать подходящее значение параметра $K = K(k)$.
Теорема 3. Представленный алгоритм возвращает “$n$-подквазигруппы порядка $ \geqslant d$ отсутствуют” тогда и только тогда, когда $n$-квазигруппа $(Q,f)$ не имеет собственных $n$-подквазигрупп порядка $ \geqslant d$. При этом в случае d = 1 параметр $K$ может быть выбран таким образом, что временная сложность составляет $O\left( {{{k}^{{\frac{{{{n}^{2}} + n + 1}}{{n + 1}}}}}{\text{lo}}{{{\text{g}}}^{{\frac{n}{{n + 1}}}}}k} \right)$, а пространственная сложность есть $O({{k}^{n}})$ при фиксированном $n$ и $k \to \infty $. В случае $d = 2$ параметр $K$ может быть выбран таким образом, что временная сложность составляет $O\left( {{{k}^{{\frac{{{{n}^{2}} + 2n + 4}}{{n + 2}}}}}{\text{lo}}{{{\text{g}}}^{{\frac{n}{{n + 2}}}}}k} \right)$, а пространственная сложность есть $O({{k}^{n}})$ при фиксированном $n \geqslant 3$ и $O({{k}^{{5/2}}}lo{{g}^{{1/3}}}k)$ при n = 2 и $k \to \infty $.
Доказательство. Корректность алгоритма непосредственно вытекает из лемм 12 и 13.
Оценим сложность алгоритма в случае d = 1. Из леммы 10 следует, что сложность построения частичных замыканий всех одноэлементных подмножеств $Q$ есть $O(k \cdot {{K}^{n}})$. Из леммы 11 вытекает, что сложность построения системы представителей равна $O\left( {k \cdot K} \right) + O({{k}^{2}} \cdot logk{\text{/}}K)$. Из лемм 10 и 11 следует, что сложность вычисления замыканий представителей есть $O({{k}^{n}} \cdot \left( {k{\text{/}}K + 1} \right) \cdot \left( {logk + 2} \right))$. Положим K(k) = $min(k - 1,\,\,[c \cdot {{({{k}^{n}} \cdot logk)}^{{1/(n + 1)}}}])$, где квадратные скобки означают взятие целой части, а $c$ – некоторая положительная наперед заданная константа. Если $K(k) < 1$, положим $K = 1$. Очевидно, что для любых $n \geqslant 2$ и $c > 0$ найдется такое ${{k}_{0}} \in \mathbb{N}$, что для любого $k \geqslant {{k}_{0}}$ выполнено равенство $K(k) = [c \cdot {{({{k}^{n}} \cdot logk)}^{{1/(n + 1)}}}]$ и неравенства
При фиксированном $n \geqslant 2$ и $k \to \infty $ верны следующие оценки (без ограничения общности считаем, что $k \geqslant {{k}_{0}}$).
Из этих оценок непосредственно следует искомая оценка временной сложности.
Объем таблицы Кэли составляет $O({{k}^{n}})$. В силу лемм 10, 11 объем дополнительной памяти есть $O(k \cdot K)$. Так как $K = o(k)$, при $n \geqslant 2$ второе значение пренебрежимо мало в сравнении с первым, откуда вытекает оценка пространственной сложности.
Перейдем к рассмотрению случая d = 2. Из леммы 10 следует, что сложность построения частичных замыканий всех двухэлементных подмножеств есть $O({{k}^{2}} \cdot {{K}^{n}})$. По лемме 11 сложность построения системы представителей равна O(k2 · K2) + + $O({{k}^{4}} \cdot logk{\text{/}}{{K}^{2}})$. Из лемм 10 и 11 вытекает, что общая сложность построения полных замыканий представителей есть
При фиксированном $n \geqslant 2$ и $k \to \infty $ верны следующие оценки (без ограничения общности считаем, что $k \geqslant {{k}_{0}}$).
Отметим, что в случае n = 2 все четыре слагаемых имеют одинаковый порядок.
Из приведенных оценок непосредственно вытекает искомая оценка временной сложности.
Объем таблицы Кэли составляет $O({{k}^{n}})$. В силу лемм 10, 11 объем дополнительной памяти есть $O({{k}^{2}} \cdot K)$. При n = 2 выполнены соотношения
При $n \geqslant 3$ выполнены соотношения
Таким образом, оценка пространственной сложности доказана. ◻
Заметим, что в случае n = 2 выигрыш во временной сложности по сравнению с работой [15] получился за счет незначительного проигрыша в пространственной сложности.
Содержательно параметр c позволяет регулировать объем памяти – увеличение c приводит к уменьшению теоретической временной сложности за счет роста теоретической пространственной сложности. На практике, однако, при реализации на OpenMP-архитектуре повышение параметра c может привести к замедлению программы из-за ограниченности пропускной способности канала обмена с памятью. Этот эффект можно наблюдать в табл. 5, 6.
Таблица 3.
Порядок сложности проверки наличия собственных $n$-подквазигрупп
| $n = 2$ | $n = 3$ | $n = 4$ |
|---|---|---|
| ${{k}^{3}}$ | ${{k}^{4}}$ | ${{k}^{5}}$ |
| ${{k}^{{7/3}}}lo{{g}^{{2/3}}}k$ | ${{k}^{{13/4}}}lo{{g}^{{3/4}}}k$ | ${{k}^{{21/5}}}lo{{g}^{{4/5}}}k$ |
Таблица 4.
Порядок сложности проверки наличия нетривиальных $n$-подквазигрупп
| $n = 2$ | $n = 3$ | $n = 4$ |
|---|---|---|
| ${{k}^{4}}$ | ${{k}^{5}}$ | ${{k}^{6}}$ |
| ${{k}^{3}}lo{{g}^{{1/2}}}k$ | ${{k}^{{19/5}}}lo{{g}^{{3/5}}}k$ | ${{k}^{{14/3}}}lo{{g}^{{2/3}}}k$ |
Таблица 5.
Время проверки существования собственных 3-подквазигрупп
| $k$ | 256 | 512 | 1024 | 2048 |
|---|---|---|---|---|
| Easy | 0 | 6 | 236 | |
| QC0.25 | 1 | 15 | 693 | |
| QC0.5 | 0 | 14 | 147 | |
| QC1 | 1 | 1 | 20 | |
| QC2 | 0 | 0 | 4 | |
| QC4 | 0 | 1 | 5 | |
| QP2C0.25 | 0 | 11 | 515 | |
| QP2C0.5 | 0 | 9 | 105 | |
| QP2C1 | 0 | 1 | 13 | |
| QP2C2 | 0 | 0 | 3 | |
| QP2C4 | 0 | 1 | 4 | |
| QP4C0.25 | 0 | 9 | 508 | |
| QP4C0.5 | 0 | 8 | 101 | |
| QP4C1 | 0 | 1 | 10 | |
| QP4C2 | 0 | 0 | 2 | |
| QP4C4 | 0 | 1 | 3 | |
| QP8C0.25 | 0 | 9 | 419 | 1887 |
| QP8C0.5 | 0 | 8 | 84 | 441 |
| QP8C1 | 0 | 1 | 11 | 58 |
| QP8C2 | 0 | 0 | 3 | 5 |
| QP8C4 | 0 | 0 | 3 | 8 |
Таблица 6.
Время проверки существования нетривиальных 3-подквазигрупп
| $k$ | 256 | 512 | 1024 | 2048 |
|---|---|---|---|---|
| Easy | 34 | 1340 | ||
| QC0.25 | 6 | 142 | 737 | |
| QC0.5 | 1 | 12 | 91 | |
| QC1 | 1 | 3 | 31 | |
| QC2 | 0 | 1 | 15 | |
| QC4 | 0 | 1 | 26 | |
| QP2C0.25 | 4 | 93 | 551 | |
| QP2C0.5 | 1 | 5 | 85 | |
| QP2C1 | 1 | 1 | 26 | |
| QP2C2 | 0 | 1 | 10 | |
| QP2C4 | 0 | 1 | 23 | |
| QP4C0.25 | 3 | 57 | 353 | |
| QP4C0.5 | 1 | 5 | 52 | |
| QP4C1 | 1 | 2 | 16 | |
| QP4C2 | 1 | 1 | 7 | |
| QP4C4 | 0 | 1 | 15 | |
| QP8C0.25 | 3 | 55 | 324 | 17 397 |
| QP8C0.5 | 1 | 5 | 46 | 1585 |
| QP8C1 | 0 | 1 | 15 | 196 |
| QP8C2 | 1 | 1 | 6 | 42 |
| QP8C4 | 0 | 1 | 11 | 84 |
Для наглядности выпишем порядки сложности полученных алгоритмов для небольших значений $n$ и отдельной строкой приведем оценки сложности, получаемые с помощью обобщения алгоритма из работы [21]. В табл. 3 сведены результаты для проверки существования произвольных собственных $n$-подквазигрупп, в табл. 4 – результаты для проверки существования нетривиальных $n$-подквазигрупп, то есть собственных $n$-подквазигрупп порядка $ \geqslant 2$. Верхняя строка таблиц соответствует обобщению [21], нижняя – оптимизированному алгоритму.
6.1. Оценка практической эффективности
Алгоритм проверки существования собственных $n$-подквазигрупп и нетривиальных $n$-подквазигрупп для 3-квазигрупп был программно реализован с поддержкой OpenMP-распараллеливания. Программа была протестирована на рабочей станции с 8-ядерным процессором i7–3770 CPU @3.40GHz и 32 гигабайтами памяти на 3-квази группах, аналогичных тестовым примерам из [14], с различными значениями параметра c.
В табл. 5 приведены максимальные времена (в секундах) проверки наличия собственных 3-подквазигрупп. Столбцы соответствуют различным порядкам 3-квазигрупп. В строке Easy приведены времена работы обобщения алгоритма из статьи [21] на одном вычислительном ядре (здесь и далее пустые клетки означают, что время счета превысило предустановленный порог, так что программа не закончила вычисления). Строки вида QPNCC соответствуют оптимизированному алгоритму, распараллеленному с помощью OpenMP на N ядер и использующему параметр-константу $c = 1{\text{/}}C$. Если пара PN не указана, вычисление проводилось на одном ядре. Заметим, что $k = 2048$ является максимально возможным порядком вида ${{2}^{m}}$, $m \in \mathbb{N}$, при котором 3-квазигруппы допускают табличное задание при 32 гигабайтах оперативной памяти.
В табл. 6 приведены аналогичные данные для проверки наличия нетривиальных 3-подквази групп.
Полученные результаты подтверждают возможность проверки за приемлемое время наличия собственных 3-подквазигрупп и нетривиальных 3-подквазигрупп в 3-квазигруппах до порядка 2048 включительно.
7. ЗАКЛЮЧЕНИЕ
В рамках работы рассматриваются $n$-квазигруппы, заданные таблицами Кэли. Представлены алгоритмы для проверки полиномиальной полноты $n$-квазигрупп и существования собственных $n$-подквазигрупп и нетривиальных $n$-подквази групп, то есть собственных $n$-подквазигрупп порядка $ \geqslant 2$. Полиномиальная полнота обеспечивает труднорешаемость задачи проверки разрешимости уравнений над заданной n-квазигруппой, то есть защиту от атак методом составления уравнений на биты ключа. Отсутствие собственных n-подквазигрупп обеспечивает невырожденность преобразования на меньшие подмножества, при этом в ряде случаев “неподвижные точки”, то есть n-подквазигруппы порядка 1, считаются допустимыми.
Известно, что полиномиальная полнота n-квазигруппы эквивалентна одновременной простоте и неаффинности. В работе представлен алгоритм проверки простоты, имеющий сложность $O({{k}^{{n + 1}}})$, и алгоритм проверки неаффинности, имеющий сложность $O({{k}^{n}})$, при фиксированном $n \geqslant 3$ и порядке n-квазигрупп k → ∞.
Для решения задачи проверки наличия собственных $n$-подквазигрупп предложен алгоритм, сложность которого составляет $O\left( {{{k}^{{\frac{{{{n}^{2}} + n + 1}}{{n + 1}}}}}lo{{g}^{{\frac{n}{{n + 1}}}}}k} \right)$ при фиксированном $n \geqslant 3$ и k → ∞. Также предложен алгоритм для проверки наличия нетривиальных n-подквазигрупп, имеющий сложность $O\left( {{{k}^{{\frac{{{{n}^{2}} + 2n + 4}}{{n + 2}}}}}lo{{g}^{{\frac{n}{{n + 2}}}}}k} \right)$ при фиксированном $n \geqslant 2$ и k → ∞ (включение n = 2 обусловлено тем, что в этом случае удалось уточнить оценку, полученную в работе [15]). Все алгоритмы были программно реализованы с использованием OpenMP-распараллеливания и протестированы на широком классе примеров.
В дальнейшем планируется изучить возможность дополнительной оптимизации алгоритмов (прежде всего проверки простоты), рассмотреть другие модели распараллеливания (в частности, MPI), а также и провести тестирование на машинах с большими объемами памяти. Отдельной задачей является исследование функционального подхода к заданию $n$-квазигрупповых операций. В частности, в случае полиномиального задания операций на первый план выходит проблема канонического представления полиномиального выражения (см., например, [22]).
Список литературы
Shannon C. Communication theory of secrecy systems // The Bell System Technical Journal, 1949. V. 28. № 4. P. 656–715.
Глухов М.М. О применениях квазигрупп в криптографии // Прикладная дискретная математика. 2008. № 2. С. 28–32.
Shcherbacov V.A. Quasigroups in cryptology // Computer Science Journal of Moldova. 2009. V. 17. № 2 (50). P. 193–228.
Gligoroski D., Ødegărd R.S., Mihova M., Knapskog S.J., Drapal A., Klíma V., Amundsen J., El-Hadedy M. Cryptographic hash function EDON-R’ // Proceedings of the 1st International Workshop on Security and Communication Networks, 2009. P. 1–9.
Dömösi P., Horváth G. A novel cryptosystem based on abstract automata and Latin cubes // Studia Scientiarum Mathematicarum Hungarica. 2015. V. 52. № 2. P. 221–232.
Xu M., Tian Z. An image cipher based on Latin cubes // Proceedings of the 3rd International Conference on Information and Computer Technologies, 2020. P. 160–168.
Dimitrova V., Mihajloska H. Classification of ternary quasigroups of order 4 applicable in cryptography // Proceedings of the 7th International Conference for Informatics and Information Technology (CIIT 2010), 2010. P. 145–148.
Галатенко А.В., Панкратьев А.Е., Староверов В.М. Проверка полиномиальной полноты $n$-квазигрупп // Материалы XVIII Международной конференции “Алгебра, теория чисел и дискретная геометрия: современные проблемы, приложения и проблемы истории”. Тула, 2020. С. 146–150.
Галатенко А.В., Панкратьев А.Е., Староверов В.М. Об одном алгоритме проверки существования нетривиальных $n$-подквазигрупп // Материалы XIX Международной конференции “Алгебра, теория чисел, дискретная геометрия и многомасштабное моделирование: современные проблемы, приложения и проблемы истории”. Тула, 2021. С. 100–103.
Artamonov V.A., Chakrabarti S., Gangopadhyay S., Pal S.K. On Latin squares of polynomially complete quasigroups and quasigroups generated by shifts // Quasigroups and Related Systems. 2013. V. 21. № 2. P. 117–130.
Horváth G., Nehaniv C.L., Szabó Cs. An assertion concerning functionally complete algebras and NP-completeness // Theoretical Computer Science. 2008. V. 407. № 1. P. 591–595.
Галатенко А.В., Панкратьев А.Е., Родин С.Б. О полиномиально полных квазигруппах простого порядка // Алгебра и логика. 2018. Т. 57. № 5. С. 509–521.
Галатенко А.В., Панкратьев А.Е. О сложности проверки полиномиальной полноты конечных квазигрупп // Дискретная математика. 2018. Т. 30. № 4. С. 3–11.
Galatenko A.V., Pankratiev A.E., Staroverov V.M. Efficient verification of polynomial completeness of quasigroups // Lobachevskii Journal of Mathematics. 2020. V. 41. № 8. P. 1444–1453.
Галатенко А.В., Панкратьев А.Е., Староверов В.М. Об одном алгоритме проверки существования подквазигрупп // Чебышевский сборник. 2021. Т. 22. № 2. С. 76–89.
Абрамов С.А., Боголюбская А.А. Семинар по компьютерной алгебре в 2019–2020 гг. // Программирование. 2021. № 2. С. 3–4.
Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2008. 384 с.
Hagemann J., Herrmann C. Arithmetical locally equational classes and representation of partial functions // Universal Algebra, Esztergom (Hungary). 1982. V. 29. P. 345–360.
Вьюкова Н.И., Галатенко В.А., Самборский С.В. Средства динамического анализа программ в компиляторах gcc и clang // Программирование. 2020. № 4. С. 46–64.
Artamonov V.A., Chakrabarti S., Pal S.K. Characterizations of highly non-associative quasigroups and associative triples // Quasigroups and Related Systems. 2017. V. 25. № 1. P. 1–19.
Собянин П.И. Об алгоритме проверки наличия подквазигруппы в квазигруппе // Интеллектуальные системы. Теория и приложения. 2019. Т. 23. № 2. С. 79–84.
Шпиз Г.Б., Крюков А.П. Каноническое представление полиномиальных выражений с индексами // Программирование. 2019. № 2. С. 66–72.
Дополнительные материалы отсутствуют.
Инструменты
Программирование


