Программирование, 2022, № 1, стр. 54-64

1.1 Структура статьи

В разделе 2 кратко перечислены некоторые специальные факты из теории поливекторов. В разделе 3 рассмотрены случаи двумерного и трех- мерного векторных пространств. Раздел 4 посвящен изложению базовых концепций геометрической алгебры – геометрического умножения и понятия мультивектора. В разделе 5 подробно разобран пример описания трехмерных вращений с помощью мультивектора особого вида, называемого ротором. В ходе изложения подчеркивается ряд преимуществ, по сравнению с кватернионами, которые на данный момент стали стандартом де-факто для описания поворотов в трехмерном евклидовом пространстве. В разделе 6 на базе изложенного материала дается обзор основных возможностей модуля Grassmann.jl. Данный модуль, как и сам язык Julia, для которого он написан, находится еще в начальной стадии развития, поэтому страдает от явных недоделок. По ходу работы над примерами встречаются несколько таких моментов.

1.2. Обозначения и соглашения

1. Контравариантные векторы (векторы) будем обозначать строчными латинскими буквами и выделять с помощью полужирного шрифта. Например: $v$, $x$ и т.д. Над греческими буквами будем ставить значок стрелки, например: $\vec {\omega }$.

2. Линейное пространство контравариантных векторов будем обозначать буквой $L$ и полагать наличие базиса $\left\langle {{{e}_{1}},\; \ldots ,\;{{e}_{n}}} \right\rangle $. Нумерацию векторов базиса будем вести нижними индексами от $1$ до $n$. Буквой $n$ всегда будем обозначать размерность $L$ т.е. $dimL = n$.

3. Под полем скаляров будем подразумевать поле действительных чисел $\mathbb{R}$, хотя многие формулы и утверждения остаются справедливыми для любого произвольного числового поля $R$. Скаляры будем обозначать строчными греческими буквами $\alpha $, $\beta $ и т.д.

4. Будем полагать, что пространство $L$ наделено структурой скалярного произведения. Кроме того, будем полагать, что в пространстве $L$ можно задать ортонормированный базис $\left\langle {{{e}_{1}},\; \ldots ,\;{{e}_{n}}} \right\rangle $.

5. Скалярное произведение векторов $u$ и v будем обозначать как $(u,v)$, векторное произведение как $[u,v]$ или $u \times v$ и смешанное произведение трех векторов как $(u,v,w)$.

2.1. Внешнее умножение и внешняя алгебра

Контравариантные кососимметричные тензоры валентности (ранга) $(0,p)$ называют p-векторами или поливекторами. Обозначать p-вектор произвольного ранга будем также, как и обычные векторы – полужирным латинскими буквами. Когда ранг непонятен из контекста, будем указывать его внизу буквы, например: $\mathop u\limits_P $.

Относительно операции сложения и умножения на скаляр, множество p-векторов образует линейные пространства, обозначаемые как ${{\Lambda }^{p}}(L)$, где пространство L – линейное пространство контравариантных векторов с базисом $\left\langle {{{e}_{1}},\; \ldots ,\;{{e}_{n}}} \right\rangle $. Полагают, что ${{\Lambda }^{0}}(L) = {\mathbf{R}}$ и ${{\Lambda }^{1}}(L) = L$, то есть 1-вектор является контравариантным вектором.

Рассмотрим пространство $\Lambda (L)$, которое представляет собой прямую сумму пространств p-векторов

Введем на этом пространстве операцию $ \wedge {\text{:}}\;\Lambda (L) \times \Lambda (L) \to \Lambda (L)$ называемую внешним произведением. Для любых поливекторов $u \in {{\Lambda }^{p}}(L)$, $v \in {{\Lambda }^{q}}(L)$, $w \in {{\Lambda }^{r}}(L)$ внешнее умножение определяется следующими свойствами:

• rank$(\mathop u\limits_p \, \wedge \mathop v\limits_q ) = p + q$.

• $u \wedge (v \wedge w) = (u \wedge v) \wedge w$ – ассоциативность.

• $1 \wedge u = u \wedge 1 = u$, где $1$ – скалярная единица (единичный элемент).

• $\alpha \wedge \beta = \alpha \cdot \beta $ – для скаляров $ \wedge $ эквивалентно простому умножению.

• $\mathop u\limits_p \wedge \mathop v\limits_q = {{( - 1)}^{{pq}}}\mathop v\limits_q \wedge \mathop u\limits_p $ – антикоммутативность для нечетных валентностей.

• $(u + v) \wedge w = u \wedge w + v \wedge w$ – дистрибутивность (правая).

• $w \wedge (u + v) = w \wedge u + w \wedge v$ – дистрибутивность (левая).

• $u \wedge (\alpha v) = (\alpha u) \wedge v = \alpha (u \wedge v)$ это свойство в купе с дистрибутивностью дает билинейность операции $ \wedge $.

Операция внешнего произведения наделяет пространство $\Lambda (L)$ структурой ассоциативной алгебры над полем скаляров. Такая алгебра называется внешней алгеброй пространства $L$ (или алгеброй Грассмана) [2].

Все возможные p-векторы ${{e}_{{{{i}_{1}}}}} \wedge {{e}_{{{{i}_{2}}}}} \wedge \; \ldots \; \wedge {{e}_{{{{i}_{p}}}}}$, составленные из базисных векторов пространства L, образуют базис пространства  p-векторов ${{\Lambda }^{p}}(L)$. Так как между собой поливекторы ${{e}_{{{{i}_{1}}}}} \wedge {{e}_{{{{i}_{2}}}}} \wedge \; \ldots \; \wedge {{e}_{{{{i}_{p}}}}}$ отличаются лишь знаком, то можно выбрать один из них, расположив индексы по возрастанию: $1 \leqslant {{i}_{1}} < {{i}_{2}} < \; \ldots \; < {{i}_{p}} \leqslant n$. Такой порядок индексов называется естественным, а выбранный базисный $p$-вектор значимым.

2.2. Размерность пространства и ранг $p$-вектора

При работе с p-векторами следует учитывать следующие размерности и ранги.

• Размерность пространства $L = \left\langle {{{e}_{1}},\; \ldots \;{{e}_{n}}} \right\rangle $ обозначается как $dimL = n$.

• Ранг p-вектора равен p. Указывается при обозначении пространства p-векторов: ${{\Lambda }^{p}}(L)$. Вместо термина ранг также часто используют термин порядок (grade) и обозначение gr [4, 13] и иногда термин step [3].

• Размерность пространства ${{\Lambda }^{p}}(L)$ равна наибольшему рангу, который может быть у ненулевого p-вектора в данном пространстве $L$. Она также равна количеству значимых базисных p-векторов и обозначается как $dim{{\Lambda }^{p}}(L) = C_{n}^{p}$.

• Размерность пространства Λ(L) = = ${{\Lambda }^{0}}(L) \oplus {{\Lambda }^{1}}(L) \oplus {{\Lambda }^{2}}(L) \oplus {{\Lambda }^{3}}(L) \oplus \; \ldots $ равна сумме размерностей всех подпространств, составляющих прямую сумму: $\sum\limits_{i = 0}^n {C_{n}^{i}} = {{2}^{n}}$.

• Формально можно полагать ранг нулевого p‑вектора любым (удобным для манипуляций).

Базис пространства ${{\Lambda }^{p}}(L)$ зависит как от ранга p, так и от $n$ (размерности $L$). $p$-вектор будет иметь разное количество компонент в зависимости от размерности пространства L на котором мы его рассматриваем.

• На ${{\Lambda }^{2}}(L)$ базис задается 2-векторами ${{e}_{{ij}}} = {{e}_{i}} \wedge {{e}_{j}}$, где $i < j$ и $i,j = 1,\; \ldots ,\;n$.

• На ${{\Lambda }^{p}}(L)$ базис задается p-векторами ${{e}_{{{{i}_{1}} \ldots {{i}_{p}}}}} = {{e}_{{{{i}_{1}}}}} \wedge \; \ldots \; \wedge {{e}_{{{{i}_{p}}}}}$, где ${{i}_{1}} < \; \ldots \; < {{i}_{p}}$ и ${{i}_{1}}, \ldots ,{{i}_{p}}$ = 1, ..., n.

• На ${{\Lambda }^{n}}(L)$ базис задается одним $n$-вектором ${{e}_{{12 \ldots n}}} = {{e}_{1}} \wedge {{e}_{2}}\; \ldots \; \wedge {{e}_{n}}$.

Обозначения ${{e}_{{ij}}}$, ${{e}_{{{{i}_{1}}{{i}_{2}}{{i}_{3}}}}}$ и т.д. мы ввели для краткости.

В литературе [4, 13] 2-вектор называют бивектором, 3-вектор – тривектором и 4-вектор – квадривектором. Для $p$-форм малой размерности таких специальных названий авторы не встречали.

2.3. Базисные n-векторы в n-мерном пространстве

Особый случай возникает, когда ранг рассматриваемого объекта совпадает с размерностью пространства L то есть $p = n = dimL$. Тогда размерность пространства ${{\Lambda }^{n}}(L)$ равна $C_{n}^{n} = 1$ и существует только один значимый базисный n-вектор:

Можно считать, что $n$-вектор ${{e}_{{12 \ldots n}}}$ имеют одну единичную компоненту.

Базисный $n$-вектор ${{e}_{{12 \ldots n}}}$ задает элемент единичного объема. В геометрической алгебре базисный $n$-вектор обозначают как ${{E}_{n}}$ или ${{I}_{n}}$.

2.4. Разложимость

Разложимым называют p-вектор $V$, который выражается через внешнее произведение p различных векторов из $L$:

В литературе на английском языке для обозначения разложимого вектора используют термин blade [3, 4]. Реже встречается термин простой (simple) вектор.

Формулировка необходимых и достаточных условий для разложимости p-вектора не является тривиальной задачей. Она была решена в работе [14]. В пространстве $L$ размерности n разложимыми являются любые p-векторы, при $p \in {\text{\{ }}0,\;1,\;n - 1,\;n{\text{\} }}$. В трехмерном пространстве все p-векторы являются разложимыми, но уже для четырехмерного пространства это неверно. Например, бивектор следующего вида

Отдельно стоит заметить, что бивектор V = = ${{V}^{{ij}}}{{e}_{i}}\, \wedge \,{{e}_{j}}$ разложим тогда и только тогда, когда $V \wedge V = 0$ [2, § 6.3.5].

2.5. Операция дополнения и ее свойства

Правым дополнением (right complement) базисного p-вектора $B \in {{\Lambda }^{p}}(L)$, где $dimL = n$ называется такой $(n - p)$-вектор $\bar {B} \in {{\Lambda }^{{n - p}}}(L)$, что

Соответственно, левым дополнением (left complement) базисного p-вектора $B \in {{\Lambda }^{p}}(L)$ называется такой $(n - p)$-вектор $\underline {\mathbf{B}} \in {{\Lambda }^{{n - p}}}(L)$, что

Иногда, базис состоящий из дополнений называют кобазисом [13].

Для любого разложимого p-вектора, в частности, для базисного $p$-вектора $B$ выполняется следующее соотношение

Данное соотношение показывает, что правое и левое дополнение совпадают в случае, если p – четное число и различаются знаком, если p – нечетное.

Также для разложимого p-вектора $B$, где p – нечетное, выполняется равенство:

Для любого разложимого $p$-вектора:

Определив операцию дополнения для базисных p-векторов, можно распространить ее на произвольный $p$-вектор, потребовав линейности:

• $\overline {\alpha V} = \alpha \bar {A}$, где $\alpha $ – скаляр.

• $\overline {A + B} = \overline A + \overline B $.

Правое дополнение должно подчиняться тем же свойствам.

После этого не составляет труда вычислять дополнительные (комплиментарные) p-векторы. Так для $v \in L$, $dimL = 3$ получим:

Вектор $v \in {{\Lambda }^{1}}(L) = L$, а бивектор $\bar {v} \in {{\Lambda }^{2}}(L)$, но благодаря одинаковым размерностям $L$ и ${{\Lambda }^{2}}(L)$ (при условии $n = dimL = 3$) возможно взаимно однозначное соответствие, устанавливаемое операцией дополнения.

3.1. Векторное произведение

Пусть $L$ есть трехмерное пространство с базисом $\left\langle {{{e}_{1}},{{e}_{2}},{{e}_{3}}} \right\rangle $. Найдем внешнее произведение двух векторов $u$ и $v$

Найдем дополнение к бивектору $u \wedge v$

Мы получили векторное произведение $u \times v$

Операция дополнения позволяет найти $1$-вектор, ортогональный бивектору $u \times v$. Если же ее применить к 1-вектору, то, наоборот, получаем бивектор, <<ортогональный>> к исходному вектору. Для больших размерностей данная интерпретация также сохраняется, но теряет наглядность.

3.2. Смешанное произведение

На том же трехмерном пространстве $L$ найдем внешнее произведение трех векторов $u$, $v$ и $w$.

Найдем дополнение к тривектору $u \wedge v \wedge w$

Это не что иное, как смешанное произведение трех векторов $u$, $v$ и $w$:

3.3. Комплексная структура

Рассмотрим теперь $L = \left\langle {{{e}_{1}},{{e}_{2}}} \right\rangle $ и некоторый вектор $u \in L$. Найдем правое дополнение к ${{e}_{1}}$, e₂

Найдем теперь дополнение к $u$:

Это не что иное, как комплексная структура на двумерном декартовом пространстве:

• поворот на угол $\frac{\pi }{2}$:

• поворот на угол $ - \tfrac{\pi }{2}$:

Вновь рассмотрим двумерное пространство L. Найдем смешанное произведение двух векторов $u$ и $v$:

Найдем дополнение от бивектора $u \wedge v$

Мы получили ориентированную площадь параллелограмма, построенного на векторах $u$ и v. Ориентированная площадь может служить геометрической интерпретацией бивектора.

4.1. Мультивекторы и геометрическое произведение

Если допустить сложение элементов $\Lambda (L)$ различного ранга, то мы получим более общую структуру, задаваемую операцией сложения и внешнего умножения. Объект из $\Lambda (L)$, состоящий из элементов различного ранга, называется мультивектором или числом Клиффорда [15]:

Поскольку $\Lambda (L)$ является градуированной алгеброй, то в этом выражении знак суммы надо воспринимать также как и знак суммы в комплексных числах и кватернионах. Этот знак связывает скаляры, векторы, бивекторы, тривекторы и т.д. в единую сущность.

Операция геометрического умножения обладает большей общностью, чем операции скалярного и внешнего произведений. Поэтому разумно определить ее аксиоматически, а не выражать через скалярное и внешнее произведения. Тем не менее, мы будем предполагать, что в пространстве $L$ задан метрический тензор $g(u,v)$.

Геометрическим произведением двух векторов $u$ и $v$ назовем отображение $L \times L \to L$, которое имеет следующие свойства.

• Геометрическое умножение двух скаляров сводится к обычному умножению, определенному в поле этих скаляров.

• Геометрическое умножение скаляра на вектор из $L$ сводится к обычному умножению, определенному в $L$.

• Геометрическое произведение вектора $u$ самого на себя равно скаляру, значения которого определяется метрическим тензором:

• Дистрибутивность:

• В силу того, что $u$ может быть скаляром, из дистрибутивности следует линейность.

• Ассоциативность: $v(uw) = (vu)w$.

Коммутативность или антикоммутативность явным образом не требуется.

Множество $\Lambda (L)$ с ассоциативной операцией геометрического произведения называется алгеброй мультивекторов и является реализацией абстрактной алгебры Клиффорда, обобщающей алгебру Грассмана и алгебру кватернионов Гамильтона.

Из аксиом следует формула

4.2. Обратный элемент и деление

Из свойства $uu = \mathop {\left\| u \right\|}\nolimits^2 \equiv {{u}^{2}}$ следует, что для любого ненулевого вектора $u$ существует обратный элемент $\tfrac{u}{{\mathop {\left\| u \right\|}\nolimits^2 }}$:

Можно определить операцию (правого) деления, как произведение справа на обратный элемент:

Если умножение произвести слева, то получим иное выражение: ${{v}^{{ - 1}}}u = \tfrac{{vu}}{{\mathop {\left\| v \right\|}\nolimits^2 }}$ так как $uv \ne vu$.

Используя операцию деления можно записать произвольный вектор $u$ относительно некоторого вектора $v$ как:

Первое слагаемое ${{u}_{{\parallel v}}}$ является проекцией вектора $u$ на $v$, а второе слагаемое ${{u}_{{ \bot v}}}$ является ортогональной компонентой вектора $u$ относительно вектора $v$.

4.3. Геометрическое произведение произвольных мультивекторов

Обобщение геометрического произведения на произвольные p-векторы, требует обощения скалярного произведения. Однако, в случае если введен ортонормированный базис, можно обойтись без такого обобщения.

Рассмотрим евклидово пространство L = = $\langle {{e}_{1}},{{e}_{2}}, \ldots ,{{e}_{n}}\rangle $ и найдем геометрические произведения базисных векторов ${{e}_{i}}$.

Произведение базисного вектора самого на себя находится из определения:

Для произведения ${{e}_{i}}{{e}_{j}}$, где $i \ne j$ можно доказать следующее равенство [3]

Где ${{e}_{i}}{{e}_{j}} = {{e}_{i}} \wedge {{e}_{j}}$. Вообще, для любого ортонормированного базиса справедливо тождество ${{e}_{{{{i}_{1}}}}}$ ... ${{e}_{{{{i}_{p}}}}}{{e}_{1}} \wedge \ldots \wedge {{e}_{p}}$ то есть базисные p-векторы могут быть записаны через геометрическое произведение.

Пользуясь указанными выше свойствами, можно находить геометрическое произведение любых мультивекторам, достаточно знать их разложение по базисным p-векторам. Например:

Это справедливо, так как

4.4. Случай трехмерного пространства

В трехмерном декартовом пространстве мультивектор в общем случае будет иметь следующий вид:

Обозначим ${{e}_{1}}{{e}_{2}}{{e}_{3}}$ как $I$. Тогда верно равенство

Также, переставляя сомножители и правильно меняя знак, можно показать, что

Видно, что $I$ коммутирует с базисными векторами и бивекторами: $I{{e}_{i}} = {{e}_{i}}I$ и $I{{e}_{i}}{{e}_{j}} = {{e}_{i}}{{e}_{j}}I$ из чего следует, что произвольный мультивектор $U$ в трехмерном пространстве коммутирует с $I$:

Также для произвольного бивектора справедливы равенства

Кроме того, с помощью $I$ можно связать внешнее и векторное произведения:

Обозначим

Данные бивекторы ведут себя точно также как и мнимые единицы кватернионов. Можно составить таблицу умножения:

Кроме того $ijk = - 1$.

Таким образом в трехмерном пространстве множество мультивекторов вида

5.1. Повороты в трехмерном пространстве

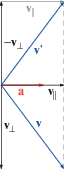
Рассмотрим вектор $v$ и умножим его слева на некоторый вектор $a$, а справа на обратный вектор a^–1. Так как операция геометрического произведения не коммутативна, то мы получим вектор $v{\text{'}}$ отличный от $v$. Пользуясь тем, что ${{u}_{{\parallel v}}} = \tfrac{{(u,v)}}{v}$ и ${{u}_{{ \bot v}}} = \tfrac{{u \wedge v}}{v}$ получим:

Таким образом, вектор $v{\text{'}}$ является отражением вектора $v$ относительно вектора $a$. Для двумерного случая данная процедура проиллюстрированна на рис. 1.

Рис. 1.

Отражение вектора $v$ относительно вектора a

Заметим, что длина (норма) вектора $v$ сохраняется. Так как по определению геометрического произведения $aa = \mathop {\left\| a \right\|}\nolimits^2 $, то

В случае единичного вектора $a$ обратный вектор ${{a}^{{ - 1}}}$ совпадает с самим $a$ так как норма a = 1 и операция отражения сводится к умножению на вектор $a$ слева и справа: $v{\text{'}} = ava$.

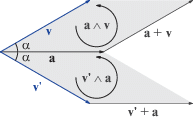
Вектор $v$ – отражение вектора $v$ относительно вектора $a$. Длины векторов $v{\text{'}}$ и $v$ совпадают и значения углов $\angle (v,a)$ и $\angle (a,v{\text{'}})$. Следовательно, геометрические произведения $av$ и $v{\text{'}}a$ совпадают:

На рис. 2 показаны бивекторы $a \wedge v$ и $v{\text{'}} \wedge a$.

Рис. 2.

Равенство бивекторных частей мультивекторов $av$ и $v{\text{'}}a$

Рис. 3.

Поворот

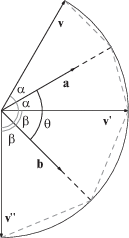
Применим к вектору $v$ последовательно два отражения: относительно вектора $a$, а затем относительно вектора $b$:

Мультивектор $ba$ обозначают как $R$ и называют ротором (вращателем).

Формула для вращения $v{\text{'}} = Rv{{R}^{{ - 1}}}$ остается справедливой для любой размерности, а не только для двумерного или трехмерного случая.

Ротор $R$ можно применять к объектам более высокого порядка, чем векторы, например:

Рассмотрим трехмерный случай для нормированных векторов $a$ и $b$. Так как

Такой ротор повернет вектор на угол $2\theta $. Если нужен поворот на угол $\theta $, то нужно взять половинный угол:

5.2. Сравнение с кватернионами

Применение мультивекторов не дает очевидного вычислительного выигрыша по сравнению с кватернионами. Однако можно выделить ряд концептуальных преимуществ

• Ротор $R$ и операция $Rv{{R}^{{ - 1}}}$ задают вращение в пространстве любой размерности.

• Операция $Rv{{R}^{{ - 1}}}$ находит геометрическую интерпретацию в виде двойного отражения. В случае кватернионов операция $qvq{\text{*}}$ вводится ad hoc.

• Угол $\theta $ имеет геометрический смысл угла между a и b. В случае кватернионов геометрическая интерпретация данного угла затруднительна.

6.1. Базовые возможности модуля Grassmann.jl

Модуль Grassmann.jl [17, 18] предназначен для языка программирования Julia. В нем реализованны все базовые операции геометрической алгебры. Одной из особенностей является поддержка смешанных численно-символьных вычислений: основные вычисления выполняются численно, но при подключении модуля Reduce появляется возможность задавать символьные компоненты и параметры.

Рассмотрим вначале базовый функционал данного модуля на примерах, повторяющих примеры изложенные нами выше. Укажем также на ошибки с которыми мы столкнулись в ходе изучения данного пакета. Наши замечания справедливы для версии библиотеки |0.7.5|. Рассмотрим следующий фрагмент кода.

1 G2 = L(ℝ^2) # DirectSum.Basis{〈++〉,4}(v, v₁,

     ↪ v₂, v₁₂)

2 @basis ℝ^2

3 complementright(e1), complementright(e2) #

     ↪ (1v₂, -1v₁)

4 complementleft(e1), complementleft(e2) #

     ↪ (-1v₂, 1v₁)

5 using Reduce

6 u = :u1 * e1 + :u2 * e2

7 complementright(u) # Error

8 u = 1*e1 + 2*e2

9 complementright(u) # -2v₁ + 1v₂

10 complementleft(u) # 2v₁ - 1v₂

Работа начинается с задания размерности пространства $L$, после чего генерируются все возможные p-векторы для пространства $\Lambda (L)$. В первой строке представлен вариант задания двумерного пространства $\Lambda (L) = \mathbb{R} \oplus L \oplus {{\Lambda }^{2}}(L)$ без экспорта сгенерированных базисных векторов в общее пространство имен, а во второй строке с экспортом.

Отметим, что для исходного кода на языке Julia общепринятым является использование различных специфических символов в кодировке Unicode. Для ввода тех символов, которые обычно используются в математике можно применять макросы ^L_A^T_E^X. Так, например, для ввода буквы $\Lambda $ в Jupyter Notebook или во встроенной оболочке, следует набрать \Lambda и нажать клавишу Tab. Некоторые макросы определены непосредственно в подключаемых пакетах. В нашем примере букву $\mathbb{R}$ можно ввести с помощью макроса /bbR, о чем, между прочим, ничего не сказано в официальной документации пакета Grassmann.

Далее (строки 3 и 4) мы применяем операции правого и левого дополнения. Вначале используется смешанный численно-символьный вариант, а затем делается попытка использовать чисто символьный вариант, однако она приводит к неудаче. Опытным путем авторами было установленно, что кроме операции внешнего произведения все остальные операции символьные вычисления не поддерживают. Ниже приведем пример вычисления ориентированной площади $S = \overline {u \wedge w} $ в символьном виде.

1 u = :u1 * e1 + :u2 * e2

2 w = :w1 * e1 + :w2 * e2

3 u ∧ w # (u1 * w2 - u2 * w1)v₁₂

4 # u = (1, 2) w = (2, 1)

5 complementright(u∧w), complementleft(u∧w) #

        ↪ -3v

6 complementright(w∧u), complementleft(w∧u) #

        ↪ +3v

Ниже показаны примеры вычисления векторного и смешанного произведений с помощью внешнего произведения и правого дополнения: $u \times w = \overline {u \wedge w} $ и $(u,{v},w) = \overline {u \wedge v \wedge w} $.

1 @basis ℝ^3

2 u∧w # (u1 * w2 - u2 * w1)v₁₂ + (u1 * w3 - u3

    ↪ * w1)v₁₃ + (u2 * w3 - u3 * w2)v₂₃

3 complementright(u∧w) # Error!

4 complementright.((e12, e13, e23)) # (1v₃,

    ↪ -1v₂, 1v₁)

Операция $ * $ переопределена для геометрического умножения. Можно перемножать мультивекторы, разложенные по базисным p-векторам, как это показано в фрагменте кода ниже.

1 (3 + 5*e1*e2 - e1*e3) * (4*e1*e2*e3) # - 4v₂

     ↪ - 20v₃ + 12v₁₂₃

2 e1*e2*e1*e2*e3 # -1v₃

3 e1*e3*e1*e2*e3 # 1v₂

Относительно операции геометрического произведения множество мультивекторов вида V = = $a + b{{e}_{{12}}}$ изоморфно множеству комплексных чисел в случае двумерного пространства $L$. Данные мультивекторы состоят только из скалярной и бивекторной части, а векторная часть равна нулю. Продемонстрируем этот факт на следующем примере, сравнив действия с мультивекторами с встроенным в язык Julia типом данных комплексных чисел.

1 (1e + 2*e12) * (2e + e12) # 0 + 5v₁₂

2 (1 + 2im)*(2 + im) # 0+5im

3 (1.0e + 2*e12) / (2.0e + e12) # 0.8 + 0.6v₁₂

4 (1 + 2im) / (2 + im) # 0.8 + 0.6im

5 sqrt(1.0e + 2*e12) # 1.2720196542002786 +

     ↪ 0.7861513560627762v₁₂

6 sqrt(1 + 2im) # 1.272019649514069 +

     ↪ 0.7861513777574233im

Отметим, что в выражении sqrt(1.0e + 2*e12) нам пришлось указать 1.0 вместо 1, так как иначе возникает ошибка извлечение квадратного корня из целого числа, появляющаяся из-за отсутствия явного приведения типов.

Стоит повысить размерность пространства $L$ до 3, как мультивекторы того же вида V = a + + $b{{e}_{{12}}} + c{{e}_{{23}}} + d{{e}_{{13}}}$ становятся изоморфными относительно операции геометрического произведения множеству кватернионов. Бивекторная часть в трехмерном пространстве имеет уже три компонента. Следующий код позволяет распечатать таблицу умножения мнимых единиц кватернионов.

1 using Printf

2 @basis ℝ^3 L e

3 i = e12; j = e23; k = e13

4 for x in (1e, i, j, k)

5 @printf “%6s|%6s|%6s|%6s\n” x*1e x*i x*j

       ↪ x*k

6 end

7 i*j*k # -1v

6.2. Реализация роторов

Рассмотрим конкретный пример вращения вектора [16]. При задании вращения в трехмерном пространстве вначале следует определить ось вращения. Для примера возьмем в качестве такой оси нормированный вектор $u = \tfrac{1}{{\sqrt 3 }}(1,\;1,\;1)$ вокруг которого на угол $\tfrac{{2\pi }}{3}$ поворачивается базисный вектор (орт) ${{e}_{1}}$. Из геометрических соображений понятно, что результатом такого вращения будет другой орт ${{e}_{2}}$.

Если необходимо задать вращение в терминах мультивекторов, то следует задавать не ось вращения, а плоскость, параллельно которой данное вращение происходит. Данная плоскость определяется некоторым бивектором вида $U = a \wedge b$. Чтобы вычислить $U$ следует взять правое дополнение от оси вращения $u$:

После чего можно вычислить ротор, используя его тригонометрическую форму:

Далее с помощью этого ротора производится вращение:

Продемонстрируем вычисление данного примера с помощью пакета Grassmann. Оператор ~ является синонимом функции reverse взятия обратного элемента.

1 u = (v1 + v2 + v3)/sqrt(3)

2 # 0.5773502691896258v₁ +

     ↪ 0.5773502691896258v₂ +

     ↪ 0.5773502691896258v₃

3 U = complementright(u)

4 # 0.5773502691896258v₁₂ -

     ↪ 0.5773502691896258v₁₃ +

     ↪ 0.5773502691896258v₂₃

5 R = cos(π/3) - sin(π/3)*U

6 # 0.5000000000000001 - 0.5v₁₂ + 0.5v₁₃ -

     ↪ 0.5v₂₃

7 R*v1*(~R)

8 # 0.0 + 1.1102230246251565e-16v₁ + 1.0v₂ -

     ↪ 1.1102230246251565e-16v₃ -

     ↪5.551115123125783e-17v₁₂₃