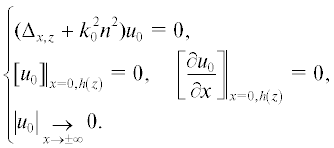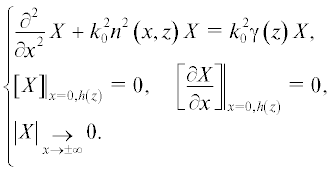Программирование, 2022, № 2, стр. 23-32
СИМВОЛЬНОЕ ИССЛЕДОВАНИЕ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК НАПРАВЛЯЕМЫХ МОД ПЛАВНО-НЕРЕГУЛЯРНЫХ ВОЛНОВОДОВ
Д. В. Диваков a, b, *, А. А. Тютюнник a, b, **
a Российский университет дружбы народов
117198 Москва, ул. Миклухо-Маклая, д. 6, Россия
b Объединенный институт ядерных исследований
141980 Московская обл., Дубна, ул. Жолио-Кюри, д. 6, Россия
* E-mail: divakov-dv@rudn.ru
** E-mail: tyutyunnik-aa@rudn.ru
Поступила в редакцию 24.08.2021
После доработки 24.08.2021
Принята к публикации 11.09.2021
- EDN: JKRTFD
- DOI: 10.31857/S0132347422020054
Аннотация
В работе рассматривается однородная система функциональных уравнений, возникающая при решении спектральной задачи, собственные функции которой описывают направляемые моды плавно-нерегулярных волноводов. Полученная система функциональных уравнений представляет собой однородную систему алгебраических уравнений при любом фиксированном значении аргумента. В рамках проведенных исследований разработан символьный метод решения систем функциональных уравнений такого типа. Метод реализован в системе компьютерной алгебры Maple. В работе приведены результаты численных расчетов, демонстрирующих эффективность разработанного символьно-численного метода по сравнению с подходом, использующим только численные методы.
1. ВВЕДЕНИЕ
Существуют различные подходы к моделированию оптических явлений, которые можно разбить на две большие группы: символьные и численные.
1.1. Символьные подходы
К символьным подходам относятся те методы, в рамках которых выделяются важные частные случаи решения, позволяющие на символьном уровне упростить уравнения модели и далее исследовать полученные упрощенные уравнения на символьном уровне [1, 2], либо с применением численных методов. Вычислительная задача в таком подходе всегда проще, чем в рамках численных подходов, описанных ниже, за счет упрощений, сделанных на символьном уровне. Кроме того, символьный подход зачастую позволяет сконструировать понятное с физической точки зрения решение.
1.2. Численные подходы
В рамках чисто численных подходов после постановки задачи сразу же следует построение приближенного метода ее решения – либо разностного [3–5], либо методов, основанных на разложениях Галеркина [6–8] (реже – методом Ритца [9]), Канторовича [10, 11] или метода конечных элементов [12, 13]. Однако, даже для генерации разностных схем также применяются системы компьютерной алгебры [14, 15].
Численный подход почти всегда исключает аналитическое упрощение представленной модели. Однако в численном подходе можно строить методы, подходящие для исследования широкого класса задач с большим произволом параметров модели.
1.3. Задача текущего исследования
Одним из первых методов исследования спектральных характеристик плавно-нерегулярных волноводов является метод поперечных сечений, предложенный в работах Каценеленбаума Б.З. [16, 17] для закрытых волноводов и обобщенный Шевченко В.В. на открытые волноводы [18, 19].
Особенностью метода поперечных сечений является символьный вид решения, в котором в явном виде присутствует искомая функция $\gamma \left( z \right)$, определяющая коэффициент фазового замедления соответствующей волноводной моды в каждом поперечном сечении волновода $z = {\text{const}}$. Для определения электромагнитного поля данной волноводной моды необходимо решать спектральную задачу специального вида, которая в фиксированном поперечном сечении волновода представляет собой задачу Штурма–Лиувилля для дифференциального оператора второго порядка на оси.
Аналогичную спектральную задачу можно получить и в рамках других подходов, например, как это сделано в работе авторов [20]. В рамках настоящей работы рассматривается система функциональных уравнений, получаемых из спектральной задачи, возникающей из метода поперечных сечений. В работе эта система функциональных уравнений исследуется на символьном уровне, для исследования разработан символьный алгоритм, реализованный в системе компьютерной алгебры Maple [21]. Зависимость $\gamma \left( z \right)$ в работе отыскивается численно.
2. МОТИВАЦИЯ
2.1. Модель распространения TE-моды в волноводе
Рассмотрим волноводное распространение TE-моды в однородном открытом диэлектрическом волноводном переходе типа “рупор”, изображенном на рисунке 1.
Рассматривать будем волноводный переход толщина которого линейно увеличивается от значения h1 при $z = 0$ до значения ${{h}_{2}}$ при $z = d$: $h(z)$ = = h1 + δz, где $\delta = \frac{{{{h}_{2}} - {{h}_{1}}}}{d} \ll 1$ – малый параметр. Ведущая компонента TE-моды Ey удовлетворяет уравнению Гельмгольца в области волноводного перехода, что соответствует $0 \leqslant z \leqslant d$ [22]:
Асимптотические условия, отвечающие направляемым модам определены следующим образом
[22]: 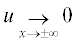 . На границах раздела сред для TE-моды должны выполняться условия сопряжения [22]:
. На границах раздела сред для TE-моды должны выполняться условия сопряжения [22]:
2.2. Разложение решения в асимптотический ряд
Так как в уравнении и граничных условиях присутствует малый параметр $\delta $ можно строить решение в виде ряда по степеням параметра $\delta $: $u = {{u}_{0}} + \delta {{u}_{1}} + {{\delta }^{2}}{{u}_{2}} + \; \ldots $. Для такого вида решения можно сформулировать уравнение:
В нулевом приближении уравнение, граничные и асимптотические условия принимают следующий вид:
2.3. Аналог разделения переменных в нулевом приближении
Классический подход к построению решения такой задачи состоит в попытке разыскать решение в виде произведения функций ${{u}_{0}}(x,z) = X(x)Z(z)$ и подстановке в уравнение из (1) с дальнейшим преобразованием уравнения в попытке разделить переменные. В данном случае аналогичная процедура приводит к следующему соотношению:
Замечание 1. Из уравнения (2) следует, что функция X должна зависеть от $x$ и $z$, что, на первый взгляд, противоречит предположению X = = X(x). Однако, если X зависит от $x$ и $z$, а величина $\left| {\frac{{\partial X}}{{\partial z}}} \right|$ имеет порядок ${{\delta }^{p}}$, где $p \geqslant 1$, то в нулевом приближении по $\delta $ выкладки вполне справедливы. Другими словами X зависит от $x$ и $z$, однако для справедливости уравнения (1.8) необходимо, чтобы зависимость X от $z$ была настолько “медленной”, чтобы выполнялось
Такую зависимость будем обозначать $X = X(x;z)$.
Замечание 2. Учитывая, что $\left| {\frac{{\partial X}}{{\partial z}}} \right|$ имеет порядок ${{\delta }^{p}}$, то в приближении порядка $p$ вклад производной $\frac{{\partial X}}{{\partial z}}$ необходимо будет учитывать.
2.4. Спектральная задача в нулевом приближении
В результате дальнейшего применения процедуры разделения переменных в нулевом приближении можно получить следующую спектральную задачу:
Искомыми величинами в задаче (3) выступают функция двух переменных X(x, z) и функция одной переменной $\gamma \left( z \right)$. Общее решение уравнения из (3), удовлетворяющее асимптотическому условию 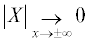 имеет следующий вид:
имеет следующий вид:
(4)
$\begin{gathered} X\left( {x,z} \right) = \\ = \;\left\{ \begin{gathered} {{A}_{c}}\left( z \right){{e}^{{ - {{p}_{c}}\left( z \right)\left( {x - h\left( z \right)} \right)}}},\quad x > h\left( z \right) \hfill \\ {{A}_{f}}\left( z \right){{e}^{{i{{p}_{f}}\left( z \right)x}}} + {{B}_{f}}\left( z \right){{e}^{{ - i{{p}_{f}}\left( z \right)x}}},\quad 0 < x < h\left( z \right) \hfill \\ {{A}_{s}}\left( z \right){{e}^{{{{p}_{s}}\left( z \right)x}}},\quad x < 0 \hfill \\ \end{gathered} \right. \\ \end{gathered} $(5)
$\begin{gathered} {{p}_{c}}\left( z \right) = {{k}_{0}}\sqrt {\gamma \left( z \right) - n_{c}^{2}} , \\ {{p}_{f}}\left( z \right) = {{k}_{0}}\sqrt {n_{f}^{2} - \gamma \left( z \right)} , \\ {{p}_{s}}\left( z \right) = {{k}_{0}}\sqrt {\gamma \left( z \right) - n_{s}^{2}} . \\ \end{gathered} $Для выполнения условий сопряжения из (3) на границах $x = 0,\;h\left( z \right)$ необходимо чтобы выполнялись следующие функциональные уравнения
(6)
$\left\{ \begin{gathered} {{A}_{f}}\left( z \right) + {{B}_{f}}\left( z \right) = {{A}_{s}}\left( z \right), \hfill \\ i{{p}_{f}}\left( z \right)\left( {{{A}_{f}}\left( z \right) - {{B}_{f}}\left( z \right)} \right) = {{p}_{s}}\left( z \right){{A}_{s}}\left( z \right), \hfill \\ {{A}_{c}}\left( z \right) = {{A}_{f}}\left( z \right){{e}^{{i{{p}_{f}}\left( z \right)h\left( z \right)}}} + {{B}_{f}}\left( z \right){{e}^{{ - i{{p}_{f}}\left( z \right)h\left( z \right)}}}, \hfill \\ - {{p}_{c}}\left( z \right){{A}_{c}}\left( z \right) = \hfill \\ = \;i{{p}_{f}}\left( z \right)({{A}_{f}}\left( z \right){{e}^{{i{{p}_{f}}\left( z \right)h\left( z \right)}}} - {{B}_{f}}\left( z \right){{e}^{{ - i{{p}_{f}}\left( z \right)h\left( z \right)}}}), \hfill \\ \end{gathered} \right.$Замечание. Зависимость $\gamma \left( z \right)$ в рамках настоящей работы отыскивается численно методом деления отрезка пополам, поэтому отысканию этой величины не будет уделено особого внимания.
Систему (6) можно записать в следующем виде:
где коэффициенты матрицы $M\left( {\gamma \left( z \right)} \right)$ зависят от искомой величины $\gamma \left( z \right)$ нелинейно, но при этом система линейна относительно искомых величин $\vec {A}\left( z \right) = {{\left( {{{A}_{c}}\left( z \right),{{A}_{f}}\left( z \right),{{B}_{f}}\left( z \right),{{A}_{s}}\left( z \right)} \right)}^{{\text{т}}}}$.При любом фиксированном $z = {{z}_{j}}$ система (7) принимает вид однородной системы уравнений вида
у которой всегда существует тривиальное решение ${{\vec {A}}_{j}} = \vec {0}$.В случае, если $\det M\left( {{{\gamma }_{j}}} \right) \ne 0$, то тривиальное решение единственно, а если $\det M\left( {{{\gamma }_{j}}} \right) = 0$, то у системы (8) кроме тривиального существует хотя бы одно нетривиальное решение.
Численные алгоритмы решения системы (7) как правило основываются на введении сетки zj, $1 \leqslant j \leqslant N$ и многократном численном решении однородной системы типа (8) при каждом фиксированном zj. При этом численное решение системы (8) состоит из двух задач:
Задача 1. Приближенное отыскание всех значений $\gamma _{j}^{s}$, являющихся корнями нелинейного уравнения $\det M\left( {{{\gamma }_{j}}} \right) = 0$.
2. Приближенное отыскание нетривиального решения однородной системы линейных алгебраических уравнений $M(\gamma _{j}^{s})\vec {A}_{j}^{s} = \vec {0}$ для каждого s.
Задача 1 в случае вещественных корней решается без каких-либо существенных сложностей в отличие от задачи 2, которая является некорректной задачей и зачастую требует применения методов регуляризации [23].
При анализе численных результатов авторами было замечено, что присутствует некая функциональная зависимость величин ${{A}_{c}}\left( z \right)$, ${{A}_{f}}\left( z \right)$, ${{B}_{f}}\left( z \right)$, ${{A}_{s}}\left( z \right)$ от ${{p}_{f}}\left( z \right)$, ${{p}_{s}}\left( z \right)$. Поэтому у авторов возникла гипотеза, что искомые величины системы (7) могут выражаться через ${{p}_{f}}\left( z \right)$ и ${{p}_{s}}\left( z \right)$ в виде простых символьных выражений. Другими словами покажем, что система (7) может иметь символьное решение в зависимости от $\gamma \left( z \right)$. Для проверки этой гипотезы был разработан символьный алгоритм исследования системы функциональных уравнений (7), который приведен в следующем разделе. Если бы у рассматриваемой системы существовало символьное решение, которое в явном виде зависит от $\gamma \left( z \right)$ и состоит из достаточно компактных символьных выражений, то оно бы избавило исследователей от отыскания решения некорректной задачи путем многократного решения системы (8) на сетке. Также наличие символьного решения упростило бы качественный анализ полученных результатов.
3. МЕТОДЫ
3.1. Численный метод отыскания $\gamma \left( z \right)$
В работе рассматривается система (7), матрица которой имеет следующий вид
(9)
$M\left( {\gamma \left( z \right)} \right) = \left( {\begin{array}{*{20}{c}} 0&1&1&{ - 1} \\ 0&{i{{p}_{f}}}&{ - i{{p}_{f}}}&{ - {{p}_{s}}} \\ 1&{ - {{e}^{{i{{p}_{f}}h}}}}&{ - {{e}^{{ - i{{p}_{f}}h}}}}&0 \\ { - {{p}_{c}}}&{ - i{{p}_{f}}{{e}^{{i{{p}_{f}}h}}}}&{i{{p}_{f}}{{e}^{{ - i{{p}_{f}}h}}}}&0 \\ {}&{}&{}&{} \end{array}} \right),$Замечание. Важно заметить, что фактически мы отыскиваем не $\gamma \left( z \right)$, а ${{\tilde {\gamma }}_{j}}$ такое, что $\left| {{{{\tilde {\gamma }}}_{j}}\, - \,\gamma ({{z}_{j}})} \right|\, < \,\varepsilon $, для $1 \leqslant j \leqslant N$, где $\varepsilon $ – погрешность приближенного решения. Однако, важно учесть, что
1. Используя числа повышенной разрядности можно добиться произвольно малой для практических расчетов погрешности $\varepsilon $;
2. Увеличивая количество узлов сетки $N$ можно добиться такой близости соседних узлов zj и ${{z}_{{j + 1}}}$, что кусочно-линейная аппроксимация $\tilde {\gamma }\left( z \right)$ гладкой функции $\gamma \left( z \right)$ была сколь угодно близка к функции $\gamma \left( z \right)$ в любой метрике.
Учитывая п. 1–2 замечания можно сказать, что величину $\gamma \left( z \right)$ можно определить с любой наперед заданной точностью. Учитывая также, что при численных расчетах все величины округляются до чисел конечной разрядности – как правило до чисел двойной точности – можно добиться одинаковой точности и величины $\gamma \left( z \right)$ и всех остальных величин, принимающих участие в численных расчетах. Поэтому величину $\gamma \left( z \right)$ можно считать численно известной.
Замечание. Как правило уравнение ${\text{det}}M(\gamma (z))$ = = 0 имеет несколько решений ${{\gamma }_{1}}\left( z \right),{{\gamma }_{2}}\left( z \right),\; \ldots $ – тем больше, чем больше толщина волновода.
3.2. Символьный метод отыскания $\vec {A}\left( z \right)$
Рассмотрим символьный алгоритм исследования системы (6), предлагаемый авторами. Учитывая изложенное в предыдущем разделе, величину $\gamma \left( z \right)$ будем считать известной. Для простоты изложения в настоящем разделе опустим зависимость от z у величин, входящих в уравнения (6).
Итак, обратим внимание на первые два уравнения системы (6)
(10)
$\left\{ \begin{gathered} {{A}_{f}} + {{B}_{f}} = {{A}_{s}}, \hfill \\ i{{p}_{f}}\left( {{{A}_{f}} - {{B}_{f}}} \right) = {{p}_{s}}{{A}_{s}}, \hfill \\ \end{gathered} \right.$(11)
${{A}_{f}}\left( {i{{p}_{f}} - {{p}_{s}}} \right) - {{B}_{f}}\left( {i{{p}_{f}} + {{p}_{s}}} \right) = 0,$(12)
$\left\{ \begin{gathered} {{A}_{f}} = A \cdot \left( {i{{p}_{f}} + {{p}_{s}}} \right), \hfill \\ {{B}_{f}} = A \cdot \left( {i{{p}_{f}} - {{p}_{s}}} \right), \hfill \\ \end{gathered} \right.$Замечание 1. Если начать рассмотрение системы (6) с последних двух уравнений, то сначала найдем из этих уравнений ${{A}_{f}}$, ${{B}_{f}}$ и ${{A}_{c}}$, а затем из первых двух определим ${{A}_{s}}$. Другими словами, из подсистемы, состоящей из двух однородных уравнений с тремя неизвестными, можно определить три неизвестных величины – то есть решить эту подсистему. Учитывая это, при реализации символьного алгоритма реализован поиск подсистем из двух уравнений с тремя неизвестными среди рассматриваемых уравнений и поочередное решение этих подсистем.
Замечание 2. После отыскания компонент решения ${{A}_{f}}$, ${{B}_{f}}$, ${{A}_{s}}$ (или ${{A}_{f}}$, ${{B}_{f}}$, ${{A}_{c}}$) оставшаяся единственная неизвестная компонента ${{A}_{c}}$ (или ${{A}_{s}}$) определяется из двух оставшихся уравнений – каждое с одной неизвестной. Однако, для определения одной неизвестной достаточно одного уравнения. Поэтому из каждого из двух оставшихся уравнений единственная неопределенная величина может определяться по-разному. Эти возможности учтены при реализации символьного алгоритма.
Замечание 3. Описанный алгоритм обобщен на случай систем уравнений произвольной размерности.
Описанный выше алгоритм реализован в системе компьютерной алгебры Maple. Он позволяет отыскивать различные представления символьного решения однородной системы уравнений типа (6). Псевдокод алгоритма приведен ниже.
3.3. Численный метод отыскания $\vec {A}\left( z \right)$
Численное отыскание $\vec {A}\left( z \right)$ состоит в приближенном отыскании нетривиального решения однородной системы $M\left( {{{{\tilde {\gamma }}}_{j}}} \right){{\vec {A}}_{j}} = \vec {0}$ на сетке ${{z}_{j}}$, $1 \leqslant j \leqslant N$, на которой приближенно определена величина $\gamma \left( z \right)$. Нетривиальное решение системы $M\left( {{{{\tilde {\gamma }}}_{j}}} \right){{\vec {A}}_{j}} = \vec {0}$ есть собственный вектор, отвечающий почти нулевому собственному значению матрицы $M\left( {{{{\tilde {\gamma }}}_{j}}} \right)$. Поэтому численное отыскание нетривиального решения осуществляется с помощью встроенного в Maple метода Eigenvectors пакета LinearAlgebra, который используюет QR-алгоритм для решения задачи.
| Algorithm 1: Algorithm for solving homogeneous system with 2 × 3 subsystem | |||||||||
| Input:eqs – ordered list of equations, vars – ordered list of variables | |||||||||
| Output: set of different possible solutions, obtained by the algorithm or empty set if the system do not contain any subsystem 2 × 3 | |||||||||
| all indexes set | |||||||||
| indx1 ← {1, 2, . . . , n}; | |||||||||
| empty set | |||||||||
| indx2 ← ∅; | |||||||||
| count of subsystems with the same | |||||||||
| variables | |||||||||
| k ← 0; | |||||||||
| fori ∈ indx1do | |||||||||
| ri ← set of variables included in i-th | |||||||||
| equation; | |||||||||
| while indx1 not emptydo | |||||||||
| a ← ${{r}_{{indx{{1}_{1}}}}}$ ; | |||||||||
| k ← k + 1; | |||||||||
| forj ∈ indx1do | |||||||||
| ifa = rj then | |||||||||
| |indx2 ← indx2 ∪{j}; | |||||||||
| indxsk ← indx2; | |||||||||
| indx1 ← indx1/indx2; | |||||||||
| indx2 ← ∅; | |||||||||
| fori ∈ [1, 2, . . . , k] do | |||||||||
| indx1 ← {1, 2, . . . , n}; | |||||||||
| indx2 ← indxsi; | |||||||||
| ifsize(indx2) = 2and | |||||||||
| size(${{r}_{{indx{{s}_{1}}}}}$) = 3then | |||||||||
| subs_def_vars ← | |||||||||
| solve(eqsj), j ∈ indx2; | |||||||||
| undef_vars ← | |||||||||
| eqsj, j ∈ indx1/indx2; | |||||||||
| undef_vars ←vars/${{r}_{{indx{{s}_{{i,1}}}}}}$; | |||||||||
| subset_eqs ← all subsets of the set | |||||||||
| undef_eqs of size | |||||||||
| size(undef_vars); | |||||||||
| for | |||||||||
| m ∈ [1, 2, . . . , size(subset_eqs)] | |||||||||
| do | |||||||||
| solution_subs ← solution_subs | |||||||||
| ∪ {solve(subset_eqsm) ∪ | |||||||||
| subs_def_vars} | |||||||||
Замечание 1. Задача отыскания нетривиального решения однородной системы $M\vec {A} = \vec {0}$ некорректна. Действительно, если вектор $\vec {A}$ есть нетривиальное решение этой системы, то вектор $\vec {B} = c \cdot \vec {A}$ также будет нетривиальным ее решением для любой константы $c \ne 0$.
Замечание 2. Для решения задачи (7) необходимо многократно для каждого $j$ на сетке ${{z}_{j}}$, $1 \leqslant j \leqslant N$ решать систему $M\left( {{{{\tilde {\gamma }}}_{j}}} \right){{\vec {A}}_{j}} = \vec {0}$. Имея два решения в соседних узлах сетки ${{\vec {A}}_{j}}$ и ${{\vec {A}}_{{j + 1}}}$ ($\left\| {{{{\vec {A}}}_{j}}} \right\| = \left\| {{{{\vec {A}}}_{{j + 1}}}} \right\|$ = 1) для обеспечения непрерывности необходимо подобрать константу $\alpha \in \mathbb{C}$, $\left| \alpha \right| = 1$ такую, что $\left\| {\alpha {{{\vec {A}}}_{{j + 1}}} - {{{\vec {A}}}_{j}}} \right\| \to \min $.
Учитывая замечания 1, 2 кроме отыскания нетривиальных решений систем $M\left( {{{{\tilde {\gamma }}}_{j}}} \right){{\vec {A}}_{j}} = \vec {0}$ для каждого j необходимо также на каждом шаге подбирать соответствующую константу $\alpha $. Решение этой задачи подбора константы подробно описано в разделе 3.5 работы [25].
4. РЕЗУЛЬТАТЫ
4.1. Символьные результаты
Применим разработанный символьный алгоритм к рассматриваемой однородной системе (6). В результате получим следующие различные символьные представления решения однородной системы (6):
(13)
${{\vec {A}}_{1}} = \left[ \begin{gathered} \frac{{{{p}_{f}}(\left( {i{{p}_{s}} + {{p}_{f}}} \right){{{\text{e}}}^{{ - i{{p}_{f}}h}}} + \left( {i{{p}_{s}} - {{p}_{f}}} \right){{{\text{e}}}^{{i{{p}_{f}}h}}})}}{{{{p}_{c}}}} \\ - {{p}_{s}} - i{{p}_{f}} \\ - i{{p}_{f}} + {{p}_{s}} \\ - 2i{{p}_{f}} \\ \end{gathered} \right],$(14)
${{\vec {A}}_{2}} = \left[ \begin{gathered} \left( { - i{{p}_{f}} + {{p}_{s}}} \right){{{\text{e}}}^{{ - i{{p}_{f}}h}}} - \left( {i{{p}_{f}} + {{p}_{s}}} \right){{{\text{e}}}^{{i{{p}_{f}}h}}} \\ - {{p}_{s}} - i{{p}_{f}} \\ - i{{p}_{f}} + {{p}_{s}} \\ - 2i{{p}_{f}} \\ \end{gathered} \right],$(15)
${{\vec {A}}_{3}} = \left[ \begin{gathered} - 2i{{p}_{f}} \\ - \left( {i{{p}_{f}} - {{p}_{c}}} \right){{{\text{e}}}^{{ - i{{p}_{f}}h}}} \\ - \left( {i{{p}_{f}} + {{p}_{c}}} \right){{{\text{e}}}^{{i{{p}_{f}}h}}} \\ \frac{{{{p}_{f}}(\left( {i{{p}_{c}} + {{p}_{f}}} \right){{{\text{e}}}^{{ - i{{p}_{f}}h}}} + \left( {i{{p}_{c}} - {{p}_{f}}} \right){{{\text{e}}}^{{i{{p}_{f}}h}}})}}{{{{p}_{s}}}} \\ \end{gathered} \right],$(16)
${{\vec {A}}_{4}} = \left[ \begin{gathered} - 2i{{p}_{f}} \\ - \left( {i{{p}_{f}} - {{p}_{c}}} \right){{{\text{e}}}^{{ - i{{p}_{f}}h}}} \\ - \left( {i{{p}_{f}} + {{p}_{c}}} \right){{{\text{e}}}^{{i{{p}_{f}}h}}} \\ \left( { - i{{p}_{f}} + {{p}_{c}}} \right){{{\text{e}}}^{{ - i{{p}_{f}}h}}} - \left( {i{{p}_{f}} + {{p}_{c}}} \right){{{\text{e}}}^{{i{{p}_{f}}h}}} \\ \end{gathered} \right].$Замечание. Решение однородной системы (6) можно отыскивать как собственный вектор матрицы коэффициентов системы, отвечающий нулевому ее собственному значению. Однако встроенный в Maple метод Eigenvectors пакета LinearAlgebra не позволяет отыскать символьные представления собственных векторов: после получаса работы метода результат вычислен не был. Тем не менее, собственные значения вычисляются методом Eigenvalues, однако символьные представления собственных значений превышают допустимый лимит длины отображения выражений в Maple. Другими словами, выражения для собственных значений слишком длинные для отображения, и, соответственно, для анализа.
Приведем также символьное выражение для определителя матрицы M, полученное с помощью встроенного в Maple метода Determinant пакета LinearAlgebra:
(17)
$\begin{gathered} \det M = (p_{f}^{2} + \left( {i{{p}_{c}} + i{{p}_{s}}} \right){{p}_{f}} - {{p}_{c}}{{p}_{s}}){{{\text{e}}}^{{ - i{{p}_{f}}h}}} + \\ + \;( - p_{f}^{2} + \left( {i{{p}_{c}} + i{{p}_{s}}} \right){{p}_{f}} + {{p}_{c}}{{p}_{s}}){{{\text{e}}}^{{i{{p}_{f}}h}}}. \\ \end{gathered} $После подстановки каждого из полученных символьных решений ${{\vec {A}}_{j}}$ в систему уравнений получим следующие вектора невязок ${{\vec {\delta }}_{j}} = M{{\vec {A}}_{j}}$:
(18)
$\begin{gathered} {{{\vec {\delta }}}_{1}} = \left[ \begin{gathered} p_{c}^{{ - 1}} \cdot \det M \\ 0 \\ 0 \\ 0 \\ \end{gathered} \right],\quad {{{\vec {\delta }}}_{2}} = \left[ \begin{gathered} 0 \\ \det M \\ 0 \\ 0 \\ \end{gathered} \right], \\ {{{\vec {\delta }}}_{3}} = \left[ \begin{gathered} 0 \\ 0 \\ - p_{s}^{{ - 1}} \cdot \det M \\ 0 \\ \end{gathered} \right],\quad {{{\vec {\delta }}}_{4}} = \left[ \begin{gathered} 0 \\ 0 \\ 0 \\ \det M \\ \end{gathered} \right]. \\ \end{gathered} $4.2. Численные результаты
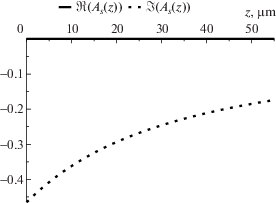
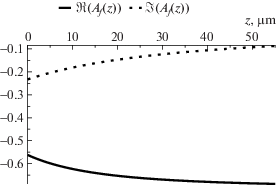
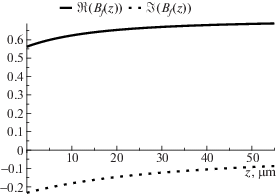
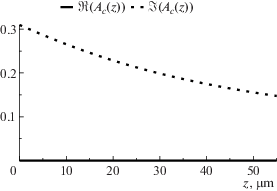
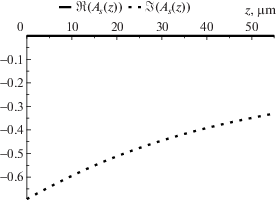
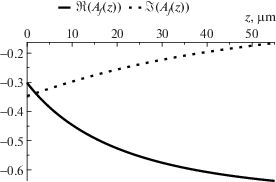
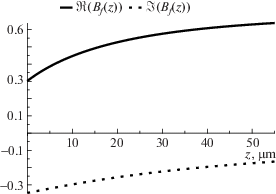
Вычислим сначала приближенно величину $\gamma (z)$, а затем вычислим $\vec {A}\left( z \right)$ на основе явных символьных выражений (13)–(16) и на основе численного алгоритма из раздела 3.3. Также численно сравним между собой величины, вычисленные по каждой из четырех формул (13)–(16).
Расчеты будем проводить для следующих значений параметров:
(19)
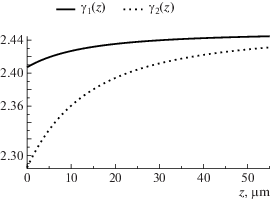
$\begin{gathered} \lambda = 0.55\;[\mu {\text{m}}];\quad {{k}_{0}} = \frac{{2\pi }}{\lambda }\;[\mu {{{\text{m}}}^{{ - 1}}}]; \\ {{n}_{c}} = 1.0;\quad {{n}_{f}} = 1.565;\quad {{n}_{s}} = 1.47; \\ h\left( z \right) = {{h}_{0}} + a \cdot z;\quad {{h}_{0}} = 2\lambda ;\quad a = 0.05. \\ \end{gathered} $Ниже приведены графики величин ${{\gamma }_{s}}\left( z \right)$, вычисленных на отрезке $z \in \left[ {0,d} \right]$, $d = 100\lambda $ на сетке zj, $1 \leqslant j \leqslant N$ для $N = 64$ с точностью $\varepsilon {{ = 10}^{{ - 15}}}$.
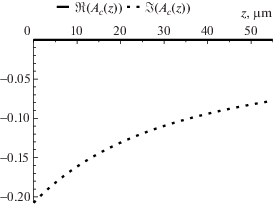
Для каждого из вычисленных ${{\gamma }_{s}}\left( z \right)$ вычислим на той же сетке численно $\vec {A}\left( z \right)$ и сравним с ${{\vec {A}}_{m}}\left( z \right)$, рассчитанными по формулам (13)–(16). Для сравнения введем следующую метрику:
(20)
$\begin{gathered} \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{m}}\left( z \right)} \right\| = \\ = \;\max {{\left\{ {{{{\left\| {\vec {A}\left( {{{z}_{j}}} \right) - {{{\vec {A}}}_{m}}\left( {{{z}_{j}}} \right)} \right\|}}_{E}}} \right\}}_{{j = 1...N}}}, \\ \end{gathered} $(21)
$\begin{gathered} \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{1}}\left( z \right)} \right\| = 1.3203943 \times {{10}^{{ - 13}}}; \\ \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{2}}\left( z \right)} \right\| = 2.2581455 \times {{10}^{{ - 13}}}; \\ \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{3}}\left( z \right)} \right\| = 2.4551606 \times {{10}^{{ - 14}}}; \\ \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{4}}\left( z \right)} \right\| = 1.9789579 \times {{10}^{{ - 13}}}. \\ \end{gathered} $Для $s = 2$ (вторая мода) данные приведены ниже.
(22)
$\begin{gathered} \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{1}}\left( z \right)} \right\| = 7.8714684 \times {{10}^{{ - 14}}}; \\ \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{2}}\left( z \right)} \right\| = 1.3160178 \times {{10}^{{ - 13}}}; \\ \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{3}}\left( z \right)} \right\| = 2.2887124 \times {{10}^{{ - 14}}}; \\ \left\| {\vec {A}\left( z \right) - {{{\vec {A}}}_{4}}\left( z \right)} \right\| = 9.9322492 \times {{10}^{{ - 14}}}. \\ \end{gathered} $Кроме того, приведем результаты сравнения величин ${{\vec {A}}_{m}}\left( z \right)$ между собой. Введем матрицу ${{\Delta }^{1}}$ (для $s = 1$) с элементами $\Delta _{{m,l}}^{1} = \left\| {{{{\vec {A}}}_{m}}\left( z \right) - {{{\vec {A}}}_{l}}\left( z \right)} \right\|$:
(23)
$\left[ {\begin{array}{*{20}{c}} 0&{2.0 \times {{{10}}^{{ - 13}}}}&{1.4 \times {{{10}}^{{ - 13}}}}&{2.4 \times {{{10}}^{{ - 13}}}} \\ {2.0 \times {{{10}}^{{ - 13}}}}&0&{2.4 \times {{{10}}^{{ - 13}}}}&{3.1 \times {{{10}}^{{ - 13}}}} \\ {1.4 \times {{{10}}^{{ - 13}}}}&{2.4 \times {{{10}}^{{ - 13}}}}&0&{2.0 \times {{{10}}^{{ - 13}}}} \\ {2.4 \times {{{10}}^{{ - 13}}}}&{3.1 \times {{{10}}^{{ - 13}}}}&{2.0 \times {{{10}}^{{ - 13}}}}&0 \end{array}} \right],$(24)
$\left[ {\begin{array}{*{20}{c}} 0&{9.9 \times {{{10}}^{{ - 14}}}}&{7.1 \times {{{10}}^{{ - 14}}}}&{1.1 \times {{{10}}^{{ - 13}}}} \\ {9.9 \times {{{10}}^{{ - 14}}}}&0&{1.2 \times {{{10}}^{{ - 13}}}}&{1.5 \times {{{10}}^{{ - 13}}}} \\ {7.1 \times {{{10}}^{{ - 14}}}}&{1.2 \times {{{10}}^{{ - 13}}}}&0&{9.7 \times {{{10}}^{{ - 14}}}} \\ {1.1 \times {{{10}}^{{ - 13}}}}&{1.5 \times {{{10}}^{{ - 13}}}}&{9.7 \times {{{10}}^{{ - 14}}}}&0 \end{array}} \right]$5. ОБСУЖДЕНИЕ
5.1. Обсуждение символьных результатов. В результате применения разработанного символьного алгоритма получилось несколько различных символьных представлений решения однородной системы (6). Похожие результаты были получены авторами в работе [25] для символьных представлений собственных векторов нормальной матрицы, элементы которой заданы символьно. В работе [25] было получено по два различных представления каждого из четырех собственных векторов матрицы, используя встроенный метод Eigenvectors в рамках авторского метода исследования собственных векторов. В настоящей работе авторы по сути также отыскивали различные символьные представления собственного вектора, отвечающего нулевому собственному значению матрицы, однако с применением другого по сравнению с [25] метода, потому что встроенный метод Eigenvectors не дал результатов для исследуемой системы: символьные представления собственных значений и векторов превышают допустимый лимит длины отображения выражений в Maple.
Для численных расчетов достаточно было бы и одного представления собственного вектора, отвечающего нулевому собственному значению, однако различных представлений получено четыре (см. (13)–(16)) в связи с чем возникает вопрос об эквивалентности этих представлений, который обсуждается ниже на основе результатов численных экспериментов.
В рамках вычисления каждого символьного представления решения однородной системы (6) также вычисляется и величина, пропорциональная определителю матрицы $M\left( {\gamma \left( z \right)} \right)$ – см. полученные невязки системы (18). Другими словами, в рамках предложенного алгоритма вместе с решением системы также отыскивается и условие существования этого самого решения: ${{\vec {\delta }}_{j}} = \vec {0}$. Поэтому для рассматриваемых систем разработанный авторами алгоритм можно применять как для поиска $\vec {A}\left( z \right)$, так и для поиска $\gamma \left( z \right)$ – то есть без использования метода Determinant пакета LinearAlgebra.
Наличие символьного представления решения $\vec {A}(z)$ также имеет важное значение для оценки применимости метода поперечных сечений, в рамках которого нужно кроме вычисления $\vec {A}(z)$ также оценивать малость величины $\frac{{d\vec {A}\left( z \right)}}{{dz}}$. Такую оценку можно провести и численно, однако располагая символьными выражениями (13)–(16) оценка сведется к анализу малости величин $\gamma \left( z \right)$ и $\frac{{d\gamma (z)}}{{dz}}$, которые вычисляются численно более устойчиво, чем $\vec {A}(z)$.
Важно также заметить, что полученные символьные представления решения $\vec {A}\left( z \right)$ выявляют связь собственной функции $X\left( {x,z} \right)$ задачи (3) с коэффициентом фазового замедления $\gamma \left( z \right)$. Описанная взаимосвязь позволяет сосредоточиться только на вычислении $\gamma \left( z \right)$, то есть отыскав все допустимые $\gamma \left( z \right)$ по явным формулам сразу же определяются и $X\left( {x,z} \right)$.
5.2. Обсуждение численных результатов
В рамках численных экспериментов мы дали ответ на вопрос о численной эквивалентности всех символьных представлений решения системы (6). Как видно из (23), (24) все четыре символьных представления решения (13)–(16) дают одинаковые с точностью до константы решения, отличия составляют не более $3.2 \times {{10}^{{ - 13}}}$. Поэтому, не имеет значение какое из полученных символьных решений (13)–(16) системы (6) выбирать для анализа и использования в численных расчетах – здесь исследователь может выбрать наиболее удобное с точки зрения дальнейших манипуляций: представляется логичным выбрать самое компактное представление как для символьных манипуляций, так и для численных расчетов.
Важно также заметить, что символьные представления решения (13)–(16) системы (6) дают примерно одинаковую с численным решением точность порядка $2.3 \times {{10}^{{ - 13}}}$ (см. (21), (22)). Однако, численный метод решения однородной системы (6) содержит специальные численные алгоритмы, обеспечивающие гладкость решения, так как задача отыскания решения системы (6) является некорректной.
Расчет решения по символьным формулам не требует использования специальных дополнительных шагов для обеспечения гладкости решения, ибо символьные выражения непрерывны и дифференцируемы столько раз, сколько дифференцируемы $\gamma (z)$ и h(z). Другими словами, полученные символьные решения (13)–(16), благодаря непрерывной зависимости от непрерывных величин $\gamma (z)$ и h(z), автоматически обладают свойством непрерывности, в отличие от решений, получаемых численно.
В работе рассмотрен простейший случай, соответствующий трехслойному волноводу с одной плоской границей x = 0 и одной криволинейной $x = h(z)$, где функция h(z) описывает переменную толщину волноводного слоя. Существуют также и более сложные конфигурации с большим количеством слоев, для которых получение символьного решения системы, аналогичной системе (6), имеет большую важность. Для таких конфигураций характерно наличие трех слоев для одного интервала значений $z$, а для другого интервала значений $z$ слоев будет уже четыре. Другими словами, для четырехслойных конфигураций характерно наличие одного слоя переменной толщины, причем для определенного интервала значений $z$ эта толщина равна нулю (то есть структура трехслойная), а для другого интервала значений $z$ толщина плавно изменяется от нуля до своего максимального значения. На границе между этими интервалами необходимо также обеспечивать непрерывность решения, для чего также необходимо использовать разработанный алгоритм. Здесь, в частности, выявится предпочтительность одних символьных представлений решения перед другими.
6. ЗАКЛЮЧЕНИЕ
В работе построен символьный метод отыскания различных символьных представлений решения системы функциональных уравнений, возникающей при решении задачи о собственных модах нерегулярного волновода.
С помощью представленного метода построены символьные решения системы функциональных уравнений для случая трехслойного волновода. На основе символьного метода построен символьно-численный метод численного отыскания решения рассматриваемой системы. В результате применения символьно-численного метода показано, что все построенные символьные решения численно эквивалентны между собой.
Полученные символьные решения рассматриваемых функциональных уравнений позволяют отказаться от использования дополнительной регуляризации численных методов решения рассматриваемых уравнений, так как символьные решения обеспечивает естественную регуляризацию. Кроме того, они дают возможность анализировать решения на символьном уровне, что необходимо для оценки применимости метода поперечных сечений.
Список литературы
Sevastyanov L.A., Sevastyanov A.L., Tyutyunnik A.A. Analytical Calculations in Maple to Implement the Method of Adiabatic Modes for Modelling Smoothly Irregular Integrated Optical Waveguide Structures // Lecture Notes in Computer Science. 2014. V. 8660. P. 419–431. doi.org/https://doi.org/10.1007/978-3-319-10515-4_30
Divakov D.V., Sevastianov A.L. The Implementation of the Symbolic-Numerical Method for Finding the Adiabatic Waveguide Modes of Integrated Optical Waveguides in CAS Maple // Lecture Notes in Computer Science. 2019. V. 11661. P. 107–121. https://doi.org/10.1007/978-3-030-26831-2_8
Yee K. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media // IEEE Transactions on Antennas and Propagation. 1966. V. 14. № 3. P. 302–307. https://doi.org/10.1109/TAP.1966.1138693
Taflove A. Application of the Finite-Difference Time-Domain Method to Sinusoidal Steady-State Electromagnetic-Penetration Problems // IEEE Transactions on Electromagnetic Compatibility. 1980. V. EMC-22. № 3. P. 191–202. https://doi.org/10.1109/TEMC.1980.30387
Joseph R., Goorjian P., Taflove A. Direct time integration of Maxwell’s equations in two-dimensional dielectric waveguides for propagation and scattering of femtosecond electromagnetic solitons // Optics Letters. 1993. V. 7. P. 491–493. https://doi.org/10.1364/OL.18.000491
Sveshnikov A.G. The incomplete Galerkin method // Dokl. Akad. Nauk SSSR. 1977. V. 236. № 5. P. 1076–1079.
Petukhov A.A. Joint application of the incomplete Galerkin method and scattering matrix method for modeling multilayer diffraction gratings // Mathematical Models and Computer Simulations. 2014. V. 6. P. 92–100. https://doi.org/10.1134/S2070048214010128
Tiutiunnik A.A., Divakov D.V., Malykh M.D., Sevastianov L.A. Symbolic-Numeric Implementation of the Four Potential Method for Calculating Normal Modes: An Example of Square Electromagnetic Waveguide with Rectangular Insert // Lecture Notes in Computer Science. 2019. V. 11661. P. 412–429. https://doi.org/10.1007/978-3-030-26831-2_27
Зорин A.В., Севастьянов Л.А., Третьяков Н.П. Компьютерное моделирование водородоподобных атомов в квантовой механике с неотрицательной функцией распределения // Программирование. 2007. № 2. С. 50–62.
Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. М.: Физматгиз, 1962.
Виницкий C.И., Гердт В.П., Гусев А.А., Касчиев М.С., Ростовцев B.А., Самойлов В.Н., Тюпикова Т.В., Чулуунбаатар О. Символьно-численный алгоритм вычисления матричных элементов параметрической задачи на собственные значения // Программирование. 2007. № 2. С. 63–76.
Bathe K.J. Finite Element Procedures in Engineering Analysis. Prentice Hall, Englewood Cliffs, 1982.
Bogolyubov A.N., Mukhartova Yu.V., Gao J., Bogolyubov N.A. Mathematical modeling of plane chiral waveguide using mixed finite elements // Progress in Electromagnetics Research Symposium. 2012. P. 1216–1219.
Блинков Ю.А., Мозжилкин В.В. Генерация разностных схем для уравнения Вюргерса построением базисов Гребнера // Программирование. 2006. № 2. С. 71–74.
Блинков Ю.А., Гердт В.П., Маринов К.Б. Дискретизация квазилинейных эволюционных уравнений методами компьютерной алгебры // Программирование. 2017. № 2. С. 28–34.
Katsenelenbaum B.Z., Mercader del Rio L., Pereyaslavets M., Sorolla Ayza M., Thumm M. Theory of Nonuniform Waveguides: the cross-section method. London: Institution of Engineering and Technology, 1998.
Каценеленбаум Б.З. Теория нерегулярных волноводов с медленно меняющимися параметрами. М.: АН СССР, 1961.
Шевченко В.В. Плавные переходы в открытых волноводах: введение в теорию. М.: Наука, 1969.
Иванов А.А., Шевченко В.В. Плоскопоперечный стык двух планарных волноводов // Радиотехника и электроника. 2009. Т. 54. № 1. С. 68–77.
Divakov D.V., Lovetskiy K.P., Sevastianov L.A., Tiutiunnik A.A. A single-mode model of cross-sectional method in a smoothly irregular transition between planar thin-film dielectric waveguides / V.L. Derbov, Eds. Saratov Fall Meeting 2020, Proc. of SPIE. V. 11846. P. 118460T. Washington: Bellingham, 2021.
Mathematics-based software and services for education, engineering, and research https://www.maplesoft.com/
Adams M.J. An Introduction to Optical Waveguides. N.Y.: Wiley, 1981.
Gevorkyan M., Kulyabov D., Lovetskiy K., Sevastia-nov L., Sevastianov A. Field calculation for the horn waveguide transition in the single-mode approximation of the cross-sections method // Proceedings of SPIE. 2017. V. 10337. № 103370H. https://doi.org/10.1117/12.2267906
Hamming R.W. Numerical Methods for Scientists and Engineers. Dover Publications; 2nd Revised ed. Edition, 1987.
Диваков Д.В., Тютюнник А.А. Символьное исследование собственных векторов для построения общего решения системы ОДУ с символьной матрицей коэффициентов // Программирование. 2021. № 1. С. 11–24. https://doi.org/10.31857/S0132347421010040
Дополнительные материалы отсутствуют.
Инструменты
Программирование