Программирование, 2022, № 2, стр. 16-22

СИМВОЛЬНЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ПОЛОЖЕНИЙ РАВНОВЕСИЯ СИСТЕМЫ ДВУХ СВЯЗАННЫХ ТЕЛ НА КРУГОВОЙ ОРБИТЕ

С. А. Гутник^a, b, *, В. А. Сарычев^c, **

^a Московский государственный институт международных отношений
119454 Москва, Проспект Вернадского, д. 76, Россия

^b Московский физико-технический институт (Национальный исследовательский университет)
141701 Долгопрудный, Московской области, Институтский переулок, д. 9, Россия

^c Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., д. 4, Россия

^* E-mail: s.gutnik@inno.mgimo.ru
^** E-mail: vas31@rambler.ru

Поступила в редакцию 14.07.2021
После доработки 09.08.2021
Принята к публикации 16.08.2021

EDN: ZLINTG
DOI: 10.31857/S0132347422020066

Полный текст (PDF)

Аннотация

Методы компьютерной алгебры применяются для определения положений равновесия системы двух тел, соединенных сферическим шарниром, движущихся в центральном ньютоновом силовом поле по круговой орбите под действием гравитационного момента. Для определения равновесных ориентаций связки двух тел проводилось преобразование системы тригонометрических уравнений, определяющих равновесия, в алгебраическую систему уравнений, которая, в свою очередь, с применением понятия результанта и символьных методов линейной алгебры была сведена к одному алгебраическому уравнению 12 степени. Классификация областей с равным числом положений равновесия выполнялась с использованием алгебраических методов построения дискриминантной гиперповерхности. Бифуркационные кривые, которые определяют границы областей с равным числом положений равновесия в пространстве параметров, были получены с использованием символьных вычислений. Положения равновесия системы двух тел в зависимости от параметров задачи определялись путем исследования числа действительных корней полученных алгебраических уравнений.

1. ВВЕДЕНИЕ

В работе представлены результаты применения методов компьютерной алгебры для исследования положений равновесия системы двух тел (спутник-стабилизатор), соединенных сферическим шарниром, движущейся в центральном ньютоновом силовом поле по круговой орбите.

Тема исследования положений равновесия связки тел на круговой орбите представляет практический интерес при проектировании пассивных гравитационных систем ориентации спутников, которые могут функционировать на орбите продолжительное время без расходования энергии. Действие стабилизатора на спутник позволяет получить новые положения равновесия системы двух тел. Подробное рассмотрение динамики различных типов составных схем гравитационной системы ориентации спутник-стабилизатор представлено в обзоре [1]. В работах [2] и [3] были найдены равновесные ориентации связки тел в плоскости орбиты в случае, когда сферический шарнир расположен на пересечении главных центральных осей инерции спутника и стабилизатора и в случае, когда шарнир расположен на линии пересечения двух плоскостей, образуемых главными центральными осями инерции спутника и стабилизатора.

В работе [4] были найдены пространственные равновесные ориентации системы спутник-стабилизатор с использованием методов компьютерной и линейной алгебры. В статье [5] главное внимание было уделено исследованию существования равновесных ориентаций системы двух тел в случаях, когда одна из главных осей инерции как первого, так и второго тела совпадает с нормалью к плоскости орбиты, радиусом вектором или касательной к орбите. Для определения равновесных ориентаций связки двух тел проводилась декомпозиция системы 12 алгебраических уравнений на ряд подсистем. Для решения каждой из подсистем алгебраических уравнений применялись алгоритмы построения базисов Гребнера.

В работе [6] исходная система 12 алгебраических уравнений, определяющая равновесия системы двух тел, была решена с применением методов построения базисов Гребнера для такой комбинации значений инерциальных и геометрических параметров двух тел, при которой коэффициенты алгебраической системы, определяющей равновесные ориентации, зависят только от одного параметра. Алгебраические методы определения положений равновесия системы двух тел, изложенные в данной работе, ранее успешно применялись авторами при анализе динамики спутника-гиростата в работах [7, 8] и динамики спутника с гравитационной системой ориентации [9]. Примеры исследования полиномиальных систем в задачах механики с применением символьных вычислений представлены в работах [10–13].

В настоящей статье проведено исследование равновесных ориентаций системы двух связанных тел в случае, когда сферический шарнир расположен на линии пересечения двух плоскостей, образуемых главными центральными осями инерции спутника и стабилизатора. Для исследования равновесных ориентаций применялся метод редукции полиномов с использованием символьного вычисления результанта. Классификация областей с равным числом положений равновесия выполнялась с применением алгебраических методов построения дискриминантной гиперповерхности.

Системы компьютерной алгебры широко используются при решении задач небесной механики, в частности, при исследовании задачи трех тел [14]. Так, с применением символьных вычислений были получены новые результаты при рассмотрении классической задачи трех тел с переменными массами в работах [15–17].

2. УРАВНЕНИЯ ДВИЖЕНИЯ

Рассмотрим задачу о движении системы двух тел, соединенных сферическим шарниром, на круговой орбите [4].

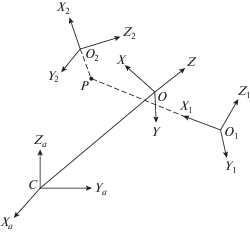
Для записи уравнений движения двух тел введем следующие правые декартовы системы координат (рис. 1): $OXYZ$ – орбитальная система координат. Ось $OZ$ направлена вдоль радиуса-вектора, соединяющего центр масс Земли $C$ и центр масс системы двух тел $O$; ось $OX$ направлена вдоль вектора линейной скорости центра масс $O$, ось $OY$ направлена по нормали к плоскости орбиты. ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$ – связанная с i-м телом система координат (i = 1, 2); ${{O}_{i}}{{x}_{i}}$, ${{O}_{i}}{{y}_{i}}$, ${{O}_{i}}{{z}_{i}}$ – главные центральные оси инерции i-го тела. Ориентацию системы координат ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$ относительно орбитальной системы координат определим с использованием самолетных углов тангажа ${{\alpha }_{i}}$, рыскания ${{\beta }_{i}}$ и крена ${{\gamma }_{i}}$ [1]

$a_{{11}}^{{(i)}} = \cos {{\alpha }_{i}}\cos {{\beta }_{i}},$

$a_{{12}}^{{(i)}} = \sin {{\alpha }_{i}}\sin {{\gamma }_{i}} - \cos {{\alpha }_{i}}\sin {{\beta }_{i}}\cos {{\gamma }_{i}},$

$a_{{13}}^{{(i)}} = \sin {{\alpha }_{i}}\cos {{\gamma }_{i}} + \cos {{\alpha }_{i}}\sin {{\beta }_{i}}\sin {{\gamma }_{i}},$

(1)

$a_{{21}}^{{(i)}} = \sin {{\beta }_{i}},\quad a_{{22}}^{{(i)}} = \cos {{\beta }_{i}}\cos {{\gamma }_{i}},$

$a_{{23}}^{{(i)}} = - \cos {{\beta }_{i}}\sin {{\gamma }_{i}},\quad a_{{31}}^{{(i)}} = - \sin {{\alpha }_{i}}\cos {{\beta }_{i}},$

$a_{{32}}^{{(i)}} = \cos {{\alpha }_{i}}\sin {{\gamma }_{i}} + \sin {{\alpha }_{i}}\sin {{\beta }_{i}}\cos {{\gamma }_{i}},$

$a_{{33}}^{{(i)}} = \cos {{\alpha }_{i}}\cos {{\gamma }_{i}} - \sin {{\alpha }_{i}}\sin {{\beta }_{i}}\sin {{\gamma }_{i}}.$

Рис. 1.

Основные системы координат.

Пусть $({{a}_{i}},{{b}_{i}},{{c}_{i}})$ – координаты сферического шарнира $P$ в связанной с телом системе координат ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$; ${{A}_{i}}$, ${{B}_{i}}$, ${{C}_{i}}$ – главные центральные моменты инерции; $M = {{M}_{1}}{{M}_{2}}{\text{/}}({{M}_{1}} + {{M}_{2}})$; ${{M}_{i}}$ – масса i-го тела; ${{\omega }_{0}}$ – угловая скорость движения центра масс системы тел по круговой орбите. Запишем выражение для кинетической энергии системы в случае, когда ${{c}_{1}} = {{c}_{2}} = 0$ и равновесные ориентации системы двух тел находятся в плоскости, перпендикулярной к плоскости орбиты (${{\alpha }_{1}} = {{\alpha }_{2}} = {{\gamma }_{1}} = {{\gamma }_{2}} = 0$, ${{\beta }_{1}} \ne 0$, ${{\beta }_{2}} \ne 0$). Тогда координаты сферического шарнира $P$ в связанной с каждым телом системе координат будут иметь значения $({{a}_{i}},{{b}_{i}},0)$ и выражение для кинетической энергии запишется в следующем виде:

$\begin{gathered} T = \frac{1}{2}({{C}_{1}} + M(a_{1}^{2} + b_{1}^{2}))\dot {\beta }_{1}^{2} + \\ + \;\frac{1}{2}({{C}_{2}} + M(a_{2}^{2} + b_{2}^{2}))\dot {\beta }_{2}^{2} - \\ \end{gathered} $

$\begin{gathered} - M(({{a}_{1}}{{a}_{2}} + {{b}_{1}}{{b}_{2}})\cos ({{\beta }_{1}} - {{\beta }_{2}}) + \hfill \\ + \;({{a}_{1}}{{b}_{2}} - {{a}_{2}}{{b}_{1}})\sin ({{\beta }_{1}} - {{\beta }_{2}})){{{\dot {\beta }}}_{1}}{{{\dot {\beta }}}_{2}} + \hfill \\ \end{gathered} $

$\begin{gathered} + \frac{1}{2}(({{B}_{1}} - {{A}_{1}}) - M(b_{1}^{2} - a_{1}^{2}))\omega _{0}^{2}{{\cos }^{2}}{{\beta }_{1}} - \\ - \;M{{a}_{1}}{{a}_{2}}\omega _{0}^{2}\cos {{\beta }_{1}}\cos {{\beta }_{2}} + \\ \end{gathered} $

$\begin{gathered} + \;\frac{1}{2}(({{B}_{2}} - {{A}_{2}}) - M(b_{2}^{2} - a_{2}^{2}))\omega _{0}^{2}{{\cos }^{2}}{{\beta }_{2}} - \\ - \;M{{b}_{1}}{{b}_{2}}\omega _{0}^{2}\sin {{\beta }_{1}}\sin {{\beta }_{2}} - \\ \end{gathered} $

(2)

$ - M\omega _{0}^{2}({{b}_{1}}\sin {{\beta }_{1}} - {{b}_{2}}\sin {{\beta }_{2}})({{a}_{1}}\cos {{\beta }_{1}} - {{a}_{2}}\cos {{\beta }_{2}}).$

Силовая функция, определяющая действие гравитационного поля Земли на систему двух тел, соединенных сферическим шарниром, запишется в виде [1]

(3)

$\begin{gathered} U = M\omega _{0}^{2}(({{a}_{1}}{{a}_{2}} + {{b}_{1}}{{b}_{2}})\cos ({{\beta }_{1}} - {{\beta }_{2}}) + \\ + \;({{a}_{1}}{{b}_{2}} - {{a}_{2}}{{b}_{1}})\sin ({{\beta }_{1}} - {{\beta }_{2}})). \\ \end{gathered} $

Используя выражения для кинетической энергии (2) и силовой функции (3), определяющей действие гравитационного поля Земли на систему двух тел, уравнения движения этой системы можно записать в форме уравнений Лагранжа второго рода

(4)

$\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{{\dot {\beta }}}_{i}}}} - \frac{{\partial T}}{{\partial {{\beta }_{i}}}} - \frac{{\partial U}}{{\partial {{\beta }_{i}}}} = 0,\quad i = \overline {1,\;2} .$

Используя возможности символьного дифференцирования в системе Wolfram Mathematica [18], запишем уравнения (4) в форме обыкновенных дифференциальных уравнений второго порядка по переменным ${{\beta }_{1}}$ и ${{\beta }_{2}}$

$({{C}_{1}} + M(a_{1}^{2} + b_{1}^{2})){{\ddot {\beta }}_{1}} - M(({{a}_{1}}{{a}_{2}} + {{b}_{1}}{{b}_{2}})\cos ({{\beta }_{1}} - {{\beta }_{2}}) + $

$\begin{gathered} + \;({{a}_{1}}{{b}_{2}} - {{a}_{2}}{{b}_{1}})\sin ({{\beta }_{1}} - {{\beta }_{2}})){{{\ddot {\beta }}}_{2}} - \\ - \;M(({{a}_{1}}{{a}_{2}} + {{b}_{1}}{{b}_{2}})\sin ({{\beta }_{1}} - {{\beta }_{2}}) - \\ \end{gathered} $

$\begin{gathered} - ({{a}_{1}}{{b}_{2}} - {{a}_{2}}{{b}_{1}})\cos ({{\beta }_{1}} - {{\beta }_{2}})){{{\dot {\beta }}}_{2}}^{2} + \\ + \;({{B}_{1}} - {{A}_{1}})\omega _{0}^{2}\sin {{\beta }_{1}}\cos {{\beta }_{1}} + \\ \end{gathered} $

$ + M\omega _{0}^{2}({{a}_{1}}\sin {{\beta }_{1}} + {{b}_{1}}\sin {{\beta }_{1}})({{a}_{1}}\cos {{\beta }_{1}} - {{b}_{1}}\sin {{\beta }_{1}}) - $

(5)

$ - M\omega _{0}^{2}({{a}_{1}}{\text{cos}}{{\beta }_{1}} - {{b}_{1}}{\text{sin}}{{\beta }_{1}})({{a}_{2}}{\text{sin}}{{\beta }_{2}} + {{b}_{2}}{\text{cos}}{{\beta }_{2}}) = 0,$

$({{C}_{2}} + M(a_{2}^{2} + b_{2}^{2})){{\ddot {\beta }}_{2}} - M(({{a}_{1}}{{a}_{2}} + {{b}_{1}}{{b}_{2}})\cos ({{\beta }_{1}} - {{\beta }_{2}}) + $

$\begin{gathered} + \;({{a}_{1}}{{b}_{2}} - {{a}_{2}}{{b}_{1}})\sin ({{\beta }_{1}} - {{\beta }_{2}})){{{\ddot {\beta }}}_{1}} + \\ + \;M(({{a}_{1}}{{a}_{2}} + {{b}_{1}}{{b}_{2}})\sin ({{\beta }_{1}} - {{\beta }_{2}}) - \\ \end{gathered} $

$\begin{gathered} - ({{a}_{1}}{{b}_{2}} - {{a}_{2}}{{b}_{1}})\cos ({{\beta }_{1}} - {{\beta }_{2}})){{{\dot {\beta }}}_{1}}^{2} + \\ + \;({{B}_{2}} - {{A}_{2}})\omega _{0}^{2}\sin {{\beta }_{2}}\cos {{\beta }_{2}} + \\ \end{gathered} $

$ + \;M\omega _{0}^{2}({{a}_{2}}\sin {{\beta }_{2}} + {{b}_{2}}\cos {{\beta }_{2}})({{a}_{2}}\cos {{\beta }_{2}} - {{b}_{2}}\sin {{\beta }_{2}}) - $

$ - M\omega _{0}^{2}({{a}_{2}}\cos {{\beta }_{2}} - {{b}_{2}}\sin {{\beta }_{2}})({{a}_{1}}\sin {{\beta }_{1}} + {{b}_{1}}\cos {{\beta }_{1}}) = 0.$

В уравнениях (5) точкой обозначено дифференцирование по времени $t$.

3. ПОЛОЖЕНИЯ РАВНОВЕСИЯ

Положив в уравнениях (5) ${{\beta }_{1}} = {\text{const}}$, ${{\beta }_{2}}$ = = const, получим при условиях ${{A}_{i}} \ne {{B}_{i}} \ne {{C}_{i}}$ уравнения

$\begin{gathered} (({{B}_{1}} - {{A}_{1}}){\text{/}}M)\sin {{\beta }_{1}}\cos {{\beta }_{1}} + \\ + \;({{a}_{1}}\sin {{\beta }_{1}} + {{b}_{1}}\cos {{\beta }_{1}})({{a}_{1}}\cos {{\beta }_{1}} - {{b}_{1}}\sin {{\beta }_{1}}) - \\ \end{gathered} $

(6)

$ - ({{a}_{1}}\cos {{\beta }_{1}} - {{b}_{1}}\sin {{\beta }_{1}})({{a}_{2}}\sin {{\beta }_{2}} + {{b}_{2}}\cos {{\beta }_{2}}) = 0,$

$\begin{gathered} (({{B}_{2}} - {{A}_{2}}){\text{/}}M)\sin {{\beta }_{2}}\cos {{\beta }_{2}} + \\ + \;({{a}_{2}}\sin {{\beta }_{2}} + {{b}_{2}}\cos {{\beta }_{2}})({{a}_{2}}\cos {{\beta }_{2}} - {{b}_{2}}\sin {{\beta }_{2}}) - \\ \end{gathered} $

$ - ({{a}_{2}}\cos {{\beta }_{2}} - {{b}_{2}}\sin {{\beta }_{2}})({{a}_{1}}\sin {{\beta }_{1}} + {{b}_{1}}\cos {{\beta }_{1}}) = 0,$

позволяющие определить положения равновесия системы двух тел, соединенных сферическим шарниром, в орбитальной системе координат. Тригонометрическую систему уравнений (6) относительно двух неизвестных самолетных углов β₁ и β₂, аналитически решить не удается.

Для решения системы (6) воспользуемся следующей универсальной заменой синусов и косинусов углов β₁ и β₂ через их тангенсы:

(7)

$\sin {{\beta }_{i}} = \frac{{{\text{tg}}{{\beta }_{i}}}}{{\sqrt {1 + {\text{t}}{{{\text{g}}}^{2}}{{\beta }_{i}}} }},\quad \cos {{\beta }_{i}} = \frac{1}{{\sqrt {1 + {\text{t}}{{{\text{g}}}^{2}}{{\beta }_{i}}} }}.$

Подставляя выражения (7) в уравнения системы (6) получим два уравнения от двух неизвестных tg${{\beta }_{1}}$ и tg${{\beta }_{2}}$

$(({{B}_{1}} - {{A}_{1}}){\text{/}}M){\text{tg}}{{\beta }_{1}} + ({{a}_{1}}{\text{tg}}{{\beta }_{1}} + {{b}_{1}})({{a}_{1}} - {{b}_{1}}{\text{tg}}{{\beta }_{1}}) - $

(8)

$ - \;({{a}_{1}} - {{b}_{1}}{\text{tg}}{{\beta }_{1}})({{a}_{2}}{\text{tg}}{{\beta }_{2}} + {{b}_{2}})\frac{{\sqrt {1 + {\text{t}}{{{\text{g}}}^{2}}{{\beta }_{1}}} }}{{\sqrt {1 + {\text{t}}{{{\text{g}}}^{2}}{{\beta }_{2}}} }} = 0,$

$(({{B}_{2}} - {{A}_{2}}){\text{/}}M){\text{tg}}{{\beta }_{2}} + ({{a}_{2}}{\text{tg}}{{\beta }_{2}} + {{b}_{2}})({{a}_{2}} - {{b}_{2}}{\text{tg}}{{\beta }_{2}}) - $

$ - \;({{a}_{2}} - {{b}_{2}}{\text{tg}}{{\beta }_{2}})({{a}_{1}}{\text{tg}}{{\beta }_{1}} + {{b}_{1}})\frac{{\sqrt {1 + {\text{t}}{{{\text{g}}}^{2}}{{\beta }_{2}}} }}{{\sqrt {1 + {\text{t}}{{{\text{g}}}^{2}}{{\beta }_{1}}} }} = 0.$

Систему уравнений (8) можно упростить. Для этого сначала умножим левую (правую) часть первого уравнения (8) на левую (правую) часть второго уравнения, а затем разделим левую (правую) часть первого уравнения (8) на левую (правую) часть второго уравнения соответственно. В результате, вводя обозначения ${{t}_{1}} = {\text{tg}}{{\beta }_{1}}$ и ${{t}_{2}} = {\text{tg}}{{\beta }_{2}}$, получим алгебраическую систему двух уравнений относительно двух неизвестных ${{t}_{1}}$ и ${{t}_{2}}$

${{\bar {a}}_{0}}t_{1}^{3} + {{\bar {a}}_{1}}t_{1}^{2} + {{\bar {a}}_{2}}{{t}_{1}} + {{\bar {a}}_{3}} = 0,$

(9)

${{\bar {b}}_{0}}t_{1}^{2} + {{\bar {b}}_{1}}{{t}_{1}} + {{\bar {b}}_{2}} = 0,$

где

$\begin{gathered} {{{\bar {a}}}_{0}} = {{b}_{1}}(({{a}_{2}}{{t}_{2}} + {{b}_{2}})({{a}_{2}}{{b}_{2}} + ({{d}_{2}} + a_{2}^{2} - b_{2}^{2}){{t}_{2}} - {{a}_{2}}{{b}_{2}}t_{2}^{2}) - \\ - \;a_{1}^{2}({{a}_{2}} - {{b}_{2}}{{t}_{2}})(1 + t_{2}^{2})), \\ \end{gathered} $

$\begin{gathered} {{{\bar {a}}}_{1}} = - {{a}_{1}}(({{a}_{2}}{{t}_{2}} + {{b}_{2}}) \times \\ \times \;({{a}_{2}}{{b}_{2}} + ({{d}_{2}} + a_{2}^{2} - b_{2}^{2})({{t}_{2}} - {{a}_{2}}{{b}_{2}}t_{2}^{2})) - \\ - ({{d}_{1}} + a_{1}^{2} - 2b_{1}^{2})({{a}_{2}} - {{b}_{2}}{{t}_{2}})(1 + t_{2}^{2})), \\ \end{gathered} $

$\begin{gathered} {{{\bar {a}}}_{2}} = {{b}_{1}}(({{a}_{2}}{{t}_{2}} + {{b}_{2}})({{a}_{2}}{{b}_{2}} + ({{d}_{2}} + a_{2}^{2} - b_{2}^{2}) \times \\ \times \;{{t}_{2}} - {{a}_{2}}{{b}_{2}}t_{2}^{2}) + ({{d}_{1}} + 2a_{1}^{2} - b_{1}^{2})({{a}_{2}} - {{b}_{2}}{{t}_{2}})(1 + t_{2}^{2})), \\ \end{gathered} $

$\begin{gathered} {{{\bar {a}}}_{3}} = - {{a}_{1}}(({{a}_{2}}{{t}_{2}} + {{b}_{2}}) \times \\ \times \;({{a}_{2}}{{b}_{2}} + ({{d}_{2}} + a_{2}^{2} - b_{2}^{2}){{t}_{2}} - {{a}_{2}}{{b}_{2}}t_{2}^{2}) - \\ - \;b_{1}^{2}({{a}_{2}} - {{b}_{2}}{{t}_{2}})(1 + t_{2}^{2})), \\ \end{gathered} $

${{\bar {b}}_{0}} = {{a}_{1}}{{b}_{1}}{{d}_{2}}{{t}_{2}},$

$\begin{gathered} {{{\bar {b}}}_{1}} = {{a}_{2}}{{b}_{2}}{{d}_{1}}t_{2}^{2} - {{d}_{1}}{{d}_{2}}{{t}_{2}} + \\ + \;(b_{1}^{2} - a_{1}^{2}){{d}_{2}}{{t}_{2}} + (b_{2}^{2} - a_{2}^{2}){{d}_{1}}{{t}_{2}} - {{a}_{2}}{{b}_{2}}{{d}_{1}}, \\ \end{gathered} $

${{\bar {b}}_{2}} = - {{a}_{1}}{{b}_{1}}{{d}_{2}}{{t}_{2}}.$

Здесь введены обозначения ${{d}_{1}} = ({{B}_{1}} - {{A}_{1}}){\text{/}}M$, d₂ = = $({{B}_{2}} - {{A}_{2}}){\text{/}}M$.

Исключая из системы (9) ${{t}_{1}}$ с использованием понятия результанта, получим путем символьных вычислений определителя матрицы результанта в системе Mathematica алгебраическое уравнение 12 порядка относительно переменной ${{t}_{2}}$, которое после факторизации представляет собой произведение трех полиномов

(10)

$P({{t}_{2}}) = {{P}_{1}}({{t}_{2}}){{P}_{2}}({{t}_{2}}){{P}_{3}}({{t}_{2}}) = 0,$

где ${{P}_{1}}({{t}_{2}})$ и ${{P}_{2}}({{t}_{2}})$ – полиномы второго порядка и имеют следующий вид: ${{P}_{1}}({{t}_{2}}) = {{a}_{1}}{{b}_{1}}{{d}_{1}}{{({{b}_{2}} + {{a}_{2}}{{t}_{2}})}^{2}}$; ${{P}_{2}}({{t}_{2}}) = {{a}_{2}}{{b}_{2}} + (a_{2}^{2} - b_{2}^{2} + {{d}_{2}}){{t}_{2}} - {{a}_{2}}{{b}_{2}}t_{2}^{2}$.

${{P}_{3}}({{t}_{2}})$ является полиномом 8 порядка

(11)

$\begin{gathered} {{p}_{0}}t_{2}^{8} + {{p}_{1}}t_{2}^{7} + {{p}_{2}}t_{2}^{6} + {{p}_{3}}t_{2}^{5} + \\ + \;{{p}_{4}}t_{2}^{4} + {{p}_{5}}t_{2}^{3} + {{p}_{6}}t_{2}^{2} + {{p}_{7}}{{t}_{2}} + {{p}_{8}} = 0, \\ \end{gathered} $

коэффициенты которого представляют собой полиномы от шести параметров системы ${{a}_{1}}$, ${{a}_{2}}$, ${{b}_{1}}$, ${{b}_{2}}$, ${{d}_{1}}$ и ${{d}_{2}}$:

${{p}_{0}} = d_{1}^{2}b_{2}^{4}(a_{1}^{2} - a_{2}^{2})(a_{2}^{2} - b_{1}^{2}),$

$\begin{gathered} {{p}_{1}} = - 2{{a}_{2}}b_{2}^{3}{{d}_{1}}({{d}_{1}}(2a_{1}^{2}a_{2}^{2} - 2a_{2}^{4} - 2a_{1}^{2}b_{1}^{2} + \\ + \;2a_{2}^{2}b_{1}^{2} - a_{1}^{2}b_{2}^{2} + 2a_{2}^{2}b_{2}^{2} - b_{1}^{2}b_{2}^{2}) + \\ \end{gathered} $

$ + \;{{d}_{2}}(a_{1}^{4} - a_{1}^{2}a_{2}^{2} + a_{2}^{2}b_{1}^{2} - b_{1}^{4}) + {{d}_{1}}{{d}_{2}}((a_{1}^{2} - 2a_{2}^{2} + b_{1}^{2})),$

$\begin{gathered} {{p}_{2}} = b_{2}^{2}(d_{1}^{2}(6a_{1}^{2}(a_{2}^{4} - 6a_{2}^{6} - 6a_{1}^{2}a_{2}^{2}b_{1}^{2} + 6a_{2}^{4}b_{1}^{2} - \\ - \;7a_{1}^{2}a_{2}^{2}b_{2}^{2} + 16a_{2}^{4}b_{2}^{2} - 2a_{1}^{2}b_{1}^{2}b_{2}^{2} - \\ \end{gathered} $

$ - \;7a_{2}^{2}b_{1}^{2}b_{2}^{2} + a_{1}^{2}b_{2}^{4} - 6a_{2}^{2}b_{2}^{4} + b_{1}^{2}b_{2}^{4}) + $

$\begin{gathered} + \;2{{d}_{1}}{{d}_{2}}(a_{1}^{2} - b_{1}^{2})(3a_{1}^{2}a_{2}^{2} - 3a_{2}^{4} + \\ + \;3a_{2}^{2}b_{1}^{2} - a_{1}^{2}b_{2}^{2} + 3a_{2}^{2}b_{2}^{2} - b_{1}^{2}b_{2}^{2}) + \\ \end{gathered} $

$ + 2d_{1}^{2}{{d}_{2}}(3a_{1}^{2}a_{2}^{2} - 6a_{2}^{4} + 3a_{2}^{2}b_{1}^{2} - a_{1}^{2}b_{2}^{2} + 6a_{2}^{2}b_{2}^{2} - b_{1}^{2}b_{2}^{2}) + $

$\begin{gathered} + \;d_{2}^{2}{{(a_{1}^{2} + b_{1}^{2})}^{2}}(a_{1}^{2} - a_{2}^{2} + b_{1}^{2}) + \\ + \;2{{d}_{1}}d_{2}^{2}(a_{1}^{2} - b_{1}^{2})(a_{1}^{2} - 3a_{2}^{2} + b_{1}^{2}) + \\ \end{gathered} $

$ + \;d_{1}^{2}d_{2}^{2}(a_{1}^{2} - 6a_{2}^{2} + b_{1}^{2})),$

$\begin{gathered} {{p}_{3}} = - 2{{a}_{2}}{{b}_{2}}(d_{1}^{2}(2a_{1}^{2}a_{2}^{4} - 2a_{2}^{6} - \\ - \;2a_{1}^{2}a_{2}^{2}b_{1}^{2} + 2a_{2}^{4}b_{1}^{2} - 4a_{1}^{2}a_{2}^{2}b_{2}^{2} + \\ \end{gathered} $

$\begin{gathered} + \;12a_{2}^{4}b_{2}^{2} - 4a_{1}^{2}b_{1}^{2}b_{2}^{2} - 4a_{2}^{2}b_{1}^{2}b_{2}^{2} + \\ + \;a_{1}^{2}b_{2}^{4} - 12a_{2}^{2}b_{2}^{4} + b_{1}^{2}b_{2}^{4} + 2b_{2}^{6}) + \\ \end{gathered} $

$\begin{gathered} + \;{{d}_{1}}{{d}_{2}}(a_{1}^{2} - b_{1}^{2})(3a_{1}^{2}a_{2}^{2} - 3a_{2}^{4} + 3a_{2}^{2}b_{1}^{2} - \\ - \;2a_{1}^{2}b_{2}^{2} + 9a_{2}^{2}b_{2}^{2} - 2b_{1}^{2}b_{2}^{2} - 3b_{2}^{4}) + \\ \end{gathered} $

$\begin{gathered} + \;d_{1}^{2}{{d}_{2}}(3a_{1}^{2}a_{2}^{2} - 6a_{2}^{4} + 3a_{2}^{2}b_{1}^{2} - \\ - \;2a_{1}^{2}b_{2}^{2} + 18a_{2}^{2}b_{2}^{2} - 2b_{1}^{2}b_{2}^{2} - 6b_{2}^{4}) + \\ \end{gathered} $

$ + \;d_{2}^{2}{{(a_{1}^{2} + b_{1}^{2})}^{2}}(a_{1}^{2} - a_{2}^{2} + b_{1}^{2} + b_{2}^{2}) + $

$\begin{gathered} + \;2{{d}_{1}}d_{2}^{2}(a_{1}^{2} - b_{2}^{2})(a_{1}^{2} - 3a_{2}^{2} + b_{1}^{2} + 3b_{2}^{2}) + \\ + \;d_{1}^{2}d_{2}^{2}(a_{1}^{2} - 6a_{2}^{2} + b_{1}^{2} + 6b_{2}^{2}) - \\ \end{gathered} $

$ - d_{2}^{3}((a_{1}^{2} + {{b}_{1}}{{)}^{2}} + 3a_{1}^{2}{{d}_{1}} - 3b_{1}^{2}{{d}_{1}} + 2d_{1}^{2})),$

$\begin{gathered} {{p}_{4}} = d_{1}^{2}(a_{1}^{2}a_{2}^{6} - a_{2}^{8} - a_{1}^{2}a_{2}^{4}b_{1}^{2} + a_{2}^{6}b_{1}^{2} - \\ - \;2a_{1}^{2}a_{2}^{4}b_{2}^{2} + 16a_{2}^{6}b_{2}^{2} - 12a_{1}^{2}a_{2}^{2}b_{1}^{2}b_{2}^{2} - \\ \end{gathered} $

$\begin{gathered} - \;2a_{2}^{4}b_{1}^{2}b_{2}^{2} - 2a_{1}^{2}a_{2}^{2}b_{2}^{4} - 36a_{2}^{4}b_{2}^{4} - \\ - \;a_{1}^{2}b_{1}^{2}b_{2}^{4} - 2a_{2}^{2}b_{1}^{2}b_{2}^{4} + a_{1}^{2}b_{2}^{6} + \\ \end{gathered} $

$\begin{gathered} + \;16a_{2}^{2}b_{2}^{6} + b_{1}^{2}b_{2}^{6} - b_{2}^{8}) + \\ + \;2{{d}_{1}}{{d}_{2}}(a_{1}^{2} - b_{1}^{2})(a_{2}^{2} - b_{2}^{2})(a_{1}^{2}a_{2}^{2} - a_{2}^{4} + \\ \end{gathered} $

$ + \;a_{2}^{2}b_{1}^{2} + a_{1}^{2}b_{2}^{2} + 8a_{2}^{2}b_{2}^{2} + b_{1}^{2}b_{2}^{2} - b_{2}^{4}) + $

$\begin{gathered} + \;2d_{1}^{2}{{d}_{2}}(a_{2}^{2} - b_{2}^{2})(a_{1}^{2}a_{2}^{2} - 2a_{2}^{4} + a_{2}^{2}b_{1}^{2} + \\ + \;a_{1}^{2}b_{2}^{2} + 16a_{2}^{2}b_{2}^{2} + b_{1}^{2}b_{2}^{2} - 2b_{2}^{4}) + \\ \end{gathered} $

$\begin{gathered} + \;d_{2}^{2}{{(a_{1}^{2} + b_{1}^{2})}^{2}}(a_{1}^{2}a_{2}^{2} - a_{2}^{4} + a_{2}^{2}b_{1}^{2} + \\ + \;a_{1}^{2}b_{2}^{2} + 4a_{2}^{2}b_{2}^{2} + b_{1}^{2}b_{2}^{2} - b_{2}^{4}) + \\ \end{gathered} $

$\begin{gathered} + \;2{{d}_{1}}d_{2}^{2}(a_{1}^{2} - b_{1}^{2})(a_{1}^{2}a_{2}^{2} - 3a_{2}^{4} + a_{2}^{2}b_{1}^{2} + \\ + \;a_{1}^{2}b_{2}^{2} + 12a_{2}^{2}b_{2}^{2} + b_{1}^{2}b_{2}^{2} - 3b_{2}^{4}) + \\ \end{gathered} $

$\begin{gathered} + \;d_{1}^{2}d_{2}^{2}((a_{1}^{2}a_{2}^{2} - 6a_{2}^{4} + a_{2}^{2}b_{1}^{2} + \\ + \;a_{1}^{2}b_{2}^{2} + 24a_{2}^{2}b_{2}^{2} + b_{1}^{2}b_{2}^{2} - 6b_{2}^{4}) - \\ \end{gathered} $

$\begin{gathered} - \;2d_{2}^{3}{{(a_{1}^{2} + b_{1}^{2})}^{2}}(a_{2}^{2} - b_{2}^{2}) - \\ - \;6{{d}_{1}}d_{2}^{3}(a_{1}^{2} - b_{1}^{2})(a_{2}^{2} - b_{2}^{2}) - \\ \end{gathered} $

$\begin{gathered} - \;4d_{1}^{2}d_{2}^{3}(a_{2}^{2} - b_{2}^{2}) - d_{2}^{4}{{(a_{1}^{2} + b_{1}^{2})}^{2}} - \\ - \;2{{d}_{1}}d_{2}^{4}(a_{1}^{2} - b_{1}^{2}) - d_{1}^{2}d_{2}^{4}, \\ \end{gathered} $

$\begin{gathered} {{p}_{5}} = - 2{{a}_{2}}{{b}_{2}}(d_{1}^{2}(a_{1}^{2}a_{2}^{4} + 2a_{2}^{6} - 4a_{1}^{2}a_{2}^{2}b_{1}^{2} + \\ + \;a_{2}^{4}b_{1}^{2} - 4a_{1}^{2}a_{2}^{2}b_{2}^{2} - 12a_{2}^{4}b_{2}^{2} - \\ \end{gathered} $

$\begin{gathered} - \;2a_{1}^{2}b_{1}^{2}b_{2}^{2} - 4a_{2}^{2}b_{1}^{2}b_{2}^{2} + 2a_{1}^{2}b_{2}^{4} + \\ + \;12a_{2}^{2}b_{2}^{4} + 2b_{1}^{2}b_{2}^{4} - 2b_{2}^{6}) + \\ \end{gathered} $

$\begin{gathered} + \;{{d}_{1}}{{d}_{2}}(a_{1}^{2} - b_{1}^{2})(2a_{1}^{2}a_{2}^{2} + 3a_{2}^{4} + \\ + \;2a_{2}^{2}b_{1}^{2} - 3a_{1}^{2}b_{2}^{2} - 9a_{2}^{2}b_{2}^{2} - 3b_{1}^{2}b_{2}^{2} + 3b_{2}^{4}) + \\ \end{gathered} $

$\begin{gathered} + \;d_{1}^{2}{{d}_{2}}(2a_{1}^{2}a_{2}^{2} + 6a_{2}^{4} + 2a_{2}^{2}b_{1}^{2} - \\ - \;3a_{1}^{2}b_{2}^{2} - 18a_{2}^{2}b_{2}^{2} - 3b_{1}^{2}b_{2}^{2} + 6b_{2}^{4}) + \\ \end{gathered} $

$ + \;d_{2}^{2}{{(a_{1}^{2} + b_{1}^{2})}^{2}}(a_{1}^{2} + a_{2}^{2} + b_{1}^{2} - b_{2}^{2}) + $

$\begin{gathered} + \;2{{d}_{1}}d_{2}^{2}(a_{1}^{2} - b_{1}^{2})(a_{1}^{2} + 3a_{2}^{2} + b_{1}^{2} - 3b_{2}^{2}) + \\ + \;d_{1}^{2}d_{2}^{2}(a_{1}^{2} + 6a_{2}^{2} + b_{1}^{2} - 6b_{2}^{2}) + \\ \end{gathered} $

$ + \;d_{2}^{3}({{(a_{1}^{2} + b_{1}^{2})}^{2}} + 3a_{1}^{2}{{d}_{1}} - 3b_{1}^{2}{{d}_{1}} + 2d_{1}^{2})),$

$\begin{gathered} {{p}_{6}} = a_{2}^{2}(d_{1}^{2}(a_{1}^{2}a_{2}^{4} - 2a_{1}^{2}a_{2}^{2}b_{1}^{2} + \\ + \;a_{2}^{4}b_{1}^{2} - 7a_{1}^{2}a_{2}^{2}b_{2}^{2} - 6a_{2}^{4}b_{2}^{2} - \\ \end{gathered} $

$\begin{gathered} - \;6a_{1}^{2}b_{1}^{2}b_{2}^{2} - 7a_{2}^{2}b_{1}^{2}b_{2}^{2} + 6a_{1}^{2}b_{2}^{4} + \\ + \;16a_{2}^{2}b_{2}^{4} + 6b_{1}^{2}b_{2}^{4} - 6b_{2}^{6}) + \\ \end{gathered} $

$\begin{gathered} + \;2{{d}_{1}}{{d}_{2}}(a_{1}^{2} - b_{1}^{2})(a_{1}^{2}a_{2}^{2} + a_{2}^{2}b_{1}^{2} - \\ - \;3a_{1}^{2}b_{2}^{2} - 3a_{2}^{2}b_{2}^{2} - 3b_{1}^{2}b_{2}^{2} + 3b_{2}^{4}) + \\ \end{gathered} $

$\begin{gathered} + \;2d_{1}^{2}{{d}_{2}}(a_{1}^{2}a_{2}^{2} + a_{2}^{2}b_{1}^{2} - 3a_{1}^{2}b_{2}^{2} - \\ - \;6a_{2}^{2}b_{2}^{2} - 3b_{1}^{2}b_{2}^{2} + 6b_{2}^{4}) + \\ \end{gathered} $

$\begin{gathered} + \;d_{2}^{2}{{(a_{1}^{2} + b_{1}^{2})}^{2}}(a_{1}^{2} + b_{1}^{2} - b_{2}^{2}) + \\ + \;2{{d}_{1}}d_{2}^{2}(a_{1}^{2} - b_{1}^{2})(a_{1}^{2} + b_{1}^{2} - 3b_{2}^{2}) \\ \end{gathered} $

$ + \;d_{1}^{2}d_{2}^{2}(a_{1}^{2} + b_{1}^{2} - 6b_{2}^{2})),$

$\begin{gathered} {{p}_{7}} = 2a_{2}^{3}{{b}_{2}}{{d}_{1}}({{d}_{1}}(a_{1}^{2}a_{2}^{2} + 2a_{1}^{2}b_{1}^{2} + a_{2}^{2}b_{1}^{2} - \\ - \;2a_{1}^{2}b_{2}^{2} - 2a_{2}^{2}b_{2}^{2} - 2b_{1}^{2}b_{2}^{2} + 2b_{2}^{4}) + \\ \end{gathered} $

$ + \;{{d}_{2}}(a_{1}^{2} - b_{1}^{2})(a_{1}^{2} + b_{1}^{2} - b_{2}^{2}) + {{d}_{1}}{{d}_{2}}(a_{1}^{2} + b_{1}^{2} - 2b_{2}^{2})),$

${{p}_{8}} = - d_{1}^{2}a_{2}^{4}(a_{1}^{2} - b_{2}^{2})(b_{1}^{2} - b_{2}^{2}).$

По определению результанта каждому корню ${{t}_{2}}$ уравнения (11) соответствует один общий корень ${{t}_{1}}$ системы (9). Число действительных корней полученного алгебраического уравнения четно и не превышает 8. Подставляя значение действительного корня ${{t}_{2}}$ алгебраического уравнения (11) в уравнения системы (9), найдем совпадающий корень ${{t}_{1}}$ этих уравнений.

Можно показать, что каждому действительному корню ${{t}_{2}}$ уравнений (10) и (11) соответствуют 4 равновесных решения исходной системы (6). Так как общее число действительных корней уравнения (10) не превышает 11, то система двух связанных тел спутник–стабилизатор в плоскости перпендикулярной плоскости орбиты может иметь не более 44 равновесных ориентаций в орбитальной системе координат.

Используя уравнения (9)–(11) для каждого набора системных параметров, мы можем определить все равновесные ориентации системы спутник–стабилизатор в орбитальной системе координат.

4. ИССЛЕДОВАНИЕ ЧИСЛА ПОЛОЖЕНИЙ РАВНОВЕСИЯ

Уравнения (9)–(11) позволяют определить все равновесные ориентации системы спутник–стабилизатор, движущейся по круговой орбите при заданных значениях параметров задачи ${{a}_{1}}$, ${{a}_{2}}$, ${{b}_{1}}$, ${{b}_{2}}$, ${{d}_{1}}$ и ${{d}_{2}}$.

Для исследования числа положений равновесия системы спутник–стабилизатор определим в пространстве 6 параметров области с одинаковым числом вещественных корней уравнения (11). Для выделения в пространстве параметров областей с одинаковым числом вещественных корней построим дискриминантную гиперповерхность полинома (11). Эта гиперповерхность содержит компоненту коразмерности 1, которая является границей областей с одинаковым числом вещественных корней. Множество особых точек дискриминантной гиперповерхности в пространстве параметров задается следующей системой алгебраических уравнений:

(12)

${{P}_{3}}({{t}_{2}}) = 0,\quad P_{3}^{'}({{t}_{2}}) = 0.$

Символ “штрих” обозначает дифференцирование по переменной ${{t}_{2}}$.

Исключая переменную ${{t}_{2}}$ из системы (12) путем символьного вычисления определителя матрицы результанта уравнений (12) с использованием матричных функций системы Mathematica, получим выражение для гиперповерхности, которое имеет очень громоздкий вид и в данной статье не приводится.

Другим способом определить число действительных корней полинома можно путем вычисления $i$-х субдискриминантов, используя теорему Якоби [10, 19].

Рассмотрим более простой случай, когда a₁ = = ${{a}_{2}} = {{b}_{1}}$ = b₂ = a. Тогда, перейдя к новым параметрам в уравнении (9) ${{d}_{{01}}} = ({{B}_{1}} - {{A}_{1}})){\text{/}}M{{a}^{2}}$, d₀₂ = = $({{B}_{2}} - {{A}_{2}}){\text{/}}M{{a}^{2}}$, получим из уравнения (11) алгебраическое уравнение 4 степени

(13)

${{P}_{4}}({{t}_{2}}) = {{p}_{{00}}}t_{2}^{4} + {{p}_{{01}}}t_{2}^{3} + {{p}_{{02}}}t_{2}^{2} + {{p}_{{03}}}{{t}_{2}} + {{p}_{{04}}} = 0,$

где

${{p}_{{00}}} = 4({{d}_{{01}}}{{d}_{{02}}} - {{d}_{{01}}} - {{d}_{{02}}})({{d}_{{01}}}{{d}_{{02}}} - {{d}_{{01}}} + {{d}_{{02}}}),$

${{p}_{{01}}} = - 4({{d}_{{02}}} - 2)(d_{{01}}^{2}d_{{02}}^{2} + d_{{01}}^{2}{{d}_{{02}}} - 2d_{{01}}^{2} + 2d_{{02}}^{2}),$

${{p}_{{02}}} = (d_{{01}}^{2}d_{{02}}^{4} + 4d_{{02}}^{4} - 16d_{{01}}^{2}d_{{02}}^{2} + 24(d_{{01}}^{2} - d_{{02}}^{2})),$

${{p}_{{03}}} = 4({{d}_{{02}}} + 2)(d_{{01}}^{2}d_{{02}}^{2} - d_{{01}}^{2}{{d}_{{02}}} - 2d_{{01}}^{2} + 2d_{{02}}^{2}),$

${{p}_{{04}}} = 4({{d}_{{01}}}{{d}_{{02}}} + {{d}_{{01}}} - {{d}_{{02}}})({{d}_{{01}}}{{d}_{{02}}} + {{d}_{{01}}} + {{d}_{{02}}}).$

Определим теперь условия существования действительных корней уравнения (13). Для этого вычислим дискриминант полинома ${{P}_{4}}({{t}_{2}})$, который задает на плоскости ${{d}_{{01}}}$, ${{d}_{{02}}}$ уравнение дискриминантной кривой. Границы областей с равным числом действительных корней на плоскости параметров ${{d}_{{01}}}$, ${{d}_{{02}}}$ определяются следующей системой алгебраических уравнений:

(14)

${{P}_{4}}({{t}_{2}}) = 0,\quad P_{4}^{'}({{t}_{2}}) = 0.$

Исключим переменную ${{t}_{2}}$ из системы (14) путем вычисления определителя результанта этих уравнений и получим уравнение дискриминантной кривой в виде

(15)

$\begin{gathered} {{P}_{5}}({{d}_{{01}}},{{d}_{{02}}}) = \\ = 1024d_{{02}}^{{12}}{{P}_{6}}({{d}_{{01}}},{{d}_{{02}}}){{P}_{7}}({{d}_{{01}}},{{d}_{{02}}}){{P}_{8}}({{d}_{{01}}},{{d}_{{02}}}) = 0. \\ \end{gathered} $

Здесь

${{P}_{6}}({{d}_{{01}}},{{d}_{{02}}}) = (d_{{01}}^{2}{{({{d}_{{02}}} - 1)}^{2}} - d_{{02}}^{2}),$

$\begin{gathered} {{P}_{7}}({{d}_{{01}}},{{d}_{{02}}}) = \\ = ((d_{{01}}^{2}d_{{02}}^{2} + 4({{d}_{{01}}} + {{d}_{{02}}}{{)}^{2}})((d_{{01}}^{2}d_{{02}}^{2} + 4({{d}_{{01}}} - {{d}_{{02}}}{{)}^{2}}), \\ \end{gathered} $

$\begin{gathered} {{P}_{8}}({{d}_{{01}}},{{d}_{{02}}}) = (d_{{01}}^{4}{{(d_{{02}}^{2} + 8)}^{2}} + \\ + \;16d_{{01}}^{2}d_{{02}}^{2}(d_{{02}}^{2} + 10) + 64d_{{02}}^{4} - 6912). \\ \end{gathered} $

Теперь мы должны проверить, как изменяется число равновесных решений при пересечении одной из кривых (15). Это можно сделать численно, определив число действительных решений в одной точке из каждой области, ограниченной кривыми (15) на плоскости $({{d}_{{01}}},{{d}_{{02}}})$.

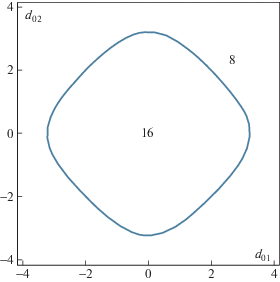
Численный анализ показал, что только кривая ${{P}_{8}}({{d}_{{01}}},{{d}_{{02}}}) = 0$ разделяет области с различным числом действительных корней уравнения (13). При пересечении границ кривых заданными уравнениями ${{P}_{6}}({{d}_{{01}}},{{d}_{{02}}}) = 0$ и ${{P}_{7}}({{d}_{{01}}},{{d}_{{02}}}) = 0$ смены числа действительных корней уравнения (13) не происходит. На рис. 2 показаны области с одинаковым числом действительных решений уравнения (13), равным 4 и 2, где существуют 16 и 8 равновесных ориентаций системы двух связанных тел соответственно. Границы этих областей задаются уравнением ${{P}_{8}}({{d}_{{01}}},{{d}_{{02}}}) = 0$. Кривые границ областей на рис. 2 построены с использованием функции $ContourPlot$ в системе Wolfram Mathematica.

Рис. 2.

Области с равным числом положений равновесия.

Таким образом, для случая a₁ = a₂ = ${{b}_{1}} = {{b}_{2}} = a$, существуют только 16 и 8 равновесных ориентаций системы спутник-стабилизатор в орбитальной системе координат в плоскости, перпендикулярной плоскости орбиты.

Применение методов компьютерной алгебры в данной работе позволило в достаточно простой форме получить решение классической задачи механики космического полета.

Список литературы

Сарычев В.А. Вопросы ориентации искусственных спутников. Итоги науки и техники. Серия Исследование космического пространства. М.: ВИНИТИ. 1978. Т. 11. 224 с.
Сарычев В.А. Положения относительного равновесия двух тел, соединенных сферическим шарниром, на круговой орбите. // Космические исследования. 1967. Т. 5. № 3. С. 360–364.
Gutnik S.A., Sarychev V.A. Symbolic investigation of the dynamics of a system of two connected bodies moving along a circular orbit // In: England M., Koepf W., Sadykov T.M., Seiler W.M., Vorozhtsov E.V. Eds. CASC 2019. LNCS. Springer, Cham, 2019. V. 11661. P. 164–178.
Гутник С.А., Сарычев В.А. Применение методов компьютерной алгебры для исследования динамики системы двух связанных тел на круговой орбите // Программирование. 2019. № 2. С. 32–40.
Гутник С.А., Сарычев В.А. Исследование стационарных движений системы двух связанных тел на круговой орбите с применением методов компьютерной алгебры // Журнал вычислительной математики и математической физики. 2020. Т. 60. № 1. С. 80–87.
Gutnik S.A., Sarychev V.A. Symbolic computations of the equilibrium orientations of a system of two connected bodies moving on a circular orbit around the Earth. // Mathematics in Computer Science. 2021. V. 15. № 3. P. 407–417.
Гутник С.А., Сарычев В.А. Символьно-численные методы исследования положений равновесия спутника-гиростата // Программирование. 2014. № 3. С. 49–58.
Гутник С.А., Сарычев В.А. Применение методов компьютерной алгебры для исследования стационарных движений спутника-гиростата // Программирование. 2017. № 2. С. 35–44.
Гутник С.А., Сарычев В.А. Символьно-аналитические методы исследования положений равновесия спутника на круговой орбите // Программирование. 2021. № 2. С. 28–33.
Батхин A.Б. Параметризация дискриминантного множества многочлена // Программирование. 2016. № 2. С. 8–21.
Батхин A.Б. Параметризация множества, определяемого обобщенным дискриминантом многочлена // Программирование. 2018. № 2. С. 5–17.
Батхин A.Б. Вычисление резонансного множества многочлена при ограничениях на коэффициенты // Программирование. 2019. № 2. С. 6–16.
Батхин A.Б. Бифуркации периодических решений системы Гамильтона с дискретной группой симметрий // Программирование. 2020. № 2. С. 14–29.
Журавлёв В.Ф., Петров А.Г., Шундерюк М.М. Избранные задачи гамильтоновой механики. М. : ЛЕНАНД, 2015. 304 с.
Прокопеня А.Н., Минглибаев М.Дж., Маемерова Г.М. Символьные вычисления в исследованиях проблемы трех тел с переменными массами // Программирование. 2014. № 2. С. 51–59.
Прокопеня А.Н., Минглибаев М.Дж., Маемерова Г.М., Иманова Ж.У. Исследование ограниченной задачи трех тел с переменными массами методами компьютерной алгебры // Программирование. 2017. № 5. С. 18–23.
Прокопеня А.Н., Минглибаев М.Дж., Шомшекова С.А. Применение компьютерной алгебры в исследованиях двухпланетной задачи трех тел с переменными массами // Программирование. 2019. № 2. С. 58–65.
http://www.wolfram.com/mathematica
Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2010.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал