Программирование, 2022, № 2, стр. 33-46

СУПЕРКОМПЬЮТЕРНАЯ СРЕДА ВЫПОЛНЕНИЯ ДЛЯ РЕКУРСИВНЫХ МАТРИЧНЫХ АЛГОРИТМОВ

Г. И. Малашонок^a, *, А. А. Сидько^a, **

^a Национальный университет “Киево-Могилянская академия”
04070 Киев, ул. Сковороды д. 2, Украина

^* E-mail: malaschonok@gmail.com
^** E-mail: a.sidko@ukma.edu.ua

Поступила в редакцию 30.06.2021
После доработки 27.08.2021
Принята к публикации 11.09.2021

EDN: MQZUTS
DOI: 10.31857/S0132347422020091

Аннотация

Предлагается новая среда выполнения для рекурсивных матричных алгоритмов на суперкомпьютере с распределенной памятью. Она предназначена как для плотных, так и для разреженных матриц. При этом обеспечивается динамическое децентрализованное управление вычислительным процессом. Как пример блочно-рекурсивного алгоритма, представлено разложение Холецкого симметричной положительно определенной матрицы в виде блочного дихотомического алгоритма. Приведены результаты экспериментов с разным количеством ядер, демонстрирующие хорошую масштабируемость полученного решения.

1. ВВЕДЕНИЕ

Современные суперкомпьютерные системы с сотнями тысяч ядер сталкиваются с проблемами в области параллельных вычислений (cм., например, [1]). Три основные проблемы – это неравномерная загрузка оборудования, накопление вычислительной погрешности в ходе вычислений с большими матрицами и возможные физические отказы отдельных процессоров в ходе вычислительного процесса.

Требуется создание новой программной инфраструктуры для организации распределенных вычислений – суперкомпьютерной среды выполнения. Такая программная среда должна поддерживать разработку и эффективное выполнение программ, предназначенных для современных кластеров.

Известно, что самой популярной сегодня средой выполнения является Hadoop. В его основе лежит парадигма MapReduce: одна задача разделяется на множество одинаковых заданий, эти задания выполняются на процессорах одного кластера, затем все сводится в один результат [2, 17].

Этот специфический класс задач оказался достаточно популярным. Однако Hadoop не может использоваться для других классов задач.

Развиваются универсальные системы, такие как OpenMP [5], StarPU [6], Legion [7], OmpSs [8], OCR [9], HPX [22], SuperGlue [5], QUARK [11], DPLASMA [12]. Каждая из них дает абстрактное описание доступных ресурсов и упрощает процесс написания параллельных программ.

Универсальная схема динамического обнаружения задач (DTD) была недавно разработана для среды выполнения PaRSEC [13, 14]. Эта среда может поддерживать как системы с общей памятью, так и системы с распределенной памятью. Новая парадигма продемонстрировала лучшую производительность по сравнению с параметризованным графиком задач, который использовался раньше.

Можно особо выделить пакет [15], предназначенный для синтеза параллельных программ на основе блочно-рекурсивных алгоритмов. Он дает возможность рассчитывать пересылку плотных блоков данных для распределенной памяти. В статье [16] представлена методология разработки блочно-рекурсивных алгоритмов в компьютерных сетях различной конфигурации. Для выделения самостоятельных вычислительных подзадач здесь используется нотация тензорного произведения.

В настоящей статье предлагается новая среда выполнения DAP для суперкомпьютера с распределенной памятью. Она предназначена для матричных задач, которые могут быть решены с помощью блочно-рекурсивных алгоритмов. Она, как и Hadoop, является узко специализированной средой выполнения.

Ее основным достоинством является обеспечение эффективного вычислительного процесса и хорошей масштабируемости программ, как для разреженных, так и для плотных матриц, на кластере с распределенной памятью. Другим достоинством является возможность перестройки вычислительного процесса при отказе отдельных узлов в ходе вычислений.

Первым подходом к созданию такой среды выполнения была схема динамического управления LLP, разработанная в лаборатории алгебраических вычислений Тамбовского государственного университета в сотрудничестве с ИСП РАН. В роли диспетчера всего вычислительного процесса тут выступал один из узлов кластера [10, 18].

Затем она была усовершенствована и была разработана схема с динамическим децентрализованным управлением [3]. Однако в этой схеме не учитывалась глубина рекурсии и невозможно было переключиться на новую задачу, пока текущая задача не была завершена.

Новая схема с децентрализованным управлением получила название DAP-схемы (Drop-Amine-Pine) [19]. В ее основе лежит дроп – вычислительная задача достаточно высокой сложности, которая может быть отделена и направлена в другой процессор. Результат вычислений дропа должен быть возвращен в тот процессор, из которого он был отправлен. Процесс вычисления дропа предполагает разворачивание его в глубину. При этом будет создан амин – соответствующий вычислительный граф, вершины которого являются дропами следующего уровня вложенности. Для хранения всех аминов, которые вычисляются на данном процессоре, создается структура, которая называется пайн. В процессе вычисления блочно-рекурсивная функция последовательно разворачивается в глубину и сохраняются все ее состояния на каждом уровне вложенности. Это позволяет любому процессору свободно переключаться с одной подзадачи на другую, не дожидаясь завершения текущей подзадачи. Кроме того, это позволяет эффективно перераспределять нагрузку в случае нерегулярных и разреженных данных.

Во втором разделе описывается граф рекурсивного алгоритма и приводятся примеры блочно-рекурсивных алгоритмов, таких как умножение матриц, обращение треугольных матрицы и дихотомический блочно-рекурсивный алгоритм для вычисления разложения Холецкого. В третьем разделе дается подробное описание новой среды выполнения. Описываются основные объекты и поля, организация потоков, алгоритмы основных процедур и функций. Четвертый раздел посвящен детальному описанию реализации блочно-рекурсивного алгоритма в среде выполнения DAP на примере алгоритма вычисления разложения Холецкого. В пятом разделе представлены результаты экспериментов. Первая серия экспериментов выполнена специально для исследования накопления вычислительной ошибки в прямых матричных алгоритмах при использовании стандартного машинного слова. В экспериментах вычислялось разложение Холецкого. В следующих сериях экспериментов демонстрировались преимущества новой среды выполнения, в частности хорошая масштабируемость. Эксперименты проводились с тремя типами алгоритмов: умножение матриц, обращение треугольных матриц и факторизация Холецкого. При этом отдельные серии экспериментов проводились для чисел, которые имеют двойную точность, и для чисел типа BigDecimal.

2. ГРАФ РЕКУРСИВНОГО АЛГОРИТМА

Рассмотрим несколько примеров блочно-рекурсивных алгоритмов, поскольку среда выполнения, которая описана в следующих разделах, предназначена для этого типа алгоритмов. Один из этих алгоритмов будет использоваться в четвертом разделе для детального описания реализации алгоритма в среде выполнения DAP.

Рассмотрим три блочно-рекурсивных алгоритма. Каждый из них содержит небольшое количество типов рекурсивных вычислительных блоков: матричное умножение, обращение и факторизация. Во всех примерах мы предполагаем, что даны квадратные матрицы, у которых количество столбцов и строк равно некоторой степени числа 2. Поэтому их легко разделить на четыре равных блока. Полученные блоки можно еще раз разделить на равные блоки, и так далее. Матрицу любого размера можно погрузить в такую квадратную матрицу, а в конце извлечь решение задачи.

Эти алгоритмы выбраны в качестве простых примеров. Отметим, что в блочно-рекурсивной форме можно записать большинство матричных алгоритмов.

2.1. МАТРИЧНОЕ УМНОЖЕНИЕ

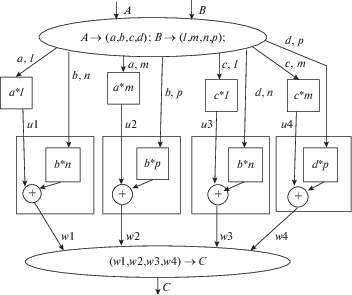
Даны две матрицы A и B. Требуется найти их произведение C = AB. Разделим эти матрицы на равные четыре блока и отдельно вычислим каждый из четырех блоков в произведении матриц:

$A \cdot B = \left( {\begin{array}{*{20}{c}} a&b \\ c&d \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} l&m \\ n&p \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{w}_{1}}}&{{{w}_{2}}} \\ {{{w}_{3}}}&{{{w}_{4}}} \end{array}} \right)$

1) ${{w}_{1}} = a \cdot l + b \cdot n$ 2) ${{w}_{2}} = a \cdot m + b \cdot p$

3) ${{w}_{3}} = c \cdot l + d \cdot n$ 4) ${{w}_{4}} = c \cdot l + d \cdot n$

Тут есть два типа блочно-рекурсивных операций: (1) AB умножение двух блоков и (2) $AB + C$ умножение двух блоков и сложение с третьим блоком.

Важно отметить, что операция сложения блоков не может составить самостоятельный дроп, из-за малой вычислительной сложности: количество операций сложения равно количеству элементов в каждом блоке.

Граф этого рекурсивного алгоритма показан на рис. 1. Здесь всего восемь дропов: четыре дропа типа (1) и четыре дропа типа (2). Верхний эллипс обозначает входную функцию, в которой происходит деление матриц A и B на блоки. А нижний эллипс обозначает выходную функцию, которая собирает из четырех блоков матрицу произведения C.

Рис. 1.

Граф блочно-рекурсивного алгоритма умножения матриц.

2.1. ОБРАЩЕНИЕ ТРЕУГОЛЬНОЙ МАТРИЦЫ

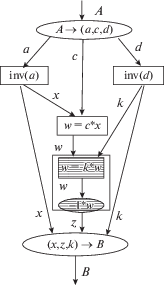
Дана нижняя треугольная матрица A, которая не имеет нулевых элементов на диагонали, поэтому ${\text{det}}(A) \ne 0$. Требуется вычислить обратную матрицу A^–1.

Обозначим блоки матрицы A через $a$, $0$, $c$, $d$, обозначим блоки матрицы A^–1 через $x$, $0$, $z$, $k$. Произведение этих матриц должно быть равно единичной матрице:

$A \cdot {{A}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} a&0 \\ c&d \end{array}} \right)\left( {\begin{array}{*{20}{c}} x&0 \\ z&k \end{array}} \right) = \left( {\begin{array}{*{20}{c}} I&0 \\ 0&I \end{array}} \right).$

Выполним умножение и приравняем соответствующие блоки в левой и правой части равенства. Получим искомые блоки обратной матрицы:

$x = {{a}^{{ - 1}}},\quad k = {{d}^{{ - 1}}},\quad z = - k \cdot c \cdot x$

Здесь есть три типа блочно-рекурсивных операций: (1) умножение двух блоков, (2) инверсия блока, (3) умножение двух блоков с инверсией знаков каждого элемента. Граф этого рекурсивного алгоритма показан на рис. 2.

Рис. 2.

Граф блочно-рекурсивного алгоритма обращения треугольной матрицы.

Здесь всего четыре дропа: два дропа типа (2), один дроп типа (1) и один дроп типа (3). Верхний эллипс – это входная функция, в которой выполняется деление входной матрицы на блоки. А нижний эллипс – это выходная функция, которая собирает из блоков вычисленную обратную матрицу.

2.2. РАЗЛОЖЕНИЕ ХОЛЕЦКОГО

Дана симметричная положительно определенная матрица $A$. Требуется найти такую нижнюю треугольную матрицу $L$, чтобы выполнялось равенство

(1)

$A = L{{L}^{T}}.$

В работе [20] приведена стандартная схема разложения Холецкого (см. алгоритм 1). Отметим, что тут происходит деление на неравные блоки. Размер ${{n}_{b}} \times {{n}_{b}}$ блока ${{A}_{{11}}}$, который отделяется в левом верхнем углу, должен быть небольшим, чтобы разложение этого блока были выполнены одним процессором: разложение ${{A}_{{11}}} = {{L}_{{11}}}L_{{11}}^{T}$ выполняется последовательным алгоритмом. Затем обратная матрица $L_{{11}}^{{ - 1}}$ вычисляется алгоритмом Гаусса. Основная часть матрицы остается в блоке ${{A}_{{22}}}$.

Algorithm 1: Стандартный блочный алгоритм разложения Холецкого [20]
1	Input:$A$
2	Output:$L$ (см. равенство (1))
	begin
		for each panel left to right do
3			Partition$A = \left( {\begin{array}{*{20}{c}} {{{A}_{{11}}}}&{A_{{21}}^{T}} \\ {{{A}_{{21}}}}&{{{A}_{{22}}}} \end{array}} \right)$,
4			where ${{A}_{{11}}}$ is ${{n}_{b}} \times {{n}_{b}}$
5			Factorize${{A}_{{11}}} = {{L}_{{11}}}L_{{11}}^{T}$ using unblocked algorithm
6			Update panel ${{A}_{{21}}} = {{A}_{{21}}}L_{{11}}^{{ - T}}$ using triangular solver
7			Update trailing matrix using symmetric rank-k update ${{A}_{{22}}} = {{A}_{{22}}} - {{A}_{{21}}}A_{{21}}^{T}$
8			Continue with $A = {{A}_{{22}}}$

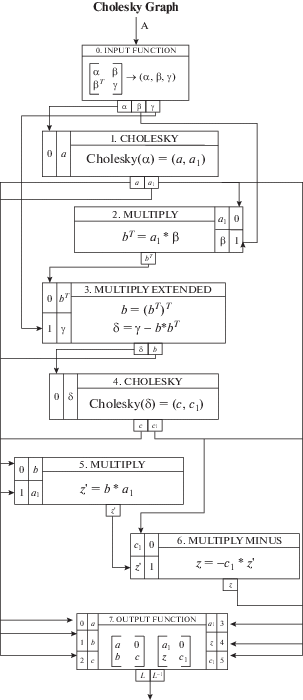
Мы предлагаем дихотомический блочно-рекурсивный алгоритм разложения Холецкого. Он отличается тем, что матрица делится на 4 одинаковых по размеру блока. И, кроме того, не требуется отдельно обращать матрицу $L$ с помощью алгоритма Гаусса. Вычислительная сложность всего алгоритма будет такой же, как и у алгоритма умножения матриц, который будет применяться для умножения блоков. Обозначим блоки матрицы А через $\alpha $, $\beta $, ${{\beta }^{T}}$, $\gamma $, обозначим блоки искомой матрицы $L$ через $a,0,b,c$ и приравняем произведение $L{{L}^{T}}$ к матрице A:

$\begin{gathered} L \cdot {{L}^{T}} = \left( {\begin{array}{*{20}{c}} a&0 \\ b&c \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{{a}^{T}}}&{{{b}^{T}}} \\ 0&{{{c}^{T}}} \end{array}} \right) = \\ = \;\left( {\begin{array}{*{20}{c}} {a{{a}^{T}}}&{a{{b}^{T}}} \\ {b{{a}^{T}}}&{b{{b}^{T}} + c{{c}^{T}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \alpha &\beta \\ {{{\beta }^{T}}}&\gamma \end{array}} \right) = A \\ \end{gathered} $

Отсюда следуют равенства для блоков:

$a{{a}^{T}} = \alpha ,\quad b = {{\beta }^{T}}{{({{a}^{{ - 1}}})}^{T}},\quad c{{c}^{T}} = \gamma - b{{b}^{T}}.$

Для вычисления блоков a, b, c необходимо выполнить блочное умножение, транспонирование, инверсию и разложение Холецкого для двух блоков.

Вычисления обратной матрицы можно избежать, если вместе с матрицей $L$ вычисляется одновременно и обратная к ней матрица L^–1.

	Algorithm 2: Дихотомический блочно-рекурсивный алгоритм разложения Холецкого (L, L^–1) = $Cholesky(A)$
	Input:$A$
	Output:$\;L,\;{{L}^{{ - 1}}}$ (см. равенство (1))
1	begin
2		if$size(A) = 1\& A = [\alpha ])$then
3			return$([{{\alpha }^{{1/2}}}],[{{\alpha }^{{ - 1/2}}}])$
4		else
5			$A - > (\alpha ,\beta ,\gamma )$ – ”we create blocks”
6			$(a,{{a}_{1}}) = Cholesky(\alpha )$ – ”${{a}_{1}} = {{a}^{{ - 1}}}$”
7			${{b}^{T}} = {{a}_{1}}*\beta ;b = ({{b}^{T}}{{)}^{T}}$
8			$\delta = \gamma - b{{b}^{T}}$
9			$(c,{{c}_{1}}) = Cholesky(\delta )$ – ”${{c}_{1}} = {{c}^{{ - 1}}}$”
10			$z = - {{c}_{1}} * b * {{a}_{1}}$
11			return$\left( {\begin{array}{{20}{c}} a&0 \\ b&c \end{array}} \right),\left( {\begin{array}{{20}{c}} {{{a}_{1}}}&0 \\ z&{{{c}_{1}}} \end{array}} \right)$

Мы расширяем процедуру вычисления разложения Холецкого таким образом, чтобы она возвращала не только матрицу $L$, но и обратную к ней матрицу L^–1. Тогда вместе с блоками a и b будут вычислены и обратные к ним a^–1 и b^–1. В этом случае обратная матрица для матрицы $L$ будет такой:

${{L}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} {{{a}^{{ - 1}}}}&0 \\ { - {{c}^{{ - 1}}}b{{a}^{{ - 1}}}}&{{{c}^{{ - 1}}}} \end{array}} \right).$

Граф этого алгоритма показан на рис. 5.

2.3. Разложение Холецкого для случая $2 \times 2$

$\left( {\left[ {\begin{array}{*{20}{c}} a&0 \\ b&c \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {\frac{1}{a}}&0 \\ {\frac{{ - b}}{{ac}}}&{\;\frac{1}{c}} \end{array}} \right]} \right) = Cholesky\left[ {\begin{array}{*{20}{c}} \alpha &\beta \\ \beta &\gamma \end{array}} \right]$

$a = \sqrt ( \alpha ),\quad b = \frac{\beta }{{\sqrt ( \alpha )}},\quad d = \frac{{\alpha * \gamma - {{\beta }^{2}}}}{\alpha },\quad c = \sqrt ( d).$

3. АРХИТЕКТУРА СРЕДЫ ВЫПОЛНЕНИЯ

3.1. ГЛАВНЫЕ ЭТАПЫ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА. ДЕРЕВО ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА

Во всех рассмотренных алгоритмах матрица дихотомически рекурсивно делится на блоки. Каждому из блоков соответствует некоторая вершина в дереве вычислительного алгоритма. К такому блоку снова применяется блочно-рекурсивный алгоритм. Это происходит до тех пор, пока блоки остаются достаточно большими.

Когда размер блока становится относительно малым, то есть когда время на пересылку данных между процессорами становится сравнимым с временем вычисления, то такой блок будет соответствовать листовой вершиной в дереве алгоритма. Он будет вычисляться последовательным алгоритмом.

Размер такого листового блока должен автоматически подбираться для конкретного оборудования, так как он зависит от физических характеристик вычислительного устройства: скорости передачи данных по сети и вычислительной мощности процессоров.

Дерево связей для вычислительных узлов формируется при передаче дропов от родительских узлов к дочерним узлам. Это дерево связей строится в соответствии с графом рекурсивного алгоритма и при наличии свободных узлов.

В первый момент все узлы свободны, а выделенный корневой узел берет на себя всю задачу и весь список свободных узлов.

Вычислительный процесс состоит из трех этапов.

3.1.1. Первый этап

На этом этапе происходит начальное построение дерева связей для вычислительных узлов. Дропы с матричными блоками отправляются из корневого узла к дочерним узлам вместе со списками свободных узлов. При этом список свободных узлов делится примерно на равные части. В дочерних узлах новые дропы отправляются дальше с соответствующими частями списка свободных узлов. Каждый раз множество свободных узлов делится примерно на равные части не зависимо от размера блока.

Каждый процессор завершает первый этап в тот момент, когда у него оказывается пустой список свободных узлов, либо, когда объем данных в полученном блоке меньше определенной границы, она называется “листовым размером”.

3.1.2. Второй этап

Процессор завершает вычисление первого полученного дропа и возвращает результат родительскому узлу. Если происходит простой некоторого процессора, либо после отправки результата, либо из-за отсутствия результата от дочернего процессора, то этот процессор добавляет свой номер к списку свободных узлов и передает его родительскому процессору.

Список свободных узлов имеет одно из двух направлений передачи: он может направляться либо родительскому процессору, либо дочерним узлам. В том случае, когда некоторые дочерние узлы не вернули результат, список свободных узлов может быть разделен на примерно равные части и отправлен тем дочерним узлам, которые имеют дропы с наименьшей глубиной рекурсии, то есть тем, у которых наибольшие по размеру блоки. Эти направления передачи чередуются.

Свободный процессор может получить новый дроп от любого процессора, который в своем списке свободных процессоров содержит его номер. И этому процессору он должен будет вернуть результат вычислений.

3.1.3. Третий этап

На этом этапе результаты возвращаются в корневую вершину, все процессоры становятся свободными и их номера передаются в список свободных вершин корневого процессора. Результат задачи будет сформирован в корневой вершине и вычисления будут завершены.

3.2. БАЛАНСИРОВКА НАГРУЗКИ

Среда выполнения осуществляет автоматическое перераспределение подзадач от перегруженных узлов на свободные узлы. Для этого предусмотрена схема передачи информации о свободных узлах и информации о перегруженных узлах.

Информация о свободных узлах распределена по спискам свободных узлов.

Информация о состоянии дочерних процессоров содержится на терминале дочерних процессоров и является целым числом, выражающим глубину рекурсии дропа, который вычисляется на дочернем процессоре.

Дочерний процессор поддерживает эту информацию актуальной и при ее изменении посылает об этом сообщение.

Пересылка списка свободных процессоров дочерним процессорам происходит в соответствии с их состоянием: дочерним процессорам, которые имеют дропы с самым низким уровнем рекурсии направляются примерно равные части списка свободных узлов.

3.3. КОМПОНЕНТЫ МЕХАНИЗМА УПРАВЛЕНИЯ ВЫЧИСЛИТЕЛЬНЫМ ПРОЦЕССОМ

Рассмотрим компоненты механизма управления вычислительным процессом (рис. 3 и рис. 4).

Рис. 3.

Механизм управления вычислительным процессом – Drop, Pine, Amine, Aerodrome, Terminal.

Рис. 4.

Механизм управления вычислительным процессом – Track, Vokzal, LeavesStack.

Рис. 5.

Граф алгоритма разложения Холецкого.

3.3.1. Дроп

Дропы – это части вычислительного графа, которые являются компактными подграфами и могут быть переданы другим процессорам. Количество машинных операций, которые требуются для вычисления дропа должно быть существенно больше чем объем данных на входе и на выходе. Например, операция суммирования двух матриц не может быть самостоятельным дропом.

На рис. 1 и 2 вершины, объединенные в один дроп, обведены прямоугольным контуром.

Для некоторых типов дропов вектор входных данных делится на две части: главную и дополнительную. Например, у дропа $A * B + C$ входной вектор $(A,B,C)$ имеет главные компоненты $(A,B, - )$ и дополнительные компоненты $( - , - ,C)$. Главных компонент достаточно, чтобы начать вычислительный процесс такого дропа. Дополнетельные компоненты могут быть доставлены позже.

В связи с этим дроп-объекты могут быть четырех разных видов, в зависимости от того какие данные присутствуют в объекте: (1) весь входной вектор, (2) главные компоненты входного вектора, (3) дополнительные компоненты входного вектора, (4) результат вычислений.

3.3.2. Амин

Процесс вычисления дропа предполагает разворачивание его в глубину. При этом будет создан амин – вычислительный граф, вершины которого являются дропами следующего уровня вложенности.

Каждый амин имеет одну входную функцию, которая принимает массив входных данных и может выполнять предварительные простые вычисления. Он имеет одну выходную функцию, которая может выполнять заключительные простые вычисления и формировать массив выходных данных.

Например, амин $A * B$ состоит из четырех дропов $A * B$, четырех дропов $A * B + C$, одной входной и одной выходной функции.

3.3.3. Пайн

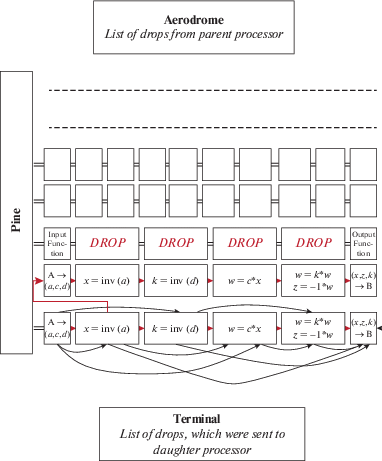
Все амины, вычисление которых происходит на одном процессоре, хранятся в общем списке, который называется Пайн (см. рис. 3).

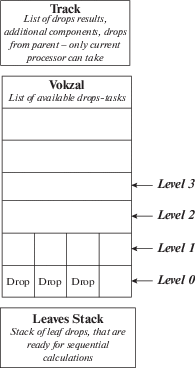
3.3.4. Вокзал

На вокзале все дроп-задания ожидают своей очереди. Эти дроп-задания расположены на разных уровнях. Уровень означает глубину рекурсии на которой находится данный дроп. С вокзала дроп может быть направлен либо на другой процессор, либо он может быть направлен для вычисления на данном процессоре. Уровень вокзала – это наименьший уровень дропа, находящегося на вокзале.

3.3.5. Аэродром

Каждый процессор, который послал дроп данному процессору, считается его родительским процессором. Список всех активных родительских процессоров называется аэродром. Родительский процессор, которому вернули результаты всех полученных от него дроп-заданий, удаляется из списка аэродром.

Однако основной родительский процессор, тот с которого был получен первый дроп, всегда сохраняется, так как список свободных процессоров должен направляеться этому родительскому процессору.

3.3.6. Терминал

Терминал используется для связи с дочерними процессорами, которым были отправлены дроп-задачи. Все дочерние процессоры регистрируются в терминале. При этом в терминале у них сохраняется текущий уровень рекурсии. Дочерние процессоры поддерживают его в актуальном состоянии и для этого посылают сообщения при смене уровня.

Дочерний процессор, который вернул результаты всех полученных дроп-заданий удаляется с терминала. Уровень терминала – это наименьший из уровней дочерних процессоров.

3.3.7. Трек

Это отдельный путь, с которого не могут отправляться дропы на другие процессоры.

Сюда передаются дропы от родительских процессоров, здесь сохраняются результаты вычислений всех дропов: и тех, которые вычислялись на данном процессоре и тех, которые получены от дочерних процессоров. Также тут сохраняются дополнительные части входных векторов дроп-заданий от родительских процессоров.

3.3.8. Листовой стек

Здесь сохраняются листовые дроп-задания, то есть те, которые должны вычисляться на данном процессоре, так как у них малый объем данных.

3.4. ОСНОВНЫЕ ПОЛЯ И ФУНКЦИИ

3.4.1. Поля дроп-обьекта

– PAD (np, na, nd) – адрес этого дропа, где np – номер процессора, na – номер амина, nd – номер дропа. Результат вычислений должен быть возвращен по этому адресу.

– Type – тип дропа (уникальный номер в списке всех типов дропов).

– InData и outData – векторы для входных и выходных данных данного дропа. Вектор InData имеет две части – главные компоненты и дополнительные. Для начала вычислений достаточно наличие главных компонент. Дополнительные компоненты могут прийти позже.

– Amine – указатель на амин, в котором находится данный дроп.

– RecNum – номер уровня, то есть номер глубины рекурсии.

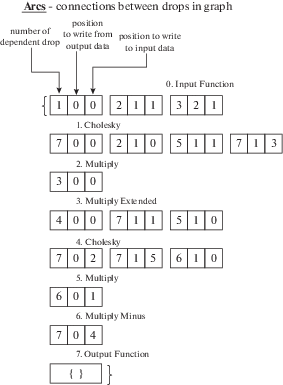
– Arcs – топология графа. Кодируется целочисленным массивом, см. пример топологии графа для алгоритма Холецкого на рис. 6.

3.4.2. Поля Амин-объекта

– PAD (np, na, nd), Type, inData, outData – такие как у дроп-обьекта.

– Drop – массив всех дропов этого амина.

3.5. ОРГАНИЗАЦИЯ ДВУХ ПОТОКОВ

Мы используем два потока: счетный поток и поток диспетчера. Эти потоки будут выполняться на каждом ядре кластера по очереди.

3.5.1. Счетный поток

Счетный поток ожидает прибытия первой дроп-задачи на вокзал и запускает соответствующие вычисления.

Объекты счетного потока:

– Pine – список аминов на этом процессоре.

– Vokzal – массив списков доступных дроп-задач.

– Aerodrome – список родительских процессоров.

– Terminal – массив списков дочерних процессоров.

– CurrentDrop – текущий дроп на выполнении.

Функции счетного потока:

– WriteResultsToAmin – вычисленный выходной вектор дропа записывается внутри его амина во входные векторы других дропов, согласно топологии графа.

– InputDataToAmin – создает амин, который соответствует данному дропу, вызывает входную функцию и передает на ее вход входной вектор.

– WriteResultsAfterInpFunc – записывает результат вычисления входной функции во все дропы амина согласно топологии графа (см. рис. 5, как пример).

– runCalcThread – это основная процедура счетного потока. Пока Track не пуст результаты вычислений дропов регистрируются согласно топологии и готовые к вычислению дропы записываются на вокзал. Дополнительные компоненты входных векторов дропов прописываются в соответствующие дропы и их входные функции вычисляются. Если приходит новое дроп-задание, то прописывается новый амин и вычисляется его входная функция. Пока Leaves Stack не пуст выполняется последовательный счет листовых дропов. Пока вокзал не пуст выполняются дроп-задания, размещенные на вокзале. Если же все эти поля пусты, то устанавливается соответствующий флаг и счетный поток переходит в режим ожидания, при этом он свой номер присоединяет к списку свободных процессоров и отправляет этот список.

3.5.2. Диспетчерский поток

Работу диспетчерского потока можно разделить на 10 процессов:

1. Ожидание сигнала завершения всех вычислений.

2. Получение дроп-задания.

3. Получение свободных процессоров.

4. Получение и запись уровня состояния дочернего процессора.

5. Получение результата вычислений от дочернего дропа и запись этого результата в соответствующий амин.

6. Получение дополнительных компонент от родительского процессора.

7. Отправка с вокзала дроп-заданий на свободные процессоры.

8. Отправка свободных процессоров дочерним процессорам или родительскому процессору. Эти действия чередуются.

9. Отправка результатов дроп-заданий родительским процессорам.

10. Отправка дополнительных компонент дочерним процессорам.

Исходный код программы доступен по ссылке: https://bitbucket.org/mathpar/dap/src/master/src/main/java/com/mathpar/parallel/dap/

4. РАЗЛОЖЕНИЕ ХОЛЕЦКОГО

В качестве иллюстрации рассмотрим подробно вычислительный процесс для алгоритма разложения Холецкого. На рис. 5 и 6 изображен рекурсивный граф алгоритма и соответствующий ему массив дуг, отображающий топологию графа. Все дропы в графе пронумерованы натуральными числами. Каждая строка в массиве Arcs соответствует одному дропу. Номер строки – это порядковый номер дропа. Каждая тройка чисел в строке указывает связь данного дропа со входами следующих дропов. Первое число – это номер дропа, который получает данные, второе – это номер компоненты в выходном векторе данного дропа и третье число – это номер компоненты во входном векторе.

Рис. 6.

Описание топологии графа разложения Холецкого.

Массив Arcs начинается с нулевой строки, которая соответствует входной функции дропа, а последняя строка предназначена для выходной функциии.

Например, вторая строка в arcs равна 7 0 0, 2 1 0, 5 1 1, 7 1 3. Рассмотрим первую тройку 7 0 0. Число 7 соответствует номеру зависимого дропа в которой нужно записать результат. Два нуля показывают, что связаны нулевая компонента выходного вектора с нулевой компонентой входного вектора.

Следующая тройка – 2 1 0. Число 2 соответствует номеру зависимого дропа, число 1 – это номер компоненты в выходном векторе, а число 0 – это номер компоненты во входном векторе.

4.1. ЧИСЛОВОЙ ПРИМЕР

Рассмотрим пример разложения Холецкого для матрицы размера 4 × 4. Разобьем матрицу А на 4 блока:

$A = \left( {\begin{array}{*{20}{c}} {16}&{24}&{28}&4 \\ {24}&{72}&{42}&{42} \\ {28}&{42}&{85}&{13} \\ 4&{42}&{13}&{74} \end{array}} \right),\quad \alpha = \left( {\begin{array}{*{20}{c}} {16}&{24} \\ {24}&{72} \end{array}} \right),$

$\beta = \left( {\begin{array}{*{20}{c}} {28}&4 \\ {42}&{42} \end{array}} \right),\quad \gamma = \left( {\begin{array}{*{20}{c}} {85}&{13} \\ {13}&{74} \end{array}} \right).$

$1.\,\,(a,{{a}_{1}}) = \left[ {\left( {\begin{array}{*{20}{c}} 4&0 \\ 6&6 \end{array}} \right),\left( {\begin{array}{*{20}{c}} {1{\text{/}}4}&0 \\ { - 1{\text{/}}4}&{1{\text{/}}6} \end{array}} \right)} \right] = Cholesky(\alpha )$

${{\alpha }_{1}} = 16,\quad {{\beta }_{1}} = 24,\quad {{\gamma }_{1}} = 72,$

$(a{\text{'}},a_{1}^{'}) = [4,1/4] = Cholesky({{\alpha }_{1}}),$

$b{\text{'}} = {{\beta }_{1}}{\text{/}}a{\text{'}} = 6,\quad {{\delta }_{1}} = {{\gamma }_{1}} - {{(b{\text{'}})}^{2}} = 36,$

$(c{\text{'}},c_{1}^{'}) = [6,1{\text{/}}6] = Cholesky({{\delta }_{1}}),$

$z{\text{'}} = - c_{1}^{'}b{\text{'}}a_{1}^{'} = - 1{\text{/}}4.$

$\begin{gathered} 2.\,\,{{b}^{T}} = {{a}_{1}} \cdot \beta = \left( {\begin{array}{*{20}{c}} {1{\text{/}}4}&0 \\ { - 1{\text{/}}4}&{1{\text{/}}6} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {28}&4 \\ {42}&{42} \end{array}} \right) = \\ = \;\left( {\begin{array}{*{20}{c}} 7&1 \\ 0&6 \end{array}} \right);\quad b = \left( {\begin{array}{*{20}{c}} 7&0 \\ 1&6 \end{array}} \right) \\ \end{gathered} $

$\begin{gathered} 3.\,\,\delta = \gamma - b \cdot {{b}^{T}} = \left( {\begin{array}{*{20}{c}} {85}&{13} \\ {13}&{74} \end{array}} \right) - \\ - \;\left( {\begin{array}{*{20}{c}} 7&0 \\ 1&6 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 7&1 \\ 0&6 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {36}&6 \\ 6&{37} \end{array}} \right) \\ \end{gathered} $

$4.\,\,(c,{{c}_{1}}) = \left[ {\left( {\begin{array}{*{20}{c}} 6&0 \\ 1&6 \end{array}} \right),\left( {\begin{array}{*{20}{c}} {1{\text{/}}6}&0 \\ { - 1{\text{/}}36}&{1{\text{/}}6} \end{array}} \right)} \right] = Cholesky(\delta )$

${{\alpha }_{2}} = 36,\quad {{\beta }_{2}} = 6,\quad {{\gamma }_{2}} = 37,$

$(a{\text{''}},a_{1}^{{''}}) = [6,1{\text{/}}6] = Cholesky({{\alpha }_{2}}),$

$b{\text{''}} = {{\beta }_{2}}{\text{/}}a{\text{''}} = 1,\quad {{\delta }_{2}} = {{\gamma }_{1}} - {{(b{\text{''}})}^{2}} = 36,$

$(c{\text{''}},c_{1}^{{''}}) = [6,1{\text{/}}6] = Cholesky({{\delta }_{2}}),$

$z{\text{''}} = - c_{2}^{{''}}b{\text{'}}a_{2}^{{''}} = - 1{\text{/}}6 \cdot 1 \cdot 1{\text{/}}6 = - 1{\text{/}}36.$

$5.\,\,z = - \left( {\begin{array}{*{20}{c}} {1{\text{/}}6}&0 \\ { - 1{\text{/}}36}&{1{\text{/}}6} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 7&0 \\ 1&6 \end{array}} \right)$

$\left( {\begin{array}{*{20}{c}} {1{\text{/}}4}&0 \\ { - 1{\text{/}}4}&{1{\text{/}}6} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - 7{\text{/}}24}&0 \\ {37{\text{/}}144}&{ - 1{\text{/}}6} \end{array}} \right)$

$L = \left( {\begin{array}{*{20}{c}} a&0 \\ b&c \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 4&0&0&0 \\ 6&6&0&0 \\ 7&0&6&0 \\ 1&6&1&6 \end{array}} \right),$

${{L}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} {{{a}_{1}}}&0 \\ z&{{{c}_{1}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\frac{1}{4}}&0&0&0 \\ { - \frac{1}{4}}&{\frac{1}{6}}&0&0 \\ { - \frac{7}{{24}}}&0&{\frac{1}{6}}&0 \\ {\frac{{37}}{{144}}}&{ - \frac{1}{6}}&{ - \frac{1}{3}6}&{\frac{1}{6}} \end{array}} \right).$

5. ЭКСПЕРИМЕНТЫ

Все вычислительные эксперименты проводились на вычислительном кластере MVS-10P CASCADE LAKE Межведомственного суперкомпьютерного центра РАН (2256 ядер, на базе Intel Xeon Platinum 8268, 28 ядер / 48 потоков, 2,9 ГГц, 35,75 МБ кэш-памяти, по 96 ГБ ОЗУ на каждый проц.)

5.1. НАКОПЛЕНИЕ ВЫЧИСЛИТЕЛЬНОЙ ПОГРЕШНОСТИ В АЛГОРИТМЕ ХОЛЕЦКОГО

Была проведена серия экспериментов для исследования накопления погрешности при вычислении разложения Холецкого [20].

Как известно, для всех прямых методов погрешность вычислений растет с увеличением размера матрицы и, соответственно, общего количества операций. Для экспериментов брались треугольные матрицы L, с целочисленными коэффициентами в промежутке [1, 9] и умножались на транспонированные матрицы ${{L}^{T}}$. Затем матрица $A = L \cdot {{L}^{T}}$ раскладывалась на множители. Полученную новую матрицу $L'$ вычитали из исходной матрицы и получали матрицу ошибок: $S = L{\text{'}} - L$. Самый большой по абсолютной величине элемент матрицы S – это погрешность вычислений в данном эксперименте.

Мы использовали числа с плавающей запятой двойной точности (стандарт IEEE 754) в первой серии экспериментов и формат BigDecimal с точностью 100 и 500 десятичных знаков во второй и третьей сериях экспериментов.

Отметим, что пакет арифметических операций для чисел типа BigDecimal дает возможность пользователю задавать желаемое количество верных десятичных знаков в дробной части числа, а последний знак округлять.

Для каждого размера матрицы мы провели серию из 100 экспериментов со случайными матрицами. Средняя ошибка и наибольшая (максимальная) ошибка в этих 100 экспериментах представлены в следующей таблице 1.

Таблица 1.

Погрешность вычислений алгоритма Холецкого для матриц размером 4, 8, 16, 32, 64

size	4	8	16	32	64
м$_{D}$	2 × 10^–13	1 × 10^–10	3 × 10^–6	0.6	142
ср$_{D}$	6 × 10^–15	4 × 10^–12	6 × 10^–8	0.01	7.9
м₁₀₀	–96	–93.22	–89.3	–79.9	–72.1
ср₁₀₀	–97	–95	–91	–81	–73.9
м₅₀₀	–497	–491	–489	–482	–470
ср₅₀₀	–498	–493	–491	–484	–472

Первые две строки (м$_{D}$ и ср$_{D}$) показывают погрешность при использовании чисел с плавающей запятой двойной точности. Для матрицы размера 64 средняя погрешность равна 7.9, а максимальная погрешность равна 142. Это при том, что искомые точные значения элементов матрицы не превосходят 9.

Для сравнения показана погрешность, которая накапливается при использовании формата BigDecimal с точностью 100 и 500 десятичных цифр. Десятичный логарифм от максимальной погрешности приведен в строках м₁₀₀ и м₅₀₀, а десятичный логарифм от средней погрешности приведен в строках ср₁₀₀ и ср₅₀₀.

Для матрицы размера 64 десятичный логарифм максимальной погрешности равен –72 и ‒470 при точности вычислений, соответственно, 100 и 500 десятичных знаков.

Эксперименты показали, что использование чисел с плавающей запятой двойной точности для матриц размера 64 и более не имеет смысла из-за накопления большой вычислительной погрешности. Для матриц, размер которых больше 64, должен использоваться формат BigDecimal.

Подробное описание всех деталей проведенных экспериментов позволяет легко повторить и проверить эти эксперименты.

5.2. ЗАВИСИМОСТЬ РАЗМЕРА МАШИННОГО СЛОВА ОТ РАЗМЕРА МАТРИЦЫ. СЛОЖНОСТЬ

Предполагая, что погрешность вычислений не должна быть больше 1, так как искомые значения – это числа в промежутке [1, 9], была проведена серия экспериментов для матриц размером 128, 256, 512, 1024. Подбор минимального необходимого количества десятичных знаков для хранения чисел показал, что увеличение числа знаков меняеться линейно с ростом размера матрицы.

Для матрицы размером 2048 требуется 700 десятичных цифр, для матриц размером 1024, 512, 256 и 128 требуется соответственно 350, 180, 90 и 50 десятичных цифр.

Таким образом, общая вычислительная сложность для плотных матриц и для стандартных алгоритмов умножения растет как пятая степень размера матрицы: сложность матричного алгоритма растет как куб, а сложность умножения двух чисел растет как квадрат.

Если применять известные быстрые алгоритмы для умножения матриц $(O({{n}^{\omega }}))$ и чисел $({{n}^{{(O(1)}}})$, то общая сложность расчетов может быть уменьшена. Например, для алгоритма В. Штрассена умножения матриц и алгоритма А. Карацубы умножения чисел [4, 21], получим алгоритм со сложностью $ \sim {\kern 1pt} {{n}^{{({{{\log }}_{2}}7 + {{{\log }}_{2}}3)}}}$.

5.3.ОСНОВНАЯ СЕРИЯ ЭКСПЕРИМЕНТОВ. МАСШТАБИРУЕМОСТЬ

5.3.1. Коэффициент потерь TLR

Для числовой характеристики масштабируемости полученных решений будем пользоваться коэффициентом потерь при передаче TLR (transmission loss ratio).

Будем проводить серии экспериментов с матрицами размеры которых увеличиваются вдвое. Тогда количество машинных операций будет увеличиваться в восемь раз. Соответственно в восемь раз будем увеличивать количество ядер. Если бы не было потерь времени на передачу данных и не было бы потерь на неравномерной загрузке оборудования, то в таком идеальном случае время вычислений сохранялось бы постянным k = $T2{\text{/}}T1$ = 1.

С другой стороны, если число операций возрастает вдвое и число ядер возрастает вдвое, а при этом время вычислений не сохраняется, а увеличивается вдвое, то это означает, что масштабирования нет.

Коэффициентом потерь TLR называется коэффициент увеличения времени вычислений $k = {{T}_{2}}{\text{/}}{{T}_{1}}$. Где T₂ – это время вычислений, которое требуется при увеличении размера задачи, когда число операций возрастает в два раза и при этом число ядер увеличивается в 2 раза.

Этот коэффициент должен находиться в интервале $1 < k < 2$, а его близость к 1 характеризует качество масштабируемости.

Во всех экспериментах, которые представлены в табл. 2–6 , дается время вычисления в минутах и находится соответствующий коэффициент TLR.

Таблица 2.

Масштабируемость алгоритма Холецкого для чисел типа BigDecimal со 100 десятичными знаками

#cores	1		8		64		512
size	256		512		1024		2048
LS		TLR		TLR		TLR
64	1.22	1.14	1.80	2.4	24.84	1.05	28.92
128	1.21	1.44	3.64	1.35	8.96	1.31	19.96
256	1.15	1.96	8.71	1.21	15.5	1.16	23.96

Таблица 3.

Масштабируемость алгоритма Холецкого для разреженных матриц плотности 3, 30 и 100% с числами имеющими двойную точность

#cores	4		32		256
matrix size	512		1024		2048
LS	32		64		128
density		TLR		TLR
3%	0.01	1.82	0.06	1.65	0.27
30%	0.019	1.65	0.085	1.21	0.15
100%	0.018	1.58	0.071	1.22	0.13

Таблица 4.

Масштабируемость алгоритма матричного умножения для разреженных матриц плотности 3, 30 и 100% для чисел типа BigDecimal со 100 десятичными знаками

#cores	4		32		256
matrix size	512		1024		2048
LS	32		64		128
density		TLR		TLR
3%	0.019	1.85	0.12	1.7	0.59
30%	0.26	1.31	0.59	1.56	2.26
100%	2.78	1.20	4.8	1.51	16.5

Таблица 5.

Масштабируемость алгоритма матричного умножения для разреженных матриц плотности 3, 30 и 100% с числами двойной точности (64 бита)

#cores	4		32		256
matrix size	512		1024		2048
LS	32		64		128
density		TLR		TLR
3%	0.017	1.86	0.11	1.7	0.54
30%	0.1	1.59	0.4	1.52	1.41
100%	0.73	1.3	1.6	1.4	4.36

Таблица 6.

Масштабируемость алгоритма обращения треугольных матриц для разреженных матриц плотности 3, 30 и 100% с числами двойной точности

#cores	4		32		256
matrix size	512		1024		2048
LS	32		64		128
density		TLR		TLR
3%	0.006	1.71	0.03	1.54	0.11
30%	0.012	1.74	0.063	1.23	0.188
100%	0.016	1.6	0.065	1.48	0.21

5.3.2. Алгоритм разложения Холецкого

В табл. 2 представлены результаты трех серий экспериментов, которые проводились на кластере. В каждой серии размер листового блока (LS), то есть такого блока, который вычислялся на одном процессоре, был постоянным. При этом в первой серии экспериментов он был равен 64, во второй – 128, а в третьей – 256.

В каждой серии экспериментов сохранялась постоянная вычислительная нагрузка на одно вычислительное ядро: при увеличении размера матрицы в 2 раза количество ядер увеличивалось в 8 раз. Поэтому количество ядер равно 1, 8, 64 и 512, а размер матрицы равен 256, 512, 1024 и 2048. Использовались числа типа BigDecimal со 100 десятичными знаками в дробной части.

Что показали эти эксперименты? Во-первых, они показали, что для данного кластера лучший размер листового блока равен 128.

Как видно по второй строчке таблицы 2, с увеличением количества ядер в 8 раз, время вычисления увеличивается в $364{\text{/}}121 = 3.0$, $896{\text{/}}364 = 2.4$ и $1996{\text{/}}896 = 2.2$ раза, соответственно. Следовательно, соответствующие значения коэффициента потерь TLR, будут равны $[\sqrt[3]{{3.0}},\sqrt[3]{{2.4}},\sqrt[3]{{2.2}}]$ = = [1.44, 1.35, 1.31].

Это говорит о хорошей масштабируемости данного программного решения.

Другая серия экспериментов (см. табл. 3), проводилась для разреженных матриц и для чисел с двойной точностью.

5.3.3. Матричное умножение

Эксперименты, продемонстрированные в табл. 4 и 5 , были проведены для алгоритма матричного умножения для умножения разреженных матриц. При этом в таблице 4 представлены результаты, полученные при использовании чисел типа BigDecimal с 100 десятичными цифрами, а в табл. 5 – при использовании чисел с двойной точностью.

5.3.4. Обращение треугольной матрицы

Эксперименты, продемонстрированные в табл. 6 были проведены для алгоритма обращения треугольной матрицы. Применялись разреженные матрицы с числами двойной точности и с разной степенью разрежения.

Можно увидеть, что для плотности 3%, коэффициент TLR хуже, чем для плотности 100%. Это связано с тем, что при малой плотности не требует так много процессоров, так как общий объем данных становится меньше в 30 раз и процессоры оказываются не догружены.

6. ЗАКЛЮЧЕНИЕ

Приведено описание среды выполнения DAP, основанной на динамической схеме управления параллельными вычислениями на распределенной памяти и предназначенной для блочно-рекурсивных матричных алгоритмов. Приведены основные объекты, их поля и функции. Описана работа двухпоточной системы. Cреда выполнения может использоваться для любых блочно-рекурсивных алгоритмов, данные могут быть как плотными, так и разряженными.

Новая среда выполнения называется DAP (drop-amine-pine). Она отличается тем, что последовательно разворачивает функции в глубину, сохраняя все состояния на любом уровне вложенности до тех пор, пока все расчеты в текущем вычислительном поддереве не будут завершены. Это позволяет любому процессору свободно переключаться с одной подзадачи на другую, не дожидаясь завершения текущей подзадачи.

Отметим важную особенность этой среды выполнения – защиту в случае выхода из строя узла во время вычислительного процесса. Родительский узел, который отправил дроп дочернему узлу должен получить результат. Однако, он может получить не результат, а сообщение об отказе дочернего узла. В этом случае дроп-задание перенаправляется на другой узел. Никаких дополнительных изменений на других узлах не требуется выполнять. Будет потеряно и заново вычислено только одно поддерево, которое соответствовало данному дропу.

Среда выполнения реализована на языке программирования Java с использованием OpenMPI. Эксперименты были проведены на алгоритме матричного умножения, матричной инверсии и алгоритме разложения Холецкого. Эксперименты продемонстрировали хорошую масштабируемость. Максимальное число ядер, которые использовались в экспериментах на кластере MVS-10P равно 512.

Список литературы

Dongarra J. With Extrim Scale Computing the Rules Have Changed. Mathematical Software. ICMS 2016, 5th International Congress, Proceedings / G.-M. Greuel, T. Koch, P. Paule, A. Sommese. Eds. Springer, LNCS, 2016. V. 9725. P. 3–8.
HDFS. Hadoop distributed file system. http://hadoop.apache.org/.
Malaschonok G.I., Ilchenko E.A. Recursive Matrix Algorithms in Commutative Domain for Cluster with Distributed Memory. 2018 Ivannikov Memorial Workshop (IVMEM), Yerevan, Armenia, 3–4 May 2018. Publisher: IEEE, 2019. P. 40–47. arXiv:1903.04394
Strassen V. Gaussian Elimination is not optimal Numerische Mathematik. 1969. V. 13. P. 354–356.
OpenMP 4.0 Complete Specifications, 2013, http://www.openmp.org/wp-content/uploads/OpenMP4.0.0.pdf
Agullo E., Aumage O., Faverge M., Furmento N., Pruvost F., Sergent M., Thibault S. Harnessing Supercomputers with a Sequential Task-based Runtime System. 2014. V. 13. № 9. P. 1–14.
Bauer M., Treichler S., Slaughter E., Aiken A. Legion: Expressing locality and independence with logical regions // International Conference for High Performance Computing, Networking, Storage and Analysis, SC., 2012. https://doi.org/10.1109/SC.2012.71
Bueno J., Planas J., Duran A., Badia R.M., Martorell X., Ayguade E., Labarta J. Productive programming of GPUclusters with OmpSs // Proceedings of the 2012 IEEE 26th International Parallel andDistributed Processing Symposium, IPDPS 2012. P. 557–568. https://doi.org/10.1109/IPDPS.2012.58
Dokulil J., Sandrieser M., Benkner S. Implementing the Open Community Runtime for Shared-Memory and Distributed-Memory Systems // Proceedings 24th Euromicro International Conference on Parallel, Distributed, and Network-Based Processing. PDP 2016. P. 364–368. https://doi.org/10.1109/PDP.2016.81
Malashonok G.I., Avetisyan A.I., Valeev Yu.D., Zuev M.S. Parallel algorithms of computer algebra // Proceedings of the Institute for System Programming, Ed. V.P. Ivannikov. M.: ISP RAS, 2004. P. 169–180.
Yarkhan A. Dynamic Task Execution on Shared and Distributed Memory Architectures. 2012. http://trace.tennessee.edu/utk
Bosilca G., Bouteiller A., Danalis A., Faverge M., Haidar A., Herault T., Kurzak J., Langou J., Lemarinier P., Ltaief H., et al. Flexible Development of Dense Linear Algebra Algorithms on Massively Parallel Architectures with DPLASMA // IEEE International Symposium on Parallel and Distributed Processing Workshops and Phd Forum. 2011. https://doi.org/10.1109/ipdps.2011.299
Bosilca G., Bouteiller A., Danalis A., Faverge M., Herault T., Dongarra J. PaRSEC: A programming paradigm exploiting heterogeneity for enhancing scalability // Computing in Science and Engineering 99. 2013. P. 1. https://doi.org/10.1109/MCSE.2013.98
Hoque R., Herault T., Bosilca G., Dongarra J. Dynamic Task Discovery in PaRSEC-A data-flow task-based Runtime. Proc. ScalA17 // Proceedings of the 8th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems, November 12–17, 2017. Denver, CO, USA.
Gupta S.K.S., Huang C.-H., Sadayappan P., Johnson R.W. A framework for generating distributed-memory parallel programs for block recursive algorithms // J. Parallel and Distributed Computing. 1996. V. 34. P. 137–153.
Fan M.-H., Huang C.-H., Chung Y.-C. A programming methodology for designing block recursive algorithms on various computer networks. 2002. P. 607–614.https://doi.org/10.1109/ICPPW.2002.1039783
Shvachko Konstantin. Apache Hadoop // The Scalability Update. 2011. V. 36. № 3. P. 7–13. ISSN 1044-6397
Malashonok G.I., Valeev Y.D. The control of parallel computations in recursive symbolic-numerical algorithms // Proceedings PaVt’2008 (St.-Petersburg). Chelyabinsk: Publishing house, 2008. P. 153–165. ISBN 978-5-696-03720-2. http://omega.sp.susu.ru/books/conference/PaVT2008/ papers/full_papers/016.pdf
Malaschonok G., Sidko A. Distributed computing: DAP-technology for parallelizing recursive algorithms. Scientific notes of NaUKMA // Computer Science. 2018. V. 1. P. 25–32.
Gustavson F.G., Karlsson L., Kagstrom B. Three Algorithms for Cholesky Factorization on Distributed Memory Using Packed Storage / In: Kagstrom B., Elmroth E., Dongarra J., Wasniewski J. Eds. Applied Parallel Computing. State of the Art in Scientific Computing. PARA 2006. Lecture Notes in Computer Science, 2007. V. 4699. Springer, Berlin, Heidelberg.
Schonhage A., Strassen V. Schnelle Multiplikation grosser Zahlen Computing. 1971. V. 7. P. 281–292.
Heller T., Kaiser H., Iglberger K. Application of the ParalleX execution model to stencil-based problems // Computer Science – Research and Development 28. 2013. V. 2–3. P. 253–261.
Tillenius M. SuperGlue: A Shared Memory Framework Using Data Versioning for Dependency-Aware Task-Based Parallelization // SIAM Journal on Scientific Computing. 2015. V. 37. № 6. P. 617–C642. https://doi.org/10.1137/140989716

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал