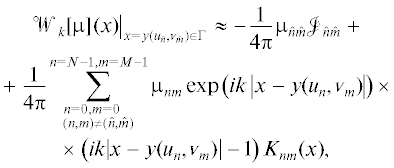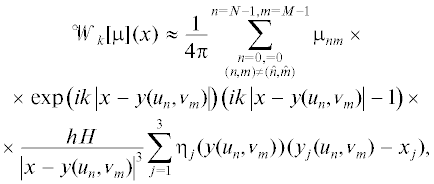Программирование, 2022, № 3, стр. 92-100

КВАДРАТУРНАЯ ФОРМУЛА ДЛЯ ПРЯМОГО ЗНАЧЕНИЯ ПОТЕНЦИАЛА ДВОЙНОГО СЛОЯ

О. И. Резниченко^a, *, П. А. Крутицкий^b, **

^a Московский государственный университет им. М.В. Ломоносова
119991 Москва, ГСП-1, Ленинские горы, д. 1-52, Россия

^b Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

^* E-mail: liorb@mail.ru
^** E-mail: biem@mail.ru

Поступила в редакцию 14.12.2021
После доработки 11.01.2022
Принята к публикации 16.01.2022

EDN: AEMAIL
DOI: 10.31857/S0132347422030098

Полный текст (PDF)

Аннотация

В работе выводится квадратурная формула для прямого значения потенциала двойного слоя с непрерывной плотностью, заданной на замкнутой либо разомкнутой поверхности. Рассматриваются потенциалы двойного слоя для уравнений Лапласа и Гельмгольца. Выведенная квадратурная формула может использоваться при численном решении краевых задач для уравнений Лапласа и Гельмгольца методом потенциалов и граничных интегральных уравнений. Предложенная квадратурная формула дает значительно более высокую точность, чем стандартная квадратурная формула, что подтверждается численными тестами, выполненными в системе компьютерных вычислений Matlab. Трудоемкие аналитические выкладки в работе выполнены с использованием системы компьютерной алгебры Symbolic Math Toolbox на базе Matlab.

ВВЕДЕНИЕ

Потенциал двойного слоя используется при численном решении краевых задач для уравнений Лапласа и Гельмгольца методом интегральных уравнений в [1–3]. С помощью потенциалов краевые задачи сводятся к интегральным уравнениям. Для численного решения интегральных уравнений нужно иметь квадратурные формулы, которые с достаточной точностью вычисляют прямые значения потенциалов на поверхности, где задана плотность потенциала. В инженерных расчетах используются стандартные квадратурные формулы для потенциалов [4], но их точность оставляет желать лучшего.

В двумерном случае улучшенная квадратурная формула для потенциала простого слоя с плотностью, заданной на разомкнутых кривых и имеющей степенные особенности на концах кривых, построена в [5, 6]. Эта формула может применяться при нахождении численных решений краевых задач для уравнений Лапласа и Гельмгольца вне разрезов и разомкнутых кривых на плоскости. Такие задачи изучались в [7–12].

В трехмерном случае улучшенная квадратурная формула для потенциала простого слоя предложена в [13], для потенциала двойного слоя в [14], а для прямого значения нормальной производной потенциала простого слоя в [15]. В настоящей работе выводится улучшенная квадратурная формула для прямого значения потенциала двойного слоя. Улучшенная формула дает значительно более высокую точность чем стандартная, что подтверждается численными тестами.

В процессе получения улучшенной квадратурной формулы одну из главных трудностей составляет вычисление так называемого канонического интеграла. Для численных тестов, а также для упрощения выкладок использовался программный пакет компьютерных вычислений Matlab [16], поскольку он содержит эффективные алгоритмы выполнения численных расчетов и систему компьютерной алгебры в виде расширения Symbolic Math Toolbox [17], которая позволяет выполнять аналитические преобразования и проверку результатов.

1. ПОСТАНОВКА ЗАДАЧИ

Введем в пространстве декартову систему координат $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}}) \in {{R}^{3}}$. Пусть $\Gamma $ – простая гладкая замкнутая либо ограниченная разомкнутая поверхность класса C², содержащая свои предельные точки. Если поверхность $\Gamma $ замкнутая, то она должна ограничивать объемно-односвязную внутреннюю область. Предположим, что поверхность $\Gamma $ параметризована так, что на нее отображается прямоугольник:

$\begin{gathered} y = ({{y}_{1}},{{y}_{2}},{{y}_{3}}) \in \Gamma ,\quad {{y}_{1}} = {{y}_{1}}(u,{v}),\quad {{y}_{2}} = {{y}_{2}}(u,{v}), \\ {{y}_{3}} = {{y}_{3}}(u,{v});\quad u \in [0,A],\quad {v} \in [0,B]; \\ \end{gathered} $

(1)

${{y}_{j}}(u,{v}) \in {{C}^{2}}\left( {[0,A] \times [0,B]} \right),\quad j = 1,\;2,\;3.$

Сфера, поверхность эллипсоида, гладкие поверхности фигур вращения, поверхность тора и многие другие более сложные поверхности можно параметризовать таким образом. Введем N точек ${{u}_{n}}$ с шагом h на отрезке $[0,A]$ и B точек ${{{v}}_{m}}$ на отрезке [0, B] и рассмотрим разбиение прямоугольника $[0,A] \times [0,B]$, который отображается на поверхность $\Gamma $

$\begin{gathered} A = Nh,\quad B = MH,\quad {{u}_{n}} = (n + 1{\text{/}}2)h, \\ n = 0,\; \ldots ,\;N - 1; \\ {{{v}}_{m}} = (m + 1{\text{/}}2)H,\quad m = 0,\; \ldots ,\;M - 1. \\ \end{gathered} $

Тем самым прямоугольник $[0,A] \times [0,B]$ разбивается на $N \times M$ маленьких прямоугольничков и через $({{u}_{n}},{{{v}}_{m}})$ обозначены серединки этих прямоугольничков.

Известно [18, Гл. 14, §1], что компоненты вектора нормали (не единичного) η(y) = (η₁(y), ${{\eta }_{2}}(y),{{\eta }_{3}}(y))$ в точке поверхности $y = ({{y}_{1}},{{y}_{2}},{{y}_{3}}) \in \Gamma $ выражаются через определители второго порядка формулами

(2)

$\begin{gathered} {{\eta }_{1}} = \left| {\begin{array}{*{20}{c}} {{{{({{y}_{2}})}}_{u}}}&{{{{({{y}_{3}})}}_{u}}} \\ {{{{({{y}_{2}})}}_{{v}}}}&{{{{({{y}_{3}})}}_{{v}}}} \end{array}} \right|,\quad {{\eta }_{2}} = \left| {\begin{array}{*{20}{c}} {{{{({{y}_{3}})}}_{u}}}&{{{{({{y}_{1}})}}_{u}}} \\ {{{{({{y}_{3}})}}_{{v}}}}&{{{{({{y}_{1}})}}_{{v}}}} \end{array}} \right|, \\ {{\eta }_{3}} = \left| {\begin{array}{*{20}{c}} {{{{({{y}_{1}})}}_{u}}}&{{{{({{y}_{2}})}}_{u}}} \\ {{{{({{y}_{1}})}}_{{v}}}}&{{{{({{y}_{2}})}}_{{v}}}} \end{array}} \right|. \\ \end{gathered} $

Положим |η(y)| = $\sqrt {{{{({{\eta }_{1}}(y))}}^{2}}\, + \,{{{({{\eta }_{2}}(y))}}^{2}}\, + \,{{{({{\eta }_{3}}(y))}}^{2}}} $. Кроме того, известно [18, Гл. 14], что

Таблица 1.

Максимальная абсолютная погрешность квадратурных формул в тестах 1–5

Номер теста	Квадратурная формула	M = N/2 = 25	M = N/2 = 50	M = N/2 = 100
1	стандартная	0.019	0.0097	0.0062
1	улучшенная	0.012	0.0063	0.0032
2	стандартная	0.019	0.0097	0.0049
2	улучшенная	0.00050	0.00014	3.8E-5
3	стандартная	0.011	0.0089	0.0062
3	улучшенная	0.011	0.0060	0.0031
4	стандартная	0.019	0.0097	0.0062
4	улучшенная	0.012	0.0063	0.0032
5	стандартная	0.011	0.0089	0.0062
5	улучшенная	0.012	0.0063	0.0032

$\int\limits_\Gamma F (y)d{{s}_{y}} = \int\limits_0^A {du} \int\limits_0^B {d{v}} F(y(u,{v}))\left| {\eta (y(u,{v}))} \right|.$

Потребуем, чтобы

(3)

$\left| {\eta (y(u,{v}))} \right| > 0,\quad \forall \;(u,{v}) \in ((0,A) \times (0,B)).$

Из условия (3) следует, что $\left| {\eta (y(u,{v}))} \right| \in {{C}^{1}}((0,A)$ × × (0, B)). Обозначим через n_y единичную нормаль в точке $y \in \Gamma $, т.е. ${{n}_{y}} = \eta (y){\text{/}}\left| {\eta (y)} \right|$. Производная по нормали n_y имеет вид

$\frac{\partial }{{\partial {{n}_{y}}}} = {{\left| {\eta (y)} \right|}^{{ - 1}}}\left( {\eta (y),{{\nabla }_{y}}} \right).$

Обозначим $\left| {x - y(u,{v})} \right|$ = = $\sqrt {{{{({{x}_{1}} - {{y}_{1}}(u,{v}))}}^{2}}\, + \,{{{({{x}_{2}} - {{y}_{2}}(u,{v}))}}^{2}}\, + \,{{{({{x}_{3}} - {{y}_{3}}(u,{v}))}}^{2}}} $ и заметим, что

$\frac{\partial }{{\partial {{n}_{y}}}}\left| {x - y} \right| = \frac{1}{{\left| {\eta (y)} \right|}}\sum\limits_{j = 1}^3 {{{\eta }_{j}}} (y)\frac{{{{y}_{j}} - {{x}_{j}}}}{{\left| {x - y} \right|}}.$

Потенциал двойного слоя для уравнения Гельмгольца используется при решении краевых задач методом интегральных уравнений. Пусть $\mu (y) \in {{C}^{0}}(\Gamma )$. Прямое значение потенциала двойного слоя в точке $x = y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}) \in \Gamma $ имеет вид

$\begin{gathered} {{\mathcal{W}}_{k}}[\mu ](x) = \frac{1}{{4\pi }}\int\limits_\Gamma \mu (y)\frac{\partial }{{\partial {{n}_{y}}}}\frac{{{{e}^{{ik|x - y|}}}}}{{\left| {x - y} \right|}}d{{s}_{y}} = \\ = \;\frac{1}{{4\pi }}\int\limits_\Gamma {\mu (y)} \frac{1}{{\left| {\eta (y)} \right|}}\frac{{\exp (ik\left| {x - y} \right|)(ik\left| {x - y} \right| - 1)}}{{{{{\left| {x - y} \right|}}^{2}}}} \times \\ \times \;\sum\limits_{j = 1}^3 {\frac{{{{\eta }_{j}}(y)({{y}_{j}} - {{x}_{j}})}}{{\left| {x - y} \right|}}} d{{s}_{y}} = \\ \end{gathered} $

(4)

$\begin{gathered} = \;\frac{1}{{4\pi }}\int\limits_0^A {du} \int\limits_0^B {d{v}} \mu (y(u,{v})) \times \\ \times \;\exp \left( {ik\left| {x - y(u,{v})} \right|} \right)\left( {ik\left| {x - y(u,{v})} \right| - 1} \right) \times \\ \times \;\sum\limits_{j = 1}^3 {\frac{{{{\eta }_{j}}(y(u,{v}))({{y}_{j}}(u,{v}) - {{x}_{j}})}}{{{{{\left| {x - y(u,{v})} \right|}}^{3}}}}} = \\ \end{gathered} $

$\begin{gathered} = \;\frac{1}{{4\pi }}\sum\limits_{n = 0}^{N - 1} {\sum\limits_{m = 0}^{M - 1} {\int\limits_{{{u}_{n}} - h/2}^{{{u}_{n}} + h/2} {du} } } \int\limits_{{{{v}}_{m}} - H/2}^{{{{v}}_{m}} + H/2} {d{v}} \mu (y(u,{v})) \times \\ \times \;\exp \left( {ik\left| {x - y(u,{v})} \right|} \right)\left( {ik\left| {x - y(u,{v})} \right| - 1} \right) \times \\ \times \;\sum\limits_{j = 1}^3 {\frac{{{{\eta }_{j}}(y(u,{v}))({{y}_{j}}(u,{v}) - {{x}_{j}})}}{{{{{\left| {x - y(u,{v})} \right|}}^{3}}}}} , \\ \end{gathered} $

где $k \geqslant 0$. Известно [19, §27.5], что прямое значение потенциала двойного слоя в наших предположениях является непрерывной на Γ функцией. Пусть ${{\mu }_{{nm}}} = \mu (y({{u}_{n}},{{{v}}_{m}}))$, тогда

$\mu (y(u,{v})) = {{\mu }_{{nm}}} + o(1),$

для $u \in [{{u}_{n}} - h{\text{/}}2,\;{{u}_{n}} + h{\text{/}}2]$ и ${v} \in [{{{v}}_{m}} - H{\text{/}}2,{{{v}}_{m}}$ + + H/2]. Так же как и в [13] можно показать, что при $u \in \left[ {{{u}_{n}} - h{\text{/}}2,\;{{u}_{n}} + h{\text{/}}2} \right]$ и ${v} \in \left[ {{{{v}}_{m}} - H{\text{/}}2,{{{v}}_{m}} + H{\text{/}}2} \right]$ выполняются оценки

$\begin{gathered} \left| {x - y(u,{v})} \right| = \left| {x - y({{u}_{n}},{{{v}}_{m}})} \right| + O(h + H), \\ \exp \left( {ik\left| {x - y(u,{v})} \right|} \right) = \\ = \;\exp \left( {ik\left| {x - y({{u}_{n}},{{{v}}_{m}})} \right|} \right) + O(h + H). \\ \end{gathered} $

Константы в оценках функций, обозначенных как $O(h + H)$, не зависят от n, m и от расположения x в узлах Γ. Следовательно,

(5)

$\begin{gathered} {{\left. {{{\mathcal{W}}_{k}}[\mu ](x)} \right|}_{{x = y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}) \in \Gamma }}} \approx \frac{1}{{4\pi }}\sum\limits_{n = 0}^{N - 1} {\sum\limits_{m = 0}^{M - 1} {{{\mu }_{{nm}}}} } \times \\ \times \;\exp \left( {ik\left| {x - y({{u}_{n}},{{{v}}_{m}})} \right|} \right)\left( {ik\left| {x - y({{u}_{n}},{{{v}}_{m}})} \right| - 1} \right) \times \\ \times \;\int\limits_{{{u}_{n}} - h/2}^{{{u}_{n}} + h/2} {du\int\limits_{{{{v}}_{m}} - H/2}^{{{{v}}_{m}} + H/2} {d{v}} } \sum\limits_{j = 1}^3 {\frac{{{{\eta }_{j}}(y(u,{v}))({{y}_{j}}(u,{v}) - {{x}_{j}})}}{{{{{\left| {x - y(u,{v})} \right|}}^{3}}}}} . \\ \end{gathered} $

Таким образом, чтобы получить квадратурную формулу для прямого значения потенциала двойного слоя при $x = y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}) \in \Gamma $, необходимо вычислить двойной интеграл в (5), который будем называть каноническим интегралом.

2. ВЫЧИСЛЕНИЕ КАНОНИЧЕСКОГО ИНТЕГРАЛА, КОГДА ТОЧКА $x$ ЛЕЖИТ В ОБЛАСТИ ИНТЕГРИРОВАНИЯ

В данном случае интегрирование ведется по прямоугольничку с центром в точке $({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$, которой отвечает точка $y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}) = x$ на поверхности Γ. Применяя формулу Тейлора с центром в точке $({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$, находим

$\begin{gathered} {{\left| {y(u,{v}) - x} \right|}^{2}} = {{\left| {y(u,{v}) - y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})} \right|}^{2}} \approx \\ \approx \;\sum\limits_{j = 1}^3 {{{{(({{y}_{j}})_{u}^{'}(u - {{u}_{{\hat {n}}}}) + ({{y}_{j}})_{{v}}^{'}({v} - {{{v}}_{{\hat {m}}}}))}}^{2}}} = \\ \end{gathered} $

$\begin{gathered} = \;\sum\limits_{j = 1}^3 {({{{(({{y}_{j}})_{u}^{'})}}^{2}}} {{(u - {{u}_{{\hat {n}}}})}^{2}} + \\ + \;{{(\left( {{{y}_{j}}} \right)_{{v}}^{'})}^{2}}{{({v} - {{{v}}_{{\hat {m}}}})}^{2}} + 2\left( {{{y}_{j}}} \right)_{u}^{'}\left( {{{y}_{j}}} \right)_{{v}}^{'}(u - {{u}_{{\hat {n}}}})({v} - {{{v}}_{{\hat {m}}}})) = \\ \end{gathered} $

$ = \;{{\alpha }^{2}}{{(u - {{u}_{{\hat {n}}}})}^{2}} + {{\beta }^{2}}{{({v} - {{{v}}_{{\hat {m}}}})}^{2}} + 2\delta (u - {{u}_{{\hat {n}}}})({v} - {{{v}}_{{\hat {m}}}}),$

$\begin{gathered} {{\alpha }^{2}} = \sum\limits_{j = 1}^3 {{{{(({{y}_{j}})_{u}^{'})}}^{2}}} , \\ {{\beta }^{2}} = \sum\limits_{j = 1}^3 {{{{(({{y}_{j}})_{{v}}^{'})}}^{2}}} ,\quad \delta = \sum\limits_{j = 1}^3 {({{y}_{j}})_{u}^{'}({{y}_{j}})_{{v}}^{'}} , \\ \end{gathered} $

где $({{y}_{j}})_{u}^{'}$ и $({{y}_{j}})_{{v}}^{'}$ берутся в точке $({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$. Заметим, что ${{\alpha }^{2}}{{\beta }^{2}} - {{\delta }^{2}} = {{\left| {\eta (x)} \right|}^{2}}$ согласно [18, Гл. 14, §1], поэтому ${{\alpha }^{2}} > 0$ и ${{\beta }^{2}} > 0$ в силу условия (3). Далее, используя формулу Тейлора в точке $({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$ с остаточным членом в форме Пеано [18, Гл. 10, §5.3], получаем

${{y}_{j}} - {{x}_{j}} = ({{y}_{j}})_{u}^{'}(u - {{u}_{{\hat {n}}}}) + ({{y}_{j}})_{{v}}^{'}({v} - {{{v}}_{{\hat {m}}}}) + $

$\begin{gathered} + \;\frac{1}{2}({{y}_{j}})_{{uu}}^{{''}}{{(u - {{u}_{{\hat {n}}}})}^{2}} + \frac{1}{2}({{y}_{j}})_{{{vv}}}^{{''}}{{({v} - {{{v}}_{{\hat {m}}}})}^{2}} + ({{y}_{j}})_{{uv}}^{{''}} \times \\ \times \;(u - {{u}_{{\hat {n}}}})({v} - {{{v}}_{{\hat {m}}}}) + o({{(u - {{u}_{{\hat {n}}}})}^{2}} + {{({v} - {{{v}}_{{\hat {m}}}})}^{2}}), \\ \end{gathered} $

$\begin{gathered} {{\eta }_{j}}(y(u,{v})) = {{\eta }_{j}}(y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})) + ({{\eta }_{j}})_{u}^{'}(u - {{u}_{{\hat {n}}}}) + \\ + \;({{\eta }_{j}})_{{v}}^{'}({v} - {{{v}}_{{\hat {m}}}}) + o(\sqrt {{{{(u - {{u}_{{\hat {n}}}})}}^{2}} + {{{({v} - {{{v}}_{{\hat {m}}}})}}^{2}}} ). \\ \end{gathered} $

Производные по u и ${v}$ берутся в точке $({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$. Легко проверить, что

$\begin{gathered} \sum\limits_{j = 1}^3 {{{\eta }_{j}}} (y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}))({{y}_{j}})_{u}^{'} = \\ = \sum\limits_{j = 1}^3 {{{\eta }_{j}}} (y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}))({{y}_{j}})_{{v}}^{'} = 0, \\ \end{gathered} $

следовательно

$\begin{gathered} \sum\limits_{j = 1}^3 {{{\eta }_{j}}} (y(u,{v}))({{y}_{j}} - {{x}_{j}}) \approx {{\xi }_{1}}{{(u - {{u}_{{\hat {n}}}})}^{2}} + \\ + \;{{\xi }_{2}}{{({v} - {{{v}}_{{\hat {m}}}})}^{2}} + {{\xi }_{3}}(u - {{u}_{{\hat {n}}}})({v} - {{{v}}_{{\hat {m}}}}), \\ \end{gathered} $

$\begin{gathered} {{\xi }_{1}} = \sum\limits_{j = 1}^3 {\left( {\frac{1}{2}{{\eta }_{j}}(y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}))({{y}_{j}})_{{uu}}^{{''}} + ({{\eta }_{j}})_{u}^{'}({{y}_{j}})_{u}^{'}} \right)} , \\ {{\xi }_{2}} = \sum\limits_{j = 1}^3 {\left( {\frac{1}{2}{{\eta }_{j}}(y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}))({{y}_{j}})_{{{vv}}}^{{''}} + ({{\eta }_{j}})_{{v}}^{'}({{y}_{j}})_{{v}}^{'}} \right)} , \\ \end{gathered} $

$\begin{gathered} {{\xi }_{3}} = \sum\limits_{j = 1}^3 {\left( {{{\eta }_{j}}(y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}))({{y}_{j}})_{{u{v}}}^{{''}}} \right.} + \\ + \,({{\eta }_{j}})_{u}^{'}({{y}_{j}})_{{v}}^{'} + \left. {({{\eta }_{j}})_{{v}}^{'}({{y}_{j}})_{u}^{'}} \right). \\ \end{gathered} $

Производные по $u$ и ${v}$ берутся в точке $({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$. Из приведенных соотношений вытекает, что в рассматриваемом случае канонический интеграл в (5) приближенно равен следующему интегралу, который обозначим через ${{\mathcal{J}}_{{\hat {n}\hat {m}}}}$

$\begin{gathered} \int\limits_{{{u}_{{\hat {n}}}} - h/2}^{{{u}_{{\hat {n}}}} + h/2} {du} \int\limits_{{{{v}}_{{\hat {m}}}} - H/2}^{{{{v}}_{{\hat {m}}}} + H/2} {d{v}} \frac{{\sum\limits_{j = 1}^3 {{\eta }_{j}}(y(u,{v}))({{y}_{j}} - {{x}_{j}})}}{{{{{\left| {x - y} \right|}}^{3}}}} \approx \\ = \;\int\limits_{ - h/2}^{h/2} {dU} \int\limits_{ - H/2}^{H/2} {dV\frac{{{{\xi }_{1}}{{U}^{2}} + {{\xi }_{2}}{{V}^{2}} + {{\xi }_{3}}UV}}{{{{{({{\alpha }^{2}}{{U}^{2}} + {{\beta }^{2}}{{V}^{2}} + 2\delta UV)}}^{{3/2}}}}}} = {{\mathcal{J}}_{{\hat {n}\hat {m}}}}, \\ \end{gathered} $

где $U = u - {{u}_{{\hat {n}}}}$, $V = {v} - {{{v}}_{{\hat {m}}}}$. Вычислим интеграл ${{\mathcal{J}}_{{\hat {n}\hat {m}}}}$ в явном виде. Перейдя к полярным координатам $\rho = \sqrt {{{U}^{2}} + {{V}^{2}}} $, $U = \rho \cos \phi $, $V = \rho \sin \phi $, мы преобразуем выражение под интегралом в сумму двух рациональных дробей. Применяя в получившися двух интегралах замены $t = {\text{tg}}\varphi $ и $t\, = \,{\text{ctg}}$ = φ соответственно, а затем сделав замену $z\, = \,t\, + \,\delta {\text{/}}{{\alpha }^{2}}$ мы приходим к табличным интегралам. В итоге получается явное выражение для ${{\mathcal{J}}_{{\hat {n}\hat {m}}}}$. Выкладки были выполнены в системе компьютерной алгебры Symbolic Math Toolbox [17] на базе пакета программ для компьютерных вычислений Matlab [16]. Подробно процесс вывода интеграла ${{\mathcal{J}}_{{\hat {n}\hat {m}}}}$ описан в работе [15]. Явное выражение для ${{\mathcal{J}}_{{\hat {n}\hat {m}}}}$ имеет вид

$\begin{gathered} {{\mathcal{J}}_{{\hat {n}\hat {m}}}} = \frac{h}{{{{\beta }^{3}}}}\left( { - \frac{{{{\xi }_{2}}z}}{{\sqrt {{{z}^{2}} + {{{(\alpha {\text{/}}\beta )}}^{2}} - {{{(\delta {\text{/}}{{\beta }^{2}})}}^{2}}} }}{{ + }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ + \;{{\xi }_{2}}\ln {\text{|}}z + \sqrt {{{z}^{2}} + {{{(\alpha {\text{/}}\beta )}}^{2}} - {{{(\delta {\text{/}}{{\beta }^{2}})}}^{2}}} {\text{|}} - \\ \end{gathered} $

$\begin{gathered} - \frac{{{{\xi }_{3}} - 2{{\xi }_{2}}\delta {\text{/}}{{\beta }^{2}}}}{{\sqrt {{{z}^{2}} + {{{(\alpha {\text{/}}\beta )}}^{2}} - {{{(\delta {\text{/}}{{\beta }^{2}})}}^{2}}} }} + \\ + \,z\left. {\left. {\frac{{{{\xi }_{2}}{{{(\delta {\text{/}}{{\beta }^{2}})}}^{2}} + {{\xi }_{1}} - {{\xi }_{3}}\delta {\text{/}}{{\beta }^{2}}}}{{({{{(\alpha {\text{/}}\beta )}}^{2}}\, - \,{{{(\delta {\text{/}}{{\beta }^{2}})}}^{2}})\sqrt {{{z}^{2}}\, + \,{{{(\alpha {\text{/}}\beta )}}^{2}}\, - \,{{{(\delta {\text{/}}{{\beta }^{2}})}}^{2}}} }}} \right)} \right|_{{ - H/h + \delta /{{\beta }^{2}}}}^{{H/h + \delta /{{\beta }^{2}}}}\, - \\ \end{gathered} $

$\begin{gathered} - \frac{H}{{{{\alpha }^{3}}}}\left( { - \frac{{{{\xi }_{1}}z}}{{\sqrt {{{z}^{2}} - {{{(\delta {\text{/}}{{\alpha }^{2}})}}^{2}} + {{{(\beta {\text{/}}\alpha )}}^{2}}} }}{{ + }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}} \right. \\ + \;{{\xi }_{1}}\ln {\text{|}}z + \sqrt {{{z}^{2}} - {{{({{{(\delta {\text{/}}{{\alpha }^{2}})}}^{2}} + {{{(\beta {\text{/}}\alpha )}}^{2}})}}^{2}}} {\text{|}} - \\ \end{gathered} $

$\begin{gathered} - \frac{{{{\xi }_{3}} - 2{{\xi }_{1}}\delta {\text{/}}{{\alpha }^{2}}}}{{\sqrt {{{z}^{2}} - {{{(\delta {\text{/}}{{\alpha }^{2}})}}^{2}} + {{{(\beta {\text{/}}\alpha )}}^{2}}} }} + \\ + \,z\left. {\left. {\frac{{{{\xi }_{1}}{{{(\delta {\text{/}}{{\alpha }^{2}})}}^{2}} + {{\xi }_{2}} - {{\xi }_{3}}\delta {\text{/}}{{\alpha }^{2}}}}{{( - {{{(\delta {\text{/}}{{\alpha }^{2}})}}^{2}}\, + \,{{{(\beta {\text{/}}\alpha )}}^{2}})\sqrt {{{z}^{2}}\, - \,{{{(\delta {\text{/}}{{\alpha }^{2}})}}^{2}}\, + \,{{{(\beta {\text{/}}\alpha )}}^{2}}} }}} \right)} \right|_{{h{\text{/}}H + \delta /{{\alpha }^{2}}}}^{{ - h{\text{/}}H + \delta /{{\alpha }^{2}}}}. \\ \end{gathered} $

3. ВЫЧИСЛЕНИЕ КАНОНИЧЕСКОГО ИНТЕГРАЛА, КОГДА ТОЧКА x НЕ ЛЕЖИТ В ОБЛАСТИ ИНТЕГРИРОВАНИЯ

Пусть точка x не принадлежит кусочку поверхности Γ, на котором изменяется точка $y = y(u,{v})$, когда $(u - {{u}_{n}}) \in \left[ { - h{\text{/}}2,h{\text{/}}2} \right]$ и $({v} - {{{v}}_{m}}) \in [ - H{\text{/}}2$, H/2]. Разложим ${{y}_{j}}(u,{v})$ по формуле Тейлора с центром в точке $({{u}_{n}},{{{v}}_{m}})$, тогда для $j = 1,\;2,\;3$ получим

${{y}_{j}}(u,{v}) = {{y}_{j}}({{u}_{n}},{{{v}}_{m}}) + {{D}_{j}} + O({{H}^{2}} + {{h}^{2}}),$

где

${{D}_{j}} = ({{y}_{j}})_{u}^{'}(u - {{u}_{n}}) + ({{y}_{j}})_{{v}}^{'}({v} - {{{v}}_{m}}).$

Здесь и далее все производные по $u$ и ${v}$ берутся в точке $({{u}_{n}},{{{v}}_{m}})$. Положим

$\begin{gathered} {{r}^{2}} = {{\left| {x - y({{u}_{n}},{{{v}}_{m}})} \right|}^{2}} = \sum\limits_{j = 1}^3 {r_{j}^{2}} \ne 0, \\ {{r}_{j}} = {{y}_{j}}({{u}_{n}},{{{v}}_{m}}) - {{x}_{j}},\quad j = 1,\;2,\;3, \\ \end{gathered} $

тогда

${{y}_{j}}(u,{v}) - {{x}_{j}} = {{r}_{j}} + {{D}_{j}} + O({{H}^{2}} + {{h}^{2}}),\quad j = 1,\;2,\;3.$

Следовательно,

$\begin{gathered} {{\left| {x - y(u,{v})} \right|}^{2}} = \sum\limits_{j = 1}^3 {{{{({{x}_{j}} - {{y}_{j}}(u,{v}))}}^{2}}} \approx \\ \approx \;\sum\limits_{j = 1}^3 {(r_{j}^{2} + 2{{r}_{j}}{{D}_{j}} + D_{j}^{2})} = \\ \end{gathered} $

$\begin{gathered} = {{r}^{2}} + 2P(u - {{u}_{n}}) + 2Q({v} - {{{v}}_{m}}) + {{\alpha }^{2}}{{(u - {{u}_{n}})}^{2}} + \\ + \,{{\beta }^{2}}{{({v} - {{{v}}_{m}})}^{2}} + 2\delta (u - {{u}_{n}})({v} - {{{v}}_{m}}) = \\ = {{\beta }^{2}}{{(V + \delta U{\text{/}}{{\beta }^{2}} + Q{\text{/}}{{\beta }^{2}})}^{2}} - {{(\delta U + Q)}^{2}}{\text{/}}{{\beta }^{2}} + \\ \, + {{\alpha }^{2}}{{U}^{2}} + 2PU + {{r}^{2}}, \\ \end{gathered} $

где $U = u - {{u}_{n}}$, $V = {v} - {{{v}}_{m}}$,

$\begin{gathered} P = \sum\limits_{j = 1}^3 {{{r}_{j}}({{y}_{j}})_{u}^{'}} ,\quad Q = \sum\limits_{j = 1}^3 {{{r}_{j}}({{y}_{j}})_{{v}}^{'}} ,\quad {{\alpha }^{2}} = \sum\limits_{j = 1}^3 {(({{y}_{j}})_{u}^{'}} {{)}^{2}}, \\ {{\beta }^{2}} = \sum\limits_{j = 1}^3 {(({{y}_{j}})_{{v}}^{'}} {{)}^{2}},\quad \delta = \sum\limits_{j = 1}^3 {({{y}_{j}})_{u}^{'}({{y}_{j}})_{{v}}^{'}} . \\ \end{gathered} $

Производные по $u$ и ${v}$ берутся в точке $u = {{u}_{n}}$, ${v} = {{{v}}_{m}}$. Используя результаты из §1 главы 14 в [18], можно показать, что ${{\alpha }^{2}}{{\beta }^{2}} - {{\delta }^{2}} = {{\left| {\eta (y({{u}_{n}},{{{v}}_{m}}))} \right|}^{2}}$. По условию (3), $\left| {\eta (y({{u}_{n}},{{{v}}_{m}}))} \right| > 0$ для всех возможных n, m, поэтому ${{\alpha }^{2}}{{\beta }^{2}} - {{\delta }^{2}} > 0$. Следовательно, ${{\alpha }^{2}} > 0$ и ${{\beta }^{2}} > 0$. Применяя формулу Тейлора в точке $({{u}_{n}},{{{v}}_{m}})$ с остаточным членом в форме Пеано, находим

$\begin{gathered} {{\eta }_{j}}(y(u,{v})) = {{\eta }_{j}}(y({{u}_{n}},{{{v}}_{m}})) + ({{\eta }_{j}})_{u}^{'}(u - {{u}_{n}}) + \\ \, + ({{\eta }_{j}})_{{v}}^{'}({v} - {{{v}}_{m}}) + o(\sqrt {{{{(u - {{u}_{m}})}}^{2}} + {{{({v} - {{{v}}_{m}})}}^{2}}} ). \\ \end{gathered} $

Производные по $u$ и ${v}$ берутся в точке $({{u}_{n}},{{{v}}_{m}})$. Для вычисления выражения

$\sum\limits_{j = 1}^3 {{{\eta }_{j}}(y(u,{v}))({{y}_{j}}(u,{v}) - {{x}_{j}})} $

с учетом формул

$\sum\limits_{j = 1}^3 {{{\eta }_{j}}(y({{u}_{n}},{{{v}}_{m}}))({{y}_{j}})_{u}^{'}} = \sum\limits_{j = 1}^3 {{{\eta }_{j}}(y({{u}_{n}},{{{v}}_{m}}))({{y}_{j}})_{{v}}^{'}} = 0,$

отражающих ортогональность вектора нормали и касательных векторов к поверхности (см. главу 14 в [18]), воспользуемся разложением по формуле Тейлора в точке $({{u}_{n}},{{{v}}_{m}})$ с остаточным членом в форме Пеано

$\begin{gathered} {{y}_{j}}(u,{v}) - {{x}_{j}} = {{r}_{j}} + ({{y}_{j}})_{u}^{'}(u - {{u}_{m}}) + ({{y}_{j}})_{{v}}^{'}({v} - {{{v}}_{m}}) + \\ + \frac{1}{2}({{y}_{j}})_{{uu}}^{{''}}{{(u - {{u}_{m}})}^{2}} + \frac{1}{2}({{y}_{j}})_{{{vv}}}^{{''}}{{({v} - {{{v}}_{m}})}^{2}} + \\ + \,({{y}_{j}})_{{u{v}}}^{{''}}(u - {{u}_{m}})({v} - {{{v}}_{m}}) + o({{(u - {{u}_{n}})}^{2}} + {{({v} - {{{v}}_{m}})}^{2}}), \\ \end{gathered} $

тогда

$\begin{gathered} \sum\limits_{j = 1}^3 {{{\eta }_{j}}(y(u,{v}))({{y}_{j}}(u,{v}) - {{x}_{j}}) \approx } \\ \approx R + {{\xi }_{4}}U + {{\xi }_{5}}V + {{\xi }_{1}}{{U}^{2}} + {{\xi }_{2}}{{U}^{2}} + {{\xi }_{2}}{{V}^{2}} + {{\xi }_{3}}UV, \\ \end{gathered} $

где $U = u - {{u}_{n}}$, $V = {v} - {{{v}}_{m}}$ и

$\begin{gathered} {{\xi }_{1}} = \sum\limits_{j = 1}^3 {\left( {\frac{1}{2}{{\eta }_{j}}(y({{u}_{n}},{{{v}}_{m}}))({{y}_{j}})_{{uu}}^{{''}} + ({{\eta }_{j}})_{u}^{'}({{y}_{j}})_{u}^{'}} \right)} , \\ {{\xi }_{2}} = \sum\limits_{j = 1}^3 {\left( {\frac{1}{2}{{\eta }_{j}}(y({{u}_{n}},{{{v}}_{m}}))({{y}_{j}})_{{{vv}}}^{{''}} + ({{\eta }_{j}})_{{v}}^{'}({{y}_{j}})_{{v}}^{'}} \right)} , \\ \end{gathered} $

${{\xi }_{3}} = \sum\limits_{j = 1}^3 {({{\eta }_{j}}(y({{u}_{n}},{{{v}}_{m}}))({{y}_{j}})_{{u{v}}}^{{''}} + ({{\eta }_{j}})_{u}^{'}({{y}_{j}})_{{v}}^{'} + ({{\eta }_{j}})_{{v}}^{'}({{y}_{j}})_{u}^{'}),} $

$\begin{gathered} {{\xi }_{4}} = \sum\limits_{j = 1}^3 {({{\eta }_{j}})_{u}^{'}{{r}_{j}},\quad {{\xi }_{5}} = \sum\limits_{j = 1}^3 {({{\eta }_{j}})_{{v}}^{'}{{r}_{j}},} } \\ R = \sum\limits_{j = 1}^3 {{{\eta }_{j}}(y({{u}_{n}},{{{v}}_{m}})){{r}_{j}}.} \\ \end{gathered} $

Все производные по u, ${v}$ берутся в точке $({{u}_{n}},{{{v}}_{m}})$. Из приведенных соотношений вытекает, что в рассматриваемом случае канонический интеграл из (5) приближенно равен следующему интегралу, который обозначим через ${{K}_{{nm}}}(x)$

(6)

$\begin{gathered} \int\limits_{{{u}_{n}} - h/2}^{{{u}_{n}} + h/2} {du\int\limits_{{{{v}}_{m}} - H/2}^{{{{v}}_{m}} + H/2} {d{v}\frac{1}{{{\text{|}}x - y(x,{v}){{{\text{|}}}^{3}}}}} } \sum\limits_{j = 1}^3 {{{\eta }_{j}}(y(u,{v}))({{y}_{j}}(u,{v}) - {{x}_{j}}) \approx } \\ \approx \int\limits_{ - h/2}^{h/2} {dU\int\limits_{ - H/2}^{H/2} {dV} } \frac{{R + {{\xi }_{4}}U + {{\xi }_{5}}V + {{\xi }_{1}}{{U}^{2}} + {{\xi }_{2}}{{V}^{2}} + {{\xi }_{3}}UV}}{{{{\beta }^{3}}{{{({{{(V + \delta U{\text{/}}{{\beta }^{2}} + Q{\text{/}}{{\beta }^{2}})}}^{2}} - {{{(\delta U + Q)}}^{2}}{\text{/}}{{\beta }^{4}} + ({{\alpha }^{2}}{{U}^{2}} + 2PU + {{r}^{2}}){\text{/}}{{\beta }^{2}})}}^{{3/2}}}}} = {{K}_{{nm}}}(x). \\ \end{gathered} $

Интеграл ${{K}_{{nm}}}(x)$ вычислен в явном виде в работе [14]. Выкладки были выполнены в системе компьютерной алгебры Symbolic Math Toolbox [17] на базе пакета программ для компьютерных вычислений Matlab [16].

4. ОСНОВНОЙ РЕЗУЛЬТАТ

Сформулируем основной результат этой работы в виде теоремы.

Теорема. Пусть $\Gamma $ – простая гладкая замкнутая поверхность класса C², ограничивающая объемно-односвязную внутреннюю область, либо простая гладкая ограниченная разомкнутая ориентированная поверхность класса C², содержащая свои предельные точки. Пусть $\Gamma $ допускает параметризацию (1) со свойством (3), и $\mu (y) \in {{C}^{0}}(\Gamma )$. Тогда для прямого значения потенциала двойного слоя (4) на $\Gamma $ при $x = y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}}) \in \Gamma $ и $k \geqslant 0$ имеет место квадратурная формула

(7)

где интеграл ${{\mathcal{J}}_{{\hat {n}\hat {m}}}}$ вычислен в явном виде в пункте 2, а интеграл ${{K}_{{nm}}}(x)$ из (6) вычислен в явном виде в работе [14].

Если k = 0, то потенциал двойного слоя для уравнения Гельмгольца переходит в потенциал двойного слоя для уравнения Лапласа, соответственно, квадратурная формула (7) при k = 0 принимает вид квадратурной формулы для прямого значения гармонического потенциала двойного слоя на поверхности $\Gamma $.

5. СТАНДАРТНАЯ КВАДРАТУРНАЯ ФОРМУЛА

Квадратурная формула (7) является альтернативой стандартной квадратурной формуле для прямого значения потенциала двойного слоя на поверхности $\Gamma $, используемой в инженерных расчетах [4, глава 2]. Стандартная квадратурная формула получается из формулы (5) заменой канонического интеграла при $x \ne y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$ на его приближенное значение

(8)

и обнулением канонического интеграла по кусочку поверхности $\Gamma $ с центром в точке $x = y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$. Обнуление канонического интеграла в данном случае можно обосновать следующим образом. Этот интеграл приближенно равен интегралу от той же функции по кусочку касательной плоскости, проведенной в точке x. Вектор нормали $\eta $ к поверхности в точке y можно приближенно заменить на вектор нормали в точке $x = y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$, а он является и вектором нормали к касательной плоскости. На касательной плоскости вектор $(y(u,{v}) - x)$ ортогонален вектору нормали в точке x, поэтому их скалярное произведение тождественно равно нулю для всех y, а значит, и интеграл по кусочку касательной плоскости равен нулю. Поскольку этот интеграл приближенно равен каноническому интегралу по кусочку поверхности $\Gamma $ с центром в точке $x = y({{u}_{{\hat {n}}}},{{{v}}_{{\hat {m}}}})$, то можно считать, что и последний интеграл приближенно равен нулю.

6. ЧИСЛЕННЫЕ ТЕСТЫ

Тестирование улучшенной (7) и стандартной (8) квадратурных формул проведено в случае, когда поверхность $\Gamma $ является сферой единичного радиуса, которая задана параметрически уравнениями:

(9)

$\begin{gathered} {{y}_{1}}(u,{v}) = \cos u\sin {v}, \\ {{y}_{2}}(u,{v}) = \sin u\sin {v},\quad {{y}_{3}}(u,{v}) = \cos {v}, \\ \end{gathered} $

причем $(u,{v}) \in \left[ {0,2\pi } \right] \times \left[ {0,\pi } \right]$. Отметим, что в данном случае $\left( {\eta (y(u,{v}))} \right]\, = \,{\text{sin}}{\kern 1pt} {\kern 1pt} {v}$ и $\left| {\eta (y(u,0))} \right|\, = \,\left| {\eta (y(u,\pi ))} \right|$ = 0 для всех $u \in \left[ {0,2\pi } \right]$. Иначе говоря, $\left| {\eta (y)} \right| = 0$ на полюсах сферы при такой параметризации, но условия теоремы выполняются.

Согласно [19, гл. 5, §27, п. 7], прямое значение потенциала двойного слоя на поверхности $\Gamma $ можно найти по формуле

${{\left. {{{\mathcal{W}}_{k}}[\mu ](x)} \right|}_{\Gamma }} = \frac{1}{2}\left[ {{{{\left. {{{\mathcal{W}}_{k}}[\mu ](x)} \right|}}_{{{{\Gamma }^{ + }}}}} + {{{\left. {{{\mathcal{W}}_{k}}[\mu ](x)} \right|}}_{{{{\Gamma }^{ - }}}}}} \right].$

Здесь поверхность $\Gamma $ рассматривается как двусторонняя, через ${{\Gamma }^{ - }}$ обозначена сторона, которую мы видим, глядя навстречу вектору нормали n_y, а через ${{\Gamma }^{ + }}$ обозначена противоположная сторона. В формуле берутся предельные значения потенциала двойного слоя на разных сторонах $\Gamma $. Отметим, что направление единичной нормали n_y совпадает с направлением нормали $\eta $, так как вектор n_y получается из $\eta $ в результате нормировки. Пусть теперь $\Gamma $ – единичная сфера, заданная параметризацией (9), тогда формулы (2) для нормали $\eta $ определяют внутреннюю нормаль на сфере, а значит, ${{\Gamma }^{ - }}$ – внутренняя сторона единичной сферы, а ${{\Gamma }^{ + }}$ – ее внешняя сторона.

В тестах точное прямое значение потенциала двойного слоя в узловых точках сравнивалось с приближенными значениями, вычисленными по квадратурным формулам – по улучшенной формуле (7) в соответствии с Теоремой и по стандартной формуле (8). В каждой узловой точке вычислялась абсолютная погрешность по обеим формулам. Вычисления проводились для разных значений M и N. Значения шагов определяются формулами $h = 2\pi {\text{/}}N$, $H = \pi {\text{/}}M$. Если $N{\text{/}}2$ = M = = 25, то $h = H \approx 0.13$; если $N{\text{/}}2 = M = 50$, то h = = $H \approx 0.063$; если $N{\text{/}}2 = M = 100$, то h = $H\, \approx \,0.031$. В таблице для каждого теста приводится максимум абсолютной погрешности вычислений по всем узловым точкам сферы. В первой строке таблицы указаны значения N, M, в последующих строках – максимальные погрешности для стандартной и улучшенной квадратурных формул в каждом тесте.

Для тестирования квадратурных формул в случае уравнений Лапласа и Гельмгольца были использованы различные плотности в потенциале. Для каждой заданной в текстах плотности известно аналитическое выражение потенциала двойного слоя и его прямого значения на единичной сфере. При этом через $\varphi $ и $\vartheta $ обозначаются азимутальный и зенитный углы в сферических координатах с началом в центре сферы. В случае уравнения Гельмгольца, значение k выбиралось равным единице.

Тест 1. Плотность потенциала $\mu (y(u,{v})) = 1$,

$\begin{gathered} {{\mathcal{W}}_{0}}[\mu ](x) = \left\{ \begin{gathered} 1\quad {\text{при}}\quad \left| x \right| < 1 \hfill \\ 0\quad {\text{при}}\;|x| > 1 \hfill \\ \end{gathered} \right., \\ {{\left. {{{\mathcal{W}}_{0}}[\mu ](x)} \right|}_{{|x| = 1}}} = \frac{1}{2}. \\ \end{gathered} $

Тест 2. Плотность потенциала $\mu (y(u,{v}))$ = cos u sin v,

$\begin{gathered} {{\mathcal{W}}_{0}}[\mu ](x) = \left\{ \begin{gathered} \frac{{2\left| x \right|\cos \varphi \sin \vartheta }}{3}\quad {\text{если}}\quad \left| x \right| < 1, \\ - \frac{{\cos \varphi \sin \vartheta }}{{3{{{\left| x \right|}}^{2}}}}\quad {\text{если}}\quad \left| x \right| > 1, \\ \end{gathered} \right. \\ {{\left. {{{\mathcal{W}}_{0}}[\mu ](x)} \right|}_{{|x| = 1}}} = \frac{{\cos \varphi \sin \vartheta }}{6}. \\ \end{gathered} $

Тест 3. Плотность потенциала μ(y(u, v)) = = $(3{\text{co}}{{{\text{s}}}^{2}}{v} - 1){\text{/}}2$,

$\begin{gathered} {{\mathcal{W}}_{0}}[\mu ](x) = \left\{ \begin{gathered} \frac{{3{{{\left| x \right|}}^{2}}(3{\text{co}}{{{\text{s}}}^{2}}\vartheta - 1)}}{{10}}\quad {\text{при}}\quad \left| x \right| < 1 \hfill \\ - \frac{{3{\text{co}}{{{\text{s}}}^{2}}\vartheta - 1}}{{5{{{\left| x \right|}}^{3}}}}\quad {\text{при}}\quad \left| x \right| > 1 \hfill \\ \end{gathered} \right., \\ {{\left. {{{\mathcal{W}}_{0}}[\mu ](x)} \right|}_{{|x| = 1}}} = \frac{{3{\text{co}}{{{\text{s}}}^{2}}\vartheta - 1}}{{20}}. \\ \end{gathered} $

Тест 4. Плотность потенциала $\mu (y(u,{v})) = k$,

$\begin{gathered} {{\mathcal{W}}_{k}}[\mu ](x) = \\ = \;\left\{ \begin{gathered} (1 - ik)\exp (ik)\frac{{\sin \left( {k\left| x \right|} \right)}}{{\left| x \right|}}\quad {\text{если}}\quad \left| x \right| < 1, \hfill \\ \left( {\sin k - k\cos k} \right)\frac{{\exp \left( {ik\left| x \right|} \right)}}{{\left| x \right|}}\quad {\text{если}}\quad \left| x \right| > 1, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

${{\left. {{{\mathcal{W}}_{k}}[\mu ](x)} \right|}_{{_{{|x| = 1}}}}} = \frac{1}{2}\left( {(2 - ik)\sin k - \cos k} \right)\exp (ik).$

Тест 5. Плотность потенциала μ(y(u, v)) = = ${{k}^{3}}{\text{cos}}{\kern 1pt} {\kern 1pt} {v}$,

$\begin{gathered} {{\mathcal{W}}_{k}}[\mu ](x) = \\ = \;\left\{ \begin{gathered} ({{k}^{2}} + 2(ik - 1))\exp (ik) \times \hfill \\ \times \;\frac{{k\left| x \right|\cos (k\left| x \right|) - \sin (k\left| x \right|)}}{{{{{\left| x \right|}}^{2}}}}{\text{cos}}\vartheta \quad {\text{если}}\quad \left| x \right|\, < \,1, \hfill \\ (2k\cos k + ({{k}^{2}} - 2)\sin k) \times \hfill \\ \times \;\frac{{\left( {ik\left| x \right| - 1} \right)\exp \left( {ik\left| x \right|} \right)}}{{{{{\left| x \right|}}^{2}}}}\cos \vartheta \quad {\text{если}}\quad \left| x \right| > 1, \hfill \\ \end{gathered} \right., \\ \end{gathered} $

$\begin{gathered} {{\left. {{{\mathcal{W}}_{k}}[\mu ](x)} \right|}_{{|x| = 1}}} = \frac{1}{2}(({{k}^{2}} + 4(ik - 1)) \times \\ \times \;(k\cos k - \sin k) + {{k}^{2}}\sin k(ik - 1))\exp (ik)\cos \vartheta . \\ \end{gathered} $

Результаты расчетов в приведенных тестовых примерах показывают, что улучшенная квадратурная формула имеет первый порядок сходимости, в то время как как стандартная формула сходится медленнее. Погрешность вычислений по улучшенной квадратурной формуле, предложенной в Теореме, меньше, чем погрешность вычислений по стандартной квадратурной формуле. Тем самым, улучшенная квадратурная формула обеспечивает более высокую точность вычислений прямого значения потенциала двойного слоя.

Отметим, что в тестовых примерах погрешность вычислений по улучшенной квадратурной формуле возрастает к полюсам сферам, которые являются особыми точками в силу выбранной параметризации (9). Вычисления по улучшенной квадратурной формуле в тесте 2 показывают более высокую точность, так как плотность в потенциале двойного слоя и его прямое значение обращаются в нуль на полюсах сферы.

Улучшенная квадратурная формула может найти применение при численном решении граничных интегральных уравнений, возникающих в процессе решения краевых задач для уравнений Лапласа и Гельмгольца методом потенциалов.

Список литературы

Белоцерковский С.М., Лифанов И.К. Численные методы в сингулярных интегральных уравнениях. М.: Наука, 1985.
Лифанов И.К. Метод сингулярных интегральных уравнений и численный эксперимент. М.: ТОО Янус, 1995.
Сетуха А.В. Численные методы в интегральных уравнениях и их приложения. М.: Аргамак-медиа, 2016.
Бреббия К., Теллес Ж., Броубел Л. Методы граничных элементов. М.: Мир, 1987.
Krutitskii P.A., Kwak D.Y., Hyon Y.K. Numerical treatment of a skew-derivative problem for the Laplace equation in the exterior of an open arc // Journal of Engineering Mathematics. 2007. V. 59. P. 25–60.
Крутицкий П.А., Колыбасова В.В. Численный метод решения интегральных уравнений в задаче с наклонной производной для уравнения Лапласа вне разомкнутых кривых // Дифференциальные уравнения. 2016. Т. 62. № 9. С. 1262–1276.
Крутицкий П.А. Смешанная задача для уравнения Лапласа вне разрезов на плоскости // Дифференциальные уравнения. 1997. Т. 33. № 9. С. 1181–1190.
Krutitskii P.A. The Dirichlet problem for the two-dimensional Laplace equation in a multiply connected domain with cuts // Proceedings of the Edinburgh Mathematical Society. 2000. V. 43. № 2. P. 325–341.
Krutitskii P.A. The Neumann problem for the 2-D Helmholtz equation in a multiply connected domain with cuts // Zeitschrift fur Analysis und ihre Anwendungen. 1997. V. 16. № 2. P. 349–361.
Krutitskii P.A. Mixed problem for the Helmholtz outside cuts in a plane // Differential Equations. 1996. V. 36. № 9. P. 1204–1212.
Krutitskii P.A. The Dirichlet problem for the 2-D Helmholtz equation in a multiply connected domain with cuts // ZAMM. 1997. V. 77. № 12. P. 883–890.
Krutitskii P.A. The Helmholtz equation in the exterior of slits in a plane with different impedance boundary conditions on opposite sides of the slits // Quarterly of Applied Mathematics. 2009. V. 67. № 1. P. 73–92.
Крутицкий П.А., Федотова А.Д., Колыбасова В.В. Квадратурная формула для потенциала простого слоя // Дифференциальные уравнения. 2019. Т. 55. № 9. С. 1269–1284.
Крутицкий П.А., Резниченко И.О. Квадратурная формула для гармонического потенциала двойного слоя // Дифференциальные уравнения. 2021. Т. 57. № 7. С. 932–950.
Крутицкий П.А., Резниченко И.О., Колыбасова В.В. Квадратурная формула для прямого значения нормальной производной потенциала простого слоя // Дифференциальные уравнения. 2020. Т. 56. № 9. С. 1270–1288.
Gdeisat M., Lilley F. Matlab by Example: Programming Basics. Elsevier, 2013.
Symbolic Math Toolbox User’s Guide. MathWorks, 2021.
Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. М.: Физматлит, 2000.
Владимиров В.С. Уравнения математической физики. М.: Физматлит, 1981.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал