Программирование, 2022, № 4, стр. 57-64

РАЗЛОЖЕНИЕ ЗАМКНУТОЙ КВАНТОВОЙ СИСТЕМЫ НА ПОДСИСТЕМЫ В КОНЕЧНОЙ КВАНТОВОЙ МЕХАНИКЕ

В. В. Корняк^a, *

^a Объединенный институт ядерных исследований
141980 Дубна, Московской области, Россия

Поступила в редакцию 17.06.2021
После доработки 29.08.2021
Принята к публикации 11.09.2021

EDN: KVSZRU
DOI: 10.31857/S0132347422020078

Аннотация

Любое гильбертово пространство с составной размерностью можно представить в виде тензорного произведения гильбертовых пространств меньших размерностей. Такая факторизация дает возможность разложить квантовую систему на подсистемы. Мы предлагаем модель, основанную на конечной квантовой механике, для конструктивного изучения разложений изолированной квантовой системы на подсистемы. Для исследования поведения составных систем, получаемых в результате разложений, мы разрабатываем алгоритмы, основанные на методах компьютерной алгебры и вычислительной теории групп.

ВВЕДЕНИЕ

Мереологией называют изучение отношений части к целому и отношений между частями внутри целого. В квантовой мереологии целое – это замкнутая квантовая система (“Вселенная”)¹ ¹ в заданном чистом состоянии, претерпевающая заданную унитарную (шредингеровскую) эволюцию.

Квантовая мереология изучает взаимосвязи между выделенными подсистемами Вселенной (“наблюдаемая система”, “наблюдатель”, “измерительный прибор”, “окружающая среда” и т.д.), возникновение геометрии и даже времени (механизм Пейджа–Вуттерса [1]) из квантовой запутанности и другие фундаментальные вопросы квантовой механики [2–4].

Разделение целого на части по своей сути произвольно – оно зависит от используемых критериев разделения. Имеется два различных аспекта разделимости квантовых систем.

1. Квантовые системы отделены друг от друга, если энергия взаимодействия между ними мала. Это более зримый, материальный критерий, хорошо согласующийся с обычной концепцией локальности. Количественно энергию взаимодействия между подсистемами $A$ и $B$ можно представить в виде

(1.1)

$\Delta E\left( {A,B} \right) = E\left( {A \cup B} \right) - E\left( A \right) - E\left( B \right).$

2. Подсистемы $A$ и $B$ разделены, если квантовые корреляции между ними малы. Этот более тонкий критерий, имеющий нелокальные проявления. Количественно квантовую запутанность между подсистемами можно описать, например, взаимной информацией

(1.2)

$\mathcal{I}\left( {A,B} \right) = S\left( A \right) + S\left( B \right) - S\left( {A \cup B} \right),$

где $S$ обозначает энтропию.

Между выражениями (1.1) и (1.2) имеется определенное структурное сходство. Однако они описывают совершенно разные типы связей между подсистемами.

Например, в модели эмерджентного времени Пейджа–Вуттерса предполагается, что вся вневременная Вселенная разделена на две подсистемы: “часы”, C, и остальную часть Вселенной, $R$. Гамильтониан Вселенной в этой модели имеет вид

$H = {{H}_{C}} \otimes {{1}_{R}} + {{1}_{C}} \otimes {{H}_{R}},$

что предполагает нулевую энергию взаимодействия между $C$ и $R$. С другой стороны, предполагается наличие нетривиальных квантовых корреляций между $C$ и $R$.

Было бы интересно внимательнее взглянуть на взаимосвязи между этими двумя различными – энергетическим и информационным – аспектами квантовой разделимости.

Мы разрабатываем и реализуем алгоритмы, основанные на методах компьютерной алгебры и вычислительной теории групп, для выполнения следующих задач. Изолированная квантовая система, построенная в рамках конечной квантовой механики, разлагается в тензорное произведение подсистем. С помощью редукции чистого квантового состояния “Вселенной”, мы получаем смешанные состояния для подсистем. В результате у нас появляется возможность изучать энергии взаимодействий и квантовые корреляции между подсистемами, а также эволюции этих величин во времени.

2. РАЗЛОЖЕНИЕ КВАНТОВОЙ СИСТЕМЫ

2.1. Тензорное произведение гильбертовых пространств

Глобальным гильбертовым пространством K‑компонентной квантовой системы является тензорное произведение локальных гильбертовых пространств компонент:

(2.1)

$\mathcal{H} = \mathop \otimes \limits_{k = 1}^K {{\mathcal{H}}_{k}}.$

Если $\dim \mathcal{H} = \mathcal{N}$ и $\dim {{\mathcal{H}}_{k}}$ = d_k, тогда $\mathcal{N}$ = = $\prod\nolimits_{k = 1}^K {{{d}_{k}}} $.

Для любого $d$-мерного гильбертова пространства i-й элемент ортонормального базиса будет обозначаться символом $\left| i \right\rangle $, т.е., $\left| 0 \right\rangle = {{(1,\;0,\; \ldots )}^{ \top }}$, $\left| 1 \right\rangle = {{\left( {0,\;1,\;0,\; \ldots } \right)}^{ \top }}$, ..., $\left| {d - 1} \right\rangle = {{\left( {0,\;0, \ldots ,\;1} \right)}^{ \top }}$.

Тензорные мономы базисных элементов локальных пространств образуют ортонормальный базис в глобальном гильбертовом пространстве:

(2.2)

$\left| i \right\rangle = \left| {{{i}_{1}}} \right\rangle \otimes \; \cdots \; \otimes \left| {{{i}_{k}}} \right\rangle \otimes \; \cdots \; \otimes \left| {{{i}_{K}}} \right\rangle ,$

где $\left| i \right\rangle \in \mathcal{H}$, $\left| {{{i}_{k}}} \right\rangle \in {{\mathcal{H}}_{k}}$ и

(2.3)

$i = \sum\limits_{k = 1}^K {{{i}_{k}}} \prod\limits_{m = k + 1}^K {{{d}_{m}}} .$

2.2. Тензорная факторизация гильбертова пространства

Мы можем обратить процедуру, поскольку (2.2) – взаимно однозначное соответствие: последовательность ${{i}_{1}},\; \ldots ,\;{{i}_{K}}$ однозначно восстанавливается из i с помощью простого алгоритма:

(2.4)

$\begin{gathered} k \leftarrow K,\quad \tilde {i} \leftarrow i \hfill \\ while{\text{ }}k \geqslant 1\;do \hfill \\ \quad {{i}_{k}} \leftarrow \tilde {i}\bmod {{d}_{k}},\quad \tilde {i} \leftarrow \left\lfloor {\tilde {i}{\text{/}}{{d}_{k}}} \right\rfloor \hfill \\ \quad k \leftarrow k - 1 \hfill \\ \end{gathered} $

Выбрав ортонормальный базис в пространстве $\mathcal{H}$ и разложение его размерности на множители $\mathcal{N} = {{d}_{1}}\; \cdots \;{{d}_{K}}$, мы можем построить конкретную биекцию вида (2.1).

Для построения произвольной биекции необходимо учесть свободу выбора базисов в гильбертовых пространствах: любой ортонормальный базис можно перевести в любой другой унитарным преобразованием.

Легко показать, что произвольный набор унитарных замен базисов во всех пространствах, фигурирующих в соотношении (2.1), эквивалентен единственной замене базиса в глобальном пространстве.

Более конкретно, любой вектор в глобальном пространстве можно представить в виде суммы тензорных произведений элементов локальных пространств

(2.5)

$\left| \psi \right\rangle = \sum\limits_\ell {\mathop \otimes \limits_{k = 1}^K } \left| {\psi _{k}^{\ell }} \right\rangle ,\quad \left| {\psi _{k}^{\ell }} \right\rangle \in {{\mathcal{H}}_{k}},\quad \left| \psi \right\rangle \in \mathcal{H}.$

Применив унитарные преобразования ко всем векторам в (2.5) и воспользовавшись свойствами тензорного произведения, мы имеем

$U\left| \psi \right\rangle = \sum\limits_\ell {\mathop \otimes \limits_{k = 1}^K } {{U}_{k}}\left| {\psi _{k}^{\ell }} \right\rangle = \mathop \otimes \limits_{k = 1}^K {{U}_{k}}\sum\limits_\ell {\mathop \otimes \limits_{k = 1}^K } \left| {\psi _{k}^{\ell }} \right\rangle $

$\quad \Downarrow $

$U{\text{'}}\left| \psi \right\rangle = \sum\limits_\ell {\mathop \otimes \limits_{k = 1}^K } \left| {\psi _{k}^{\ell }} \right\rangle ,\quad {\text{где}}\quad U{\text{'}} = {{\left( {\mathop \otimes \limits_{k = 1}^K {{U}_{k}}} \right)}^{{ - 1}}}U.$

Таким образом, тензорная факторизация гильбертова пространства $\mathcal{H}$ полностью характеризуется следующими двумя установками² ²:

1. разложением размерности на множители $\dim \mathcal{H} = {{d}_{1}}\; \cdots \;{{d}_{K}}$,

2. и унитарным преобразованием $U$, фиксирующим базис в глобальном гильбертовом пространстве $\mathcal{H}$.

2.3. Декомпозиция чистого квантового состояния

Любое смешанное состояние квантовой системы можно получить с помощью разложения Шмидта [7] чистого состояния в гильбертовом пространстве большей размерности, которое можно сконструировать с помощью процедуры называемой расширением до чистого состояния. Естественно предположить, что при фундаментальном подходе состояние изолированной системы должно быть чистым³ ³.

Для данной факторизации $\mathcal{H} = {{\mathcal{H}}_{1}} \otimes \; \cdots \; \otimes {{\mathcal{H}}_{K}}$ мы вводим множество индексов (которые удобно представлять себе как “(пре)геометрические точки”)

$X = \left\{ {1,\; \ldots ,\;K} \right\}.$

Подсистемы квантовой системы отождествляются с подмножествами $A \subseteq X$. Матрица плотности чистого состояния $\left| \psi \right\rangle \in \mathcal{H}$ глобальной системы представляет собой проектор ранга один вида

${{\rho }_{X}} = \frac{{\left| \psi \right\rangle \left\langle \psi \right|}}{{\left\langle {\psi |\psi } \right\rangle }}.$

В соответствии с законами квантовой механики статистическое поведение подсистемы $A$ правильно описывается редуцированной матрицей плотности ${{\rho }_{A}} = {\text{t}}{{{\text{r}}}_{{X\backslash A}}}{{\rho }_{X}}$, которая вычисляется из глобальной матрицы плотности взятием частичного следа по дополнению к A.

Более подробно, вычисление редуцированной матрицы плотности сводится к следующему. Согласно (2.2) базис глобального гильбертова пространства можно представить как декартово произведение локальных базисов

${{B}_{X}} = \prod\limits_{k \in X} {{{B}_{k}}} .$

Аналогичным образом мы вводим множества

${{B}_{A}} = \prod\limits_{k \in A} {{{B}_{k}}} \quad {\text{и}}\quad {{B}_{{X\backslash A}}} = \prod\limits_{k \in X\backslash A} {{{B}_{k}}} .$

В компонентах глобальную матрицу плотности можно написать в виде

${{\rho }_{X}} = {{\left( {{{\rho }_{X}}} \right)}_{{{{i}_{X}}{{j}_{X}}}}}\left| {{{i}_{X}}} \right\rangle \left\langle {{{j}_{X}}} \right|,$

где ${{i}_{X}} \simeq \left\{ {{{i}_{1}},\; \ldots ,\;{{i}_{K}}} \right\}$, ${{j}_{X}} \simeq \left\{ {{{j}_{1}}, \ldots ,\;{{j}_{K}}} \right\} \in {{B}_{X}}$, а эквивалентность $ \simeq $ обеспечивается формулой (2.3) и алгоритмом (2.4). Процедуру вычисления редуцированной матрицы плотности легко реализовать, запрограммировав формулу

${{\left( {{{\rho }_{A}}} \right)}_{{{{i}_{A}}{{j}_{A}}}}} = \sum\limits_{\substack{ {{m}_{{X\backslash A}}} \in {{B}_{{X\backslash A}}} \\ {{i}_{X}} = {{i}_{A}} \sqcup {{m}_{{X\backslash A}}} \\ {{j}_{X}} = {{j}_{A}} \sqcup {{m}_{{X\backslash A}}} } } {{\left( {{{\rho }_{X}}} \right)}_{{{{i}_{X}}{{j}_{X}}}}},\quad {\text{где}}\quad {{i}_{A}},{{j}_{A}} \in {{B}_{A}}.$

3. КОНЕЧНАЯ КВАНТОВАЯ МЕХАНИКА

Мы используем версию квантовой теории [9–11] в которой группы Ли унитарных эволюций заменяются линейными представлениями конечных групп, а поле комплексных чисел заменяется его плотными конструктивными подполями, которые естественным образом строятся из натуральных чисел и корней из единицы. Такая модификация квантового формализма “can accurately reproduce all of the results of conventional quantum mechanics” [12].

3.1. Перестановочное гильбертово пространство

Любое линейное представление конечной группы – в силу простого математического факта такое представление всегда унитарно – является подпредставлением некоторого перестановочного представления. Из этого следует, что формализм квантовой механики можно полностью⁴ ⁴ воспроизвести исходя из перестановок некоторого множества

(3.1)

$\Omega = \left\{ {{{e}_{1}},\; \ldots ,\;{{e}_{\mathcal{N}}}} \right\} \cong \left\{ {1,\; \ldots ,\;\mathcal{N}} \right\}$

первичных (“онтических”) объектов, на котором действует некоторая подгруппа $G$ симметрической группы ${{{\text{S}}}_{\mathcal{N}}}$.

Гильбертово пространство на множестве $\Omega $, необходимое для вычислений в квантовой теории, можно наиболее экономным образом построить используя только два примитивных понятия:

1. натуральные числа $\mathbb{N} = \left\{ {0,\;1, \ldots } \right\}$ – абстракция счета,

2. корни из единицы – абстракция периодичности.

Поле $\mathcal{I}$, достаточное для всех потребностей квантового формализма – в частности для расщепления любого представления любой подгруппы группы $G$ на неприводимые компоненты – можно построить, добавив к натуральным числам примитивный корень из единицы $\ell $-й степени ${{\zeta }_{\ell }}$, где $\ell $ – наименьшее общее кратное периодов (порядков) всех элементов группы $G$, называемое экспонентой группы.

Примитивный корень из единицы ${{\zeta }_{\ell }}$ является алгебраическим целым, поскольку он является корнем полинома ${{\Phi }_{\ell }}\left( x \right)$ с целыми коэффициентами и единичным старшим коэффициентом. ${{\Phi }_{\ell }}\left( x \right)$ называется $\ell $-м циклотомическим полиномом (или $\ell $-м многочленом деления круга). Алгебраическое целое ${{\zeta }_{\ell }}$ можно записать в виде комплексного числа: ${{\zeta }_{\ell }} = {{e}^{{2\pi {\mathbf{i}}k/\ell }}}$, где натуральное число $k < \ell $ является взаимно простым с $\ell $. Мы будем всегда подразумевать, что $k = 1$, а соответствующий примитивный корень из единицы ${{\zeta }_{\ell }} = {{e}^{{2\pi {\mathbf{i}}/\ell }}}$ называть основным⁵ ⁵.

Добавив ${{\zeta }_{\ell }}$ к натуральным числам, мы расширяем полукольцо $\mathbb{N}$ в кольцо $\mathbb{N}\left[ {{{\zeta }_{\ell }}} \right]$ (исключив тривиальный случай $\ell = 1$). Далее, построив поле частных кольца $\mathbb{N}\left[ {{{\zeta }_{\ell }}} \right]$, мы получаем циклотомическое расширение поля рациональных чисел $\mathcal{F} = \mathbb{Q}({{\zeta }_{\ell }}).$ При $\ell > 2$ поле $\mathcal{I}$, будучи плотным подполем комплексного поля $\mathbb{C}$, эмпирически неотличимо от $\mathbb{C}$.

Интерпретируя множество $\Omega $ как базис, мы приходим к $\mathcal{N}$-мерному гильбертову пространству ${{\mathcal{H}}_{\mathcal{N}}}$ над полем $\mathcal{F}$. Действие $G$ на $\Omega $ определяет перестановочное представление $\mathcal{P}$ в пространстве ${{\mathcal{H}}_{\mathcal{N}}}$ матрицами вида

(3.2)

$\mathcal{P}{{\left( g \right)}_{{i,j}}} = {{\delta }_{{ig,j}}},$

где $ig$ обозначает действие (справа) элемента группы $g \in G$ на элемент множества $i \in \Omega $.

3.2. Разложение перестановочного представления

Перестановочное представление любой группы имеет тривиальное одномерное подпредставление в пространстве, состоящем из векторов с равными компонентами. В качестве базисного элемента тривиального подпространства мы будем использовать вектор

$\left| \omega \right\rangle = (\underbrace {1,1,\; \ldots ,\;1}_\mathcal{N}{{)}^{{\text{т}}}}.$

Дополнение к тривиальному подпредставлению называется стандартным представлением. Оператор проектирования в $\left( {\mathcal{N} - 1} \right)$-одномерное стандартное пространство ${{\mathcal{H}}_{ \star }}$ имеет вид

${{{\text{P}}}_{ \star }} = {{1}_{\mathcal{N}}} - \frac{{\left| \omega \right\rangle \left\langle \omega \right|}}{\mathcal{N}}.$

Квантовомеханическое поведение (интерференция и т.д.) проявляется именно в стандартном пространстве ${{\mathcal{H}}_{ \star }}$. Том Бэнкс сделал глубокое наблюдение [12], что проекция классических перестановочных эволюций во всем пространстве ${{\mathcal{H}}_{\mathcal{N}}}$ приводит к истинно квантовым эволюциям в его подпространстве ${{\mathcal{H}}_{ \star }} < {{\mathcal{H}}_{\mathcal{N}}}$. Бэнкс также показал, что наиболее естественным выбором является полная группа всех перестановок онтических элементов $G = {{{\text{S}}}_{\mathcal{N}}}$, где $\mathcal{N}$ – число фундаментальных (планковских) элементов реальности⁶ ⁶.

Для пояснения соответствия между конечной квантовой механикой и традиционной теорией, основанной на непрерывных унитарных группах, Бэнкс указал на наличие связи между симметрической группой на $\mathcal{N}$ элементах и унитарной группой в размерности $\mathcal{N} - 1$. А именно, для достаточно большого⁷ ⁷ числа $\mathcal{N}$ наиболее общая конечная подгруппа $G$ группы ${\text{SU}}\left( {\mathcal{N} - 1} \right)$ имеет структуру полупрямого произведения абелевой группы A и симметрической группы ${{{\text{S}}}_{\mathcal{N}}}$

$G = A \rtimes {{{\text{S}}}_{{\mathcal{N}}}} < {\text{SU}}\left( {\mathcal{N} - 1} \right).$

3.3. Онтические состояния

${{{\text{S}}}_{{\mathcal{N}}}}$ – рационально представляемая группа, т.е., любое ее неприводимое представление (в частности, стандартное) можно реализовать над $\mathbb{Q}$ (или, эквивалетно, над $\mathbb{Z}$). Это означает, что для описания квантовых состояний в ${{\mathcal{H}}_{ \star }}$ достаточно только векторов с рациональными компонентами⁸ ⁸.

Легко показать, что любое квантовое состояние в ${{\mathcal{H}}_{ \star }}$ можно получить как проекцию целочисленного вектора из неотрицательного ортанта $\mathcal{H}_{\mathcal{N}}^{ + } \subset {{\mathcal{H}}_{\mathcal{N}}}$. Пусть $\left| x \right\rangle = {{({{x}_{1}},\; \ldots ,\;{{x}_{{_{\mathcal{N}}}}})}^{{\text{т}}}} \in \mathcal{H}_{\mathcal{N}}^{ + }$ – вектор с неотрицательными рациональными компонентами. Тогда его проекция на ${{\mathcal{H}}_{ \star }}$ является $\left( {\mathcal{N} - 1} \right)$-мерным вектором вида

(3.3)

$\left| y \right\rangle = {{({{y}_{1}},\; \ldots ,\;{{y}_{{_{{\mathcal{N} - 1}}}}})}^{{\text{т}}}} = {{{\text{P}}}_{ \star }}\left| x \right\rangle .$

Удобным для наших целей базисом в ${{\mathcal{H}}_{ \star }}$ является множество

(3.4)

$\left\{ {\left| 0 \right\rangle - \left| {\mathcal{N} - 1} \right\rangle ,\; \ldots ,\;\left| {\mathcal{N} - 2} \right\rangle - \left| {\mathcal{N} - 1} \right\rangle } \right\},$

где $\left\{ {\left| 0 \right\rangle ,\; \ldots ,\;\left| {\mathcal{N} - 1} \right\rangle } \right\}$ – базис в ${{\mathcal{H}}_{\mathcal{N}}}$. В базисе (3.4), соотношение (3.3) в компонентах имеет вид

${{y}_{1}} = {{x}_{1}} - {{x}_{\mathcal{N}}},$

$\quad \vdots $

${{y}_{{\mathcal{N} - 1}}} = {{x}_{{\mathcal{N} - 1}}} - {{x}_{\mathcal{N}}}.$

Очевидно, что любой набор величин ${{y}_{1}},\; \ldots ,\;{{y}_{{_{{\mathcal{N} - 1}}}}}$ можно получить, используя только неотрицательные величины ${{x}_{1}},\; \ldots ,\;{{x}_{\mathcal{N}}}$.

Поскольку квантовые состояния являются лучами в гильбертовом пространстве, мы можем заменить неотрицательные рациональные векторы |x〉 натуральными векторами

$\left| n \right\rangle = {{\left( {{{n}_{1}},\; \ldots ,\;{{n}_{\mathcal{N}}}} \right)}^{{\text{т}}}} \in {{\mathbb{N}}^{\mathcal{N}}} \subset \mathcal{H}_{\mathcal{N}}^{ + }.$

Чтобы строить конструктивные модели, необходимо выбрать конечное подмножество в ${{\mathbb{N}}^{\mathcal{N}}}$. Простейшим выбором являются векторы с координатами из множества {0, 1}, т.е., битовые строки длины $\mathcal{N}$, которые мы будем называть онтическими векторами или онтическими состояниями. Эти состояния привлекательны как по онтологическим, так и по вычислительным причинам.

Интерпретируя онтическое состояние |q〉 как характеристическую функцию, мы можем отождествить его с подмножеством $q \subset \Omega $ или, эквивалентно, с разбиением онтического множества (3.1) на два нетривиальных подмножества

$\Omega = q \sqcup \sim q,\quad \sim q = \Omega {{\backslash }}q,$

где $ \sim $ обозначает теоретико-множественное дополнение (или побитовую инверсию). Полное множество онтических состояний имеет вид

$Q{{ = 2}^{\Omega }}{{\backslash }}\left\{ {\not {0},\Omega } \right\}.$

Число онтических состояний экспоненциально зависит от $\mathcal{N}$: $\left| Q \right|{{ = 2}^{\mathcal{N}}} - 2$. Поэтому для больших $\mathcal{N}$ они порождают достаточно большие множества квантовых состояний в стандартном пространстве и его подпространствах.

Операция дополнения, примененная к онтическому состоянию, вызывает изменение знака соответствующего квантового состояния в стандартном пространстве:

$\left| \psi \right\rangle = {{{\text{P}}}_{ \star }}\left| q \right\rangle \Rightarrow \left| \psi \right\rangle = {{{\text{P}}}_{ \star }}\left| { \sim q} \right\rangle .$

Скалярное произведение нормализованных проекций онтических векторов |q〉 и |r〉 в пространство ${{\mathcal{H}}_{ \star }}$ имеет вид

$S\left( {q,r} \right) \equiv \frac{{\left\langle {q\left| {{{{\text{P}}}_{ \star }}} \right|r} \right\rangle }}{{\sqrt {\left\langle {q\left| {{{{\text{P}}}_{ \star }}} \right|q} \right\rangle \left\langle {r\left| {{{{\text{P}}}_{ \star }}} \right|r} \right\rangle } }} = \frac{{\mathcal{N}\left\langle {q\& r} \right\rangle - \left\langle q \right\rangle \left\langle r \right\rangle }}{{\sqrt {\left\langle q \right\rangle \left\langle { \sim q} \right\rangle \left\langle r \right\rangle \left\langle { \sim r} \right\rangle } }},$

где $\& $ – побитовое И для битовых строк, а $\left\langle \cdot \right\rangle $ обозначает вес Хэмминга (число заполнения).

Из очевидных тождеств $\left\langle { \sim a} \right\rangle = \mathcal{N} - \left\langle a \right\rangle $ и $\left\langle {a\& b} \right\rangle + \left\langle {a\& \sim b} \right\rangle = \left\langle a \right\rangle $ легко выводятся следующие симметрии относительно операций дополнения, примененных к онтическим состояниям

$S\left( {q,r} \right) = - S\left( { \sim q,r} \right) = - S\left( {q, \sim r} \right) = S\left( { \sim q, \sim r} \right).$

4. ОНТИЧЕСКИЙ И ЭНЕРГЕТИЧЕСКИЙ БАЗИСЫ

4.1. Онтический базис

Исходный перестановочный базис в пространстве ${{\mathcal{H}}_{\mathcal{N}}}$, т.е. множество Ω, мы будем называть онтическим базисом. В этом базисе матрица плотности онтического состояния $\left| q \right\rangle \in {{\mathcal{H}}_{\mathcal{N}}}$ в пространстве ${{\mathcal{H}}_{ \star }}$ имеет вид

(4.1)

$\rho _{q}^{o} = \frac{1}{\mathcal{N}}\frac{{\left( {\left| q \right\rangle - \alpha \left| \omega \right\rangle } \right)\left( {\left\langle q \right| - \alpha \left\langle \omega \right|} \right)}}{{\alpha \left( {1 - \alpha } \right)}},$

где $\alpha = \left\langle q \right\rangle {\text{/}}\mathcal{N}$ – плотность заполнения.

Имеется очевидная двойственность: выражение для матрицы плотности дополнения к онтическому состоянию |q〉 получается из (4.1) заменами $q \to \, \sim q$ и $\alpha \to 1 - \alpha $

$\rho _{q}^{o}\xrightarrow{\begin{subarray}{l} q \to \sim q \\ \alpha \to 1 - \alpha \end{subarray} }\rho _{{ \sim q}}^{o}.$

Заметим, что онтический базис не зависит ни от состояния, ни от эволюции квантовой системы, а полностью определяется числом $\mathcal{N}$. Поэтому его можно рассматривать как прообраз, из которого любой другой базис можно получить подходящим унитарным преобразованием.

4.2. Энергетический базис

В континуальной квантовой механике эволюция изолированной квантовой системы описывается однопараметрической унитарной группой U_t = e^–iHt, порождаемой гамильтонианом H. Собственные значения гамильтониана называются энергиями.

В конечной квантовой механике эволюция описывается циклической группой $U{{\left( g \right)}^{t}}$, порождаемой элементом $U\left( g \right) \in \mathcal{P}\left( G \right)$, где $\mathcal{P}\left( G \right)$ – перестановочное представление группы $G$, определяемое формулой (3.2), а время t – целочисленный параметр. Мы называем энергетическим базисом ортонормальный базис в пространстве ${{\mathcal{H}}_{\mathcal{N}}}$, в котором матрица $U\left( g \right)$ диагональна. Этот базис зависит от заданной эволюции.

Формула Планка $E = h\nu $ выражает связь энергии $E$ с частотой $\nu $ – величиной, обратной периоду соответствующего циклического процесса.

Любую перестановку можно представить как произведение непересекающихся циклов. Поучительно посмотреть, как часто циклы разной длины встречаются в группе всех перестановок ${{{\text{S}}}_{\mathcal{N}}}$. Простое комбинаторное вычисление показывает, что общее число циклов длины $\ell $ во всей симметрической группе ${{{\text{S}}}_{\mathcal{N}}}$ равно $\mathcal{N}!{\text{/}}\ell $, и, следовательно, ожидаемое число $\ell $-циклов в одной перестановке равно $1{\text{/}}\ell $. То есть в нашей модели Вселенной, основанной на перестановках, преобладают эволюции с высокими энергиями⁹ ⁹.

Матрица цикла длины $\ell $ имеет вид

${{C}_{\ell }} = \left( {\begin{array}{*{20}{c}} 0&1&0& \cdots &0 \\ 0&0&1& \cdots &0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1&0&0& \cdots &0 \end{array}} \right),$

т.е. ${{\left( {{{C}_{\ell }}} \right)}_{{ij}}} = {{\delta }_{{i - j + 1(\bmod \ell )}}}$ . Эта матрица имеет следующую диагональную форму

${{F}_{\ell }}{{C}_{\ell }}F_{\ell }^{{ - 1}} = \left( {\begin{array}{*{20}{c}} 1&0&0& \cdots &0 \\ 0&{{{\zeta }_{\ell }}}&0& \cdots &0 \\ 0&0&{\zeta _{\ell }^{2}}& \cdots &0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&0&0& \cdots &{\zeta _{\ell }^{{\ell - 1}}} \end{array}} \right),$

где ${{\zeta }_{\ell }} = {{e}^{{2\pi {\mathbf{i}}/\ell }}}$ – $\ell $-й основной примитивный корень из единицы, а

${{F}_{\ell }} = \frac{1}{{\sqrt \ell }}\left( {\begin{array}{*{20}{c}} 1&1&1& \ldots &1 \\ 1&{\zeta _{\ell }^{{ - 1}}}&{\zeta _{\ell }^{{ - 2}}}& \cdots &{\zeta _{\ell }^{{ - \left( {\ell - 1} \right)}}} \\ 1&{\zeta _{\ell }^{{ - 2}}}&{\zeta _{\ell }^{{ - 4}}}& \cdots &{\zeta _{\ell }^{{ - 2\left( {\ell - 1} \right)}}} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1&{\zeta _{\ell }^{{ - \left( {\ell - 1} \right)}}}&{\zeta _{\ell }^{{ - 2\left( {\ell - 1} \right)}}}& \cdots &{\zeta _{\ell }^{{ - \left( {\ell - 1} \right)\left( {\ell - 1} \right)}}} \end{array}} \right)$

– матрица преобразования Фурье. Матрица ${{F}_{\ell }}$ является одновременно унитарной и симметрической, что позволяет легко написать обратную матрицу

$F_{\ell }^{{ - 1}} = F_{\ell }^{\dag } = F_{\ell }^{*} \Rightarrow {{(F_{\ell }^{{ - 1}})}_{{ij}}} = \frac{1}{{\sqrt \ell }}\zeta _{\ell }^{{\left( {i - 1} \right)\left( {j - 1} \right)}}.$

В общем случае матрица перестановочного представления элемента $g \in {{{\text{S}}}_{\mathcal{N}}}$ является прямой суммой циклических матриц $U\left( g \right) = \mathop \oplus \limits_{m = 1}^M {{C}_{{{{\ell }_{m}}}}}$, а соответствующая диагонализирующая матрица – матрица перехода от онтического к энергетическому базису – имеет вид $F = \mathop \oplus \limits_{m = 1}^M {{F}_{{{{\ell }_{m}}}}}$.

Матрицу плотности онтического состояния |q〉 в энергетическом базисе можно вычислить из (4.1) по формуле

$\rho _{q}^{\varepsilon } = F\rho _{q}^{o}F{\text{*}}.$

4.3. Замечание о базисах

Как показано в разделе 2.2, выбор базиса в гильбертовом пространстве замкнутой квантовой системы имеет решающее значение для выделения подсистем в рассматриваемой системе.

Наиболее универсальным является онтический базис, не требующий никаких данных, характеризующих квантовую систему, кроме числа онтических элементов. Для построения разложения замкнутой системы в этом базисе достаточно задать только ее квантовое состояние.

Если данные, описывающие систему, помимо состояния, включают унитарную эволюцию, то наиболее адекватным с точки зрения физики является энергетический базис, связанный с разложением оператора эволюции на неприводимые компоненты.

В [12] в качестве универсального энергетического базиса, сопряженного к онтическому, предлагается использовать базис, диагонализирующий цикл максимальной возможной длины. Энергия основного состояния такого цикла является минимально возможной для Вселенной, состоящей из $\mathcal{N}$ онтичеких элементов.

5. МЕРЫ КВАНТОВОЙ ЗАПУТАННОСТИ

Количественно квантовые корреляции описываются мерами запутанности, в основе которых лежит понятие энтропии. Чаще всего в физике используется энтропия фон Неймана

(5.1)

${{S}_{1}}\left( \rho \right) = - {\text{tr}}\left( {\rho \log \rho } \right).$

Широко используются также энтропии из семейства Реньи [14]

(5.2)

${{S}_{\alpha }}\left( \rho \right) = \frac{1}{{1 - \alpha }}\log {\text{tr}}({{\rho }^{\alpha }}),\quad \alpha \geqslant 0,\quad \alpha \ne 1.$

Общим свойством для энтропий фон Неймана и Реньи является аддитивность на комбинациях вероятностных распределений, задаваемых собственными значениями матриц плотности, если эти распределения независимы.

Энтропию фон Неймана предпочитают потому, что она дополнительно имеет более сильное свойство – цепное правило для условных энтропий. В принципе, семейство Реньи можно пополнить энтропией фон Неймана с помощью предельного перехода $\alpha \to 1$.

В наших вычислениях мы используем 2-ю энтропию Реньи (называемую также энтропией столкновений)

${{S}_{2}}\left( \rho \right) = - \log {\text{tr}}({{\rho }^{2}})$

по следующим причинам:

• Ее легко вычислять. Для матрицы плотности размера $n \times n$ мы имеем

${{S}_{2}}\left( \rho \right) = - \log \left( {\sum\limits_{i = 1}^n {\rho _{{ii}}^{2}} + 2\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^n {{{{\left| {{{\rho }_{{ij}}}} \right|}}^{2}}} } } \right).$

• ${\text{tr}}({{\rho }^{2}})$ – это величина, называемая чистотой квантового состояния $\rho $. Чистота лежит в интервале $\left[ {1{\text{/}}n,1} \right]$, достигая верхнего значения 1 только для чистых состояний (отсюда название).

${\text{tr}}({{\rho }^{2}})$ совпадает с борновской вероятностью: “система наблюдает саму себя”.

• ${\text{tr}}({{\rho }^{2}}) \equiv {{\left\langle \rho \right\rangle }_{\rho }}$ – ожидаемое значение наблюдаемой $\rho $ в состоянии $\rho $.

• ${\text{tr}}({{\rho }^{2}}) \equiv \left\| \rho \right\|_{{\text{F}}}^{2}$ – квадрат нормы Фробениуса (Гильберта–Шмидта) матрицы плотности.

Скалярное произведение Фробениуса для двух матриц (или скалярное произведение Гильберта–Шмидта для двух операторов) a и b определяется как ${{\left\langle {a|b} \right\rangle }_{{\text{F}}}} = {\text{tr}}({{a}^{\dag }}b)$, а соответствующая норма имеет вид ${{\left\| a \right\|}_{{\text{F}}}} = \sqrt {{{{\left\langle {a|a} \right\rangle }}_{{\text{F}}}}} .$

Можно показать, что любые конструкции, используемые при изучении квантовых корреляций и основанные на энтропии фон Неймана, можно переформулировать в терминах матричных метрик.

Например, в моделях эмерджентной геометрии [3, 15, 16] расстояния между подсистемами $A$ и $B$ моделируются функциями взаимной информации

(5.3)

$\mathcal{F}\left( {A,B} \right) = {{S}_{1}}\left( {{{\rho }_{A}}} \right) + {{S}_{1}}\left( {{{\rho }_{B}}} \right) - {{S}_{1}}\left( {{{\rho }_{{A \cup B}}}} \right).$

Заменив в (5.3) энтропию фон Неймана 2-й энтропией Реньи, мы получаем выражение

(5.4)

${{\mathcal{F}}_{2}}\left( {A,B} \right) = {{S}_{2}}\left( {{{\rho }_{A}}} \right) + {{S}_{2}}\left( {{{\rho }_{B}}} \right) - {{S}_{2}}\left( {{{\rho }_{{A \cup B}}}} \right)$

экспонента которого имеет вид

(5.5)

$\frac{{{\text{tr}}(\rho _{{A \cup B}}^{2})}}{{{\text{tr}}(\rho _{A}^{2}){\text{tr}}(\rho _{B}^{2})}} \equiv \frac{{\left\| {{{\rho }_{{A \cup B}}}} \right\|_{{\text{F}}}^{2}}}{{\left\| {{{\rho }_{A}} \otimes {{\rho }_{B}}} \right\|_{{\text{F}}}^{2}}}.$

Очевидно, оба выражения (5.4) и (5.5) хорошо описывают отклонение от сепарабельности вызываемое запутанностью – хотя (5.4) и не имеет той вероятностной интерпретации, которая присущя выражению (5.3).

6. НЕКОТОРЫЕ ВЫЧИСЛИТЕЛЬНЫЕ НАБЛЮДЕНИЯ

Алгоритмы для построения тензорных разложений и вычисления квантовых корреляций реализованы в виде программы на языке Си.

Для иллюстрации вычислений с помощью этой программы рассмотрим однородную квантовую систему, т.е., систему, гильбертово пространство которой разлагается в тензорное произведение локальных гильбертовых пространств одинаковой размерности

$\mathcal{H} = \mathop \otimes \limits_{x \in X} {{\mathcal{H}}_{x}},$

где $X = \left\{ {1,\; \ldots ,\;\left| X \right|} \right\}$ – множество “геометрических точек”, $\dim {{\mathcal{H}}_{x}} = d$ для всех $x \in X$.

Предварительные вычисления указывают на то, что разложения с меньшими локальными размерностями демонстрируют более интересное поведение. Рассмотрим пример с d = 2 и |X| = 23. В этом случае размерность глобального пространства $\dim \mathcal{H} = 8388608$. В качестве меры расстояния между точками воспользуемся аналогом взаимной информации (5.4). Вычисления (5.4) на всех ребрах $\left( {x,y} \right) \in X \times X$ полного графа на вершинах $X$ дают разброс величин в два порядка. Типичный результат вычислений

${{\mathcal{I}}_{2}}\left( {x,y} \right) \in [5.3 \times {{10}^{{ - 8}}},7 \times {{10}^{{ - 6}}}]\,.$

Большой разброс расстояний между точками можно рассматривать как признак нетривиальности предполагаемой эмерджентной геометрии в данном примере.

В примере с несколько большей локальной размерностью, $d = 7$ и $\left| X \right| = 7$ (следовательно $\dim \mathcal{H}$ = = 823 543), аналогичное вычисление дает

${{\mathcal{I}}_{2}}\left( {x,y} \right) \in \left[ {0.0037,\;0.0041} \right].$

То есть, геометрия близка к тривиальной – все точки почти эквидистантны и их можно интерпретировать как вершины близкого к правильному симплекса в $6$-мерном евклидовом пространстве.

Более детальные вычисления показывают, что основной вклад в нетривиальность геометрии вносят локальные размерности d, а не число точек |X|.

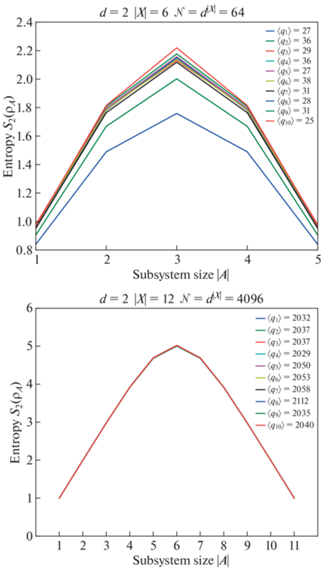
На рис. 1 приведены результаты вычисления энтропий подсистем всех возможных размеров для квантовых систем с локальной размерностью $d = 2$, но с двумя разными количествами геометрических точек: $\left| X \right| = 6$ и $\left| X \right| = 12$. В обоих случаях использовалось по 10 случайно сгенерированных онтических состояний, в легендах указаны их веса Хэмминга. Данные, представленные на рисунке, демонстрируют следующие особенности:

Рис. 1.

Энтропии подсистем.

• Тенденция к универсальности (слабой зависимости от квантовых состояний) с ростом |X| : визуально все графики почти идентичны в “большем” случае $\left| X \right| = 12$.

• Симметрия ${{S}_{2}}\left( {{{\rho }_{A}}} \right) = {{S}_{2}}\left( {{{\rho }_{{X\backslash A}}}} \right)$ – это проявление свойств разложения Шмидта [7] чистого состояния: обе матрицы ${{\rho }_{A}}$ и ${{\rho }_{{X\backslash A}}}$ имеют идентичные наборы ненулевых собственных значений.

• Для подсистем, размеры которых |A| заметно меньше чем |X|/2, редуцированные состояния близки к максимально смешанным состояниям: ${{S}_{2}}({{\rho }_{A}}) \approx \left| A \right|\log d$. Напомним, что максимально смешанным называют состояние, матрица плотности которого описывает равномерное распределение вероятностей, т.е., все ее собственные значения равны.

Список литературы

Page D.N., Wootters W.K. Evolution without evolution: Dynamics described by stationary observables // Phys. Rev. D. 1983. V. 27. P. 2885–2892. URL: https://link.aps.org/doi/10.1103/PhysRevD.27.2885.
Carroll S.M. Singh Ashmeet. Quantum mereology: Factorizing Hilbert space into subsystems with quasiclassical dynamics // Physical Review A. 2021. V. 103. № 2. URL: https://doi.org/10.1103/PhysRevA.103.022213
Cao ChunJun, Carroll Sean M., Michalakis Spyridon. Space from Hilbert space: Recovering geometry from bulk entanglement // Physical Review D. 2017. V. 95. № 2. URL: https://doi.org/10.1103/PhysRevD.95.024031
Woods Mischa. The Page-Wootters mechanism 36 years on: a consistent formulation which accounts for interacting systems // Quantum Views. 2019. V. 3. P. 16. URL: https://doi.org/10.22331/qv-2019-07-21-16.
Zanardi Paolo. Virtual Quantum Subsystems // Physical Review Letters. 2001. V. 87. № 7. URL: https://doi.org/10.1103/PhysRevLett.87.077901
Zanardi Paolo, Lidar Daniel A., Lloyd Seth. Quantum Tensor Product Structures are Observable Induced // Physical Review Letters. 2004. V. 92. № 6. URL: https://doi.org/10.1103/PhysRevLett.92.060402
Nielsen M.A., Chuang I.L. Quantum Computation and Quantum Information (10th Anniversary edition). USA: Cambridge University Press, 2016. ISBN: 978-1-10-700217-3.
Gleason A.M. Measures on the closed subspaces of a Hilbert space // Journal of Mathematics and Mechanics. 1957. V. 6. № 6. P. 885–893. URL: http://www.jstor.org/stable/24900629.
Kornyak V.V. Quantum models based on finite groups // Journal of Physics: Conference Series. 2018. V. 965. P. 012023. URL: https://doi.org/10.1088/1742-6596/965/1/012023.
Kornyak V.V. Modeling Quantum Behavior in the Framework of Permutation Groups // EPJWeb of Conferences. 2018. V. 173. P. 01007. URL: https://doi.org/10.1051/epjconf/201817301007.
Kornyak V.V. Mathematical Modeling of Finite Quantum Systems // Lect. Notes Comput. Sci. 2012. V. 7125. P. 79–93. 1107.5675.
Banks T. Finite Deformations of Quantum Mechanics. 2020. 2001.07662.
Collins M.J. On Jordan’s theorem for complex linear groups // Journal of Group Theory. 2007. V. 10. № 4. P. 411–423. URL: https://doi.org/10.1515/JGT.2007.032
Rényi A. On measures of entropy and information / Proc. 4th Berkeley Symp. Math. Stat. Probab. 1961. V. 1. P. 547–561.
Van Raamsdonk M. Building up spacetime with quantum entanglement // Gen. Rel. Grav. 2010. V. 42. P. 2323–2329. 1005.3035.
Maldacena J., Susskind L. Cool horizons for entangled black holes // Fortschritte der Physik. 2013. V. 61. № 9. P. 781–811. URL: https://doi.org/10.1002/prop.201300020

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал