Программирование, 2022, № 4, стр. 50-56
АЛГОРИТМ ВЫЧИСЛЕНИЯ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ДВУМЕРНОГО РАЗНОСТНОГО УРАВНЕНИЯ С НАЧАЛЬНЫМИ ДАННЫМИ, ЗАДАННЫМИ В “ПОЛОСЕ”
М. С. Апанович a, *, А. П. Ляпин b, **, К. В. Шадрин a, ***
a Красноярский государственный медицинский университет имени профессора В.Ф. Войно-Ясенецкого
660022 Красноярск, ул. Партизана Железняка, 1, Россия
b Сибирский федеральный университет
660041 Красноярск, пр. Свободный, 79, Россия
* E-mail: marina.apanovich@list.ru
** E-mail: aplyapin@sfu-kras.ru
*** E-mail: kvsh_buffon@mail.ru
Поступила в редакцию 16.07.2021
После доработки 13.12.2021
Принята к публикации 31.01.2022
- EDN: PPSFHS
- DOI: 10.31857/S0132347422040021
Аннотация
Представлен алгоритм вычисления решения задачи Коши для двумерного разностного уравнения с постоянными коэффициентами в точке по коэффициентам разностного уравнения и начальным данным задачи Коши, заданными в “полосе”, методами компьютерной алгебры. Для автоматизации процесса вычисления решения данной задачи был разработан алгоритм в среде MATLAB, где входными данными являются матрица коэффициентов двумерного полиномиального разностного уравнения, координаты матрицы начальных данных, регламентирующей структуру разностного уравнения, координаты точки, задающей размерность матрицы начальных данных; матрица начальных данных. Результатом работы алгоритма является решение задачи Коши, начальные данные которой заданы в “полосе”, для двумерного разностного уравнения, представляющее собой значение функции в искомой точке.
1. ВВЕДЕНИЕ
Линейные разностные уравнения возникают в различных областях математики, следовательно, поиск решений таких уравнений является одной из математических задач, имеющей многочисленные приложения в различных областях науки и техники. Например, разностные уравнения часто используются в моделях динамики с дискретным временем [1, 2], а также для приближенного решения дифференциальных уравнений [3], в комбинаторном анализе разностные уравнения в сочетании с методом производящих функций дают мощный аппарат исследования перечислительных задач (см., например, [4–6]). Алгоритм вычисления производящей функции решения задачи Коши для двумерного разностного уравнения с постоянными коэффициентами по коэффициентам разностного уравнения и начальным данным задачи Коши представлен в работе [7]. В работе [8] представлен алгоритм вычисления решения задачи Коши для двумерного разностного уравнения с постоянными коэффициентами в точке по коэффициентам разностного уравнения и начальным данным задачи Коши. В данной работе представлен алгоритм вычисления решения задачи Коши для двумерного разностного уравнения с постоянными коэффициентами по коэффициентам разностного уравнения и начальным данным задачи Коши, которые заданы в “полосе”.
2. ПОСТАНОВКА ЗАДАЧИ И ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ
Обозначим $\mathbb{Z}$ – множество целых чисел, ${{\mathbb{Z}}^{2}} = \mathbb{Z} \times \mathbb{Z}$ – двумерная целочисленная решетка и $\mathbb{Z}_{ + }^{2}$ – подмножество этой решетки, состоящее из точек с целыми неотрицательными координатами. Пусть δ1 – оператор сдвига по переменной $x$, т.е. ${{\delta }_{1}}f(x,y) = f(x + 1,y)$, а ${{\delta }_{2}}$ – оператор сдвига по переменной $y$, т.е. ${{\delta }_{2}}f(x,y) = f(x,y + 1)$. Зададим “полосу”, $\Pi = \{ (x,y) \in {{\mathbb{Z}}^{2}},0 \leqslant x \leqslant B,y \geqslant 0\} $ в положительном октанте целочисленной решетки, число $B + 1$ будем называть шириной “полосы” $\Pi $. Рассмотрим разностный полиномиальный оператор с постоянными коэффициентами вида
(1)
$P({{\delta }_{1}},{{\delta }_{2}}) = \sum\limits_{j = 0}^m {\sum\limits_{i = 0}^b {} {{c}_{{ij}}}} \delta _{1}^{i}\delta _{2}^{j} = \sum\limits_{j = 0}^m {{{P}_{j}}} ({{\delta }_{1}})\delta _{2}^{j},$Многочлен $P(z,w) = \sum\limits_{j = 0}^m {\sum\limits_{i = 0}^b {{{c}_{{ij}}}} } {{z}^{i}}{{w}^{j}}$ называется характеристическим. Степень $m$ многочлена $P(z,w)$ по переменной $w$ будем называть порядком разностного оператора $P({{\delta }_{1}},{{\delta }_{2}})$ и предполагать, что $b < B$.
Зафиксируем $\beta = \left( {{{x}_{\beta }},m} \right)$ такое, что ${{c}_{\beta }} \ne 0$, и рассмотрим множество Πβ = {(x, y) ∈ $\mathbb{Z}_{ + }^{2}$: $0 \leqslant x - {{x}_{\beta }} \leqslant $ B – b, y > m – 1}. Обозначим ${{L}_{\beta }} = \Pi {{\backslash }}{{\Pi }_{\beta }}$ и сформулируем следующую задачу:
найти решение разностного уравнения
удовлетворяющее условиюгде $g(x,y)$ и $\varphi (x,y)$ – заданные функции целочисленных аргументов.Задачу (2)–(3) назовем задачей Коши для полиномиального разностного оператора (1) и приведем легко проверяемое условие ее разрешимости.
Известно (см. [9]), что задача (2)–(3) однозначно разрешима, если выполняется условие
(4)
$\left| {{{c}_{\beta }}} \right| \geqslant \sum\limits_{|\alpha | = 0,\alpha \ne \beta }^b {\left| {{{c}_{\alpha }}} \right|.} $Поставим задачу вычислить значение функции $f(x,y)$ в точке A с координатами $\left( {{{x}_{A}},{{y}_{A}}} \right)$, т.е. $f\left( {{{x}_{A}},{{y}_{A}}} \right)$.
3. ОПИСАНИЕ ВХОДНЫХ ДАННЫХ
Решение задачи Коши (2)–(3) для двумерного разностного уравнения с постоянными коэффициентами в точке $z = ({{x}_{z}},{{y}_{z}})$ представляет собой значение функции $f(x,y)$ в этой точке.
Алгоритм вычисления значения функции $f(x,y)$ в заданной точке A c координатами $({{x}_{A}},{{y}_{A}})$ имеет рекурсивный характер и сводится к вычислению значений функции $f(x,y)$ на конечном подмножестве точек $\left( {x,y} \right) \in {{L}_{\beta }} = \Pi {{\backslash }}{{\Pi }_{\beta }}$.
Начальные данные (3) задаются матрицей F размерности $(B + 1) \times ({{y}_{A}} + 1)$, содержащей конечное подмножество значений начальных данных задачи Коши.
Коэффициенты двумерного разностного уравнения задаются матрицей $C$, имеющей прямоугольный вид (размерность: $(m + 1) \times (b + 1)$).
Проиллюстрируем процедуру задания функции начальных данных на примере.
Для разностного уравнения
(5)
$\begin{gathered} {{c}_{{00}}}f(x,y) + {{c}_{{10}}}f(x + 1,y) + {{c}_{{20}}}f(x + 2,y) + \\ + \;{{c}_{{01}}}f(x,y + 1) + {{c}_{{11}}}f(x + 1,y + 1) + \\ + \;{{c}_{{21}}}f(x + 2,y + 1) + {{c}_{{02}}}f(x,y + 2) + \\ + \;{{c}_{{12}}}f(x + 1,y + 2) + {{c}_{{22}}}f(x + 2,y + 2) = 0 \\ \end{gathered} $Здесь элементы, обозначенные $*$, вычисляются при выполнении алгоритма. При этом, вычислить элемент $\varphi (1,\;2)$ не представляется возможным без вычисления элемента $\varphi (2,\;2)$. Таким образом, для нахождения неизвестных элементов необходимо решить систему линейных разностных уравнений вида (5) с использованием начальных данных $\varphi (i,j)$, где $i = 0,\; \ldots ,\;4$, $j = 0,\;1$ и $\varphi (0,\;2)$, а именно:
Все, что нам известно, перенесем вправо и получим константы:
Матрица полученной системы уравнений будет иметь вид:
Поскольку на всех диагоналях матрицы, параллельных главной диагонали и на самой главной диагонали, элементы матрицы одинаковые, то такая матрица является теплицевой [10].
Вернемся к входным данным. Входные данные конечны и имеют вид:
1. точка $\beta = \left( {{{x}_{\beta }},m} \right)$;
2. прямоугольная марица коэффициентов $C = ({{c}_{\alpha }})$, $\alpha = \left( {{{\alpha }_{1}},{{\alpha }_{2}}} \right)$, ${{\alpha }_{1}} = 0,\; \ldots ,\;b$, ${{\alpha }_{2}} = 0,\; \ldots ,\;m$ размера $(m + 1) \times (b + 1)$ из коэффициентов ${{c}_{\alpha }}$ полиномиального разностного оператора (1);
3. точка $A$ с координатами $({{x}_{A}},{{y}_{A}})$, определяющая координаты искомого значения функции $f(x,y)$ и размерность матрицы начальных данных $F$;
4. матрица начальных данных $F = (\varphi (x,y))$, размера $(B + 1) \times ({{y}_{A}} + 1)$, где $(x,y) \in {{L}_{\beta }}$, для всех остальных значений (x, y) значения $\varphi (x,y) = 0$.
Для технической реализации алгоритма целесообразно отразить матрицы коэффициентов C и начальных данных $F$ зеркально отностельно горизонтальной оси. Поскольку координаты элементов матрицы коэффициентов разностного оператора и матрицы начальных данных в декартовой системе координат $(X,Y)$ не совпадают с их координатами в зеркально отраженной матрице (строка$ \times $столбец), то следует перейти из декартовой системы координат $\left( {D\left( {{{d}_{1}},{{d}_{2}}} \right)} \right)$ в “матричную” $\left( {M\left( {{{m}_{1}},{{m}_{2}}} \right)} \right)$ по правилу: $D\left( {{{d}_{1}},{{d}_{2}}} \right) \to M\left( {{{m}_{1}},{{m}_{2}}} \right)$, где ${{m}_{1}} = 1 + {{d}_{2}}$, ${{m}_{2}} = 1 + {{d}_{1}}$.
Например, элемент ${{c}_{{00}}}$ матрицы коэффициентов C, имеющий в декартовой системе координат координаты $\left( {{{d}_{1}},{{d}_{2}}} \right)$ = (0, 0), в “матричной” системе координат будет иметь координаты $({{m}_{1}},{{m}_{2}})$ = = (1, 1), а, например, элемент $\varphi $(1, 0) матрицы начальных данных $F$ в “матричной” системе координат будет иметь координаты (1, 2).
Далее необходимо будет проверить задачу Коши (2)–(3) на разрешимость, т.е. проверить, выполняется ли условие (4) для коэффициентов разностного оператора (1).
4. ПРИМЕР
Алгоритм был реализован в среде MatLab2014 32bit. Вычисления производились на машине Intel(R) Core(TM) i5-3330S CPU 2.70 GHz, 32bit, ОЗУ 4.00 Гб под управлением Windows 7 Корпоративная SP1. Время счета для приведенного примера составило менее 1 секунды.
В качестве примера рассмотрим задачу о распределении температуры в некотором образце. Требуется оценить распределение температуры в образце в течение некоторого времени, если заданы начальное распределение температуры в образце и изменение температуры на концах образца с течением времени. Для конкретизации задачи положим, что требуется определить температуру через четыре временных шага и четыре шага по координате.
Зафиксируем $\beta = ({{x}_{\beta }},m)$, ${{x}_{\beta }} = 2$, $m = 1$, $b = 3$, $B = 5$.
Для полиномиального разностного оператора
(6)
$\begin{gathered} P({{\delta }_{1}},{{\delta }_{2}}) = {{c}_{{00}}} + {{c}_{{10}}}{{\delta }_{1}} + \\ + \;{{c}_{{20}}}\delta _{1}^{2} + {{c}_{{30}}}\delta _{1}^{3} + {{c}_{{01}}}{{\delta }_{2}} + \\ + \;{{c}_{{11}}}{{\delta }_{1}}{{\delta }_{2}} + {{c}_{{21}}}\delta _{1}^{2}{{\delta }_{2}} + {{c}_{{31}}}\delta _{1}^{3}{{\delta }_{2}} \\ \end{gathered} $(7)
$\begin{gathered} {{c}_{{00}}}f(x,y) + {{c}_{{10}}}f(x + 1,y) + \\ + \;{{c}_{{20}}}f(x + 2,y) + {{c}_{{30}}}f(x + 3,y) + \\ + \;{{c}_{{01}}}f(x,y + 1) + {{c}_{{11}}}f(x + 1,y + 1) + \\ + \;{{c}_{{21}}}f(x + 2,y + 1) + \\ + \;{{c}_{{31}}}f(x + 3,y + 1) = 0,(x,y) \in \Pi , \\ f(x,y) = \varphi (x,y),(x,y) \in {{L}_{{\left( {2,1} \right)}}}, \\ \end{gathered} $Зададим матрицу коэффициентов полиномиального разностного оператора (6)
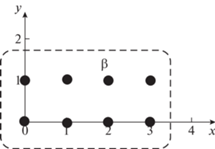
Расположение элементов матрицы $C$ в декартовой системе координат представлено на рис. 1.
Поставим задачу: найти значения функции $f(x,y)$ в точке $A$ с координатами (4, 4), т.е. $f$(4, 4).
Зададим матрицу начальных данных:
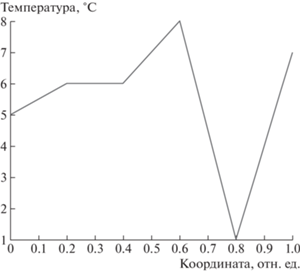
Распределение температуры в образце в начальный момент времени, т.е. последняя строка матрицы $F$, имеет форму, представленную на рис. 2.
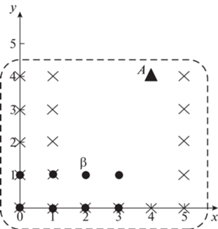
Расположение элементов матрицы $F$ в декартовой системе координат представлено на рис. 3.
1. Переход из декартовой системы координат в “матричную” осуществляется путем отражения матриц начальных данных и коэффициентов зеркально относительно горизонтальной оси, поэтому точка $\beta $ с координатами (2, 1) переходит в точку с координатами (2, 3) в “матричной” системе координат.
Пусть $p$ – количество столбцов матрицы коэффициентов, а $i$ – количество столбцов матрицы начальных данных. Тогда для рассматриваемого примера $p = 4$ и $i = 6$.
“Матричная” система координат для матрицы коэффициентов разностного оператора (6) имеет вид, представленный в табл. 1:
“Матричная” система координат для матрицы начальных данных $F$ имеет вид, представленный в табл. 2:
Таблица 2
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | $ \times $ | $ \times $ | $ \times $ | $ \times $ | $ \times $ | $ \times $ |
| 2 | $ \times $ | $ \times $ | $ \times $ | |||
| 3 | $ \times $ | $ \times $ | $ \times $ | |||
| 4 | $ \times $ | $ \times $ | $ \times $ | |||
| 5 | $ \times $ | $ \times $ | $A$ | $ \times $ |
В табл. 2 знак $ \times $ – начальные данные. Точка $A$ имеет координаты [5, 5 ] в “матричной” системе координат.
2. Проверка на разрешимость задачи Коши (7), т.е. выполняется ли условие (4) для коэффициентов полиномиального разностного оператора (6). Так как
3. Зеркальное отражение относительно горизонтальной оси матрицы коэффициентов C и матрицы начальных данных $F$:
4. Последняя строка в матрице ${{C}_{{work}}}$:
5. Получение общей Теплицевой матрицы [10, 11], размер которой зависит от искомого значения.
Для построения теплицевой матрицы необходимы два вектора $colum{{n}_{c}}$ и $ro{{w}_{c}}$. Пусть матрица $neiz{{v}_{1}}$ – несимметричная Теплицева матрица размера $\left( {i - p + 1} \right) \times \left( {i - p + 1} \right)$ (в рассматриваемом примере 3 × 3), построенная на основе правила, что элементы вектора $colum{{n}_{c}}$ – ее первый столбец, а элементы вектора $ro{{w}_{c}}$ – ее первая строка, причем первые элементы векторов $colum{{n}_{c}}$ и $ro{{w}_{c}}$ совпадают. В случае, если количество элементов в векторах $colum{{n}_{c}}$ и $ro{{w}_{c}}$ меньше $\left( {i - p + 1} \right)$, то вектор меньшего размера дополняется нулями. Элементы векторов $colum{{n}_{c}}$ и $ro{{w}_{c}}$ берутся из вектора $a$. В вектор $colum{{n}_{c}}$ попадают элементы, начиная с ${{c}_{\beta }} = {{c}_{{21}}}$ в порядке уменьшения номера элемента, т.е. $colum{{n}_{c}} = {{\left( {\begin{array}{*{20}{c}} {{{c}_{{21}}}}&{{{c}_{{11}}}}&{{{c}_{{01}}}} \end{array}} \right)}^{{\text{т}}}} = {{\left( {\begin{array}{*{20}{c}} {10}&3&1 \end{array}} \right)}^{{\text{т}}}}$, а в вектор $ro{{w}_{c}}$ попадают элементы, начиная ${{c}_{\beta }} = {{c}_{{21}}}$ в порядке увеличения номера элемента, т.е. rowc = = $\left( {\begin{array}{*{20}{c}} {{{c}_{{21}}}}&{{{c}_{{31}}}} \end{array}} \right)$ = (10 1). Поскольку длина вектора $ro{{w}_{c}}$ меньше $\left( {i - p + 1} \right)$, то дополним его нулем: $ro{{w}_{c}}$ = = (10 1 0). Таким образом, матрица $neiz{{v}_{1}}$ имеет вид
6. Решение системы линейных уравнений с целью нахождения значений $f\left( {x,y} \right)$, которые могут потребоваться для вычисления искомого значения в точке $A\left( {{{x}_{A}},{{y}_{A}}} \right)$.
Количество неизвестных для каждого значения $m$ (т.е. номера строки матрицы $F$ в декартовой системе координат), показывающего номер “слоя”, на каждом шаге алгоритма одинаково. Поэтому размер матрицы Теплица остается постоянным. На каждом шаге алгоритма происходит запись найденных значений функции $f\left( {x,y} \right)$ в матрицу начальных данных $F$.
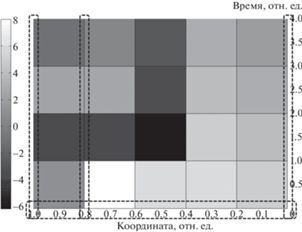
На рис. 4 представлено итоговое распределение температуры в образце в течение четырех временных шагов.
Рис. 4.
Изменение температуры в образце в течение 4 временных шагов (пунктиром выделено множество начальных данных).
7. Переход к декартовой системе координат $f(4,4)$ = F[5, 5].
Output: значение функции $f\left( {x,y} \right)$ в искомой точке $A\left( {4,\;4} \right)$ равно 0.19.
Входными данными для работы алгоритма в этом случае будут:
1. $\beta = (2,\;1)$;
2. матрица коэффициентов
3. $A = (4,\;4);$
4. матрица начальных данных
| Алгоритм 1: Пример оформления алгоритма | |||||||||||||||||
| Input: Точка β, матрица коэффициентов C, точка A, матрица начальных данных F. | |||||||||||||||||
| Output: Значение функции $f(x,y)$ в точке $A$ с координатами $({{x}_{A}},{{y}_{A}})$. | |||||||||||||||||
| begin | |||||||||||||||||
| $i: = $ количество столбцов матрицы $F$ | |||||||||||||||||
| $p: = $ количество столбцов матрицы $C$ | |||||||||||||||||
| $w: = $ количество строк матрицы $C$ | |||||||||||||||||
| $neiz{{v}_{1}}: = $ теплицевая матрица размера $\left( {i - p + 1} \right) \times \left( {i - p + 1} \right)$ | |||||||||||||||||
| $v: = $ количество строк в матрице $neiz{{v}_{1}}$ | |||||||||||||||||
| ${{\beta }_{1}}: = $ координаты точки $\beta $ в “матричной” системе координат | |||||||||||||||||
| ${{A}_{1}}: = $ координаты точки $A$ в “матричной” системе координат | |||||||||||||||||
| if$\left| {C\left( {{{\beta }_{1}}\left( 1 \right),{{\beta }_{1}}\left( 2 \right)} \right)} \right| \leqslant \sum \left( {\left| {C\left( {{{\beta }_{1}}\left( 1 \right),:} \right)} \right|} \right) - \left| {C\left( {{{\beta }_{1}}\left( 1 \right),{{\beta }_{1}}\left( 2 \right)} \right)} \right|$ | |||||||||||||||||
| then | |||||||||||||||||
| return Ошибка ввода матрицы C | |||||||||||||||||
| ${{C}_{{work}}}: = $ матрица $C$, зеркально отраженная относительно горизонтальной оси | |||||||||||||||||
| ${{F}_{{work}}}: = $ матрица $F$, зеркально отраженная относительно горизонтальной оси | |||||||||||||||||
| $a: = $ последняя строка в матрице ${{C}_{{work}}}$ | |||||||||||||||||
| $e: = {{\beta }_{1}}(2)$ | |||||||||||||||||
| $colum{{n}_{c}}: = zeros(i - (p - 1),1)$ | |||||||||||||||||
| $col: = 1$ | |||||||||||||||||
| while$e \geqslant 1$do | |||||||||||||||||
| $colum{{n}_{c}}(col): = a(e)$ | |||||||||||||||||
| $col: = col + 1$ | |||||||||||||||||
| $e: = e - 1$ | |||||||||||||||||
| $ro{{w}_{c}}: = zeros(l,i - (p - 1))$ | |||||||||||||||||
| $e: = {{\beta }_{1}}(2)$ | |||||||||||||||||
| $r: = 1$ | |||||||||||||||||
| for$h$from${{\beta }_{1}}(2)$to$l$do | |||||||||||||||||
| $ro{{w}_{c}}(r) = a(e)$ | |||||||||||||||||
| $r: = r + 1$ | |||||||||||||||||
| $e: = e + 1$ | |||||||||||||||||
| $neiz{{v}_{1}}: = toeplitz(colum{{n}_{c}},ro{{w}_{c}})$ | |||||||||||||||||
| for$k$from${{\beta }_{1}}(1)$to${{A}_{1}}(1)$do | |||||||||||||||||
| $b: = zeros({v},1)$ | |||||||||||||||||
| for$i$from 0 to${v} - 1$do | |||||||||||||||||
| $P: = {{F}_{{work}}}((k - (w - 1)):k,(1 + i):i + p)$ | |||||||||||||||||
| ${{P}_{{work}}}: = P \circ {{C}_{{work}}}$ | |||||||||||||||||
| $(b(i + 1) = - (sum(sum({{P}_{{work}}})))$ | |||||||||||||||||
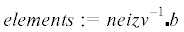 |
|||||||||||||||||
| for$s$from$1$tovdo | |||||||||||||||||
| ${{F}_{{work}}}(k,e - 1 + s): = elements(s)$ | |||||||||||||||||
| return$f\left( {{{x}_{A}},{{y}_{A}}} \right)$ | |||||||||||||||||
Список литературы
Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. М.: Мир, 1988.
Изерман Р. Цифровые системы управления. М.: Мир, 1984. 541 с.
Рябенький В.С. Введение в вычислительную математику: учеб. пособие, изд. 2-е, исправл. М. : ФИЗМАТЛИТ, 2000. 296 с.
Стенли Р. Перечислительная комбинаторика: Пер. с англ. М.: Мир, 1990. 440 с.
Стенли Р. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции: Пер. с англ. М.: Мир, 2005. 767 с.
Ляпин А.П. Последовательности Риордана и двумерные разностные уравнения // Журн. СФУ. Сер. Матем. и физ. 2009. Т. 2. Вып. 2. С. 210–220.
Кытманов А.А., Ляпин А.П., Садыков Т.М. Алгоритм вычисления рациональной производящей функции решения задачи Коши двумерного разностного уравнения с постоянными коэффициентами // Программирование. 2017. Вып. 2. С. 54–62.
Апанович М.С., Ляпин А.П., Шадрин К.В. Применение методов компьютерной алгебры для вычисления решения задачи Коши для двумерного разностного уравнения в точке // Программирование. 2021. Вып. 1. С. 1–5.
Рогозина М.С. Разрешимость разностной задачи Коши для многослойных неявных разностных схем // Вестник СибГАУ. Математика, механика, информатика. 2014. Т. 55. № 3. С. 126–130.
Иохвидов И.С. Ганкелевы и теплицевы матрицы. М.: Наука, 1974. 264 с.
Апанович М.С., Ляпин А.П., Шадрин К.В. Вычисление последовательности главных миноров теплицевой ленточной матрицы // Прикладная математика и физика. 2020. Т. 52. № 1. С. 5–10.
Дополнительные материалы отсутствуют.
Инструменты
Программирование