1. На главную
  2. Электронные версии
  3. Программирование
  4. № 2, 2023

Программирование, 2023, № 2, стр. 54-68

РАЗРАБОТКА АЛГОРИТМИЧЕСКОГО И ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ МОДЕЛИРОВАНИЯ УПРАВЛЯЕМЫХ ДИНАМИЧЕСКИХ СИСТЕМ С ПРИМЕНЕНИЕМ СИМВОЛЬНЫХ ВЫЧИСЛЕНИЙ И СТОХАСТИЧЕСКИХ МЕТОДОВ

А. В. Демидова a, *, О. В. Дружинина b, **, О. Н. Масина c, ***, А. А. Петров c, ****

a Российский университет дружбы народов
117198 Москва, ул. Миклухо-Маклая, д. 6, Россия

b Федеральный исследовательский центр “Информатика и управление” РАН
119333 Москва, ул. Вавилова, д. 44, кор. 2, Россия

c Елецкий государственный университет им. И.А. Бунина
399770 Липецкая обл., Елец, ул. Коммунаров, д. 28, Россия

* E-mail: demidova-av@rudn.ru
** E-mail: ovdruzh@mail.ru
*** E-mail: olga121@inbox.ru
**** E-mail: xeal91@yandex.ru

Поступила в редакцию 01.07.2022
После доработки 29.07.2022
Принята к публикации 30.10.2022

Полный текст (PDF)

Аннотация

Разработка нового программного обеспечения для решения задач синтеза и анализа управляемых моделей с учетом детерминированного и стохастического описания является актуальным научным направлением. В статье представлены результаты разработки программного комплекса моделирования динамических систем, поведение которых может быть описано одношаговыми процессами. В качестве примеров рассмотрены модели популяционной динамики. Программный комплекс с использованием на входе детерминированного описания модели позволяет получить соответствующую стохастическую модель в символьном виде, а также провести детальный анализ модели (расчет траекторий в детерминированном и стохастическом случаях, поиск управляющих функций, графическая визуализация результатов). Важным аспектом разработки программного комплекса является применение методов компьютерной алгебры в задачах анализа модели и синтеза управлений. В программном комплексе реализованы методы и алгоритмы, базирующиеся на детерминированных и стохастических методах Рунге–Кутты, методах теории устойчивости и теории управления, методе построения самосогласованных стохастических моделей, алгоритмах численной оптимизации и искусственного интеллекта. Предложенный программный комплекс разрабатывается на основе языков высокого уровня Python и Julia. В качестве базового инструментального программного обеспечения используются высокопроизводительные библиотеки для векторно-матричных расчетов, библиотеки символьных вычислений, библиотеки для численного решения обыкновенных дифференциальных уравнений, библиотеки алгоритмов глобальной оптимизации.

1. ВВЕДЕНИЕ

Разработка инструментального обеспечения для моделирования динамических систем с применением символьных вычислений является актуальной проблемой [1–4]. В частности, теоретический и прикладной интерес представляет разработка средств получения формализованного представления динамических моделей популяционной динамики исходя из общего описания принципов взаимодействия популяций. Проблема формализации и изучения многомерных динамических моделей популяционной динамики относится к многоплановым и многоаспектным проблемам, требующим как понимания сущности процессов взаимодействия фазовых переменных, так и привлечения современных методов теории детерминированных и стохастических дифференциальных уравнений, теории устойчивости, теории управления.

Развиваемый в настоящей работе подход к разработке инструментально-методического обеспечения базируется на реализации возможностей построения и исследования нелинейных динамических систем, поведение которых может быть описано одношаговыми процессами. Как известно, класс одношаговых процессов охватывает многие процессы физики, химии, экологии, демографии, социологии. Для дифференциальных уравнений, описывающих одношаговые процессы, применяется ряд методов интегрирования, например, явные и неявные методы Рунге–Кутты [5]. Особый интерес для численного изучения представляют стохастические дифференциальные уравнения, моделирующие одношаговые процессы [6, 7]. Однако реализация стохастических методов Рунге–Кутты в рамках прикладных пакетов и математических библиотек развиты недостаточно. Для конкретных научных задач часто приходится разрабатывать собственную реализацию для численного решения стохастических дифференциальных уравнений [8–11]. В [10] дано описание комплекса программ, предназначенного для моделирования одношаговых стохастических процессов и реализующего модифицированные методы Рунге–Кутты. Указанный программный комплекс реализован на языке программирования Python с использованием библиотек NumPy и SymPy.

Отметим, что в [8–11] рассматривались такие задачи реализации алгоритмов моделирования одношаговых стохастических процессов, которые в качестве входных параметров используют вектор сносов и матрицу диффузии в уравнении Фоккера–Планка. В настоящей работе проблема ставится шире: требуется разработать единый инструмент для формализованного построения детерминированных моделей, поиска состояний равновесия с помощью символьных вычислений, а также усовершенствовать формализованное построение стохастических моделей. Кроме того, требуется учитывать управляющие воздействия в системе и построить управляющие функции с применением современных алгоритмов глобальной оптимизации [12]. Важность создания алгоритмов численной оптимизации в контексте данного научного направления связана с расширением требований к управлению экосистемами, в частности к управлению численностью популяций ценных промысловых видов.

В процессе стохастического моделирования возникает вопрос о механизме ввода стохастических членов в детерминированное уравнение [13, 14]. Часто стохастизация выполняется аддитивно с учетом добавления члена со стохастической переменной. Однако большей информативностью обладает подход, базирующийся на использовании стохастической части, согласованной с детерминированной. Этот подход реализуется в случае, если обе части (детерминированная и стохастическая) получаются из одного уравнения. Такую возможность предоставляет метод построения самосогласованных стохастических моделей [8, 11, 15]. В основе данного метода лежит комбинаторная методология [16, 17]. Данный метод предполагает, что эволюция во времени многомерных систем рождения-гибели может быть рассмотрена как результат индивидуальных взаимодействий между элементами этой системы. Согласно этому методу для описания системы используется основное кинетическое уравнение (Master equation). Это уравнение описывает эволюцию распределения вероятностей в цепи Маркова с непрерывным временем и представляет собой балансовое уравнение для вероятности каждого состояния системы. Кроме того, предполагается, что вероятность перехода из одного состояния в другое состояние (являющееся следствием рассматриваемого взаимодействия) пропорциональна числу возможных взаимодействий данного типа. Указанный метод позволяет выполнить переход к стохастической модели, важным этапом изучения которой является оценка влияния стохастики на качественные свойства системы.

В настоящей работе в качестве примеров реализации рассмотрены задачи моделирования систем популяционной динамики. Необходимость изучения экологических систем с различными взаимосвязями между подсистемами и изменение структуры этих взаимосвязей в процессе функционирования часто приводят к построению математических моделей, аналитическое исследование которых весьма затруднительно. Об актуальности проблем математической биологии свидетельствуют публикации последнего десятилетия (например, [18, 19]). Различные обобщения и модификации классических моделей экологических процессов [20] рассматривались в многочисленных работах исследователей (см., например, [21–23]). При аналитическом исследовании эффективно применяются методы Ляпунова [24–26]. В [27–31] предложено построение новых детерминированных моделей популяционной динамики, разработаны конкретизации метода стохастических самосогласованных моделей. Проведено численное исследование, дан сравнительный анализ траекторий. Поставлены и в ряде случаев решены задачи оптимального управления с разработкой и реализацией ряда алгоритмов численной оптимизации.

Модули разработанного в рамках настоящего исследования программного комплекса решают следующие задачи: расчет траекторий детерминированных динамических систем размерности $n \geqslant 2$; получение символьных выражений для перехода к стохастическим моделям; детальная формализация структуры стохастических систем; поиск управляющих функций в детерминированном случае. Программный комплекс включает в себя библиотеку алгоритмов численной оптимизации; библиотеку нейронных сетей и машинного обучения; графический модуль.

Предложенный программный комплекс разрабатывается на основе языков высокого уровня Python [32–36] и Julia [37]. В качестве базового инструментального программного обеспечения используются высокопроизводительные библиотеки для векторно-матричных расчетов (NumPy, LinearAlgebra.jl), библиотеки символьных вычислений (SymPy), библиотеки для численного решения обыкновенных дифференциальных уравнений (SciPy, DifferentialEquations.jl), библиотеки алгоритмов глобальной оптимизации (дифференциальная эволюция, генетический алгоритм, NES из состава BlackBoxOptim.jl). К задачам, решаемым в статье с помощью методов компьютерной алгебры, относятся нахождение состояний равновесия динамических моделей с помощью библиотеки SymPy, построение стохастических моделей в символьном виде (авторские программные модули), синтез управляющих функций с использованием полиномиальной регрессии и библиотек глобальной оптимизации.

Структура статьи следующая. В разделе 2 проведен сравнительный анализ используемого в работе программного обеспечения и средств символьных вычислений, приведена общая структура разработанного программного комплекса. В разделе 3 описано методическое обеспечение для построения детерминированной модели. В разделе 4 представлено алгоритмическое и программное обеспечение стохастического моделирования. В разделе 5 рассмотрены принципы построения модуля программного комплекса для получения управляющих функций. Раздел 6 посвящен вопросам получения и визуализации численных решений. В разделе 7 представлены результаты тестирования производительности в рамках отдельных задач, решаемых программным комплексом.

2. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ИНСТРУМЕНТАЛЬНОГО ОБЕСПЕЧЕНИЯ ДЛЯ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКИХ СИСТЕМ

В настоящем разделе мы проводим анализ инструментального обеспечения для моделирования динамических систем, поведение которых может быть описано одношаговыми процессами, при этом накладываются требования учета управляющих воздействий и перехода к стохастизации. Новые эффекты в динамических системах часто связаны с управляющими воздействиями и необходимостью перехода к стохастической структуре модели, обеспечивающей более реалистичное описание свойств. Используемое в работе инструментальное обеспечение должно предоставлять эффективные средства для решения комплекса задач в рамках изучаемой проблемы:

• построение детерминированных моделей динамических систем;

• построение стохастических моделей динамических систем;

• численное решение обыкновенных дифференциальных уравнений и стохастических дифференциальных уравнений;

• аналитический вывод в символьном виде (в частности, символьное решение систем нелинейных уравнений для поиска состояний равновесия);

• матрично-векторные расчеты;

• построение логических регуляторов (в том числе на основе искусственного интеллекта);

• глобальная параметрическая оптимизация.

Помимо возможностей инструментального обеспечения особое внимание уделяется доступности результатов. По этой причине в рамках исследования используется открытое программное обеспечение.

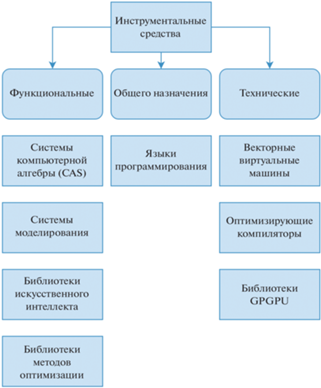
Для используемых в работе инструментальных программных средств можно выделить три категории, которые представлены на рис. 1.

Рис. 1.

Дерево инструментальных средств.

Функциональные инструментальные средства непосредственно направлены на решение задач исследования. По внутренней структуре указанные средства представляют собой интегрированные комплексы высокоэффективных алгоритмов. Технические инструментальные средства направлены на ускорение разработки, улучшение читаемости программного кода и эффективное использование современных программно-аппаратных платформ. Инструментальные средства общего назначения направлены на решение широкого спектра задач, например, на интеграцию разработанных модулей в единый программный комплекс.

Мы используем инструментальные средства, приведенные в табл. 1.

Таблица 1.

Перечень инструментальных средств, использованных при разработке программного комплекса

Инструментальные средства
Функциональные Технические Общего назначения
SymPy/SciPy (Python) NumPy (Python) Python
Symbolics.jl (Julia) Numba (Python) Julia
Maxima ArrayFire (Python, Julia)  
BlackBoxOptim.jl (Julia) Matplotlib (NumPy)  

В качестве основного языка разработки используется мультипарадигменный язык Python в сочетании с библиотеками SymPy/SciPy, NumPy, Matplotlib. Пакет SymPy/SciPy представляет собой решение CAS-класса (CAS – англ. Computer Algebra Software, система компьютерной алгебры), которое позволяет решать ряд научных задач с использованием инструментария, близкого по возможностям к коммерческим решениям. Данный пакет содержит, в том числе, инструменты численного решения обыкновенных дифференциальных уравнений, а также библиотеки глобальной параметрической оптимизации (дифференциальная эволюция, имитация отжига и другие методы) [38].

Тем не менее, существенным недостатком указанного инструментального ПО является относительно невысокая производительность в ряде задач, среди которых можно отметить численное решение дифференциальных уравнений, а также аналитический вывод выражений. Указанный недостаток непосредственно влияет на время поиска состояний равновесия модели, а также на возможности применения машинного обучения с подкреплением для управления. Более подробно вопросы производительности рассмотрены в разделе 7.

Для того, чтобы компенсировать указанный недостаток, возможно использование дополнительных инструментальных средств, позволяющих достичь более высокой производительности разработанного ПО в определенных задачах.

Для решения обыкновенных дифференциальных уравнений при реализации машинного обучения с подкреплением мы используем язык Julia с библиотеками bboxoptim.jl и Symbolics.jl. Библиотека Symbolics.jl, аналогично SymPy, представляет собой решение CAS-класса, которое может быть расширено библиотекой моделирования динамических систем ModelingToolkit.jl. Для нахождения состояний равновесия модели используются пакеты SymPy и Maxima, обеспечивающие высокую производительность в символьных вычислениях.

Отдельным вопросом является выявление условий эффективного применения технических инструментальных средств для увеличения производительности разработанного ПО при решении описанных выше задач моделирования. Совместно с языком Python используется оптимизирующий компилятор Numba, который позволяет многократно увеличить скорость выполнения некоторых участков кода благодаря использованию JIT-компиляции и автоматическому распараллеливанию. Кроме того, важной задачей является реализация гетерогенных вычислений (в частности, GPGPU) с высокой степенью переносимости в рамках разрабатываемого программного комплекса. Для интеграции указанной возможности в программный комплекс используется пакет ArrayFire, который позволяет производить “ленивые” вычисления с применением широкого спектра ускорителей вычислений. Преимуществами указанного пакета является высокий уровень абстракции по отношению к аппаратному обеспечению, что дает высокую переносимость разработанного программного обеспечения.

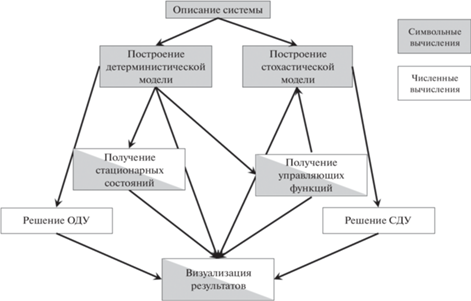
На основе выбранных инструментальных средств разработан авторский программный комплекс для проведения всестороннего анализа систем с взаимодействующими популяциями. Структура указанного программного комплекса представлена на рис. 2. Реализация проведена с использованием языка Python с применением компьютерной алгебры. При создании программного комплекса использован ряд результатов, полученных в [10].

Рис. 2.

Структура программного комплекса.

Отметим, что разработанный программный комплекс комбинирует численные и символьные вычисления для увеличения степени универсальности по отношению к многообразию изучаемых систем. В последующих разделах основные принципы работы программного комплекса рассматриваются на примерах, конкретизациях и обобщениях. Листинги обсуждаемых в настоящей статье программ и примеры их использования доступны по адресу https://github.com/demidav/one-step-to-sdu.

3. ПОСТРОЕНИЕ ДЕТЕРМИНИРОВАННОЙ МОДЕЛИ

Модели взаимодействия популяций в общем виде можно записать в форме векторного дифференциального уравнения:

(3.1)
$\dot {x} = {{f}_{p}}\left( x \right),\quad x \in {{\mathbb{R}}^{n}},$
где ${{f}_{p}}(x)$ – параметрическая функция, определяющая взаимодействия в системе, x – фазовый вектор плотности популяций. Конкретный вид параметрической функции определяется существенными для модели факторами (наличием конкуренции, мутуализма, миграции, видом трофических цепей).

Кроме того, интерес представляет изучение модификаций модели (3.1) с учетом воздействия внешних факторов, в частности, управления. В таком случае уравнение (3.1) можно записать в виде:

(3.2)
$\dot {x} = {{f}_{p}}\left( x \right) - u\left( {x,t} \right),\quad x \in {{\mathbb{R}}^{n}},$
где $u(x,t)$ – управление. Характерной особенностью данной модели является ограничение на управление $u(x,t) > 0$, поскольку непосредственное управление возможно, как правило, только путем изъятия особей из популяции. Пример управляемой модели рассматривается в разделе 0.

Рассмотрим модель “жертва–два хищника” без управления, рассмотренную в работе [22]. Уравнения указанной модели имеют вид

(3.3)
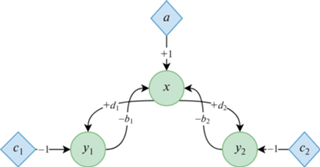
$\begin{gathered} \dot {x} = ax - {{b}_{1}}x{{y}_{1}} - {{b}_{2}}x{{y}_{2}}, \\ {{{\dot {y}}}_{1}} = - {{c}_{1}}{{y}_{1}} + {{d}_{1}}x{{y}_{1}},\quad {{{\dot {y}}}_{2}} = - {{c}_{2}}{{y}_{2}} + {{d}_{2}}x{{y}_{2}}, \\ \end{gathered} $
где $x$ – плотность популяции жертвы, ${{y}_{1}}$, ${{y}_{2}}$ – плотности популяции хищника, $a$ – коэффициент естественного прироста популяции жертвы, ${{c}_{1}},$ ${{c}_{2}}$ – коэффициенты естественной смертности хищника, ${{b}_{1}}$, ${{b}_{2}}$ – коэффициенты убыли популяции жертв, ${{d}_{1}}$, ${{d}_{2}}$ – коэффициенты прироста популяции хищника. Модель (3.3) можно представить в виде графа взаимодействий, который имеет вид, представленный на рис. 3.

Рис. 3.

Граф взаимодействий модели (3.3).

На рис. 3 кругами обозначены плотности популяций, ромбами обозначены источники естественного прироста/смертности, ребрами графа обозначены взаимодействия между популяциями.

Важным вопросом при изучении моделей вида (3.3) является существование положительных состояний равновесия. Для предварительного анализа устойчивости модели (3.3) необходимо найти особые точки для уравнений системы, что приводит к необходимости решения уравнений вида

${{f}_{p}}\left( x \right) = 0,\quad x \in {{\mathbb{R}}^{n}},$
что для (3.3) эквивалентно

$\begin{gathered} ax - {{b}_{1}}x{{y}_{1}} - {{b}_{2}}x{{y}_{2}} = 0, \\ - {{c}_{1}}{{y}_{1}} + {{d}_{1}}x{{y}_{1}} = 0,\quad - {{c}_{2}}{{y}_{2}} + {{d}_{2}}x{{y}_{2}} = 0. \\ \end{gathered} $

Для символьного решения уравнений используется функция solve из состава библиотеки SymPy. Особые точки для модели (3.3) имеют вид

$\left[ {(0,0,0),\;\left( {\frac{{{{c}_{1}}}}{{{{d}_{1}}}},\frac{a}{{{{b}_{1}}}},0} \right),\left( {\frac{{{{c}_{2}}}}{{{{d}_{2}}}},0,\frac{a}{{{{b}_{2}}}}} \right)} \right].$

Следует отметить, что отсутствие положительных нетривиальных решений для уравнений (3.3) не является достаточным условием невозможности перманентного сосуществования популяций.

Упрощением модели (3.3) является модель, уравнения которой имеют вид:

(3.4)
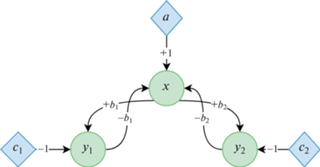
$\begin{gathered} \dot {x} = ax - {{b}_{1}}x{{y}_{1}} - {{b}_{2}}x{{y}_{2}}, \\ {{{\dot {y}}}_{1}} = - {{c}_{1}}{{y}_{1}} + {{b}_{1}}x{{y}_{1}}, \\ {{{\dot {y}}}_{2}} = - {{c}_{2}}{{y}_{2}} + {{b}_{2}}x{{y}_{2}}, \\ \end{gathered} $
где ${{b}_{1}}$, ${{b}_{2}}$ – коэффициенты трофических взаимодействий. Модель (3.4) представляет собой “уравновешенный” вариант модели (3.3), где скорость поглощения популяции жертвы соответствует скорости прироста популяции хищников. Граф указанной модели представлен на рис. 4.

Рис. 4.

Граф модели (3.4).

Обозначения аналогичны рис. 3. Состояния равновесия модели (3.4) имеют вид

$\left[ {(0,0,0),\;\left( {\frac{{{{c}_{1}}}}{{{{b}_{1}}}},\frac{a}{{{{b}_{1}}}},0} \right),\left( {\frac{{{{c}_{2}}}}{{{{b}_{2}}}},0,\frac{a}{{{{b}_{2}}}}} \right)} \right].$

По аналогии с моделью (3.3), модель (3.4) не имеет положительных нетривиальных решений. Следует отметить, что модели (3.3) и (3.4) оперируют рядом допущений (в частности, отсутствует внутривидовая конкуренция и конкуренция между жертвами). Однако, качественный и численный анализ указанных моделей, а также построение управлений является необходимым для апробации разработанного программного комплекса. При исследовании моделей вида (3.3) и (3.4), а также их многомерных модификаций и обобщений возникают задачи, связанные с символьными вычислениями. Разработанный программный комплекс позволяет выполнять исследование устойчивости многофакторных моделей.

4. АЛГОРИТМИЧЕСКОЕ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТОХАСТИЧЕСКОЙ МОДЕЛИ

В основе рассматриваемого подхода к моделированию лежит метод построения самосогласованных стохастических моделей [8–11]. При использовании данного метода динамика изменения численности популяций рассматривается как случайный одношаговый процесс. На первом этапе необходимо сформулировать в терминах одношаговых процессов все взаимодействия, проходящие в системе между ее элементами. Далее требуется составить схему взаимодействия, под которой понимается символическая запись всех возможных взаимодействий между элементами системы с помощью оператора состояния системы и оператора изменения состояния системы. На основе схемы взаимодействий с помощью преобразований можно получить коэффициенты сноса и диффузии для уравнения Фоккера–Планка, что позволяет записать это уравнение и эквивалентное ему стохастическое дифференциальное уравнение в форме Ланжевена. Таким образом, можно одновременно получить как детерминированное описание системы, которому соответствует вектор сносов уравнения Фоккера–Планка, так и стохастическое описание, которое обеспечивается стохастическим дифференциальным уравнением в форме Ланжевена. Далее приведен алгоритм применения метода построения самосогласованных стохастических моделей.

Входные данные: Описание системы
Выходные данные: Детерминированная и стохастическая модели (системы ОДУ и СДУ)
 begin
  1. Добавление взаимодействий в модель
  2. Построение схемы взаимодействия модели
  3. Получение операторов состояния системы из схемы взаимодействия
  4. Получение оператора изменения состояния системы
  5. Получение интенсивностей переходов
  6. Получение коэффициентов уравнения Фоккера–Планка
 end

Алгоритм 1: Алгоритм применения метода построения самосогласованных стохастических моделей.

Опишем основные этапы этого алгоритма более подробно.

4.1. Описание системы и построение схемы взаимодействия

В [10] были формализованы шаги (3–6), в данной работе сделана формализация 1 и 2 шагов, а именно, формализация определения уравнений и построение схемы взаимодействия. Таким образом, в качестве входных данных используется не схема взаимодействия, а описание взаимодействий, имеющихся в системе, что упрощает построение.

Для этого был реализован класс PopModel с использование библиотеки sympy и символьных вычислений. Исходными данными является описание происходящих в системе взаимодействий. Вызов конструктора PopModel(n) создает такой объект класса, который является формальной моделью системы, содержащей описание всех взаимодействий, происходящих в системе. Здесь $n$ – это размерность системы. Для класса PopModel реализованы следующие методы:

• interaction(self,type_int);

• coef(self);

•adder(self,type_int,id_pop_1, id_pop_2,coef=0);

• matr_M(self);

• matr_N(self);

• display_infos(self,model,X,coef).

Метод adder(self, type_int, id_pop_1, id_pop_2, coef=0) является основным методом класса для добавления уравнений в схему взаимодействия. type_int – тип взаимодействия; id_pop_1 – идентификатор 1-й взаимодейтствующей популяции, id_pop_2 – идентификатор 2‑й взаимодействующей популяции (соответствует индексу элемента в векторе состояния системы), coef – коэффициенты взаимодействия (по умолчанию принимает значение ki).

Метод interaction(self,type_int) – вспомогательный метод, содержащий описание различных взаимодействий. В моделировании популяционных систем принято выделять такие виды взаимодействий, как естественное размножение, естественная гибель, конкуренция, симбиоз, отношения хищник-жертва и др [22]. Типы взаимодействий, реализованных в классе PopModel представлены в табл. 2.

Таблица 2.

Описание параметров метода interaction() класса PopModel

type_int id_pop_1 id_pop_2 Тип взаимодействия
 1 $i$ 0 Естественное размножение
 2 $i$ 0 Естественная гибель
 3 $i$ $j$ Симбиоз
 4 $i$ $j$ Хищник–жертва
 5 $i$ 0 Внутривидовая конкуренция
 6 $i$ $j$ Межвидовая конкуренция
 7 $i$ $j$ Миграция

Метод coef(self) – вспомогательный метод, используется для определения коэффициентов взаимодействия, если они не заданы пользователем.

Методы matr_M(self) и matr_N(self) служат для получения матриц $M$ и $N$ в символьном виде, описывающих состояние системы до взаимодействия и после него.

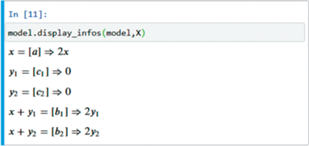
Метод display_infos(self,model,X) предназначен для символьного отображения схемы взаимодействия.

Пример реализации. Для верификации полученных результатов рассмотрим трехмерную популяционную модель “два хищника–жертва” вида (3.4). В данной модели учитывается естественное размножение жертвы, естественная смертность хищников, а также убыль популяции жертвы и прирост популяции хищников происходит за счет взаимодействий типа “хищник–жертва”.

Импортируем необходимые библиотеки:

import sympy as sp

import numpy as np

import IS

Зададим вектор состояний системы x = (x, ${{y}_{1}},{{y}_{2}})$ в символьном виде:

X = sp.Matrix(['x', 'y_1', 'y_2'])

Создадим объект класса размерности 3:

model = IS.PopModel(3)

Добавим описание взаимодействий:

model.adder(type_int=1,1,0,"a")

model.adder(type_int = 2,2,0,"c_1")

model.adder(type_int = 2,3,0,"c_2")

model.adder(type_int = 4,1,2,"b_1")

model.adder(type_int = 4,1,3,"b_2")

В данном описании первая строка описывает размножение жертв (type_int=1, id_pop_1=1). Строки 2 и 3 соответствуют естественной убыли популяций хищников (type_int=2, id_pop_1=2 и id_pop_1=3 соответственно). Строки 4 и 5 описывают отношения типа хищник–жертва (type_int=4) жертвы с первым хищником (id_pop_1=1, id_pop_2=2) и со вторым хищником (id_pop_1=1, id_pop_2=3).

Далее с помощью метода display_infos можно вывести схему взаимодействия. При использовании интерактивной оболочки Jupyter вывод будет иметь вид, представленный на рис. 5.

Рис. 5.

Результат вывода метода display_infos.

После получения схемы взаимодествия можно перейти к этапу построения стохастических дифференциальных уравнений.

4.2. Построение коэффициентов уравнения Фоккера–Планка

Подробное описание модуля (IStoDE.py) получения коэффициетов уравнения Фоккера–Планка из схемы взаимодействия дано в [10]. Здесь дадим краткое описание. Алгоритм получения коэффициентов уравнения Фоккера–Планка из схемы взаимодействия (шаги 3–6 алгоритма 1) реализован как последовательность операций над векторными данными.

В качестве входных данных принимаются матрицы M и N (атрибуты объекта класса PopModel) состояний системы до взаимодействия и после, векторы K_plus и K_minus – коэффициенты взаимодействия и вектор X – вектор состояния системы. В качестве результата получаем символьную запись коэффициентов уравнения Фоккера–Планка. Использование библиотеки SymPy позволяет получить также и код этих коэффициентов в TeX, что упрощает их чтение.

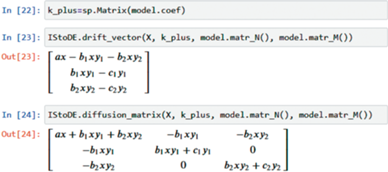
Основными функциями данного модуля являются drift_vector для получения вектора сносов A и diffusion_matrix для получения матрицы диффузии В.

Пример реализации. На рис. 6 представлен результат работы функций получения коэффициентов уравнения Фоккера–Планка для модели (3.4).

Рис. 6.

Результат вывода функций drift_vector и diffusion_matrix.

Согласно рис. 6, вектор сносов полностью соответствует правой части системы уравнений для модели (3.4), что позволяет использовать этот вектор для исследования детерминированного поведения системы.

В результате проведенных символьных вычислений мы получаем стохастическую и детерминированную модели популяционной динамики. Далее могут быть применены остальные модули программного комплекса для исследования системы, такие как добавление и исследование управления, символьное и численное получение стационарных состояний системы, получение численных решений.

5. БАЗОВЫЙ АЛГОРИТМ МОДУЛЯ ПРОГРАММНОГО КОМПЛЕКСА ДЛЯ ПОЛУЧЕНИЯ УПРАВЛЯЮЩИХ ФУНКЦИЙ

С учетом управляющих воздействий модель (3.4) можно записать в виде

(5.1)
$\begin{gathered} \dot {x} = ax - {{b}_{1}}x{{y}_{1}} - {{b}_{2}}x{{y}_{2}} - {{u}_{1}}(t)x, \\ {{{\dot {y}}}_{1}} = {{c}_{1}}{{y}_{1}} + {{d}_{1}}x{{y}_{1}} - {{u}_{2}}(t){{y}_{1}}, \\ {{{\dot {y}}}_{2}} = - {{c}_{2}}{{y}_{2}} + {{d}_{2}}x{{y}_{2}} - {{u}_{3}}(t){{y}_{2}}, \\ \end{gathered} $
где ${{u}_{1}}$, ${{u}_{2}}$, ${{u}_{3}}$ – функции управления. Рассматривается задача оптимального управления, состоящая в построении такого управления, которое позволяет с учетом выбранного критерия качества реализовать траекторию L при условиях:

$\begin{gathered} x(0) = {{x}_{0}},\quad {{y}_{1}}(0) = {{y}_{{10}}},\quad {{y}_{2}}(0) = {{y}_{{20}}}, \\ x({{t}_{1}}) = {{x}_{1}},\quad {{y}_{1}}({{t}_{1}}) = {{y}_{{11}}},\quad {{y}_{2}}({{t}_{2}}) = {{y}_{{21}}}. \\ \end{gathered} $

Будем рассматривать функции управления в виде нормированных полиномов. Примем

$U = \left( {\begin{array}{*{20}{c}} {{{u}_{1}}} \\ {{{u}_{2}}} \\ {{{u}_{3}}} \end{array}} \right).$

С учетом полиномиального управления имеет место равенство

$U = \left\| {PT} \right\|,\quad P = \left( {\begin{array}{*{20}{c}} {{{p}_{{11}}}}&{{{p}_{{12}}}}&{{{p}_{{13}}}} \\ {{{p}_{{21}}}}&{{{p}_{{22}}}}&{{{p}_{{23}}}} \\ {{{p}_{{31}}}}&{{{p}_{{32}}}}&{{{p}_{{33}}}} \end{array}} \right),$
где P – матрица коэффициентов, $T = (1,t,{{t}^{2}}){\kern 1pt} *$.

Следует отметить, что размерность матрицы коэффициентов определяет порядок управляющих полиномов, а нормирование матричного произведения осуществляется построчно. С учетом того, что начальные условия для системы (5.1) известны, критерий оптимальности можно записать в виде:

$\left\| {X({{t}_{1}}) - {{X}_{1}}} \right\| \to \min ,$
где $X = (x(t),{{y}_{1}}(t),{{y}_{2}}(t))$, ${{X}_{1}} = ({{x}_{1}},{{y}_{{11}}},{{y}_{{21}}})$.

Для нахождения матрицы коэффициентов разработан алгоритм на основе машинного обучения с подкреплением (см. алгоритм 2).

Входные данные: ${{X}_{1}},X(0)$
Выходные данные: $P$
Function Loss($P$, $X(0)$):
   prob$_{1}$ = ODEProblem(ecosystem, ${{X}_{0}}$, ${{t}_{1}}$)
   sol$_{1}$ = solve(prob$_{1}$, *args)
   return norm(sol$_{1}$.y[end] - ${{X}_{1}}$)
   
Function Main:
   $P$ = optimize(Loss, array(9), *args)
   serialize($P$)
   return 0
 return

Алгоритм 2: Алгоритм поиска коэффициентов управления.

Алгоритм 2 реализован на языке Julia с применением дифференциальной эволюции из состава пакета BlackBoxOptim.jl. Значения коэффициентов для ${{X}_{1}} = (10,10,15)$ имеют вид

$P = \left( {\begin{array}{*{20}{c}} { - 5.13979}&{2.68192}&{ - 0.233943} \\ { - 1.67237}&{4.09481}&{ - 0.367989} \\ {2.71886}&{0.457653}&{ - 0.015932} \end{array}} \right).$

Графическое представление плотностей популяций хищника и жертвы для управляемого случая при рассмотренных условиях приведено в разделе 6.

Разработанный модуль программного комплекса позволяет строить функции управления для многомерных систем популяционной динамики с учетом различных критериев качества. Взаимодействие указанного модуля с программным комплексом осуществляется посредством сериализации полученных данных. Отметим, что возможно расширение модуля на основе предложенного в [28] способа построения нейроуправления.

6. ПОЛУЧЕНИЕ И ВИЗУАЛИЗАЦИЯ ЧИСЛЕННЫХ РЕШЕНИЙ

Как известно, для численного решения систем обыкновенных дифференциальных уравнений и соответствующих им стохастических дифференциальных уравнений часто используются методы Рунге–Кутты и их модификации. Для решения обыкновенных дифференциальных уравнений в данной работе используется программная реализация стандартных методов Рунге–Кутты четвертого порядка. Для стохастических дифференциальных уравнений используется специально разработанная библиотека, подробное описание которой приведено в [8, 9].

В настоящей работе для получения численных решений применительно к блоку IStoDE.py реализована функция преобразования символьных данных в численные:

def func_for_rk(x, p, f):

 F = sp.lambdify(args=(*x, *p),

      expr=f,

      modules=’numpy’)

 def func_f(t, x, p):

   return F(*x, *p).flatten()

   return func_f

def func_for_sdu(x, p, g):

   G = sp.lambdify(args=(*x, *p),

       expr=g,

       modules=’numpy’)

   def func_g(x, p):

      return G(*x, *p)#.flatten()

   return func_g

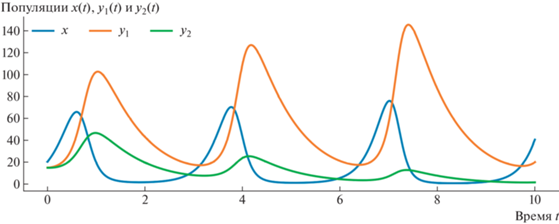
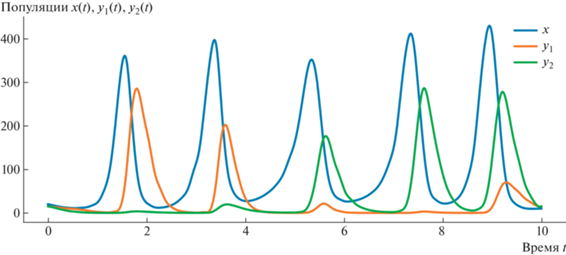
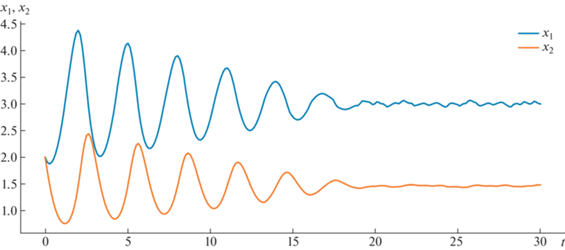
В качестве иллюстрации приведена визуализация численного решения для детерминированного случая (рис. 7) и для стохастического случая (рис. 8). На рис. 9 приведена визуализация численного решения для управляемой детерминированной модели.

Рис. 7.

Пример визуализации численного решения детерминированной модели при параметрах (a, b1, b2, c1, c2) = = $[4.5,1.2,1.1,0.07,0.05]$. Начальные значения $(x(0),{{y}_{1}}(0),{{y}_{2}}(0)) = [20,15,15]$.

Рис. 8.

Пример визуализации численного решения стохастической модели при параметрах (a, b1, b2, c1, c2) = = $[4.5,1.2,1.1,0.07,0.05]$. Начальные значения $(x(0),{{y}_{1}}(0),{{y}_{2}}(0)) = [20,15,15]$.

Рис. 9.

Пример визуализации численного решения детерминированной модели с управлением при параметрах (a, b1, b2, c1, c2) = $[4.5,1.2,1.1,0.07,0.05]$. Начальные значения $(x(0),{{y}_{1}}(0),{{y}_{2}}(0)) = [20,15,15]$.

7. ТЕСТИРОВАНИЕ ПРОИЗВОДИТЕЛЬНОСТИ В РАМКАХ ОТДЕЛЬНЫХ ЗАДАЧ, РЕШАЕМЫХ ПРОГРАММНЫМ КОМПЛЕКСОМ

Мы изучаем вопросы производительности инструментальных средств на примере модифицированной для управляемого случая известной модели Лотки–Вольтерры вида:

(7.1)
$\begin{array}{*{20}{c}} {{{{\dot {x}}}_{1}} = \left( {\alpha - \beta {{x}_{2}}} \right){{x}_{1}} - {v},} \\ {{{{\dot {x}}}_{2}} = \left( { - \gamma + \delta {{x}_{1}}} \right){{x}_{2}},} \end{array}$
где ${{x}_{1}}$, ${{x}_{2}}$ – плотности популяций жертвы и хищника соответственно, $\alpha ,\beta ,\gamma ,\delta $ – коэффициенты взаимодействия, ${v}$ – переключаемое управление, реализующее скользящий режим с законом управления:

$\begin{array}{*{20}{c}} {{{x}_{1}} < 3:{v} = 0,} \\ {{{x}_{1}} \geqslant 3:{v} = 0.25.} \end{array}$

Экологический смысл указанного управления заключается в регулировании плотности популяции жертвы. Мы производим тестирование скорости работы кода при численном интегрировании методом Рунге–Кутты четвертого порядка для языков Python (Scipy.integrate) и Julia (DifferentialEquations.jl). Для указанных решателей используются настройки по умолчанию. Отметим, что для Julia не учитывается время компиляции программы. Конфигурация используемой ЭВМ: ЦП AMD Ryzen 5 5600X, 16 GB RAM.

Фрагмент тестовой программы на языке Python 3 приведен в листинге 1.

class lotki_volterra :

def __init__ (self , alpha ,

   beta , gamma , delta ):

self . alpha = alpha

self . beta = beta

self . gamma = gamma

self . delta = delta

self .v = 0

def __call__ (self , t, y):

   a,b,g,d,v = ( self .alpha ,

     self .beta ,

     self .gamma ,

     self .delta ,

     self .v)

   x1, x2 = y

   dx1 = (a - b*x2)*x1 - v

   dx2 = (-g + d*x1)*x2

   if x1 < 3: self .v = 0

   else : self .v = 0.25

   return dx1 , dx2

model1 = lotki_volterra (1.5 , 1, 3, 1)

solution = solve_ivp ( model1 , (0 ,30) ,

   (2 ,2) , t_eval =(0 , 30, 240) )

Листинг 1: Тестовая программа для расчета траекторий (Python 3)

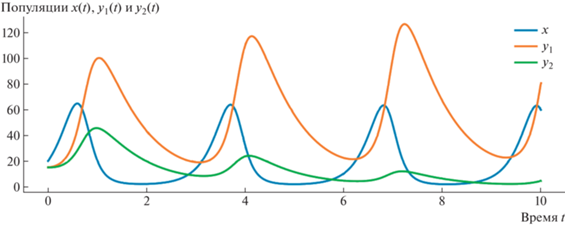
Результатом работы программы являются графики плотностей популяций, представленные на рис. 10.

Рис. 10.

Плотности популяций хищника и жертвы для модели (7.1) при выбранных начальных условиях.

Для замера производительности использована директива %timeit из пакета JupyterLab. Скорость выполнения функции solve_ivp составляет 8.43 ms ± 120 μs per loop (mean ± std. dev. of 7 runs, 100 loops each). Рассмотрим аналогичную реализацию модели (7.1) на языке Julia, которая приведена на листинге 2.

function lotki_volterra (du , u, p, t)

   a,b,g,d,c = p

 du [1] = (a - b*u [2]) *u [1] - v

 du [2] = (-g + d*u [1]) *u [2]

end

switch_condition1 (u, t, integrator ) =

 integrator .u [1] < 3

affect1 !( integrator ) = integrator .p [5]

 = 0

switch_condition2 (u, t, integrator ) =

 integrator .u [1] >= 3

affect2 !( integrator ) = integrator .p [5]

 = 0.25

cb1 = DiscreteCallback (

 switch_condition1 , affect1 !)

cb2 = DiscreteCallback (

 switch_condition2 , affect2 !)

cbs = CallbackSet (cb1 , cb2 )

u0 = [2.0; 2.0]

p = [1.5 , 1., 3., 1., 0]

prob = ODEProblem (lotki_volterra , u0

 ,(0.0 , 30.0) ,p)

sol = solve (prob , RK4 () , callback =

 cbs)

Листинг 2: Тестовая программа для расчета траекторий (Julia)

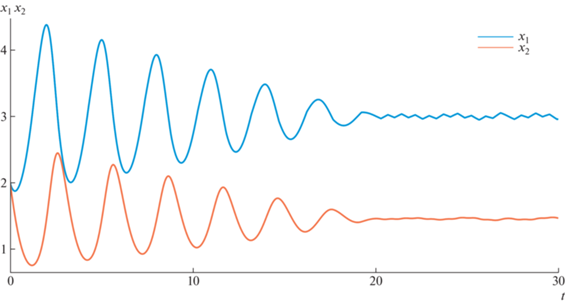
Результат работы программы представляет собой график, аналогичный рис. 10, который приведен на рис. 11.

Рис. 11.

Плотности популяций хищника и жертвы для модели (7.1) при выбранных начальных условиях (Julia).

Для замера производительности использован пакет BenchmarkTools.jl (макрос @btime). Скорость работы функции 42.091 μs (1021 allocations: 98.25 KiB). Таким образом, программа на языке Julia показывает в 195.53 меньшее время выполнения задачи построения траекторий управляемой системы (7.1). Несмотря на то, что программы на языке Julia требуют продолжительной предварительной компиляции, более высокая скорость работы имеет существенное значение при решении задач, требующих многократного решения обыкновенного дифференциального уравнения с разными параметрами. К таким задачам можно отнести, в частности, машинное обучение с подкреплением или анализ устойчивости модели. Далее рассмотрим производительность программного кода для поиска состояний равновесия экологических моделей. Как известно, задача нахождения особых точек уравнений вида

$\dot {x} = f\left( x \right),\quad x \in {{\mathbb{R}}^{n}},$
требует решения уравнения

$f\left( x \right) = 0.$

Уравнения моделей взаимодействия популяций, как правило, имеют нелинейный характер правых частей. Мы изучаем пример, когда правые части модели задаются полиномами второго порядка:

(7.2)
$\begin{array}{*{20}{c}} {{{{\dot {y}}}_{1}} = {{k}_{1}} + {{k}_{2}}{{y}_{1}} + {{k}_{3}}y_{2}^{2},} \\ {{{{\dot {y}}}_{2}} = {{k}_{1}} + {{k}_{2}}{{y}_{2}} + {{k}_{3}}y_{1}^{2}.} \end{array}$

Программный код на языке Python 3 с применением библиотеки SymPy приведен в листинге 3.

from sympy import *

init_printing ( use_latex ='mathjax ')

k1 ,k2 ,k3 ,k4 ,y1 ,y2 = symbols ('k1 k2 k3

k4 y1 y2 ')

eq1 = k1 + k2*y1 + k3*y2 **2

eq2 = k1 + k2*y2 + k3*y1 **2

solution = solve (( eq1 , eq2 ), (y1 , y2))

for sol in solution : display ( sol )

Листинг 3: Тестовая программа для поиска состояний равновесия (Python 3)

Программа, представленная в листинге 3, предназначена для поиска состояний равновесия для модели в форме дифференциальных уравнений. Для замера производительности использована директива %timeit из пакета JupyterLab. Скорость выполнения функции solve составляет 32.6 ms ± 634 μs per loop (mean ± std. dev. of 7 runs, 10 loops each).

Далее рассмотрим решение приведенных уравнений в Maxima. Для расчета состояний равновесия используются следующие команды:

s:[ k1 + k2*y1 + k3*y2 ^2, k1 + k2*y2 +

     k3*y1 ^2]

solve (s, [y1 , y2 ])

Время работы символьного решателя оценено с помощью встроенной функции time и составляет 0.002234 сек. (2.234 ms). Таким образом, время решения системы уравнений (7.2) для символьного решателя системы компьютерной алгебры Maxima составляет менее 7% от времени решения для пакета SymPy.

Полученные при тестировании производительности результаты свидетельствуют о том, что для решаемых научных задач целесообразно создавать интегрированные программные средства, базирующиеся на инструментах различных языков программирования. Одним из перспективных направлений развития работы является интеграция CAS Maxima со средствами символьного решения уравнений в рамках разрабатываемого программного комплекса.

8. ЗАКЛЮЧЕНИЕ

Таким образом, разработанный программный комплекс продемонстрировал возможности решения таких задач, как получение формализованного описания детерминированных моделей, получение символьных выражений для перехода к стохастическим моделям, детальная формализация структуры стохастических систем, расчет траекторий многомерных динамических систем, поиск управляющих функций. В программном комплексе находят реализацию методы и алгоритмы, базирующиеся на детерминированных и стохастических методах Рунге–Кутты, методах теории устойчивости и теории управления, методе построения самосогласованных стохастических моделей, алгоритмах численной оптимизации и искусственного интеллекта.

Методология, предложенная в работе, позволяет осуществлять построение моделей любой размерности, однако необходимо учитывать производительность используемого компьютера и возможности пакетов компьютерной алгебры. В настоящей работе задействованы несколько языков программирования и пакетов компьютерной алгебры, что позволило в полной мере использовать преимущества каждого из них и реализовать многоплановость и многоаспектность поставленной задачи моделирования динамических систем с учетом стохастизации и управления.

Разработанный программный комплекс допускает дальнейшее расширение и усовершенствование. В качестве перспективных направлений исследования можно выделить разработку модуля для моделирования динамики переключаемых систем популяционной динамки (например, с учетом сезонных изменений условий взаимодействия популяций), совершенствование модулей программного комплекса с учетом возможностей эффективного применения современных аппаратных средств, разработка модуля с учетом распространения изучаемых моделей популяционной динамики на нестационарный случай (например, для учета трофических функций, зависящих от времени). Кроме того, важным направлением работы является достижение более высокой плотности интеграции модулей с учетом реализации на различных языках программирования.

Список литературы

  1. Кулябов Д.С., Кокотчикова М.Г. Аналитический обзор систем символьных вычислений // Вестник РУДН. Серия: Математика. Информатика. Физика. 2007. № 1–2. С. 38–45.

  2. Алтунин К.Ю., Сениченков Ю.Б. О возможности символьных вычислений в пакетах визуального моделирования сложных динамических систем // Информатика, телекоммуникации и управление. 2009. № 3(80). С. 153–158.

  3. Малашонок Г.И., Рыбаков М.А. Решение систем линейных дифференциальных уравнений и расчет динамических характеристик систем управления в веб-сервисе mathpartner // Вестник российских университетов. Математика. 2014. № 2. С. 517–529.

  4. Банщиков А.В., Бурлакова Л.А., Иртегов В.Д., Титоренко Т.Н. Символьные вычисления в моделировании и качественном анализе динамических систем // Вычислительные технологии. 2014. № 6. С. 3– 18.

  5. Фалейчик Б.В. Одношаговые методы численного решения задачи Коши. Минск: БГУ, 2010.

  6. Platen E. An introduction to numerical methods for stochastic differential equations // Acta Numerica. 1999. V. 8. P. 197–246.

  7. Kulchitskiy O., Kuznetsov D. Numerical methods of modeling control systems described by stochastic differential equations // Journal of Automation and Information Sciences. 1999. 06. V. 31. P. 47–61.

  8. Gevorkyan M.N., Velieva T.R., Korolkova A.V. et al. Stochastic Runge–Kutta software package for stochastic differential equations // Dependability Engineering and Complex Systems / Ed. by Wojciech Zamojski, Jacek Mazurkiewicz, Jarosllaw Sugier Cham: Springer International Publishing, 2016. P. 169–179.

  9. Gevorkyan M.N., Demidova A.V., Korolkova A.V., Kulyabov D.S. Issues in the software implementation of stochastic numerical Runge–Kutta // Distributed Computer and Communication Networks / Ed. by Vladimir M. Vishnevskiy, Dmitry V. Kozyrev. Cham: Springer International Publishing, 2018. V. 919 of Communications in Computer and Information Science. P. 532–546. arXiv: 1811.01719.

  10. Геворкян М.Н., Демидова А.В., Велиева Т.Р. и др. Реализация метода стохастизации одношаговых процессов в системе компьютерной алгебры // Программирование. 2018. № 2. С. 18–27.

  11. Демидова А.В. Уравнения динамики популяций в форме стохастических дифференциальных уравнений // Вестник РУДН. Серия: Математика. Информатика. Физика. 2013. № 1. С. 67–76. URL: https://journals.rudn.ru/miph/article/ view/8319.

  12. Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы, вдохновленные природой. 2-е изд. изд. Москва: МГТУ им. Н.Э. Баумана, 2016.

  13. Firsov A.N., Inovenkov I.N., Nefedov V.V., Tikhomirov V.V. Numerical study of the effect of stochastic disturbances on the behavior of solutions of some differential equations // Modern Information Technologies and IT-Education. 2021. V. 17. № 1. P. 37–43.

  14. Mao X. Stochastic Differential Equations and Applications, 2nd ed. Cambridge: Woodhead Publ, 2008.

  15. Korolkova A., Kulyabov D. Onestep stochastization methods for open systems // EPJ Web of Conferences. 2020. V. 226. P. 02014. URL: https://doi.org/10.1051/epjconf/202022602014

  16. Gardiner C.W. Handbook of Stochastic Methods: For Physics, Chemistry and the Natural Sciences. Heidelberg: Springer, 1985.

  17. Van Kampen N. Stochastic Processes in Physics and Chemistry. Amsterdam: Elsevier, 1992.

  18. Bairey E., Kelsic E.D., Kishony R. High-order species interactions shape ecosystem diversity // Nature Communications. 2016. V. 7. P. 12285.

  19. Голубятников В.П., Подколодная О.А., Подколодный Н.Л., Аюпова Н.Б., Кириллова Н.Е., Юношева Е.В. Об условиях существования циклов в двух базовых моделях циркадного осциллятора млекопитающих // Сиб. журн. индустр. матем. 2021. Т. 24. № 4. С. 39–53.

  20. Вольтерра В. Математическая теория борьбы за существование. Москва: Наука, 1976.

  21. Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. Москва: Наука, 1978.

  22. Базыкин А.Д. Нелинейная динамика взаимосвязанных популяций. Москва–Ижевск: Институт компьютерных исследований, 2003.

  23. Dilao R. Mathematical Models in Population Dynamics and Ecology // In Biomathematics: Modelling and Simulation. Singapore: World Scientific, 2006. P. 399–449.

  24. Четаев Н.Г. Устойчивость движения. Москва: ГИТТЛ, 1964.

  25. Пых Ю.А. Равновесие и устойчивость в моделях популяционной динамики. Москва: Наука, 1983.

  26. Шестаков A.А. Обобщенный прямой метод Ляпунова для систем с распределенными параметрами. Москва: Наука, 1990.

  27. Demidova A.V., Druzhinina O.V., Jacimovic M. et al. The generalized algorithms of global parametric optimization and stochastization for dynamical models of interconnected populations // Optimization and Applications. OPTIMA 2020. Lecture Notes in Computer Science / Ed. by Nicholas Olenev, Yuri Evtushenko, Michael Khachay, Vlasta Malkova. V. 12422. Cham: Springer, 2020. P. 40–54.

  28. Demidova A.V., Druzhinina O.V., Masina O.N., Petrov A.A. Synthesis and computer study of population dynamics controlled models using methods of numerical optimization, stochastization and machine learning // Mathematics. 2021. V. 9. № 24. URL: https: //www.mdpi.com/2227-7390/9/24/3303.

  29. Demidova A.V., Druzhinina O.V., Jacimovic M., Masina O.N., Mijajlovic N. Synthesis and analysis of multidimensional mathematical models of population dynamics // Proceedings of the Selected Papers of the 10th International Congress on Ultra Modern Telecommunications and Control Systems ICUMT (Moscow, Russia, November 5–9, 2018). New York: IEEE Xplore Digital Library, 2018. IEEE Catalog Number CFP 1863G-USB. P. 361–366. https://doi.org/10.1109/ICUMT.2018.8631252

  30. Demidova A., Druzhinina O., Jacimovic M. et al. Problems of synthesis, analysis and optimization of parameters for multidimensional mathematical models of interconnected populations dynamics // Optimization and Applications. OPTIMA 2019. Communications in Computer and Information Science / Ed. by Milojica Jacimovic, Michael Khachay, Vlasta Malkova, Mikhail Posypkin. V. 1145. Cham: Springer, 2020. P. 56–71.

  31. Demidova A.V., Druzhinina O.V., Masina O.N., Petrov A.A. Computer research of the controlled models with migration rows // Proceedings of the Selected Papers of the 10th International Conference “Information and Telecommunication Technologies and Mathematical Modeling of High-Tech Systems” (ITTMM-2020). CEUR Workshop Proceedings. 2020. V. 2639. P. 117–129.

  32. Harris C.R., Millman K.J., van der Walt S.J. et al. Array programming with NumPy // Nature. 2020. V. 585. № 7825. P. 357–362. URL: https://doi.org/10.1038/s41586-020-2649-2

  33. Fuhrer C., Solem J., Verdier O. Scientific Computing with Python 3. Packt Publishing, 2016.

  34. Lamy R. Instant SymPy Starter. Packt Publishing, 2013.

  35. Oliphant T.E. Guide to NumPy. 2nd edition. North Charleston, SC, USA: CreateSpace Independent Publishing Platform, 2015. ISBN: 151730007X.

  36. Virtanen P., Gommers R., Oliphant T.E. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python // Nature Methods. 2020. V. 17. P. 261–272. URL: https://doi.org/10.1038/s41592-019-0686-2

  37. Bezanson J., Edelman A., Karpinski S., Shah V.B. Julia: A fresh approach to numerical computing // SIAM Review. 2017. V. 59. № 1. P. 65–98.

  38. Meurer A., Smith C.P., Paprocki M. et al. SymPy: symbolic computing in Python // PeerJ Computer Science. 2017. V. 3. P. e103. URL: https://doi.org/10.7717/ peerj-cs.103

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал