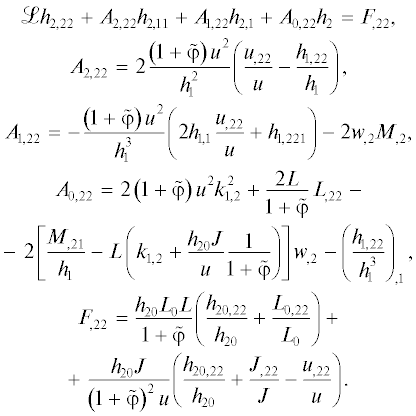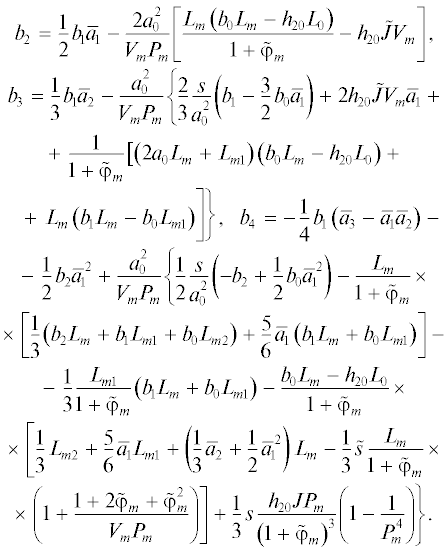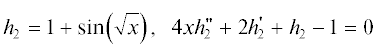Радиотехника и электроника, 2019, T. 64, № 1, стр. 82-95
Геометризованная теория ленточных релятивистских электронных пучков в φ-представленииВ. А. Сыровой
В. А. Сыровой *
Всероссийский электротехнический институт
111250 Москва, ул. Красноказарменная, 12, Российская Федерация
* E-mail: red@cplire.ru
Поступила в редакцию 20.06.2017
После доработки 20.06.2017
Принята к публикации 18.02.2018
Аннотация
Сформулировано второе приближение теории узких ленточных пучков с криволинейной осью и плоскосимметричных потоков. Построена полная гидродинамическая картина течения вблизи стартовой поверхности при эмиссии в $\rho $- и Т-режимах. Исследована окрестность особых точек, соответствующих экстремумам потенциала на базовой трубке тока при его немонотонном изменении.
ВВЕДЕНИЕ
В работе [1] представлен новый вариант геометризованной теории плотных электронных пучков, в которой, помимо введения заранее неизвестной системы координат ${{x}^{i}}$ (i = 1, 2, 3), связанной с траекториями (линии ${{x}^{1}}$) или трубками тока (поверхности ${{x}^{2}} = {\text{const}}$), в качестве продольной координаты использован потенциал электрического поля $\varphi $ ($\varphi $-представление). При тестировании двумерных геометризованных моделей на наборе эталонных точных решений в [2] обнаружено, что построенное в $\varphi $-формализме приближенное решение может иметь бóльшую точность по сравнению со случаем использования длины дуги l образующей трубки тока (l-представление) в качестве продольной координаты.
В отличие от l-варианта геометризованной теории плотных электронных пучков $\varphi $-вариант в большей степени связан с физической картиной явления, которую образуют не только траектории или трубки тока, но и эквипотенциальные поверхности. В рамках $\varphi $-представления автоматически появляется информация об углах наклона траекторий или трубок тока к эквипотенциальным поверхностям, получение которой в l-варианте теории, как и построение поверхностей $\varphi = {\text{const,}}$ представляет самостоятельную задачу.
Уравнения, описывающие $\varphi $-геометризацию, нельзя получить из системы l-варианта по формулам перехода от одной криволинейной системы к другой. Потенциал $\varphi $, меняя свой статус искомой функции и становясь независимой переменной, уменьшает число зависимых переменных на единицу при сохранении числа уравнений; порядок уравнения Пуассона при этом снижается со второго на первый. В результате в $\varphi $-варианте система уравнений геометризованной теории становится полной и элемент ${{g}_{{12}}}$ метрического тензора ${{g}_{{ik}}}$ перестает быть произвольной функцией, специализацию которой определяет требование регуляризации решения.
В то время как классическая параксиальная теория [3, 4] оперирует с асимптотическим рядом по малому геометрическому параметру, геометризованный подход основан на построении ряда Тэйлора по поперечной координате. Сравнение на эталонных точных решениях асимптотической и геометризованной моделей [2] дает основание для предпочтения второй из них уже в первом приближении, если критерием является точность результата. Кроме того, геометризованное описание позволяет рассматривать случай произвольной ориентации магнитного поля на катоде, недоступный классическому подходу. В результате появляется возможность синтеза электронно-оптической системы магнетронно-инжекторных пушек в осесимметричном [5] или планарном [6] варианте.
В последнее десятилетие существенно возрос интерес к ленточным пучкам для различных приборов СВЧ (см., например, [7] и приведенную там библиографию). Цель работы – построение второго приближения геометризованной модели в $\varphi $‑варианте для описания непараксиальных ленточных пучков с искривленной осью и плоскосимметричных потоков. Помимо этого необходимо исследовать сингулярности, источником которых в $\varphi $-представлении является немонотонное поведение потенциала на базовой поверхности.
В работе используются обычные тензорные обозначения [4, 8] и релятивистские нормировки, позволяющие исключить из уравнений все физические постоянные выбранной системы единиц.
1. ГЕОМЕТРИЗОВАННЫЕ УРАВНЕНИЯ ЛЕНТОЧНОГО ПУЧКА В $\varphi $-ПРЕДСТАВЛЕНИИ
В системе ${{x}^{i}}$ (i = 1, 2, 3), где уравнение ${{x}^{1}} = {\text{const}}$ определяет эквипотенциальные поверхности, ${{x}^{2}} = {\text{const}}$ – трубки тока, ${{x}^{3}} = x$ – циклическая декартова координата примем следующие обозначения для основных параметров задачи: ${{g}_{{ik}}}$ – метрический тензор, g – его детерминант; ${{\theta }_{{12}}}$ – угол между касательными к осям ${{x}^{1}},$ ${{x}^{2}};$ u – косоугольная проекция продольной скорости, w – сносовая скорость по оси x; $\vec {H} = {\text{rot}}{\kern 1pt} \vec {A}$ – вектор напряженности магнитного поля с косоугольными проекциями L, M на оси ${{x}^{1}},$ ${{x}^{2}}$ и компонентой N по оси x; $\rho $ – плотность пространственного заряда; J – плотность тока эмиссии. Для обозначения частных производных по криволинейным координатам использованы сокращения типа ${{h}_{{1,1}}} \equiv {{\partial {{h}_{1}}} \mathord{\left/ {\vphantom {{\partial {{h}_{1}}} {\partial {{x}^{1}}}}} \right. \kern-0em} {\partial {{x}^{1}}}},$ ${{g}_{{12,12}}} \equiv {{{{\partial }^{2}}{{g}_{{12}}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{g}_{{12}}}} {\partial {{x}^{1}}\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{1}}\partial {{x}^{2}}}};$ тильдой отмечены исчезающие в нерелятивистском пределе члены.
Метрический тензор gik имеет следующие компоненты:
(1)
$\begin{gathered} {{g}_{{11}}} \equiv h_{1}^{2},\,\,\,\,{{g}_{{22}}} \equiv h_{2}^{2},\,\,\,\,{{g}_{{33}}} = 1,\,\,\,\,{{g}_{{12}}} = {{h}_{1}}{{h}_{2}}\cos {\kern 1pt} {{\theta }_{{12}}}, \\ {{g}^{{11}}} = \frac{1}{{h_{1}^{2}{{{\sin }}^{2}}{{\theta }_{{12}}}}},\,\,\,\,{{g}^{{22}}} = \frac{1}{{h_{2}^{2}{{{\sin }}^{2}}{{\theta }_{{12}}}}}, \\ {{g}^{{12}}} = - \frac{{\cos {{\theta }_{{12}}}}}{{{{h}_{1}}{{h}_{2}}{{{\sin }}^{2}}{{\theta }_{{12}}}}},\,\,\,\,{{g}^{{33}}} = 1, \\ {{g}_{{13}}} = {{g}_{{23}}} = {{g}^{{13}}} = {{g}^{{23}}} = 0,\,\,\,\,\sqrt g = {{h}_{1}}{{h}_{2}}\sin {\kern 1pt} {{\theta }_{{12}}}. \\ \end{gathered} $Контравариантные компоненты скорости ${{v}^{{{\kern 1pt} i}}}$ определены соотношениями
(2)
${{v}^{{{\kern 1pt} 1}}} = \frac{{d{{x}^{1}}}}{{dt}},\,\,\,\,{{v}^{{{\kern 1pt} 2}}} = \frac{{d{{x}^{2}}}}{{dt}},\,\,\,\,{{v}^{3}} = \frac{{d{{x}^{3}}}}{{dt}} = w,\,\,\,u = {{h}_{1}}{{v}^{1}}.$Условие евклидовости пространства, которому удовлетворяет тензор ${{g}_{{ik}}},$ имеет вид [4]
(3)
$\begin{gathered} {{h}_{2}}{{h}_{{2,11}}} - {{g}_{{12,12}}} + {{h}_{1}}{{h}_{{1,22}}} + \frac{1}{{{{{\sin }}^{2}}{{\theta }_{{12}}}}} \times \\ \times \,\,\left\{ { - \left( {h_{{2,1}}^{2} + h_{{1,2}}^{2}} \right){{{\cos }}^{2}}{{\theta }_{{12}}} + \frac{{{{h}_{{1,1}}}}}{{{{h}_{1}}}}\left( {{{g}_{{12,2}}} - {{h}_{{{\kern 1pt} 2}}}{{h}_{{2,1}}}} \right)} \right. + \\ + \,\,\frac{{{{h}_{{2,2}}}}}{{{{h}_{2}}}}\left( {{{g}_{{12,1}}} - {{h}_{1}}{{h}_{{1,2}}}} \right) + \left[ { - {{h}_{{1,1}}}{{h}_{{2,2}}} + \left( {\frac{1}{{{{h}_{1}}}}{{g}_{{12,1}}} + {{h}_{{1,2}}}} \right)} \right. \times \\ \times \,\,\left. {\left. {{{h}_{{2,1}}} - \frac{1}{{{{h}_{2}}}}\left( {\frac{1}{{{{h}_{1}}}}{{g}_{{12,1}}} - {{h}_{{1,2}}}} \right){{g}_{{12,2}}}} \right]\cos {{\theta }_{{12}}}} \right\} = 0. \\ \end{gathered} $У трех уравнений движения моноэнергетического пучка есть два интеграла:
(4)
$\begin{gathered} 1 + \varphi = \frac{1}{{\sqrt {1 - {{u}^{2}} - {{w}^{2}}} }},\,\,\,\,\left( {1 + \tilde {\varphi }} \right)w + {{A}_{3}} = P\left( {{{x}^{2}}} \right), \\ w{{P}_{{,2}}} = u\left\{ {\frac{1}{{{{h}_{1}}}}{{{\left[ {\left( {1 + \tilde {\varphi }} \right)\frac{{{{g}_{{12}}}u}}{{{{h}_{1}}}}} \right]}}_{{,1}}} - \frac{1}{{{{h}_{1}}}}{{{\left[ {\left( {1 + \tilde {\varphi }} \right){{h}_{1}}u} \right]}}_{{,2}}} + {{h}_{2}}\sin {{\theta }_{{12}}}N} \right\}. \\ \end{gathered} $Уравнения Пуассона и сохранения тока описываются формулами
(5)
$\begin{gathered} {{\left( {\frac{{{{h}_{2}}}}{{{{h}_{1}}\sin {\kern 1pt} {{\theta }_{{12}}}}}} \right)}_{{,1}}} - {{\left( {{\text{ctg}}{{\theta }_{{12}}}} \right)}_{{,2}}} = {{h}_{1}}{{h}_{2}}\sin {\kern 1pt} {{\theta }_{{12}}}\rho , \\ {{\left( {{{h}_{2}}\sin {\kern 1pt} {\kern 1pt} {{\theta }_{{12}}}\rho u} \right)}_{{,1}}} = 0. \\ \end{gathered} $Самосогласованное магнитное поле $\vec {H}$ выражается через векторный потенциал ${{A}_{3}}$ и удовлетворяет уравнениям Максвелла
(6)
$\begin{gathered} {{h}_{2}}\sin {\kern 1pt} {{\theta }_{{12}}}L = {{A}_{{3,2}}},\,\,\,\,{{h}_{1}}\sin {\kern 1pt} {{\theta }_{{12}}}M = - {{A}_{{3,1}}}, \\ {{H}_{{3,1}}} = 0,\,\,\,\,{{H}_{{3,2}}} = {{h}_{2}}\sin {{\theta }_{{12}}}\tilde {\rho }u,\,\,\,\,{{H}_{3}} \equiv N = N\left( {{{x}^{2}}} \right); \\ {{\left[ {{{h}_{2}}\left( {M + L\cos {\kern 1pt} {{\theta }_{{12}}}} \right)} \right]}_{{,1}}} - {{\left[ {{{h}_{1}}\left( {L + M\cos {{\theta }_{{12}}}} \right)} \right]}_{{,2}}} = \\ = {{h}_{1}}{{h}_{2}}\sin {\kern 1pt} {{\theta }_{{12}}}\tilde {\rho }w, \\ {{\left( {{{h}_{2}}\sin {\kern 1pt} {{\theta }_{{12}}}L} \right)}_{{,1}}} + {{\left( {{{h}_{1}}\sin {\kern 1pt} {{\theta }_{{12}}}M} \right)}_{{,2}}} = 0. \\ \end{gathered} $2. ПРЕОБРАЗОВАННАЯ ФОРМА УРАВНЕНИЙ ЛЕНТОЧНОГО ПУЧКА
В работе [9] показано, что уравнения двумерных пучков в $\varphi $-формализме могут быть представлены в виде соотношений на трубке тока, имеющих вид обыкновенных дифференциальных уравнений с входящей в их коэффициенты координатой ${{x}^{2}}$ в качестве параметра и системы эволюционных уравнений, выражающих поперечные производные ${\partial \mathord{\left/ {\vphantom {\partial {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}}$ искомых функций через зависящие от ${{x}^{1}}$ распределения на трубке тока.
Соотношения на трубке тока. Для криволинейного ленточного пучка на трубке тока справедливо соотношение
(7)
$\begin{gathered} \times \,\,\left[ {k_{1}^{2} + f\frac{{{{k}_{{1,1}}}}}{{{{h}_{1}}}}} \right. + {{\sin }^{2}}{{\theta }_{{12}}}\left( {3{{{\cos }}^{2}}{{\theta }_{{12}}} - 1} \right){{\left( {\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right)}^{2}} - \\ \left. { - \,\,\sin {\kern 1pt} {{\theta }_{{12}}}\cos {{\theta }_{{12}}}\frac{1}{{{{h}_{1}}}}{{{\left( {\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right)}}_{{,1}}}} \right]{{u}^{2}} + \frac{L}{{1 + \tilde {\varphi }}} \times \\ \times \,\,\left[ {2\left( {1 + \tilde {\varphi }} \right){{k}_{1}}w + \frac{{wN}}{u} + {{H}_{l}}} \right] - {{k}_{1}}w{{H}_{l}} + \sin {{{\kern 1pt} }^{2}}{{\theta }_{{12}}} \times \\ \times \,\,\cos {{\theta }_{{12}}}wM\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}} - \frac{w}{{{{h}_{1}}\sin {\kern 1pt} {{\theta }_{{12}}}}}\left( {{{M}_{{,1}}} + \cos {\kern 1pt} {{\theta }_{{12}}}{{L}_{{,1}}}} \right) + \\ \end{gathered} $Здесь ${{k}_{1}}$ – кривизна трубки тока, нижний индекс нуль указывает на значение функции на катоде ${{x}^{1}} = 0.$
К уравнению (7) необходимо добавить зависимости, определяющие изменение угла ${{\theta }_{{12}}}$ и сносовой скорости w вдоль трубки тока:
(8)
$\begin{gathered} \left( {1 - {{h}_{1}}wM{{{\sin }}^{3}}{{\theta }_{{12}}}{\kern 1pt} } \right)\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}} = \frac{{{{h}_{{1,1}}}}}{{h_{{{\kern 1pt} 1}}^{2}}}f - \frac{{2{{k}_{1}}}}{{{{{\left( {1 + \tilde {\varphi }} \right)}}^{2}}}} - \\ - \,\,\left[ {\left( {1 + \tilde {\varphi }} \right){{k}_{{1,1}}} + {{{\tilde {k}}}_{1}}} \right]{{u}^{2}} + \left[ {2\left( {1 + \tilde {\varphi }} \right){{k}_{1}} - \frac{N}{u}} \right]w{{w}_{{,1}}} + \\ + \,\,\frac{1}{{{{{\left( {1 + \tilde {\varphi }} \right)}}^{3}}}}\frac{N}{u} + {{\left( {wL} \right)}_{{,1}}} + {{\left( {wM} \right)}_{{,1}}}\cos {{\theta }_{{12}}}, \\ {{w}_{{,1}}} = \frac{1}{{1 + \tilde {\varphi }}}\left( {{{h}_{1}}M\sin {{\theta }_{{12}}} - \tilde {w}} \right). \\ \end{gathered} $Эволюционные уравнения. Изменение в поперечном направлении декартовых координат z, y, угла $\theta $ между касательной к трубке тока и осью z и функции ${{h}_{{\,1}}}$ описывается уравнениями
(9)
$\begin{gathered} {{z}_{{,2}}} = {{h}_{2}}\cos {\kern 1pt} \vartheta ,\,\,\,\,{{y}_{{,2}}} = {{h}_{2}}\sin \vartheta ,\,\,\,\,\vartheta = \theta + {{\theta }_{{12}}}; \\ {{\theta }_{{,2}}} = \sin {\kern 1pt} {{\theta }_{{12}}}\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}} + {{h}_{2}}\cos {{\theta }_{{12}}}\left( {{{k}_{1}} - {{{\sin }}^{2}}{\kern 1pt} {{\theta }_{{12}}}\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right), \\ {{h}_{{1,2}}} = {{h}_{1}}{{h}_{2}}\sin {\kern 1pt} {{\theta }_{{12}}}\left( {{{{\sin }}^{2}}{{\theta }_{{12}}}\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}} - {{k}_{1}}{\kern 1pt} } \right) + {{h}_{{2,1}}}\cos {\kern 1pt} {{\theta }_{{12}}}. \\ \end{gathered} $Для производной ${{k}_{{1,2}}}$ имеем
(10)
$\begin{gathered} {{k}_{{1,2}}} = \frac{{{{h}_{2}}}}{{{{h}_{1}}}}\cos {{\theta }_{{12}}}{{k}_{{1,1}}} + {{h}_{2}}\sin {\kern 1pt} {{\theta }_{{12}}}k_{1}^{2} + \sin {{\theta }_{{12}}}\frac{1}{{{{h}_{1}}}}{{\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}}} \right)}_{{,1}}} + \\ + \,\,{{h}_{2}}{{\sin }^{3}}{{\theta }_{{12}}} \times \\ \times \,\,\left[ { - \frac{f}{{{{h}_{1}}}}{{{\left( {\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right)}}_{{,1}}} + \left( {3{{{\cos }}^{2}}{{\theta }_{{12}}} - 1} \right){{{\left( {\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right)}}^{2}} - 2f\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}{{h}_{2}}}}\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right]. \\ \end{gathered} $Производные от компонент скорости в поперечном направлении определены соотношениями
(11)
$u{\kern 1pt} {{u}_{{,2}}} = - w{\kern 1pt} {{w}_{{,2}}},\,\,\,\,{{w}_{{,2}}} = - \frac{1}{{1 + \tilde {\varphi }}}\left[ {{{h}_{2}}L\sin {\kern 1pt} {{\theta }_{{12}}} - {{{\left( {{{h}_{2}}L} \right)}}_{0}}} \right].$Для компонент магнитного поля получаем
(12)
$\begin{gathered} \frac{1}{{{{h}_{2}}}}{{H}_{{l,2}}} = \sin {{\theta }_{{12}}}{{k}_{1}}{{H}_{l}} + \frac{{\sin {{{\kern 1pt} }^{2}}{{\theta }_{{12}}}}}{{{{h}_{1}}}}\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{2}}}} - \sin {{\theta }_{{12}}}{{f}_{{,1}}}} \right)M + \\ + \frac{1}{{{{h}_{1}}}}{{M}_{{,1}}} + \frac{1}{{{{h}_{1}}}}{{L}_{{,1}}}\cos {\kern 1pt} {{\theta }_{{12}}} - \frac{{{{h}_{{20}}}\tilde {J}w}}{{{{h}_{2}}u}}, \\ \frac{1}{{{{h}_{2}}}}{{\left( {M\sin {\kern 1pt} {{\theta }_{{12}}}} \right)}_{{,2}}} = \\ = - \sin {\kern 1pt} {{\theta }_{{12}}}\left[ {\frac{1}{{{{h}_{1}}}}\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{2}}}} - \sin {{\theta }_{{12}}}\cos {{\theta }_{{12}}}{{f}_{{,1}}}} \right)L + \frac{{{{L}_{{,1}}}}}{{{{h}_{1}}}}} \right] - \\ - M\sin {{\theta }_{{12}}}\left[ {\frac{1}{{{{h}_{1}}}}\left( {{{{\sin }}^{3}}{{\theta }_{{12}}}{{f}_{{,1}}} + \frac{{{{h}_{{2,1}}}}}{{{{h}_{2}}}}\cos {{\theta }_{{12}}}} \right) - {{k}_{1}}\sin {{\theta }_{{12}}}} \right], \\ {{N}_{{,2}}} = {{h}_{{20}}}\tilde {J}. \\ \end{gathered} $Эволюция функции f в ${{x}^{2}}$-направлении описывается формулой
(13)
$\begin{gathered} \left. { - \,\,\sin {{\theta }_{{12}}}\cos {{\theta }_{{12}}}\left[ {\frac{1}{{{{h}_{1}}}}{{{\left( {\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right)}}_{{,1}}} + 2\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}{{h}_{2}}}}\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right]} \right\}{{u}^{2}} - \\ - \,\,\frac{1}{{\left( {1 + \tilde {\varphi }} \right){{h}_{2}}}}\left[ {{{h}_{2}}\sin {{\theta }_{{12}}}L - {{{\left( {{{h}_{2}}L} \right)}}_{0}}} \right] \times \\ \end{gathered} $3. ВТОРОЕ ПРИБЛИЖЕНИЕ ТЕОРИИ УЗКИХ КРИВОЛИНЕЙНЫХ ЛЕНТОЧНЫХ ПУЧКОВ
Соотношения на трубке тока (7), (8) и эволюционная система (9)–(13) описывают первое приближение теории узких пучков, позволяющее по информации на базовой трубке тока сконструировать первые члены рядов Тэйлора по поперечной координате ${{x}^{2}} \equiv \xi .$ Уже в этом приближении, в отличие от классической параксиальной теории, где член порядка $\varepsilon $ описывает внешнее поле, учитывается пространственный заряд пучка.
Для построения второго приближения представим уравнение (7) в виде
(14)
$\begin{gathered} + \,\,{{\sin }^{2}}{{\theta }_{{12}}}\left( {3{{{\cos }}^{2}}{{\theta }_{{12}}} - 1} \right){{\left( {\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right)}^{2}} - \\ \left. { - \,\,\sin {{\theta }_{{12}}}\cos {{\theta }_{{12}}}\frac{1}{{{{h}_{1}}}}{{{\left( {\frac{{{{f}_{{,1}}}}}{{{{h}_{1}}}}} \right)}}_{{,1}}}} \right]{{u}^{2}} + \frac{L}{{1 + \tilde {\varphi }}} \times \\ \end{gathered} $Уравнение (7) представляет собой точное соотношение на трубке тока, содержащее координату ${{x}^{2}}$ как параметр. По этой причине его можно дифференцировать по ${{x}^{2}}$ для получения уравнения относительно ${{h}_{{\,2,2}}}$ – функции, через которую могут быть выражены параметры потока во втором приближении теории:
(15)
$\mathcal{L}{{h}_{{2,2}}} + {{A}_{{2,2}}}{{h}_{{2,11}}} + {{A}_{{1,2}}}{{h}_{{2,1}}} + {{A}_{{0,2}}}{{h}_{2}} = {{F}_{{,2}}}.$Полученный результат проиллюстрируем двумя первыми коэффициентами:
(16)
$\begin{gathered} {{A}_{{2,2}}} = 2\left( {1 + \tilde {\varphi }} \right)\frac{{{{u}^{2}}}}{{h_{1}^{2}}}\left( {\frac{{{{u}_{{,2}}}}}{u} - \frac{{{{h}_{{1,2}}}}}{{{{h}_{1}}}}} \right), \\ {{A}_{{1,2}}} = - \left( {1 + \tilde {\varphi }} \right)\frac{{{{u}^{2}}}}{{{{h}_{1}}}}\left\{ {\frac{{{{h}_{{1,21}}}}}{{{{h}_{1}}}} + 2\frac{{{{u}_{{,2}}}}}{u}\left( {\frac{{{{h}_{{1,1}}}}}{{{{h}_{1}}}} - 2\frac{{f{{f}_{{,1}}}}}{{1 + {{f}^{2}}}}} \right) - } \right. \\ - \,\,3\frac{{h_{{1,1}}^{2}}}{{h_{1}^{2}}} - \left. {\frac{2}{{1 + {{f}^{2}}}}\left[ {\frac{{1 - {{f}^{2}}}}{{1 + {{f}^{2}}}}{{f}_{{,1}}}{{f}_{{,2}}} + f\left( {{{f}_{{,21}}} - 2\frac{{{{h}_{{1,2}}}}}{{{{h}_{1}}}}{{f}_{{,1}}}} \right)} \right]} \right\} + \\ + \,\,\sin {\kern 1pt} {{\theta }_{{12}}}\left[ {\frac{{wM}}{{{{h}_{1}}}}\left( {\frac{{{{h}_{{1,2}}}}}{{{{h}_{1}}}} + \frac{{f{{f}_{{,2}}}}}{{1 + {{f}^{2}}}}} \right) - {{{\left( {wM} \right)}}_{{,2}}}} \right]. \\ \end{gathered} $Уравнения эволюционной системы (9)–(13) дают возможность исключить производные по ${{x}^{2}}$ из коэффициентов уравнения (15), после чего оно будет иметь тот же вид, что и соотношение на трубке тока (14).
4. ТЕОРИЯ ПЛОСКОСИММЕТРИЧНЫХ ПУЧКОВ
Первое приближение. Соотношения, описывающие плоскосимметричные потоки, значительно проще по сравнению с соотношениями в случае искривленной оси в силу того, что ряд параметров на оси обращается в нуль, а система криволинейных координат на ней локально-ортогональна:
(17)
$\begin{gathered} {{k}_{1}} = 0,\,\,\,\,\theta = 0,\,\,\,\,f = 0,\,\,\,\,w = 0,\,\,\,M = 0, \\ {{N}_{s}} = 0,\,\,\,\,{{\theta }_{{12}}} = \frac{\pi }{2},\,\,\,\,{{u}^{2}} = \frac{{\varphi \left( {2 + \tilde {\varphi }} \right)}}{{{{{\left( {1 + \tilde {\varphi }} \right)}}^{2}}}}, \\ \end{gathered} $где ${{N}_{s}}$ – собственное магнитное поле. Обращаются в нуль на оси и производные по ${{x}^{2}}$ для параметров задачи, являющихся четными функциями ${{x}^{2}}\,:$
(18)
${{z}_{{,2}}} = 0,\,\,\,\,{{h}_{{1,2}}} = 0,\,\,\,\,{{u}_{{,2}}} = 0,\,\,\,\,{{L}_{{,2}}} = 0,\,\,\,\,{{J}_{{,2}}} = 0.$Соотношение на трубке тока (7) описывается уравнением
(19)
$\begin{gathered} \mathcal{L}{{h}_{2}} \equiv \frac{{\left( {1 + \tilde {\varphi }} \right){{u}^{2}}}}{{{{h}_{1}}}}{{\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}}} \right)}_{{,1}}} + \frac{{{{h}_{{2,1}}}}}{{h_{1}^{2}}} + \left( {\frac{{{{L}^{2}}}}{{1 + \tilde {\varphi }}} - \frac{{{{h}_{{1,1}}}}}{{h_{1}^{3}}}} \right){{h}_{2}} = \\ = \frac{{{{h}_{{20}}}{{L}_{0}}L}}{{1 + \tilde {\varphi }}} + \frac{{{{h}_{{20}}}J}}{u}\frac{1}{{{{{\left( {1 + \tilde {\varphi }} \right)}}^{2}}}}. \\ \end{gathered} $Система эволюционных уравнений для нечетных функций принимает вид
(20)
$\begin{gathered} {{y}_{{,2}}} = {{h}_{2}},\,\,\,\,{{\theta }_{{,2}}} = \frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}},\,\,\,\,{{k}_{{1,2}}} = {{h}_{2}}k_{1}^{2} + \frac{1}{{{{h}_{1}}}}{{\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}}} \right)}_{{,1}}}, \\ {{w}_{{,2}}} = \frac{1}{{1 + \tilde {\varphi }}}\left[ {{{{\left( {{{h}_{2}}L} \right)}}_{0}} - {{h}_{2}}L} \right], \\ \frac{1}{{{{h}_{2}}}}{{M}_{{,2}}} = \frac{1}{{{{h}_{1}}}}\left( {{{L}_{{,1}}} - \frac{{{{h}_{{2,1}}}}}{{{{h}_{2}}}}L} \right),\,\,\,\,{{N}_{{,2}}} = {{h}_{{20}}}\tilde {J}, \\ \frac{1}{{{{h}_{2}}}}{{f}_{{,2}}} = - \frac{{\left( {1 + \tilde {\varphi }} \right){{u}^{2}}}}{{{{h}_{2}}}}{{\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}}} \right)}_{{,1}}} + \\ + \,\,\frac{1}{{1 + \tilde {\varphi }}}\frac{{{{h}_{1}}}}{{{{h}_{2}}}}\left\{ {\left[ {{{{\left( {{{h}_{2}}L} \right)}}_{0}} - {{h}_{2}}L} \right]L - {{h}_{{20}}}\tilde {J}u} \right\}. \\ \end{gathered} $Второе приближение. Уравнение (15) для ${{h}_{{2,2}}}$ в случае прямой оси имеет тривиальное решение, а следующее приближение сводится к получению уравнения для ${{h}_{{2,22}}}.$ Для этого необходимо продифференцировать по ${{x}^{2}}$ уравнение (15) и перейти к прямой оси с учетом соотношений (17), (18). Вторые производные от четных функций удовлетворяют эволюционной системе высшего порядка, построение которой на основании связей (9)–(12) проводится по аналогичному алгоритму; вторые производные функций из (20) на оси обращаются в нуль.
Соотношение на трубке тока в высшем приближении имеет вид
Эволюционные соотношения высшего порядка. Коэффициенты в уравнении (21) становятся известными функциями продольной координаты при использовании формул
(22)
$\begin{gathered} {{h}_{{1,22}}} = - {{h}_{1}}{{h}_{2}}{{k}_{{1,2}}} + {{\left( {{{h}_{2}}{{f}_{{,2}}}} \right)}_{{,1}}},\,\,\,\,{{u}_{{,22}}} = - \frac{{w_{{,2}}^{2}}}{u}, \\ {{L}_{{,22}}} = {{h}_{2}}L{{k}_{{1,2}}} + \frac{{{{h}_{2}}}}{{{{h}_{1}}}}\left( {{{M}_{{,21}}} + {{L}_{{,1}}}{{f}_{{,2}}}} \right) + \left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}} - 2{{f}_{{,2}}}} \right){{M}_{{,2}}}. \\ \end{gathered} $Параметры потока во втором приближении теории. Зная функцию ${{h}_{{{\kern 1pt} 2,22}}},$ можно построить решение с учетом более высоких степеней поперечной координаты ${{x}^{2}} \equiv \xi ,$ чем вторая:
(23)
$\begin{gathered} z = \frac{1}{2}{{z}_{{,22}}}{{\xi }^{2}} + \frac{1}{{24}}{{z}_{{,2222}}}{{\xi }^{4}},\,\,\,\,y = {{y}_{{,2}}}\xi + \frac{1}{6}{{y}_{{,222}}}{{\xi }^{3}}, \\ \theta = {{\theta }_{{,2}}}\xi + \frac{1}{6}{{\theta }_{{,222}}}{{\xi }^{3}},\,\,\,\,f = {{f}_{{,2}}}\xi + \frac{1}{6}{{f}_{{,222}}}{{\xi }^{3}}, \\ u = {{u}_{a}} + \frac{1}{2}{{u}_{{,22}}}{{\xi }^{2}} + \frac{1}{{24}}{{u}_{{,2222}}}{{\xi }^{4}}, \\ w = {{w}_{{,2}}}\xi + \frac{1}{6}{{w}_{{,222}}}{{\xi }^{3}}, \\ \end{gathered} $где ${{u}_{a}}$ – скорость на оси.
Входящие в формулы (23) производные определены выражениями
(24)
$\begin{gathered} {{f}_{{,222}}} = - 2\left( {1 + \tilde {\varphi }} \right)u{{u}_{{,22}}}{{\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}}} \right)}_{{,1}}} - \left( {1 + \tilde {\varphi }} \right) \times \\ \times \,\,{{u}^{2}}{{\left[ {\left( {\frac{{{{h}_{{2,221}}}}}{{{{h}_{1}}}} - \frac{{{{h}_{{2,1}}}{{h}_{{1,22}}}}}{{h_{1}^{2}}}} \right)} \right.}_{{,1}}} - 2{{f}_{{,2}}}{{\left( {\frac{{{{h}_{2}}{{f}_{{,21}}}}}{{{{h}_{1}}}}} \right)}_{{,1}}} - \\ - \,\,f_{{,2}}^{2}{{\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}}} \right)}_{{,1}}} + \left. {2{{h}_{2}}\left( {{{f}_{{,2}}}{{k}_{{1,21}}} + {{h}_{1}}k_{{1,2}}^{2} - \frac{{f_{{,21}}^{2}}}{{{{h}_{1}}}}} \right)} \right] + \\ + \,\,2{{f}_{{,2}}}\left[ {\frac{1}{{{{h}_{1}}}}{{{\left( {{{h}_{2}}{{f}_{{,2}}}} \right)}}_{{,1}}} - {{h}_{2}}{{k}_{{1,2}}}} \right] - \\ - \,\,\frac{{{{h}_{1}}L}}{{1 + \tilde {\varphi }}}\left[ {{{h}_{2}}L\left( {\frac{{{{L}_{{,22}}}}}{L} + \frac{{{{h}_{{2,22}}}}}{{{{h}_{2}}}} - f_{{,2}}^{2}} \right) - } \right. \\ \end{gathered} $Для компонент L, M магнитного поля получаем
(25)
$\begin{gathered} + \,\,{{h}_{2}}L{{k}_{{1,222}}} + 3\left( {{{h}_{{2,22}}}L - {{h}_{2}}f_{{,2}}^{2}L + {{h}_{2}}{{L}_{{,22}}}} \right){{k}_{{1,2}}} - \\ - \,\,\frac{{{{h}_{{20}}}\tilde {J}}}{u}\left[ {{{w}_{{,222}}} - 3\left( {\frac{{{{u}_{{,22}}}}}{u} - \frac{{{{h}_{{20,22}}}}}{{{{h}_{{20}}}}} - \frac{{{{J}_{{,22}}}}}{J}} \right){{w}_{{,2}}}} \right], \\ {{M}_{{,222}}} = - {{h}_{2}}\left[ {\frac{{{{L}_{{,221}}}}}{{{{h}_{1}}}} + \frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}{{h}_{2}}}}{{L}_{{,22}}} - \left( {\frac{{{{h}_{{1,22}}}}}{{{{h}_{1}}}} - \frac{{{{h}_{{2,22}}}}}{{{{h}_{2}}}} - f_{{,2}}^{2}} \right)\frac{{{{L}_{{,1}}}}}{{{{h}_{1}}}}} \right. + \\ \end{gathered} $Выражения для z, y из (23) при фиксированных значениях $\xi $ или ${{x}^{1}}$ определяют параметрические уравнения трубки тока или эквипотенциали.
5. РЕШЕНИЕ ВБЛИЗИ СТАРТОВОЙ ПОВЕРХНОСТИ ПРИ ЭМИССИИ В $\rho $-РЕЖИМЕ
Форма решения. При эмиссии в $\rho $-режиме структура особенности в прикатодной зоне описывается разложениями по параметру $t = {{\varphi }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}$ [1] с сингулярным элементом ${{g}_{{11}}}$ метрического тензора:
(26)
$\begin{gathered} {{h}_{1}} = {{a}_{0}}{{t}^{{ - 1}}}\left( {1 + {{{\bar {a}}}_{1}}t + {{{\bar {a}}}_{2}}{{t}^{2}} + ...} \right), \\ {{h}_{2}} = {{b}_{0}}\left( {1 + {{{\bar {b}}}_{3}}{{t}^{3}} + {{{\bar {b}}}_{4}}{{t}^{4}} + ...} \right), \\ {{g}_{{21}}} = {{f}_{0}}\left( {1 + {{{\bar {f}}}_{1}}t + {{{\bar {f}}}_{2}}{{t}^{2}} + ...} \right), \\ u = {{U}_{0}}{{t}^{2}}\left( {1 + {{{\bar {U}}}_{1}}t + {{{\bar {U}}}_{2}}{{t}^{2}} + ...} \right), \\ w = {{W}_{0}}{{t}^{3}}\left( {1 + {{{\bar {W}}}_{1}}t + {{{\bar {W}}}_{2}}{{t}^{2}} + ...} \right), \\ \rho = {{\rho }_{0}}{{t}^{{ - 2}}}\left( {1 + {{{\bar {\rho }}}_{1}}t + {{{\bar {\rho }}}_{2}}{{t}^{2}} + ...} \right), \\ L = {{L}_{0}} + {{L}_{1}}t + {{L}_{2}}{{t}^{2}} + ..., \\ M = {{M}_{0}} + {{M}_{1}}t + {{M}_{2}}{{t}^{2}} + ... \\ \end{gathered} $Условия ${{b}_{1}} = {{b}_{2}} = 0$ обеспечивают конечное значение кривизны эмитирующей поверхности.
В каждом n-м приближении по t возникают связанные через коэффициенты предыдущих приближений системы алгебраических уравнений, причем интеграл энергии из (4) устанавливает соотношения между величинами ${{U}_{k}}$ и ${{W}_{k}};$ уравнение движения из (4) служит для определения ${{g}_{{12}}};$ уравнения Пуассона и сохранения тока (5) порождают связи между ${{g}_{{11}}}$ и ρ; условие евклидовости (3) определяет ${{g}_{{22}}};$ связь сносовой скорости w с магнитным полем и компоненты L, M самосогласованного магнитного поля регламентированы уравнениями для ${{w}_{{,1}}}$ из (6) и (8).
При решении упомянутых алгебраических систем используются вспомогательные разложения
(27)
$\begin{gathered} \cos {\kern 1pt} {{\theta }_{{12}}} = {{c}_{0}}t\left( {1 + {{{\bar {c}}}_{1}}t + {{{\bar {c}}}_{2}}{{t}^{2}} + ...} \right), \\ \sin {{\theta }_{{12}}} = 1 + {{s}_{2}}{{t}^{2}} + {{s}_{3}}{{t}^{3}} + ... \\ \end{gathered} $Выражения для коэффициентов разложений. Первые алгебраические системы приводят к следующему результату:
(28)
$\begin{gathered} U_{0}^{2} = 2,\,\,\,\,a_{0}^{2} = \frac{{{{U}_{0}}}}{{4J}},\,\,\,\,{{\rho }_{0}} = \frac{J}{{{{U}_{0}}}},\,\,\,\,{{W}_{0}} = \frac{4}{3}{{a}_{0}}{{M}_{0}}, \\ {{f}_{0}} = - \frac{4}{3}\frac{{a_{0}^{2}{{b}_{0}}}}{{{{U}_{0}}}}N,\,\,\,\,{{c}_{0}} = - \frac{4}{3}\frac{{{{a}_{0}}N}}{{{{U}_{0}}}}. \\ \end{gathered} $Для коэффициентов с индексом 1 получаем
(29)
$\begin{gathered} {{a}_{1}} = {{U}_{1}} = {{\rho }_{1}} = {{L}_{1}} = 0,\,\,\,\,{{W}_{1}} = \frac{2}{3}a_{0}^{2}{{U}_{0}}{{L}_{0}}N, \\ {{M}_{1}} = \frac{4}{3}\frac{{{{a}_{0}}{{L}_{0}}N}}{{{{U}_{0}}}},\,\,\,{{f}_{1}} = \frac{2}{3}a_{0}^{3}{{b}_{0}}{{L}_{0}}{{M}_{0}},\,\,\,{{c}_{1}} = \frac{2}{3}a_{0}^{2}{{L}_{0}}{{M}_{0}}. \\ \end{gathered} $Решение алгебраических систем для следующего набора коэффициентов имеет вид
(30)
$\begin{gathered} {{{\bar {a}}}_{2}} = - a_{0}^{2}\left( {\frac{1}{9}M_{0}^{2} - \frac{1}{3}{{N}^{2}}} \right),\,\,\,\,{{{\bar {U}}}_{2}} = - \frac{4}{9}a_{0}^{2}M_{0}^{2}, \\ {{W}_{2}} = - \frac{8}{{15}}a_{0}^{3}{{M}_{0}}\left( {L_{0}^{2} + \frac{1}{6}M_{0}^{2} + \frac{1}{6}{{N}^{2}}} \right), \\ {{L}_{2}} = \frac{4}{9}a_{0}^{2}{{L}_{0}}{{N}^{2}},\,\,\,\,{{M}_{2}} = - \frac{2}{3}a_{0}^{2}L_{0}^{2}{{M}_{0}}, \\ {{{\bar {\rho }}}_{2}} = - \frac{4}{9}a_{0}^{2}\left( {M_{0}^{2} - {{N}^{2}}} \right),\,\,\,\,{{f}_{2}} = \frac{8}{{15}}\frac{{a_{0}^{4}{{b}_{0}}N}}{{{{U}_{0}}}} \times \\ \times \,\,\left( {L_{0}^{2} - \frac{2}{3}M_{0}^{2} - \frac{2}{3}{{N}^{2}}} \right) + \frac{4}{5}{{a}_{0}}{{a}_{{0,2}}},\,\,\,\,{{s}_{2}} = - \frac{4}{9}a_{0}^{2}{{N}^{2}}, \\ {{c}_{2}} = \frac{{a_{0}^{3}N}}{{{{U}_{0}}}}\left( {\frac{8}{{15}}L_{0}^{2} - \frac{{68}}{{135}}M_{0}^{2} + \frac{4}{{45}}{{N}^{2}}} \right) + \frac{4}{5}\frac{{{{a}_{{0,2}}}}}{{{{b}_{0}}}}. \\ \end{gathered} $Коэффициенты с индексами 3 определяются по формулам
(31)
$\begin{gathered} {{L}_{3}} = - \frac{4}{3}\frac{1}{{{{b}_{0}}}}{{\left( {{{a}_{0}}{{M}_{0}}} \right)}_{{,2}}} - {{L}_{0}}{{{\bar {b}}}_{3}} - \frac{4}{9}a_{0}^{3}{{U}_{0}}L_{0}^{2}{{M}_{0}}N, \\ {{M}_{3}} = \frac{4}{3}\frac{{{{a}_{0}}}}{{{{b}_{0}}}}{{L}_{{0,2}}} + \frac{8}{{15}}{{L}_{0}}\frac{{{{a}_{{0,2}}}}}{{{{b}_{0}}}} - {{M}_{0}}{{{\bar {b}}}_{3}} + \\ + \,\,\frac{{a_{0}^{3}{{L}_{0}}N}}{{{{U}_{0}}}}\left[ { - \frac{8}{{15}}L_{0}^{2} + \frac{{68}}{{135}}\left( {M_{0}^{2} + {{N}^{2}}} \right)} \right],\,\,\,\,{{{\bar {\rho }}}_{3}} = - {{{\bar {b}}}_{3}}, \\ {{f}_{3}} = - \frac{{59}}{{45}}a_{0}^{2}{{b}_{0}}{{U}_{0}}N{{{\bar {b}}}_{3}} - a_{0}^{5}{{b}_{0}}{{L}_{0}}{{M}_{0}} \times \\ \end{gathered} $Для коэффициентов при ${{t}^{4}}$ имеем
(32)
$\begin{gathered} - \,\,\frac{{a_{0}^{2}{{M}_{0}}N}}{{{{U}_{0}}{{b}_{0}}}}\left( {\frac{{40}}{9}\frac{{{{a}_{{0,2}}}}}{{{{a}_{0}}}} + \frac{{28}}{9}\frac{{{{M}_{{0,2}}}}}{{{{M}_{0}}}}} \right) + a_{0}^{4}L_{0}^{2}{{M}_{0}} \times \\ \times \,\,\left( {\frac{8}{{45}}L_{0}^{2} - \frac{{56}}{{135}}M_{0}^{2} + \frac{{128}}{{135}}{{N}^{2}}} \right),\,\,\,\,{{{\bar {\rho }}}_{4}} = - {{{\bar {b}}}_{4}} - \frac{8}{{15}}\frac{{{{a}_{{0,2}}}}}{{{{b}_{0}}}} + \\ + \,\,a_{0}^{4}\left[ {M_{0}^{2}\left( { - \frac{2}{{15}}L_{0}^{2} + \frac{{32}}{{135}}M_{0}^{2} + \frac{{124}}{{405}}{{N}^{2}}} \right)} \right. + \\ \left. { + \,\,{{N}^{2}}\left( {\frac{2}{{45}}L_{0}^{2} + \frac{4}{{15}}{{N}^{2}}} \right)} \right],\,\,\,\,{{f}_{4}} = - \frac{{136}}{{63}}\frac{{a_{0}^{2}{{b}_{0}}N}}{{{{U}_{0}}}}{{{\bar {b}}}_{4}} + \\ + \,\,\frac{4}{5}a_{0}^{3}{{b}_{0}}{{L}_{0}}{{M}_{0}}{{{\bar {b}}}_{3}} + \left( {\frac{{32}}{{315}}L_{0}^{2} - \frac{{24}}{{35}}M_{0}^{2} + } \right. \\ \end{gathered} $В случае отсутствия однородного внешнего магнитного поля по оси x формулы при учете релятивистских эффектов не упрощаются. Для заданных конечных размеров эмитирующей поверхности и распределения плотности тока на ней собственное поле с компонентой N равно нулю только в одной точке и нарастает по мере удаления от нее в соответствии с формулой для ${{N}_{{,2}}}$ из (12):
При этом оно влияет на компоненты по двум другим осям через коэффициенты ${{M}_{1}},$ ${{L}_{2}}.$
Коэффициенты пятого приближения приведем для случая $N \equiv 0,$ который возможен для нерелятивистских потоков:
(34)
$\begin{gathered} + \,\,\frac{{a_{0}^{3}}}{{{{b}_{0}}}}\left[ {\frac{2}{3}{{L}_{0}}{{M}_{0}}{{L}_{{0,2}}} + \left( {\frac{2}{3}L_{0}^{2} + \frac{1}{3}M_{0}^{2}} \right){{M}_{{0,2}}}} \right], \\ {{M}_{5}} = - {{M}_{0}}{{{\bar {b}}}_{5}} + \frac{{16}}{{15}}a_{0}^{2}L_{0}^{2}{{M}_{0}}{{{\bar {b}}}_{3}} + \frac{{a_{0}^{2}{{L}_{0}}}}{{{{b}_{0}}}} \times \\ \end{gathered} $Асимптотика функции $h{{{\kern 1pt} }_{2}}.$ Условия евклидовости пространства (3) позволяет получить выражения для функций ${{\bar {b}}_{4}},$ ${{\bar {b}}_{5}}\,:$
(35)
$\begin{gathered} {{{\bar {b}}}_{4}} = - \frac{4}{3}\frac{{a_{0}^{2}}}{{{{U}_{0}}}}\left( {2\frac{{{{a}_{{0,2}}}}}{{{{a}_{0}}{{b}_{0}}}}N + \tilde {J}} \right),\,\,\,\,{{{\bar {b}}}_{5}} = \frac{2}{5}a_{0}^{3} \times \\ \times \,\,\left[ {{{L}_{0}}{{M}_{0}}\left( {4\frac{{{{a}_{{0,2}}}}}{{{{a}_{0}}{{b}_{0}}}} + \frac{2}{3}\frac{{{{b}_{{0,2}}}}}{{b_{0}^{2}}}} \right) + {{M}_{0}}\frac{{{{L}_{{0,2}}}}}{{{{b}_{0}}}} + {{L}_{0}}\frac{{{{M}_{{0,2}}}}}{{{{b}_{0}}}}} \right] - \\ - \,\,\frac{1}{{15}}a_{0}^{2}\left( {M_{0}^{2} + {{N}^{2}}} \right){{{\bar {b}}}_{3}}. \\ \end{gathered} $Коэффициент ${{\bar {b}}_{3}}$ определяется через кривизну ${{\kappa }_{1}}$ стартовой поверхности, для которой в силу локальной ортогональности системы координат при ${{x}^{1}} = 0$ справедлива формула
Трубки тока и эквипотенциали. Связь декартовых y, z и криволинейных ${{x}^{1}},$ ${{x}^{2}}$ координат описывается уравнениями [1]
(37)
${{y}_{{,11}}} = \Gamma _{{11}}^{1}{{y}_{{,1}}} + \Gamma _{{11}}^{2}{{y}_{{,2}}},\,\,\,\,{{z}_{{,11}}} = \Gamma _{{11}}^{1}{{z}_{{,1}}} + \Gamma _{{11}}^{2}{{z}_{{,2}}},$где $\Gamma _{{kl}}^{i}$ – символы Кристоффеля:
(38)
$\begin{gathered} \Gamma _{{11}}^{1} = \frac{1}{{{{h}_{1}}{{{\sin }}^{2}}{{\theta }_{{12}}}}}\left[ {{{h}_{{1,1}}} - \frac{{\cos {{\theta }_{{12}}}}}{{{{h}_{2}}}}\left( {{{g}_{{12,1}}} - {{h}_{1}}{{h}_{{1,2}}}} \right)} \right], \\ \Gamma _{{11}}^{2} = \frac{1}{{{{h}_{2}}{{{\sin }}^{2}}{{\theta }_{{12}}}}}\left[ {\cos {\kern 1pt} {{\theta }_{{12}}}{\kern 1pt} {{h}_{{1,1}}} + \frac{1}{{{{h}_{2}}}}\left( {{{g}_{{12,1}}} - {{h}_{1}}{{h}_{{1,2}}}} \right)} \right]. \\ \end{gathered} $В окрестности катода будем искать решение в виде
(39)
$\begin{gathered} y = Y + {{Y}_{3}}{{t}^{3}} + {{Y}_{4}}{{t}^{4}} + ..., \\ z = Z + {{Z}_{3}}{{t}^{3}} + {{Z}_{4}}{{t}^{4}} + ... \\ \end{gathered} $с сохранением в (39) членов с седьмой степенью t. Используя приведенное выше локальное решение уравнений пучка, получаем
(40)
$\begin{gathered} + \,\,a_{0}^{4}\left( {\frac{7}{{27}}L_{0}^{2} - \frac{{218}}{{1215}}M_{0}^{2} - \frac{{377}}{{1215}}{{N}^{2}}} \right) - \frac{{\widetilde {19}}}{{36}}; \\ \Gamma _{{11}}^{2} = {{t}^{{ - 4}}}\left( {{{\gamma }_{{20}}} + {{\gamma }_{{21}}}t + {{\gamma }_{{22}}}{{t}^{2}} + {{\gamma }_{{23}}}{{t}^{3}}} \right), \\ {{\gamma }_{{20}}} = - \frac{1}{3}\frac{{a_{0}^{2}N}}{{{{b}_{0}}{{U}_{0}}}},\,\,\,\,{{\gamma }_{{21}}} = \frac{1}{3}\frac{{a_{0}^{3}{{L}_{0}}{{M}_{0}}}}{{{{b}_{0}}}}, \\ \end{gathered} $Коэффициенты ${{Y}_{k}}$ в формулах (39) могут быть выражены через параметры из (40):
(41)
$\begin{gathered} {{Y}_{4}} = 4{{\gamma }_{{20}}}{{Y}_{{,2}}},\,\,\,\,{{Y}_{5}} = \frac{8}{5}\left( {{{\gamma }_{{21}}}{{Y}_{{,2}}} + \frac{3}{4}{{\gamma }_{{12}}}{{Y}_{3}}} \right), \\ {{Y}_{6}} = \frac{8}{9}\left[ {\left( {{{\gamma }_{{22}}} + 4{{\gamma }_{{20}}}{{\gamma }_{{12}}}} \right){{Y}_{{,2}}} + \frac{3}{4}{{\gamma }_{{13}}}{{Y}_{3}}} \right], \\ {{Y}_{7}} = \frac{4}{7}\left[ {\left( {{{\gamma }_{{23}}} + 2{{\gamma }_{{12}}}{{\gamma }_{{21}}} + 4{{\gamma }_{{13}}}{{\gamma }_{{20}}}} \right){{Y}_{{,2}}} + \frac{{}}{{}}} \right. \\ \left. { + \,\,\frac{3}{4}\left( {{{\gamma }_{{14}}} + 2{{\gamma }_{{12}}}} \right){{Y}_{3}} + {{\gamma }_{{20}}}{{Y}_{{3,2}}}} \right]. \\ \end{gathered} $Формулы для ${{Z}_{k}}$ получаются при помощи замены ${{Y}_{k}} \to {{Z}_{k}}$ в (41).
Коэффициенты с индексом 3 связаны с ориентацией нормали к стартовой поверхности:
(42)
$\begin{gathered} y = Y({{x}^{2}}),\,\,\,\,z = Z({{x}^{2}}); \\ {{Y}_{3}} = \frac{4}{3}{{a}_{o}}\frac{{{{Z}_{{,2}}}}}{{\sqrt {Y_{{,2}}^{2} + Z_{{,2}}^{2}} }},\,\,\,\,{{Z}_{3}} = \frac{4}{3}{{a}_{o}}\frac{{{{Y}_{{,2}}}}}{{\sqrt {Y_{{,2}}^{2} + Z_{{,2}}^{2}} }}. \\ \end{gathered} $Уравнения (39) с коэффициентами (40) являются параметрическими уравнениями трубки тока при ${{x}^{2}} = {\text{const}}$ или эквипотенциали при ${{x}^{1}} = {\text{const}}{\text{.}}$ Построение нормальных к эквипотенциалям кривых показывает, насколько трубки тока отклоняются от силовых линий электрического поля.
6. РЕШЕНИЕ ВБЛИЗИ СТАРТОВОЙ ПОВЕРХНОСТИ ПРИ ЭМИССИИ В Т-РЕЖИМЕ
Форма решения. При эмиссии в Т-режиме решение в прикатодной зоне может быть представлено разложениями по полуцелым степеням потенциала [1]:
(43)
$\begin{gathered} {{h}_{{\,1}}} = {{a}_{0}}\left( {1 + {{{\bar {a}}}_{1}}t + {{{\bar {a}}}_{2}}{{t}^{2}} + ...} \right), \\ {{h}_{2}} = {{b}_{0}}\left( {1 + {{{\bar {b}}}_{1}}t + {{{\bar {b}}}_{2}}{{t}^{2}} + ...} \right), \\ {{g}_{{12}}} = {{f}_{0}}\left( {1 + {{{\bar {f}}}_{1}}t + {{{\bar {f}}}_{2}}{{t}^{2}} + ...} \right), \\ u = {{U}_{0}}t\left( {1 + {{{\bar {U}}}_{1}}t + {{{\bar {U}}}_{2}}{{t}^{2}} + ...} \right), \\ w = {{W}_{0}}{{t}^{2}}\left( {1 + {{{\bar {W}}}_{1}}t + {{{\bar {W}}}_{2}}{{t}^{2}} + ...} \right), \\ \rho = {{\rho }_{0}}{{t}^{{ - 1}}}\left( {1 + {{{\bar {\rho }}}_{1}}t + {{{\bar {\rho }}}_{2}}{{t}^{2}} + ...} \right), \\ L = {{L}_{0}} + {{L}_{1}}t + {{L}_{2}}{{t}^{2}} + ..., \\ M = {{M}_{0}} + {{M}_{1}}t + {{M}_{2}}{{t}^{2}} + ... \\ \end{gathered} $В дальнейшем будем использовать следующие сокращенные обозначения (Е – электрическое поле на катоде):
(44)
$\begin{gathered} {{{\bar {L}}}_{0}} = \frac{{{{L}_{0}}}}{E},\,\,\,\,{{{\bar {M}}}_{0}} = \frac{{{{M}_{0}}}}{E},\,\,\,\bar {J} = \frac{J}{{{{E}^{2}}}},\,\,\,{{{\bar {L}}}_{{0,2}}} = \frac{{{{L}_{{0,2}}}}}{{{{b}_{0}}{{E}^{2}}}}, \\ {{{\bar {E}}}_{{,2}}} = \frac{{{{E}_{{,2}}}}}{{{{b}_{0}}{{E}^{2}}}},\,\,\,\,{{{\bar {J}}}_{{,2}}} = \frac{{{{J}_{{,2}}}}}{{{{b}_{0}}{{E}^{3}}}}, \\ {{{\bar {L}}}_{{0,22}}} = \frac{{{{L}_{{0,22}}}}}{{b_{0}^{2}{{E}^{3}}}},\,\,\,\,{{{\bar {E}}}_{{,22}}} = \frac{{{{E}_{{,22}}}}}{{b_{0}^{2}{{E}^{3}}}}. \\ \end{gathered} $Выражения для коэффициентов разложений. В нулевом приближении по t получаем
(45)
$\begin{gathered} {{a}_{0}} = \frac{1}{E},\,\,\,\,U_{0}^{2} = 2,\,\,\,\,{{W}_{0}} = {{{\bar {M}}}_{0}},\,\,\,{{\rho }_{0}} = \frac{J}{{{{U}_{0}}}}, \\ {{f}_{0}} = - \frac{1}{2}\frac{{{{b}_{0}}{{U}_{0}}}}{E}\bar {N},\,\,\,\,{{c}_{0}} = - \frac{1}{2}{{U}_{0}}\bar {N}. \\ \end{gathered} $Значение ${{a}_{0}}$ следует из определения нормального электрического поля на катоде:
(46)
$E = {{\left( {\frac{1}{{{{h}_{1}}}}\frac{{\partial \varphi }}{{\partial {{x}^{1}}}}} \right)}_{0}} = \frac{1}{{{{a}_{0}}}}.$Для коэффициентов с индексом 1 имеем
(47)
$\begin{gathered} {{U}_{1}} = {{L}_{1}} = {{\rho }_{1}} = 0,\,\,\,{{{\bar {a}}}_{1}} = - {{U}_{0}}\bar {J}, \\ {{W}_{1}} = \frac{2}{3}{{U}_{0}}\left( { - \bar {J}{{{\bar {M}}}_{0}} + \frac{1}{2}{{{\bar {L}}}_{0}}\bar {N}} \right),\,\,\,\,{{M}_{1}} = \frac{1}{2}{{U}_{0}}E{{{\bar {L}}}_{0}}\bar {N}, \\ {{f}_{1}} = \frac{{{{b}_{0}}}}{E}\left( { - \frac{2}{3}{{{\bar {E}}}_{{,2}}} + \frac{1}{3}{{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}} + \frac{5}{3}\bar {J}\bar {N}} \right), \\ {{c}_{1}} = - \frac{2}{3}{{{\bar {E}}}_{{,2}}} + \frac{1}{3}{{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}} + \frac{2}{3}\bar {J}\bar {N}. \\ \end{gathered} $Во втором приближении получаем
(48)
$\begin{gathered} {{{\bar {a}}}_{2}} = {{{\bar {b}}}_{2}} + 3{{{\bar {J}}}^{2}} + \frac{1}{4}{{{\bar {N}}}^{2}},\,\,\,\,{{{\bar {U}}}_{2}} = - \frac{1}{4}\bar {M}_{0}^{2} - \frac{{\tilde {3}}}{4}, \\ {{W}_{2}} = - \frac{1}{6}{{{\bar {L}}}_{0}}{{{\bar {E}}}_{{,2}}} + \frac{1}{2}{{L}_{{0,2}}} + \frac{3}{2}{{{\bar {J}}}^{2}}{{{\bar {M}}}_{0}} - \\ - \,\,\frac{1}{6}\bar {L}_{0}^{2}{{{\bar {M}}}_{0}} - \frac{1}{6}\bar {J}{{{\bar {L}}}_{0}}\bar {N} - {{{\tilde {M}}}_{0}},\,\,\,\frac{{{{L}_{2}}}}{E} = {{{\bar {M}}}_{0}}{{{\bar {E}}}_{{,2}}} - {{{\bar {M}}}_{{0,2}}} - \\ - \,\,{{{\bar {L}}}_{0}}\left( {{{{\bar {b}}}_{2}} - \frac{1}{4}{{{\bar {N}}}^{2}}} \right),\,\,\,\frac{{{{M}_{2}}}}{E} = - \frac{1}{3}{{{\bar {L}}}_{0}}{{{\bar {E}}}_{{,2}}} + {{{\bar {L}}}_{{0,2}}} - \\ - \,\,{{{\bar {M}}}_{0}}{{{\bar {b}}}_{2}} - \frac{1}{3}\bar {L}_{0}^{{{\kern 1pt} 2}}{{{\bar {M}}}_{0}} - \frac{2}{3}\bar {J}{\kern 1pt} {{{\bar {L}}}_{0}}\bar {N},\,\,\,\,{{{\bar {\rho }}}_{2}} = - {{{\bar {b}}}_{2}} + \frac{1}{4}\bar {M}_{0}^{2} + \\ + \,\,\frac{1}{4}{{{\bar {N}}}^{2}} + \frac{{\tilde {3}}}{4},\,\,\,{{f}_{2}} = \frac{{{{b}_{0}}}}{{{{U}_{0}}E}}\left[ {\frac{{22}}{3}\bar {J}{{{\bar {E}}}_{{,2}}} - {{{\bar {J}}}_{{,2}}} - \frac{3}{2}\bar {J}{\kern 1pt} {{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}}} \right. + \\ \left. {\left. { + \,\,\bar {N}\left( { - 2{{{\bar {b}}}_{2}} - \frac{{35}}{6}{{{\bar {J}}}^{2}} + } \right.\frac{1}{6}\bar {L}_{0}^{{{\kern 1pt} 2}} - \frac{1}{4}\bar {M}_{0}^{2} - \frac{1}{4}{{{\bar {N}}}^{2}} + \frac{{\tilde {1}}}{4}} \right)} \right], \\ {{s}_{2}} = - \frac{1}{4}{{{\bar {N}}}^{2}},\,\,\,\,{{c}_{2}} = \frac{1}{{{{U}_{0}}}}\left[ {6\bar {J}{{{\bar {E}}}_{{,2}}} - {{{\bar {J}}}_{{,2}}} - \frac{5}{6}\bar {J}{\kern 1pt} {{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}}} \right. + \\ \left. {\left. { + \,\,\bar {N}\left( { - 2{{{\bar {b}}}_{2}} + \frac{{103}}{{56}}{{{\bar {J}}}^{2}} + } \right.\frac{1}{6}\bar {L}_{0}^{{{\kern 1pt} 2}} - \frac{1}{4}\bar {M}_{0}^{2} - \frac{1}{2}{{{\bar {N}}}^{2}} + \frac{{\tilde {1}}}{4}} \right)} \right]. \\ \end{gathered} $Коэффициенты при t3 определены формулами
(49)
$\begin{gathered} \times \,\,\left. {\left( {\frac{1}{2}{{{\bar {b}}}_{2}} - \frac{{103}}{{72}}{{{\bar {J}}}^{2}} - \frac{1}{{12}}\bar {L}_{0}^{{{\kern 1pt} 2}} + \frac{1}{8}\bar {M}_{0}^{2} + \frac{3}{8}{{{\bar {N}}}^{2}} - \frac{{\tilde {1}}}{8}} \right)} \right], \\ {{{\bar {\rho }}}_{3}} = - {{{\bar {b}}}_{3}} + \frac{{{{U}_{0}}{{{\bar {M}}}_{0}}}}{3}\left( {\bar {J}{{{\bar {M}}}_{0}} - \frac{1}{2}{{{\bar {L}}}_{0}}\bar {N}} \right),\,\,\,\,{{f}_{3}} = \frac{{{{b}_{0}}}}{E} \times \\ \end{gathered} $Для коэффициентов с индексом 4 имеем
(50)
$\begin{gathered} + \,\,\left( {{{{\bar {b}}}_{2}} - \frac{3}{2}{{{\bar {J}}}^{2}} + \frac{1}{6}\bar {L}_{0}^{{{\kern 1pt} 2}} - \frac{1}{2}{{{\bar {N}}}^{2}}} \right){{{\bar {M}}}_{{0,2}}} + \\ + \,\,\bar {L}_{0}^{2}{{{\bar {M}}}_{0}}\left( {\frac{1}{{18}}{{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}} + \frac{{23}}{{36}}\bar {J}\bar {N}} \right) - {{{\bar {L}}}_{0}}{{{\bar {N}}}^{2}}\left( {\frac{3}{4}{{{\bar {b}}}_{2}} - \frac{{29}}{{24}}{{{\bar {J}}}^{2}}} \right. - \\ \left. { - \,\,\frac{1}{{12}}\bar {L}_{0}^{{{\kern 1pt} 2}} + \frac{1}{8}\bar {M}_{0}^{2} - \frac{{\tilde {1}}}{8}} \right),\,\,\,\,\frac{1}{E}{{M}_{4}} = - \frac{2}{5}{{{\bar {L}}}_{0}}\frac{{{{{\bar {b}}}_{{2,2}}}}}{{{{b}_{0}}E}} + \\ + \,\,{{{\bar {M}}}_{0}}\left( { - {{{\bar {b}}}_{4}} + \bar {b}_{2}^{2}} \right) - \frac{3}{5}{{U}_{0}}{{{\bar {L}}}_{0}}\bar {N}{{{\bar {b}}}_{3}} + \frac{1}{6}{{{\bar {M}}}_{0}}\left( {{{{\bar {E}}}_{{,22}}} + \bar {E}_{{,2}}^{2}} \right) - \\ \end{gathered} $Влияние собственного магнитного поля начинает проявляться в коэффициентах ${{M}_{1}},$ ${{L}_{2}}$ при членах порядка $\sqrt \varphi $ и φ, в то время как в $\rho $-режиме соответствующие слагаемые имели порядок $\sqrt[4]{\varphi }$ и $\sqrt \varphi .$
Асимптотика функции ${{h}_{2}}.$ Рассматривая уравнение (3), можно вычислить коэффициенты ${{b}_{3}},$ ${{b}_{4}},$ определяющие поведение элемента ${{g}_{{22}}}$ в окрестности особенности на катоде:
(51)
$\begin{gathered} {{{\bar {b}}}_{3}} = \frac{1}{3}{{U}_{0}}\left( { - 2{{{\bar {b}}}_{2}}\bar {J} + 2\bar {N}{{{\bar {E}}}_{{,2}}} - \tilde {J}} \right), \\ {{{\bar {b}}}_{4}} = - {{{\bar {E}}}_{{,22}}} - \frac{1}{2}\left( {{{{\bar {E}}}_{{,2}}} + \bar {J}\bar {N}} \right)\frac{{{{b}_{{0,2}}}}}{{b_{0}^{2}E}} - \\ - \,\,\left( {\frac{1}{3}{{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}} + \frac{{23}}{6}\bar {J}\bar {N}} \right){{{\bar {E}}}_{{,2}}} + \frac{1}{2}{{{\bar {b}}}_{2}}\left( {{{{\bar {b}}}_{2}} + 4{{{\bar {J}}}^{2}} + \frac{1}{2}{{{\bar {N}}}^{2}}} \right) + \\ + \,\,\frac{1}{6}{{{\bar {M}}}_{0}}{{{\bar {L}}}_{{0,2}}} + \frac{1}{6}{{{\bar {L}}}_{0}}{{{\bar {M}}}_{{0,2}}} + \frac{5}{2}\bar {N}{\kern 1pt} {{{\bar {J}}}_{{,2}}} + \frac{{11}}{4}{{{\tilde {\bar {J}}}}^{2}}. \\ \end{gathered} $Трубки тока и эквипотенциали. Используя соотношения (37), (38), будем искать решение в виде
(52)
$\begin{gathered} y = Y + {{Y}_{2}}{{t}^{2}} + {{Y}_{3}}{{t}^{3}} + {{Y}_{4}}{{t}^{4}} + {{Y}_{5}}{{t}^{5}}, \\ z = Z + {{Z}_{2}}{{t}^{2}} + {{Z}_{3}}{{t}^{3}} + {{Z}_{4}}{{t}^{4}} + {{Z}_{5}}{{t}^{5}}. \\ \end{gathered} $Для символов Кристоффеля на основании результатов разд. 6 имеем
(53)
$\begin{gathered} {{{\bar {a}}}_{2}} = {{{\bar {b}}}_{2}} + 3{{{\bar {J}}}^{2}} + \frac{1}{4}{{{\bar {N}}}^{2}},\,\,\,\,{{{\bar {U}}}_{2}} = - \frac{1}{4}\bar {M}_{0}^{2} - \frac{{\tilde {3}}}{4}, \\ {{W}_{2}} = - \frac{1}{6}{{{\bar {L}}}_{0}}{{{\bar {E}}}_{{,2}}} + \frac{1}{2}{{L}_{{0,2}}} + \frac{3}{2}{{{\bar {J}}}^{2}}{{{\bar {M}}}_{0}} - \\ - \,\,\frac{1}{6}\bar {L}_{0}^{2}{{{\bar {M}}}_{0}} - \frac{1}{6}\bar {J}{{{\bar {L}}}_{0}}\bar {N} - {{{\tilde {M}}}_{0}},\,\,\,\frac{{{{L}_{2}}}}{E} = {{{\bar {M}}}_{0}}{{{\bar {E}}}_{{,2}}} - {{{\bar {M}}}_{{0,2}}} - \\ - \,\,{{{\bar {L}}}_{0}}\left( {{{{\bar {b}}}_{2}} - \frac{1}{4}{{{\bar {N}}}^{2}}} \right),\,\,\,\frac{{{{M}_{2}}}}{E} = - \frac{1}{3}{{{\bar {L}}}_{0}}{{{\bar {E}}}_{{,2}}} + {{{\bar {L}}}_{{0,2}}} - \\ - \,\,{{{\bar {M}}}_{0}}{{{\bar {b}}}_{2}} - \frac{1}{3}\bar {L}_{0}^{{{\kern 1pt} 2}}{{{\bar {M}}}_{0}} - \frac{2}{3}\bar {J}{\kern 1pt} {{{\bar {L}}}_{0}}\bar {N},\,\,\,\,{{{\bar {\rho }}}_{2}} = - {{{\bar {b}}}_{2}} + \frac{1}{4}\bar {M}_{0}^{2} + \\ + \,\,\frac{1}{4}{{{\bar {N}}}^{2}} + \frac{{\tilde {3}}}{4},\,\,\,{{f}_{2}} = \frac{{{{b}_{0}}}}{{{{U}_{0}}E}}\left[ {\frac{{22}}{3}\bar {J}{{{\bar {E}}}_{{,2}}} - {{{\bar {J}}}_{{,2}}} - \frac{3}{2}\bar {J}{\kern 1pt} {{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}}} \right. + \\ \left. {\left. { + \,\,\bar {N}\left( { - 2{{{\bar {b}}}_{2}} - \frac{{35}}{6}{{{\bar {J}}}^{2}} + } \right.\frac{1}{6}\bar {L}_{0}^{{{\kern 1pt} 2}} - \frac{1}{4}\bar {M}_{0}^{2} - \frac{1}{4}{{{\bar {N}}}^{2}} + \frac{{\tilde {1}}}{4}} \right)} \right], \\ {{s}_{2}} = - \frac{1}{4}{{{\bar {N}}}^{2}},\,\,\,\,{{c}_{2}} = \frac{1}{{{{U}_{0}}}}\left[ {6\bar {J}{{{\bar {E}}}_{{,2}}} - {{{\bar {J}}}_{{,2}}} - \frac{5}{6}\bar {J}{\kern 1pt} {{{\bar {L}}}_{0}}{{{\bar {M}}}_{0}}} \right. + \\ \left. {\left. { + \,\,\bar {N}\left( { - 2{{{\bar {b}}}_{2}} + \frac{{103}}{{56}}{{{\bar {J}}}^{2}} + } \right.\frac{1}{6}\bar {L}_{0}^{{{\kern 1pt} 2}} - \frac{1}{4}\bar {M}_{0}^{2} - \frac{1}{2}{{{\bar {N}}}^{2}} + \frac{{\tilde {1}}}{4}} \right)} \right]. \\ \end{gathered} $Коэффициенты ${{Y}_{k}}$ из (52) могут быть выражены через ${{\gamma }_{{1k}}},$ ${{\gamma }_{{2k}}}$ при помощи соотношений
(54)
$\begin{gathered} {{Y}_{3}} = \frac{4}{3}\left( {{{\gamma }_{{10}}}{{\gamma }_{2}} + {{\gamma }_{{20}}}{{Y}_{{,2}}}} \right), \\ {{Y}_{4}} = \frac{1}{2}\left[ {\left( {2\gamma _{{10}}^{2} + {{\gamma }_{{11}}}} \right){{Y}_{2}} + \left( {2{{\gamma }_{{20}}}{{\gamma }_{{11}}} + {{\gamma }_{{21}}}} \right){{Y}_{{,2}}}} \right], \\ {{Y}_{5}} = \frac{4}{{15}}\left[ {\left( {{{\gamma }_{{12}}} + 3{{\gamma }_{{10}}}{{\gamma }_{{11}}} + 2\gamma _{{10}}^{3}} \right){{Y}_{2}} + } \right. \\ + \,\,\left( {{{\gamma }_{{22}}} + 2{{\gamma }_{{11}}}{{\gamma }_{{20}}} + {{\gamma }_{{10}}}{{\gamma }_{{21}}}} \right. + \left. {\left. {2\gamma _{{10}}^{2}{{\gamma }_{{20}}}} \right){{Y}_{{,2}}} + {{\gamma }_{{20}}}{{Y}_{{2,2}}}} \right]. \\ \end{gathered} $Формулы для ${{Z}_{k}}$ получаются при помощи замены ${{Y}_{k}} \to {{Z}_{k}},$ а компоненты нормали ${{Y}_{2}},$ ${{Z}_{2}}$ описываются выражениями (42).
7. ИНТЕГРИРОВАНИЕ СООТНОШЕНИЙ НА БАЗОВОЙ ТРУБКЕ ТОКА
Пучки с искривленной осью. Уравнения (7), (8) в случае криволинейного ленточного пучка в правых частях имеют члены, обращающиеся в бесконечность или содержащие неопределенности. Для учета первых и раскрытия вторых следует использовать прикатодные асимптотики, приведенные в разд. 5, 6. Структура особенностей решения сводится к трехчленной формуле с двумя выделенными точками ветвления в ρ-режиме эмиссии и к двучленной формуле в случае Т-режима [10]. По этой причине при интегрировании уравнения (7) необходимо использовать для ${{h}_{{\,2}}}$ разложения с сохранением коэффициентов ${{b}_{4}},$ ${{b}_{5}}$ (ρ-режим) или ${{b}_{3}}$ (Т-режим). Значение кривизны ${{\kappa }_{1}}$ катода на оси пучка определяет коэффициенты ${{b}_{3}},$ ${{b}_{2}}$ соответственно:
(55)
${{\kappa }_{1}} = - \frac{{{{{\bar {b}}}_{3}}}}{{{{a}_{0}}}},\,\,\,\,{{\kappa }_{1}} = - \frac{{{{{\bar {b}}}_{2}}}}{{{{a}_{0}}}}.$При интегрировании уравнения (15) первого приближения асимптотика функции ${{h}_{{\,2,2}}}$ описывается коэффициентами ${{b}_{{3,2}}},$ ${{b}_{{4,2}}},$ ${{b}_{{5,2}}}$ или ${{b}_{{2,2}}},$ ${{b}_{{3,2}}},$ первые из которых выражаются через производную кривизны катода ${{\kappa }_{{1,2}}},$ оставшиеся получаются при дифференцировании формул (35), (51) по ${{x}^{2}}.$ Таким образом, в рассматриваемой модели необходимо задать геометрию катода через кривизну и ее производные и распределения прочих параметров на стартовой поверхности.
Функция ${{b}_{0}}\left( {{{x}^{2}}} \right)$ связана со способом отсчета поперечной координаты и не ограничена никакими другими требованиями. При длине дуги этой оси в качестве ${{x}^{2}}$ имеем ${{b}_{0}} \equiv 1$. В работе [2] показано, что точность приближенного решения зависит от выбора функции ${{b}_{0}}({{x}^{2}}).$
Случай прямой оси. Для плоскосимметричных потоков система координат ${{x}^{i}}$ локально-ортогональна не только на катоде, но и при $y = 0.$ В результате уравнения (8) удовлетворяются тождественно и задача сводится к интегрированию соотношений (19), (20). Для функций, входящих в первое из них, справедливы следующие асимптотики:
(56)
$\begin{gathered} {{h}_{2}} = {{b}_{0}} + {{b}_{3}}{{t}^{3}} + {{b}_{4}}{{t}^{4}} + {{b}_{5}}{{t}^{5}},\,\,\,\,t = {{\varphi }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}, \\ L = {{L}_{0}} - \left( {{{{\bar {b}}}_{3}}{{L}_{0}} + \frac{4}{3}\frac{{{{a}_{0}}}}{{{{b}_{0}}}}{{M}_{{0,2}}}} \right){{t}^{3}} + 0 \cdot {{t}^{4}}; \\ {{h}_{2}} = {{b}_{0}} + {{b}_{2}}{{t}^{2}} + {{b}_{3}}{{t}^{3}} + {{b}_{4}}{{t}^{4}},\,\,\,\,t = {{\varphi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ L = {{L}_{0}} - \left( {{{{\bar {b}}}_{2}}{{L}_{0}} + \frac{1}{{{{E}^{2}}{{b}_{0}}}}{{M}_{{0,2}}}} \right){{t}^{2}} + \\ + \,\,\frac{2}{3}\frac{{{{U}_{0}}J}}{{{{E}^{2}}}}\left( {{{{\bar {b}}}_{2}}\frac{{{{L}_{0}}}}{E} - \frac{1}{{{{E}^{2}}{{b}_{0}}}}{{M}_{{0,2}}} + \frac{{{{{\tilde {L}}}_{0}}}}{E}} \right){{t}^{3}}. \\ \end{gathered} $Функция ${{h}_{1}}({{x}^{1}})$ на оси связана с распределением потенциала $\varphi = \varphi \left( z \right)$ соотношением
(57)
${{h}_{1}}\left( \varphi \right) = \frac{1}{{\varphi {\text{'}}\left( {z\left( \varphi \right)} \right)}}$и на основании результатов разд. 5, 6 определена разложениями
(58)
$\begin{gathered} {{h}_{{\,1}}} = \sqrt {\frac{{{{U}_{0}}}}{{4J}}} \,{{t}^{{ - 1}}}\left[ {1 + \frac{4}{5}{{{\bar {b}}}_{3}}{{t}^{3}} + \left( {\frac{5}{6}{{{\bar {b}}}_{4}} - \frac{{\widetilde {19}}}{{36}}} \right){{t}^{4}}} \right. + \\ \left. { + \,\,\left( {\frac{6}{7}{{{\bar {b}}}_{5}} - \frac{8}{{81}}\frac{{a_{0}^{3}}}{{{{b}_{0}}}}{{L}_{0}}{{M}_{{0,2}}}} \right){{t}^{5}}} \right]; \\ {{h}_{1}} = \frac{1}{E}\left\{ {1 - {{U}_{0}}\bar {J}t + \left( {{{{\bar {b}}}_{2}} + 3{{{\bar {J}}}^{2}}} \right){{t}^{2}} + \frac{{}}{{}}} \right. \\ + \,\,\left. {\left[ {{{{\bar {b}}}_{3}} + {{U}_{0}}\left( { - \frac{4}{3}{{{\bar {b}}}_{2}}\bar {J} - 9{{{\bar {J}}}^{3}} + \frac{1}{8}\tilde {\bar {J}}} \right)} \right]{{t}^{3}}} \right\}. \\ \end{gathered} $При интегрировании уравнения (21) функция ${{h}_{{\,2,22}}}$ в окрестности катодных сингулярностей имеет вид
(59)
$\begin{gathered} {{h}_{{2,22}}} = {{b}_{{0,22}}} + {{b}_{{3,22}}}{{t}^{3}} + {{b}_{{4,22}}}{{t}^{4}} + {{b}_{{5,22}}}{{t}^{5}},\,\,\,\,t = {{\varphi }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}; \\ {{h}_{{2,22}}} = {{b}_{{0,22}}} + {{b}_{{2,22}}}{{t}^{2}} + {{b}_{{3,22}}}{{t}^{3}} + {{b}_{{4,22}}}{{t}^{4}},\,\,\,t = {{\varphi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $Величины ${{b}_{{3,22}}},$ ${{b}_{{2,22}}}$ могут быть выражены через вторую производную ${{\kappa }_{{1,22}}}$ кривизны катода
(60)
$\begin{gathered} {{\kappa }_{{1,22}}} = - \frac{{{{b}_{{3,22}}}}}{{{{a}_{0}}{{b}_{0}}}} - {{\kappa }_{1}}\left( {\frac{{{{a}_{{0,22}}}}}{{{{a}_{0}}}} + \frac{{{{b}_{{0,22}}}}}{{{{b}_{0}}}}} \right),\,\,\,\frac{{{{a}_{{0,22}}}}}{{{{a}_{0}}}} = - \frac{1}{2}\frac{{{{J}_{{,22}}}}}{J}; \\ {{\kappa }_{{1,22}}} = - \frac{{{{b}_{{2,22}}}}}{{{{a}_{0}}{{b}_{0}}}} - {{\kappa }_{1}}\left( {\frac{{{{a}_{{0,22}}}}}{{{{a}_{0}}}} + \frac{{{{b}_{{0,22}}}}}{{{{b}_{0}}}}} \right),\,\,\,\frac{{{{a}_{{0,22}}}}}{{{{a}_{0}}}} = - \frac{{{{E}_{{,22}}}}}{E}. \\ \end{gathered} $Другие коэффициенты в формулах (59) получаются при дифференцировании соответствующих величин из (35), (51) и переходе к оси:
(61)
$\begin{gathered} \frac{{{{b}_{{4,22}}}}}{{b_{0}^{3}}} = - \frac{1}{{12}}\frac{{{{{\tilde {J}}}_{{,22}}}}}{{b_{0}^{2}J}} - \frac{1}{3}\frac{{{{{\tilde {b}}}_{{0,22}}}}}{{b_{0}^{3}}},\,\,\,\,\frac{{{{b}_{{5,22}}}}}{{b_{0}^{3}}} = \frac{2}{5}a_{0}^{3} \times \\ \times \,\,\left[ {{{L}_{0}}\frac{{{{M}_{{0,2}}}}}{{{{b}_{0}}}}\left( { - \frac{{11}}{2}\frac{{{{J}_{{,22}}}}}{{b_{0}^{2}J}} + \frac{4}{3}\frac{{{{b}_{{0,22}}}}}{{b_{0}^{3}}}} \right)} \right. + {{L}_{0}}\frac{{{{M}_{{0,222}}}}}{{b_{0}^{3}}} + \\ \left. { + 3\frac{{{{M}_{{0,2}}}}}{{{{b}_{0}}}}\frac{{{{L}_{{0,22}}}}}{{b_{0}^{2}}} - \frac{1}{3}{{{\bar {b}}}_{3}}\left( {\frac{{M_{{0,2}}^{2}}}{{b_{0}^{2}}} + \tilde {J}} \right)} \right];\,\,\,\,\frac{{{{b}_{{3,22}}}}}{{b_{0}^{3}}} = \frac{{{{U}_{0}}J}}{{{{E}^{2}}}} \times \\ \times \,\,\left[ {\left( {\frac{2}{3}{{{\bar {b}}}_{3}} + \frac{{\tilde {1}}}{3}} \right)\frac{{{{J}_{{,22}}}}}{{b_{0}^{2}J}} + \left( {2{{{\bar {b}}}_{2}} + \frac{{\tilde {4}}}{3}} \right)\frac{{{{E}_{{,22}}}}}{{b_{0}^{2}E}} - \frac{2}{3}\frac{{{{b}_{{2,22}}}}}{{b_{0}^{3}}} - \frac{1}{3}\frac{{{{{\tilde {b}}}_{{0,22}}}}}{{b_{0}^{3}}}} \right]. \\ \end{gathered} $Коэффициенты уравнения (21) вблизи катода, как и асимптотики (56), подсчитываются при использовании разложений разд. 5, 6. Например, для функции ${{L}_{{,22}}}$ при эмиссии в $\rho $-режиме имеем
(62)
$\begin{gathered} {{L}_{{,22}}} = {{L}_{{0,22}}} + {{L}_{{2,22}}}{{t}^{2}} + {{L}_{{3,22}}}{{t}^{3}} + {{L}_{{4,22}}}{{t}^{4}}, \\ \frac{1}{{b_{0}^{2}}}{{L}_{{2,22}}} = \frac{8}{9}a_{0}^{2}{{L}_{0}}{{{\tilde {J}}}^{2}},\,\,\,\,\frac{1}{{b_{0}^{2}}}{{L}_{{3,22}}} = - \frac{4}{3}\frac{{a_{0}^{{}}}}{{b_{0}^{3}}}{{M}_{{0,222}}} - \\ - \,\,4\frac{{{{a}_{{,22}}}}}{{b_{0}^{2}}}\frac{{{{M}_{{0,2}}}}}{{{{b}_{0}}}} - {{{\bar {b}}}_{3}}\frac{{{{L}_{{0,22}}}}}{{b_{0}^{2}}} - {{L}_{0}}\frac{{{{{\bar {b}}}_{{3,22}}}}}{{b_{0}^{2}}} - \frac{8}{9}{{a}_{0}}\frac{{{{M}_{{0,2}}}}}{{{{b}_{0}}}}\tilde {L}_{0}^{2}, \\ \frac{1}{{b_{0}^{2}}}{{L}_{{4,22}}} = {{L}_{0}}\frac{{{{{\bar {b}}}_{{4,22}}}}}{{b_{0}^{2}}} - {{{\bar {b}}}_{4}}\frac{{{{L}_{{0,22}}}}}{{b_{0}^{2}}} + \frac{{L_{0}^{3}}}{{8{{J}^{2}}}}\left( {\frac{4}{9}\frac{{M_{{0,2}}^{2}}}{{b_{0}^{2}}} - \frac{{16}}{{45}}{{{\tilde {J}}}^{2}}} \right) - \\ - \,\,\frac{1}{3}\frac{{{{{\tilde {L}}}_{{0,22}}}}}{{b_{0}^{2}}} - 2{{{\tilde {L}}}_{0}}\left( {\frac{{12}}{5}\frac{{{{a}_{{0,22}}}}}{{{{a}_{0}}b_{0}^{2}}} + \frac{{{{L}_{{0,22}}}}}{{{{L}_{0}}b_{0}^{2}}}} \right). \\ \end{gathered} $Из формул (56), (61), (62) видно, что распределения плотности тока эмиссии J, компонент магнитного поля L, M, электрического поля Е, задаваемые с необходимой степенью подробности, относятся к входной информации задачи.
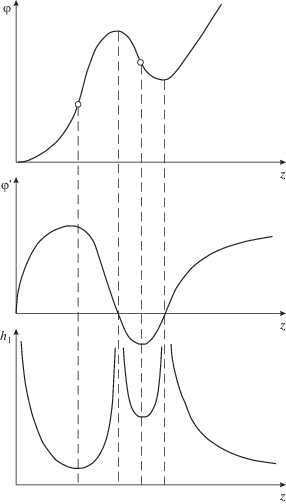
Из формулы (57) следует, что функция ${{h}_{{\,1}}}$ обращается в бесконечность при $\varphi {\text{'}}\left( z \right) = 0.$ Одну связанную с этим особенность на катоде мы уже исследовали. Дополнительные сингулярности со своей асимптотикой возникают в точках, соответствующих экстремумам потенциала при его немонотонном поведении. На рисунке 1 представлены подобное распределение $\varphi \left( z \right)$ на оси, производная $\varphi {\text{'}}\left( z \right)$ и функция ${{h}_{{\,1}}}$. В отмеченных точках перегиба кривой $\varphi \left( z \right)$ она принимает минимальное и максимальное значения.
8. РЕШЕНИЕ В ОКРЕСТНОСТИ ЭКСТРЕМУМОВ ПОТЕНЦИАЛА
Структура решения. В окрестности не связанных с режимом эмиссии особых точек главным членом разложения потенциала по z является квадратичный:
где $\bar {\varphi } = {{\varphi }_{m}} - \varphi ,$ $\varphi - {{\varphi }_{m}}$ – разность текущего значения $\varphi $ и значения ${{\varphi }_{m}}$ в экстремуме для максимума и минимума соответственно; координата z в (63) отсчитывается от точки экстремума ${{z}_{m}}.$
Обратное разложение имеет вид
(64)
$\begin{gathered} z = {{z}_{1}}t + {{z}_{2}}{{t}^{2}} + {{z}_{3}}{{t}^{3}} + ...,\,\,\,\,t = {{{\bar {\varphi }}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}; \\ {{z}_{1}} = \frac{1}{{\sqrt {{{U}_{2}}} }},\,\,\,\,{{z}_{2}} = - \frac{{{{U}_{3}}}}{{2U_{2}^{2}}},\,\,\,\,{{z}_{3}} = \frac{5}{8}\frac{{U_{3}^{2}}}{{U_{2}^{3}\sqrt {{{U}_{2}}} }} - \\ - \,\,\frac{1}{2}\frac{{{{U}_{4}}}}{{U_{2}^{2}\sqrt {{{U}_{2}}} }},\,\,\,\,{{z}_{4}} = - \frac{{U_{3}^{3}}}{{U_{2}^{5}}} + \frac{1}{2}\frac{{{{U}_{3}}{{U}_{4}}}}{{U_{2}^{4}}} - \frac{1}{2}\frac{{{{U}_{5}}}}{{U_{2}^{3}}}. \\ \end{gathered} $Асимптотику ${{h}_{{\,1}}}$ определим из формулы
(65)
$\begin{gathered} dz = \frac{{dz}}{{d\varphi }}d\bar {\varphi } = {{h}_{1}}d\bar {\varphi },\,\,\,\,{{h}_{{\,1}}} = {{a}_{0}}{{t}^{{ - 1}}}\left( {1 + {{{\bar {a}}}_{1}}t + {{{\bar {a}}}_{2}}{{t}^{2}} + ...} \right), \\ {{a}_{0}} = \frac{1}{2}{{z}_{1}},\,\,\,\,{{a}_{1}} = {{z}_{2}},\,\,\,\,{{a}_{2}} = \frac{3}{2}{{z}_{3}},\,\,\,\,{{a}_{4}} = 2{{z}_{4}}. \\ \end{gathered} $Имея в виду, что магнитное поле на оси в области экстремумов является регулярной функцией z, будем искать решение в виде
(66)
$\begin{gathered} {{h}_{{\,2}}} = {{b}_{0}} + {{b}_{1}}t + {{b}_{2}}{{t}^{2}} + {{b}_{3}}{{t}^{3}} + {{b}_{4}}{{t}^{4}} + ...,\,\,\,\,t = {{{\bar {\varphi }}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ L = {{L}_{m}} + {{\Lambda }_{1}}z + {{\Lambda }_{2}}{{z}^{2}} + ... = \\ = {{L}_{m}} + {{L}_{{m1}}}t + {{L}_{{m2}}}{{t}^{2}} + ..., \\ {{L}_{{m1}}} = {{\Lambda }_{1}}{{z}_{1}},\,\,\,\,{{L}_{{m2}}} = {{\Lambda }_{1}}{{z}_{2}} + {{\Lambda }_{2}}z_{1}^{2}. \\ \end{gathered} $При подстановке функций (66) в уравнения пучка следует иметь в виду, что продольные производные для максимума и минимума будут различаться по знаку:
(67)
${{f}_{{,1}}} \equiv \frac{{\partial f}}{{\partial \varphi }} = s\frac{{\partial f}}{{\partial{ \bar {\varphi }}}} = \frac{1}{2}s{{t}^{{ - 1}}}\frac{{\partial f}}{{\partial t}},\,\,\,\,s = \pm 1.$Подставляя функции (65), (66) в уравнение (19), при любом числе n сохраненных членов приходим к неполной системе из n – 2 соотношений. Дефицит уравнений необходимо дополнить физическими соображениями.
Регуляризация уравнения для ${{h}_{2}}.$ Воспользуемся определением кривизны поверхностей ${{x}^{1}} = {\text{const}}$ в случае неортогональной системы координат [4], записывая это выражение на оси пучка и преобразуя при его помощи уравнение (5):
(68)
$\begin{gathered} {{\kappa }_{1}} = \frac{1}{{{{h}_{1}}{{h}_{2}}}}\left[ {{{{\left( {\frac{{{{g}_{{12}}}}}{{{{h}_{2}}}}} \right)}}_{{,2}}} - {{h}_{{2,1}}}} \right] = \frac{{{{f}_{{,2}}}}}{{{{h}_{2}}}} - \frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}{{h}_{2}}}}, \\ {{\kappa }_{1}} + \frac{{{{h}_{{1,1}}}}}{{h_{1}^{2}}} + {{h}_{1}}\frac{{{{h}_{{20}}}J}}{{{{h}_{2}}u}} = 0. \\ \end{gathered} $Введем для скорости и импульса в точках экстремума обозначения ${{V}_{m}}$ и ${{P}_{m}}\,:$
(69)
${{V}_{m}} = \sqrt {\frac{{{{\varphi }_{m}}\left( {2 + {{{\tilde {\varphi }}}_{m}}} \right)}}{{1 + {{{\tilde {\varphi }}}_{m}}}}} ,\,\,\,\,{{P}_{m}} = \left( {1 + {{{\tilde {\varphi }}}_{m}}} \right){{V}_{m}}$и подсчитаем первые члены разложения функции ${{\kappa }_{1}}$ вблизи $z = {{z}_{m}}\,:$
(70)
$\begin{gathered} {{\kappa }_{1}} = - \frac{1}{{{{b}_{0}}}}\left[ {\frac{{{{V}_{m}}{{P}_{m}}}}{{2{{a}_{0}}}}\left( {{{b}_{2}} - \frac{1}{2}{{b}_{1}}{{{\bar {a}}}_{1}}} \right) + \frac{{{{a}_{0}}{{L}_{m}}}}{{1 + {{{\tilde {\varphi }}}_{m}}}}} \right. \times \\ \left. {\frac{{^{{}}}}{{}} \times \,\,\left( {{{b}_{0}}{{L}_{m}} - {{h}_{{20}}}{{L}_{0}}} \right) + {{a}_{0}}{{h}_{{20}}}{{V}_{m}}\tilde {J}} \right]{{t}^{{ - 1}}} + {{\kappa }_{{1m}}}{{t}^{0}} + ..., \\ {{\kappa }_{{1m}}} = - \frac{1}{{{{b}_{0}}}}\left\{ {\frac{{{{V}_{m}}{{P}_{m}}}}{{{{a}_{0}}}}} \right.\left[ {\frac{3}{2}{{b}_{3}} - {{b}_{2}}{{{\bar {a}}}_{1}} + \frac{1}{2}{{b}_{1}}\left( { - {{{\bar {a}}}_{2}} + \bar {a}_{1}^{2}} \right)} \right] + \\ + \,\,\frac{{{{a}_{0}}}}{{1 + {{{\tilde {\varphi }}}_{m}}}}\left[ {{{L}_{m}}\left( {{{b}_{1}}{{L}_{m}} + {{b}_{0}}{{L}_{{m1}}}} \right) + \left( {{{L}_{{m1}}} + {{{\bar {a}}}_{1}}{{L}_{m}}} \right)} \right. \times \\ \times \,\,\left. {\left. {\left( {{{b}_{0}}{{L}_{m}} - {{h}_{{20}}}{{L}_{0}}} \right)} \right] + \frac{1}{2}s\frac{{{{b}_{1}}}}{{{{a}_{0}}}}} \right\}. \\ \end{gathered} $Конечное значение кривизны эквипотенциали $\varphi = {{\varphi }_{m}}$ на оси пучка требует обращения в нуль коэффициента при ${{t}^{{ - 1}}}$ в формуле (70). Члены того же порядка в уравнении (68) должны балансироваться независимо от ${{\kappa }_{1}},$ и в результате коэффициент ${{b}_{0}}$ определяется следующим образом:
(71)
$ - \frac{s}{{2{{a}_{0}}}} + \frac{{{{a}_{0}}{{h}_{{20}}}}}{{{{b}_{0}}{{V}_{m}}}} = 0,\,\,\,\,{{b}_{0}} = s\frac{{2a_{0}^{2}{{h}_{{20}}}J}}{{{{V}_{m}}}}.$Решение уравнения для h2. Балансы членов порядка ${{t}^{0}},$ t и ${{t}^{2}}$ позволяют выразить коэффициенты ${{b}_{2}}$, ${{b}_{3}}$, ${{b}_{4}}$ через ${{b}_{1}}$:
Для электростатических потоков формулы (69) существенно упрощаются:
(73)
$\begin{gathered} {{b}_{0}} = 2s\frac{{a_{0}^{2}{{h}_{{\,20}}}J}}{{\sqrt {2{{\varphi }_{m}}} }},\,\,\,\,{{b}_{2}} = \frac{1}{2}{{b}_{1}}{{{\bar {a}}}_{1}},\,\,\,{{b}_{3}} = \frac{1}{3}{{b}_{1}}{{{\bar {a}}}_{2}} - \\ - \,\,\frac{1}{3}\frac{s}{{{{\varphi }_{m}}}}\left( {{{b}_{1}} - \frac{3}{2}{{b}_{0}}{{{\bar {a}}}_{1}}} \right),\,\,\,\,{{b}_{4}} = - \frac{1}{4}{{b}_{1}}\left( {{{{\bar {a}}}_{3}} - {{{\bar {a}}}_{1}}{{{\bar {a}}}_{2}} + \bar {a}_{1}^{3}} \right) - \\ - \,\,\frac{1}{{4{{\varphi }_{m}}}}\left[ {\frac{1}{2}s\left( {{{b}_{0}}\bar {a}_{1}^{2} - {{b}_{1}}{{{\bar {a}}}_{1}}} \right) + \frac{1}{3}\frac{{{{b}_{0}}}}{{{{\varphi }_{m}}}}} \right]. \\ \end{gathered} $Обозначим ${{z}_{*}}$ координату, определяющую границу зоны действия асимптотики. Коэффициент ${{b}_{1}}$ может быть найден из условия сопряжения функции ${{h}_{{\,2}}}$ при $z = z{\text{*}}\,:$
(74)
${{h}_{{2*}}} = {{h}_{2}}\left( {{{z}_{*}}} \right) = {{b}_{0}} + {{b}_{1}}{{z}_{*}} + {{b}_{2}}z_{*}^{2} + {{b}_{3}}z_{*}^{3} + {{b}_{4}}z_{*}^{4}.$Функция ${{h}_{{\,2}}}$ удовлетворяет уравнению второго порядка, и ее значение ${{b}_{0}}$ в точке экстремума известно (формула (71)). При сращивании решения в разных областях естественно было бы следить за непрерывностью производных до второго порядка включительно, однако эти требования переопределяют систему уравнений для ${{b}_{k}}.$ По какой причине способ (74) замыкания системы является правильным, следует из тестовой задачи.
Тестовая задача. Рассмотрим функцию ${{h}_{{\,2}}}$, удовлетворяющую дифференциальному уравнению второго порядка:
при известном до решения уравнения значении ${{h}_{2}}\left( 0 \right) \equiv {{b}_{0}} = 1.$ Построение решения в виде ряда приводит к балансу членов порядка $\sqrt x ,$ 1, х:
(76)
$\begin{gathered} {{h}_{{\,2}}} = {{b}_{0}} + {{b}_{1}}\sqrt x + {{b}_{2}}x + {{b}_{3}}x\sqrt x + ..., \\ 6{{b}_{3}} + {{b}_{1}} = 0,\,\,\,2{{b}_{1}} + {{b}_{0}} - 1 = 0,\,\,\,\,12{{b}_{4}} + {{b}_{2}} = 0. \\ \end{gathered} $Коэффициенты с четными индексами связаны только между собой и в силу ${{b}_{2}} = 0$ обращаются в нуль, что свидетельствует о нечетности искомой функции. В результате нечетные коэффициенты могут быть выражены через ${{b}_{1}}$, а ряд для ${{h}_{{\,2}}}$ принимает вид
Сращивание функций при $x = x{\text{*}}$ с точным значением ${{h}_{{2*}}}$ приводит к следующему значению ${{b}_{1}}$:
(78)
${{b}_{1}} = \frac{{\sin {\kern 1pt} \left( {\sqrt {{{x}_{*}}} } \right)}}{{\sqrt {{{x}_{*}}} \left( {1 - {{{{x}_{*}}} \mathord{\left/ {\vphantom {{{{x}_{*}}} 6}} \right. \kern-0em} 6}} \right)}}.$На значительном удалении ${{x}_{*}} = 0.64$ от особенности при $x = 0$ формула (78) приводит к значению ${{b}_{1}}$=1.00377 вместо точной величины ${{b}_{1}} = 1$.
ЗАКЛЮЧЕНИЕ
На основе декомпозиции уравнений релятивистского ленточного пучка, сводящейся к формулировке соотношений на трубке тока и уравнений эволюционной системы, построено второе приближение $\varphi $-варианта геометризованной теории, позволяющее описывать непараксиальные пучки при произвольной ориентации магнитного поля на катоде. Первый блок трансформированной системы имеет вид трех обыкновенных дифференциальных уравнений по продольной координате ${{x}^{1}} = \varphi ,$ роль которой играет потенциал электрического поля. Поперечная координата ${{x}^{2}} = \xi $ связана с геометрией трубок тока. Второй блок образован системой уравнений для первых производных по $\xi $ от параметров потока, выражаемых через продольные распределения на базовой поверхности.
Для плоскосимметричных течений второе приближение теории позволяет описывать параметры пучка, определяемые нечетными функциями $\xi $, с сохранением кубических членов по этой координате и четные функции с членами порядка ${{\xi }^{4}}$.
Исходными данными для решения задачи являются распределение потенциала на оси, трансформируемое в элемент метрического тензора ${{g}_{{11}}}$, и распределение продольного магнитного поля. Форма катода задается через кривизну и ее вторую производную на оси, где также с необходимой точностью через производные должны быть описаны распределения плотности тока эмиссии, компонент магнитного поля, нормального к катоду электрического поля. Перечисленные распределения являются свободными управляющими функциями задачи.
Как и l-вариант геометризованной теории, $\varphi $-построение позволяет рассчитывать магнетронно-инжекторные пушки, которые не могут быть описаны в рамках классического параксиального подхода.
Тестовые исследования дают основание считать, что $\varphi $-вариант теории может приводить к более точному описанию электронного потока по сравнению с l-приближением, создавая при этом максимально информативную картину трубок тока и эквипотенциальных поверхностей. Оба подхода представляют альтернативу лобовому численному счету уравнений пучка, в то время как численные алгоритмы следовало бы включать после синтеза электронно-оптической системы на основании моделей, оперирующих с обыкновенными дифференциальными уравнениями и правильно описывающих окрестности особых точек как в пучке, так и в лапласовской области вблизи кромки катода.
Список литературы
Cыpoвoй B.A. // PЭ. 2013. T. 58. № 6. C. 614.
Сапронова Т.М., Сыровой В.А. // РЭ. 2010. Т. 55. № 6. С. 726.
Данилов В.Н. // Журн. прикл. механики и техн. физики. 1968. № 5. С. 3.
Сыровой В.А. // Теория интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Cыpoвoй B.A. // PЭ. 2002. T. 47. № 9. C. 1114.
Cыpoвoй B.A. // PЭ. 2016. T. 61. № 3. C. 263.
Cыpoвoй B.A. // PЭ. 2017. T. 62. № 5. C. 493.
Мак-Конел А.Дж. Введение в тензорный анализ. М.: Физматгиз, 1963.
Cыpoвoй B.A. // PЭ. 2017. T. 62. № 5. C. 502.
Cыpoвoй B.A. // PЭ. 2005. T. 50. № 7. C. 875.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника