Радиотехника и электроника, 2019, T. 64, № 1, стр. 54-64

ВВЕДЕНИЕ

Нелинейные СВЧ-колебания намагниченности в магнитных диэлектриках привлекают внимание исследователей [1]. Стремление преодолеть низкий уровень ограничения амплитуды колебаний, обусловленный возбуждением обменных волн [2], требует нормального намагничивания пластины, где углы прецессии достигают десятков градусов [3–6]. Некоторые виды такой прецессии описаны в обзоре [7], где постоянное поле превышает размагничивание формы, так что вектор намагниченности ориентирован по нормали к плоскости пластины. В поле, меньшем размагничивания вектор намагниченности отклонен от нормали [8]. При этом под действием переменного поля положение равновесия намагниченности прецессирует (прецессия второго порядка) [9, 10]. То есть вектор намагниченности участвует в прецессии как вокруг положения равновесия, так и вокруг направления поля.

Период прецессии второго порядка в несколько раз превышает период возбуждающего поля, поперечные компоненты динамической намагниченности меняются по синусоидальному закону со сдвигом фаз на 90°, а прецессионный (параметрический) портрет имеет форму большого кругового кольца, равномерно заполненного вдоль образующей малыми кольцами [9, 10].

В работе [11] выявлены пять различных режимов прецессии второго порядка: № 1 – малоамплитудная круговая прецессия, № 2 – прецессия положения равновесия без охвата центра, № 3 – незатухающая прецессия положения равновесия с охватом центра, № 4 – затухающая прецессия положения равновесия с охватом центра, № 5 – развернутая круговая прецессия. Переходы между режимами рассмотрены на основе трехмерной модели потенциала.

В работах [12, 13] рассмотрены случаи несимметричного постоянного и переменного поля. В этом случае прецессия положения равновесия приобретает характер неправильных импульсов, а на прецессионном портрете появляется сгущение малых колец, интерпретированное на основе векторной модели.

В работах [14, 15] прецессия положения равновесия рассмотрена в среде с одноосной и кубической анизотропией. Анизотропные свойства среды также приводят к импульсному характеру прецессии, результатом чего являются сгущения малых колец, отражающие расположение осей анизотропии.

Все перечисленные работы относятся к случаю чисто магнитной среды. Однако в реальных магнетиках на поведении намагниченности в значительной степени сказывается магнитострикция. Так, в работе [16] на примере пленок ферритов-гарантов показано, что магнитоупругое взаимодействие оказывает существенное влияние на ориентационный переход намагниченности, меняет поле перехода и характер установления намагниченности во времени.

Таким образом, можно ожидать, что магнитоупругое взаимодействие также может изменить характер прецессии второго порядка [17]. Настоящая работа посвящена более подробному рассмотрению этого вопроса.

1. ГЕОМЕТРИЯ И ОБЩИЕ ПАРАМЕТРЫ ЗАДАЧИ

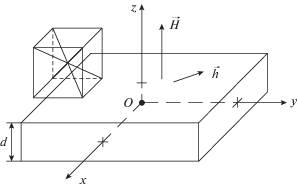
Подобно [18], рассмотрим ферритовую пластину, намагниченную по нормали к ее плоскости, в геометрии, показанной на рис. 1. Пусть феррит по магнитным свойствам – изотропен, а по упругим и магнитоупругим обладает кубической симметрией типа (100). Упругие свойства описываются константой ${{c}_{{44}}},$ магнитоупругие – константой ${{B}_{2}}.$ Задача решается в декартовой системе координат $Oxyz,$ ось $Oz$ перпендикулярна плоскости пластины. Поле имеет вид $\vec {H} = \left\{ {{{h}_{x}};{{h}_{y}};{{H}_{0}}} \right\},$ где ${{H}_{0}}$ – постоянное поле, ${{h}_{{x,\,y}}}$ – компоненты переменного поля. Полная плотность энергии пластины имеет вид [19–22]

Рис. 1.

Геометрия задачи.

где $\vec {m}\,\, = \,\,{{\vec {M}} \mathord{\left/ {\vphantom {{\vec {M}} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}$ – нормированный вектор намагниченности, ${{M}_{0}}$ – намагниченность насыщения; ${{x}_{i}}$ – координаты, $i = x,y,z,$

– тензор деформаций (${{u}_{i}}$ – компоненты упругого смещения).

Материал пластины – тербиевый феррит-гранат (ТбФГ) [20] с параметрами: $4\pi {{M}_{0}}$ = 280 Гс, ${{{\text{c}}}_{{44}}} = 7.64 \times {{10}^{{11}}}$ эрг/см³, ${{B}_{2}} = 3.0 \times {{10}^{7}}$ эрг/см³; $\rho = 5.17$ г/см³ или железоиттриевый гранат (ЖИГ) [1, 20]: $4\pi {{M}_{0}}$ = 1750 Гс, ${{B}_{2}} = 66.96 \times {{10}^{6}}$ эрг/см³. Толщина пластины – 1 мкм, параметры затухания: $\alpha $ = 0.3; $\beta \,$ = 10⁹ см^–1.

Постоянное поле ${{H}_{0}}$ примем равным 265 Э, амплитуды переменного поля ${{h}_{{0x}}} = {{h}_{{0y}}} = $ 3 Э (поле круговое), частота переменного поля f = 100 МГц.

2. ОРИЕНТАЦИОННЫЙ ПЕРЕХОД В МАГНИТОУПРУГОЙ СРЕДЕ

Реализация прецессии второго порядка требует, чтобы вектор намагниченности находился в условиях ориентационного перехода [16, 17]. Благодаря симметрии задачи (см. рис. 1) вектор намагниченности в равновесном состоянии находится в плоскости $Oxz,$ т.е. ${{m}_{y}} = 0,$ пластина деформируется в той же плоскости, т.е. ${{u}_{{xy}}} = {{u}_{{yz}}} = 0.$ В равновесии переменное поле отсутствует: ${{h}_{x}} = {{h}_{y}} = 0.$ При этом плотность энергии (1) принимает вид

где в силу нормировки имеем

Минимизируя плотность энергии (3) с учетом (4) по ${{m}_{z}}$ и ${{u}_{{xz}}},$ получаем систему уравнений для равновесной намагниченности и упругого смещения:

Из (6) с учетом (4) получим важное вспомогательное соотношение:

Подставляя это выражение в (5), получаем уравнение для определения ${{m}_{z}}\,:$

где

– поле магнитоупругого взаимодействия.

Вводя обозначения

приводим уравнение (8) к каноническому виду:

Это – классическое “неполное” кубическое уравнение [23, 24], способ разрешения которого определяется знаком его детерминанта:

В работе [17] показано, что при принятых здесь параметрах материала детерминант положителен вплоть до значений константы магнитоупругости ${{B}_{2}}\sim 15 \times {{10}^{7}}$ эрг/см³. Положительность детерминанта позволяет для решения (8) использовать метод Кардано [23, 24]. В результате, подобно [16], получаем

где

Поскольку ${{m}_{x}}$ определяется соотношением (4), то этими двумя формулами (14) и (15) равновесные компоненты намагниченности определены полностью.

Согласно [17], интервал применимости решения Кардано имеет вид

При ${{B}_{2}} \to \infty $ вектор намагниченности отклонен на 45°, так что

3. РАВНОВЕСНЫЕ КОМПОНЕНТЫ НАМАГНИЧЕННОСТИ

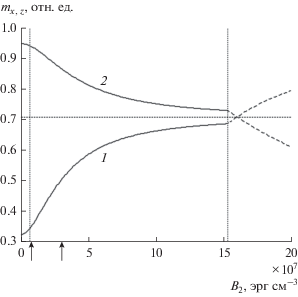
Поведение компонент намагниченности ${{m}_{{x,z}}}$ в зависимости от величины константы ${{B}_{2}}$ иллюстрируется рис. 2. Компоненты намагниченности ${{m}_{x}}$ (кривая 1) и ${{m}_{z}}$ (кривая 2) рассчитаны по формуле Кардано (15). По мере увеличения магнитоупругого взаимодействия вектор намагниченности поворачивается ближе к плоскости пластины. Горизонтальная точечная линия проведена на уровне ${{m}_{{x,z}}} = 0.7071,$ что соответствует ${{B}_{2}} \to \infty $ (17). На верхней границе интервала Кардано величины ${{m}_{{x,z}}}$ отличаются от этого значения на 3%. Стрелками показаны значения констант магнитоупругости: левая соответствует ЖИГ, правая – ТбФГ. Оба значения находятся вблизи нижней границы решения Кардано, так что использование (17) допустимо.

Рис. 2.

Зависимости равновесных компонент намагниченности ${{m}_{x}}$ (1) и ${{m}_{z}}$ (2) от константы магнитоупругого взаимодействия при поле ${{H}_{0}}$ = 265 Э. Вертикальные точечные линии – границы применимости решения Кардано (15).

4. УРАВНЕНИЯ ДВИЖЕНИЯ

Для исследования динамики намагниченности воспользуемся аппаратом, развитым в [9–16, 18]. Уравнения движения для намагниченности имеют вид

где $\gamma $ – гиромагнитная постоянная, $\alpha $ – параметр затухания, уравнения для ${{m}_{{y,z}}}$ получаем циклической перестановкой x, y, z. Считаем прецессию однородной, а продольные колебания вдоль оси Oz – отсутствующими. Эффективные поля имеют вид

Уравнения для упругого смещения имеют вид

где β – параметр затухания упругих колебаний, ρ – плотность материала пластины. Граничные условия на поверхностях пластины следующие:

Систему (18)–(22) решали численно методом Рунге–Кутты [24].

А. Развитие колебаний во времени

На рис. 3 показаны зависимости от времени поперечных компонент намагниченности ${{m}_{{x,\,y}}}$ (а, б) и упругого смещения ${{u}_{{x,\,y}}}$ (в) при отсутствии магнитоупругой связи (рис. 3а) и при ее наличии (рис. 3б).

Рис. 3.

Развитие колебаний во времени в отсутствие (а) и при наличии (б, в) магнитоупругой связи: а, б – компоненты намагниченности; в – компоненты упругого смещения. Сплошные линии – компоненты ${{m}_{x}},$ ${{u}_{x}},$ пунктирные – ${{m}_{y}},$ ${{u}_{y}};$ ${{B}_{2}} = 0$ (а) и ${{B}_{2}} = 3 \times {{10}^{7}}$ эрг/см³ (б, в).

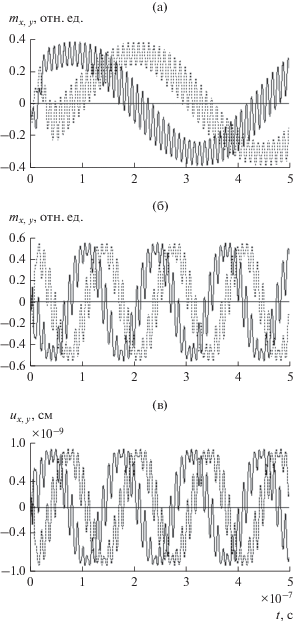
Из рисунка видно, что колебания намагниченности имеют две составляющие: малоамплитудную быструю, синхронную с возбуждающим полем, и высокоамплитудную медленную с периодом, во много раз меньшим [9]. Медленные колебания компонент ${{m}_{x}}$ и ${{m}_{y}}$ сдвинуты по фазе на 90°. Амплитуда медленных колебаний при включении магнитоупругой связи возрастает, а их период уменьшается. Период быстрых колебаний не меняется. Колебания компонент упругого смещения (рис. 3в) синхронны колебаниям компонент намагниченности (рис. 3б), причем те и другие находятся в противофазе.

Б. Параметрические портреты

На рис. 4 представлены параметрические портреты – зависимости ${{m}_{y}}$ от ${{m}_{x}}$ (а) и ${{u}_{y}}$ от ${{u}_{x}}$ (б), когда время является параметром. Из рисунка видно, что при увеличении константы магнитоупругого взаимодействия диаметры больших колец увеличиваются, а их ширина уменьшается. Сравнение средних радиусов колец со значениями ${{m}_{x}}$ (см. рис. 2) показывает совпадение с точностью 2.5%. То есть средний радиус колец определяется равновесным значением поперечной компоненты намагниченности.

Рис. 4.

Параметрические портреты для компонент намагниченности (а) и упругого смещения (б) при различных значениях константы магнитоупругой связи: ${{B}_{2}} = 0$ (1, 4), ${{B}_{2}} = 3 \times {{10}^{7}}$ эрг/см³ (2, 5); ${{B}_{2}} = 10 \times {{10}^{7}}$ эрг/см³ (3, 6).

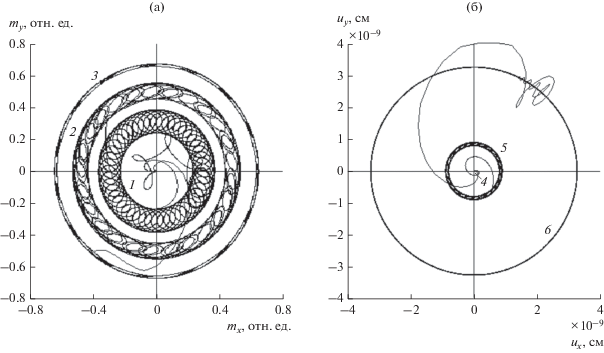
Сужение большого кольца при увеличении ${{B}_{2}}$ означает уменьшение размера малых колец в радиальном направлении при его сохранении в касательном. Уменьшение ширины кольца для упругости аналогично подобному уменьшению для намагниченности, однако эллиптичность выражена сильнее благодаря пропорциональности диаметра большого кольца величине ${{B}_{2}}.$

В. Колебания при различной степени связи

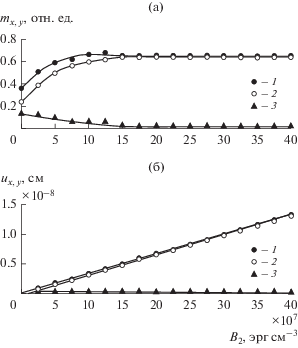
На рис. 5а для компонент намагниченности показаны зависимости внешнего и внутреннего радиусов большого кольца и его ширины от величины константы ${{B}_{2}}$. По мере увеличения ${{B}_{2}}$ радиусы сначала увеличиваются, а затем принимают стационарное значение ${{m}_{{x,y}}} \approx 0.7$ отн. ед., что соответствует равновесному отклонению намагниченности от нормали на 45° (кривая 1 на рис. 2). Из рис. 5а (кривая 3) видно, что ширина кольца при этом уменьшается, стремясь к 0.01 отн. ед. На рис. 5б показаны подобные зависимости для компонент упругого смещения. Здесь радиусы кольца увеличиваются прямо пропорционально ${{B}_{2}}$, как видно из формулы (7). Сужение кольца повторяет аналогичное сужение, имеющее место для намагниченности.

Рис. 5.

Характеристики колец параметрических портретов для намагниченности (а) и упругого смещения (б) при различных значениях магнитоупругой связи. Точки – результат машинного эксперимента, линии построены, исходя из плавного соединения точек: 1 – наружный радиус большого кольца портрета, 2 – внутренний радиус, 3 – ширина большого кольца портрета.

5. ДЕФОРМАЦИЯ БОЛЬШОГО КОЛЬЦА ПО МОДЕЛИ ПОТЕНЦИАЛА

Как отмечено в разделах 4А и 4Б, при увеличении константы ${{B}_{2}}$ диаметр большого кольца увеличивается, а его ширина уменьшается. Покажем, что оба эти свойства обусловлены изменением потенциальной энергии (3) при изменении ${{B}_{2}}.$ Ограничимся рассмотрением только намагниченности.

Плотность потенциальной энергии, выраженная через продольную компоненту намагниченности ${{m}_{z}}$, имеет вид (3) с учетом (4). Прецессионные портреты (см. рис. 4а) содержат только поперечные компоненты ${{m}_{x}}$ и ${{m}_{y}},$ роль которых симметрична, поэтому рассмотрим лишь компоненту ${{m}_{x}}\,:$

Пользуясь выражением ${{u}_{{xz}}}$ в соответствии с (7) с учетом (4), получаем

Это выражение дает зависимость плотности энергии от ${{m}_{x}}$. Его минимум соответствует равновесному состоянию намагниченности.

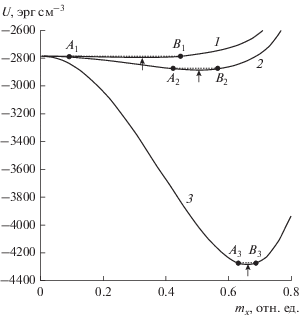
На рис. 6 показаны зависимости плотности энергии (24) от компоненты намагниченности ${{m}_{x}}$ при различных значениях ${{B}_{2}}.$ Кривая 1 соответствует ${{B}_{2}} = 0,$ кривые 2 и 3 – тем же значениям ${{B}_{2}},$ что использовались при построении портретов на рис. 4а. Стрелками показаны минимумы кривых, соответствующие равновесному положению намагниченности. Точки ${{A}_{{1,2,3}}},$ ${{B}_{{1,2,3}}},$ а также соединяющие их горизонтальные точечные линии соответствуют равным значениям потенциала на высоте 7.9460 эрг/см³, которое обеспечивается уровнем возбуждения ${{h}_{{x,y}}}.$ Компонента намагниченности ${{m}_{x}}$ колеблется в потенциальной яме, ограниченной точками ${{A}_{{1,2,3}}}$ и ${{B}_{{1,2,3}}}.$ Видно, что ${{A}_{1}}{{B}_{1}} > {{A}_{2}}{{B}_{2}} > {{A}_{3}}{{B}_{3}},$ т.е. кольцо по мере увеличения ${{B}_{2}}$ сужается. По мере увеличения ${{B}_{2}}$ положения минимумов смещаются в сторону больших значений ${{m}_{x}},$ т.е. диаметр кольца увеличивается.

Рис. 6.

Зависимости потенциала от поперечной компоненты намагниченности при ${{B}_{2}} = \,\,0$ (1), ${{B}_{2}} = 3 \times {{10}^{7}}$ эрг/см³ (2), ${{B}_{2}} = 10 \times {{10}^{7}}$ эрг/см³ (3).

Таким образом, рассмотренная модель потенциала описывает свойства большого кольца прецессионного портрета вполне адекватно.

6. ПЕРИОД МЕДЛЕННЫХ КОЛЕБАНИЙ ПРИ ИЗМЕНЕНИИ МАГНИТОУПРУГОЙ СВЯЗИ

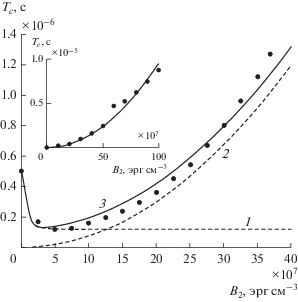
Рассмотрим теперь период медленных колебаний при различной величине магнитоупругой связи, для чего обратимся к рис. 7, точки на котором получены путем расчета развития колебаний во времени по системе (18)–(22). Пунктирными линиями показаны результаты двух модельных расчетов, а сплошной линией – их сумма. Из расположения точек можно видеть, что после включения магнитоупругого взаимодействия период колебаний резко уменьшается. Спад продолжается от нуля до ${{B}_{2}} = 5 \times {{10}^{7}}$ эрг/см³, после чего период возрастает – сначала медленно, до ${{B}_{2}} = 10 \times {{10}^{7}}$ эрг/см³, а затем все быстрее, вплоть до конца исследованного диапазона ${{B}_{2}} = 40 \times {{10}^{7}}$ эрг/см³.

Рис. 7.

Зависимость периода медленных колебаний от константы магнитоупругой связи. Точки – результат машинного эксперимента. Пунктирные линии – модельные расчеты, сплошная линия – их сумма. Кривые построены по формулам: 1 – (28); 2 – (29); 3 – (30). На врезке – зависимость, построенная по формуле (29), в более широком диапазоне изменения ${{B}_{2}}.$

Такой характер изменения периода свидетельствует о наличии двух механизмов, один из которых приводит к уменьшению периода при увеличении ${{B}_{2}},$ а второй – к его увеличению. Рассмотрим эти механизмы по отдельности на основе моделей эффективных полей и квадратичной магнитоупругой связи.

7. МОДЕЛЬ ЭФФЕКТИВНЫХ ПОЛЕЙ

В работах [9, 10], выполненных в случае ${{B}_{2}}$ = 0, на основе векторной модели показано, что период медленных колебаний определяется выражением

где h – внешнее переменное поле, $A = {{A}_{0}} \times {{10}^{{ - 6}}}$ с Э² (${{A}_{0}}$ – постоянный коэффициент). В работе [9], показано, что ${{A}_{0}} = 1.03...1.45,$ здесь же для простоты будем считать ${{A}_{0}} = 1.00.$

Возбуждаемые за счет магнитных упругие колебания сами создают магнитные поля, действующие на намагниченность. То есть имеет место самосогласованный процесс, выравнивающий времена релаксации магнитных и упругих колебаний [18].

Примем теперь, что в связанной магнитоупругой системе роль внешних полей h играют эффективные поля ${{H}_{{ex,{\text{ }}y}}},$ определяемые выражением (19). При этом формула (25) с учетом (2) принимает вид

где учтена симметрия относительно x и y. Подставляя (7) в (26), получаем

Видно, что при увеличении ${{B}_{2}}$ период должен уменьшаться. В соответствии с такой моделью кривая 1 на рис. 7 построена по формуле

где введен близкий к единице коэффициент 1.06 и постоянная добавка, поднимающая кривую для согласования с точками при ${{B}_{2}} = 5 \times {{10}^{7}}$ эрг/см³.

8. МОДЕЛЬ КВАДРАТИЧНОЙ МАГНИТОУПРУГОЙ СВЯЗИ

Модель эффективных полей описывает только спад зависимости периода при малых значениях ${{B}_{2}}.$ Теперь рассмотрим модель, обеспечивающую рост зависимости при больших значениях ${{B}_{2}}.$ Учтем, что пластина с магнитоупругой связью представляет собой совокупность двух связанных через ${{B}_{2}}$ колебательных систем – магнитной и упругой. Переменное поле возбуждает магнитную систему, из которой часть энергии передается упругой системе. Упругая система нагружает магнитную, приводя к увеличению ее инерционности т.е. к увеличению периода собственных колебаний.

Следуя такой идеологии, в [17] на основе векторной модели [12, рис. 4] предложена механическая модель, учитывающая гироскопические свойства намагниченности и предсказывающая рост периода колебаний, пропорциональный квадратичному увеличению ${{B}_{2}}.$ На рис. 7 кривая 2 построена по формуле

где коэффициент $8.{\text{7}} \times {{10}^{{ - 24}}}$ выбран исходя из согласия кривой с точками.

Для построения результирующей зависимости (сплошная кривая 3 на рис. 7) принято суммарное действие обоих механизмов:

Из рис. 7 видно, что кривая 3 совпадает с приведенными точками с довольно высокой точностью: даже в области ${{В }_{2}} \approx 15 \times {{10}^{7}}$ эрг/см³. На врезке показано, что модель квадратичной связи обеспечивает хорошее соответствие вплоть до ${{В }_{2}} = 100 \times {{10}^{7}}$ эрг/см³, это с избытком перекрывает весь диапазон значений константы ${{B}_{2}}$ для реальных материалов.

А. Возможные способы интерпретации квадратичности магнитоупругой связи

Рассмотрим аналитическую интерпретацию модели квадратичной магнитоупругой связи. Предварительное исследование показало, что квадратичность не является специфическим свойством прецессии второго порядка, а имеет место и при обычной собственной прецессии намагниченности. При этом квадратичность проявляется как в нелинейном, так и в линейном режиме.

Нахождение частоты собственной прецессии в магнитоупругой среде из решения системы уравнений (18)–(22), связано с определенными математическими трудностями (см. [18]), поэтому здесь рассмотрим два более простых варианта решения. Сначала проведем грубую оценку частоты из анализа уравнений движения в линейном приближении. Затем выполним более точное рассмотрение на основе приема, предложенного в работах [25–28], состоящего в сведении системы из семи уравнений первого порядка к системе из двух уравнений второго порядка при помощи квадратичного приближения, что позволяет рассмотреть задачу на модели связанных колебаний двух осцилляторов – магнитного и упругого.

Б. Квадратичность связи из уравнений движения

Рассмотрим малые свободные колебания намагниченности, т.е. положим ${{h}_{{x,y}}}$ = 0, ${{m}_{{x,y}}} \ll 1$, ${{m}_{z}}$ = 1, а также $\alpha $ = 0. Тогда уравнения движения для намагниченности (18) принимают вид

где эффективные поля (19)–(20) будут иметь вид

Учитывая круговой характер прецессии, положим $\left| {{{m}_{x}}} \right| = \left| {{{m}_{y}}} \right|,$ $\left| {{{u}_{x}}} \right| = \left| {{{u}_{y}}} \right|$, а также ${{H}_{{ey}}}$ = 0. Введем обозначение

и приведем поля к виду

Из первого уравнения системы (31)–(32) выразим ${{m}_{y}}\,:$

Дифференцируя по времени, получаем

Подставляя это выражение во второе уравнение системы (31)–(32), получаем

Подставляя ${{H}_{{ez}}}$ в виде (35), в линейном приближении, получаем

Здесь ${{H}_{{ex}}}$ определяется выражением (33), в которое входит производная ${{\partial {{u}_{x}}} \mathord{\left/ {\vphantom {{\partial {{u}_{x}}} {\partial z}}} \right. \kern-0em} {\partial z}}.$ Согласно [18, формула (55)], эта производная имеет вид

где ${{v}_{x}}$ – решение неоднородной задачи с нулевыми граничными условиями. На поверхностях пластины $z = \pm {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2},$ т.е. второе слагаемое равняется нулю. Оценка показывает, что при ${{B}_{2}} \leqslant 10 \times {{10}^{7}}$ эрг/см³ второе слагаемое остается меньше первого на порядок, поэтому примем:

где учтено, что ${{m}_{z}}$ = 1. Подставляя это выражение в поле ${{H}_{{ex}}}$ (37), входящее в (43), получаем уравнение свободных колебаний ${{m}_{x}}$

частота которых равна:

Учитывая малость второго слагаемого по сравнению с единицей, получаем

где для получения ${{T}_{m}}$ в секундах следует брать $\gamma $ = = 2.8 МГц/Э. Согласно формуле (48), период при ${{B}_{2}} = 0$ соответствует таковому в нормально намагниченной пластине при классическом ферромагнитном резонансе [1]:

Из (48) видно, что период пропорционален квадрату константы ${{B}_{2}}.$

В. Квадратичность связи на основе квадратичного приближения по намагниченности

Рассмотрим получение частоты прецессии намагниченности на основе квадратичного приближения по намагниченности [25–28]. Согласно [27, формулы (19)–(21)], а также [27, формула (30)], уравнение для компоненты намагниченности ${{m}_{x}}$ имеет вид

где введены вспомогательные обозначения:

В случае собственных колебаний положим ${{h}_{{x,y}}} = 0$, а также ${{\alpha }^{2}} \ll 1,$ тогда

Отвлекаясь от динамической связи между системами, т.е. полагая в (54) последние два слагаемых равными нулю, получаем

То есть частота собственных колебаний магнитной системы будет равна:

а период свободной прецессии намагниченности имеет вид

где $\gamma $ = 2.8 МГц/Э.

В приближении ${{b}_{1}} \ll {{H}_{p}}$ период принимает вид

откуда с учетом (51), (52) получаем

Видно, что с точностью до обозначений эта формула совпадает с (48), полученной на основе оценки в линейном приближении. То есть формула (59) описывает квадратичную зависимость периода прецессии от константы ${{B}_{2}}$ как в линейном, так и в нелинейном режиме с точностью, определяемой корректностью квадратичного разложения намагниченности [25–28].

9. СРАВНЕНИЕ С МАШИННЫМ ЭКСПЕРИМЕНТОМ

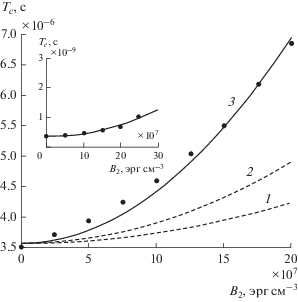
Рассмотрим теперь работу механизма квадратичной магнитоупругой связи на примере свободной прецессии намагниченности в условиях ферромагнитного резонанса при внешнем поле, превышающем поле размагничивания формы. Сравним расчет по полной системе (18)–(22) с зависимостью, описываемой формулами (48), (59). На рис. 8 показана зависимость периода свободной прецессии от константы ${{B}_{2}},$ точки – результаты машинного эксперимента с использованием системы (18)–(22), кривая 1 построена по формуле (59) без каких-либо изменений. Видно, что такая кривая, хотя и отражает рост периода по мере увеличения ${{B}_{2}}$, но везде, кроме своего начала (т.е. уже при ${{B}_{2}} \geqslant 2 \times {{10}^{7}}$ эрг/см³), проходит значительно ниже экспериментальных точек. Кривая 2 построена по той же формуле, но перед вторым слагаемым в скобках введен поправочный коэффициент 2. В этом случае кривая, хотя и повышается, но все же проходит еще намного ниже точек. Дальнейшее увеличение поправочного коэффициента до 6, хотя и приводит к более или менее приемлемому согласию с точками, но с позиции физики явления это недостаточно оправдано. Поэтому более логичным было принято введение поправки в величину ${{B}_{2}}$, возводимую далее в квадрат. Так, кривая 3 построена при замене в формуле (59) величины ${{B}_{2}}$ на $2.25{{B}_{2}}.$ Видно, что в этом случае кривая соответствует точкам вполне удовлетворительно. Наибольшее расхождение вблизи ${{B}_{2}}\sim 7 \times {{10}^{7}}$ эрг/см³ не превышает 5% (считая от нуля периода). При этом в остальной области изменения ${{B}_{2}}$ точность еще выше, а при ${{B}_{2}}\sim (15...20) \times {{10}^{7}}$ эрг/см³ имеет место совпадение не хуже 1%.

Рис. 8.

Зависимость периода свободной прецессии от константы магнитоупругой связи; точки – результаты машинного эксперимента; кривые построены по формуле (59) без коэффициентов (1); с коэффициентом 2 перед вторым слагаемым (2); с коэффициентом 2.25 при ${{B}_{2}}$ (3). Параметры: $4\pi {{M}_{0}} = 1750$ Гс; ${{H}_{0}} = 2750$ Э.

Необходимость введения поправочного коэффициента, по-видимому, обусловлена недостаточным учетом динамической магнитоупругой связи, т.е. пренебрежением двумя последними слагаемыми в формуле (54), что было вызвано стремлением выявить квадратичный характер магнитоупругой связи наиболее простым путем.

Следует отметить, что хорошая квадратичная зависимость периода от константы ${{B}_{2}}$ получается только при умеренных ее значениях. Так, при увеличении ${{B}_{2}}$ выше ${\text{30}} \times {{10}^{7}}$ эрг/см³ квадратичный рост сменяется значительно более быстрым, напоминающим расходимость (см. рис. 8, врезка). Можно полагать, что столь быстрый рост периода происходит благодаря вступлению в игру эффективных полей по нормали к плоскости пластины. Такой механизм рассмотрен в [17], однако там показано, что в случае прецессии второго порядка квадратичную зависимость он описывает значительно хуже, чем формула (59), поэтому здесь не приводится.

ЗАКЛЮЧЕНИЕ

Рассмотрена вынужденная нелинейная прецессия вектора намагниченности в нормально намагниченной пластине, обладающей магнитоупругими свойствами. В условиях ориентационного перехода переменное поле круговой поляризации вызывает прецессию положения равновесия вектора намагниченности, причем за счет магнитоупругости свойства такой прецессии существенно изменяются.

Подробно рассмотрен ориентационный переход вектора намагниченности, состоящий в изменении положения его равновесия при изменении константы магнитоупругости. На основе минимизации плотности энергии для случая кубической анизотропии с ориентацией типа (100) получена система уравнений относительно компонент намагниченности и упругого смещения, описывающая равновесное положение вектора намагниченности. Показана возможность сведения такой системы к одному алгебраическому уравнению третьего порядка, путем решения которого методом Кардано получена аналитическая зависимость продольной и поперечной компонент намагниченности от константы магнитоупругости и других параметров материала и поля.

На основе связанной системы уравнений движения для намагниченности и упругого смещения проанализированы свойства прецессии второго порядка в магнитоупругой среде. Получены параметрические портреты для намагниченности и упругого смещения. По мере увеличения магнитоупругой связи диаметр больших колец параметрических портретов увеличивается, причем для компонент намагниченности – сначала линейно с последующим насыщением и выходом на горизонтальный участок, а для компонент упругого смещения – линейно. Ширина больших колец при этом сначала уменьшается, а по мере увеличения магнитоупругой связи стремится к нулю. При этом малые кольца вдоль образующей большого кольца превращаются в узкие эллипсы, вытянутые вдоль такой образующей. Характер изменения геометрических параметров колец параметрических портретов объяснен на основе соответствия радиусов больших колец величинам равновесных значений поперечных компонент намагниченности. Уменьшение ширины колец по мере увеличения константы магнитоупругости определяется сужением потенциальной ямы, дно которой соответствует равновесному значению намагниченности.

Исследована зависимость периода прецессии от величины константы магнитоупругого взаимодействия. При малых значениях этой константы период резко уменьшается, тогда как при средних стабилизируется, а при больших – плавно увеличивается тем быстрее, чем значение константы больше. Для интерпретации наблюдаемого изменения периода медленных колебаний прецессии предложено две модели: эффективных полей и квадратичности магнитоупругой связи. Резкий спад периода при малых значениях константы магнитоупругости можно описать путем введения добавки эффективного поля магнитоупругости, обусловленного поперечной составляющей намагниченности, к поперечной составляющей переменного поля, возбуждающего прецессию.

Для интерпретации увеличения периода при больших значениях константы рассмотрена простая (первого порядка) свободная прецессия намагниченности. Период такой прецессии прямо пропорционален квадрату константы вплоть до довольно значительных ее значений.

В результате совокупного рассмотрения обеих моделей получена аналитическая формула, дающая не только качественное, но и количественное описание зависимости периода прецессии второго порядка от константы магнитоупругой связи с точностью до единиц процентов.

Численный анализ развития колебаний во времени выполнен за счет гранта Российского фонда фундаментальных исследований (проект № 17-02-01138-а).

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 14-22-00279).