Радиотехника и электроника, 2019, T. 64, № 10, стр. 962-969

ВВЕДЕНИЕ

Как известно, в нанопроводах (цилиндрах) из серебра и золота в оптическом диапазоне волн существуют резонансы поверхностных волн (плазмон-поляритонов). Поэтому такие нанопровода находят применение в спектроскопии, а также используются в качестве сенсоров [1]. Спектры рассеяния и поглощения на одиночных цилиндрах с прямоугольной формой поперечного сечения рассчитаны в [2–4]. В работах [5, 6] исследовано рассеяние на золотых и серебряных цилиндрах эллиптического сечения. Многоэлементные оптические резонаторы из серебряных цилиндров прямоугольного сечения рассмотрены в [3, 4], а для случая двух эллиптических цилиндров – в [7]. Достоинством таких резонаторов является возможность управлять резонансной частотой путем изменения расстояния между цилиндрами. Случай двух сплошных или полых цилиндров из метаматериала рассматривался в [8].

В работе [9] утверждалось, что в оптическом диапазоне длин волн кластер, состоящий из трех (а также четырех или шести) самоподобных серебряных шаров, способен усиливать поле проходящей плоской волны в сотни (тысячи) раз. Для обоснования такого утверждения использовалось решение соответствующей задачи статики (статическое приближение), предположение об отсутствии потерь серебра и взаимного влияния шаров. Отметим, что строгое электродинамическое решение такой задачи не рассматривалось. Физически очевидно, что двумерным аналогом кластера из нескольких шаров является кластер, состоящий из двух серебряных цилиндров. При этом явления (усиление поля проходящей волны), свойственные случаю шаров, должны иметь место и в случае цилиндров.

Цель данной работы состоит в строгом электродинамическом исследовании особенностей резонансного рассеяния плоской волны светового диапазона длин волн кластером, образованным двумя самоподобными серебряными цилиндрами разного радиуса.

1. ФОРМУЛИРОВКА ЗАДАЧИ. МЕТОД РЕШЕНИЯ

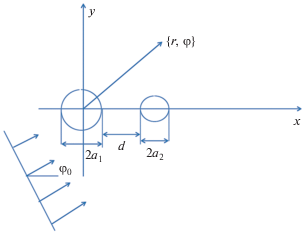
Рассматриваются двумерные задачи дифракции плоской электромагнитной волны на кластере (структуре), состоящем из двух самоподобных серебряных цилиндров различного радиуса. Считается, что радиусы ${{a}_{i}}$ ($i = 1,2$) двух цилиндров и расстояние $d$ между ними удовлетворяет соотношению ${{a}_{{i + 1}}} = \chi {{a}_{i}}$ ($\chi $ – коэффициент подобия), $d = \chi {{a}_{{i + 1}}}$, $\chi = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ (или 1/3) [9]. Предполагается, что длина электромагнитной волны $\lambda $ принадлежит световому диапазону ($\lambda \approx 300...900\,\,нм$), а электрические радиусы $k{{a}_{i}}$ цилиндров в этом диапазоне таковы, что $k{{a}_{i}} \ll 1,$ где $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }.$

Геометрия исследуемой задачи представлена на рис. 1. Диэлектрическую проницаемость серебра 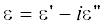≡ $\operatorname{Re} (\varepsilon ) - i\operatorname{Im} (\varepsilon )$ определяли путем аппроксимации кубичными сплайнами экспериментальных данных работы [10]. Отметим, что использование результатов работы [10], так же как и теории Друде [1], накладывает ограничение на минимальный диаметр $2{{a}_{i}}$ серебряных цилиндров $2{{a}_{i}} \geqslant 10$ нм, так как при $2{{a}_{i}} < 10$ нм необходимо учитывать явления пространственной дисперсии [1].

Рис. 1.

Геометрия задачи.

Таким образом, с точки зрения классической электродинамики речь идет о решении задачи дифракции плоской электромагнитной волны на двух цилиндрах из диэлектрика.

Исследуется случай ТМ-поляризации, когда в электромагнитном поле присутствуют компоненты ${{H}_{z}}(x,y),$ ${{E}_{x}}(x,y),$ ${{E}_{y}}(x,y).$ Задача дифракции в этом случае сводится к нахождению скалярной функции $U(x,y) = {{H}_{z}}(x,y),$ а волновое поле падающей плоской волны задается выражением

где угол ${{\varphi }_{0}}$ определяет направление распространения волны. Используется гауссовская система физических единиц, зависимость от времени выбрана в виде $\exp (i\omega t).$

Полное поле $U(x,y)$ в кусочно-однородной среде удовлетворяет уравнению Гельмгольца

где диэлектрическая проницаемость $\varepsilon (x,y)$ среды определяется выражением

для задачи, геометрия которой представлена на рис. 1.

Уравнение (2) необходимо дополнить условием непрерывности величин

на границах цилиндров, где $N$ обозначает нормаль к границам цилиндров.

Полное поле вне цилиндров состоит из падающего ${{U}^{0}}$ и рассеянного ${{U}^{S}}$ полей

Рассеянное поле ${{U}^{S}}$ в цилиндрической системе координат ($x = r\cos \varphi ,\,\,y = r\sin \varphi $) должно удовлетворять в дальней зоне условию излучения

где $\Phi (\varphi )$ – диаграмма рассеяния кластера. Полное сечение рассеяния ${{\sigma }_{s}}$ и сечение поглощения ${{\sigma }_{a}}$ выражаются через решение краевой задачи (1)–(5) по формулам

Интегрирование в (8) проводится по внешним контурам цилиндров ${{S}_{1}}$ и ${{S}_{2}}.$

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численное решение краевой задачи проводилось модифицированным методом дискретных источников [11–13]. Точность численного решения оценивалась невязкой граничных условий $\Delta $ в линейной норме на цилиндрах и во всех расчетах была не хуже, чем $\Delta = {{10}^{{ - 3}}}.$

Рассмотрим сначала случай, когда значения радиусов цилиндров из реального серебра были: ${{a}_{1}} = 45$ нм и ${{a}_{2}} = 15$ нм ($\chi = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$); расстояние между ними – $d = 5$ нм ($d = \chi {{a}_{2}} = {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} 3}} \right. \kern-0em} 3}$); угол падения плоской волны принимал значения: ${{\varphi }_{0}} = 0,$ $\pi ,\,\,{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2},$ ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0em} 4},\pi + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ На рис. 2 представлены результаты расчетов спектра нормированного поперечника рассеяния $k{{\sigma }_{S}}.$ Из рисунка видно, что все кривые имеют два максимума. Однако наибольшее значение из всех максимумов $k{{\sigma }_{S}}$ имеет тот, для которого угол падения ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}.$ Этому углу соответствует случай, когда падающее поле распространяется вдоль оси $у$. При этом компонента электрического поля ${{E}_{x}}$ направлена по оси x, т.е. пересекает оба цилиндра.

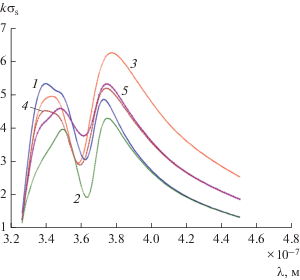
Рис. 2.

Спектр поперечника рассеяния для кластера из двух серебряных наноцилиндров при различных углах падения плоской волны: φ₀ = 0 (1), π (2), ‒π/2 (3), –π/4 (4), π + π/4 (5) и при а₁ = 45 нм, а₂ = = 15 нм, χ = 1/3.

Для того чтобы понять происхождение двух максимумов $k{{\sigma }_{S}},$ рассмотрим результаты расчетов спектров поперечника рассеяния $k{{\sigma }_{S}}$ при различных значениях мнимой части относительной диэлектрической проницаемости серебра $\operatorname{Im} (\varepsilon ),$ которые определяют потери серебра (см. рис. 3). При расчете $k{{\sigma }_{S}}$ полагали, что ${{a}_{1}} = 45$ нм, ${{a}_{2}} = 15\,\,{\text{нм}}$, $d = 5$ нм, ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ (эти данные аналогичны данным работы [9]). Из результатов, представленных на рис. 3 следует, что главный максимум кривой 1 соответствует дипольному резонансу плазмонов. Второй максимум этой кривой связан с слиянием полей мультипольных резонансов плазмонов, которые начинают проявляться лишь при малых ($0.001\operatorname{Im} (\varepsilon ),$ кривая 3) потерях серебра.

Рис. 3.

Спектр поперечника рассеяния кластера из двух серебряных наноцилиндров для разных потерь серебра цилиндров: кривая 1 – $\operatorname{Im} (\varepsilon ),$ кривая 2 – $0.1\operatorname{Im} (\varepsilon ),$ кривая 3 – $0.001\operatorname{Im} (\varepsilon )$ и при ${{a}_{1}} = 45$ нм, ${{a}_{2}} = 15$ нм, $\chi = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},$ ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}.$

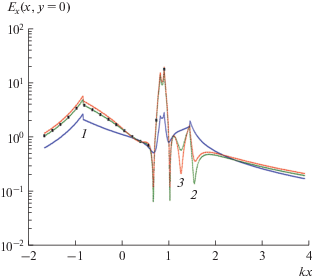
Рисунок 4 иллюстрирует результаты расчета модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ вдоль оси $x$ в котором ${{a}_{1}} = 45$ нм, ${{a}_{2}} = 15$ нм, $d = 5$ нм, при длине волны $\lambda = 342$ нм (при такой длине волны имеет место первый максимум $k{{\sigma }_{S}},$ см. рис. 2 кривая 3), угле падения ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ и различных потерях серебра. Из рис. 4 видно, что максимальные значения модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ достигаются в промежутке между цилиндрами, а не на выходе кластера в точке с координатами $x = {{a}_{1}} + d + 2{{a}_{2}}.$ На выходе кластера электрическая компонента E_x (x = = a₁ + d + + 2a₂, y = 0) увеличивает свою амплитуду примерно в два раза по отношению к амплитуде $E_{x}^{0} = 1$ падающей волны.

Рис. 4.

Пространственное распределение компоненты электрического поля ${{E}_{x}}(x,y = 0)$ в кластере из двух серебряных наноцилиндров для разных потерь серебра цилиндров: кривая 1 – $\operatorname{Im} (\varepsilon ),$ кривая 2 – $0.1\operatorname{Im} (\varepsilon ),$ кривая 3 – $0.001\operatorname{Im} (\varepsilon )$ и при ${{a}_{1}} = 45$ нм, ${{a}_{2}} = 15$ нм, $\chi = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},$ ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}.$

На рис. 5 изображены результаты расчета модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ вдоль оси x кластера, в котором цилиндры из реального серебра имели радиусы: ${{a}_{1}} = 45$ нм, ${{a}_{2}} = 15$ нм, $d = 5$ нм; угол падения волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2};$ длины волн λ = 378, 359 и 342 нм. Из рис. 5 видно, что и здесь максимальные значения модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ достигаются в промежутке между цилиндрами. Отметим, что при длине волны $\lambda = 378\,\,{\text{нм}}$ (при дипольном резонансе) на выходе кластера электрическая компонента ${{E}_{x}}(x = {{a}_{1}} + d + 2{{a}_{2}},y = 0)$ имеет амплитуду примерно в пять раз большую, чем амплитуда $E_{x}^{0}$ падающей волны. При остальных длинах волн значения амплитуды поля E_x (x = a₁ + d + 2a₂, y = 0) меньше трех. Это означает, что такой кластер не способен значительно усиливать электрическое поле проходящей волны.

Рис. 5.

Пространственное распределение компоненты электрического поля ${{E}_{x}}(x,y = 0)$ в кластере из двух серебряных наноцилиндров для разных длин волн: λ = 378 (1), 359 (2) и 342 нм (3) и при а₁ = 45 нм, а₂ = = 15 нм, χ = 1/3, φ₀ = –π/2.

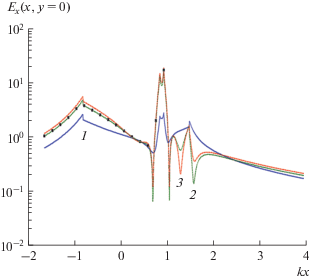
Рис. 6 посвящен исследованию влияния расстояния между серебряными цилиндрами на поперечник рассеяния $k{{\sigma }_{S}}.$ При расчетах спектров нормированного поперечника рассеяния kσ_S полагалось, что радиусы цилиндров имели значения: ${{a}_{1}} = 45$ нм, ${{a}_{2}} = 15$ нм; угол падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2};$ расстояния между цилиндрами $d = 0.1{{a}_{2}},$ $0.2{{a}_{2}},$ ${{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} 3}} \right. \kern-0em} 3},0.5{{a}_{2}},0.75{{a}_{2}},{{a}_{2}}.$ При малом расстоянии между цилиндрами $d = 0.1{{a}_{2}}$ поперечник рассеяния $k{{\sigma }_{S}}$ имеет три максимума. Увеличение расстояния между цилиндрами $d$ приводит к вырождению (уменьшение числа) максимумов поперечника рассеяния $k{{\sigma }_{S}}.$

Рис. 6.

Спектр поперечника рассеяния для кластера из двух серебряных наноцилиндров при различных расстояниях между цилиндрами: $d = 0.1{{a}_{2}}$ (1), 0.2а₂ (2), а₂/3 (3), 0.5а₂ (4), 0.75а₂ (5), а₂ (6) и при а₁ = 45 нм, а₂ = 15 нм, χ = 1/3, φ₀ = –π/2.

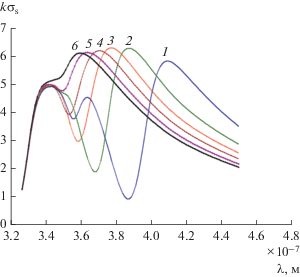
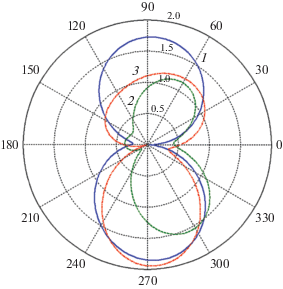
Рисунок 7 иллюстрирует результаты расчетов диаграммы рассеяния $k{{\sigma }_{S}}$ для кластера, образованного серебряными цилиндрами с радиусами $d$ ${{a}_{1}} = 45$ нм, ${{a}_{2}} = 15$ нм, при угле падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ и трех значениях длины волны λ = 378, 359 и 342 нм. Эти длины волн соответствуют двум максимумам и минимуму графика поперечника рассеяния $k{{\sigma }_{S}},$ представленного на рис. 3 (кривая 1). Из рис. 7 следует, что в случае дипольного резонанса (λ = 359 нм) диаграмма рассеяния представляет собой практически симметричную двухлепестковую кривую, которая имеет два максимума в направлениях ${{\varphi }_{m}} = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2}.$ В остальных случаях диаграмма рассеяния имеет асимметричные лепестки разной амплитуды. При этом направления максимумов отличается от углов ${{\varphi }_{m}} = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2}.$

Рис. 7.

Диаграмма рассеяния кластера из двух серебряных наноцилиндров для разных длин волн: λ = = 378 (1), 359 (2) и 342 нм (3) и при а₁ = 45 нм, а₂ = = 15 нм, χ = 1/3, φ₀ = –π/2.

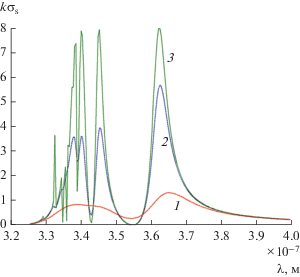
В рассмотренных выше случаях величина $k{{a}_{1}}$ изменялась в пределах $1.41 < k{{a}_{1}} < 1.76$ (при 320 нм < $ < \lambda < 400\,\,{\text{нм}}$). Это означает, что мы находились в резонансном диапазоне длин волн. Если взять кластер, цилиндры которого имеют радиусы ${{a}_{1}} = 18\,\,{\text{нм,}}$ ${{a}_{2}} = 6\,\,{\text{нм}}$ и $\chi = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},$ то величина $k{{a}_{1}}$ будет изменяться в пределах $0.56 < k{{a}_{1}} < 0.7,$ что соответствует положению границы квазистатики. На рис. 8 представлены результаты расчетов поперечника рассеяния для такого кластера и трех случаев потерь серебряных цилиндров. Из рисунка следует, что и в этом случае реальные потери серебра приводят не только к уменьшению амплитуды поперечника рассеяния $k{{\sigma }_{S}},$ но и к исчезновению мультипольных резонансов.

Рис. 8.

Спектр поперечника рассеяния кластера из двух серебряных наноцилиндров для разных потерь серебра цилиндров: кривая 1 – $\operatorname{Im} (\varepsilon ),$ кривая 2 – $0.1\operatorname{Im} (\varepsilon ),$ кривая 3 – $0.001\operatorname{Im} (\varepsilon )$ и при а₁ = 18 нм, а₂ = = 6 нм, χ = 1/3, φ₀ = –π/2.

На рис. 9 даны результаты расчета модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ вдоль оси x такого кластера при трех длинах волн: λ = = 365, 355 и 340 нм. Такие длины волн соответствуют двум максимумам и минимуму графика поперечника рассеяния (см. рис. 8 кривая 1) для данного кластера. Из рис. 9 видно, что и здесь максимальные значения модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ достигаются в промежутке между цилиндрами при малых потерях серебра. Однако по сравнению со случаем кластера, у которого ${{a}_{1}} = 45\,\,{\text{нм,}}$ значения электрического поля здесь примерно в три раза больше. На выходе кластера (в точке с координатами $x = {{a}_{1}} + d + 2{{a}_{2}}$) значение электрической компоненты E_x (x = a₁ + + d + 2a₂, y = 0) максимально при длине падающей волны $\lambda = 365\,\,{\text{нм}}$ и примерно в десять раз больше, чем амплитуда падающей волны. При остальных длинах волн значения амплитуды поля ${{E}_{x}}(x = {{a}_{1}} + d + 2{{a}_{2}},y = 0)$ меньше примерно в два раза. Это свидетельствует о том, что и такой кластер не способен значительно усиливать электрическое поле проходящей волны.

Рис. 9.

Пространственное распределение компоненты электрического поля ${{E}_{x}}(x,y = 0)$ в кластере из двух серебряных наноцилиндров для разных длин волн: λ = 365 (1), 355 (2) и 340 нм (3) и при а₁ = 18 нм, а₂ = = 6 нм, χ = 1/3, φ₀ = –π/2.

Рассмотрим теперь кластер, образованный двумя серебряными наноцилиндрами с радиусами ${{a}_{1}} = 20\,\,{\text{нм,}}$ ${{a}_{2}} = 10\,\,{\text{нм}}$ и коэффициентом самоподобия $\chi = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ (см. рис. 10–14) . В этом случае величина $k{{a}_{1}} < 1.$ Это значит, что выполняется условие нахождения параметров кластера в области квазистатики.

Рис. 10.

Спектр поперечника рассеяния для кластера из двух серебряных наноцилиндров при различных углах падения плоской волны: φ₀ = 0 (1), π (2), ‒π/2 (3), –π/4 (4), π + π/4 (5) и при а₁ = 20 нм, а₂ = = 10 нм, χ = 1/2.

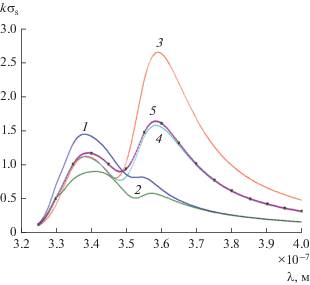
Рис. 11.

Спектр поперечника рассеяния кластера из двух серебряных наноцилиндров для разных потерь серебра цилиндров: кривая 1 – $\operatorname{Im} (\varepsilon ),$ кривая 2 – $0.1\operatorname{Im} (\varepsilon ),$ кривая 3 – $0.001\operatorname{Im} (\varepsilon )$ и при а₁ = 20 нм, а₂ = = 10 нм, χ = 1/2, φ₀ = –π/2.

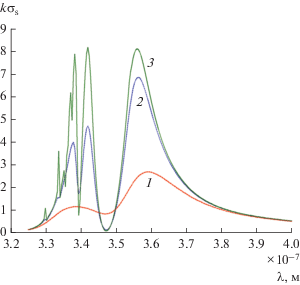
Рис. 12.

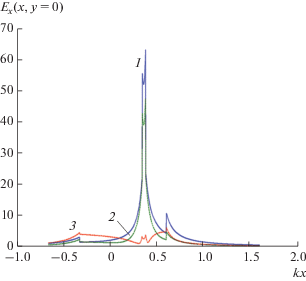
Пространственное распределение компоненты электрического поля ${{E}_{x}}(x,y = 0)$ в кластере из двух серебряных наноцилиндров для разных длин волн: λ = 360 (1), 347 (2) и 339 нм (3) и при а₁ = 20 нм, а₂ = 10 нм, χ = 1/2, φ₀ = –π.

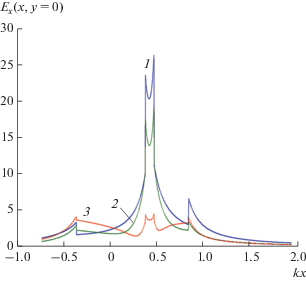
Рис. 13.

Спектр поперечника рассеяния для кластера из двух серебряных наноцилиндров при различных расстояниях между цилиндрами: $d = 0.1{{a}_{2}}$ (1), 0.2а₂ (2), а₂/3 (3), 0.5а₂ (4), 0.75а₂ (5), а₂ (6) и при а₁ = 20 нм, а₂ = 10 нм, χ = 1/2, φ₀ = –π/2.

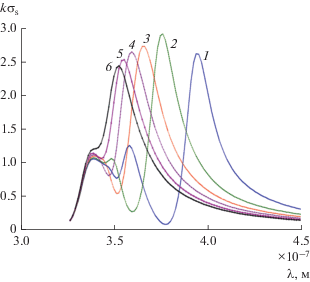
Рис. 14.

Диаграмма рассеяния кластера из двух серебряных наноцилиндров для разных длин волн: λ = 360 (1), 347 (2) и 339 нм (3) и при а₁ = 20 нм, а₂ = 10 нм, χ = = 1/2, φ₀ = –π/2.

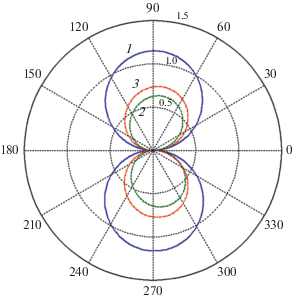
Рисунок 10 иллюстрирует результаты расчетов спектра нормированного поперечника рассеяния $k{{\sigma }_{S}}$ для случая кластера, образованного серебряными наноцилиндрами с радиусами ${{a}_{1}} = 20$ нм, ${{a}_{2}} = 10$ нм ($\chi = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$) и расстоянием между ними $d = 5\,\,{\text{нм}}{\text{.}}$ Расчеты проводились при пяти различных углах падения плоской волны: ${{\varphi }_{0}} = 0,\pi ,{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2},$ ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0em} 4},\pi + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ Из рис. 10 видно, что все кривые имеют два максимума. Однако для кривых 1 и 2 их главный максимум $k{{\sigma }_{S}}$ является первым максимумом $k{{\sigma }_{S}},$ и он располагается при меньших значениях $\lambda $, чем их второй максимум $k{{\sigma }_{S}}.$ У кривых 3–5, в отличие от кривых 1 и 2, главный максимум $k{{\sigma }_{S}}$ является вторым максимумом $k{{\sigma }_{S}}$ и располагается при бóльших значениях $\lambda $, чем первый максимум $k{{\sigma }_{S}}$. При этом наибольшее значение из всех максимумов $k{{\sigma }_{S}}$ имеет тот, для которого угол падения ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}.$ Этому углу соответствует случай, когда падающее поле распространяется вдоль оси $у$. При этом компонента электрического поля ${{E}_{x}}$ направлена по оси $x$, т.е. пересекает оба цилиндра.

Для того чтобы понять происхождение двух максимумов $k{{\sigma }_{S}},$ обратимся к результатам расчетов спектров поперечника рассеяния $k{{\sigma }_{S}}$ при различных значениях мнимой части относительной диэлектрической проницаемости серебра $\operatorname{Im} (\varepsilon )$ представленных на рис. 11. Из рисунка следует, что главный максимум кривой 1 определяется дипольным резонансом плазмонов, а второй максимум кривой 1 – является результатом слияния полей мультипольных резонансов плазмонов. При этом выделение мультипольных резонансов плазмонов происходит лишь при малых ($0.001\operatorname{Im} (\varepsilon ),$ кривая 3) потерях серебра.

На рис. 12 приведены результаты расчета модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ вдоль оси $x$ кластера, в котором цилиндры из реального серебра имели радиусы: ${{a}_{1}} = 20$ нм, ${{a}_{2}} = 10$ нм, $d = 5\,\,{\text{нм;}}$ угол падения волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2};$ и трех значениях длины волны: λ = = 360, 347 и 339 нм. Из рис. 12 видно, что максимальные значения модуля электрической компоненты $\left| {{{E}_{x}}(kx,y = 0)} \right|$ достигаются в промежутке между цилиндрами. На выходе кластера в точке с координатами $x = {{a}_{1}} + d + 2{{a}_{2}}$ амплитуда электрического поля меньше, чем в промежутке. При длине волны λ = 360 нм (при дипольном резонансе) на выходе кластера электрическая компонента ${{E}_{x}}(x = {{a}_{1}} + d + 2{{a}_{2}},\,\,y = 0)$ имеет амплитуду примерно в пять раз большую, чем амплитуда $E_{x}^{0}$ падающей волны. При остальных длинах волн значения амплитуды поля E_x (x = a₁ + d + 2a₂, y = 0) меньше трех. Это означает, что и такой кластер не способен значительно усиливать электрическое поле проходящей волны.

Также было исследовано влияние расстояния между серебряными цилиндрами в кластере (см. рис. 13). На этом рисунке представлены расчеты спектров нормированного поперечника рассеяния $k{{\sigma }_{S}}$ при различных значениях параметра, характеризующего расстояние между цилиндрами: $d = 0.1{{a}_{2}},0.2{{a}_{2}},$ ${{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} 3}} \right. \kern-0em} 3},0.5{{a}_{2}},0.75{{a}_{2}},{{a}_{2}}.$ Полагалось, что радиусы серебряных цилиндров имели следующие значения: ${{a}_{1}} = 20\,\,{\text{нм,}}$ ${{a}_{2}} = 10\,\,{\text{нм;}}$ угол падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}.$ При малых расстояниях между цилиндрами $d = (0.1...0.3){{a}_{2}}$ поперечник рассеяния $k{{\sigma }_{S}}$ имеет три максимума. С увеличением расстояния между цилиндрами $d$ происходит вырождение (уменьшение числа) максимумов поперечника рассеяния $k{{\sigma }_{S}}.$

Наконец рис. 14 иллюстрирует результаты расчетов диаграммы рассеяния для кластера, образованного серебряными цилиндрами с радиусами ${{a}_{1}} = 20\,\,{\text{нм,}}$ ${{a}_{2}} = 10\,\,{\text{нм,}}$ $\chi = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ при угле падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ и трех значениях длины волны: λ = 360, 347 и 339 нм. Эти длины волн соответствуют двум максимумам и минимуму графика поперечника рассеяния $k{{\sigma }_{S}}$, представленного кривой 1 на рис. 11. Из рис. 14 следует, что в случае дипольного резонанса (λ = 360 нм) диаграмма рассеяния представляет собой симметричную двухлепестковую кривую, которая имеет два максимума в направлениях ${{\varphi }_{m}} = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2}.$ В остальных случаях диаграмма рассеяния также имеет двухлепестковую структуру с незначительной асимметрией лепестков (максимумы излучения немного смещены по отношению к направлениям ${{\varphi }_{m}} = {{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2}$).

ЗАКЛЮЧЕНИЕ

Численно исследована двумерная задача дифракции ТМ-поляризованной плоской волны на кластере, состоящем из двух самоподобных серебряных круговых цилиндров разного диаметра. Исследовано влияние угла падения, расстояния между цилиндрами, коэффициента самоподобия и потерь серебра на спектры поперечника рассеяния и диаграмму рассеяния в световом диапазоне длин волн. Показано, что реальные потери серебра относительно слабо влияют на дипольный резонанс и сильно сказываются на мультипольных резонансах – приводят к слиянию полей мультипольных резонансов в один общий резонанс. Обнаружены эффекты “вырождения” резонансов в кластере из двух серебряных цилиндров разного диаметра. Показано, что такой кластер не может быть нанолинзой, т.е. системой существенно увеличивающей поле на выходе кластера.

ФИНАНСИРОВАНИЕ РАБОТЫ

Работа выполнена за счет частичного бюджетного финансирования в рамках государственного задания по теме 0030-2019-0014 и частичной финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-02-00654).