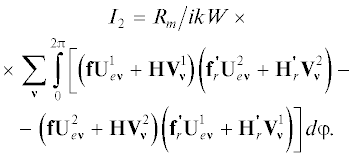Радиотехника и электроника, 2019, T. 64, № 11, стр. 1049-1060

1. ПОСТАНОВКА ЗАДАЧИ

Интерес к ПС и структурам на их основе стимулируется развитием научного направления, связанного с созданием и исследованием новых искусственных сред, получивших название метаматериалов (ММ) [1]. Чаще всего они имеют упорядоченную структуру в виде кристаллической решетки. Поэтому логично было бы называть данный вид ММ метакристаллами. Частицы, образующие ММ могут быть достаточно сложными объектами, которые отличаются от частиц традиционных искусственных сред необычными пространственными и частотными свойствами. Благодаря им появляется новый класс электромагнитных явлений, характерных исключительно для ММ [2, 3].

Среди них отметим создание непрозрачных ПС, в которых в любом направлении отсутствуют распространяющиеся волны. Впервые такие среды были созданы и изучены в оптическом диапазоне. Поэтому они получили название фотонных кристаллов (ФК) [4]. Их аналогами в микроволновом диапазоне являются электромагнитные кристаллы (ЭМК) [5]. В ряде работ (см., например, [6, 7]) было показано, что внесение дефектов в кристаллическую решетку позволяет создавать в метакристаллах волноводные элементы, способные выполнять функции пространственной и временной обработки и формирования полей и сигналов.

Проектирование таких устройств связано с их электродинамическим моделированием, которое требует решения граничных задач для неоднородных ПС. Современные средства численного электродинамического моделирования [8] в принципе позволяют решать такие задачи. Однако следует отметить, что неоднородные ПС и волноведущие структуры на их основе являются весьма неудобным для численного решения объектом. Дело в том, что, как отмечалось выше, частицы, формирующие ПС, имеют сложную малоразмерную пространственную структуру. Поэтому для точного описания поля в ПС необходимо использовать соответствующие сетки с относительно малыми ячейками. В то же время область, в которой ищется решение, может иметь большие электрические размеры. Таким образом, общее число определяющее размерность ячеек решаемой численно задачи оказывается большой величиной второго порядка.

Описанная выше ситуация делает актуальной задачу поиска альтернативного описания электромагнитного поля в неоднородной ПС. Такое описание должно с самого начала учитывать особенности взаимодействия электромагнитных (ЭМ) волн, характерные для ПС, и за счет этого обеспечивать относительную простоту формулировки граничных задач и высокую эффективность алгоритмов их численного решения. Платой за приобретаемые преимущества будет потеря универсальности, поскольку предлагаемое альтернативное описание поля потребует определенных ограничений на параметры ПС.

Наиболее близким к излагаемому подходу является метод обобщенной матрицы рассеяния (ОМР), который активно развивается рядом авторов [9, 10]. Основная идея метода состоит в том, что поле в окрестности элемента ПС представляется в виде совокупности падающих и отраженных волн, амплитуды которых связаны матричным оператором, аналогичным матрице рассеяния в теории СВЧ-многополюсников [11]. Взаимодействие элементов ПС описывается с помощью специальной процедуры, связывающей волны разных частиц ПС друг с другом.

Метод ОМР используется для эффективного численного анализа фазированных антенных решеток больших, но конечных электрических размеров, а также непериодических решеток. Отмечается его высокая численная эффективность, многократно превосходящая эффективность прямых численных методов, таких как метод конечных элементов [8]. В работе [12] одна из версий метода ОМР использована для электродинамического моделирования неоднородного ММ.

Метод компенсирующих источников (МКИ), предложенный в работе [13] также можно рассматривать как вариант метода ОМР. Однако он существенно развивает его. Важным отличием МКИ является применение виртуальных сторонних источников и, что наиболее существенно, решение задачи о возбуждении этими источниками однородной ПС, которое представляется в виде ее функции Грина.

Применение функции Грина существенно уменьшает размерность систем линейных алгебраических уравнений (СЛАУ), к которым сводятся задачи электродинамического анализа неоднородных ПС.

Цель данной работы – развитие идей, положенных в основу МКИ и нашедших отражение в монографии [5]. Будет показано, что принципы, использованные в методах ОМР и МКИ, позволяют не только создавать эффективные численные алгоритмы решения граничных задач электродинамики ПС, но по-новому, не прибегая непосредственно к векторам поля $\vec {E},$ $\vec {H},$ описывать электромагнитные процессы в неоднородных ПС. Соответствующий математический аппарат можно рассматривать как специализированную электродинамику таких сред. Она не противоречит традиционной универсальной электродинамике, но является ее новой и, мы надеемся, более эффективной формулировкой, ориентированной на применение к относительно узкому классу объектов.

2. ЧАСТИЦЫ ПС И ОПЕРАТОРЫ РАССЕЯНИЯ ЭМ-ВОЛН НА ЧАСТИЦАХ

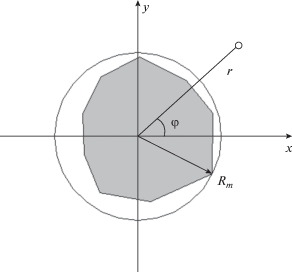
Обсудим ограничения, которые необходимо наложить на частицы, формирующие ПС, и операторы рассеяния, получающиеся из решения задачи возбуждения уединенной частицы внешним полем. Частицы, из которых состоит двумерная ПС, представляют собой цилиндры, имеющие в общем случае произвольную образующую (см. рис. 1). В рамках развиваемого подхода будем рассматривать только ПС, образованные изолированными частицами, которые можно полностью вписать в окружность, радиус которой R_m. При этом период Р кристаллической решетки ПС больше R_m. Для простоты ограничимся решетками с квадратной сеткой.

В двумерном случае поле в однородной среде можно представить в виде разложения по цилиндрическим волнам. Возбуждающее и рассеянное частицей поля E_e,s запишем в следующем виде:

где r, φ – локальные цилиндрические координаты (см. рис. 1), k – волновое число свободного пространства, J_n, $H_{n}^{{\left( {\text{2}} \right)}}$ – функции Бесселя и Ганкеля второго рода, U_e, sn – амплитуды возбуждающих и рассеянных волн, J, H – векторы-строки, а U_e, s – векторы-столбцы, произведение типа JU – это скалярное произведение векторов. Выбор параметра $N$обсудим ниже. Отметим, что представление для E_s верно только в области r > R_m.

В двумерных задачах поле разделяется на два независимых класса электрических и магнитных волн. Здесь и далее мы будем рассматривать электрические волны, у которых компонента H_z = 0. Волны этого типа имеют одну компоненту электрического поля Е_z, поэтому индекс z мы опускаем. Анализ магнитных волн полностью аналогичен анализу, представленному ниже.

Оператор рассеяния L связывает амплитудные векторы U_e, s:

Можно также записать возбуждающее поле в виде разложения по функциям Ганкеля первого рода. Тогда пространственные гармоники имеют смысл падающих и отраженных волн с амплитудами U_i, rn. Вводя векторы U_i, r, получаем связь между ними, аналогичную (2), через матрицу рассеяния S. Матрицы L, S связаны соотношением: S = E + 2L, где E – единичная матрица. Нам будут полезны оба представления поля. Отметим, что для матрицы S взаимной и недиссипативной структуры справедливы известные из теории многополюсников [11] соотношения:

С учетом (1), (2) запишем полное поле вокруг частицы E = E_e + E_s:

В ПС каждую частицу, положение которой описывается векторными (двумерными) индексами ν(ν_x, ν_y), можно охарактеризовать падающим и рассеянным полями и соответствующими амплитудными векторами U_e, sν. Падающее на ν-ю частицу поле, в свою очередь, является полем, рассеянным всеми остальными частицами ПС. Поэтому без потери общности мы можем считать, что полное поле в ПС является суммой рассеянных полей всеми ее частицами:

Таким образом, видно, что знания множества векторов U_sν достаточно для однозначного определения поля в ПС. Поэтому переход от векторов поля к амплитудным векторам происходит без потери информации о поле, которое всегда может быть найдено по известному множеству U_sν.

Нашей целью является вывод уравнений, которым удовлетворяют векторы U_sν, и формулировка граничных задач для них в том случае, когда в ПС присутствуют дефекты, т.е. ПС является неоднородной.

Определение сторонних источников – важный этап дальнейшего анализа. Зададим их как виртуальные источники, создающие в частице с индексом ξ дополнительное рассеянное поле Е с амплитудным вектором V_ξ:

Этот вектор не связан с возбуждающим полем соотношением (2).

3. УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ЭМ-ВОЛН В ПС

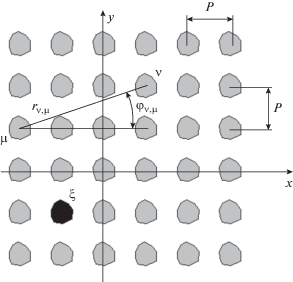
Получим уравнение, описывающее в терминах амплитудных векторов распространение ЭМ-волн в ПС. Выделим в бесконечной ПС ν-й элемент. Пусть в ξ-й частице существует источник. Поле, рассеянное μ-й частицей, записывается в виде (1) в связанной с ней системе координат. Для определения амплитуд волн, падающих на выделенную частицу, надо перейти в систему координат, привязанную к ν-й частице. Это можно сделать с помощью теоремы сложения для цилиндрических функций [14]. Применяя ее, получим следующее соотношение:

Аналогичный вид имеет вклад в вектор U_eν от стороннего источника. Смысл параметров, входящих в (7), поясняется на рис. 2. Суммируя по всем частицам ПС, применяя соотношение (2) и добавляя сторонние источники, получаем искомое уравнение:

Суммирование по μ в (8) ведется по всем значениям индекса, кроме μ = ν. Уравнение (8) описывает процесс распространения ЭМ-волн в ПС, возбуждаемой сторонним источником V_ξ. Оно является существенно нелокальным уравнением, поскольку перейти к суммированию по конечной области вокруг ν-й частицы не представляется возможным из-за того, что элементы матрицы M_{ν, μ} медленно убывают с ростом расстояния r_{ν, μ}.

Нелокальную природу уравнения (8) удобно проследить, перейдя к однородному уравнению (V_ξ = 0) и взяв от него двумерное дискретное преобразование Фурье (ДПФ). Матрица M_{ν, μ} зависит только от разности индексов ν, μ. Поэтому если мы возьмем ДПФ, то можем воспользоваться теоремой о свертке. В результате получаем

Здесь g_s(χ) – фурье-образ векторов U_sν, а G(χ) – ДПФ от матрицы M_{ν, μ}, χ(κ, α) – векторный (двумерный) спектральный параметр ДПФ. Матрица G(χ) периодична по обоим переменным κ, α с периодом 2π/Р.

Характер зависимости данной матрицы от аргументов κ,α определяется степенью локальности уравнения (8). Отметим, что в силу периодичности элементы матрицы можно представить рядами Фурье. Если они меняются относительно медленно, то ряды быстро сходятся, что эквивалентно быстрому убыванию элементов матрицы M_{ν, μ} при увеличении r_ν, μ. Можно показать, что элементы G(χ) имеют периодически повторяющиеся полюса при κ²+ α² = k². Наличие полюсов свидетельствует о быстром изменении фурье-образа и, следовательно, о высокой степени нелокальности уравнения (8).

Причина появления полюсов матрицы G(χ) физически понятна. Она связана с эффектами синфазного сложения рассеянных элементами ПС волн, падающих на некоторый выделенный ее элемент. В подобном режиме синхронизма сумма малых воздействий от бесконечного числа источников может порождать волны сколь угодно большой амплитуды.

Уравнение (8) может и будет использовано ниже при решении граничных задач для частных структур. Однако представляет интерес задача его локализации, т.е. такого преобразования, при котором процесс распространения волн можно описать, учитывая вклады частиц, расположенных в некоторой ограниченной области. Строго локализовать уравнение (8) не представляется возможным. Тем не менее можно предложить приближенную процедуру локализации. Ее идея состоит в следующем.

Рассмотрим линейное преобразование А:

где A_λ, ν – скалярные величины, а суммирование ведется по ограниченной области. Возьмем от него ДПФ и получим по аналогии с (8) следующее выражение:

где a(χ) – фурье-образ ${{A}_{{\lambda {\mathbf{,}}\nu }}}.$ Если параметры ${{A}_{{{\mathbf{\lambda ,\nu }}}}}$ таковы, что функция a(χ) имеет нули при $\left| {\mathbf{\chi }} \right| = k$ (κ²+ α² = k²), то, применяя данное линейное преобразование к уравнению (9), устраняем полюсы матрицы G(χ). Новая матрица a(χ)G(χ) содержит гладкие функции, которые можно с хорошей точностью аппроксимировать конечным числом членов ряда Фурье. Переходя обратно в пространство оригиналов, получаем квазилокальное однородное уравнение распространения:

Расчеты показали, что решение задачи определения матрицы А возможно с очень высокой точностью. Средняя погрешность, с которой найденная функция a(χ) обращается в нуль на окружности $\left| \chi \right| = k,$ не превышает ${{10}^{{ - 6}}}.$ Интересно, что для kP < 1 матрица А имеет всего лишь третий порядок, т.е. линейное преобразование охватывает центральный элемент и окружающие его соседние элементы. Поскольку их амплитудные векторы можно выразить через конечные разности вида ${{\Delta }_{x}}{{U}_{{sn,\,m}}} = $ $ = {{U}_{{sn + 1,\,m}}} - {{U}_{{sn,\,m}}},$ то уравнение (12) можно рассматривать в качестве разностного аналога дифференциального волнового уравнения Гельмгольца, описывающего распространение ЭМВ в непрерывной двумерной среде. Проведенный большой объем численных исследований показал, что размерность матрицы А ни разу не превысила 5 × 5. Это свидетельствует о высокой эффективности предложенной процедуры локализации уравнения (8).

4. РЕШЕНИЕ ОДНОРОДНОГО УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ. СОБСТВЕННЫЕ ВОЛНЫ ПС

Ищем решение уравнения (8) при V_ξ = 0 в виде плоской волны:

где χ₀ – неизвестный волновой вектор собственной волны ПС. Подставим соотношение (13) в уравнение (8) и применим к нему ДПФ:

где ${\mathbf{U}}\delta (\chi - {{\chi }_{0}})$ – двумерная дельта-функция. Уравнение (14) имеет нетривиальные решения при выполнении следующего условия:

Соотношение (15) является дисперсионным уравнением собственных волн однородной ПС. В него входят две неизвестные переменные, являющиеся проекциями волнового вектора χ₀ на оси координат: χ_0x, y. Одну из них можно зафиксировать, а вторую находить из уравнения (15). Возможны другие варианты исследования решений уравнения (15). Например, можно положить константе угол распространения волны и искать модуль волнового вектора, имеющий смысл постоянной распространения волны.

При выводе соотношения (15) мы использовали нелокальное уравнение (8). Процедура, аналогичная изложенной выше процедуре и примененная к локализованному уравнению (12), приводит нас к дисперсионному уравнению, отличающемуся от (15) множителем a(χ):

Выше мы отмечали, что умножение матрицы G(χ) на функцию a(χ) устраняет полюсы при |χ| = k. После этого элементы матрицы можно описать сравнительно быстро сходящимися бесконечными тригонометрическими рядами, которые допустимо заменить аппроксимациями в виде сумм конечного порядка. При этом определитель матрицы и дисперсионное уравнение (16) также будут представляться суммой тригонометрических функций вида cos(nαP), cos(nκP). Число учитываемых членов бесконечного ряда определяет число корней дисперсионного уравнения. При этом следует иметь в виду, что в силу периодичности функций, входящих в левую часть уравнения (16), каждому корню в главном периоде при $\left| {\kappa ,\alpha } \right| < {\pi \mathord{\left/ {\vphantom {\pi P}} \right. \kern-0em} P}$ соответствует бесконечное число периодически смещенных на πn/P корней. Под решением дисперсионного уравнения понимаем только корень, лежащий в главном периоде.

Функции в (12), (13) являются четными функциями своих аргументов, поэтому их корни по любой из проекций волнового вектора, например по проекции на ось 0x – κ, располагаются парами ±κ_n, n = 1, 2, … Строго говоря, число таких корней бесконечно. Однако, как отмечалось выше, ограничивая порядок аппроксимации, мы одновременно ограничиваем число корней дисперсионного уравнения однородной ПС.

Как следует из разд. 3, порядок аппроксимации, в свою очередь, связан с размерностью матрицы А, которая определяет степень локализации уравнения, описывающего распространение ЭМ волн в ПС. В простейшем случае, который имеет место при относительно малых периодах ПС, достаточно учесть только взаимодействие соседних частиц. При этом дисперсионное уравнение имеет одну пару корней ±κ₁, соответствующих волнам одного типа, распространяющихся в противоположных направлениях. Такую ПС можно назвать одноволновой средой.

Из сказанного выше видно, что в общем случае ПС является многоволновой средой. Чаще всего достаточно учитывать две волны: основную с n = 1 и волну высшего типа с n = 2. В случаях, представляющих практический интерес, все волны высших типов являются нераспространяющимися. У них при отсутствии диссипативных потерь Re κ_n = 0, Im κ_n ≠ 0. Все волны в ФК и ЭМК, включая основную волну, в рабочей области параметров являются нераспространяющимися волнами.

5. РЕШЕНИЕ НЕОДНОРОДНОГО УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ. ФУНКЦИЯ ГРИНА ПС

Будем понимать под функцией Грина ПС решение уравнения (8) при

где ${{\delta }_{{\xi {\text{,}}\tau }}}$ – символ Кронекера. Таким образом, источник сосредоточен в единственной частице ПС с индексом τ. Применим к уравнению (8) двукратное ДПФ: где χτ – скалярное произведение двух векторов. Далее находим вектор g_s(χ):

Для определения векторов U_sν берем от выражения (19) обратное ДПФ:

Введем обозначение

Матрица ${\mathbf{Q}}(\nu - \tau )$ выполняет для ПС функцию, аналогичную функции Грина однородной непрерывной среды, поэтому логично ее также называть функцией Грина ПС. При ее помощи можем записать решение задачи возбуждения ПС произвольным распределением сторонних источников:

Обратную матрицу в выражении (20) можно представить в следующем виде:

Здесь D(χ) – определитель исходной матрицы E – LG(χ), а B(χ) – матрица, элементы которой являются регулярными функциями без особенностей.

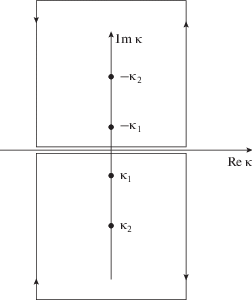
Двойной интеграл в формуле (20) сводится к однократному, если интеграл, например по переменной κ, взять по теореме Коши как сумму вычетов. Для этого нужно перейти от интеграла на интервале [–π/P, π/P] к интегралу по замкнутому контуру, показанному на рис. 3.

Нижний контур берется при ν_x – τ_x < 0, а верхний при ν_x – τ_x > 0. Интегралы по вертикальным участкам компенсируют друг друга в силу периодичности подынтегральной функции. Интегралы по горизонтальным участкам, удаленным от оси Im κ = 0 на бесконечность, равны нулю благодаря экспоненциальному множителю. Таким образом, интеграл по контуру равен исходному интегралу по действительной оси.

Расположение полюсов на рис. 3 приведено с учетом того, что при Re κ_n > 0 мнимая часть Im κ_n < 0. Такое соотношение между действительной и мнимой частями постоянной распространения волны соответствует зависимости от времени exp(iωt).

Если взять вычеты в полюсах подынтегральной функции, то получим представление функции Грина в виде разложения по собственным волнам ПС:

Верхний знак берется при ν_x – τ_x > 0, а нижний при ν_x – τ_x < 0. Выражение D' означает производную от функции по аргументу κ.

Из соотношения (21) видно, что элементы матрицы Q(ν – τ) соответствующей ФК или ЭМК, быстро убывают при увеличении разности индексов ν – τ, поскольку все постоянные распространения собственных волн чисто мнимые, а экспоненты в (21) оказываются быстро убывающими функциями.

6. КВАДРАТИЧНЫЕ СООТНОШЕНИЯ ЭЛЕКТРОДИНАМИКИ ПС

В данном разделе мы получим так называемые квадратичные соотношения для амплитудных векторов, которые являются аналогами известных соотношений электродинамики: леммы Лоренца, теоремы взаимности, теоремы об активной мощности.

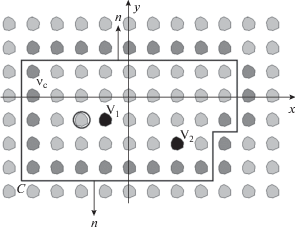
Рассмотрим однородную бесконечную ПС, в которой имеются два источника ${{{\mathbf{V}}}_{{1,\,2}}}.$ Введем в ней замкнутый контур С, как показано на рис. 4, который включает в себя внешнюю часть и окружности радиусом R_m, окружающие частицы, попавшие внутрь контура. Нормаль n внешняя на внешней части контура, на окружностях она направлена к центру. Внешняя часть контура проходит не произвольно, а по границам периодов ПС. Пусть периоды, касающиеся контура левыми и нижними границами, имеют индексы ν_c (показаны на рис. 4 темно-серым цветом). Частицы с источниками (черный цвет) находятся внутри контура и не входят в множество пограничных частиц с индексами ν_c.

Введя в контур окружности, охватывающие внутренние частицы, мы исключили из рассмотрения внутреннюю область частицы, поле в которой в рамках данного подхода неизвестно. Во внешней по отношению к частице области поле полностью определяется амплитудными векторами. Кроме того, в анализируемой области отсутствуют сторонние источники. Применим с учетом этого обстоятельства к контуру C лемму Лоренца [15]:

Наша задача состоит в том, чтобы выразить интеграл из левой части выражения (25) через амплитудные векторы, источники и связанные с ними матрицы. Представим полное, т.е. возбуждающее плюс рассеянное электрическое поле в пределах некоторого периода следующим образом:

Здесь вектор-строка f определяет зависимость поля пространственных гармоник от координат. Магнитное поле находим из (26) с помощью уравнений Максвелла:

где W₀ – волновое сопротивление свободного пространства.

Введем следующие матрицы M_x, y:

В соотношениях (28) f^T означает транспонированный вектор-строку, т.е. столбец, произведение которого на вектор-строку дает матрицу. Первое равенство в (28) берется при x = –P/2, а второе при у = –Р/2, т.е. на левой и нижней границах периода. С учетом того как была проведена внешняя часть контура C, можем записать интеграл (25) по внешней части контура C – I₁:

где i, j – орты декартовой системы координат, ${{\vec {n}}_{{\mathbf{\nu }}}}$ – вектор нормали к контуру интегрирования, зависящий от индекса суммирования. Нам необходимо различать векторы в физическом пространстве и амплитудные векторы и связанные с ними матрицы. Векторы в физическом пространстве будем дополнительно выделять курсивом.

Для дальнейшего преобразования интеграла (25) нам нужно учесть вклады от интегралов вокруг внутренних частиц. Некоторые из них содержат источники. Поэтому модифицируем представление (26), добавив к полю соответствующие слагаемые:

Интеграл I₂ по внутренним контурам имеет следующий вид:

Суммирование в (31) ведется по всем внутренним частицам. В выражение (31) входят производные от векторов ${\mathbf{f}}$ по радиальной координате ${\mathbf{f}}_{r}^{'}.$ Векторы и их производные берутся при $r = {{R}_{m}}.$ Вычисление интегралов по угловой координате следует вести с учетом ортогональности пространственных гармоник. Важно отметить, что ортогональными оказываются гармоники с индексами, одинаковыми по модулю, но противоположными по знаку. Полезным оказывается также соотношение для цилиндрических функций Z_n:

Рассмотрим более подробно преобразование интеграла I₂. Интегрирование по координате $\varphi $ приводит к сумме по индексу ${\mathbf{\nu }}$ следующих слагаемых S:

В формуле (33) временно опускаем индекс ν. В нее входят производные от цилиндрических функций по их аргументу $kr$ (для сокращения записи аргументы функций также опущены); индекс $n$ – номер пространственной гармоники.

С помощью соотношения (32) и замены индекса суммирования нетрудно показать, что

С помощью выражений (34) слагаемое $S$ приобретает компактный вид:

Запишем равенство (35) в векторной форме:

Используя формулу (36), получаем окончательное выражение для интеграла ${{I}_{2}}{\text{:}}$

Матрица q имеет простую структуру. У нее все элементы, кроме элементов на побочной диагонали равны нулю. На побочной диагонали элементы матрицы равны (–1)ⁿ. Объединяя интегралы I_{1, 2}, получаем

Равенство (38) является формулировкой леммы Лоренца для произвольной ПС в терминах амплитудных векторов.

Воспользуемся далее соотношением (2) и получим

Для ПС, состоящей из взаимных частиц, удовлетворяющих соотношению (3), имеет место следующее равенство:

Применяя его, приходим к формулировке леммы Лоренца для взаимной ПС:

Отметим, что во вторую сумму из соотношения (41) входят только слагаемые, соответствующие частицам с источниками.

Обычно теорему эквивалентности получают из леммы Лоренца, устремляя поверхность, охватывающую источники, на бесконечность [15]. При этом интеграл по ней оказывается равным нулю благодаря условиям излучения на бесконечность, которые фиксируют вид электромагнитного поля на бесконечно большом расстоянии от источников. В случае ПС воспользоваться этим приемом мы не можем, так как рядом с любой точкой наблюдения находятся частицы, являющиеся вторичными источниками поля, которое не подчиняется указанным условиям.

Обойти данную сложность и доказать теорему взаимности не трудно для случая ФК и ЭМК. Для этого достаточно воспользоваться представлением функции Грина (21), из которого следует, что амплитудные векторы в таких ПС экспоненциально убывают при удалении от источников. По этой причине первая сумма в выражении (38) при удалении внешней части контура на бесконечность будет стремиться к нулю, и получаем искомую формулировку теоремы взаимности:

Видимо, соотношение (42) сохраняется и для ПС более общего вида, в которой могут существовать распространяющиеся собственные волны. Если допустить наличие в среде тепловых потерь, пусть даже и бесконечно малых, то утверждение об экспоненциальном затухании амплитудных векторов сохраняется вместе с равенством (42).

Из теоремы взаимности (42) следует соотношение для функции Грина взаимной ПС. Для его доказательства достаточно выразить вектор U_eν через вектор U_sν при помощи соотношения (2), а затем вектор U_sν через вектор V, используя соотношение (21). В результате получаем

В заключение данного раздела рассмотрим теорему об активной мощности [16] и ее запись в терминах амплитудных векторов. Доказательство данного квадратичного соотношения во многом аналогично доказательству леммы Лоренца. Для удобства записи будем использовать вместо амплитудных векторов возбуждающих и рассеянных волн амплитудные векторы падающих и отраженных волн, которые связаны при помощи матрицы рассеяния S.

Рассмотрим тот же контур C (см. рис. 4). Для представления интеграла по внешней части контура введем матрицы K_x,y, аналогичные матрицам M_x, y (25):

С помощью соотношений (44) и теоремы об активной мощности [16] получаем

Соотношение (45) является искомой записью теоремы об активной мощности в терминах амплитудных векторов.

Из равенства (3), которое справедливо для ПС без потерь следует, что последнее слагаемое в (45) равно нулю. С учетом этого получаем формулировку теоремы об активной мощности для ПС без потерь:

В выражении (45) третье слагаемое в правой части равенства описывает процесс поглощения электромагнитной энергии в частицах ПС. Первое и второе слагаемые, пропорциональные векторам источников, описывают выделение энергии. Левая часть равенства имеет смысл, аналогичный вектору Пойнтинга. Она описывает излучение через замкнутую поверхность.

8. ДЕФЕКТЫ В ПС И ФОРМУЛИРОВКА ГРАНИЧНОЙ ЗАДАЧИ ДЛЯ ПС С ДЕФЕКТАМИ

Под дефектом регулярной ПС будем понимать любой элемент решетки с оператором рассеяния L_d отличным от L:

Полученные выше соотношения позволяют нам сформулировать граничную задачу в терминах амплитудных векторов и источников. Для этого воспользуемся следующей схемой. Пусть в бесконечной регулярной ПС существуют дефектные элементы, характеризуемые индексами τ. Оператор рассеяния L_d может зависеть от данного индекса. Допустим, что рассматриваемая среда по-прежнему регулярна, но в дефектных частицах располагаются источники V_τ. Амплитудный вектор рассеянных волн таких частиц подчиняется соотношению

Отметим, что виртуальным источникам, вводимым в частицы с целью выполнения условия (47), было дано название компенсирующих источников (КИ) [5], чтобы подчеркнуть их отличие от сторонних источников произвольного типа.

Потребуем, чтобы для вектора U_s выполнялось соотношение (47). Тогда получаем

Выразим из (47) вектор U_e через вектор U_s и подставим этот результат в формулу (49). Далее находим U_s:

Соотношение (50) можно рассматривать как граничное условие для вектора U_s на дефекте ПС.

Для окончательной постановки граничной задачи необходимо применить к источникам V_μ формулу (22) и найти множество амплитудных векторов U_sν:

Подставим в соотношение (51) выражение для U_sν (50):

Выражение (52) является искомой СЛАУ относительно векторов КИ, к которой сводится граничная задача для ПС с дефектами.

Важно отметить, что размерность СЛАУ равна (2N – 1)N_d, где 2N – 1 – размерность амплитудного вектора, а N_d – число дефектов. Таким образом, в отличие от многих методов решения граничных задач электродинамики неоднородных ПС (см., например, [17, 18]), размерность СЛАУ пропорциональна не общему числу частиц, находящихся в области, в которой ищется поле, а только числу дефектов, расположенных в той же области. Данное обстоятельство определяет высокую эффективность алгоритмов численного решения, которые могут быть построены на основе соотношения (52).

Говоря о размерности СЛАУ, нельзя обойти вниманием вопрос о выборе размерности амплитудного вектора, которая задается параметром N. Здесь нужно отметить, что в интересных для практики случаях период решетки P является достаточно малой в электрическом смысле величиной. Параметр kP редко превышает значение π. Еще меньшей величиной является kR_m, так как R_m < P. Известно [19], что число пространственных гармоник, необходимых для точного описания рассеянного цилиндром поля, пропорционально kR_m. Отсюда следует, что приемлемую точность его представления в практически интересных случаях можно обеспечить сравнительно небольшим числом гармоник.

Строго говоря, параметр N должен выбираться из условия сходимости решения СЛАУ (52):

где ε – некоторая априорно заданная малая величина.

Численные расчеты показали, что параметр N весьма редко больше двух, т.е. максимальная размерность амплитудного вектора, при которой достигается нужная точность решения, не более пяти. Данное обстоятельство подтверждает, что размерность СЛАУ (52) сравнительно невелика.

9. КАНОНИЧЕСКИЕ ЗАДАЧИ ЭЛЕКТРОДИНАМИКИ НЕОДНОРОДНЫХ ПС

Рассмотрим несколько достаточно простых структур, которые неоднократно обсуждались в литературе и исследовались преимущественно численными методами. Назовем их каноническими, так же как и соответствующие граничные задачи. Получим для них аналитические решения, т.е. выразим интересующие нас параметры через функцию Грина (21). Естественно, что сама функция Грина за исключением простейших случаев должна определяться численно.

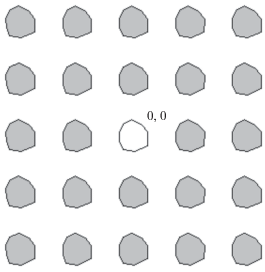
Резонатор в ФК. Структура, получаемая путем удаления из кристаллической решетки одной частицы, рассматривалась в работе [17]. Интерес к ней обусловлен тем, что если ПС демонстрирует свойства ФК, то удаление из нее одного элемента создает полость, в которой может накапливаться электромагнитная энергия. Это обусловлено тем, что излучаться за пределы полости поле не может, так как в ФК отсутствуют распространяющиеся волны.

С точки зрения развиваемого подхода удаление частицы из решетки ПС эквивалентно присутствию в ней частицы с нулевым оператором рассеяния: L_d = 0.

Если из решетки, как показано на рис. 5, удален один элемент, то СЛАУ (52) приобретает следующий вид:

Соотношение (54) представляет собой однородную СЛАУ порядка $2N - 1$ × $2N - 1.$ Равенство нулю ее определителя дает нам характеристическое уравнение, которое необходимо решать относительно частоты f:

Возможно только численное решение уравнения (55).

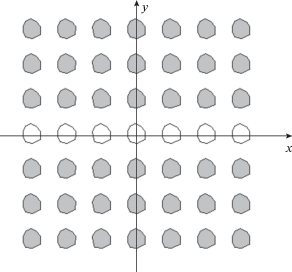
Бесконечный волновод. Пусть теперь из бесконечной среды удален ряд элементов, как показано на рис. 6. В соответствии с представленной выше методикой введем в частицы с дефектами КИ V_n, 0. Мы раскрыли векторный индекс и заменили его двумя индексами n, 0. Первый из них описывает положение частицы на оси 0x, а второй на оси 0y. Для записи СЛАУ воспользуемся представлением функции Грина (21):

Ищем решение в виде бегущей волны:

где V – собственный вектор волны, а κ₀ – ее постоянная распространения.

Подставим выражение (57) в СЛАУ (56) и воспользуемся следующим известным соотношением:

Поскольку пределы интегрирования по κ ограничены, то вклад в интеграл в (56) дает лишь ограниченное число дельта-функций из (50). Рассмотрим типичный случай, когда необходимо учесть только основное слагаемое с m = 0:

Опуская не равный нулю экспоненциальный множитель в формуле (59), получаем однородную СЛАУ, решение которой определяет собственные волны бесконечного волновода в ПС. Данная СЛАУ имеет нетривиальные решения, когда ее определитель равен нулю:

Уравнение (60) является дисперсионным уравнением волновода, из которого находятся постоянные распространения собственных волн κ₀.

Возбуждение бесконечного волновода. В заключение данного раздела рассмотрим задачу возбуждения волновода сторонним источником W_0, 0. Пусть наряду с КИ в частице с нулевыми индексами расположен сторонний источник. Тогда вместо СЛАУ (56) мы получим неоднородную СЛАУ:

Ищем решение в виде интеграла Фурье:

где g(ξ) – неизвестный вектор. Подставив выражение (62) в СЛАУ (61) и воспользовавшись еще раз соотношением (58), получим

Применим к уравнению (63) ДПФ и найдем вектор g(ξ):

Подставляя полученное решение в соотношение (62), получаем представление КИ в виде интеграла Фурье:

Под интегралом в формуле (65) стоит обратная матрица, которую можно представить по аналогии с (23) в виде отношения некоторой матрицы B(ξ) и функции D(ξ), совпадающей с левой частью дисперсионного уравнения (60):

Подставим соотношение (66) в (65) и возьмем интеграл по теореме Коши, представляя его в виде суммы вычетов. Вычеты берем в нулях функции D(ξ), которые совпадают с постоянными распространения собственных волн волновода ±κ_m:

Соотношение (67) является представлением решения задачи о возбуждении волновода в виде разложения по его собственным волнам.

ЗАКЛЮЧЕНИЕ

В работе развит новый подход к постановке и решению граничных задач электродинамики ПС, основанный на переходе от традиционного описания поля в виде векторных функций пространственных координат к его описанию при помощи амплитудных векторов.

Важно отметить, что в рамках предложенного подхода сложная задача определения поля в неоднородной ПС разделяется на ряд более простых задач. На первом этапе определяется оператор рассеяния L, который выше мы полагали известным. Для круговых цилиндров они действительно хорошо известны. Для цилиндров более общей формы можно воспользоваться численными решениями, что не нарушает общую схему метода, изложенную выше. Важно, что довольно сложная задача рассеяния на частице решается предварительно, а ее решение, представленное в требуемой форме, используется в рамках данного подхода как готовый результат, получение которого не требует новых затрат ресурсов.

Следующий этап формулировки граничной задачи, который непосредственно решен в данной работе, – это возбуждение однородной ПС сторонним источником и определение функции Грина. Знание функции Грина позволяет нам далее действовать аналогично методу интегральных уравнений в традиционной электродинамике и получить СЛАУ, являющуюся эквивалентом интегрального уравнения. Отметим, что замена интегрального уравнения СЛАУ является прямым следствием дискретного характера ПС, который в данном случае только облегчает решение граничной задачи, так как избавляет от процедуры алгебраизации интегрального уравнения, сразу сводя задачу к СЛАУ.

В работе анализируется метод перехода от нелокального уравнения распространения к его локализованной форме, который существенно облегчает построение алгоритма вычисления функции Грина, не обсуждавшегося в данной работе. Процедура локализации, связанная с построением функции a(χ), позволяет с высокой точностью осуществить аппроксимацию ДПФ функции Грина простыми тригонометрическими функциями с известным расположением нулей, что, в свою очередь, дает возможность использовать представление в виде разложения по собственным волнам ПС, которое в вычислительном смысле намного эффективнее исходной формы (21).

Важным для данного метода моментом являются квадратичные соотношения (разд. 6). С их помощью можно получить априорную информацию о свойствах функции Грина взаимной и недиссипативной ПС. В традиционной электродинамике теорема взаимности используется для доказательства ортогональности собственных волн направляющих структур. Было бы интересно рассмотреть этот вопрос применительно к волнам однородной ПС и волновода, используя соотношение (41).

Следует отметить, что перечень задач, ждущих своего решения, можно было бы еще продолжить. Это говорит о том, что представленный выше подход является не застывшей схемой, а руководством к действию, которое можно и нужно развивать далее.