Радиотехника и электроника, 2019, T. 64, № 11, стр. 1079-1087

ВВЕДЕНИЕ

Исследование особенностей распространения электромагнитных колебаний в нерегулярных волноводах приводит к решению краевых задач на системе уравнений Максвелла со сложными граничными условиями. В большинстве случаев такие задачи не имеют аналитических решений, в связи с чем возникает проблема построения приближенных решений, реализуемых, как правило, численно на ЭВМ.

Математические методы исследования нерегулярных волноводов зависят от характера нерегулярности. В тех случаях, когда нерегулярный волновод мало отличается от регулярного и удается выделить малый параметр нерегулярности, можно использовать асимптотические методы [1–3]. В частности, для волноводов с координатными нерегулярностями можно использовать метод частичных областей (МЧО) [4], для плавно-нерегулярных волноводов – метод поперечных сечений [5], а для волноводов с относительно малым пространственным периодом параметра нерегулярности – импедансный метод [6]. Строгая идеология исследования нерегулярных (в частности, гофрированных) волноводов предлагает обращаться к сложным строго обоснованным методам, например, к методу, использующему переход от нерегулярного волновода с изотропным заполнением к регулярному волноводу с анизотропным заполнением [7]. В данной работе для расчета нерегулярных волноводов предложен метод интегральных уравнений, основанный на лемме Лоренца.

1. СОСТАВЛЕНИЕ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

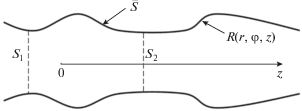
Рассмотрим пространство, ограниченное поверхностью S, описываемой непрерывной функцией $R\left( {r,\varphi ,z} \right),$ где $r,\varphi ,z$ – цилиндрические координаты (рис. 1). Соответствующая поверхности S продольная координата $z \subset \left( { - \infty ,\infty } \right).$ Внутри указанного пространства расположены источники

которые создают поля

Таким образом, имеем N неоднородных краевых задач, пространства которых объединены одной общей областью $S = \bar {S} + {{S}_{1}} + {{S}_{2}},$ где $\bar {S}$ – боковая поверхность выделенного объема, ${{S}_{{1,\,2}}}$ – торцевые поверхности (поперечные сечения волновода), ограничивающие с двух сторон объем V.

Все источники (1) находятся в конечной области V, под которой можно понимать либо продольно-нерегулярный волновод (в частности, периодически-нерегулярный), либо нерегулярный участок волноводного тракта, либо волноводный переход.

Если электромагнитные поля ${{\vec {E}}_{i}},$ ${{\vec {H}}_{i}}$ удовлетворяют граничному условию

то они соответствуют собственным волнам рассматриваемого волновода. Поля ${{\vec {E}}_{i}},$ ${{\vec {H}}_{i}},$ на которые не накладывают условие (3), удовлетворяют условию излучению на бесконечности.

Таким образом, волны ${{\vec {E}}_{i}},$ ${{\vec {H}}_{i}}$ могут быть как направляемыми волноводными волнами, так и волнами, излучаемыми в открытое пространство, т.е. волны ${{\vec {E}}_{i}},$ ${{\vec {H}}_{i}}$ могут соответствовать различным краевым задачам. При этом пространства, соответствующие различным краевым задачам, имеют одну общую область V, в которой распределены источники (1), создающие поля (2), т.е. указанные пространства объединяются областью источников.

Поля первого типа (обозначим их ${{\vec {E}}_{k}},$ ${{\vec {H}}_{k}}$), удовлетворяющие граничному условию (3), соответствуют собственным волнам нерегулярного экранированного волновода. Поля второго типа (обозначим их ${{\vec {E}}_{n}},$ ${{\vec {H}}_{n}}$), удовлетворяющие условию излучения, могут принимать на поверхности $\bar {S}$ любые конечные значения. Поля ${{\vec {E}}_{k}},$ ${{\vec {H}}_{k}}$ будем полагать искомыми решениями краевой задачи, поля ${{\vec {E}}_{n}},$ ${{\vec {H}}_{n}}$ будем рассматривать как вспомогательные. Источники, создающие поля первого типа, обозначим $\vec {j}_{k}^{{e,m}},$ источники, создающие поля второго типа, обозначим $\vec {j}_{n}^{{e,m}}.$

Для полей ${{\vec {E}}_{k}},$ ${{\vec {H}}_{k}}$ и ${{\vec {E}}_{n}},$ ${{\vec {H}}_{n}}$ в объеме V запишем лемму Лоренца в виде

где S − поверхность, ограничивающая объем V.

При ${{S}_{{1,\,2}}} \to \pm \infty $ с учетом конечности площади поперечного сечения рассматриваемого нерегулярного волновода перепишем уравнение (4):

В безграничном пространстве ($\bar {S} \to \infty $) источники $\vec {j}_{k}^{{e,m}}$ создадут поля расходящихся сферических волн, удовлетворяющих условию излучения, которые на поверхности $\bar {S} \to \infty $ обращаются в нуль. Обозначив эти поля $\vec {E}_{k}^{0},$ $\vec {H}_{k}^{0},$ перепишем уравнение (5) в виде

При этом интеграл по бесконечному объему в (6) тождественно совпадает с интегралом по конечной области источников в (5), т.е. $\int_{V\infty } { \equiv \int_V . } $

Исключая из уравнения (5) с помощью соотношения (6) токи $\vec {j}_{k}^{{e,m}},$ получим

Выбрав в качестве источников $\vec {j}_{n}^{{e,m}}$ элементарные диполи:

где ${{\vec {r}}_{{j_{n}^{{e,m}}}}}$ − координаты вспомогательных источников, и воспользовавшись свойством $\delta $-функции, из соотношения (7) получаем

В уравнении (8) $E_{k}^{0}\left( {{{{\vec {r}}}_{{j_{n}^{e}}}}} \right),$ ${{E}_{k}}\left( {{{{\vec {r}}}_{{j_{n}^{e}}}}} \right),$ $H_{k}^{0}\left( {{{{\vec {r}}}_{{j_{n}^{m}}}}} \right),$ $H_{k}^{{}}\left( {{{{\vec {r}}}_{{j_{n}^{m}}}}} \right)$ – проекции векторов на направления элементарных диполей $\vec {j}_{n}^{{e,m}}.$

Поля ${{\vec {E}}_{k}},$ ${{\vec {H}}_{k}}$ в (8), удовлетворяющие граничным условиям

(${{E}_{\parallel }}$ − касательная составляющая электрического поля; ${{H}_{ \bot }}$ − нормальная составляющая магнитного поля), можно рассматривать как поля собственных волн в волноводе с идеально проводящей экранирующей поверхностью $\bar {S}$. В решаемой задаче эти поля будут искомыми полями нерегулярного волновода. Поля $\vec {E}_{k}^{0},$ $\vec {H}_{k}^{0},$ ${{\vec {E}}_{n}}$ в (8) являются вспомогательными. Они создаются диполями $\vec {j}_{{k,n}}^{{e,m}}$ в неограниченном пространстве и стремятся к нулю при удалении от источников как поля расходящихся сферических волн.

Расположим излучатели $\vec {j}_{n}^{{e,m}}$ в сечении $z = 0,$ а $\vec {j}_{k}^{{e,m}},$ как источники, создающие поля собственных волн рассматриваемого волновода, отнесем в сечение $z \to - \infty .$ Поскольку $\vec {E}_{k}^{0},$ $\vec {H}_{k}^{0}$ – поля сферических волн, создаваемых источниками, отнесенными в бесконечность, то в сечении $z = 0,$ где расположены диполи $\vec {j}_{n}^{{e,m}},$ их вклад пренебрежимо мал в силу неравенств

Поэтому в правой части уравнения (8) эти поля можно опустить и переписать уравнение в следующем виде:

Уравнение (10) является интегральным (в общем случае интегро-дифференциальным) уравнением относительно полей ${{\vec {E}}_{k}},$ ${{\vec {H}}_{k}}.$ В тех случаях, когда вводится один вспомогательный источник (одного типа), из (10) получаем уравнения

Амплитуды вспомогательных источников, входящие в обе части уравнений (11а) и (11б), в процессе решения уравнений сокращаются, поскольку ${{\vec {E}}_{n}}\sim I_{n}^{{e,m}}.$

Поскольку согласно решению задачи о возбуждении волн экранированного волновода источники $\vec {j}_{k}^{{e,m}}$ создают в общем случае бесконечные наборы собственных волн, поля ${{\vec {E}}_{k}}$ и ${{\vec {H}}_{k}}$ следует представить в виде

для каждого фиксированного k, т.е. для каждого источника.

Уравнения (11а), (11б) можно свести к алгебраическим, если подставить в них поля в виде (12) и записать их в точках расположения вспомогательных источников, число которых выбирают в соответствии с числом членов в суммах (12). Поля ${{\vec {E}}_{\nu }},$ ${{\vec {H}}_{\nu }}$ в каждом сечении z записывают как поля волновода сравнения, соответствующего этому сечению. Суммирование в (12) проводят по полям волновода сравнения толщиной dz, удовлетворяющим в пределах этого волновода граничным условиям (9). Это обеспечивает выполнение граничных условий в целом. Непрерывность поля по продольной координате обеспечивается самими интегральными уравнениями (11а) и (11б). Каждому источнику $\vec {j}_{k}^{{e,m}}$ соответствует свой набор полей (12), определяющий k-ю волну нерегулярного волновода. Номер собственной волны нерегулярного волновода определяется порядковым номером корня трансцендентного дисперсионного уравнения.

2. НЕРЕГУЛЯРНЫЙ ЦИЛИНДРИЧЕСКИЙ ВОЛНОВОД

Рассмотрим реализацию предлагаемого метода в частном случае, когда функция R, описывающая экранирующую поверхность нерегулярного волновода, зависит только от продольной координаты. При этом подход к решению краевой задачи не потеряет своей общности и в том случае, когда $R = R\left( {\varphi ,z} \right).$

Выясним, в каком случае предлагаемая постановка задачи требует обращения лишь к одному из уравнений: (11а) или (11б), а в каком – к обоим. В том случае, когда функция $R\left( z \right)$ зависит только от одной продольной координаты, имеем дело с круглым гофрированным волноводом. Рассматривать такой волновод удобно в цилиндрической системе координат $\left( {r,\varphi ,z} \right).$ Граничные условия (9) можно записать в виде

Приведенные выше соотношения устанавливают связь между компонентами поля на поверхности $\bar {S}$ волновода, которая используется в поверхностных интегралах (11а) и (11б), обеспечивая выполнение граничных условий задач Дирихле и Неймана на поверхности $\bar {S}.$

Если волны не имеют угловой зависимости поля, у них отсутствуют азимутальные компоненты: либо ${{Е}_{\varphi }}$ (Е-волны), либо ${{Н}_{\varphi }}$ (Н-волны). При этом для выполнения граничных условий (9) достаточно выполнения одного из условий: (13а) или (13б). В этом случае граничные условия указанных краевых задач выполняются при наличии одной из продольных компонент поля, т.е. волны, распространяющиеся в волноводе, классифицируются как Е- и Н-волны.

Выбор интегрального уравнения (11а) или (11б) определяется заданием вспомогательных источников. Если задается электрический диполь, ориентированный вдоль оси z, то предполагается существование Е-волны, для которой краевая задача является полной при наличии одного условия (13а). В этом случае нужно решать интегральное уравнение (11а) с граничным условием (13а), что соответствует краевой задаче о распространении в нерегулярном волноводе Е-волны. Когда же в качестве вспомогательного источника задается магнитный диполь, ориентированный вдоль оси z, то отличной от нуля должна быть правая часть уравнения (11б), что свидетельствует о наличии у распространяющейся волны продольной компоненты магнитного поля. В этом случае полнота краевой задачи, соответствующей Н-волнам, обеспечивается уравнением (11б) и граничным условием (13б).

Таким образом, уравнение (11а) описывает волны, у которых отсутствует азимутальное электрическое поле, уравнение (11б) – волны, у которых отсутствует азимутальное магнитное поле. Полнота краевой задачи, описывающей волны, имеющие все компоненты поля, обеспечивается двумя интегральными уравнениями, (11а), (11б), решаемыми при граничных условиях (13а), (13б). В этом случае, как следует из (13а), (13б), присутствуют обе продольные компоненты поля (${{Е}_{z}}$ и ${{H}_{z}}$), через которые на поверхности $\bar {S}$ должны быть выражены азимутальные компоненты. Соотношения (13а), (13б) не дают связи между указанными компонентами на поверхности $\bar {S}.$ Эту связь следует устанавливать на основе уравнений Максвелла, из которых получаем

Из (14) видно, что присутствие азимутальных компонент поля приводит к появлению в каждом из уравнений (11а), (11б) двух неизвестных функций: ${{Е}_{z}}$ и ${{H}_{z}}.$ Таким образом волны, имеющие обе азимутальные компоненты, являются гибридными и расчет их полей требует совместного решения интегральных уравнений (11а), (11б) относительно двух неизвестных компонент ${{Е}_{z}}$ и ${{H}_{z}}.$ Через указанные компоненты с использованием соотношений (13а), (13б), (14) можно выразить остальные компоненты:

Таким образом, в общем случае, когда волны нерегулярного волновода гибридные и имеют все шесть компонент поля, необходимо решать систему двух интегральных уравнений (11а), (11б) относительно функций E_z и H_z. С учетом соотношений (13а), (13б)–(15) уравнения (11а), (11б) следует рассматривать как интегро-дифференциальные. При этом в подынтегральных выражениях указанные функции определяются как

где $\left( {r,\;\varphi ,\;z} \right)$ – цилиндрические координаты точек на экранирующей поверхности $\bar {S};$ $\left( {r{\text{'}},\;\varphi {\text{'}},\;z{\text{'}}} \right)$ – цилиндрические координаты вспомогательных источников. Если последние размещены в сечении $z = 0,$ то в (16) $z{\text{'}} = 0.$ Тогда в правых частях уравнений (11а), (11б) имеем

где ${{E}_{k}}$ и ${{H}_{k}}$ – проекции полей на направления соответствующих диполей.

Продольные компоненты полей волн, распространяющихся в нерегулярном волноводе, представим в виде

где $\alpha _{\nu }^{e}\left( z \right)$ и $\alpha _{\nu }^{m}\left( z \right)$ – корни уравнений:

соответствующих задачам Дирихле и Неймана, решаемым для каждого круга радиусом $R\left( z \right)$ в поперечного сечении $z = {\text{const}}$. Значения $\alpha _{\nu }^{{e,m}}\left( z \right)$ находятся из уравнений (19а), (19б) в том случае, когда радиальная зависимость поля в (18) описывается цилиндрическими функциями, т.е. когда каждому сечению $z = {\text{const}}$ соответствует цилиндрический волновод сравнения (ВС), радиус которого $R\left( z \right).$ В общем случае радиальная зависимость в (18) определяется краевыми задачами Дирихле (19а) и Неймана (19б) для ВС, соответствующими геометрии экранирующей поверхности волновода.

Суммирование в (18) производится по корням уравнений (19а), (19б). Азимутальная зависимость поля в рассматриваемом случае считается фиксированной. Каждой волне соответствует свое значение k, и она состоит из бесконечного набора волн фиксированной поляризации с индексами $\nu $.

Компоненты поля, представляемые на поверхности волновода выражениями (13а), (13б), (15), (18), далее подставляют в интегральные уравнения (11а), (11б). Эти уравнения, записанные в точках, где расположены вспомогательные источники (в узлах коллокаций), образуют систему линейных однородных алгебраических уравнений относительно коэффициентов $A_{\nu }^{{\left( k \right)}},$ $В_{\nu }^{{\left( k \right)}}.$ Из условия нетривиальности ее решений получаем трансцендентное дисперсионное уравнение волн $H{{E}_{{kq}}}$ ($E{{H}_{{kq}}}$), где q – порядковый номер корня указанного дисперсионного уравнения.

Возможен другой вариант сведения интегральных уравнений к алгебраическим, если для сечения, в котором расположены вспомогательные источники, можно сформулировать краевую задачу Штурма–Лиувилля. В этом случае координаты точек указанного сечения можно отождествить с точками, по которым непрерывно распределены вспомогательные источники. Применяя условия ортогональности собственных функций краевой задачи для указанного поперечного сечения, получим систему линейных однородных алгебраических уравнений относительно неизвестных коэффициентов разложений полей волн нерегулярного волновода и поля в сечении, в котором расположены вспомогательные источники. Условие нетривиальности решений этой системы также приводит к дисперсионному уравнению волн рассматриваемого нерегулярного волновода.

3. КРУГЛЫЙ ГОФРИРОВАННЫЙ ВОЛНОВОД

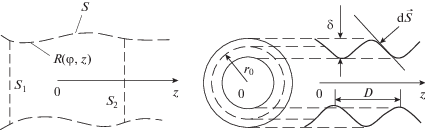
В качестве примера реализации предлагаемого метода рассмотрим расчет дисперсии симметричной волны магнитного типа в круглом гофрированном волноводе (рис. 2), уравнение поверхности которого имеет вид

где $\Delta = {\delta \mathord{\left/ {\vphantom {\delta {2{{r}_{0}}}}} \right. \kern-0em} {2{{r}_{0}}}},$ $\delta $ – глубина гофра, r₀ – средний (по глубине гофра) радиус волновода.

В качестве вспомогательного источника возьмем продольный магнитный диполь. Симметричные Н-волны будут описываться уравнением (11б), решение которого представим в виде

где ${{\alpha }_{m}} = \sqrt {\varepsilon \mu {{\omega }^{2}} - \beta _{m}^{2}} ,$ ${{\beta }_{m}} = {{\beta }_{0}} + \frac{{2\pi m}}{D},$ $D$ – период гофра, $m = 0\,;\;1\,;\;2...,$ ${{J}_{0}}\left( {{{\alpha }_{m}}r} \right)$ – функция Бесселя нулевого порядка.

Ввиду периодичности направляющей структуры поле (20) представляется набором пространственных гармоник. В m-м приближении имеем 2m + 1 неизвестных амплитудных коэффициентов. При $m \to \infty $ решение рассматриваемой задачи становится инвариантным по отношению к размещению вспомогательных источников. Перемещая последние в сечении $z = 0$ (используя коллокацию по вспомогательным источникам), запишем уравнение (11б) в (m + 1) точках $\left( {r,\varphi } \right)$. В результате получаем систему (2m + 1) линейных однородных алгебраических уравнений относительно коэффициентов ${{А}_{m}}.$ Запись условия нетривиальности её решений дает дисперсионное уравнение симметричных Н-волн, решаемое в плоскости $\left( {\omega ,{{\beta }_{0}}} \right).$

Решение уравнения (11б) в виде (20) соответствует симметричным волнам Н_0q круглого периодически нерегулярного волновода. Для волноводов с другими поперечными сечениями общий вид записи решения сохранится. Изменятся лишь базисные функции поперечных координат. Так, в эллиптическом волноводе [4, 8] это будут функции Матье, в прямоугольном – тригонометрические функции. В том случае, когда поперечное сечение волновода не “вписывается” ни в одну из ортогональных систем координат (т.е. границы сечения не совпадают с координатными линиями), определить базис, по которому нужно проводить разложение искомого поля, значительно сложнее. Для этого предварительно необходимо решить, например, с помощью МЧО задачу о распространении поля в соответствующем, в общем случае, зависящем от продольной координаты, волноводе сравнения.

Подставив решение (20) в уравнение (11б), получаем

где α_m – поперечное волновое число волновода сравнения, соответствующее m-й пространственной гармонике;

${{k}_{0}} = \omega \sqrt {\varepsilon \mu } ;$ $r$ – радиальная координата вспомогательного источника, расположенного в плоскости $z = 0$ цилиндрической системы координат $\left( {r,\varphi ,z} \right),$ связанной с волноводом; $\tilde {k} = {{k}_{0}}{{r}_{0}}.$

В нулевом приближении $\left( {m = 0} \right),$ располагая вспомогательный источник вдоль оси волновода, после разделения в (21) действительной и мнимой частей получаем систему двух уравнений:

где

Выразив поперечное волновое число через продольное, решаем систему уравнений (22) при заданной частоте в плоскости $\left( {\alpha ,\beta } \right).$

При $\delta \to 0,$ т.е. при переходе к гладкому волноводу, систему (22) можно преобразовать к уравнению

Так как в гладком круглом волноводе волновые числа связаны соотношением ${{\alpha }^{2}} + {{\beta }^{2}} = k_{0}^{2},$ то уравнение (23) – обычное уравнение для определения поперечных волновых чисел $\alpha $ симметричных Н-волн: $J_{0}^{'}\left( {\alpha {{r}_{0}}} \right) = 0.$

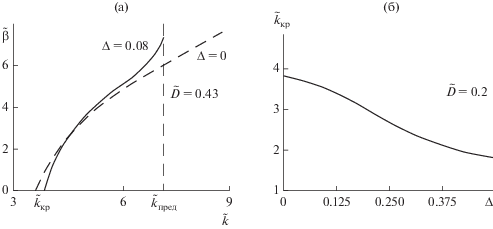
На рис. 3а приведены результаты расчета дисперсии ($\tilde {\beta }$ = β₀), полученные из решения системы (22), сплошная кривая соответствует гофрированному волноводу с $\Delta = 0.08,$ а штриховая − гладкому волноводу ($\Delta = 0$).

Полоса пропускания периодической замедляющей системы ограничена значением продольного волноводного числа

где $\tilde {D} = {D \mathord{\left/ {\vphantom {D {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}},$ r₀ – средний радиус гофра (см. рис. 2). Например, при периоде гофра $\tilde {D} = 0.43$ получаем, что ${{\tilde {k}}_{{{\text{пред}}}}} = 7.3.$

Расчеты дисперсионных характеристик на основе решения системы (22) дали значение $\tilde {k}_{{{\text{пред}}}}^{{}}$ несколько большее, чем значение, полученное с использованием выражения (24). Это объясняется тем, что расчеты проводили без учета пространственных гармоник, а соотношение (24) строго справедливо лишь для диафрагмированного волновода с периодом $\tilde {D}$.

На рис. 3б приведены результаты расчета на основе (22) критических частот (${{\tilde {k}}_{{{\text{кр}}}}} = \tilde {k}$ при $\tilde {\beta } = 0$) волны Н₀₁ в зависимости от глубины гофра для случая $\tilde {D}$ = 0.2.

Сравнение с [7] показывает, что при $\Delta = 0.08$ и $\tilde {D} = 0.43$ погрешность в вычислении критических частот по отношению к результатам этой работы, полученным в 7-м приближении, составляет ~0.1%; по отношению к результатам, полученным в 13-м приближении, ~0.8%. Результаты работы [7] в силу их теоретически обоснованной точности можно рассматривать как эталонные.

Таким образом, интегральное уравнение (11б) относительно поля в продольно-нерегулярном волноводе с использованием граничных условий (13) на экранирующей поверхности, описываемой аналитической функцией, дает хорошие результаты уже при достаточно низких приближениях. Инвариантность решения задачи по отношению к месту расположения вспомогательных источников, имеющая место в высоких приближениях, делает метод теоретически обоснованным.

4. РАСЧЕТ СТУПЕНЧАТОЙ НЕРЕГУЛЯРНОСТИ В КРУГЛОМ ВОЛНОВОДЕ

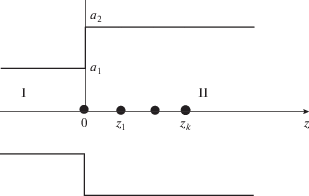
Предлагаемый метод может быть использован для расчета характеристик передачи нерегулярных участков волноводных трактов. Рассмотрим процедуру расчета характеристик передачи скачкообразной нерегулярности в круглом экранированном волноводе. Рассматриваемая структура изображена на рис. 4. На стык двух волноводов из $z \to - \infty $ со стороны волновода I падает волна Н₀₁ единичной амплитуды. В результате дифракции этой волны на стыке в волноводе I образуется бесконечный набор симметричных отраженных волн магнитного типа с коэффициентами отражения ${{R}_{m}},$ в волноводе II – бесконечный набор прошедших волн того же типа с коэффициентами прохождения ${{B}_{r}}.$

Продольные компоненты векторов Герца, через которые выражаются поля в регулярных волноводах I и II, запишем в виде

где ${{\alpha }_{m}}$ – m-й корень уравнения $J_{0}^{'}\left( {{{\alpha }_{m}}{{r}_{1}}} \right) = 0,$ ${{\alpha }_{n}}$ − n-й корень уравнения $J_{0}^{'}\left( {{{\alpha }_{n}}{{r}_{2}}} \right) = 0;$ ${{r}_{1}} = {{a}_{1}};$ ${{r}_{2}} = {{a}_{2}}.$

Выражая компоненты поля через векторы Герца (25) и подставляя их в уравнение (11б), получаем интегральное уравнение

которое связывает искомые поля ${{\vec {H}}_{{I,II}}}$ в стыкуемых волноводах с полями $\vec {E},$ создаваемыми вспомогательными магнитными источниками $\vec {j}_{2}^{m},$ имеющими амплитуду $I_{2}^{m}.$ Интегрирование в (26) проводят по всей поверхности S исследуемой структуры. Если в качестве вспомогательных источников выбрать элементарные магнитные диполи, расположенные вдоль оси волноводов в точках с координатами ${{z}_{k}},$ то создаваемое ими поле можно записать в виде [6] где ${{k}_{0}} = {{\omega }_{0}}\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} ,$ $\sin \Theta = {r \mathord{\left/ {\vphantom {r {{{{\left[ {{{r}^{2}} + {{{\left( {z - {{z}_{k}}} \right)}}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left[ {{{r}^{2}} + {{{\left( {z - {{z}_{k}}} \right)}}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$

После интегрирования (26), где в качестве ${{\vec {H}}_{{I,II}}}$ были подставлены поля, выражаемые через векторы Герца (25), получим систему из k алгебраических уравнений (k – число вспомогательных источников). При этом часть интегралов в левой части (26) берется аналитически; к остальным применяется численное интегрирование. В случае конечного числа вспомогательных источников их координаты ${{z}_{k}}$ выбирают из условия наилучшего выполнения закона сохранения энергии. При одномодовом режиме рассеяния на ступеньке, который имеет место при выполнении неравенства ${\text{3}}{\text{.832}}\left( {{{a{}_{{\text{1}}}} \mathord{\left/ {\vphantom {{a{}_{{\text{1}}}} {{{a}_{2}}}}} \right. \kern-0em} {{{a}_{2}}}}} \right) < {{\left( {2\pi {{a}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {2\pi {{a}_{2}}} \right)} \lambda }} \right. \kern-0em} \lambda } < 7.016,$ закон сохранения энергии записывается в виде

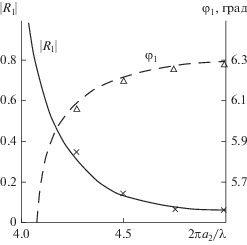
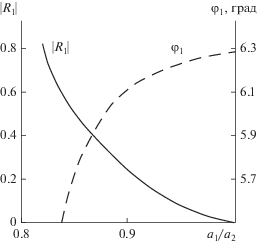
где N – коэффициент, учитывающий различие площадей поперечных сечений стыкуемых волноводов. На рис. 5, 6 приведены результаты расчета модуля $\left| {{{R}_{1}}} \right|$ и фазы ${{\varphi }_{1}}$ коэффициента отражения волны ${{H}_{{01}}}$ от стыка для случая, когда в стыкуемых волноводах учитывается по две волны. На рис. 5 приведены зависимости $\left| {{{R}_{1}}} \right|$ и ${{\varphi }_{1}}$ от частоты при ${{a{}_{{\text{1}}}} \mathord{\left/ {\vphantom {{a{}_{{\text{1}}}} {{{a}_{2}}}}} \right. \kern-0em} {{{a}_{2}}}} = 0.95,$ на рис. 6 – от высоты ступеньки ${{a{}_{{\text{1}}}} \mathord{\left/ {\vphantom {{a{}_{{\text{1}}}} {{{a}_{2}}}}} \right. \kern-0em} {{{a}_{2}}}}$ при ${{\left( {2\pi {{a}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {2\pi {{a}_{2}}} \right)} \lambda }} \right. \kern-0em} \lambda } = 5.0.$ Крестиками на рисунках показаны значения $\left| {{{R}_{1}}} \right|$, а треугольниками − значения ${{\varphi }_{1}},$ взятые из работы [9]. Как видно из рисунков, расхождения между этими значениями и результатами, полученными в данной работе, незначительны и не превышают несколько процентов. При этом следует отметить, что результаты [9] достаточно точные, поскольку задачу там решали на основе метода полуобращений в высоких приближениях, когда в стыкуемых волноводах учитывали большое число волн − более десяти в каждом волноводе.

Таким образом, метод интегральных уравнений, основанный на лемме Лоренца, позволяет производить расчет характеристик ступенчатых нерегулярностей с высокой точностью уже в низших приближениях. При этом точки, где располагаются вспомогательные источники, отождествляются с узлами коллокаций интегральных уравнений (11а), (11б).

Поскольку запись интегральных уравнений (11а), (11б) в узлах коллокаций является строгой, точность результатов зависит от числа учитываемых волн высших типов и сходимости разложений (22), которая определяется величиной скачка ${{a{}_{{\text{1}}}} \mathord{\left/ {\vphantom {{a{}_{{\text{1}}}} {{{a}_{2}}}}} \right. \kern-0em} {{{a}_{2}}}}$ параметров волноводов.

Рассмотренная задача, разумеется, является тестовой и может быть решена более строго [9], в частности, и в рамках предлагаемого метода. Располагая вспомогательные источники непрерывно по радиальной координате в пределах поперечного сечения $z = 0,$ переход от интегральных уравнений к алгебраическим можно осуществить на основе процедуры Галеркина, поскольку стыкуемые волноводы имеют координатные границы и для них известны строгие решения задач Дирихле и Неймана. В общем случае (при произвольной поверхности нерегулярного участка) для такого перехода может быть использована общая теория Фредгольма [10]. Первоначально идеология предлагаемого метода была сформулирована в работе [11]. Метод хорошо зарекомендовал себя при расчете характеристик передачи нерегулярных участков волноводных трактов [12–17]. В предлагаемом варианте он обобщен на произвольное число источников в интегральной записи леммы Лоренца.

ЗАКЛЮЧЕНИЕ

На основе обобщенной записи леммы Лоренца предложена формулировка метода интегральных уравнений для расчета нерегулярных экранированных волноводов. Обобщение леммы Лоренца заключается в объединении в ее записи нескольких краевых задач: для волн, направляемых экранированной структурой, и волн, создаваемых вспомогательными источниками в открытом пространстве, удовлетворяющих условию излучения. Метод является универсальным, пригодным для расчета как неограниченных продольно-нерегулярных экранированных направляющих структур, так и отдельных нерегулярных (плавных и скачкообразных) участков волноводного тракта, в том числе и неоднородно заполненных. Сведение интегральных уравнений к алгебраическим осуществлено на основе метода коллокаций, который в данном случае является физически обоснованным, поскольку в качестве узлов коллокаций выбраны точки, в которых расположены вспомогательные источники.

Для демонстрации практического использования предлагаемого метода решены две тестовые задачи: о расчете круглого гофрированного волновода и стыка двух регулярных круглых волноводов с различными размерами поперечных сечений.