1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 64, № 11, 2019

Радиотехника и электроника, 2019, T. 64, № 11, стр. 1122-1125

Осевые и винтовые метачастицы импульсных волновых полей

В. В. Шевченко *

Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

* E-mail: sto@cplire.ru

Поступила в редакцию 25.03.2019
После доработки 17.04.2019
Принята к публикации 19.04.2019

Полный текст (PDF)

Аннотация

Представлены свойства импульсных волновых полей осевых и винтовых метачастиц. Рассмотрен пример излучения таких метачастиц апертурным источником. Приведен расчет ширины поля и плотности энергии основной (нулевой) метачастицы в дальней зоне от излучающей апертуры.

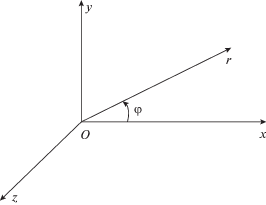
1. В работе [1] были введены понятия метачастиц импульсных волновых полей (электромагнитного, акустического), направленно излученных апертурными источниками (антеннами, лазерами, акустическими мембранами) и распространяющихся в свободном пространстве и в однородных изотропных средах. Структурные функции полей метачастиц представлены в цилиндрических координатах r, φ, z (рис. 1). В работе [2] рассмотрен пример излучения метачастиц с осесимметричными, не зависящими от угла φ структурными функциями полей при излучении апертурным источником осесимметричного волнового импульса в направлении оси z.

Рис. 1.

Применяемая система координат.

В данной статье рассмотрены свойства и излучение волнового импульса с неосесимметричным полем, представленного здесь несколько иначе, чем в [1]: в виде набора осевых и винтовых метачастиц. При этом используются указанные упрощенные названия метачастиц: с осесимметричными полями – осевые метачастицы, а с неосесимметричными полями – винтовые метачастицы. Случай набора только осевых метачастиц, как сказано выше, рассмотрен в статье [2].

2. Функции полей осевых и винтовых метачастиц представим в виде

(1)
$\begin{gathered} {{f}_{{lmn}}}\left( {r,\varphi ,z,t} \right) = {{{\bar {C}}}_{l}}{{{\bar {U}}}_{l}}\left( {z,t} \right){{{\bar {C}}}_{{mn}}}\bar {V}_{n}^{{\left( m \right)}}\left( {r,\varphi ,z} \right) \times \\ \times \,\,{\text{exp}}\left[ { - i\left( {kz - \omega t} \right)} \right], \\ \end{gathered} $
где l = 0, 1, 2, …, m = 0 у осевых метачастиц, m = 1, 2, 3… у винтовых метачастиц, n = 0, 1, 2, …, ${{\bar {C}}_{l}}$, $~{{\bar {C}}_{{mn}}}$ – амплитудные константы, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda } = {\omega \mathord{\left/ {\vphantom {\omega {v}}} \right. \kern-0em} {v}},$ λ – длина волны, ω – круговая частота поля, v – скорость распространения импульсных волновых метачастиц, v = с – для электромагнитных метачастиц в свободном пространстве, t – время.

Структурную функцию полей метачастиц $~{{\overline {~U} }_{l}}\left( {z,t} \right)$ представим с учетом внесенной в [2] поправки в виде

(2)
${{\bar {U}}_{l}}\left( {z,t} \right) = {{U}_{l}}\left( \zeta \right) = N_{l}^{{ - 1}}{{H}_{l}}\left( \zeta \right){\text{exp}}\left( {{{ - {{\zeta }^{2}}} \mathord{\left/ {\vphantom {{ - {{\zeta }^{2}}} 2}} \right. \kern-0em} 2}} \right),$
где ${{N}_{l}} = {{\left( {{{2}^{l}}l!\sqrt \pi } \right)}^{{1{\text{/}}2}}},$ ${{H}_{l}}\left( \zeta \right)$ – полином Эрмита [3‒10],
(3)
$\begin{gathered} \zeta = {{\left( {z - \nu t} \right)} \mathord{\left/ {\vphantom {{\left( {z - \nu t} \right)} L}} \right. \kern-0em} L} = {{\delta }_{L}}\left( {kz - \omega t} \right), \\ {{\delta }_{L}} = \frac{1}{{kL}} = \frac{1}{\pi }\frac{\lambda }{{2L}},\,\,\,\,~\delta _{L}^{2} \ll 1\,\,\,\,{\text{при}}\,\,\,\,\frac{\lambda }{{2L}} \leqslant 1, \\ \end{gathered} $
L – эффективная полудлина импульса поля метачастицы вдоль оси z, ω – средняя (несущая) частота узкой, при условии (3), полосы частот импульса метачастицы [2].

Аналогично представим функцию $\bar {V}_{n}^{{\left( m \right)}}\left( {r,\varphi ,z} \right)~$ в виде

(4)
$\begin{gathered} \bar {V}_{n}^{{\left( m \right)}}\left( {r,\varphi ,z} \right) = V_{n}^{{\left( m \right)}}\left( {\rho ,\varphi ,z} \right) = \\ = {{\left( {{{{\bar {N}}}_{{mn}}}} \right)}^{{ - 1}}}W_{n}^{{\left( m \right)}}\left( {\rho ,z} \right){\text{exp}}\left( { - im\varphi } \right), \\ \end{gathered} $
где ${{\bar {N}}_{{mn}}} = \sqrt {2\pi } \cos \sigma {{N}_{{mn}}},$ ${{N}_{{mn}}} = {{\left[ {{{\left( {m + n} \right)!} \mathord{\left/ {\vphantom {{\left( {m + n} \right)!} {n!}}} \right. \kern-0em} {n!}}} \right]}^{{1{\text{/}}2}}},$
(5)
$\begin{gathered} W_{n}^{{\left( m \right)}}\left( {\rho ,z} \right) = \cos \sigma K_{n}^{{\left( m \right)}}\left( \rho \right) \times \\ \times \,\,{\text{exp}}\left\{ {{{ - {{\rho }^{2}}} \mathord{\left/ {\vphantom {{ - {{\rho }^{2}}} 2}} \right. \kern-0em} 2} + i\left[ {\left( {1 + m + 2n} \right)\sigma - {{{{u}_{z}}{{\rho }^{2}}} \mathord{\left/ {\vphantom {{{{u}_{z}}{{\rho }^{2}}} 2}} \right. \kern-0em} 2}} \right]} \right\}~, \\ \end{gathered} $
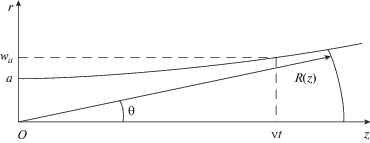
$K_{n}^{{\left( m \right)}}\left( \rho \right) = {{\rho }^{m}}L_{n}^{{\left( m \right)}}\left( {{{\rho }^{2}}} \right),$ $L_{n}^{{\left( m \right)}}\left( {{{\rho }^{2}}} \right)~$ – обобщенный полином Лагерра [3–10], $\rho = {r \mathord{\left/ {\vphantom {r {{{w}_{a}}}}} \right. \kern-0em} {{{w}_{a}}}},$ $~{{w}_{a}} = {a \mathord{\left/ {\vphantom {a {{\text{cos}}\sigma }}} \right. \kern-0em} {{\text{cos}}\sigma }},$ $~\sigma = {\text{arctg}}{{u}_{z}},$ $~{\text{cos}}\sigma = {{\left( {1 + u_{z}^{2}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ ${{u}_{z}} = {{{{\delta }_{a}}z} \mathord{\left/ {\vphantom {{{{\delta }_{a}}z} a}} \right. \kern-0em} a} = \delta _{a}^{2}kz,$
(6)
${{\delta }_{a}} = \frac{1}{{ka}} = \frac{1}{\pi }\frac{\lambda }{{2a}},\,\,\,\,~~~\delta _{a}^{2} \ll 1\,\,\,\,{\text{при}}\,\,\,\,\frac{\lambda }{{2a}} \leqslant 1,$
a – радиус круглой излучающей апертуры (рис. 2).

Рис. 2.

Функция изменения эффективной полуширины (радиуса) поля метачастицы ${{w}_{a}}\left( z \right)~$ при распространении метачастицы вдоль оси z [1], где предельный угол $\theta \leqslant {\text{tg}}\theta $ = $\mathop {\lim }\limits_{z \to \infty } ({{{{w}_{a}}} \mathord{\left/ {\vphantom {{{{w}_{a}}} z}} \right. \kern-0em} z})$ = ${{\delta }_{a}} = {1 \mathord{\left/ {\vphantom {1 {\left( {ka} \right)}}} \right. \kern-0em} {\left( {ka} \right)}}.$

Для структурных функций (2), (4) выполняются условия ортонормировки [1, 2, 5]:

(7)
$\int\limits_{ - \infty }^\infty {{{U}_{l}}\left( \zeta \right){{U}_{{l{\text{'}}}}}\left( \zeta \right)d\zeta } = \left\{ {\begin{array}{*{20}{c}} {1\,\,\,\,~{\text{при}}~\,\,\,\,l = l{\text{'}},} \\ {~0~\,\,\,\,{\text{при}}\,\,\,\,l \ne l{\text{'}},} \end{array}} \right.~~~~~$
(8)
$\begin{gathered} \int\limits_0^\infty {\left[ {\int\limits_{ - {\pi }}^{\pi } {V_{n}^{{\left( m \right)}}\left( {\rho ,\varphi ,z} \right)V_{{n{\text{'}}}}^{{\left( {m{\text{'}}} \right)*}}\left( {\rho ,\varphi ,z} \right)d\varphi } } \right]2\rho d\rho } = \\ = \left\{ {\begin{array}{*{20}{l}} {1~\,\,\,\,{\text{при}}\,\,\,\,~m{\text{'}} = m,\,\,n{\text{'}} = n,} \\ {0~\,\,\,\,{\text{при}}\,\,\,\,~m{\text{'}} \ne m,} \\ {0~\,\,\,\,{\text{при}}\,\,\,\,n' \ne n.} \end{array}} \right. \\ \end{gathered} $

Последнее выражение следует из того, что при этом выполняются соотношения [6–10]:

(9)
$\begin{gathered} \int\limits_{ - {\pi }}^{\pi } {\exp \left( { - im\varphi } \right)\left[ {{\text{exp}}\left( { - im{\text{'}}\varphi } \right)} \right]{\text{*}}d\varphi } = \\ = \frac{{2\sin \left( {m - m{\text{'}}} \right)\pi }}{{m - m{\text{'}}}} = \left\{ {\begin{array}{*{20}{c}} {2\pi ~\,\,\,\,{\text{при}}\,\,\,\,m{\text{'}} = m,} \\ {0\,\,\,\,{\text{при}}\,\,\,\,m{\text{'}} \ne m,} \end{array}} \right.~ \\ \end{gathered} $
(10)
$\begin{gathered} \int\limits_0^\infty {W_{n}^{{\left( m \right)}}\left( {\rho ,z} \right)W_{{n{\text{'}}}}^{{\left( m \right)*}}\left( {\rho ,z} \right)2\rho d\rho } = \\ = \left\{ {\begin{array}{*{20}{l}} {{{{\cos }}^{2}}\sigma ~N_{{mn}}^{2}\,\,\,\,{\text{при}}~\,\,\,\,n{\text{'}} = n,} \\ {~0\,\,\,\,{\text{при}}\,\,\,\,n{\text{'}} \ne n.} \end{array}} \right. \\ \end{gathered} $

3. Условия ортонормировки (7), (8) дают возможность стандартным способом [1–5] вычислять амплитудные коэффициенты ${{\bar {C}}_{l}},~\,{{\bar {C}}_{{mn}}}~$ при разложении в ряд по метачастицам поле волнового импульса, излученного источником, апертура которого расположена в плоскости z = 0 (см. рис. 2). Представим функцию поля такого импульса на апертуре в виде

(11)
$f\left( {r,\varphi ,~0,t} \right) = M\left( {\zeta ,\rho } \right)U\left( \zeta \right)V\left( {\rho ,\varphi } \right){\text{exp}}\left( {i\omega t} \right),$
где $\zeta = {{ - \nu t} \mathord{\left/ {\vphantom {{ - \nu t} L}} \right. \kern-0em} L},$ $~\rho = {r \mathord{\left/ {\vphantom {r a}} \right. \kern-0em} a}$ при z = 0,

(12)
$M\left( {\zeta ,\rho } \right) = \left\{ {\begin{array}{*{20}{l}} {1~\,\,\,\,{\text{при}}\,\,\,\, - 1 \leqslant {\zeta } \leqslant 1,\,\,\rho \leqslant 1,} \\ {0\,\,\,\,{\text{при}}\,\,\,\,\zeta < - 1,\,\,~1 < \zeta ,\,\,1 < \rho ,} \end{array}} \right.$
(13)
$\begin{gathered} U\left( \zeta \right) = \mathop \sum \limits_{l = 0}^\infty {{{\bar {C}}}_{l}}{{U}_{l}}\left( \zeta \right), \\ V\left( {\rho ,\varphi } \right) = \sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{{{\bar {C}}}_{{mn}}}V_{n}^{{\left( m \right)}}\left( {\rho ,\varphi ,0} \right)} } . \\ \end{gathered} $

Тогда коэффициенты разложения поля излученного импульса равны

(14)
$\begin{gathered} {{{\bar {C}}}_{l}} = \int\limits_{ - 1}^1 {U\left( \zeta \right){{U}_{l}}\left( \zeta \right)d\zeta } , \\ {{{\bar {C}}}_{{mn}}} = \int\limits_0^1 {\left[ {\int\limits_{ - {\pi }}^{\pi } {V\left( {\rho ,\varphi } \right)V_{n}^{{\left( m \right)*}}\left( {\rho ,\varphi ,0} \right)d\varphi } } \right]} 2\rho d\rho , \\ \end{gathered} $
причем не только для разложения поля импульса на апертуре, т.е. в плоскости z = 0, но и в пространстве при z > 0:
(15)
$\begin{gathered} \bar {U}\left( {z,t} \right) = U\left( \zeta \right) = \sum\limits_{l = 0}^\infty {{{{\bar {C}}}_{l}}{{U}_{l}}\left( \zeta \right)} , \\ \bar {V}\left( {r,\varphi ,z} \right) = V\left( {\rho ,\varphi ,z} \right) = \sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{{{\bar {C}}}_{{mn}}}V_{n}^{{\left( m \right)}}\left( {\rho ,\varphi ,z} \right)} } , \\ \end{gathered} $
где $\zeta = {{\left( {z - \nu t} \right)} \mathord{\left/ {\vphantom {{\left( {z - \nu t} \right)} L}} \right. \kern-0em} L},$ $\rho = ({r \mathord{\left/ {\vphantom {r a}} \right. \kern-0em} a})$cosσ.

В результате функцию поля импульса, излученного апертурным источником, можно представить в виде суммы функций полей метачастиц:

(16)
$\begin{gathered} f\left( {r,\varphi ,~z,t} \right) = \sum\limits_{l = 0}^\infty {\sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{{f}_{{lmn}}}\left( {r,\varphi ,~z,t} \right)} } } = \\ = \sum\limits_{l = 0}^\infty {{{{\bar {C}}}_{l}}{{U}_{l}}\left( \zeta \right)} \sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{{{\bar {C}}}_{{mn}}}V_{n}^{{\left( m \right)}}\left( {\rho ,\varphi ,z} \right)} } \times \\ \times \,\,{\text{exp}}\left[ { - i\left( {kz - \omega t} \right)} \right], \\ \end{gathered} $
где амплитудные коэффициенты ${{\bar {C}}_{l}},$ ${{\bar {C}}_{{mn}}}$ вычисляются по формулам (14).

При этом относительная (безразмерная [1, 2]) энергия, переносимая излученным импульсом, равна сумме долей энергии, переносимых метачастицами:

(17)
${\bar {Э}} = \sum\limits_{l = 0}^\infty {\sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{{{{\bar {Э}}}}_{{lmn}}}} } } ,$
где соответствующие доли энергии метачастиц равны

(18)
${{{\bar {Э}}}_{{lmn}}} = \bar {C}_{l}^{2}\bar {C}_{{mn}}^{2}.$

4. Рассмотрим конкретный пример. Пусть функции $U\left( \zeta \right),$ $~V\left( {\rho ,\varphi } \right)$ в выражении (11) для поля на апертуре источника, т.е. при z = 0, имеют вид

(19)
$\begin{gathered} U\left( \zeta \right) = e\left( {{{\sqrt[4]{\pi }} \mathord{\left/ {\vphantom {{\sqrt[4]{\pi }} 2}} \right. \kern-0em} 2}} \right)\exp \left( {{{ - {{\zeta }^{2}}} \mathord{\left/ {\vphantom {{ - {{\zeta }^{2}}} 2}} \right. \kern-0em} 2}} \right), \\ V\left( {\rho ,\varphi } \right) = \left( {e\sqrt {2{\text{/}}\pi } } \right){\text{exp}}\left[ {{{ - \left( {{{\rho }^{2}} + i\varphi } \right)} \mathord{\left/ {\vphantom {{ - \left( {{{\rho }^{2}} + i\varphi } \right)} 2}} \right. \kern-0em} 2}} \right]. \\ \end{gathered} $

Тогда для четных и нечетных l: l = $~2\upsilon ,$ l = $2\upsilon - 1,$ получим, как в работе [2]:

(20)
${{\bar {C}}_{{\upsilon = 0}}} = 2,\,\,\,\,{{\bar {C}}_{{{\text{2}}\upsilon }}} = \mp \frac{1}{{\sqrt {\left( {2\upsilon } \right)!} }},\,\,\,\,{{\bar {C}}_{{2\upsilon - 1}}} = 0,$
где $\upsilon = 1,~\,2,~\,3\, \ldots ,$ а на основании [6–10] и изложенного выше получим
(21)
${{\bar {C}}_{{mn}}} = {{C}_{m}}{{C}_{{mn}}},$
где m = 0, 1, 2, …, n = 0, 1, 2, …,
(22)
$\begin{gathered} {{C}_{m}} = \frac{1}{{2\pi }}\int\limits_{ - {\pi }}^{\pi } {\exp \left[ {i\left( {{{m - 1} \mathord{\left/ {\vphantom {{m - 1} 2}} \right. \kern-0em} 2}} \right)\varphi } \right]d\varphi } = \\ = \frac{{2\sin \left[ {{{\left( {2m - 1} \right)\pi } \mathord{\left/ {\vphantom {{\left( {2m - 1} \right)\pi } 2}} \right. \kern-0em} 2}} \right]}}{{\pi \left( {2m - 1} \right)}}~\,\, = \,\,~\frac{{2{{{\left( { - 1} \right)}}^{{m - 1}}}}}{{\pi \left( {2m - 1} \right)}}~, \\ \end{gathered} $
(23)
$\begin{gathered} {{C}_{{mn}}} = \frac{e}{{{{N}_{{mn}}}}}\int\limits_0^1 {\exp \left( { - {{\rho }^{2}}} \right)K_{n}^{{\left( m \right)}}\left( \rho \right)2\rho d\rho } = \\ = \frac{e}{{{{N}_{{mn}}}}}\int\limits_0^1 {\exp \left( { - x} \right){{x}^{{m{\text{/}}2}}}L_{n}^{{\left( m \right)}}\left( x \right)dx} = \\ = \frac{e}{{{{{\left[ {\left( {m + n} \right)!n!} \right]}}^{{1{\text{/}}2}}}}}\sum\limits_{k = 0}^\infty {\frac{{\left( {m + n + k} \right)!{{{\left( { - 1} \right)}}^{k}}}}{{\left( {m{\text{/}}2 + k + 1} \right)\left( {m + k} \right)!k!}}} , \\ \end{gathered} $
(24)
$\begin{gathered} {{C}_{{00}}} = e\sum\limits_{k = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{k}}}}{{\left( {k + 1} \right)!}}} = e - 1,\,\,\,\,{{C}_{{01}}} = e\sum\limits_{k = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{k}}}}{{\left( k \right)!}}} = 1, \\ ~{{C}_{{10}}} = 2e\sum\limits_{k = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{k}}}}{{\left( {2k + 3} \right)k!}}} ,\,\,\,\,{{C}_{{11}}} = e\sqrt 2 \sum\limits_{k = 0}^\infty {\frac{{\left( {k + 2} \right){{{\left( { - 1} \right)}}^{k}}}}{{\left( {2k + 3} \right)k!}}} , \\ \end{gathered} $
и аналогично остальные ${{C}_{{mn}}}.$ Здесь представлены первые четыре коэффициента, имеющие наибольшие значения величины модуля.

Оценочный численный расчет энергии рассматриваемого импульса проведем приближенно по формулам (20)–(24), учитывая только старшие (существенные по величине модулей) коэффициенты 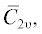${{\bar {C}}_{{mn}}}$ в разложении поля излученного импульса. Для первых восьми метачастиц получим 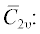${{\bar {C}}_{0}} = 2,$ ${{\bar {C}}_{2}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }};$ ${{C}_{m}}{\text{:}}$ $~{{C}_{0}} = {2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi },$ ${{C}_{1}} = {2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi };$ ${{C}_{{mn}}}{\text{:}}$ ${{C}_{{00}}} = e - 1,$ ${{C}_{{11}}} = 1.07,$ ${{C}_{{01}}} = 1,$ ${{C}_{{10}}} = 0.88.$ Доли энергии метачастиц при этом равны: ${{{\bar {Э}}}_{{000}}} = 4.79,$ ${{{\bar {Э}}}_{{011}}} = 1.85,$ ${{{\bar {Э}}}_{{001}}} = 1.62,$ ${{\overline {~{\text{Э}}} }_{{010}}} = 1.27,$ ${{\overline {~{\text{Э}}} }_{{100}}} = 0.60,$ ${{{\bar {Э}}}_{{111}}} = 0.23,$ ${{{\bar {Э}}}_{{101}}} = 0.20,$ ${{{\bar {Э}}}_{{110}}} = 0.16.$ Суммарная же относительная энергия составляет ${\bar {Э}}\left( {{\Sigma } = 8} \right) = $ $ = 10.72.$ Поскольку первые четыре метачастицы имеют энергию $~{\bar {Э}}\left( {{\Sigma } = 4} \right) = 9.53,$ то оказывается, что эти метачастицы (две осевые с m = 0 и две винтовые с m = 1) переносят около 90% энергии рассматриваемого импульса, так как ${{{\bar {Э}}\left( {{\Sigma } = 4} \right)} \mathord{\left/ {\vphantom {{{\bar {Э}}\left( {{\Sigma } = 4} \right)} {{\bar {Э}}\left( {{\Sigma } = 8} \right)}}} \right. \kern-0em} {{\bar {Э}}\left( {{\Sigma } = 8} \right)}} \approx 0.9.$

5. В заключение приведем оценочный расчет размера ширины поля и плотности энергии нулевой (000) метачастицы в общем случае и отдельно для дальней зоны от излучающей апертуры.

Эффективный размер полуширины (радиуса) поля нулевой метачастицы (см. п. 2) равен

(25)
${{w}_{a}} = a{{\left[ {1 + {{{\left( {\frac{{{{\delta }_{a}}z}}{a}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\,\,\,\,{\text{и}}\,\,\,\,{{w}_{a}} \approx {{\delta }_{a}}z = \frac{{\lambda z}}{{2\pi a}}$
при ${{({{{{\delta }_{a}}z} \mathord{\left/ {\vphantom {{{{\delta }_{a}}z} a}} \right. \kern-0em} a})}^{2}} \gg 1.$ При следующих параметрах: радиусы апертуры источника света a = 5; 0.5 и 0.05 м, длина волны $\lambda $ = 0.4 × 10–6 м и расстояние от Земли до Луны z ≈ 400 × 106 м [11], приведем в качестве примера размеры светового пятна на поверхности Луны: 2wa ≈ 10√2, 100 и 1000 м.

Средняя за период колебания плотность энергии метачастицы изменяется вдоль оси z от значения Па = ${{{{{{\bar {Э}}}}_{{000}}}} \mathord{\left/ {\vphantom {{{{{{\bar {Э}}}}_{{000}}}} {{{V}_{a}}}}} \right. \kern-0em} {{{V}_{a}}}}$ в области апертуры до Пw = ${{{{{{\bar {Э}}}}_{{000}}}} \mathord{\left/ {\vphantom {{{{{{\bar {Э}}}}_{{000}}}} {{{V}_{w}}}}} \right. \kern-0em} {{{V}_{w}}}},$ где отношение эффективных объемов поля метачастицы ${{{{V}_{w}}} \mathord{\left/ {\vphantom {{{{V}_{w}}} {{{V}_{a}}}}} \right. \kern-0em} {{{V}_{a}}}} = {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {w_{a}^{2}}}} \right. \kern-0em} {w_{a}^{2}}}.$

Отсюда имеем

(26)
$\frac{{{{{\text{П}}}_{w}}}}{{{{{\text{П}}}_{a}}{\text{ }}}} = {{\left( {\frac{a}{{{{w}_{a}}}}} \right)}^{2}} = {{\left[ {1 + {{{\left( {\frac{{{{\delta }_{a}}z}}{a}} \right)}}^{2}}} \right]}^{{ - 1}}}\,\,\,\,{\text{и}}\,\,\,\,\frac{{{{{\text{П}}}_{w}}}}{{{{{\text{П}}}_{a}}{\text{ }}}} \approx {{\left( {\frac{{{\text{2}}\pi {{a}^{2}}{\text{ }}}}{{\lambda z}}} \right)}^{2}}$
при ${{({{\delta }_{a}}z} \mathord{\left/ {\vphantom {{({{\delta }_{a}}z} a}} \right. \kern-0em} a}{{)}^{2}} \gg 1.$ Для отношения указанных плотностей энергии метачастицы вблизи поверхности Луны и в области около апертуры источника на Земле в приведенном выше примере получим Пw/Пa ≈ 0.5, 10–4, 10–6.

Работа выполнена за счет бюджетного финансирования в рамках государственного задания по теме 0030-2019-0014.

Список литературы

  1. Шeвчeнкo B.B. // PЭ. 2018. T. 63. № 9. C. 899.

  2. Шeвчeнкo B.B. // PЭ. 2019. T. 64. № 3. C. 265.

  3. Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.

  4. Katsenelenbaum B.Z. High-frequency Electrodynamics. Weinheim: Wiley-VCH, 2006.

  5. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Дрофа, 2006.

  6. Бронштейн И.Н., Семендяев К.А. Справочник по математике. М.: Наука, 1964.

  7. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1962.

  8. Справочник по специальным функциям. Сб. статей / Под ред. Абрамовица М. и Стиган И. М.: Наука, 1979.

  9. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Специальные функции. М.: Наука, 1983.

  10. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Элементарные функции. М.: Наука, 1981.

  11. Шевченко В.В. Луна. Физическая энциклопедия. М.: Cов. энциклопедия, 1990. Т. 2. С. 613.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал