Радиотехника и электроника, 2019, T. 64, № 12, стр. 1190-1196

Вычислительно-эффективный алгоритм оценивания частоты сигналов на выходе канала с белым гауссовским шумом и узкополосными помехами

Л. Н. Казаков^1, *, И. В. Лукьянов², Б. И. Шахтарин^3, **

¹ Ярославский государственный университет им. П.Г. Демидова
150000 Ярославль, ул. Советская, 14, Российская Федерация

² НПП “ЛАМА”
152907 Рыбинск, просп. Серова, 89, Российская Федерация

³ Московский государственный технический университет им. Н.Э. Баумана
105005 Москва, ул. 2-я Бауманская, 5, стр. 1, Российская Федерация

^* E-mail: kazakov@uniyar.ac.ru
^** E-mail: shakhtarin@mail.ru

Поступила в редакцию 16.05.2018
После доработки 16.05.2018
Принята к публикации 27.06.2018

DOI: 10.1134/S003384941910005X

Полный текст (PDF)

Аннотация

Предложен вычислительно-эффективный алгоритм оценивания частоты квазигармонического сигнала при наличии узкополосных помех, основанный на итерационном вычислении автокорреляционной последовательности. Особенностью алгоритма является применение дополнительной процедуры фильтрации, повышающей его устойчивость. Результаты моделирования подтвердили близость полученных оценок к теоретическим границам.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим модель комплексного сигнала на выходе канала с аддитивным белым гауссовским шумом (АБГШ) и узкополосными помехами:

(1)

$\begin{gathered} x[n] = {{A}_{0}}\exp \left( {j\left[ {2\pi {{f}_{0}}n + {{\varphi }_{0}}} \right]} \right) + \\ + \,\,\sum\limits_{m = 1}^M {{{A}_{m}}\exp \left( {j\left[ {2\pi {{f}_{m}}n + {{\varphi }_{m}}} \right]} \right)} + \dot {v}[n], \\ \end{gathered} $

где n = 0, 1, …, N – 1 – номер отсчета; N – размер выборки; A₀, f₀, φ₀ – амплитуда, нормированная частота и начальная фаза полезного сигнала; M – количество узкополосных помех; A_m, f_m, φ_m – амплитуда, нормированная частота и начальная фаза узкополосных помех; $\dot {v}[n]$ – комплексные отсчеты АБГШ с дисперсией σ².

Из [1] известно, что при воздействии узкополосных помех максимально правдоподобная (МП) оценка частоты определяется выражением

(2)

${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }_{{{\text{МП}}}}} = \mathop {{\text{argmax}}}\limits_f \left( {P{\text{(}}f)} \right),$

где P(f) – периодограмма сигнала и помехи с неперекрывающимися спектрами.

При наличии узкополосных помех, близких по частоте к полезному сигналу, распространенной техникой их ослабления является оконное взвешивание – умножение отсчетов исходного сигнала на отсчеты заданной параметрически оконной функции

$w{\text{[}}n] = w(n,\theta ),$

где $\theta $ – вектор параметров оконной функции [2].

При этом оценка (2) выполняется над выборкой

(3)

${{x}_{w}}[n] = x[n]w[n].$

Однако техника оконного взвешивания увеличивает эквивалентную шумовую полосу, в результате этого возрастает дисперсия оценки. В [1] показано, что среднеквадратическая ошибка (СКО) оценки частоты сигнала (3) соотносится с границей Рао–Крамера (ГРК) как

(4)

$\frac{{{{\varepsilon }^{2}}}}{{{\text{VAR(}}\hat {f}{\text{)}}}} = \frac{{{{N}^{3}}\sum\limits_{n = 0}^{N - 1} {w{{{[n]}}^{2}}{{{\left( {n - {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }}{{12{{{\left( {\sum\limits_{n = 0}^{N - 1} {w[n]{{{\left( {n - {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } \right)}}^{2}}}}.$

Здесь ${\text{VAR(}}\hat {f}{\text{)}}$ – ГРК; ε – СКО оценки частоты сигнала, вычисляемая по формуле

(5)

$\varepsilon = \sqrt {\frac{1}{K}\sum\limits_{i = 0}^{K - 1} {{{{\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }}_{i}} - {{f}_{0}}} \right)}}^{2}}} } ,$

где ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }_{i}}$ – оценка нормированной частоты; ${{f}_{0}}$ – истинное значение нормированной частоты; K – число экспериментов.

Логичным выходом из данной ситуации может стать адаптация параметров $\theta $ взвешивающего окна путем решения оптимизационной задачи вида

(6)

$\begin{gathered} L\left( \theta \right) \to \min , \\ L(\theta ) = {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }}_{n}}\Delta f + \sum\limits_{m = 1}^M {\int\limits_{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }}_{0}} - {{\Delta f} \mathord{\left/ {\vphantom {{\Delta f} 2}} \right. \kern-0em} 2}}^{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }}_{0}} + {{\Delta f} \mathord{\left/ {\vphantom {{\Delta f} 2}} \right. \kern-0em} 2}} {{{P}_{w}}(\theta ,f - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }}_{m}})df} } , \\ \end{gathered} $

где Δf – ширина главного лепестка оконной функции; ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{n}}$ – оценка спектральной плотности мощности (СПМ) широкополосного шума; ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }_{0}},$ ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} }_{m}}$ – оценки частот полезного сигнала и узкополосных помех соответственно; ${{P}_{w}}$ – квадрат модуля аналитически заданного преобразования Фурье оконной функции.

Задача в похожей постановке решается в [3]. Недостатком такого подхода является высокая вычислительная сложность, обусловленная необходимостью предварительной оценки частот компонентов смеси (1) и численного решения (6). Практическим компромиссом может служить выбор оконной функции с фиксированными параметрами и малой эквивалентной шумовой полосой (например, окно Бартлетта [2]) и последующее вычисление МП-оценки по (2). Однако вычисление МП-оценок связано с высокими вычислительными затратами, обусловленными необходимостью вычисления большого количества спектральных отсчетов с малым частотным шагом. В связи с этим остается актуальной задача поиска эффективных в вычислительном плане альтернативных методов.

2. АЛГОРИТМ НИКИФОРОВА

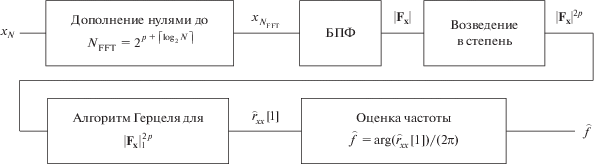
Эффективный вычислительный алгоритм оценивания частоты в условиях АБГШ предложен Никифоровым [4, 5]. Алгоритм основан на увеличении отношения сигнал/шум (ОСШ) с помощью процедуры итерационного вычисления автокорреляционной последовательности (АКП) и последующем вычислением авторегрессионной (АР) оценки частоты [6]. Вычислительная эффективность алгоритма достигается за счет вычислений в спектральной области. Процедура итерационного вычисления АКП заменяется возведением в степень спектральных отсчетов, полученных с помощью быстрого преобразования Фурье (БПФ). В [7] экспериментально показано, что этот алгоритм после ряда доработок обеспечивает оценку частоты, близкую к ГРК, и там же предложена модификация алгоритма Никифорова, обеспечивающая снижение количества вычислительных операций (рис. 1).

Рис. 1.

Схема модифицированного алгоритма Никифорова.

Недостатком алгоритма Никифорова и его модификации является низкая устойчивость к мощным узкополосным помехам. Покажем это. Для упрощения положим в модели (1) σ² = 0. Известно, что АКП такого процесса определяется выражением [8]

${{r}_{{xx}}}[n] = \sum\limits_{m = 0}^M {A_{m}^{2}\exp \left( {j\left[ {2\pi {{f}_{m}}n} \right]} \right)} .$

После p итераций вычисления АКП имеем

${{r}_{{pxx}}}[n] = \sum\limits_{m = 0}^M {A_{m}^{{{{2}^{p}}}}\exp \left( {j\left[ {2\pi {{f}_{m}}n} \right]} \right)} .$

Тогда согласно алгоритму, представленному на рис. 1, оценка частоты определяется выражением

(7)

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} = \frac{1}{{2\pi }}{\text{arg}}\left( {{{r}_{{pxx}}}[1]} \right) = \frac{1}{{2\pi }}{\text{arg}}\left( {\sum\limits_{k = 0}^M {{{{\vec {R}}}_{k}}} } \right),$

где

(8)

$\begin{gathered} {{{\vec {R}}}_{k}} = [A_{0}^{{{{2}^{p}}}}\exp \left( {j2\pi {{f}_{0}}} \right),A_{1}^{{{{2}^{p}}}}\exp \left( {j2\pi {{f}_{1}}} \right), \ldots , \\ A_{M}^{{{{2}^{p}}}}\exp \left( {j2\pi {{f}_{M}}} \right)]. \\ \end{gathered} $

Представив элементы вектора (8) на комплексной плоскости и воспользовавшись теоремой косинусов, можно показать, что оценка (7) будет смещена на

(9)

$\Delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} = \frac{1}{{2\pi }}\arccos \left( {\frac{{A_{0}^{{{{2}^{p}}}} - \left| {{{{\vec {A}}}_{R}}} \right|\cos \gamma }}{{\sqrt {A_{0}^{{{{2}^{{p + 1}}}}} + {{{\left| {{{{\vec {A}}}_{R}}} \right|}}^{2}} - 2A_{0}^{{{{2}^{p}}}}\left| {{{{\vec {A}}}_{R}}} \right|\cos \gamma } }}} \right),$

где ${{\vec {A}}_{R}} = \sum\nolimits_{k = 1}^M {{{{\vec {R}}}_{k}}} $ – векторное представление ошибки, вносимой узкополосными помехами; γ – угловое расстоянием между $\exp \left( {j2\pi \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} } \right)$ и $\exp \left( {j2\pi {{f}_{0}}} \right).$

Из выражения (9) видно, что смещение оценки нелинейно увеличивается при возрастании уровня помехи. Особенностью является увеличение ошибки при отдалении помехи от полезного сигнала в спектральной области. Следует отметить, что у известного алгоритма МП-оценки [9] ошибка в этом случае уменьшается [1]. Полученные результаты объясняются несогласованностью порядка АР-процесса (1) и модели AР-1, на которой основан алгоритм. Для снижения ошибки необходимо увеличить порядок АР-модели до количества комплексных экспонент, присутствующих в сигнале. Однако это приводит к необходимости предварительной оценки количества комплексных экспонент в процессе (1) и к значительному увеличению вычислительных затрат, что ставит под сомнение эффективность применения АР-оценивания в целом. Вместе с тем увеличение количества итераций p обеспечивает повышение отношения полезный сигнал/узкополосная помеха в соответствии с выражениями:

(10)

${{\eta }_{{\text{1}}}} = {{\left( {\frac{{\left| {{{A}_{0}}} \right|}}{{\left| {{{A}_{m}}} \right|}}} \right)}^{2}},\,\,\,\,{{\eta }_{p}} = {{\left( {\frac{{\left| {{{A}_{0}}} \right|}}{{\left| {{{A}_{m}}} \right|}}} \right)}^{{{{2}^{p}}}}} = \eta _{1}^{{{{2}^{{p - 1}}}}}.$

Согласно (10) ослабление помех возможно только при A₀ > A_m. Однако увеличение числа итераций p приводит к снижению вычислительной эффективности, дополнительному расходу памяти и риску переполнения разрядной сетки.

3. АВТОРЕГРЕССИОННЫЙ АЛГОРИТМ ОЦЕНКИ ЧАСТОТЫ, УСТОЙЧИВЫЙ К УЗКОПОЛОСНЫМ ПОМЕХАМ

Для подавления узкополосных помех возможно применение полосового фильтра, настроенного на полосу полезного сигнала. Такая процедура может быть эффективно встроена в алгоритм оценки – она заключается в умножении СПМ сигнала на прямоугольное окно

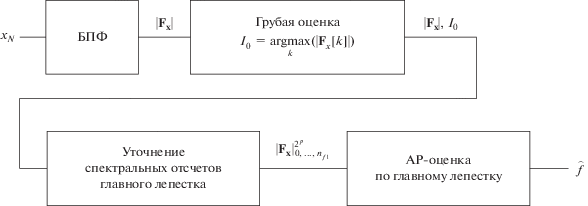
$W[k] = \left\{ {\begin{array}{*{20}{c}} {1,}&{{{k}_{0}} \leqslant k \leqslant {{k}_{1}},} \\ 0&{k < {{k}_{0}},\,\,\,k > {{k}_{1}},} \end{array}} \right.$

где k₀ и k₁– абсциссы нулей главного лепестка СПМ.

Применение этого подхода позволяет не только повысить устойчивость алгоритма, но и снизить количество сложений, умножений и требуемый объем памяти, поскольку необходим расчет спектральных отсчетов только в пределах главного лепестка СПМ. Такая процедура эффективно выполняется с помощью дискретного преобразования Фурье (ДПФ) или алгоритма Герцеля, а необходимость в дополнении исходной выборки нулями отпадает. С учетом этого был разработан новый алгоритм оценки (рис. 2).

Рис. 2.

Схема предложенного алгоритма.

На первом этапе вычисляли БПФ F_x исходного сигнала, после чего проводили грубую оценку частоты и определяли индекс

${{I}_{0}} = \mathop {{\text{argmax}}}\limits_k \left( {\left| {{{{\mathbf{F}}}_{x}}[k]} \right|} \right).$

Учитывая узкополосную модель полезного сигнала в (1) и эффект “растекания спектра” при частоте, не кратной частотной сетке БПФ, положим, что главный лепесток локализован в ${{n}_{f}} = 5$ спектральных отсчетах, а искомая оценка

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \in \left[ {df\left( {{{I}_{0}} - 2} \right),df\left( {{{I}_{0}} + 2} \right)} \right],$

где df – частотная дискрета БПФ. Далее вычисляли ${{n}_{{{{f}_{1}}}}} = {{n}_{f}}{{2}^{p}}$ спектральных отсчетов и оценку частоты по формулам

${{{\text{F}}}_{{{\text{xx}}}}}[k] = {{\left| {\sum\limits_{n = 0}^{N - 1} {x[n]\exp \left( {\frac{{ - 2\pi jn\left( {{{I}_{0}}{{2}^{p}} - \frac{{{{n}_{{{{f}_{1}}}}}}}{2} + k} \right)}}{{{{2}^{p}}N}}} \right)} } \right|}^{{{{2}^{p}}}}},$

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} = \frac{{\text{1}}}{{{\text{2}}\pi }}\arg \left( {\sum\limits_{n = 0}^{{{n}_{{{{f}_{1}}}}} - 1} {{{{\text{F}}}_{{{\text{xx}}}}}[n]\exp \left( {\frac{{2\pi j\left( {{{I}_{0}}{{2}^{p}} - \frac{{{{n}_{{{{f}_{1}}}}}}}{2} + n} \right)}}{{{{2}^{p}}N}}} \right)} } \right),$

где $k = 0,...,{{n}_{{{{f}_{1}}}}} - 1$.

4. ВЫЧИСЛИТЕЛЬНАЯ СЛОЖНОСТЬ АЛГОРИТМА

В таблице 1 представлена оценка количества вычислительных операций исходного алгоритма Никифорова для комплексных отсчетов [5], алгоритма, рассмотренного в [7], и алгоритма, предложенного в данной работе.

Таблица 1.

Сравнение вычислительной сложности рассмотренных алгоритмов

Алгоритм	Операции
Алгоритм	действительных умножений	действительных сложений	сравнений
Никифорова	${{2}^{p}}N(3{{\log }_{2}}N + 4p + 2)$	${{2}^{p}}N(5{{\log }_{2}}N + 5p + 1)$	–
Модифицированный Никифорова	${{2}^{p}}N(2{{\log }_{2}}N + 3p + 4)$	${{2}^{p}}N(3{{\log }_{2}}N + 3p + 3)$	–
Предложенный	$\begin{gathered} 2N({{\log }_{2}}N + 1) + \\ + 5 \times {{2}^{p}}(4N + p + 4) - 10 \\ \end{gathered} $	$\begin{gathered} N\left( {3{{{\log }}_{2}}N + 1} \right) + \\ + \,\,5 \times {{2}^{p}}\left( {3 + 4N} \right) - 5 \\ \end{gathered} $	N

Введем коэффициенты уменьшения вычислительных операций:

$\begin{gathered} {{K}_{{1{\text{умн}}}}} = \frac{{{{M}_{{1{\text{умн}}}}}}}{{{{M}_{{3{\text{умн}}}}}}},\,\,\,\,{{K}_{{1{\text{сл}}}}} = \frac{{{{M}_{{1{\text{сл}}}}}}}{{{{M}_{{3{\text{сл}}}}}}},\,\,\,\,{{K}_{{2{\text{умн}}}}} = \frac{{{{M}_{{2{\text{умн}}}}}}}{{{{M}_{{3{\text{умн}}}}}}}, \\ {{K}_{{2{\text{сл}}}}} = \frac{{{{M}_{{2{\text{сл}}}}}}}{{{{M}_{{3{\text{сл}}}}}}}, \\ \end{gathered} $

где М_1умн, М_1сл – количество операций умножения и сложения алгоритма Никифорова [5]; М_2умн, М_2сл – алгоритма [7]; М_3умн, М_3сл – предложенного алгоритма. Зависимости этих коэффициентов от размера выборки N представлены на рис. 3. Как видно из рисунка, количество операций умножения и сложения для больших выборок и при высоком порядке АКП значительно снижается. Так, при N = 1024 и p = 3 количество операций умножения и сложения по сравнению с исходным алгоритмом Никифорова сокращается примерно в 2.2 и 3.1 раза соответственно, а при N = 32 768 – в 2.8 и 4.4 раза соответственно. При малых же объемах выборок (до 32 отсчетов) предложенный алгоритм проигрывает алгоритму Никифорова в вычислительной эффективности.

Рис. 3.

Зависимость коэффициентов уменьшения вычислительных операций умножения (а, в) и сложения (б, г) от размера выборки N и количества итераций вычисления АКП p = 2 (1), 3 (2), 4 (3) и 5 (4) для алгоритма Никифорова (а, б) и предложенного алгоритма (в, г).

5. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

5.1. Оценка частоты сигнала на выходе канала с АБГШ

Результаты численного исследования по установлению зависимости СКО оценки (5) (количество экспериментов K = 10 000) от ОСШ на выходе канала с АБГШ представлены на рис. 4а, 4б.

Рис. 4.

Зависимость СКО оценки от ОСШ на выходе канала с АБГШ, p = 3 (а) и р = 2 (б) для предложенного алгоритма (1–6) и для ГРК (7–12) с размером выборки N = 128 (1, 7), 256 (2, 8), 512 (3, 9), 1024 (4, 10), 4096 (5, 11) и 16384 отсчета (6, 12).

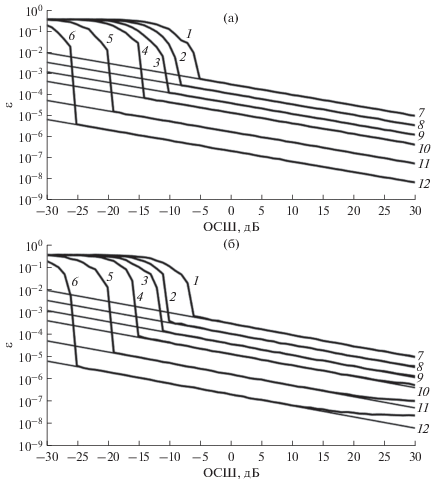
По представленным результатам видно, что при p = 3 кривые зависимости СКО оценки от ОСШ приближаются к ГРК (см. рис. 4а). Кроме того, данные рис. 4б подтверждают, что для коротких выборок достаточно двух итераций для получения оценки, близкой к ГРК.

Наблюдаемый “пороговый эффект”, ниже которого существует расхождение с ГРК, обусловлен превышением уровней спектральных отсчетов шума над уровнем спектрального отсчета полезного сигнала, следствием чего является ошибка определения индекса I₀.

5.2. Оценка частоты сигнала на выходе канала с АБГШ и узкополосными помехами

На рис. 5а, 5б представлены зависимости СКО оценки (5) от ОСШ соответственно для алгоритма Никифорова с окном Бартлетта и для предложенного алгоритма с окном Бартлетта (количество экспериментов K = 10 000, шум предполагается широкополосным) при наличии узкополосной помехи с частотой ${{f}_{m}},$ равномерно распределенной в диапазоне нормированных частот (–0.5; 0.5), и амплитудой A_m = 0.5A₀, размер выборки N = 2048.

Рис. 5.

Зависимость СКО оценки от ОСШ на выходе канала с АБГШ и узкополосной помехой для алгоритма Никифорова (а) и предложенного алгоритма (б) с окном Бартлетта при различном количестве итераций вычисления АКП: p = 1 (1), 2 (2), 3 (3) и 4 (4) 5 (5), кривая 6 – ГРК.

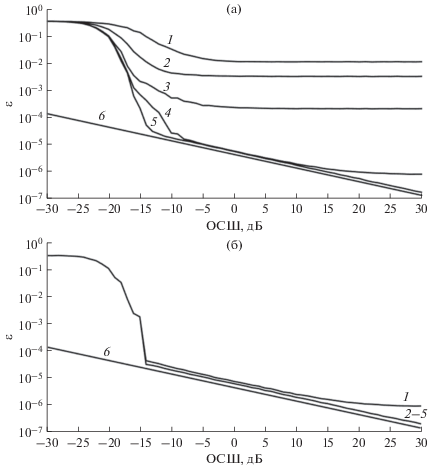
Представленные результаты демонстрируют, что подавление узкополосной помехи при использовании алгоритма Никифорова возможно только при количестве итераций вычисления АКП больше четырех, в то время как предложенный алгоритм обеспечивает устойчивость к таким помехам уже при двух итерациях вычисления АКП.

На рис. 6а, 6б представлены зависимости СКО оценки (5) (количество экспериментов K = 10 000) от разности нормированной номинальной частоты и нормированной частоты узкополосной помехи $\Delta f = {{f}_{0}} - {{f}_{m}}$ также для алгоритма Никифорова и для предложенного алгоритма; уровень широкополосного шума фиксирован, ОСШ составляет 15 дБ.

Рис. 6.

Зависимости СКО оценки от частоты узкополосной помехи для алгоритма Никифорова, p = 4 (а) и предложенного алгоритма, p = 2 (б): кривая 1 – с прямоугольным окном, кривая 2 – с окном Бартлетта, кривая 3 – ГРК.

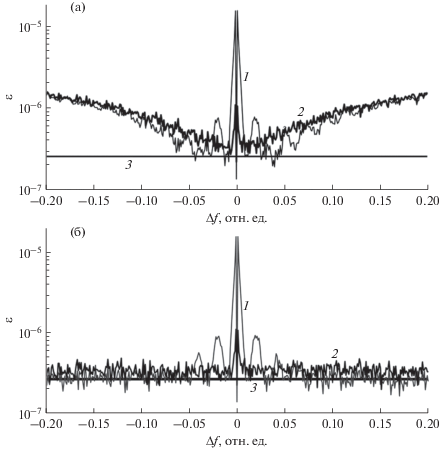
Приведенные результаты подчеркивают рост ошибки алгоритма Никифорова при удалении частоты помехи от частоты полезного сигнала. Предложенный алгоритм свободен от этого недостатка.

ВЫВОДЫ

1. Предложен алгоритм оценивания частоты квазигармонического сигнала в условиях АБГШ и узкополосных помех. Алгоритм согласует модель сигнала с АР-моделью первого порядка за счет процедуры узкополосной фильтрации. Совмещение процедуры фильтрации с оценкой частоты позволило снизить количество операций умножения и сложения (в 2.8 и 4.4 раза соответственно при размере выборки 32768 отсчетов).

2. Предложенный алгоритм обеспечивает оценку частоты в условиях АБГШ с дисперсией, отклоняющейся от границы Рао–Крамера не более чем на 0.2 и 0.4 дБ при четырех и трех итерациях вычисления АКП соответственно вплоть до области порогового эффекта. Также показано, что при двух итерациях вычисления АКП для выборок размером менее 1024 отсчетов дисперсия отклоняется от ГРК не более чем на 1.2 дБ. При длинных выборках и высоких ОСШ наблюдается некоторое смещение оценки.

3. В канале с узкополосными помехами алгоритм также демонстрирует результаты, близкие к теоретически возможным. При оценивании частоты сигнала в присутствии мощных узкополосных помех дисперсия оценки с применением окна Бартлетта отклоняется от теоретической границы не более чем на 0.52, 0.74 и 1.3 дБ при четырех, трех и двух итерациях вычисления АКП соответственно в исследованном диапазоне ОСШ вплоть до области порогового эффекта.

Список литературы

Schuster S., Scheiblhofer S., Stelzer. A. // IEEE Trans. 2009. V. IM-58. № 6. P. 1975.
Дворкович В.П., Дворкович A.В. Оконные функции для гармонического анализа сигналов. М.: Техносфера, 2014.
Давыдочкин В.М. Весовые функции и алгоритмы для повышения точности оценки частоты и амплитуды выборки гармонического сигнала на фоне сигналоподобных помех. Автореф. … канд. техн. наук. Рязань: Рязанский гос. радиотехн. ун-т, 2008. 18 с.
Никифоров А.А. // Механизация строительства. 2013. № 11. С. 53.
Никифоров А.А. Идентификация и оценка информационных параметров навигационных систем с кодовым разделением. Дис. … канд. техн. наук. М.: МГТУ им. Н. Э. Баумана, 2014. 139 с.
Останин С.А. // Журн. радиоэлектроники. 2011. № 12. http://jre.cplire.ru/win/dec11/13/text.pdf.
Волков В.Г., Кривов Ю.Н., Лукьянов И.В. // Журн. радиоэлектроники. 2016. № 10. http://jre.cplire.ru/ jre/oct16/6/pdf
Марпл С.Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990.
Boorstyn R.R., Rife D.C. // IEEE Trans. 1974. V. IT-20. № 5. P. 591.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал