Радиотехника и электроника, 2019, T. 64, № 12, стр. 1228-1237

ВВЕДЕНИЕ

Магнитные гетероструктуры с протекающим по ним спин-поляризованным током находят практическое применение в терагерцовой спинтронике, в трехмерных наномагнитных устройствах, сенсорах, запоминающих устройствах [1–16]. Поляризация спинов протекающего в гетероструктуре тока может приводить к значительному неравновесному накоплению спинов в ограниченном объеме ферромагнитного материала. Спиновая релаксация неравновесных электронов может происходить через взаимодействие с ферромагнитной решеткой, возбуждая осцилляции намагниченности или переключая намагниченность [17, 18]. В меньшей степени изучено взаимодействие спинов электронов проводимости и магнитной решетки ферромагнетика при резонансных условиях для релаксационных процессов (в том числе и фотоэмиссионных), вызванных переворотом спина проводящих (s) электронов [19–24]. Спин-релаксационные переходы электронов проводимости между спиновыми подзонами ферромагнетика стимулированы опосредованно через sd-обменное взаимодействие с электромагнитной волной. Такие спин-флип-переходы электронов могут сопровождаться испусканием или поглощением фотонов [25] с частотой, определяемой энергией эффективного обменного расщепления спиновых подзон. Для ряда переходов энергия расщепления спиновых подзон соответствует энергии фотонов терагерцового диапазона частот [26–32]. В этом случае появляется возможность технических применений гетероструктур как основы компактных терагерцовых источников излучения, в том числе работающих при комнатной температуре.

Электроны проводимости могут взаимодействовать с электромагнитным внешним излучением через sd-обмен, с включением вектор-потенциала $\vec {A}$ внешнего поля в энергию обменного sd-взаимодействия [24]. Излучение через такую релятивистскую поправку к импульсу электронов проводимости (s-электронов) “модулирует” sd-взаимодействие и может вызвать излучательные переходы s-электронов с переворотом спинов. Такой канал взаимодействия на порядки более эффективен, чем стандартные мультипольные каналы [33]. Его высокая эффективность показана в работе [24] с помощью оценок вероятности электронных переходов с переворотом спина. При этом не учитывалось влияние динамики неравновесной заселенности электронных подзон, а также влияние термостата электронной системы на вероятность энергетических переходов электронов с переворотом спина. Для более корректного описания механизма излучения фотонов ранее была предложена модель спин-флип-переходов на основе вывода уравнений динамики магнитного момента [31, 32], определяющих временную зависимость изменения среднего магнитного момента неравновесных инжектированных электронов и пространственной неоднородности распределения носителей заряда. В данной работе показано, что на базе уравнений динамики магнитного момента [31, 32] можно получить уравнение для неравновесной спиновой поляризации в магнитных переходах, а его решение позволяет рассчитать частоты испускания или поглощения фотонов при непрямых энергетических переходах электронов с переворотом спина.

1. МОДЕЛЬ МАГНИТНОГО ПЕРЕХОДА

Рассмотрим схему типичного магнитного перехода аналогично работе [29] (рис. 1). Здесь неравновесная спиновая заселенность в ферромагнетике достигается с помощью эффективной спиновой инжекции при протекании электрического тока.

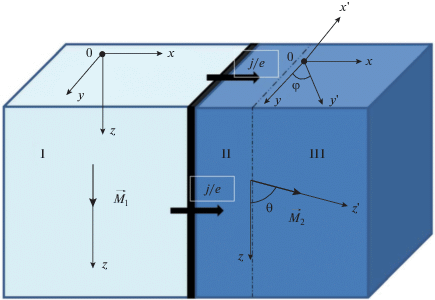
При выводе исходных уравнений учтем зависимость неравновесной спиновой поляризации от координат x, y, z [29] и будем считать, что изменение начального состояния спиновой поляризации со временем происходит благодаря приложению импульса тока инжекции. Импульс электрического тока протекает через границу металлических ферромагнетиков I и II, векторы намагниченности которых ${{\vec {M}}_{1}}$ и ${{\vec {M}}_{2}}$ параллельны осям квантования в средах I и II; $\theta $ – угол между векторами ${{\vec {M}}_{1}}$ и ${{\vec {M}}_{2}}$ (см. рис. 1). Обменное взаимодействие между ферромагнетиками I и II устранено благодаря наличию сверхтонкого буферного слоя из немагнитного диэлектрика или металла. При прохождении тока через спин-инжекционный переход из первого ферромагнетика (область I) происходит инжекция нескомпенсированных спинов в область II второго ферромагнетика (далее – рабочая область магнитного перехода). Затем инжектированные носители заряда стекают через область III, выполняющую роль коллектора.

Изменение квазиуровней Ферми для средних заселенностей спиновых подзон в областях I, II (с обозначением энергетических релаксационных переходов электронов с переворотом спина в области II) показано на рис. 2 [29]. В терагерцовом диапазоне частот можно приближенно считать, что колебания намагниченности решеток ферромагнетиков слабо выражены (типичные собственные частоты таких колебаний ~10¹⁰…10¹¹ Гц), поэтому в первом приближении будем считать магнитную решетку неподвижной. Кроме того, колебания и перемагничивание решетки ферромагнетика из-за передачи ей крутильного момента от s-электронов наблюдаются в слоях магнетиков толщиной порядка нескольких нанометров. Далее мы полагаем, что толщина слоя области сохранения спинового состояния (толщина рабочего слоя) много больше этого размера. Как следствие, энергетически выгодным становятся состояния со стационарным направлением намагниченности ферромагнетика. При этом частоты колебаний спиновой подсистемы s-электронов много больше частот 3d‑электронов, “локализованных” на атомах кристаллической решетки и связанных с ее намагниченностью. Перечисленное выше дает нам основания пренебречь динамикой магнитной решетки на терагерцовых частотах.

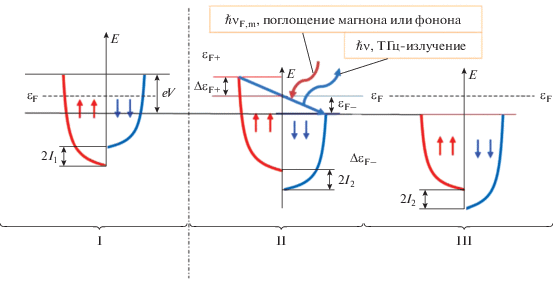
Далее принимаем, что электроны проводимости имеют изотропный параболический спектр энергий с некоторой эффективной массой. Учитываем воздействие на них обменного взаимодействия с d-электронами (sd-обмен), внешнего электромагнитного поля и внешней равновесной системы “термостата”. Обменное взаимодействие s‑электронов, определяющих проводимость ферромагнитного металла, c d-электронами, “локализованными” на атомах кристаллической решетки, зависит от спинового состояния s- и d‑электронов, при этом спиновое состояние d‑электронов считается связанным с намагниченностью кристаллической решетки ферромагнетика. Такое взаимодействие описывается по механизму sd-обмена [34]. При рассмотрении средних заселенностей инжектированных электронов по спиновым подзонам можно ввести для них квазистационарные уровни Ферми в каждой из подзон как добавку к равновесному значению ферми-уровня. Кроме этого, учитываем условие электронейтральности так, чтобы общее число электронов в рабочей области магнитного перехода оставалось постоянным. В результате возникает разница в положениях квазиуровней в спиновых подзонах и, таким образом, при инжекции спинов током в магнитном переходе может возникнуть отрицательная спиновая температура, предсказанная в [35].

2. ГАМИЛЬТОНИАН ИНЖЕКТИРОВАННЫХ ЭЛЕКТРОНОВ

Гамильтониан одного инжектированного электрона с учетом взаимодействия с электромагнитной волной для уравнения Паули можно представить в виде [24, 31, 32]

Здесь ${{\hat {H}}_{k}}$ – оператор кинетической энергии электрона, равный произведению ${{\vec {\hat {p}}}^{2}}$/2m* на единичную матрицу 2 × 2; ${{\hat {H}}_{{sd}}}$ – оператор sd-обменного взаимодействия, в общем виде он задается выражением где векторная матрица с использованием орт осей координат равна $\vec {\hat {\sigma }} = \vec {x}{{\hat {\sigma }}_{x}} + \vec {y}{{\hat {\sigma }}_{y}} + \vec {z}{{\hat {\sigma }}_{z}},$ $\vec {H}_{{sd}}^{0}$ – встроенное эффективное sd-обменное поле, а ${{\mu }_{{\text{B}}}}$ – магнетон Бора; ${{\hat {H}}_{A}}$ – оператор взаимодействия с электромагнитной волной с векторным потенциалом $\vec {A}$ определяется как [24]

где индуцированное электромагнитной волной sd-обменное поле равно

Используя первые два члена гамильтониана (1), получаем решение в виде спиноров со спином “вверх” или “вниз”, соответствующих двум параболическим спиновым подзонам, расщепленным по энергии на величину $2{{\mu }_{{\text{B}}}}\left| {\vec {H}_{{sd}}^{0}} \right|.$ Третий член гамильтониана (1) можно рассматривать как возмущение, вызывающее излучательные переходы между спиновыми подзонами с переворотом спина электрона под действием электромагнитной волны с вектор-потенциалом $\vec {A}.$

Поскольку для переходных металлов спин атома определяется главным образом спином d‑электронов, то используем формулу для оценки обменного sd-взаимодействия [34] и вводим тензор s-обмена [31, 32]

где по одинаковым индексам идет суммирование. Используя формулу (3) для вычисления индуцированного электромагнитной волной sd-обменного поля ${{\vec {H}}_{A}}$ с помощью формулы (5), легко показать, что векторы $\vec {H}_{{sd}}^{0}$ и ${{\vec {H}}_{A}}$ коллинеарны, если среда изотропна. В то же время из-за различия диагональных компонент тензора sd-обмена (при приведении к главным осям тензора) поля $\vec {H}_{{sd}}^{0}$ и ${{\vec {H}}_{A}}$ неколлинеарны и, следовательно, среда излучения анизотропна. Лишь в этом случае в рамках рассматриваемой модели возможны излучательные переходы с переворотом спина электронов, находящихся в редуцированных состояниях. Это существенно изменяет рассмотрение процесса спин-инжекционного излучения по сравнению с [26].

Согласно формулам (2)–(4), для удобства дальнейших преобразований можно ввести вектор $\vec {I},$ имеющий размерность энергии, через встроенное эффективное sd-обменное поле $\vec {H}_{{sd}}^{0}\,:$

где $G{{\left( {\vec {p}} \right)}_{{}}} = {{\alpha }_{{i\,j}}}\left( {\vec {p}} \right)$ – тензор sd-обмена (отметим, что в тонких монокристаллических пленках с кубической симметрией могут возникать выделенные направления анизотропии [34]). Также можно ввести вектор $\vec {J}$ через индуцированное электромагнитной волной sd-обменное поле ${{\vec {H}}_{A}}$:

Вектор $\vec {H}_{{sd}}^{{}}$, определяющий sd-обменное поле с учетом добавки от внешнего электромагнитного поля, введем как

Отметим, что, помимо координатной составляющей, поле $\vec {H}_{{sd}}^{{}}$ включает временную составляющую $\vec {J}$ с частотой колебания, задаваемой внешним электромагнитным полем. Частоту внешнего поля полагаем равной частоте перехода электрона с переворотом спина между подзонами ${{\omega }_{{12}}} \approx {{\left( {2{{I}_{z}}} \right)} \mathord{\left/ {\vphantom {{\left( {2{{I}_{z}}} \right)} \hbar }} \right. \kern-0em} \hbar }.$ Если частота внешнего поля сравнима с частотой перехода между подзонами (которая на несколько порядков превосходит частоту ферромагнитного резонанса пленки), то намагниченность решетки, как мы уже отмечали, не успевает следовать за внешним полем и сохраняет свое исходное положение. Далее мы пренебрегаем динамикой магнитной решетки. Ограничимся рассмотрением только поперечных компонент $\vec {A}\left( {z,t} \right),$ например, компонент ${{A}_{x}}\left( {z,t} \right)$ и ${{A}_{y}}\left( {z,t} \right).$ Таким образом, гамильтониан неравновесных инжектированных электронов будет определяться обменным полем, которое модулировано внешним излучением. Анизотропия обменного взаимодействия и наличие внешнего поля приводит к существованию в гамильтониане (1) слагаемого, которое описывает возмущение и содержит недиагональные компоненты, приводящие к перевороту спина.

3. АНАЛОГ УРАВНЕНИЯ БЛОХА ДЛЯ ИНЖЕКТИРОВАННЫХ ЭЛЕКТРОНОВ С УЧЕТОМ ТРАНСПОРТА ЭЛЕКТРОНОВ

Для описания кинетики изменения намагниченности инжектированных электронов удобно рассмотреть аналог модифицированного уравнения Блоха (с транспортным членом) и учесть взаимодействия инжектированных электронов с электромагнитным полем. С помощью такого уравнения можно исследовать не только релаксационные, но и излучательные процессы, а также транспорт неравновесных спинов. Для учета транспортного члена в аналоге уравнения Блоха необходимо принять во внимание пространственную неоднородность спинового распределения. Вывод такого уравнения приведен в нашей работе [32].

Аналог уравнения Блоха с транспортной частью для намагниченности инжектированных электронов, учитывающего транспорт и взаимодействие электронов проводимости с электромагнитной волной через sd-взаимодействие, имеет вид (поперечное и продольное затухание из-за безызлучательных спиновых релаксаций при взаимодействии со средой введены феноменологически):

Здесь фигурные скобки { , } обозначают антикоммутатор, ${{\hat {p}}_{k}}$ – оператор импульса электрона, ${{\vec {\mu }}_{\parallel }},$ ${{\vec {\mu }}_{ \bot }}$ – продольная и поперечная компоненты магнитного момента спинов инжектированных электронов, ${{\tau }_{\parallel }}$ – время продольной (спиновой) релаксации инжектированных электронов, $\tau _{ \bot }^{{}}$ – время релаксации поперечной составляющей спина, которую мы приписываем действию механизма Слончевского–Берже [17]. Время релаксации поперечной составляющей спина мало и релаксация происходит при распространении волны на расстояние порядка единиц нанометров [17]. Время продольной спиновой релаксации намного больше и релаксация происходит при распространении волны на расстояние в несколько десятков нанометров. Система уравнений (9) и ее решение описывают процесс, когда время продольной релаксации определяется интенсивностью процессов обмена энергии между инжектированными электронами и решеткой [36], а время поперечной релаксации определяется тем, как быстро нарушается синхронность прецессии магнитных диполей [17]. Релаксация поперечной компоненты спина происходит достаточно быстро в масштабе времени продольной релаксации. Именно при релаксации поперечной компоненты спина происходит передача крутильного момента спина магнитной решетке ферромагнетика. При этом могут иметь место осцилляции намагниченности или переключение намагниченности ферромагнетика [1–10], которые мы в данной работе не учитываем. Дальнейший процесс релаксации спина происходит путем перехода электронов между неравновесными квазиуровнями Ферми с переворотом спина, что и может приводить к терагерцовому и дальнему инфракрасному излучению.

Из системы уравнений (9) следует, что состояние инжектированных неравновесных электронов будет изменяться со временем под влиянием sd-обмена, внешнего электромагнитного поля, нерадиационных процессов релаксации и процессов переноса носителей заряда, а также транспорта электронов. Далее будет показано, что на основе уравнений (9) возможно получение уравнения для неравновесной спиновой поляризации в магнитных переходах с учетом пространственной неоднородности спиновой поляризации.

4. УРАВНЕНИЕ ДЛЯ НЕРАВНОВЕСНОЙ СПИНОВОЙ ПОЛЯРИЗАЦИИ В МАГНИТНЫХ ПЕРЕХОДАХ

Рассмотрим случай, когда электрический ток протекает через границу однородных ферромагнетиков, векторы намагниченности которых (они же соответствуют осям квантования в разных средах) образуют некоторый угол рассогласования $\varphi $. Введем обозначения: ${{P}_{1}}$ – равновесная спиновая поляризация инжектора (ферромагнетика, из которого инжектируются спин-поляризованные электроны, см. рис. 1), ${{P}_{2}}$ – равновесная спиновая поляризация рабочей области магнитного перехода, в который инжектируются спин-поляризованные электроны. Пусть электрический ток протекает вдоль оси х через границу ферромагнетиков. Будем для упрощения считать, что плотность электрического тока j не изменяется как вдоль поперечного сечения, так и вдоль оси х магнитного контакта. Далее считаем анизотропию обменного взаимодействия пренебрежимо малой, т.е. компоненты обменного поля (определяемые внешним электромагнитным полем) равны нулю, а релаксация продольной компоненты магнитного момента электрона проводимости полностью определяется взаимодействием спиновой системы электронов проводимости с термостатом.

Запишем определение тензора потока намагниченности [34]:

где ${{\Psi }_{{\vec {p},s}}}(\vec {r},t)$ – волновая функция электрона с импульсом $\vec {p}$ в спиновом состоянии $s$, ${{\mu }_{{\text{B}}}}$ – магнетон Бора, $\vec {\sigma } = \left\{ {{{\sigma }^{x}},{{\sigma }^{y}},{{\sigma }^{z}}} \right\}$ – вектор-матрица Паули; спиновые индексы записаны снизу, векторные сверху; $\hat {v} = - ({{i\hbar } \mathord{\left/ {\vphantom {{i\hbar } m}} \right. \kern-0em} m})\nabla $ – оператор скорости. При использовании определения для ${{\Pi }_{k}}$ (10) и формулы (11) видно, что величины $n\left\langle {{{\Pi }_{k}}{{\mu }_{ \bot }}} \right\rangle $ и $n\left\langle {{{\Pi }_{k}}{{\mu }_{\parallel }}} \right\rangle $ в выбранной нами геометрии в формулах (11) являются усредненным компонентами тензора потока намагниченности.

Выясним, как преобразуется в выбранной нами геометрии компонента потока намагниченности инжектора

при переходе к новой оси квантования. Такой переход может быть связан как с переходом электрона в другую магнитную среду с иным направлением оси квантования, так и с поворотом (например, с помощью внешнего магнитного поля) оси квантования однородной среды. Повороту координатных осей на угол $\varphi $ вокруг оси x соответствует матрица преобразования спиновых волновых функций [37]

Отсюда следует, что при переходе к новой оси квантования рассматриваемая компонента тензора намагниченности будет преобразовываться по закону

поскольку по условию ${{J}^{{y{\kern 1pt} {\kern 1pt} x}}} = 0.$ При этом появляется также ортогональная компонента ${{J}^{{y'{\kern 1pt} {\kern 1pt} x}}},$ определяемая как

Таким образом, при переходе потока намагниченности (и соответствующего ему спинового потока) из инжектора ${{J}^{{z{\kern 1pt} x}}}$ в среду с новой осью квантования он преобразуется в поток, имеющий компоненту $n\left\langle {{{\Pi }_{k}}{{\mu }_{\parallel }}} \right\rangle $ = ${{J}^{{z{\kern 1pt} x}}}\cos \varphi $ с поляризацией вдоль новой оси квантования и компоненту $n\left\langle {{{\Pi }_{k}}{{\mu }_{ \bot }}} \right\rangle $ = ${{J}^{{z{\kern 1pt} x}}}\sin \varphi $ с перпендикулярной оси квантования поляризацией. Поскольку продольной и поперечной поляризациям соответствуют существенно различающиеся времена спиновой релаксации, за пределами слоя толщиной порядка длины поперечной релаксации (“слоя Слончевского-Берже”) остается только продольная поляризация. В дальнейшем нас будет интересовать область вне этого слоя, при этом из уравнений (9) выпадает член с векторным произведением $\vec {\mu } \times \vec {H}_{{sd}}^{*}.$ Таким образом, для получения уравнения для неравновесной спиновой поляризации мы будем использовать только второе уравнение системы уравнений (9).

Магнитное состояние электронов проводимости будет описываться локальной спиновой поляризацией

где ${{n}_{{ + ( - )}}}(x)$ – парциальные концентрации электронов проводимости со спином, параллельным (антипараллельным) оси квантования соответствующего ферромагнетика, $n = {{n}_{ + }}(x) + {{n}_{ - }}(x)$ – полная концентрация, предполагаемая не зависящей от координаты в силу нейтральности металла. Учитывая (12), введем плотность спинового потока и получим

где ${{j}_{ \pm }}$ – парциальные плотности электрического (зарядового) тока.

В этом случае второе уравнение в системе (9) с учетом (16), (17) в стационарных условиях (${{\partial {{{\vec {\mu }}}_{\parallel }}} \mathord{\left/ {\vphantom {{\partial {{{\vec {\mu }}}_{\parallel }}} {\partial {\kern 1pt} t}}} \right. \kern-0em} {\partial {\kern 1pt} t}} = 0$) можно переписать в виде

При наличии электрического поля $E(x)$ и градиентов парциальных концентраций возникают парциальные плотности электрического (зарядового) тока

где ${{\mu }_{ \pm }}$ и ${{D}_{ \pm }}$ – парциальные подвижности и коэффициенты диффузии электронов соответственно.

Полная плотность $j = {{j}_{ + }}(x) + {{j}_{ - }}(x)$ в стационарном состоянии не зависит от $x$. Выражая $E(x)$ через $j$, получим с учетом (17) для плотности спинового потока

где

Предположим, что в обеих подзонах носители тока имеют одинаковые подвижности и коэффициенты диффузии: ${{\mu }_{--}} = {{\mu }_{ + }} = \mu ,$ ${{D}_{ - }} = {{D}_{ + }} = D.$ В этом случае $Q\left( P \right) = P,$ $D\left( P \right) = D$, и подстановка (20) в (18) с учетом условия сохранения электрического заряда $\nabla \vec {j} = 0$ дает уравнение [26]

где $\tau $ – время релаксации спинов, ${{j}_{D}} = {{enD} \mathord{\left/ {\vphantom {{enD} l}} \right. \kern-0em} l} = {{enl} \mathord{\left/ {\vphantom {{enl} \tau }} \right. \kern-0em} \tau }$ – плотность тока диффузии электронов, $l = \sqrt {D\tau } $ – длина спиновой релаксации, $n$ – концентрация электронов в металле.

5. НЕРАВНОВЕСНАЯ СПИНОВАЯ ПОЛЯРИЗАЦИЯ В МАГНИТНЫХ ПЕРЕХОДАХ

Решение уравнение (22) имеет вид [29]

где

Здесь нижние индексы 1, 2 означают знаки “–”, “+” соответственно. При записи решения (22) его можно упростить при условии:

Поскольку длина спиновой диффузии l = $ = \sqrt {D\tau } \sim 3 \times {{10}^{{ - 6}}}$ см, концентрация электронов проводимости в металле $n\sim {{10}^{{22}}}$ см^–3 и время продольной (спиновой) релаксации инжектированных электронов ${{\tau }_{\parallel }}\sim 3 \times {{10}^{{ - 13}}}$ с [6, 7], то получаем следующую оценку плотности тока диффузии электронов ${{j}_{D}} = {{enl} \mathord{\left/ {\vphantom {{enl} \tau }} \right. \kern-0em} \tau }\sim 1.6 \times {{10}^{{10}}}$ А/см². Так как используемые в эксперименте максимальные плотности токов в магнитных переходах, как правило, на порядок меньше полученной величины, то можно считать, что условие (25) хорошо выполняется. В этом случае решение (23) можно переписать в виде

Поскольку $P\left( \infty \right) = {{P}_{2}},$ то ${{С}_{2}} = 0.$ Постоянную интегрирования ${{C}_{1}}$ определим из условия непрерывности спинового потока на границе между двумя ферромагнетиками [6]

Граничное условие (27) записано при условии, что спиновая поляризация инжектора остается неизменной величиной или возмущается крайне слабо, что, как показано в работе [6], вполне возможно осуществить подбором соответствующих материалов. Кроме того, считаем, что влиянием отраженного от границы потока электронов на спиновую поляризацию прошедших в рабочую область магнитного перехода электронов можно пренебречь.

Подстановка (23) в (27) дает

Учитывая (28), распределение спиновой поляризации электронов проводимости в рабочей области принимает следующий вид:

Формула (29а) верна при ${j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}} \ll 1,$ eе можно представить в более простом виде

В другом пределе, когда $j \to \infty $ ($j \gg {{j}_{D}}$), из (24) и (29а) получаем

Из (29в) следует, что при ${j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}} \to 0$ спиновая поляризация инжектированных электронов перестает зависеть от расстояния до инжектора и $P(x) \to {{P}_{1}}\cos \varphi .$ Последнее означает, что невозможно создать спиновую поляризацию в рабочей области магнитного перехода большую, чем спиновая поляризация в инжектируемом потоке.

Из формул (29а), (29б), (29в) следует, что по мере удаления от инжектора спиновая поляризация, как и ожидалось, монотонно приближается к равновесному значению для рабочего тела. Наибольшее отклонение спиновой поляризации от неравновесной $\Delta P = P - {{P}_{2}}$ достигается на границе ферромагнетиков

При ${j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}} \ll 1$ формула (30а) принимает вид

6. ЭНЕРГЕТИЧЕСКИЕ ПЕРЕХОДЫ ЭЛЕКТРОНОВ С ПЕРЕВОРОТОМ СПИНА

Неравновесные электроны имеют соответствующие им неравновесные квазиуровни Ферми ${{\varepsilon }_{{F + }}}$ и ${{\varepsilon }_{{F - }}},$ отсчитываемые от дна нижней спиновой подзоны (рис. 2). В неравновесных условиях возможны электронные переходы из занятых состояний, расположенных ниже квазиуровня Ферми ${{\varepsilon }_{{{\text{F}} + }}}$ для, например, минорной спиновой подзоны, в свободные электронные состояния, расположенные выше квазиуровня Ферми ${{\varepsilon }_{{F - }}}$ для мажорной спиновой подзоны (см. рис. 2). Если квазиуровень Ферми ${{\varepsilon }_{{F + }}}$ смещен относительно равновесного значения уровня Ферми рабочей области на величину $\Delta {{\varepsilon }_{{F + }}} = {{\varepsilon }_{{F + }}} - ({{\varepsilon }_{{F0 + }}} - {{eV} \mathord{\left/ {\vphantom {{eV} 2}} \right. \kern-0em} 2}),$ а квазиуровень Ферми ${{\varepsilon }_{{F - }}}$ на величину $\Delta {{\varepsilon }_{{F - }}} = ({{\varepsilon }_{{F0 - }}} - {{eV} \mathord{\left/ {\vphantom {{eV} 2}} \right. \kern-0em} 2}) - {{\varepsilon }_{{F - }}},$ то максимальную частоту излучения можно также представить в виде суммы величин $\Delta {{\varepsilon }_{{F + }}}$ и $\Delta {{\varepsilon }_{{F - }}},$ деленной на постоянную Планка [26]:

Мы ввели здесь знаки модуля, чтобы эта формула соответствовала любому знаку ΔP.

Значения квазиуровней подзон зависят от неравновесной спиновой поляризации и энергетического обменного расщепления (I₂):

Здесь учтено, что на один электрон приходится фазовый объем ${{(2\pi \hbar )}^{3}},$ а количество электронов с одним направлением спина ${{n}_{{ - , + }}} = n(1 \pm {{P)} \mathord{\left/ {\vphantom {{P)} 2}} \right. \kern-0em} 2}$ равно объему сферы с радиусом, равным импульсу Ферми, деленному на ${{(2\pi \hbar )}^{3}}.$ Далее удобнее выразить изменение спиновой поляризации квазиуровней через равновесное значение (${{P}_{2}}$) и неравновесную добавку ($\Delta P$) следующим образом:

В формулах (32) и (33) знак изменений квазиуровней зависит от знака неравновесной спиновой добавки и может быть как положительным, так и отрицательным.

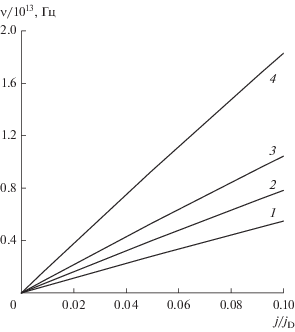
На рис. 3 представлена зависимость частоты излучения $\nu $ от приведенной плотности тока, рассчитанная по формулам (31)–(33). Согласно рис. 3 диапазону частот спин-инжекционного излучения 5…20 ТГц соответствуют плотности тока примерно на два порядка меньшие, чем плотность тока диффузии. Исходя из оценки плотности тока диффузии ${{j}_{D}}\sim {{10}^{{10}}}{{...10}^{{11}}}$ А/см², получаем плотности тока в магнитном переходе ${{j}_{{}}}\sim {{10}^{8}}{{...10}^{9}}$ А/см², что достижимо экспериментально без теплового пробоя магнитного контакта. Низкие частоты излучения соответствуют меньшим плотностям тока. Необходимо также учитывать затухание электромагнитных волн, возникающее главным образом благодаря поглощению волн свободными носителями в материалах магнитного перехода. Как показано в работе [24], для превышения уровня мощности излучения, соответствующего потерям из-за затухания и тепловых шумов, необходимо преодолеть некоторое пороговое значение плотности тока ${{j}_{{{\text{пр}}}}}\sim {{10}^{7}}{{...10}^{8}}$ А/см².

7. ВЕРОЯТНОСТЬ КВАНТОВЫХ ПЕРЕХОДОВ

Согласно работе [31], из уравнений (9) можно найти вероятность переходов (количество квантовых переходов в единицу времени):

Здесь ${{n}_{{{\text{эн}}}}}$ – концентрация инжектированных неравновесных по спину электронов в металле, $H_{A}^{{( \bot )}} = {{({{H}^{2}}_{{sd}}^{{(х)}} + {{H}^{2}}_{{sd}}^{{{\text{(}}y{\text{)}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – модуль поперечной компоненты обменного поля, ${{P}_{z}}(0)$ – неравновесная спиновая поляризация в начальный момент времени, $P_{z}^{e}$ – равновесная спиновая поляризация в ферромагнетике.

В режиме низкой добротности при ${{\omega }_{{{\text{пр}}}}}{{\tau }_{{{\text{эф}}}}} \ll 1$ (${{\tau }_{{{\text{эф}}}}} = \sqrt {{{\tau }_{ \bot }}{{\tau }_{\parallel }}} ,$ ${{\omega }_{{{\text{пр}}}}} \approx \gamma H_{A}^{{( \bot )}}$ – частота прецессии) вероятность квантовых переходов согласно (34) равна

Для режима высокой добротности прецессии при ${{\omega }_{{{\text{пр}}}}}{{\tau }_{{{\text{эф}}}}} \gg 1$ учтем, что приближенная формула (34) совпадает с численным решением системы (9) при $t \approx 10{{\tau }_{\parallel }}.$ В этом случае вероятность переходов, как следует из (34), равна

и определяется поперечным временем спиновой релаксации.

Из формулы (34) следуют интересные свойства процессов релаксации. При ${{\omega }_{{{\text{пр}}}}}{{\tau }_{{{\text{эф}}}}} \gg 1$ и $t \gg {{{{\tau }_{\parallel }}} \mathord{\left/ {\vphantom {{{{\tau }_{\parallel }}} {{{\omega }_{{{\text{пр}}}}}{{\tau }_{{{\text{эф}}}}}}}} \right. \kern-0em} {{{\omega }_{{{\text{пр}}}}}{{\tau }_{{{\text{эф}}}}}}}$ заселенности верхнего и нижнего электронных подуровней выравниваются. В режиме высокой добротности прецессии, т.е. при достаточно большом внешнем электромагнитном поле (${{H_{A}^{{( \bot )}}} \mathord{\left/ {\vphantom {{H_{A}^{{( \bot )}}} {H_{{sd}}^{{{\text{*(}}z{\text{)}}}}}}} \right. \kern-0em} {H_{{sd}}^{{{\text{*(}}z{\text{)}}}}}}$ = 0.1), скорость поступления энергии от поля может превосходить скорость отбора энергии колебаний магнитного момента термостатом. В результате компенсируется отбор и отдача энергии электромагнитному полю осциллятором, система переходит в состояние равновесия с действующим полем и имеет место так называемый эффект насыщения [38].

Вероятность переходов электронов проводимости с переворотом спином при их взаимодействии с термостатом определяется формулой (35) (вклад излучательных переходов в эту вероятность определим далее). Если предположить, что квантовый выход равен единице (оценка по верхнему пределу), то согласно формуле (35) количество излучательных переходов для плотности неравновесных электронов ${{n}_{{{\text{эн}}}}} \approx {{10}^{{19}}}$ см^–3 (плотность тока ${{10}^{8}}\,{{\text{A}} \mathord{\left/ {\vphantom {{\text{A}} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}}},$ см. формулу (29)) ${{W}_{r}} \approx {{10}^{{31}}}$ с^–1 см^–3. Выделяемая при этом в единице объема мощность излучения P_i определяется количеством переходов, умноженным на энергию кванта $\hbar \,\omega $. Для ${{\omega }_{{12}}}$ = 30 ТГц получаем

Объем активной области излучателя будет определяться площадью магнитного перехода и длиной спиновой релаксации. При диаметре перехода порядка 1 мкм и длине спиновой релаксации 10 нм получим объем активной области $V = \pi {{d}^{2}}l \approx {{10}^{{ - 15}}}\,\,{\text{с}}{{{\text{м}}}^{3}}.$ Таким образом, в активной области согласно (37) может выделяться максимальная мощность излучения около ${{P}_{i}} \approx {{10}^{{ - 4}}}\,\,{\text{Вт}}{\text{.}}$ Столь высокое оценочное значение мощности получено без учета того, что квантовый выход на практике будет значительно меньше единицы, а число неравновесных электронов не равно максимально возможному (${{10}^{{19}}}$ см^–3) при данной плотности тока [29].

ЗАКЛЮЧЕНИЕ

Получено уравнение для неравновесной спиновой поляризации в магнитных переходах на основе уравнения динамики движения магнитного момента, усредненного по ансамблю неравновесных спин-инжектированных при учете пространственной неоднородности распределения. При решении уравнения для неравновесной спиновой поляризации на границе магнитного контакта (образованного двумя ферромагнетиками) с протекающим по контакту током выведены формулы для расчета частот испускания или поглощения фотонов при непрямых энергетических переходах электронов с переворотом спина. Показано, что при плотности тока, превышающей пороговый уровень, излучение может выходить из области контакта, а соответствующие частоты лежат в терагерцовом диапазоне частот. В целом частоты испускания или поглощения фотонов при непрямых энергетических переходах электронов с переворотом спина определяются плотностью тока, углом между направлениями намагниченности инжектора и рабочего слоя, а также величиной спиновой поляризации электронов проводимости. При плотностях тока, намного превышающих плотности тока диффузии электронов, достигается максимально возможная неравновесная спиновая поляризация в рабочем слое, и соответствующие частоты испускания или поглощения фотонов достигают насыщения. Полученные результаты могут быть использованы для разработки компактных источников излучения терагерцового диапазона частот.