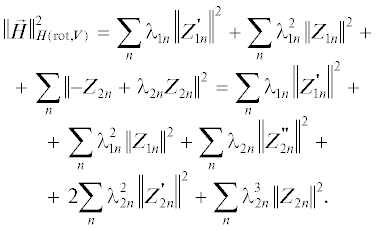Радиотехника и электроника, 2019, T. 64, № 12, стр. 1151-1166

1.1. Постановка задачи

С физической точки зрения задача о возбуждении волновода представляет собой задачу об излучении электромагнитного поля в цилиндре токами и зарядами, гармонически зависящими от времени.

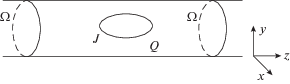
Рассмотрим задачу в цилиндре Q = $ = \left\{ {(x,y) \in \Omega ,z \in ( - \infty ,\infty )} \right\},$ сечение цилиндра $\Omega $ – произвольная односвязная область с кусочно-гладкой границей. Будем считать, что граница области $\Omega $ состоит из конечного числа бесконечно дифференцируемых дуг, соединяющихся под ненулевыми углами. Считаем, что токи и заряды и возбуждаемое ими поле имеют гармоническую зависимость от времени ${\text{exp}}( - i\omega t).$ Требуется найти электромагнитное поле, удовлетворяющее уравнениям Максвелла в цилиндре $Q$

где $k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c},$ $\vec {D} = \varepsilon \vec {E},$ $\vec {B} = \mu \vec {H}.$ Матрицы диэлектрической и магнитной проницаемости имеют зависимость только от поперечных координат $x,y.$ Считаем, что матрицы $\varepsilon ,\mu $ эрмитовы, положительно определены, кусочно-непрерывны и имеют вид

$\varepsilon _{{ij}}^{*}$ означает комплексное сопряжение к ${{\varepsilon }_{{ij}}}.$

Считаем, что сечение $\Omega $ представимо в виде $\bar {\Omega } = \cup \mathop {\bar {\Omega }}\nolimits_i ,$ причем области ${{\Omega }_{i}}$ имеют кусочно-гладкие границы и в областях ${{\Omega }_{i}}$ матрицы ${{\varepsilon }_{{ij}}},{{\mu }_{{ij}}}$ бесконечно дифференцируемы. На границе цилиндра поставим условия, соответствующие идеально проводящей стенке

На поверхностях разрыва $S$ диэлектрической и магнитной проницаемостей поставим условия сопряжения

Считаем, что токи и заряды $\vec {j} = \vec {j}(x,y,z),$ $\rho = \rho (x,y,z),$ возбуждающие поле, являются заданными функциями, локализованными в конечной области ${\text{supp}}\vec {j} \subset ((x,y)$ $ \in $ $\Omega ,z \in [{{z}_{1}},{{z}_{2}}]),$ удовлетворяют условиям $\vec {j} \in {{L}_{2}},$ $\rho \in {{L}_{2}},$ ${{\partial {{j}_{x}}} \mathord{\left/ {\vphantom {{\partial {{j}_{x}}} {\partial x}}} \right. \kern-0em} {\partial x}} \in {{L}_{2}},$ ${{\partial {{j}_{y}}} \mathord{\left/ {\vphantom {{\partial {{j}_{y}}} {\partial y}}} \right. \kern-0em} {\partial y}} \in {{L}_{2}},$ ${{\partial {{j}_{z}}} \mathord{\left/ {\vphantom {{\partial {{j}_{z}}} {\partial z}}} \right. \kern-0em} {\partial z}} \in {{L}_{2}}.$ Кроме того, считаем, что удовлетворяется уравнение непрерывности, имеющее после сокращения на временной множитель вид:

Поскольку задача рассматривается в неограниченной области, для постановки задачи (1)–(4) необходимо поставить условия излучения при $z \to + \infty ,$ $z \to - \infty .$

Перейдем к изложению предлагаемого метода. Запишем систему уравнений Максвелла в виде

При рассмотрении краевых задач электродинамики основную роль играет обычно вихревая пара системы уравнений Максвелла. Аналогичную роль играют уравнения (6, 7).

Системы уравнений (6), (7) и (8), (9) связаны соотношениями, подобными в некотором смысле соотношениям, связывающим (1) и (2).

Из уравнений (6), (7) в качестве следствия получаем

Если поле удовлетворяет дополнительным условиям, например стремится к нулю на бесконечности, то из этих уравнений следует, что имеют место уравнения (8), (9).

Введем обозначения:

Запишем в обозначениях (10) уравнения (6), (7) в виде

Уравнения (13) являются дальнейшим объектом исследования, для которого поставим краевую задачу в цилиндре.

1.2. Спектральная задача теории регулярных волноводов

Вне области, занятой токами, поле ${{\vec {A}}_{1}},\,\,{{\vec {A}}_{2}}$ удовлетворяет однородным уравнениям

Будем искать решения системы (14) при краевых условиях и условиях сопряжения (3), (4), которые удовлетворяют однородным уравнениям (8), (9) и имеют вид

Введем обозначения для сокращения записи:

а под $\varepsilon ,\mu $ будем подразумевать матрицы ${{\varepsilon }_{{ij}}},\,\,{{\mu }_{{ij}}},\,\,(i,j = 1,2).$

Относительно вектора ${{\vec {A}}_{1}} = ({{\vec {B}}_{ \bot }},{{E}_{z}})$ в обозначениях (15), (16) после сокращения на экспоненциальный множитель получим

Дополним уравнения (17), (18) краевыми условиями

и условиями сопряжения, принимающими вид

где $\vec {n}$ – нормаль к границе или линии разрыва S. Условия сопряжения (21) являются записью условий

выраженных через вектор ${{({{\vec {B}}_{ \bot }},\,\,{{E}_{z}})}^{T}}.$ Кроме того, учитывая, что область $\Omega $ может иметь входящие углы, необходимо поставить условия на ребре, в качестве которых потребуем выполнения

Пусть ${{\vec {A}}_{{{{1}_{n}}}}}$ – собственный вектор задачи (17)–(21). Тогда векторы ${{\vec {A}}_{{{{1}_{n}}}}}$ и ${{\vec {A}}_{{{{2}_{n}}}}} = - i\tfrac{1}{{{{{\gamma }}_{n}}}}{\mathbf{d}}_{1}^{{ - 1}}{{{\mathbf{a}}}_{1}}{{\vec {A}}_{{{{1}_{n}}}}}$ – являются решением спектральной задачи, возникающей для уравнений (14). При этом основные граничные условия и условия сопряжения выполняются в силу определения векторов ${{\vec {A}}_{{{{1}_{n}}}}}$ и ${{\vec {A}}_{{{{2}_{n}}}}},$ а дополнительные условия, как было показано, являются их следствиями. Таким образом, задача для уравнений (14) и задача (17)–(21) имеют одни и те же собственные значения. Зная собственные векторы задачи (17)–(21), можно определить собственные векторы задачи для уравнений (14). Для присоединенных векторов могут быть проведены аналогичные выкладки.

Для того чтобы сформулировать обобщенную постановку задачи, напомним определения некоторых функциональных пространств. Следуя [32], введем гильбертово пространство:

со скалярным произведением ${{({{\vec {A}}_{ \bot }},\,\,{{\vec {B}}_{ \bot }})}_{{H({\text{div}})}}}$ = $ = {{({{\vec {A}}_{ \bot }},\,\,{{\vec {B}}_{ \bot }})}_{{{{L}_{2}}}}}$ + ${{({\text{div}}{{\vec {A}}_{ \bot }},\,\,{\text{div}}{{\vec {B}}_{ \bot }})}_{{{{L}_{2}}}}}$ и нормой $\left\| {{{{\vec {A}}}_{ \bot }}} \right\|_{{H({\text{div}})}}^{2}$ = = $\left\| {{{{\vec {A}}}_{ \bot }}} \right\|_{{{{L}_{2}}}}^{2} + \left\| {{\text{div}}{{{\vec {A}}}_{ \bot }}} \right\|_{{{{L}_{2}}}}^{2},$ а также пространство ${{H}_{0}}({\text{div}})$

Введем гильбертово пространство

т.е. пространство векторов ${{\vec {A}}_{ \bot }} \in {{H}_{0}}({\text{div}}),$ ${{A}_{z}} \in {{\dot {H}}^{1}}.$ В пространстве $W$ введем скалярное произведение ${{(\vec {A},\tilde {A})}_{W}}$ = ${{({{\vec {A}}_{ \bot }},{{\vec {\tilde {A}}}_{ \bot }})}_{{H({\text{div}})}}}$ + ${{({{A}_{z}},{{\tilde {A}}_{z}})}_{{{{H}^{1}}}}}$ и норму $\left\| {\vec {A}} \right\|_{W}^{2} = $ = $\left\| {{{{\vec {A}}}_{ \bot }}} \right\|_{{H({\text{div}})}}^{2}$ + $\left\| {{{A}_{z}}} \right\|_{{{{H}^{1}}}}^{2}.$

Предположим, что $\vec {A},\gamma $ – классическое решение задачи (17)–(21). Умножим систему (17)–(18) на произвольный достаточно гладкий вектор $\vec {\tilde {A}},$ удовлетворяющий граничным условиям и условиям сопряжения (19)–(21), и проинтегрируем по частям.

Введем полуторалинейные формы в пространстве W:

Рассмотрим задачу поиска обобщенного решения (17)–(21) в пространстве W. Задача формулируется следующим образом: найти $\vec {A} \in W$ и комплексное число γ, такие что

Классическое решение задачи (17)–(21) удовлетворяет уравнению (25), т.е. является обобщенным решением задачи.

Отметим следующую особенность задачи (25), рассматриваемой в пространстве $W$. Множество векторов вида ${{({\text{rot}}\varphi ,\,\,ik\varphi )}^{T}}$ являются решением задачи, рассматриваемой в пространстве W, отвечающем нулевому собственному значению. Таким образом, у задачи (25) существует бесконечномерное ядро. В то же время корневые векторы задачи, отвечающие ненулевым собственным значениям $\gamma _{n}^{2},$ удовлетворяют, как легко убедиться, уравнению

Данное уравнение представляет собой обобщенную запись одного из уравнений Максвелла, не использованного при постановке задачи.

Отметим, что $({\text{rot}}\varphi ,\,\, - ik\varphi )$ является ядром сопряженной к (25) задачи. То есть одно из уравнений представляет собой условие ортогональности ядру сопряженной задачи.

Введем пространство

Будем рассматривать далее спектральную задачу в пространстве V. Норма пространства V определяется так же, как норма пространства W.

Перейдем теперь к вопросу о полноте системы корневых векторов задачи (25). Система векторов ${{\vec {A}}_{n}}$ называется полной в некотором пространстве V, если замыкание линейной оболочки векторов ${{\vec {A}}_{n}}$ совпадает с $V$ [33].

Полуторалинейная форма $a(\vec {A},\vec {\tilde {A}})$ определяет в гильбертовом пространстве $V$ скалярное произведение

В силу ограниченности и положительной определенности тензоров $\varepsilon ,\mu $ формы $b(\vec {A},\vec {\tilde {A}}),\,\,c(\vec {A},\vec {\tilde {A}})$ и теоремы Рисса существуют линейные ограниченные операторы $C,H$ такие, что:

Дальнейшее изложение существенно опирается на компактность вложения пространства $V$ в ${{({{L}_{2}})}^{3}}.$

Доказательство компактности вложения основано на аналоге теоремы [32] о разложении произвольного векторного поля из ${{L}_{2}}$ на вихревую и потенциальную части.

Теорема 1. Для любого вектора $\vec {A} \in {{L}_{2}}$ справедливо представление в виде

где $\psi \in {{H}^{1}},\,\,\,\,\chi \in {{\dot {H}}^{1}}.$

Теорема 2. Пространство $V$ компактно вложено в ${{({{L}_{2}})}^{3}}.$

В силу компактности вложения $V$ в ${{({{L}_{2}})}^{3}}$ операторы $C$ и $H$ компактны. В силу того, что уравнение (25) справедливо для любого $\tilde {A} \in V,$ задача (25) эквивалентна в пространстве $V$ спектральной задаче для операторного пучка:

Операторы $C$ и $H$ компактны, оператор $H$ самосопряжен и аннулируется только в нуле, т.е. из условия $H\vec {A} = 0$ следует $\vec {A} = 0.$

Справедлива следующая теорема.

Теорема 3. Оператор $H$ – оператор Гильберта–Шмидта, т.е. $\sum\nolimits_k {\nu _{k}^{2} < \infty } ,$ где ${{\nu }_{k}}$ – собственные значения оператора H.

Таким образом, операторный пучок $M(\gamma )$ удовлетворяет теореме Келдыша о полноте корневых векторов операторного пучка [34]. Напомним ее формулировку применительно к рассматриваемой задаче.

Пусть дан операторный пучок $I + C + {{\gamma }^{2}}H,$ где операторы $C$ и $H$ – компактны, $H$ – полный самосопряженный оператор конечного порядка. Тогда система корневых векторов операторного пучка полна в пространстве V. Пусть дан операторный пучок $I + C + {{\gamma }^{2}}H,$ где операторы $C,H$ – компактные, $H$ – полный самосопряженный оператор конечного порядка. Тогда система корневых векторов операторного пучка двукратно полна в пространстве V, т.е. полна в пространстве $V \oplus V.$

В результате справедлива следующая теорема.

Теорема 4. Система корневых векторов задачи (25) полна в пространстве V.

Кроме того, справедливы утверждения, имеющие место для задач, описываемых келдышевским пучком.

1. Все собственные значения, кроме, может быть, конечного числа лежат в секторе $\left| {{\text{arg}}\left( {\gamma _{{{\text{max}}}}^{2} - {{\gamma }^{2}}} \right)} \right| < \beta ,$ где $\beta $ сколь угодно мало, $\gamma _{{{\text{max}}}}^{2}$ – некоторая константа.

2. Квадраты постоянных распространения имеют асимптотику $\gamma _{n}^{2} = O(n),$ $n \to \infty .$

3. Существует лишь конечное число вещественных положительных $\gamma _{n}^{2}.$

Справедлива следующая теорема.

Теорема 5. Система корневых векторов задачи (25) удовлетворяет уравнениям (17), (18) и условиям (19)–(21) всюду, кроме угловых точек, в классическом смысле.

Будем для упрощения записей считать, что вещественным собственным значениям ${{\gamma }_{n}}$ соответствуют только собственные векторы, присоединенные векторы отсутствуют. Несложно выписать биортогональную систему к системе корневых векторов ${{\vec {A}}_{{1n}}}.$ В качестве биортогональной системы можно выбрать систему корневых векторов задачи, сопряженной к задаче (17–21).

Отметим, что после умножения системы уравнений (17), (18) на матрицу $\nu = \left( {\begin{array}{*{20}{c}} 1&{} \\ {}&{ - 1} \end{array}} \right)$ система уравнений принимает симметричный вид:

В результате

квадраты собственных значений $\gamma _{n}^{2}$ задачи (17), (21) расположены симметрично относительно вещественной оси.

Собственные и присоединенные векторы ${{\vec {A}}_{{1n}}}$ в силу симметрии уравнений (17), (18) указанного вида удовлетворяют обобщенным условиям ортогональности:

Будем обозначать собственные векторы сопряженной задачи $\vec {A}_{n}^{1}.$

Данные векторы имеют вид

и представляют собой элементы биортогональной системы к корневым векторам задачи (17)–(21)

1.3. Существование решения задачи возбуждения волновода

Рассмотрим задачу о возбуждении волновода (1)–(4). Необходимо поставить краевую задачу для уравнений

с краевыми условиями и условиями сопряжения (3), (4).

Существует конечное число вещественных положительных собственных значений $\gamma _{n}^{2},$ которым отвечают бегущие волны, т.е. не затухающие при $z \to \infty $ решения. Решение вне области, занятой токами, представимо в виде суммы конечного числа бегущих волн и стремящейся к 0 при $z \to \pm \infty $ части.

Итак, можно поставить условия излучения следующим образом. Будем искать решения вида

где ${{\vec {\bar {A}}}_{1}} \in {{L}_{2}}({{Q}_{i}}),$ ${{\vec {\bar {A}}}_{2}} \in {{L}_{2}}({{Q}_{i}}),$ ${{Q}_{1}} = \left\{ {(x,y) \in \Omega ,\,\,z \leqslant {{z}_{1}}} \right\},$ ${{Q}_{2}} = \left\{ {(x,y) \in \Omega ,\,\,z \geqslant {{z}_{2}}} \right\}.$

Произвольный вектор $\vec {J}$ не удовлетворяет уравнению (26), которое выполняется для корневых векторов задачи (25). Считаем, что ток $\vec {J}$ имеет конечный носитель и удовлетворяет уравнению непрерывности, которое запишем в обобщенном виде:

Справедлива теорема о разложении векторного поля.

Теорема 6. Пусть $\Omega $ – область с кусочно-гладкой границей. $\vec {A} \in {{L}_{2}}(\Omega ).$ Тогда найдутся $\varphi \in {{\dot {H}}^{1}},$ и $\vec {F} \in H({\text{div}}) \oplus {{H}^{1}},$ такие что

или

Задачу для системы (31) можно свести к задаче для одного уравнения путем введения нового неизвестного вектора $\vec {A}.$ Рассмотрим уравнение

с краевыми условиями и условиями сопряжения

Зная решение этого уравнения, можно определить решения уравнений (31) по формулам

Задачу (34), (35) необходимо дополнить условиями излучения. Отметим, что в области, не занятой токами, поиск решения сводится к спектральной задаче для уравнения

т.е. к задаче (17)–(21). Для вектора $\vec {A}$ получаем спектральную задачу, такую же, как для вектора ${{\vec {A}}_{1}}.$ Поэтому в области, не занятой токами, вектор $\vec {A}$ имеет тот же вид, что вектор ${{\vec {A}}_{1}}.$

Поставим следующие условия излучения. Пусть существует $N$ вещественных собственных значений. Будем считать, что присоединенные векторы отсутствуют. Пусть $\vec {A}$ представим при $z \leqslant {{z}_{1}},$ $z \geqslant {{z}_{2}}$ в виде

Здесь $\vec {\bar {A}} \in {{L}_{2}}({{Q}_{i}}),$ где ${{Q}_{i}}$ – полуцилиндры ${{Q}_{1}} = ((x,y) \in \Omega ,$ $z \in ( - \infty ,{{z}_{1}})),$ ${{Q}_{2}} = ((x,y) \in \Omega ,$ $z \in ({{z}_{2}},\infty )).$

В случае стремления решения на бесконечности к нулю естественным представляется поставить условия $\vec {A} \in {{L}_{2}}(W;( - \infty ,\infty )),$ т.е. условие

Следует отметить, что в силу наличия в общем случае бегущих волн, соответствующих вещественным положительным $\gamma _{n}^{2},$ условие принадлежности решения пространству ${{L}_{2}}(V; - \infty ,\infty )$ не может быть использовано в качестве условия на бесконечности. Обобщенным решением задачи (34)–(38) будем называть вектор $\vec {A}(x,y,z),\,\,\vec {A} \in W$ при почти всех z, удовлетворяющий уравнению

и условиям (38).

При сделанном предположении о том, что частота электромагнитного поля не совпадает с частотой отсечки, множество собственных значений задачи (37) состоит из нулевого собственного значения, которому соответствуют собственные векторы вида $\vec {N} = {{({\text{rot}}\varphi ,ik\varphi )}^{T}},$ $\forall \varphi \in {{\dot {H}}^{1}}$ и ненулевых собственных значений, которым соответствуют корневые векторы, принадлежащие пространству V.

Отметим, что вектор $\vec {J}$ не удовлетворяет условию (26), которому удовлетворяют корневые векторы, отвечающие ненулевым собственным значениям. Будем использовать следующий метод построения решения $\vec {A} \in W,$ удовлетворяющего уравнению (39):

и условиям излучения (38).

Представим вектор $\vec {J}$ в виде суммы двух слагаемых

где ${{\vec {J}}_{1}}$ удовлетворяет условию (26), ${\mathbf{d}}_{2}^{{ - 1}}{{\vec {J}}_{2}}$ принадлежит ядру спектральной задачи (25), рассматриваемой в пространстве W. Возможность подобного представления установлена в теореме 6. Разобьем исследование задачи для уравнения (40) на три задачи.

Найти $\vec {A} \in W,$ удовлетворяющее уравнению:

с условиями при $z \leqslant {{z}_{1}},$ $z \geqslant {{z}_{2}}{\text{:}}$

Данные условия соответствуют тому, что при $z \leqslant {{z}_{1}},$ $z \geqslant {{z}_{2}}$ поле ${{\partial{ \vec {A}}} \mathord{\left/ {\vphantom {{\partial{ \vec {A}}} {\partial z}}} \right. \kern-0em} {\partial z}} = {{\vec {A}}_{1}}$ обращается в нуль, поскольку ток ${{\vec {J}}_{2}}$ не принадлежит пространству $V$ и возбуждает поле в ближней зоне. Поскольку требуется найти поле, а не потенциал, то можно ограничиться поиском ${{\partial{ \vec {A}}} \mathord{\left/ {\vphantom {{\partial{ \vec {A}}} {\partial z}}} \right. \kern-0em} {\partial z}}.$ При этом, как легко видеть,

Ток ${{\vec {J}}_{1}}$ представим в виде суммы:

Ток $\vec {J}_{1}^{N}$ представляет собой проекцию вектора ${{\vec {J}}_{1}}$ на конечномерное пространство собственных векторов, обозначенных ${{\vec {A}}_{n}}$ и отвечающих бегущим волнам. Собственные векторы сопряженной задачи будем обозначать ${{\vec {A}}_{n}}$ = $\nu {\mathbf{d}}_{2}^{{ - 1}}{{\vec {A}}_{n}}{\text{:}}$

Для вектора $\vec {J}_{1}^{N}$ будем рассматривать задачу

с условиями излучения при $z \leqslant {{z}_{1}},$ $z \geqslant {{z}_{2}}{\text{:}}$

Решение данной задачи сводится к решению конечного числа обыкновенных дифференциальных уравнений.

Ток ${{\vec {\bar {J}}}_{1}}$ удовлетворяет условиям ортогональности

При этих условиях, накладываемых на правую часть уравнения, существует решение уравнения

удовлетворяющее условиям

Сумма решений этих трех задач (41)–(43) будет удовлетворять уравнению (39) и условиям излучения (38).

Теорема 7. Существует решение задачи возбуждения (39), удовлетворяющее условиям излучения (38).

1.4. Пример комплексных собственных значений

Задача поиска мод регулярных волноводов с диэлектрическим заполнением сводится к спектральной задаче для несамосопряженного оператора даже в случае отсутствия потерь в среде. Собственные значения могут быть комплексными, при этом в случае кратных собственных значений помимо собственных векторов могут существовать присоединенные векторы. Кроме того, возможны участки дисперсионных кривых, для которых ${{d\gamma } \mathord{\left/ {\vphantom {{d\gamma } {dk}}} \right. \kern-0em} {dk}} < 0,$ т.е. фазовая и групповая скорости направлены в противоположные стороны. Примеры подобных эффектов приведены в работах [35, 36].

Покажем, что они возникают для волновода квадратного сечения с анизотропным заполнением даже в случае постоянных коэффициентов. Решение этой задачи выписывается в явном виде. В работе [37] рассмотрено качественное поведение дисперсионных кривых.

Рассмотрим задачу о волноводе прямоугольного сечения с анизотропным заполнением. Требуется найти электромагнитное поле в цилиндре

Диэлектрическая проницаемость задается тензором:

Магнитная проницаемость $\mu = 1.$

Будем искать решения системы (17), (18) в виде

где ${{H}_{x}},{{H}_{y}},{{E}_{z}}$ – константы. Решение данной задачи выписывается явным образом. Оно позволяет рассмотреть качественное поведение дисперсионных кривых.

Существование комплексных волн и обратных волн хорошо известно в теории электромагнитных и упругих волноводов. Тем не менее случай касания дисперсионной кривой с осью ${{k}^{2}}$ обнаружен не был. Возбуждение волновода имеет принципиально иной характер для подобной точки. Квадрат постоянной распространения ${{\gamma }^{2}}$ для определенного участка дисперсионной кривой имеет ненулевую вещественную и мнимую части.

Кривые, описывющие зависимости собственных значений $\gamma $ от волнового числа $k,$ или, что эквивалентно, частоты ω, называют дисперсионными кривыми. Частота изменяется в пределах от $0$ до $ + \infty .$

Наложим ограничения на параметры тензора диэлектрической проницаемости. Значения величин ε₁ и ε₂ зафиксируем, считая, что они равны двум произвольным константам, удовлетворяющим условию $0 < {{\varepsilon }_{1}} < {{\varepsilon }_{2}}.$ Параметр ε₃ будем изменять. В зависимости от принадлежности ε₃ интервалу (ε₁, ε₂), поведение дисперсионных кривых может иметь качественно различный характер.

Прямыми волнами называют моды волновода, для которых ${{d\gamma } \mathord{\left/ {\vphantom {{d\gamma } {dk}}} \right. \kern-0em} {dk}} > 0,$ обратными – моды, для которых ${{d\gamma } \mathord{\left/ {\vphantom {{d\gamma } {dk}}} \right. \kern-0em} {dk}} < 0.$

Если ${{\varepsilon }_{3}} < {{\varepsilon }_{1}}$ или ${{\varepsilon }_{3}} > {{\varepsilon }_{2}},$ то дисперсионные кривые являются монотонными функциями и существуют только прямые волны. При значениях ε₃, расположенных между ε₁ и ε₂$\left( {{{\varepsilon }_{1}} < {{\varepsilon }_{3}} < {{\varepsilon }_{2}}} \right),$ при определенных значениях частот появляются точки ветвления дисперсионной кривой. В этих точках возникают парами прямая и обратная волны. Для обратной волны дисперсионная кривая убывает, а не возрастает. Кроме того, в этих точках рождаются комплексно-сопряженные пары комплексных волн. Под комплексными волнами подразумеваются волны с ненулевыми значениями как вещественной, так и мнимой частей постоянной распространения. Подобные моды существуют в волноводенесмотря на отсутствие в среде, заполняющей волновод, т.е. вещественный характер тензора диэлектрической проницаемости.

Будем называть далее дисперсионной кривой зависимость квадрата постоянной распространения от квадрата волнового числа ${{\gamma }^{2}}({{k}^{2}}).$ Это удобнее для качественного анализа поведения дисперсионных кривых, например, потому что в случае постоянного заполнения в подобных переменных дисперсионные кривые являются прямыми.

Рассмотрим дисперсионные кривые, соответствующие $n = 1,$ $m = 1.$ Из точки касания выходят две ветви дисперсионных кривых, которые соответствуют прямой и обратной волнам. Для прямых волн квадрат постоянной распространения является возрастающей функцией квадрата частоты, для обратных – убывающей.

На рис. 2 представлены дисперсионные кривые при ε₃ меньше ε₁, которые имеют стандартный монотонный характер и качественно соответствуют кривым полого волновода. Для полого волновода дисперсионные кривые в переменных квадрат частоты – квадрат постоянной распространения являются прямыми. В случае наличия анизотропии происходит деформация этих кривых, однако монотонность сохраняется.

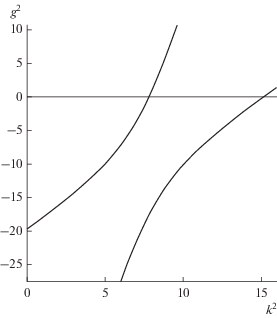
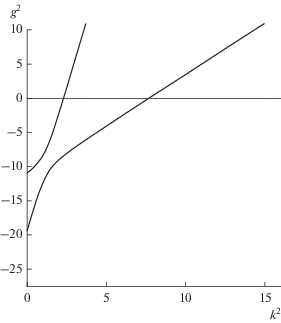
При ${{\varepsilon }_{3}} = {{\varepsilon }_{1}}$ и ${{\varepsilon }_{3}} = {{\varepsilon }_{2}}$ дисперсионные кривые становятся прямыми. При увеличении параметра ${{\varepsilon }_{3}}$ происходит качественное изменение поведения дисперсионной кривой. Появляются участки убывания, а не роста дисперсионной кривой. Эти участки соответствуют существованию обратных волн. Типичное поведение дисперсионной кривой приведено на рис. 3. Участок, отмеченный на кривой точками $A$ и $B$ отвечает обратной волне. Поскольку на отмеченном участке ${{\gamma }^{2}}({{k}^{2}})$ вещественно, то волна, отвечающая этим значениям $\gamma $ является бегущей.

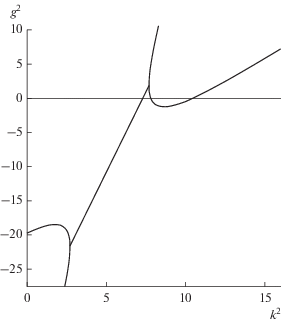
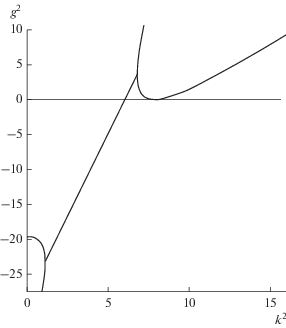
При значении ε₃, среднем гармоническим между ε₁ и ε₂, возникает явление касания дисперсионной кривой оси абсцисс (рис. 4).

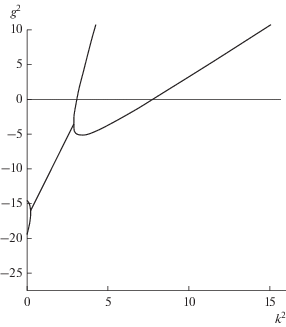
Дальнейшее увеличение параметра ε₃ приводит вновь к пересечению дисперсионной кривой с осью абсцисс (рис. 5).

При значениях ε₃, больших ε₂, как уже отмечалось, обратные волны пропадают (см. рис. 6).

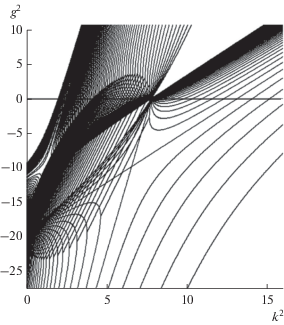
На рис. 7 изображена общая картина поведения дисперсионных кривых при изменении ε₃ от ε₁ до ε₂.

Множество критических точек дисперсионных кривых, соответствующих различным значениям ε₃ образует кривую, напоминающую эллипс.

Справедливо следующее утверждение.

Утверждение 1. Множество особых точек дисперсионных кривых анизотропного волновода квадратного сечения является эллипсом.

Этот эллипс касается оси ординат при значении ε₃ = ${{({{\varepsilon }_{1}} + {{\varepsilon }_{2}})} \mathord{\left/ {\vphantom {{({{\varepsilon }_{1}} + {{\varepsilon }_{2}})} 2}} \right. \kern-0em} 2}$ и имеет тангенс наклона большой оси к оси абсцисс, равный ${{({{\varepsilon }_{1}} + {{\varepsilon }_{2}})} \mathord{\left/ {\vphantom {{({{\varepsilon }_{1}} + {{\varepsilon }_{2}})} 2}} \right. \kern-0em} 2}.$

Моды более высокого порядка, отвечающие одинаковым значениям чисел $n$ и $m$ $(n = m),$ определяют эллипсы, подобные случаю $n = 1,$ $m = 1.$

Вопрос о существовани параметров анизотропии, при которых множество комплексных собственных значений спектральной задачи (17), (18) бесконечно, также может быть разрешен. Приведем следующий пример. Пусть ${{\varepsilon }_{3}} = \tfrac{1}{2}({{\varepsilon }_{1}} + {{\varepsilon }_{2}}).$

Тогда справедливо утверждение.

Утверждение 2. Множество комплексных собственных значений задачи (17), (18) бесконечно.

1.5. Стабилизация решения и резонансное возбуждение

Задача о формулировке условий излучения и применении принципа предельной амплитуды в полом волноводе была решена в работах А.Г. Свешникова (см. [8, 9]). Для возбуждения волновода на частотах, равных частотам отсечки, Раммом и Вернером [38] установлено, что поле неограниченно растет, причем скорость роста пропорциональна $\sqrt t ,$ а не t, как в резонаторе.

Значительно более сложный характер имеет задача возбуждения волновода с неоднородным заполнением. Основная сложность связана с несамосопряженным характером вспомогательной спектральной задачи, даже в случае отсутствия у среды, заполняющей волновод, поглощения. При этом возможно возникновение качественно новых явлений.

В качестве простой частной задачи, которая отражает основные характерные черты общей задачи, продолжим рассмотрение задачи с постоянным, но анизотропным заполнением [39].

Рассмотрим начально-краевую задачу для системы уравнений Максвелла

Будем использовать нулевые начальные условия:

и граничные условия, соответствующие идеально-проводящей стенке:

Задача рассматривается в цилиндре $Q = $ $ = \left\{ {(x,y) \in \Omega ,\,\,\,\,z \in ( - \infty ,\infty )} \right\}$ с квадратным сечением $\Omega = \left\{ {0 < x < 1,\,\,\,\,0 < y < 1} \right\}.$

Данная задача допускает точное решение. Оно легко получается при помощи преобразования Лапласа по временной переменной и преобразования Фурье по координате z. Анализ аналитического решения позволяет сформулировать следующие утверждения.

Утверждение 3. При условии, что частота ${{\omega }_{0}}$ не является критической точкой дисперсионной кривой, решение стабилизируется к гармоническому при стремлении $t$ к бесконечности.

При этом доказано, что возможно возбуждение как прямых волн, так и обратных. Для прямых волн в области стабилилизации решение имеет зависимость от времени и от координаты z, соответствующую уходящей, а для обратных волн приходящей из бесконечности волны. Например, при положительных $z$ для прямой волны имеем зависимость ${\text{exp}}( - i(\omega t - \gamma z)),$ а для обратной ${\text{exp}}( - i(\omega t + \gamma z)).$

Если ${{\gamma }_{2}}({{\omega }_{0}}) = 0$ решение возрастает как $\sqrt t .$ Это соответствует задаче, исследованной Рамом и Вернером, рассматривавшим полый волновод при ${{\omega }_{0}}$ равной частоте отсечки. Принципиально отличным является в анизотропном волноводе касание дисперсионной кривой с осью $\gamma = 0.$ На подобной частоте отсечки обратная волна преобразуется в прямую. Подобная точка возникает при ${{\varepsilon }_{3}} = {{(2{{\varepsilon }_{1}}{{\varepsilon }_{2}}} \mathord{\left/ {\vphantom {{(2{{\varepsilon }_{1}}{{\varepsilon }_{2}}} {({{\varepsilon }_{1}} + {{\varepsilon }_{2}})}}} \right. \kern-0em} {({{\varepsilon }_{1}} + {{\varepsilon }_{2}})}})$ при ${{k}^{2}} = {{\pi }^{2}}({1 \mathord{\left/ {\vphantom {1 {{{\varepsilon }_{1}}}}} \right. \kern-0em} {{{\varepsilon }_{1}}}} + {1 \mathord{\left/ {\vphantom {1 {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}}).$ Дисперсионная кривая изображена на рис. 1.

Справедливо следующее утверждение.

Утверждение 4. В указанной точке касания дисперсионной кривой с осью ${{\gamma }^{2}} = 0$ решение растет как $t{\text{exp}}( - i{{\omega }_{0}}t).$

В результате при резонансном возбуждении волновода поле может нарастать не только как $\sqrt t ,$ но и линейно t, как в резонаторе.

1.6. Применение смешанных конечных элементов

Как было показано выше, задача возбуждения волновода сводится к вычислению мод волновода. Для построения приближенного решения большую популярность приобрел метод смешанных конечных элементов [40–42]. Применение лагранжевых конечных элементов приводит к возникновению нефизических решений [43]. Нулевое собственное значение бесконечной кратности исходной задачи переходит в совокупность ненулевых собственных значений дискретной. Эти ложные собственные значения расположены среди истинных. Их число равно примерно трети от общего числа собственных значений. Подобные решения отсутствуют при применении смешанных конечных элементов, введенных в двумерном случае Равьяром и Тома [40], а в трехмерном Неделеком [42]. Для спектральной задачи теории волноводов, рассматриваемой относительно параметра ${{k}^{2}},$ доказательство сходимости метода смешанных конечных элементов было дано в работе Бермудеса и Педрейры [43]. При этом задача становится самосопряженной, и ее спектр чисто вещественный. Разработанный в работе [43] метод применим для рассматриваемой нами несамосопряженной задачи [44].

Остановимся на основных этапах доказательства сходимости решений дискретной спектральной задачи. Рассмотрим задачу относительно постоянной распространения $\gamma $ и вектора $({{\vec {H}}_{ \bot }},\,\,{{E}_{z}}).$ Будем считать, что магнитная проницаемость $\mu = 1,$ область $\Omega $ – выпуклый многоугольник. Будем рассматривать задачу в гильбертовом пространстве $W = {{H}_{0}}({\text{div}}) \oplus H_{0}^{1},$ ${{\vec {H}}_{ \bot }} \in {{H}_{0}}({\text{div}}),$ ${{E}_{z}} \in H_{0}^{1}.$

Введем в пространстве W полуторалинейные формы:

Будем искать $\vec {A} \in W,$ ${{\gamma }^{2}} \in C,$ удовлетворяющие уравнению

Вектор $\vec {A},$ удовлетворяющий (49) будем называть слабым решением спектральной задачи.

Полуторалинейная форма $a\left( {\vec {A},\vec {\tilde {A}}} \right),$ как легко видеть, удовлетворяет условию W-эллиптичности

где ${{\lambda }_{0}} > \mathop {max}\limits_{(x,y) \in \Omega } \varepsilon (x,y),$ C – константа. В силу теоремы Лакса–Мильграма существует ограниченный оператор T: ${{({{L}_{2}})}^{3}} \to W,$ определяемый равенством

Таким образом, задача (49) эквивалентна спектральной задаче

Особенностью задачи (52) является некомпактность оператора $T$ в пространстве $W$. Некомпактность этого оператора связана с существованием бесконечнократного собственного значения, равного ${{\lambda }_{0}},$ которому отвечает множество собственных векторов вида

Отметим, что оператор $T$ будет компактным в подпространстве $V$ пространства W, выделяемым дополнительным условием:

Напомним, что данное уравнение является слабой формой уравнения (8) и отвечающие ненулевым собственным значениям корневые векторы задачи (49) удовлетворяют этому уравнению.

Рассмотрим вопрос о применении метода смешанных конечных элементов к задаче (49). Будем использовать смешанные конечные элементы, конформные в пространстве $H({\text{div}}).$ Напомним определение смешанных конечных элементов [40].

Считаем, что область $\Omega $ – выпуклый многоугольник. Разобьем область $\Omega $ на треугольники ${{K}_{i}}:\Omega = \cup {{K}_{i}}.$ Введем пространство полиномов

где ${{P}_{{k - 1}}}$ – пространство полиномов, зависящих от $x,y$ степени $k - 1,$ ${{\tilde {P}}_{{k - 1}}}$ – пространство однородных полиномов степени $k - 1,$ r – радиус-вектор.

Введем пространство:

Рассмотрим задачу поиска собственных значений и корневых подпространств в пространстве ${{W}_{h}}{\text{:}}$

В силу W-эллиптичности формы $\bar {a}\left( {\vec {A},{{{\vec {\tilde {A}}}}_{h}}} \right)$ существует оператор ${{T}_{h}}$ такой, что

Таким образом, задача (54) эквивалентна задаче

Максимальный диаметр треугольника ${{K}_{i}}$ обозначим h. Рассмотрим вопрос о сходимости не равных ${{\lambda }_{0}}$ собственных значений и соответствующих им корневых векторов задачи (56) к решениям задачи (52) при $h \to 0.$ Пусть $\sigma (T)$ – множество точек спектра оператора $T,$ $\sigma ({{T}_{h}})$ – оператора ${{T}_{h}}.$

Используем известную теорему о дискретизации задачи на собственные значения с некомпактным оператором, доказанную Деклу, Нассифом и Раппазом [45].

Пусть выполнены условия:

Тогда справедливы утверждения:

1) для любой замкнутой области $D$, не имеющей точек пересечения с $\sigma (T),$ найдется ${{h}_{0}}$ такое, что при $h \leqslant {{h}_{0}}$ область $D$ не имеет точек пересечения с $\sigma ({{T}_{h}});$

2) для любого изолированного собственного значения кратности m найдется m характеристических значений ${{\lambda }_{{ih}}} \to \lambda $ при h, стремящемся к нулю;

3) корневые подпространства оператора ${{T}_{h}}$ сходятся к корневым пространствам оператора $T$ при h, стремящемся к нулю.

В работе [44] доказано, что задача (56) удовлетворяет условиям приведенной теоремы. Доказательство в целом является применением метода работы [43] к нашей задаче.

Таким образом, применение смешанных конечных элементов позволяет правильно аппроксимировать дифференциальную задачу.

2.1. Постановка задачи

Рассмотрим вопрос о существовании решения задачи дифракции на диэлектрическом теле в волноводе. Исследование энергетических оценок, дающих решение подобной задачи, проводилось в случае рассеивателя с поглощением в работе [11]. В наших работах [29–31] предположение о наличии в среде поглощения отсутствует.

Задача рассматривается в цилиндре Q = $ = ((x,y) \in \Omega ,$ $z \in ( - \infty ,\infty )).$ Область $\Omega $ – односвязная, граница области $\partial \Omega $ состоит из конечного числа бесконечно дифференцируемых дуг и удовлетворяет условию конуса. Задача описывается системой уравнений Максвелла, приведенной к виду

На боковой поверхности всюду за исключением угловых точек поставим граничные условия

Параметр $k$ – вещественный. Функция $\varepsilon $ удовлетворяет условию $1 \leqslant \varepsilon \leqslant {{\varepsilon }_{{{\text{max}}}}}$ в области ${{V}_{0}},$ занятой диэлектрическим телом, $\varepsilon \equiv 1,\,\,(x,y,z) \notin {{V}_{0}}.$ Считаем, что диэлектрическое тело лежит в области ${{z}_{1}} + \tau < z < {{z}_{2}} - \tau .$ Область ${{\overline V }_{0}}$ представима в виде объединения конечного числа областей ${{\overline V }_{0}} = \bigcup\nolimits_i {{{{\overline V }}_{i}}} .$ В областях ${{V}_{i}}$ с кусочно-гладкими границами функция $\varepsilon $ бесконечно-дифференцируемая. Будем искать решение $\vec {H},$ бесконечно дифференцируемое, в областях ${{\overline V }_{i}}$ всюду за исключением ребер и конических точек.

На гладких участках поверхностей разрыва $S$ диэлектрической проницаемости поставим условия сопряжения

В качестве условия на ребре потребуем

т.е. условие ограниченности ${{L}_{2}}$ нормы векторов $\vec {H}$ и ${\text{rot}}\vec {H}$ в любой конечной подобласти цилиндра $Q.$

Поставим парциальные условия излучения Свешникова [8] в качестве условий на бесконечности: в областях $z < {{z}_{1}} + \tau ,$ $z > {{z}_{2}} - \tau .$

Пусть ${{\chi }_{n}},{{\psi }_{n}}$ – собственные функции задачи

Обозначим

Считаем, что ${{k}^{2}} \ne {{\lambda }_{{1n}}},$ ${{k}^{2}} \ne {{\lambda }_{{2n}}}$. Считаем, что из $ - \infty $ падает нормальная волна вида $\vec {H} = A{\text{rot}}{{\chi }_{m}}{{\vec {e}}_{z}}{\text{exp}}(i{{\gamma }_{{1m}}})z,$ где $A$ – константа, $m \leqslant {{N}_{1}}.$ Условия излучения представим в виде требования о представимости вектора $Н$ при $z < {{z}_{1}} + \tau ,$ $z > {{z}_{2}} - \tau $ в виде сходящихся в ${{({{L}_{2}}(\Omega ))}^{2}}$ рядов

2.2. Слабое решение задачи рассеяния

Умножая уравнение (57) на произвольный достаточно гладкий вектор $\vec {\tilde {H}},$ удовлетворяющий граничным условиям (58) и условиям сопряжения (59), и интегрируя по частям с учетом парциальных условий излучения (62), (63), получим

Введем полуторалинейные формы

и линейную форму

В обозначениях (64) уравнение (65) примет вид

Для определения слабого решения задачи (57)–(63) необходимо ввести векторное функциональное пространство, в котором будем рассматривать задачу.

В областях $z \leqslant {{z}_{1}} + \tau ,$ $z \geqslant {{z}_{2}} - \tau $ компоненты магнитного поля H, представимого в виде рядов (62)–(63) связаны соотношениями

Введем функциональное пространство, на элементы которого наложим условия (69) на следы вектора H:

Условия (69) являются необходимым элементом определения пространства $\mathcal{V}$. Они приводят к компактности вложения пространства $\mathcal{V}$ в ${{L}_{2}}.$ В то же время эти условия не являются излишне ограничительными и не препятствуют тому, чтобы слабое решение задачи являлось классическим.

Будем называть вектор $\vec {H} \in \mathcal{V}$ слабым решением задачи (57)–(63), если он удовлетворяет уравнению (68) для любого $\vec {\tilde {H}} \in \mathcal{V}.$

Рассмотрим сначала вопрос о существовании слабого решения задачи (57)–(63), т.е. решения задачи (68). Это решение является и классическим решением задачи (57)–(63).

Полуторалинейная форма $a\left( {\vec {H},\vec {\tilde {H}}} \right)$ задает скалярное произведение в пространстве $\mathcal{V}$. Пространство $\mathcal{V}$ является гильбертовым с нормой, порождаемой скалярным произведением $a\left( {\vec {H},\vec {\tilde {H}}} \right).$

Для элементов пространства $\mathcal{V}$ определена полуторалинейная форма $b\left( {\vec {H},\vec {\tilde {H}}} \right).$ Доказательство этого утверждения будет дано ниже.

В силу теоремы Рисса существует ограниченный в пространстве $\mathcal{V}$ оператор $T$ и вектор $\vec {F},$ такие что

Уравнение (68) сводится к уравнению

Справедлива следующая теорема.

Теорема 8. Оператор $T$ компактный в пространстве $\mathcal{V}$.

Отсюда следует не только фредгольмовость, но и существование решения задачи (57)–(63). Действительно, справедливо утверждение.

Утверждение 5. Если при некотором вещественном $k$ существует нетривиальное решение однородного уравнения (71), то ядро сопряженного уравнения ортогонально правой части уравнения (68).

Значение параметра может отвечать ловушечной моде. Утверждение 5 означает, что это не влияет на существование решения задачи рассеяния. В то же время возможна потеря единственности решения.

Доказательство компактности оператора $T$ сводится к следующему утверждению.

Утверждение 6. Из любой ограниченной в норме пространства $\mathcal{V}$ последовательности, можно выделить фундаментальную подпоследовательность по норме, которую обозначим ${{\left\| {\vec {H}} \right\|}_{W}}{\text{:}}$

Утверждение разобьем на две теоремы.

Теорема 9. Пространство $\mathcal{V}$ компактно вложено в ${{({{L}_{2}}(V))}^{3}}.$

Теорема 10. Из любой ограниченной по норме $\mathcal{V}$ последовательности можно выделить сходящуюся подпоследовательность по полунорме

В результате, оператор $T$ – компактный. Тогда задача (68) разрешима.

Утверждение 7. Слабое решение задачи (68) является классическим.

То, что это решение является классическим в областях, в которых диэлектрическая проницаемость гладкая функция, а также то, что решение удовлетворяет в классическом смысле условиям сопряжения на гладких участках поверхностей разрыва, доказывается стандартно. Интерес представляет вопрос о поведении решения вблизи сечений ${{\Omega }_{i}}$. Доказано [29], что слабое решение является классическим.

2.3. Теоремы вложения для векторных функциональных пространств

Векторное функциональное пространство $H({\text{rot}}) \cup {{H}_{0}}({\text{div}})$ содержит в себе соболевское пространство ${{\dot {H}}^{1}}(V).$ Однако в случае кусочно-гладкой границы области $V$ оно не является подмножеством ${{H}^{1}}(V).$ Теоремам вложения для векторных функциональных пространств посвящено большое количество работ.

Применяемый в наших работах [29] метод доказательства теорем вложения использовался для учета граничных условий на сечениях цилиндра. В то же время он применим для областей достаточно общего вида. Поясним метод вначале для следующей частной задачи. Пусть $V$ – цилиндр конечной высоты:

Основание цилиндра $\Omega $ – односвязная область с границей, состоящей из конечного числа гладких дуг, соединяющихся под ненулевыми углами.

Справедлива следующая теорема.

Теорема 11. Пространство $H({\text{rot}},V) \cap {{H}_{0}}({\text{div}},V)$ вложено в ${{L}_{2}}(V)$ компактно.

Для доказательства достаточно рассмотреть случай когда векторы $H$ удовлетворяют условию ${\text{div}}\vec {H} = 0.$ Представим вектор $\vec {H}$ в виде ряда

и учтем, что

Учитывая граничные условия, имеем

Учитывая, что $\left\| {\vec {H}} \right\|_{{{{L}_{2}}(V)}}^{2}$ равна

приходим к доказательству теоремы.

Теорема может быть распространена на некоторые области более широкого класса. Пусть область ${{V}_{1}}$ гладко взаимно однозначно отображается в цилиндр $V$ указанного ранее вида.

Введем криволинейные координаты (x¹, x², x³) и декартовы координаты (y¹, y², y³), такие что

Считаем, что область изменения координат (x¹, x², x³) – цилиндр V, ось x³ направлена вдоль оси цилиндра: $V = \left\{ {\left( {{{x}^{1}},{{x}^{2}}} \right) \in \Omega ,\,\,\,\,{{x}^{3}} \in \left[ {x_{1}^{3},x_{2}^{3}} \right]} \right\}.$ Отображение цилиндра $V$ в область ${{V}_{1}}$

удовлетворяет условию

где

– метрический тензор. Считаем, что

где $g = {\text{det}}{{g}_{{ij}}}.$ Запишем выражение ${\text{rot}}H$ и ${\text{div}}H$ в криволинейной системе координат относительно ковариантных координат вектора $H$

${{r}^{i}}$ – вектор с координатами ${{\partial {{y}^{j}}} \mathord{\left/ {\vphantom {{\partial {{y}^{j}}} {\partial {{x}^{i}}}}} \right. \kern-0em} {\partial {{x}^{i}}}}.$

Вектор $\sqrt g {{g}^{{ij}}}{{H}_{j}}$ – контравариантный. В результате на границе прямолинейного цилиндра $V$ выполняются условия

где ${{n}_{j}}$ – вектор нормали к границе цилиндра $V$, поскольку

где ${{\vec {n}}_{1}}$ – вектор нормали к границе области ${{V}_{1}}.$

Кроме того,

Поскольку

то

Следовательно, если ввести обозначения

то в прямолинейном цилиндре $V$ получим

В результате из любой ограниченной по норме пространства $H({\text{rot}},{{V}_{1}})$ последовательности ${{H}_{n}},$ такой что ${\text{div}}{{\vec {H}}_{n}}0,$ ${{\left. {{{{\vec {H}}}_{n}}\vec {n}} \right|}_{{\partial {{V}_{1}}}}} = 0,$ можно выделить фундаментальную последовательность ${{\vec {A}}_{n}}$ в пространстве ${{L}_{2}}(V).$ Поскольку

то фундаментальной является и последовательность ${{\vec {H}}_{n}}$ в пространстве ${{L}_{2}}({{V}_{1}}).$

Если область ${{V}_{2}}$ может быть покрыта конечным числом перекрывающихся областей типа ${{V}_{1}},$ то для нее, очевидно, имеет место сформулированная теорема вложения. Аналогичным образом могут быть рассмотрены конические точки границы. Указанный метод доказательства разрешимости задачи рассеяния в волноводе применим и к задаче рассеяния в свободном пространстве. Общность используемого подхода позволяет учитывать рассеиватели, представляющие собой как магнитодиэлектрические, так и металлические тела.