Радиотехника и электроника, 2019, T. 64, № 12, стр. 1181-1189
Обнаружение групп точечных объектов в пространствах различных размерностей по признаку пространственной компактности
А. В. Кревецкий *
Поволжский государственный технологический университет
424000 Йошкар-Ола, пл. Ленина, 3, Российская Федерация
* E-mail: KrevetskyAV@volgatech.net
Поступила в редакцию 22.12.2017
После доработки 16.03.2019
Принята к публикации 25.03.2019
Аннотация
Рассмотрены изображения групп точечных объектов (ГТО), заданных в одномерном, двумерном и трехмерном пространствах. Показано, что введение абстрактного математического объекта – ассоциированного сплошного образа (АСО), связывающего элементы ГТО, позволяет использовать инвариантную к конфигурации ГТО меру пространственной компактности. Задача обнаружения компактных, в том числе частично маскированных ГТО, сведена к простой в вычислительном плане и инвариантной к ракурсу наблюдения процедуре обнаружения контрастных площадных объектов или аналогичной по результату задаче структурного анализа графа иерархической группировки элементов ГТО сцены. Получены характеристики обнаружения ГТО для различных условий наблюдения.
ВВЕДЕНИЕ
Изображения групп точечных объектов (ГТО) в задачах распознавания образов часто ассоциируют с локационными отметками групп обнаруженных малоразмерных объектов, созвездиями, особыми точками изображений крупноразмерных объектов, представлениями кластеров сигналов в признаковом пространстве [1–4]. Сложность распознавания ГТО как для человеческого сознания, так и для технической системы во многом определяется несвязностью элементов изображения ГТО [1, 4], что затрудняет восприятие ГТО как целостного объекта, обладающего формой. В отличие от крупноразмерных объектов, распознавание ГТО по их первичным описаниям затруднено также из-за узости главного лепестка автокорреляционной функции их изображений по параметрам смещения, масштаба и углового рассогласования, из-за координатных шумов и других помех.
В различные годы большой вклад в развитие методов и систем обработки изображений ГТО внесли авторы работ [1, 2, 4–8].
Установлена высокая информативность формы взаимного расположения объектов ГТО для их распознавания. Проанализированы применяемые модели описания формы ГТО в виде различных графов, вектор-пучков, матриц геометрии при их задании на плоскости или пространстве действительного, комплексного или кватернионного переменного [10–14]. В последние годы вышел ряд работ, связанных с распознаванием 3D и обобщенных в монографии [1].
В перечисленных выше работах [1, 4, 9–11, 13] речь идет о ГТО со стационарной конфигурацией, элементы которых статистически связаны с эталонными положениями, и делается допущение о принадлежности множества наблюдаемых точечных объектов одному ГТО. Это может не соблюдаться в реальной ситуации из-за ошибок первого и второго рода при обнаружении элементов ГТО, отсутствии сведений о числе ГТО в сцене, ГТО может быть нестационарным и частично маскированным.
Преодолеть указанные трудности можно, перейдя к распознаванию ГТО по вторичным признакам. Однако для этого сначала необходимо обнаружить и пространственно разрешить ГТО.
В работе рассмотрен подход, позволяющий за счет введения в модель описания ГТО абстрактного математического объекта – ассоциированного сплошного образа – решить задачу обнаружения пространственно компактных ГТО на фоне из ложных отметок инвариантно к конфигурации ГТО и ракурсу наблюдения. Данный подход обобщен на изображения ГТО в пространствах различной размерности.
1. ПОСТАНОВКА ЗАДАЧИ
Предположим, что задачи обнаружения отдельных точечных и малоразмерных объектов на фоне крупноразмерных объектов решены, а результаты обнаружения предъявлены в виде множества
(1)
$V = \left\{ {{{{v}}_{n}}} \right\} = \left\{ {{{{\mathbf{x}}}_{n}},{{s}_{n}}} \right\},\,\,\,\,n = 1,2,...,N,$Данное множество можно представить в виде
(2)
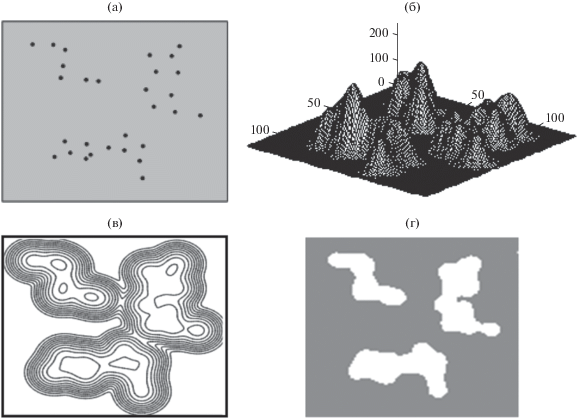
$s\left( {\mathbf{x}} \right) = \sum\limits_{n = 1}^N {{{s}_{n}}\delta \left( {{\mathbf{x}} - {{{\mathbf{x}}}_{n}}} \right)} ,\,\,\,\,{\mathbf{x}} \in {\mathbf{X}},$Рис. 1.
Примеры изображений с ГТО: а – в криволинейной системе координат; б – на плоскости; в – в трехмерном пространстве.

С учетом возможных ошибок обнаружения точечных и малоразмерных объектов наблюдаемую точечную сцену можно представить в виде смеси ложных ${{s}_{b}}\left( {\mathbf{x}} \right)$ = $\sum\nolimits_{n = 1}^{{{N}_{b}}} {{{s}_{{bn}}}\delta \left( {{\mathbf{x}} - {{{\mathbf{x}}}_{{bn}}}} \right)} $ и правильно обнаруженных полезных отметок ${{s}_{g}}\left( {\mathbf{x}} \right)$ = = $\sum\nolimits_{n = 1}^{{{N}_{g}}} {{{s}_{{gn}}}\delta \left( {{\mathbf{x}} - {{{\mathbf{x}}}_{{gn}}}} \right)} {\text{:}}$
(3)
$s\left( {\mathbf{x}} \right) = {{s}_{b}}\left( {\mathbf{x}} \right) + \Theta {{s}_{g}}\left( {\mathbf{x}} \right),$2. МОДЕЛЬ ГТО С АССОЦИИРОВАННЫМ СПЛОШНЫМ ОБРАЗОМ
Не нарушая общности, введем в выражения (3) новый математический объект h(x) – ассоциированный сплошной образ (АСО), – представляющий собой сплошное, т.е. в отличие от ГТО связное изображение, ограничивающее область расположения ГТО своими ненулевыми значениями:
(4)
$\begin{gathered} {{s}_{g}}\left( {\mathbf{x}} \right) = h\left( {{\mathbf{x}},{{{\mathbf{x}}}_{0}},\mu ,{{\varphi }_{0}}} \right)\sum\limits_{n = 1}^{{{N}_{g}}} {{{s}_{n}}\delta \left( {{\mathbf{x}} - {{{\mathbf{x}}}_{n}}} \right)} , \\ \delta \left( {{{{\mathbf{x}}}_{n}}} \right)h\left( {{\mathbf{x}},{{{\mathbf{x}}}_{0}},\mu ,{{\varphi }_{0}}} \right) \ne 0\forall n. \\ \end{gathered} $Здесь добавление аргументов ${{{\mathbf{x}}}_{0}},\mu ,{{\varphi }_{0}}$ формально показывает смещение, масштаб и разворот ГТО в системе координат точечной сцены по отношению к его эталонному описанию. Введя нулевую гипотезу (${{h}_{0}}\left( {\mathbf{x}} \right) = 0\forall {\mathbf{x}}$), с учетом (4) модель наблюдаемого ГТО k-го класса примет вид
(5)
$s\left( {\mathbf{x}} \right) = {{s}_{b}}\left( {\mathbf{x}} \right) + {{h}_{k}}\left( {{\mathbf{x}},{{{\mathbf{x}}}_{0}}\mu ,{{\varphi }_{0}}} \right){{s}_{{gk}}}\left( {\mathbf{x}} \right).$Отметим, что формальное введение в модель наблюдаемого изображения ГТО ассоциированного образа никак не изменяет равенство выражений (3) и (5), но добавляет важные параметры геометрических рассогласований.
3. МОДЕЛИ ФОРМИРОВАНИЯ АСО
В качестве модели АСО был использован результат пороговой обработки расфокусированного изображения ГТО (рис. 2):
(6)
$\begin{gathered} h\left( {\mathbf{x}} \right) = \left\{ {\begin{array}{*{20}{l}} {1,\,\,{\text{if}}\,\,F\left( {\mathbf{x}} \right) \geqslant t,} \\ {0,\,\,{\text{if}}\,\,F\left( {\mathbf{x}} \right) < t,} \end{array}} \right. \\ F\left( {\mathbf{x}} \right) = \int\limits_X {s\left( {\mathbf{v}} \right)a\left( {{\mathbf{x}} - {\mathbf{v}}} \right)d{\mathbf{v}}} = \sum\limits_{n = 1}^N {{{s}_{n}}a\left( {{\mathbf{x}} - {{{\mathbf{x}}}_{n}}} \right)} , \\ \end{gathered} $(7)
$a\left( {{\mathbf{x}}{\text{|}}b} \right) = \exp \left( { - {{{{{\left\| {\mathbf{x}} \right\|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left\| {\mathbf{x}} \right\|}}^{2}}} {2{{b}^{2}}}}} \right. \kern-0em} {2{{b}^{2}}}}} \right),$(8)
$a\left( {\left. {\mathbf{x}} \right|b} \right) = \left\{ {\begin{array}{*{20}{c}} {1,\,\,{\text{if}}\,\,\left\| {\mathbf{x}} \right\| \leqslant b,} \\ {0,\,\,{\text{if}}\,\,\left\| {\mathbf{x}} \right\| > b,} \end{array}} \right.$Рис. 2.
Формирование АСО: а – машинный кадр $s\left( {\mathbf{x}} \right),$ б – рельефный портрет расфокусированного изображения, в – линии уровня яркостного рельефа, г – ассоциированные сплошные образы.
Значение t пороговой яркости целесообразно назначать на уровне максимального градиента склона границы расфокусированного изображения F(x): t > 0 – для (8), $t = \exp \left( {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}} \right) \approx 0.607$ – для (7).
Отметим, что АСО вводится как дополнительный математический объект, использующийся далее для связывания элементов ГТО в единый образ, пространственного ограничения (разрешения) ГТО и определения дополнительных признаков распознавания – площади (или объема), формы занимаемой ГТО области и мощности ГТО. Привычная ассоциация расфокусировки изображений крупноразмерных объектов с потерей информации и ухудшением качества изображения здесь не имеет значения – исходные данные о координатах точечных объектов сцены хранятся в памяти вычислителя, никуда не исчезают и используются в дальнейшем.
4. МЕРА ПРОСТРАНСТВЕННОЙ КОМПАКТНОСТИ
Как показано в [9], при неизвестной заранее форме АСО важнейшим информативным признаком, отличающим область расположения ГТО от фона из ложных отметок, служит более высокая плотность точечных объектов. Плотность характеризует степень пространственной близости (компактности) бесконечных полей точечных объектов. Результаты ее измерения по ограниченным в пространстве выборкам зависят от размеров и формы апертуры измерителя, подсчитывающего локальное число точечных объектов. Рассмотрим не зависящий от апертуры и, следовательно, от конфигурации ГТО механизм измерения компактности множеств точечных объектов в пространстве.
Из рассмотренной модели АСО следует “естественный” в данном случае критерий компактности множества точек и мера компактности точек ГТО. Два множества точек ${{Q}_{i}}$ и ${{Q}_{j}}$ при заданном уровне ограничения по яркости t и радиусе дефокусирующего фильтра b являются компактными, если все их элементы располагаются во внутренней области общего АСО:
(9)
${{J}_{C}}\left( {{{Q}_{i}},{{Q}_{j}}} \right) = \left\{ {\begin{array}{*{20}{c}} {0,\,\,{\text{if}}\,\,{{h}_{i}}\left( {\mathbf{x}} \right) \cap {{h}_{j}}\left( {\mathbf{x}} \right) = 0,} \\ {1,\,\,{\text{if}}\,\,{{h}_{i}}\left( {\mathbf{x}} \right) \cap {{h}_{j}}\left( {\mathbf{x}} \right) \ne 0.} \end{array}} \right.$Тогда роль меры компактности этих двух множеств может играть минимальный “радиус” b импульсной характеристики дефокусирующего фильтра, при котором АСО этих двух множеств начинают сливаться:
(10)
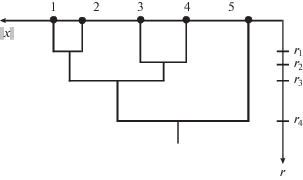
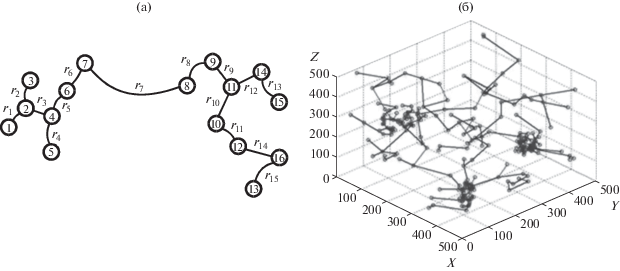
$r\left( {{{Q}_{i}},{{Q}_{j}}} \right) = \mathop {\inf }\limits_b \left( {{{{\left. {{{J}_{C}}\left( {{{Q}_{i}},{{Q}_{j}}} \right)} \right|}}_{b}} = 1} \right).$Таким образом, для определения компактности всех пар подмножеств точек в сцене s(x) необходимо, монотонно изменяя b, фиксировать его значения в моменты слияния их АСО. Результатом такой процедуры становится граф (дендрограмма) иерархической группировки (рис. 3, 4).
Рис. 4.
Изображение дендрограмм иерархической группировки в виде графа на плоскости исходной точечной сцены (а) и в трехмерном пространстве (б).
Следует отметить, что при использовании импульсной характеристики дефокусирующего фильтра (8) для формирования АСО мера $r\left( {{{Q}_{i}},{{Q}_{j}}} \right)$ соответствует евклидовому расстоянию r = 2b между ближайшими точками подмножеств. При использовании колоколообразного фильтра (7) из-за кумулятивности F(x) величина $r\left( {{{Q}_{i}},{{Q}_{j}}} \right)$ не соответствует евклидовому расстоянию, так как компактные подмножества из большего числа точек будут объединяться при меньших r нежели подмножества меньшей мощности при прочих равных условиях. Аналитически соотнести меру $r\left( {{{Q}_{i}},{{Q}_{j}}} \right)$ с евклидовым расстоянием легко лишь для случая всего двух одинаковых по яркости точек – их АСО сольются, если они будут на расстоянии $r = b2\sqrt {1 + 2\ln 2} \approx 3.09b$ [12].
Рассмотренная мера компактности подобна мере для построения графа иерархической группировки в методе потенциальных функций теории обучения машин [15 ] . Алгоритм ее вычисления не зависит от конфигурации ГТО, т.е. инвариантен к его классу и ракурсу наблюдения.
5. ПОСТАНОВКА ЗАДАЧИ ОБНАРУЖЕНИЯ ПРОСТРАНСТВЕННО КОМПАКТНЫХ ГТО
Очевидно, что мощность k связных графом иерархической группировки подмножеств точек на заданном уровне компактности $r \leqslant {{r}_{0}}$ статистически связана с плотностью точек. Это обстоятельство позволяет допустить использование k в качестве локальных мер плотности точек.
Относительно наблюдения s(x) выдвинем две альтернативные статистические гипотезы:
1) H0 – группа образована исключительно ложными отметками,
2) H1 – группа представляет собой смесь точек ГТО и ложных отметок. Необходимо вынести обоснованное решение Н в пользу одной из данных гипотез, если условные относительно r распределения вероятностей мощности k для пространственно компактных групп из смеси точек ГТО и фона $P(z = k{\text{|}}{{H}_{1}},\,\,r \leqslant {{r}_{0}})$ = ${{W}_{z}}\left( {k{\text{|}}{{H}_{1}},\,\,r \leqslant {{r}_{0}}} \right),$ а также групп исключительно из точек фона ${{W}_{z}}\left( {k{\text{|}}{{H}_{0}},\,\,r \leqslant {{r}_{0}}} \right)$ заданы. Здесь z – случайная величина мощности множества точек инцидентных смежным ребрам произвольного подграфа минимального дерева сцены с компактностью $r \leqslant {{r}_{0}}$ ($r$ – длина ребра графа иерархической группировки точечной сцены, ${{r}_{0}}$ – пороговая длина ребра).
6. СИНТЕЗ ОПТИМАЛЬНЫХ РЕШАЮЩИХ ПРАВИЛ
В общем виде оптимальный в байесовском смысле алгоритм обнаружения ГТО при такой постановке задачи состоит в вычислении функций правдоподобия двух гипотез путем подстановки в указанные условные распределения вероятностей мощности k каждой группы точек, инцидентных $k - 1$ смежным ребрам минимального дерева точечной сцены, вычислению отношения правдоподобия $\lambda \left( k \right)$ и сравнению его с порогом:
(11)
$\lambda \left( k \right) = \frac{{{{W}_{z}}\left( {k\left| {{{H}_{1}},\,\,r \leqslant {{r}_{0}}} \right.} \right)}}{{{{W}_{z}}\left( {k\left| {{{H}_{0}},\,\,r \leqslant {{r}_{0}}} \right.} \right)}}\begin{array}{*{20}{c}} {\mathop > \limits^{{{H}_{1}}} } \\ {\mathop < \limits_{{{H}_{0}}} } \end{array}{{\lambda }_{0}},$Для вычисления (11) и получения характеристик обнаружения необходимо знать соответствующие распределения вероятностей, которые в реальных условиях обычно неизвестны. Однако для получения нижних оценок вероятностей правильного обнаружения можно задаться случаем наибольшей априорной неопределенности касательно конфигурации ГТО. Этому случаю соответствует случайное равномерное поле точечных отметок в пределах занимаемой ГТО области с плотностью ${{p}_{g}}.$ Так как пороги обнаружения элементов ГТО в сцене стараются локально оптимизировать по критерию Неймана–Пирсона, то в качестве модели ложных отметок также примем случайное равномерное поле с плотностью ${{p}_{b}}.$ Конкретизируем участвующие в (11) законы распределения вероятностей для приведенных допущений.
Пусть $\xi $ – случайная длина ребра в минимальном дереве точечной сцены, соответствующем графу иерархической группировки (см. рис. 3, 4). Тогда функцию распределения вероятностей мощности z компактной случайной группы можно представить в виде
где $g = P\left( {\xi \leqslant {{r}_{0}}} \right)$ – вероятность непревышения значения $\xi $ порога r0. Закон распределения дискретной случайной мощности z выразим через разность функций распределения вероятностей:(13)
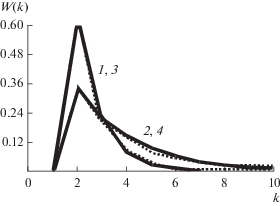
$\begin{gathered} {{W}_{z}}\left( k \right) = P\left( {z = k} \right) = P\left( {z < k} \right) - \\ - \,\,P\left( {z < k - 1} \right) = \left( {1 - g} \right){{g}^{{k - 2}}},\,\,\,\,k = 2,3,... \\ \end{gathered} $На рис. 5 приведены теоретические (сплошные кривые) и полученные по методу Монте-Карло экспериментальные (пунктирные) распределения вероятностей мощности компактных групп случайных равномерных полей точек с параметрами g = 0.7 и 0.4.
Рис. 5.
Рассчитанные (1, 2) и экспериментальные полученные методом Монте-Карло (3, 4) распределения вероятностей мощности компактных групп при g = = 0.7 (1, 3), 0.4 (2, 4).
Чтобы конкретизировать $g = P\left( {\xi \leqslant {{r}_{0}}} \right)$, выполним шаги, подобные (12) и (13) для пространств различной размерности.
1. Одномерное пространство:
(14)
$g = P\left( {\xi \leqslant r} \right) = 1 - P\left( {\xi > r} \right) = 1 - {{\left( {1 - p} \right)}^{r}}$(15)
${{r}_{0}} = \frac{{\ln \left( {1 - {{F}_{r}}} \right)}}{{\ln \left( {1 - {{p}_{b}}} \right)}}.$2. Двумерная точечная сцена. Поскольку даже в растровом изображении длина ребра, соединяющего точки, может принимать нецелые значения, целесообразно воспользоваться асимптотикой Пуассона:
Эта формула определяет вероятность того, что ни одна случайная отметка потока интенсивности p не попадет в полукруг радиусом r. Тогда
(16)
$g = P\left( {\xi \leqslant r} \right) = 1 - \exp \left( {{{ - p\pi {{r}^{2}}} \mathord{\left/ {\vphantom {{ - p\pi {{r}^{2}}} 2}} \right. \kern-0em} 2}} \right),$На рис. 6 представлены рассчитанные и экспериментально полученные законы распределения длин ребер минимального дерева для двух параметров: $p = {{50} \mathord{\left/ {\vphantom {{50} {\left( {256 \times 256} \right)}}} \right. \kern-0em} {\left( {256 \times 256} \right)}}$ и $p = {{20} \mathord{\left/ {\vphantom {{20} {\left( {256 \times 256} \right)}}} \right. \kern-0em} {\left( {256 \times 256} \right)}}.$
Рис. 6.
Рассчитанные (1, 2) и экспериментальные (3, 4) распределения длин ребер минимального дерева в 2D-пространстве при 50/(256 × 256) (1, 3) и р = = 20/(256 × 256) (2, 4).
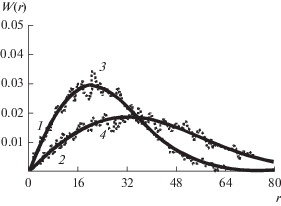
Из (16) по аналогии с (15) следует
(17)
${{r}_{0}} = {{\left( { - \frac{{2\ln \left( {1 - {{F}_{r}}} \right)}}{{{{p}_{b}}\pi }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$3. Трехмерное пространство:
$P\left( {\xi > r} \right)$ = ${{\left( {1 - p} \right)}^{{{{2{\pi }{{r}^{3}}} \mathord{\left/ {\vphantom {{2{\pi }{{r}^{3}}} 3}} \right. \kern-0em} 3}}}}$ ∼ $\exp \left( {{{ - p2\pi {{r}^{3}}} \mathord{\left/ {\vphantom {{ - p2\pi {{r}^{3}}} 3}} \right. \kern-0em} 3}} \right)$ – вероятность непопадания в полушарие с радиусом r соседней отметки,
(18)
$g = P\left( {\xi \leqslant r} \right) = 1 - \exp \left( {{{ - p2\pi {{r}^{3}}} \mathord{\left/ {\vphantom {{ - p2\pi {{r}^{3}}} 3}} \right. \kern-0em} 3}} \right),$${{W}_{\xi }}\left( r \right) = \frac{{dP\left( {\xi \leqslant r} \right)}}{{dr}}$ = $\frac{{{{r}^{2}}}}{{{{\sigma }^{2}}}}\exp \left( {\frac{{ - {{r}^{3}}}}{{3{{\sigma }^{2}}}}} \right)$ – плотность вероятности длин ребер минимального дерева трехмерной точечной сцены, ${{\sigma }^{2}} = {1 \mathord{\left/ {\vphantom {1 {p2\pi }}} \right. \kern-0em} {p2\pi }},$
(19)
${{r}_{0}} = \sqrt[3]{{{{ - 3\ln \left( {1 - {{F}_{r}}} \right)} \mathord{\left/ {\vphantom {{ - 3\ln \left( {1 - {{F}_{r}}} \right)} {{{p}_{b}}2\pi }}} \right. \kern-0em} {{{p}_{b}}2\pi }}}}\,.$На рис. 7 приведены теоретические плотности распределения вероятностей (сплошные кривые) и соответствующие им выборочные распределения (штрихпунктирные) для интенсивностей точечных отметок p = 50/(255 × 255 × 255) и p = = 20/(255 × 255 × 255).
Рис. 7.
Рассчитанные (1, 2) и экспериментальные (3, 4) распределения длин ребер минимального дерева в 3D-пространстве при 50/(256 × 256 × 256) (1, 3) и р = = 20/(256 × 256 × 256) (2, 4).
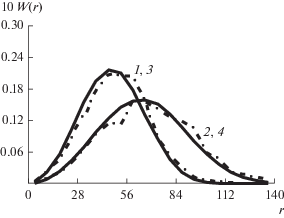
Все рассмотренные в данном разделе теоретические законы распределения вероятностей соответствуют экспериментальным по двустороннему критерию согласия для уровня значимости 0.05.
Подставим в отношение правдоподобия (11) условные законы (13) с параметрами (14), (16) или (18) при соответствующих плотностях ${{\left. p \right|}_{{{{H}_{0}}}}} = {{p}_{b}}$ для фона из ложных отметок и ${{\left. p \right|}_{{{{H}_{1}}}}} = {{p}_{{bg}}}$ = ${{p}_{g}} + {{p}_{b}}$ для области смеси элементов ГТО и фона. После логарифмирования и приведения подобных слагаемых получим, что оптимальный алгоритм обнаружения ГТО по признаку пространственной компактности на основе минимальной достаточной статистики сводится к следующему.
Шаг 1. Выполняется дефокусировка точечной сцены фильтром с радиусом импульсной характеристики b, соответствующим уровню компактности r0, и формирование ассоциированных сплошных образов (6).
Шаг 2. Осуществляется группировка подмножеств точечных отметок путем пространственной локализации ассоциированными сплошными образами с компактностью $r \leqslant {{r}_{0}}.$ (Отметим, что Шаг 2 может выполняться двумя способами: 1) на основе определения цвета в координатах каждого точечного объекта сцены после заливки каждого АСО сцены своим цветом (например, с кодом, равным номеру соответствующего замкнутого контура яркой области [9]); 2) на основе определения связных вершин после разрушения длинных ребер ($r > {{r}_{0}}$) минимального остовного дерева точечной сцены.)
Шаг 3. Принимается решение для каждой компактной группы на основе сравнения ее мощности k с порогом k0:
(20)
$H = \left\{ {\begin{array}{*{20}{c}} {{{H}_{1}},\,\,{\text{if}}\,\,k \geqslant {{k}_{0}},} \\ {{{H}_{0}},\,\,{\text{if}}\,\,k < {{k}_{0}}.} \end{array}} \right.$Для критерия Неймана–Пирсона значение порога k0 – квантиль закона распределения вероятностей ${{W}_{z}}\left( {k{\text{|}}{{H}_{0}},\,\,r \leqslant {{r}_{0}}} \right),$ который находится по заданному уровню ложных тревог Fk из уравнения
7. ХАРАКТЕРИСТИКИ ОБНАРУЖЕНИЯ И ПРОСТРАНСТВЕННОЙ ЛОКАЛИЗАЦИИ ГТО
С учетом обозначений $g = P\left( {\xi \leqslant {{r}_{0}}{\text{|}}{{H}_{0}}} \right) = {{F}_{r}}$ и $g = P\left( {\xi \leqslant {{r}_{0}}{\text{|}}{{H}_{1}}} \right) = {{D}_{r}}$ запишем условные законы распределения компактности (длин ребер минимального дерева) полей точечных отметок, формулы для расчета оптимальной пороговой компактности и расчета вероятности правильной локализации точечных отметок, инцидентных одному ребру минимального дерева. В скобках в верхнем индексе укажем размерность пространства:
(22)
$\begin{gathered} W_{\xi }^{{\left( 1 \right)}}\left( {r\left| {{{H}_{0}}} \right.} \right) = {{p}_{b}}{{\left( {1 - {{p}_{b}}} \right)}^{{r - 1}}}, \\ W_{\xi }^{{\left( 1 \right)}}\left( {r\left| {{{H}_{1}}} \right.} \right) = {{p}_{{bg}}}{{\left( {1 - {{p}_{{bg}}}} \right)}^{{r - 1}}}, \\ r_{0}^{{\left( 1 \right)}} = \frac{{\ln \left( {1 - {{F}_{r}}} \right)}}{{\ln \left( {1 - {{p}_{b}}} \right)}},\,\,\,\,D_{r}^{{\left( 1 \right)}} = 1 - {{\left( {1 - {{p}_{{bg}}}} \right)}^{{{{r}_{0}}}}}, \\ \end{gathered} $(23)
$\begin{gathered} W_{{\xi }}^{{\left( 2 \right)}}\left( {r\left| {{{H}_{0}}} \right.} \right) = \frac{r}{{\sigma _{1}^{2}}}\exp \left( {\frac{{ - {{r}^{2}}}}{{2\sigma _{1}^{2}}}} \right), \\ W_{{\xi }}^{{\left( 2 \right)}}\left( {r\left| {{{H}_{1}}} \right.} \right) = \frac{r}{{\sigma _{2}^{2}}}\exp \left( {\frac{{ - {{r}^{2}}}}{{2\sigma _{2}^{2}}}} \right), \\ r_{0}^{{\left( 2 \right)}} = \sqrt { - 2\sigma _{1}^{2}\ln \left( {1 - {{F}_{r}}} \right)} , \\ D_{r}^{{\left( 2 \right)}} = 1 - \exp \left( { - \frac{{r_{0}^{2}}}{{2\sigma _{2}^{2}}}} \right), \\ \end{gathered} $(24)
$\begin{gathered} W_{{\xi }}^{{\left( 3 \right)}}\left( {r\left| {{{H}_{0}}} \right.} \right) = \frac{{{{r}^{2}}}}{{\sigma _{3}^{2}}}\exp \left( {\frac{{ - {{r}^{3}}}}{{3\sigma _{3}^{2}}}} \right), \\ W_{{\xi }}^{{\left( 3 \right)}}\left( {r\left| {{{H}_{1}}} \right.} \right) = \frac{{{{r}^{2}}}}{{\sigma _{4}^{2}}}\exp \left( {\frac{{ - {{r}^{3}}}}{{3\sigma _{4}^{2}}}} \right), \\ r_{0}^{{\left( 3 \right)}} = \sqrt[3]{{ - 3\sigma _{3}^{2}\ln \left( {1 - {{F}_{r}}} \right)}}, \\ D_{r}^{{\left( 3 \right)}} = 1 - \exp \left( { - \frac{{r_{0}^{3}}}{{3\sigma _{4}^{2}}}} \right), \\ \end{gathered} $Подстановка в (13) вероятностей образования ложных и правильных компактных ребер вместо величины g дает общие для различных размерностей пространств выражения условных законов для отношения правдоподобия (11):
(25)
$\begin{gathered} {{W}_{z}}\left( {k\left| {{{H}_{0}}} \right.} \right) = \left( {1 - {{F}_{r}}} \right)F_{r}^{{k - 2}}, \\ {{W}_{z}}\left( {k\left| {{{H}_{1}}} \right.} \right) = \left( {1 - {{D}_{r}}} \right)D_{r}^{{k - 2}}, \\ \end{gathered} $а также вероятностей ложной тревоги и правильного обнаружения ГТО:
(26)
$\begin{gathered} {{F}_{k}} = P\left( {k \geqslant {{k}_{0}}{\text{|}}{{H}_{0}}} \right) = F_{r}^{{{{k}_{0}} - 1}}, \\ {{D}_{k}} = P\left( {k \geqslant {{k}_{0}}{\text{|}}{{H}_{1}}} \right) = D_{r}^{{{{k}_{0}} - 1}}. \\ \end{gathered} $Для построения характеристик обнаружения достаточно для фиксированного значения ${{F}_{k}}$ по заданному ${{k}_{0}}$ определить ${{F}_{r}} = \sqrt[{{{k}_{0}} - 1}]{{{{F}_{k}}}},$ затем по формулам (22), (23) или (24) рассчитать ${{D}_{r}}$ и подставить их в (26).
Проиллюстрируем анализ характеристик обнаружения ГТО на примере двухмерного пространства. В этом случае
(27)
${{D}_{k}} = {{\left( {1 - {{{\left( {1 - {{F}_{r}}} \right)}}^{d}}} \right)}^{{{{k}_{0}} - 1}}} = {{\left( {1 - {{{\left( {1 - \sqrt[{{{k}_{0}} - 1}]{{{{F}_{k}}}}} \right)}}^{d}}} \right)}^{{{{k}_{0}} - 1}}},$Рис. 8.
Характеристики обнаружения ГТО: а – рассмотренного алгоритма при k0 = 10 для уровней ложных тревог ${{F}_{k}}$ = 10–1, 10–2, 10–3, 10–4 (сплошные кривые 1–4) и при ${{F}_{k}} = {{10}^{{ - 2}}}$ и ${{k}_{0}}$ = 13, 11, 9, 7, 5 (пунктир 5–9); б – сравнение известного (1–4) и рассмотренного (5–8, 9–12) алгоритма обнаружения пространственно компактных ГТО при различных параметрах (см. текст).
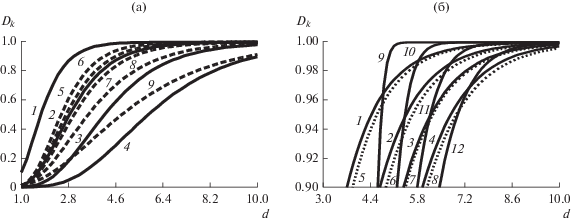
На рис. 8б сопоставлены характеристики рассмотренного нами и известного ранее алгоритмов обнаружения ГТО на фоне ложных отметок. Графики 1–4 соответствуют характеристикам известного двумерного аналога цифрового обнаружителя “k из n” [9] с окном подсчета числа точечных отметок, согласованным с АСО площадью 2500 пикселей. Зависимости ${{D}_{k}}\left( d \right)$ получены для ${{F}_{k}}$ = 10–1, 10–2, 10–3, 10–4 (см. слева направо) для плотности ложных отметок ${{p}_{b}}$ = 50/256 × 256 и ${{p}_{{bg}}} = d{{p}_{b}}.$ Указанные уровни ложных тревог достигаются здесь при порогах по мощности ${{k}_{0}}$ ≈ 4, 5, 6, 7 соответственно.
Графики 5–8 соответствуют характеристикам рассмотренного алгоритма для случайного равномерного ГТО. Те же уровни ложных тревог и близкие значения ${{D}_{k}}$ достигаются при порогах по мощности ${{k}_{0}}$ = 6, 10, 14, 17, т.е. в 1.5–2.4 раза более строгих. Графики 9–12 соответствуют исследуемому алгоритму при обнаружении существенно более регулярного ГТО с расстоянием между соседними элементами, распределенном по нормальному закону ${{W}_{{\xi }}}\left( r \right) = N\left( {{{m}_{r}},{{\sigma }_{r}}} \right),$ ${{m}_{r}} = {{\left[ {{{p}_{b}}\left( {d - 1} \right)} \right]}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$ В связи со слабой зависимостью ${{D}_{k}}\left( d \right)$ от ${{F}_{k}}$ и ${{k}_{0}}$ графики 9–12 построены для фиксированных ${{F}_{k}} = {{10}^{{ - 4}}}$ и ${{k}_{0}} = 3,$ отличающихся значениями СКО: ${{\sigma }_{r}}$ = 5, 10, 15, 20% от ${{m}_{r}}$ (см. слева направо). Так, при обнаружении ГТО с достаточно регулярным расположением элементов Dk = 0.95 достигается при пороговых отношениях плотностей фона и ГТО, близких к таковым значениям аналога обнаружителя “k из n” на основе подсчета точек в окне заданной формы [9].
ЗАКЛЮЧЕНИЕ
Таким образом, исследованный в работе метод обнаружения ГТО использует связывание точечных отметок ГТО ассоциированным сплошным образом или графом иерархической группировки по введенной мере компактности. Алгоритм синтезируется подобно цифровому обнаружителю, но в качестве отсчетов используется не интенсивность точечных отметок, а длины ребер графа.
Версия алгоритма обнаружения ГТО на основе формирования ассоциированного сплошного образа оказывается менее “жадной” в вычислительном плане по сравнению с графовой. По результатам моделирования в двумерных сценах выигрыш наступает, когда число точек в сцене начинает превышать 100.
Достоинства описанного алгоритма обнаружения ГТО заключаются в следующем: 1) инвариантность к ракурсу наблюдения вследствие инвариантности алгоритмов локализации ГТО к соответствующим преобразованиям, 2) инвариантность к форме и, следовательно, к номеру класса ГТО, поскольку точки группируются естественным образом по критерию компактности, 3) попутное формирование оценок вторичных признаков ГТО, необходимых для последующего распознавания (таких как мощность, занимаемая площадь, форма АСО, статистические параметры законов распределения расстояний между соседними элементами), 4) для формализации параметров алгоритма достаточно знать лишь среднюю плотность ложных отметок.
Отсутствие априорной информации о конфигурации ГТО компенсируется приемлемым для практики увеличением порогового числа точек ГТО или соответствующим ему увеличению пороговой плотности ГТО.
Список литературы
Фурман Я.А., Роженцов А.А., Хафизов Р.Г. и др. Точечные поля и групповые объекты. М.: Физматлит, 2014.
Верба В.С. Обнаружение наземных объектов. Радиолокационные системы обнаружения и наведения воздушного базирования. М.: Радиотехника, 2007.
Мандель И.Д. Кластерный анализ. М.: Финансы и статистика, 1988.
Анисимов В.В., Курганов В.Д., Злобин В.К. Распознавание и цифровая обработка изображений. М.: Высш. школа, 1983.
Gowda K.C., Krishna G. // Pattern Recognition. 1978. V. 10. № 2. P. 105.
Ogawa H. // Pattern Recognition. 1984. V. 17. № 5. P. 569.
Fränti P., Virmajoki O., Hautamäki V. // IEEE Trans. 2006. V. PAMI-28. № 11. P. 1875. Warnekar C.S., Krishna G.A. // Pattern Recognition, 1979. V. 11. № 2. P. 85.
Фурман Я.А., Кревецкий А.В., Передреев А.К. и др. Введение в контурный анализ; приложения к обработке изображений и сигналов. 2-е изд. М.: Физматлит, 2003.
Фурман Я.А., Кревецкий А.В., Роженцов А.А. и др. Комплекснозначные и гиперкомплексные системы в задачах обработки многомерных сигналов. М.: Физматлит, 2004.
Кревецкий А.В. // Программные системы и вычислительные методы. 2016. № 4. С. 392.
Кревецкий А.В. // Вестник МарГТУ. Радиотехнические и инфокоммуникационные системы. 2011. № 1. С. 47.
Кревецкий А.В., Чесноков С.Е. // Автометрия, 2002. № 3. С. 80.
Кревецкий А.В., Чесноков С.Е. // Кибернетика и программирование. 2016. № 6. С. 30.
Дуда Р., Харт П. Распознавание образов и анализ сцен. М.: Мир, 1976.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника