Радиотехника и электроника, 2019, T. 64, № 2, стр. 116-122
Формовременная динамика субнаносекундных радиоимпульсов при распространении в гетерогенных средах
М. С. Костин 1, *, В. М. Викулов 1, С. С. Тамбовский 1
1 МИРЭА – Российский технологический университет
119454 Москва, просп. Вернадского, 78, Российская Федерация
* E-mail: mihailkos@mail.ru
Поступила в редакцию 12.04.2018
После доработки 01.06.2018
Принята к публикации 11.06.2018
Аннотация
Представлены результаты радиофизических исследований формовременной динамики субнаносекундных импульсов при их распространении в гетерогенных средах: отражение от наклонной плоской поверхности; прохождение через диэлектрик. Исследовано влияние эффективной площади рассеяния облучаемой поверхности, а также влияния диэлектрических потерь на формочастотную динамику распределения напряженности поля гауссовских радиоимпульсов. Показаны особенности формовременной и спектральной трансформации распределения напряженности электрической компоненты поля сверхкороткоимпульсных сигналов. Сформулированы основные результаты исследований.
ВВЕДЕНИЕ
Для сверхкоротких импульсов (СКИ), аппроксимируемых гауссовской моделью, при тех же преобразованиях, что и для узкополосных (сложение, вычитание, дифференцирование и интегрирование), свойственно изменение не только перечисленных параметров, но и трансформация распределения напряженности электрической компоненты поля – формы радиоимпульса.
Исследование механизма формоизменения гауссовского СКИ без несущего частотного заполнения является чрезвычайно важным, поскольку для решения ряда задач субнаносекундной радиолокации и сверхширокополосной радиосвязи необходимо учитывать факторы, влияющие на формоизменение СКИ, например, при оценке импульсной характеристики облучаемой цели или в решении радиотехнических задач обнаружения или оптимальной фильтрации сверхширокополосных сигналов [1].
Пусть цифровым приемопередатчиком сформирован видеосигнал s, который токовым импульсом поступает на антенну. Первое изменение его профиля ${{s}_{1}} = {{ds(t)} \mathord{\left/ {\vphantom {{ds(t)} {dt}}} \right. \kern-0em} {dt}}$ – моноцикл Гаусса, происходит в момент излучения, поскольку известно, что напряженность электрического поля, излучаемого антенной, изменяется пропорционально производной тока в антенне. Второе изменение профиля СКИ может происходить в том случае, когда пространственная протяженность импульса, определяемая произведением $c{{{\tau }}_{S}}$ (${{{\tau }}_{S}}$ – длительность радиоимпульса, c – скорость света в вакууме), меньше линейного размера излучателя. В этом случае импульсы электромагнитной волны будут излучаться, образуя серию ${{s}_{2}}$ из суммы СКИ, смещенных во времени на величину ${{\tau }_{k}}\,:$
(1)
${{s}_{2}} = \sum\limits_{k = 1}^N {ds(} t + {{{{\tau }_{k}})} \mathord{\left/ {\vphantom {{{{\tau }_{k}})} {dt}}} \right. \kern-0em} {dt}}.$Третье изменение профиля СКИ ${{s}_{3}}$ происходит при его отражении от зондируемой поверхности, которая в общем случае может представлять собой структуру из отражающих элементов, образующих профильную геометрию конструкции длиной L. В том случае, если $c{{\tau }_{s}} \ll L,$ импульс ${{s}_{3}}$ поочередно отражается от отдельных элементов поверхности, образуя импульсную последовательность, параметры которой (число импульсов, взаимная обратная задержка во времени ${{\tau }_{m}},$ интенсивность) зависят от геометрической структуры поверхности и импульсных характеристик ${{h}_{m}}$ ее элементов. При этом импульсная последовательность формируется за время $\Delta t = {{2L} \mathord{\left/ {\vphantom {{2L} c}} \right. \kern-0em} c}$ и представляет собой распределение функции [2]:
(2)
${{s}_{3}} = \sum\limits_{m = 1}^M {\sum\limits_{k = 1}^N {\int {\frac{{d{{s}_{1}}(t + {{\tau }_{k}} + {{\tau }_{m}})}}{{dt}}} } } {{h}_{m}}(t - {{\tau }_{m}} - {{\tau }_{s}})dt.$Отсюда ЭПР облучаемой поверхности становится динамической во времени и, как следствие, диаграмма рассеяния, сформированная облучаемой поверхностью – нестационарной. Отсутствие интерференции СКИ-сигналов, отраженных от элементов поверхности, исключает нули в диаграмме рассеяния, т.е. явление интерференции носит слабо выраженный характер. Элементы поверхности могут выполнять роль частотных фильтров, что приводит к дополнительному изменению формы профиля СКИ. Четвертое формоизменение СКИ происходит в момент его радиоприема по аналогии с излучением: импульсы тока, наведенного полем в разных частях антенны, будут сдвинуты во времени из-за разности хода сигнала. Пятое формоизменение СКИ возможно при его распространении через диэлектрические среды за счет затухания различных участков его спектра [2].
Из перечисленных особенностей формовременной динамики СКИ без несущего заполнения можно сделать вывод о принципиально малой эффективности их согласованной фильтрации, поскольку априори предсказать формоизменение профиля СКИ – затруднительная радиофизическая задача. Тем не менее формоизменения, связанные с приемом и излучением, достаточно успешно поддаются расчету, в то время другие электродинамические процессы как, например, отражение, прохождение через диэлектрические препятствия, в некотором смысле, остаются мало изученными.
Цель данной работы – исследование влияния угла наклона облучаемой поверхности, а также диэлектрические потери на особенности формовременной и спектральной трансформации распределения напряженности электрической компоненты поля СКИ.
1. ВЛИЯНИЕ ЭФФЕКТИВНОЙ ПЛОЩАДИ РАССЕЯНИЯ ОБЛУЧАЕМОЙ ПОВЕРХНОСТИ НА ФОРМОДИНАМИКУ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕННОСТИ ПОЛЯ СКИ
Как показывают исследования, характер формоизменения отраженных от поверхности СКИ во многом будет зависеть не только от радиофизических свойств материала этой поверхности, но и во многом от показателя эффективной площади ее рассеяния (ЭПР), которая в общем представлении имеет следующий вид:
(3)
${{\sigma }_{{{\text{Э П Р }}}}} = 4\pi {{r}^{2}}{{E_{{{\text{о т р }}}}^{2}} \mathord{\left/ {\vphantom {{E_{{{\text{о т р }}}}^{2}} {E_{{{\text{п а д }}}}^{2}}}} \right. \kern-0em} {E_{{{\text{п а д }}}}^{2}}},$По существу, в этом выражении сравниваются плотности мощности двух волн – отраженной и падающей на поверхность; оно может быть выражено через пиковые значения полей:
(4)
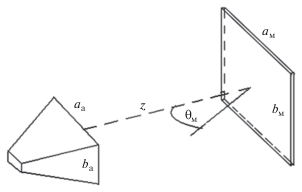
${{\sigma }_{{{\text{Э П Р }}}}} = 4\pi {{r}^{2}}{{\left| {\frac{{{{E}_{{{\text{о т р (м а к с )}}}}}}}{{{{E}_{{{\text{п а д (м а к с )}}}}}}}} \right|}^{2}}.$Исследуем влияния угла наклона ${{\theta }_{{\text{м }}}}$ и ЭПР металлической пластины (площадь ${{S}_{{\text{м }}}},$ стороны ${{а }_{{\text{м }}}}$ и ${{b}_{{\text{м }}}}$) на формовременную трансформацию распределения электрической компоненты поля СКИ (рис. 1). Для этого произведем численное моделирование СКИ-волнового процесса во временной области.
Рис. 1.
Схема расположения плоской отражательной поверхности пластины относительно раскрыва антенны.
В качестве зондирующей антенны используем апертурную с раскрывом ${{S}_{{\text{а }}}}$ и сторонами ${{а }_{{\text{а }}}}$ и ${{b}_{{\text{а }}}},$ поскольку для нее известно решение поля в дальней зоне. Положим, что распределение поля и тока в раскрыве – равномерные; форма поля, возбуждающего антенну имеет вид гауссовского видеоимпульса
(5)
${{s}^{{(n)}}}(t) = {{G}_{0}}\frac{{{{d}^{n}}}}{{d{{t}^{n}}}}\left( {\exp \left( { - \frac{{{{t}^{2}}}}{{2\sigma _{s}^{2}}}} \right)} \right),$Далее будем считать, что функция распределения поля равна ${{E}_{{\text{a}}}}(t) = s(t);$ причем ${{E}_{0}} = {{G}_{0}};$ также будем полагать, что падающая на поверхность волна отражается без потерь; относительно линии визирования пластина повернута в горизонтальной плоскости на угол ${{\theta }_{{\text{м }}}}.$
Как известно, в дальней зоне (при $z \gg {{b}_{{\text{а }}}},{{a}_{{\text{a}}}}$) распределение электрического поля апертурной антенны имеет следующее решение:
(6)
$E(t) = \frac{{1 + \cos {{\theta }_{{\text{а }}}}}}{{4\pi с z}}\int\limits_{{{ - {{a}_{а }}} \mathord{\left/ {\vphantom {{ - {{a}_{а }}} 2}} \right. \kern-0em} 2}}^{{{{{a}_{а }}} \mathord{\left/ {\vphantom {{{{a}_{а }}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{b}_{а }}} \mathord{\left/ {\vphantom {{ - {{b}_{а }}} 2}} \right. \kern-0em} 2}}^{{{{{b}_{а }}} \mathord{\left/ {\vphantom {{{{b}_{а }}} 2}} \right. \kern-0em} 2}} {\frac{{d{{E}_{{\text{a}}}}\left( {t - \frac{{z{\text{'}}}}{c}} \right)}}{{dt}}} } dxdy,$Полагая, что ${{\theta }_{{\text{а }}}},{{\varphi }_{{\text{а }}}} = 0,$ подставим в подынтегральное выражение (6) видеоимпульс (5). Тогда функция распределения напряженности поля падающей на поверхность волны имеет вид
(7)
${{E}_{{{\text{п а д }}}}}(t) = \frac{{t{{S}_{{\text{а }}}}{{E}_{{\text{а }}}}}}{{\pi zc\sigma _{s}^{2}}}\exp \left( { - \frac{{{{t}^{2}}}}{{\sigma _{s}^{2}}}} \right)$(8)
$\left| {{{E}_{{{\text{п а д (м а к с )}}}}}} \right| = \frac{{{{S}_{{\text{a}}}}{{E}_{0}}}}{{\pi zc{{\sigma }_{s}}\sqrt {2e} }}.$Распределение поля на пластине характеризуется формой падающей на ее поверхность волны. При повороте пластины на угол ${{\theta }_{{\text{м }}}}$ переизлученное поле в дальней зоне по аналогии с (6) имеет вид
(9)
$E\left( t \right) = \frac{{1 + \cos {{\theta }_{{\text{м }}}}}}{{4\pi с z}}\int\limits_{{{ - {{a}_{{\text{м }}}}} \mathord{\left/ {\vphantom {{ - {{a}_{{\text{м }}}}} 2}} \right. \kern-0em} 2}}^{{{{{a}_{{\text{м }}}}} \mathord{\left/ {\vphantom {{{{a}_{{\text{м }}}}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{b}_{{\text{м }}}}} \mathord{\left/ {\vphantom {{ - {{b}_{{\text{м }}}}} 2}} \right. \kern-0em} 2}}^{{{{{b}_{{\text{м }}}}} \mathord{\left/ {\vphantom {{{{b}_{{\text{м }}}}} 2}} \right. \kern-0em} 2}} {\frac{{d{{E}_{{{\text{п а д }}}}}\left( {t - {{z{\text{'}}} \mathord{\left/ {\vphantom {{z{\text{'}}} c}} \right. \kern-0em} c}} \right)}}{{dt}}} } dxdy,$где $z{\text{'}} = z - \sin {{\theta }_{{\text{м }}}}(x\cos {{\varphi }_{{\text{м }}}} + y\sin {{\varphi }_{{\text{м }}}})$ – расстояние от поверхности до раскрыва антенны. Считая ${{\varphi }_{{\text{м }}}} = 0,$ проинтегрируем выражение (9) по переменной y, тогда
(10)
$\begin{gathered} {{E}_{{{\text{о т р }}}}}(t) = \frac{{\left( {1 + \cos {{\theta }_{{\text{м }}}}} \right){{b}_{{\text{м }}}}}}{{4\pi с z}} \times \\ \times \,\,\int\limits_{ - \frac{{{{a}_{{\text{м }}}}}}{2}}^{\frac{{{{a}_{{\text{м }}}}}}{2}} {\frac{{d{{E}_{{{\text{п а д }}}}}\left( {t - \frac{{x\sin ({{\theta }_{{\text{м }}}})}}{c}} \right)}}{{dt}}} dx. \\ \end{gathered} $Подставив (7) в (10), получим выражение, описывающее распределение напряженности поля отраженной волны (рис. 2):
(11)
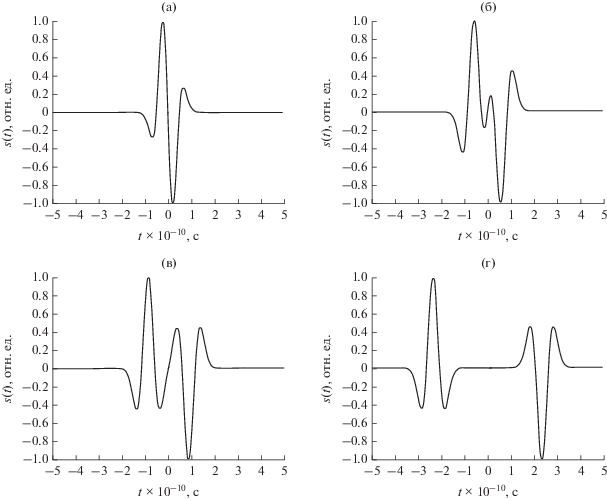
$\begin{gathered} {{E}_{{{\text{о т р }}}}}(t) = \frac{{\left( {1 + \cos {{\theta }_{{\text{м }}}}} \right){{b}_{{\text{м }}}}{{E}_{0}}{{S}_{{\text{а }}}}}}{{8{{{\left( {\pi zc{{\sigma }_{s}}} \right)}}^{2}}\sin {{\theta }_{{\text{м }}}}}} \times \\ \times \,\,\left[ {A\exp \left( { - \frac{{{{A}^{2}}}}{{2c\sigma _{s}^{2}}}} \right) + A{\text{'}}\exp \left( { - \frac{{A{{{\text{'}}}^{2}}}}{{2c\sigma _{s}^{2}}}} \right)} \right], \\ \end{gathered} $Рис. 2.
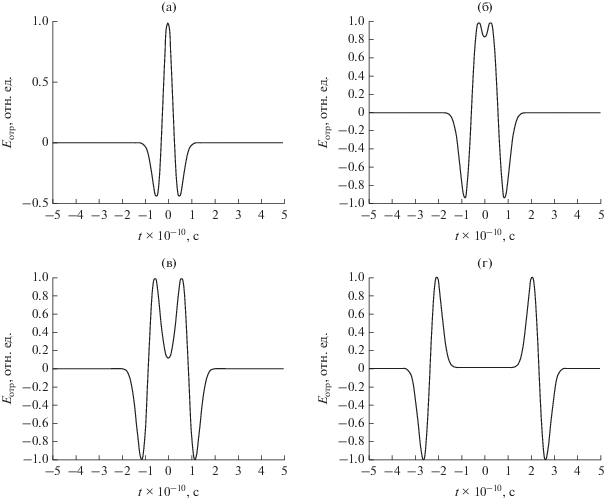
Нормированные эпюры функции ${{E}_{{{\text{о т р }}}}}(t)$ для СКИ длительностью 200 пс, ${{a}_{{\text{м }}}} = 20$ см при θм = 0 (а), 10 (б), 15 (в) и 45 град (г).
где $A = {{a}_{{\text{м }}}}\sin {{\theta }_{{\text{м }}}} - 2tc;$ $A{\text{'}} = {{a}_{{\text{м }}}}\sin {{\theta }_{{\text{м }}}} + 2tc.$
По аналогии с (11) можно получить выражение для связи распределения поля при наклоне поверхности и в вертикальном направлении, найдя полное решение для поля из интегрального выражения (9).
Проанализируем выражение (11). На рис. 2 приведены графики распределения напряженности электрического поля отраженной волны в зависимости от угла наклона поверхности ${{\theta }_{{\text{м }}}}$ при ${{a}_{{\text{м }}}} = {{b}_{{\text{м }}}} = 20$ см (из условия программно-численного эксперимента).
При ${{\theta }_{{\text{м }}}} \to 0$ функция (11) описывает модель СКИ второго порядка ${{s}^{{(2)}}}(t)$ (рис. 2а):
(12)
${{E}_{{{\text{о т р }}}}}(t) = \frac{{{{E}_{0}}{{S}_{{\text{а }}}}{{S}_{{\text{м }}}}}}{{2{{{\left( {\pi zc\sigma _{s}^{2}} \right)}}^{2}}}}\left[ {\left( {2{{t}^{2}} - \sigma _{s}^{2}} \right)\exp \left( { - \frac{{{{t}^{2}}}}{{\sigma _{s}^{2}}}} \right)} \right],$(13)
$\left| {{{E}_{{{\text{о т р (м а к с )}}}}}} \right| = \frac{{{{E}_{0}}{{S}_{{\text{а }}}}{{S}_{{\text{м }}}}}}{{2{{{\left( {\pi zc{{\tau }_{s}}} \right)}}^{2}}}}.$Таким образом, увеличение угла наклона зондируемой поверхности (рис. 2б–2г) влияет на формоизменение СКИ, выраженное перераспределением напряженности поля радиоимпульса, что в данном случае, при ${{\theta }_{{\text{м }}}} \geqslant 20^\circ ,$ ведет к образованию импульсной последовательности. Следовательно, в случае опрокидывающих пластину моментов ЭПР будет носить динамический характер и согласно (11) экспоненциально убывать с увеличением угла ${{\theta }_{{\text{м }}}}.$
Учитывая формоизменение СКИ в момент приема при его прохождении через антенну, на входе приемного устройства для эпюр ${{E}_{{{\text{о т р }}}}}(t)$ (рис. 2) соответственно будем иметь радиоимпульсы третьего порядка ${{s}^{{(3)}}}(t)$ (рис. 3).
Подставляя в выражение (4) формулы (8) и (13) – максимальные значения электрических полей, получим выражение для ЭПР исследуемой пластины, расположенной перпендикулярно к линии визирования:
(14)
${{\sigma }_{{{\text{Э П Р (С К И )}}}}} = \frac{{2eS_{{\text{м }}}^{2}}}{{\pi {{{\left( {c{{\tau }_{s}}} \right)}}^{2}}}}.$При этом выражение для ЭПР пластины, облучаемой узкополосным гармоническим сигналом с длиной волны λ, имеет вид
(15)
${{{\sigma }}_{{{\text{Э П Р (У С )}}}}} = {{4{\pi }S_{{\text{м }}}^{2}} \mathord{\left/ {\vphantom {{4{\pi }S_{{\text{м }}}^{2}} {{{\lambda }^{2}}}}} \right. \kern-0em} {{{\lambda }^{2}}}}.$При сравнении выражений (14) и (15) видна аналогия между длиной волны $\lambda $ и пространственной длиной импульса $c{{\tau }_{s}}$ СКИ. Так, в случае равенства $c{{\tau }_{s}} = \lambda $ ЭПР пластины, облучаемой сверхкоротким радиоимпульсом, в 1.3 раза выше, чем в случае с гармоническим сигналом. Действительно, приравняв выражение (14) и (15), получаем соотношение между СКИ и гармоническим сигналом $c{{\tau }_{s}} = 1.3\lambda \,.$
Таким образом, изменение угла наклона ${{\theta }_{{\text{м }}}}$ плоской отражающей поверхности влияет на ЭПР, а следовательно, и на перераспределение напряженности электрического поля отраженной волны субнаносекундного колебания.
2. ВЛИЯНИЕ ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ НА ФОРМОДИНАМИКУ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕННОСТИ СКИ
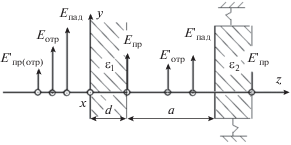
Будем полагать, что электромагнитное поле, облучающее диэлектрическое препятствие, имеет вид плоской волны, нормально падающей на полупространство препятствия с диэлектрической проницаемостью ${{\varepsilon }_{r}}$ и толщиной d (рис. 4). Как известно, коэффициент прохождения t в этом случае выражается через соответствующие импедансы ${{Z}_{i}}$ и волновые числа ${{k}_{i}}\,:$
(16)
$\begin{gathered} t = \frac{{{{E}_{{{\text{п р }}}}}}}{{{{E}_{{{\text{п а д }}}}}}} = \frac{{2{{Z}_{2}}}}{{{{Z}_{2}} + {{Z}_{1}}}} = \frac{{2{{k}_{0}}}}{{{{k}_{0}} + {{k}_{1}}}}{\text{,}} \\ {\text{г д е }}\,\,\,\,{{Z}_{1}} = \frac{{{{E}_{{{\text{п а д }}}}}}}{{{{H}_{{{\text{п а д }}}}}}};\,\,\,\,{{Z}_{2}} = \frac{{{{E}_{{{\text{п р }}}}}}}{{{{H}_{{{\text{п р }}}}}}}, \\ \end{gathered} $(17)
$r = \frac{{{{E}_{{{\text{о т р }}}}}}}{{{{E}_{{{\text{п а д }}}}}}} = \frac{{{{Z}_{2}} - {{Z}_{1}}}}{{{{Z}_{2}} + {{Z}_{1}}}} = \frac{{{{k}_{0}} - {{k}_{1}}}}{{{{k}_{0}} + {{k}_{1}}}}.$Рис. 4.
Характер прохождения СКИ через диэлектрик толщиной d (магнитные составляющие поля не показаны); $E_{{{\text{п р (о т р )}}}}^{'}$ – напряженность электрического поля волны, отраженной от зондируемой поверхности и прошедшей через диэлектрическое препятствие в обратном направлении.
Для каждой гармоники в спектре СКИ коэффициенты прохождения будут иметь свои значения.
Из граничных условий для схемы, приведенной на рис. 4, в общем случае известно решение результирующего коэффициента отражения [3]:
(18)
$\begin{gathered} R(f) = \frac{{E_{{{\text{п р (о т р )}}}}^{'}}}{{{{E}_{{{\text{п а д }}}}}}} = {{K}^{{ - 1}}}\{ ({{r}_{2}} + {{r}_{3}}\exp \left( {j2{{k}_{0}}a} \right) \times \\ \times \,\,\exp \left( {j2{{k}_{1}}d} \right) + {{r}_{1}}(1 + {{r}_{2}}{{r}_{3}}\exp \left( {j2{{k}_{0}}a} \right)\} , \\ \end{gathered} $Исследуем влияние экранирующего диэлектрического слоя ε1 на формоизменение профиля прошедшего СКИ. Для этого удобно выразить коэффициент прохождения через стационарную передаточную функцию и рассматривать его в спектральной области как частотно зависимый коэффициент передачи, который можно аппроксимировать функцией вида
где α – табличный коэффициент затухания в диэлектрике.
Амплитудный спектр прошедшего СКИ ${{S}_{{{\text{п р }}}}}(\omega )$ определяется как результат прохождения зондирующего сигнала со спектром ${{S}_{{{\text{п а д }}}}}(\omega )$ через диэлектрик:
В случае интраскопического облучения металлизированной поверхности через диэлектрик амплитудный спектр обратного прохождения имеет вид
Отсюда можно заключить, что, как и в случае отражения СКИ от проводящей пластины, прохождение субнаносекундного радиоимпульса через однородные диэлектрические среды приводит к перераспределению напряженности электрического поля. Это объясняется тем, что спектр зондирующих импульсов расположен в высокочастотной области, в которой имеет место сильное поглощение спектральных составляющих высших гармоник, и коэффициент прохождения для них мал. Вследствие квадратичной зависимости затухания волны в прямом и обратном прохождении при значительной толщине диэлектрика и величине диэлектрических потерь формоизменения СКИ становятся значительными.
На рис. 5 приведены результаты моделирования, отражающие качественный характер влияния спектропоглощения диэлектриком (${{\varepsilon }_{r}} = 10,$ $\alpha = 10{\text{ }}{{{\text{д Б }}} \mathord{\left/ {\vphantom {{{\text{д Б }}} {{\text{(м }}\,\,{\text{М Г ц )}}}}} \right. \kern-0em} {{\text{(м }}\,\,{\text{М Г ц )}}}},$ $d = 100$ см) на формоизменение временных характеристик для двух аналитических моделей СКИ:
Рис. 5.
Нормированные эпюры распределения напряженности электрического поля СКИ падающего (сплошная кривая) и прошедшего через диэлектрик (пунктирная кривая): а – модель СКИ вида (21); б – модель СКИ вида (22).
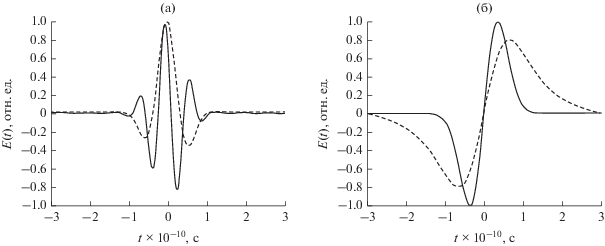
1) с несущим частотным заполнением на частоте ${{f}_{{\text{н }}}}$ (гауссиана) –
(21)
${{s}_{1}}(t) = {{A}_{1}}\exp ({{ - \pi {{t}^{2}}} \mathord{\left/ {\vphantom {{ - \pi {{t}^{2}}} {\sigma _{s}^{2}}}} \right. \kern-0em} {\sigma _{s}^{2}}})\cos (2\pi {{f}_{{\text{н }}}}t)$2) без несущего частотного заполнения –
(22)
${{s}_{2}}(t) = {{A}_{2}}t\exp ({{ - {{t}^{2}}} \mathord{\left/ {\vphantom {{ - {{t}^{2}}} {\sigma _{s}^{2}}}} \right. \kern-0em} {\sigma _{s}^{2}}}).$По результатам численного моделирования, проведенных на базе программной модели, реализующей принцип высокоскоростной атактовой оцифровки СКИ [4] следует (см. рис. 5), что гауссовский СКИ без несущего частотного заполнения, в отличие от гауссиана – с частотным заполнением, претерпевает незначительные изменения профиля поля при прохождении через диэлектрическое препятствие.
Это обусловлено тем, что спектр используемой в работе модели СКИ расположен вблизи нулевого отсчета оси частот, в то время как спектры вещественных моделей типа гауссиан сдвинуты в верхнюю область на несущую частоту ${{f}_{{\text{н }}}}.$ Поскольку влияние диэлектрических потерь существенно в области верхних частот, боковые лепестки СКИ без несущего заполнения становятся более пологими.
ЗАКЛЮЧЕНИЕ
Рассмотренный в работе механизм формовременной и спектральной трансформации распределения напряженности электрической компоненты поля гауссовских СКИ без несущего частотного заполнения при их распространении, отражении и поглощении в гетерогенных средах позволяет судить не только об особенностях применения таких сигналов в сверхширокополосной радиосвязи, но и о возможности применения субнаносекундных радиоимпульсов в таких актуальных направлениях радиофизики, как радиовидение и радиофотонные системы обработки сигналов [5]. Проведенный анализ электродинамических явлений и процессов, влияющих на формоизменение СКИ в неоднородных средах, показал следующие результаты: изменение угла наклона плоской отражающей поверхности влияет на ЭПР, а следовательно, и на перераспределение напряженности электрического поля отраженной волны субнаносекундного колебания; гауссовский СКИ, в отличие от гауссиана, спектр которого сдвинут на несущую частоту заполнения, при прохождении через диэлектрик претерпевает незначительные изменения профиля электрического поля, однако ввиду существенного влияния диэлектрических потерь в области верхних частот боковые лепестки распределения напряженности электрического поля гауссовского СКИ стремятся к более пологой форме.
Полученные в работе результаты аналитических исследований могут быть полезны при оценке и априорном построении импульсной характеристики облучаемой цели, а также в решении задач статистической радиотехники при обнаружении или оптимальной фильтрации сверхширокополосных сигналов.
Список литературы
Budagyan I.F., Kostin M.S. // J. Communications Technology and Electronics. 2015. № 8. V. 60. P. 871–879.
Budagyan I.F., Kostin M.S., Shil’tsin A.V. // J. Comm. Technol. Electron. 2017. V. 62. № 5. P. 512.
Будагян И.Ф., Костин М.С. // Радиоэлектронная техника: межвуз. сб. науч. тр. РАН. Ульяновск: УлГТУ, 2015. С. 104.
Будагян И.Ф., Костин М.С. // Журн. Радиоэлектроника. 2016. № 3. URL: http://jre.cplire.ru/mac/ mar16/5/text.html.
Белкин М.Е., Кудж С.А., Сигов А.С. // Рос. технол. журн. 2016. Т. 4. № 1. С. 4. https://rtj.mirea.ru/upload/ medialibrary/984/rtzh_1_2016_05_07_watermark_updated.pdf.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника