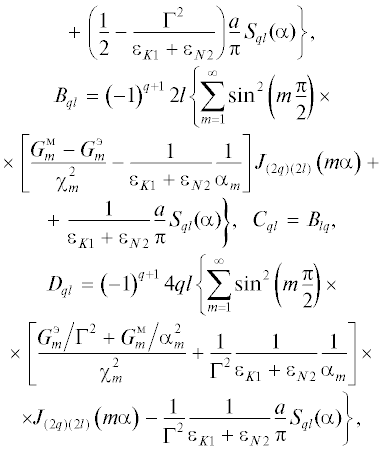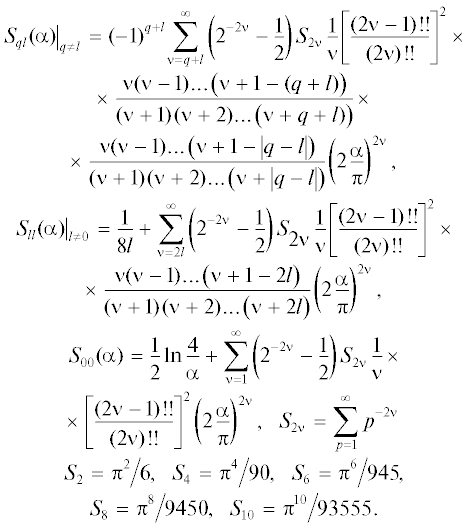Радиотехника и электроника, 2019, T. 64, № 2, стр. 108-115

Проекционный метод построения электродинамических моделей полосковых линий

А. Н. Коваленко^*

МИРЭА – Российский технологический университет
119454 Москва, просп. Вернадского, 78, Российская Федерация

Поступила в редакцию 12.04.2018
После доработки 01.06.2018
Принята к публикации 11.06.2018

DOI: 10.1134/S0033849419020128

Аннотация

Разработан численно-аналитический метод расчета собственных волн полосковых линий, позволяющий получить численные результаты с высокой точностью и с малыми вычислительными затратами. Построена алгебраическая модель микрополосковой линии в многослойной диэлектрической среде. Элементы матрицы системы линейных алгебраических уравнений преобразованы в быстросходящиеся ряды. Получены асимптотические выражения для матричных коэффициентов и асимптотическое решение бесконечной системы линейных алгебраических уравнений. Представлены результаты численного исследования сходимости метода, подтверждающие его эффективность.

ВВЕДЕНИЕ

Полосковые линии различного типа (микрополосковые, щелевые, компланарные и др.) широко используются в радиоэлектронной аппаратуре в качестве линий передач, а также в качестве различных устройств СВЧ. Они составляют основу интегральных схем (ИС) СВЧ. Построение адекватной математической модели сложного СВЧ-устройства, которая как электродинамическая система полностью определяется матрицей рассеяния, практически возможно лишь с использованием декомпозиционного подхода [1]. Декомпозиционный подход позволяет определить матрицу рассеяния сложного полоскового устройства через матрицы рассеяния простейших типовых СВЧ-элементов, которые называют базовыми. К ним относятся отрезки регулярных линий, повороты, тройники, скачкообразные изменения ширины полосковых проводников и др. От того, насколько точно известны матрицы рассеяния каждого базового элемента, зависит конечный результат проектирования всего устройства, в котором общее число базовых элементов может быть весьма большим. Высокую точность расчета характеристик ИС СВЧ могут обеспечить лишь математические модели полосковых линий электродинамического уровня строгости, или электродинамические модели. Построение электродинамических моделей полосковых линий основано на решении краевых задач для уравнений Максвелла. Решение этих задач возможно лишь с использованием численных методов, на основе которых разрабатываются вычислительные алгоритмы и реализующие их компьютерные программы. Наиболее универсальным является проекционный метод построения математических моделей электродинамических систем [2]. Проекционный метод основан на представлении решения краевой задачи, формулируемой как некоторое операторное уравнение, в виде разложения по полной системе функций, образующей базис. Коэффициенты разложения определяются из системы линейных алгебраических уравнений (СЛАУ) путем проектирования операторного уравнения на тот же или другой базис. Эту систему называют проекционной, или алгебраической моделью исходной краевой задачи. Проекционный метод позволяет получить решение граничной задачи, теоретически, с любой степенью точности, но для достижения высокой точности требуется разработка проекционного метода для того или иного класса электродинамических задач. При построении математических моделей полосковых линий проекционным методом возникают сложные проблемы, связанные с учетом особенности поля на металлическом ребре, с явлением относительной сходимости, медленной сходимости бесконечных рядов для матричных коэффициентов СЛАУ, неустойчивостью численных результатов и обоснованием их достоверности. В данной статье эти проблемы решены на основе подхода, предложенного в работе [3], позволяющего свести исходную граничную задачу электродинамики нахождения собственных волн полосковых линий к бесконечной СЛАУ с матрицей коэффициентов, имеющей явно выраженный диагональный характер.

1. ОСНОВНЫЕ РАСЧЕТНЫЕ СООТНОШЕНИЯ

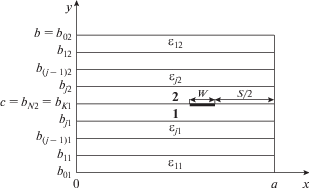
Рассмотрим многослойную направляющую структуру в идеальном прямоугольном экране с размерами $а ,b$ (рисунок 1). В сечении $y = c$ расположен полосковый проводник. В области 1, ниже полоскового проводника ($y < c$), имеется K слоев, в области 2, выше полосковых проводников – N слоев, ${{{\varepsilon }_{{j1,2}}}}$ – относительная диэлектрическая проницаемость среды в j-м слое областей 1 и 2.

Рис. 1.

Поперечное сечение многослойной направляющей структуры.

Решая задачу возбуждения прямоугольного волновода со слоистым диэлектриком поверхностным электрическим током на полосковом проводнике, выразим поле собственных волн через составляющие электрического и магнитного векторных потенциалов ${{U}^{{\text{э }}}}$ и ${{U}^{{\text{м }}}}$ по оси $y$ и представим в виде [3]

(1)

$\begin{gathered} {{E}_{x}} = \frac{{{{\partial }^{{\text{2}}}}{{U}^{{\text{э }}}}}}{{\partial x\partial y}} + {{W}_{{\text{0}}}}\Gamma {{U}^{{\text{м }}}},{{E}_{z}} = - {\text{i}}\Gamma \frac{{\partial {{U}^{{\text{э }}}}}}{{\partial y}} - {\text{i}}{{{\text{W}}}_{{\text{0}}}}\Gamma \frac{{\partial {{U}^{{\text{м }}}}}}{{\partial x}}{\text{,}} \\ {{E}_{y}} = \frac{{{{\partial }^{{\text{2}}}}{{U}^{{\text{э }}}}}}{{\partial {{y}^{{\text{2}}}}}} + {{\varepsilon }_{{j1,2}}}{{U}^{{\text{э }}}}{\text{,}}\,\,\,\,{{H}_{{\text{x}}}} = \frac{{{{\partial }^{{\text{2}}}}{{U}^{{\text{м }}}}}}{{\partial x\partial y}} - \frac{{{{\varepsilon }_{{j1,2}}}}}{{{{W}_{{\text{0}}}}}}\Gamma {{U}^{{\text{э }}}}, \\ {{H}_{z}} = - {\text{i}}\Gamma \frac{{\partial {{U}^{{\text{м }}}}}}{{\partial y}} + {\text{i}}\frac{{{{\varepsilon }_{{j1,2}}}}}{{{{W}_{{\text{0}}}}}}\frac{{\partial {{U}^{{\text{э }}}}}}{{\partial x}}{\text{,}}\,\,\,\,{{H}_{y}} = \frac{{{{\partial }^{{\text{2}}}}{{U}^{{\text{э }}}}}}{{\partial {{y}^{{\text{2}}}}}} + {{\varepsilon }_{{j1,2}}}{{U}^{{\text{м }}}}{\text{,}} \\ \end{gathered} $

где ${{{W}_{0}} = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} }$ – волновое сопротивление свободного пространства, Γ – нормированная (к волновому числу ${{{k}_{0}} = \omega \sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} }$) постоянная распространения. В (1) и последующих выражениях опущен множитель ${\exp (i(\omega t - \Gamma z))}$ и используются безразмерные координаты и элементы длины, переход к которым осуществляется путем умножения их размерных аналогов на волновое число свободного пространства ${{{k}_{{\text{0}}}}}.$

Представим функции ${{U}^{{\text{э }}}}$ и ${{U}^{{\text{м }}}}$ в виде разложений в ряды Фурье по координате x:

$\begin{gathered} {{U}^{{\text{э }}}} = \sum\limits_{m = 1}^\infty {U_{m}^{{\text{э }}}(y)\sin ({{\alpha }_{m}}x)} , \\ {{U}^{{\text{м }}}} = \sum\limits_{m = 0}^\infty {U_{m}^{{\text{м }}}(y)} \cos ({{\alpha }_{m}}x),\,\,\,\,{{\alpha }_{m}} = \frac{\pi }{a}m. \\ \end{gathered} $

Используя неоднородные волновые уравнения для составляющих ${{E}_{y}}$ и ${{H}_{y}}$

$\begin{gathered} \frac{{{{\partial }^{2}}{{E}_{y}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{E}_{y}}}}{{\partial {{x}^{2}}}} + ({{\varepsilon }_{{j1,2}}} - {{{\text{Г }}}^{2}}){{E}_{y}} = \\ = i\frac{{{{W}_{0}}}}{{{{\varepsilon }_{{j1,2}}}}}\left( {\frac{{\partial {{\eta }_{x}}}}{{\partial x}} - i{\text{Г }}{{\eta }_{z}}} \right)\delta {\text{'}}\left( {y - c} \right), \\ \end{gathered} $

$\begin{gathered} \frac{{{{\partial }^{2}}{{H}_{y}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{H}_{y}}}}{{\partial {{x}^{2}}}} + ({{\varepsilon }_{{j1,2}}} - {{{\text{Г }}}^{2}}){{H}_{y}} = \\ = \left( {\frac{{\partial {{\eta }_{z}}}}{{\partial x}} + i{\text{Г }}{{\eta }_{x}}} \right)\delta \left( {y - c} \right) \\ \end{gathered} $

и разложения в ряды Фурье составляющих ${{E}_{y}}$ и ${{H}_{y}}$

$\begin{gathered} {{E}_{y}} = \sum\limits_{m = 1}^\infty {\chi _{m}^{2}U_{m}^{{\text{э }}}(y)\sin ({{\alpha }_{m}}x)} , \\ {{H}_{y}} = \sum\limits_{m = 0}^\infty {\chi _{m}^{2}U_{m}^{м }(y)} \cos ({{\alpha }_{m}}x),\,\,\,\,\chi _{m}^{2} = \alpha _{m}^{2} + {{{\text{Г }}}^{2}}, \\ \end{gathered} $

получим следующие выражения для определения коэффициентов разложений $U_{m}^{{\text{э }}}(y)$ и $U_{m}^{{\text{м }}}(y)$:

$\begin{gathered} \sum\limits_{m = 1}^\infty {\left( {\frac{{{{d}^{2}}U_{m}^{{\text{э }}}}}{{d{{y}^{2}}}} + \beta _{{mj1,2}}^{2}U_{m}^{{\text{э }}}} \right)} \chi _{m}^{2}\sin ({{\alpha }_{m}}x) = \\ = i\frac{{{{W}_{0}}}}{{{{\varepsilon }_{{j1,2}}}}}\left( {\frac{{\partial {{\eta }_{x}}}}{{\partial x}} - i{\text{Г }}{{\eta }_{z}}} \right)\delta '\left( {y - c} \right), \\ \end{gathered} $

$\begin{gathered} \sum\limits_{m = 0}^\infty {\left( {\frac{{{{d}^{2}}U_{m}^{{\text{м }}}}}{{d{{y}^{2}}}} + \beta _{{mj1,2}}^{2}U_{m}^{{\text{м }}}} \right)} \chi _{m}^{2}\cos ({{\alpha }_{m}}x) = \\ = \left( {\frac{{\partial {{\eta }_{z}}}}{{\partial x}} + i{\text{Г }}{{\eta }_{x}}} \right)\delta \left( {y - c} \right), \\ \end{gathered} $

где $\beta _{{mj1,2}}^{2} = {{\varepsilon }_{{j1,2}}} - \chi _{m}^{2},$ ${{{\eta }_{x}}{\text{,}}{{\eta }_{z}}}$ – составляющие поверхностной плотности тока на полосковом проводнике, $\delta {\text{'}}(x)$ – производная δ-функции.

Применяя обратное преобразование Фурье, приведем выражения для функций ${{U}^{{\text{э }}}}$ и ${{U}^{{\text{м }}}}$ к следующему виду [3]:

(2)

$\begin{gathered} {{{U}^{{\text{э }}}} = - \frac{{2\Gamma {{W}_{0}}}}{{a{{\varepsilon }_{{j12}}}}}\sum\limits_{m = 1}^\infty {\frac{{dG_{m}^{{\text{э }}}}}{{dy}}\left( {{{I}_{{zm}}} - \frac{{{{\alpha }_{m}}}}{{{{{\text{Г }}}^{2}}}}{{I}_{{xm}}}} \right)\frac{{{\text{sin(}}{{\alpha }_{m}}x)}}{{\chi _{m}^{2}}}} }, \\ {{{U}^{{\text{м }}}} = - \frac{1}{a}\sum\limits_{m = {\text{0}}}^\infty {G_{m}^{{\text{м }}}\left( {{{I}_{{xm}}} + {{\alpha }_{m}}{{I}_{{zm}}}} \right)\frac{{{{\varepsilon }_{m}}\cos ({{\alpha }_{m}}x)}}{{\chi _{m}^{2}}}} }, \\ \end{gathered} $

где

${{\varepsilon }_{m}} = \left\{ \begin{gathered} 1\,\,\,\,{\text{п р и }}\,\,\,\,m = 0 \hfill \\ {\text{2}}\,\,\,\,{\text{п р и }}\,\,\,\,m \ne 0 \hfill \\ \end{gathered} \right.,$

$\begin{gathered} {{{I}_{{zm}}} = \int\limits_{{{x}_{0}} - {W \mathord{\left/ {\vphantom {W 2}} \right. \kern-0em} 2}}^{{{x}_{0}} + {W \mathord{\left/ {\vphantom {W 2}} \right. \kern-0em} 2}} {{{\eta }_{z}}} \left( {x{\text{'}}} \right){\text{sin(}}{{\alpha }_{m}}x{\text{')}}dx{\text{'}}}, \\ {{{I}_{{xm}}} = \int\limits_{{{x}_{0}} - {W \mathord{\left/ {\vphantom {W 2}} \right. \kern-0em} 2}}^{{{x}_{0}} + {W \mathord{\left/ {\vphantom {W 2}} \right. \kern-0em} 2}} {i{{\eta }_{x}}} \left( {x{\text{'}}} \right){\text{cos(}}{{\alpha }_{m}}x{\text{')}}dx{\text{'}}}, \\ \end{gathered} $

${{{\eta }_{z}}\,\,{\text{и }}\,\,{{\eta }_{x}}}$ – продольная и поперечная составляющие плотности тока на полосковом проводнике, $W$ – ширина полоскового проводника, ${{x}_{0}}$ – расстояние от плоскости $x = 0$ до центра проводника.

Одномерные функции Грина ${G_{m}^{{\text{э }}}\left( y \right)}$ и ${G_{m}^{{\text{м }}}\left( y \right)}$ определяются как решения уравнения

${\frac{{{{d}^{{\text{2}}}}G_{m}^{{{\text{э ,м }}}}}}{{d{{y}^{2}}}} + \beta _{{mj1,2}}^{2}G_{m}^{{{\text{э ,м }}}} = - \delta \left( {y - c} \right)},$

${{{\beta }_{{mj1,2}}} = \sqrt {{{\varepsilon }_{{j1,2}}} - \chi _{m}^{2}} {\text{,}}\,\,\,\chi _{m}^{2} = {{\alpha }_{m}} + {{\Gamma }^{{\text{2}}}}{\text{,}}\,\,\,\,{{\alpha }_{m}} = \frac{\pi }{a}m{\text{,}}}$

обеспечивающие выполнение граничных условий электродинамики на экране и межслойных сечениях.

Эффективный алгоритм построения функции Грина предложен в [4]. При этом задача сводится к определению собственных волн в двухслойной структуре с импедансными граничными условиями на (K – 1)-м и (N – 1)-м межслойных сечениях. Используя условие равенства нулю тангенциальной составляющей напряженности электрического поля на поверхности полоскового проводника, получим следующую систему интегральных уравнений специального вида относительно продольной и поперечной составляющих плотности тока на проводнике:

(3)

$\begin{gathered} \sum\limits_{m = 1}^\infty {\frac{2}{{\chi _{m}^{2}}}} [({{\Gamma }^{2}}G_{m}^{{\text{э }}} + \alpha _{m}^{2}G_{m}^{{\text{м }}}){{I}_{{zm}}} + \\ + \,\,{{\alpha }_{m}}(G_{m}^{{\text{м }}} - G_{m}^{{\text{э }}}){{I}_{{xm}}}]\sin ({{\alpha }_{m}}x) = 0, \\ \sum\limits_{m = 0}^\infty {\frac{{{{\varepsilon }_{m}}}}{{\chi _{m}^{2}}}\left[ {{{\alpha }_{m}}(G_{m}^{{\text{м }}} - G_{m}^{{\text{э }}}){{I}_{{zm}}} + \left( {\frac{{\alpha _{m}^{2}}}{{{{\Gamma }^{2}}}}G_{m}^{{\text{э }}} + G_{m}^{{\text{м }}}} \right){{I}_{{xm}}}} \right] \times } \\ \times \,\,\cos ({{\alpha }_{m}}x) = 0, \\ \end{gathered} $

где $\left| {x - {{x}_{0}}} \right| \leqslant {W \mathord{\left/ {\vphantom {W 2}} \right. \kern-0em} 2},$

$\begin{array}{*{20}{c}} \begin{gathered} G_{m}^{{{\text{э ,м }}}} = ({1 \mathord{\left/ {\vphantom {1 {Z_{{mK1}}^{{{\text{э ,м }}}}}}} \right. \kern-0em} {Z_{{mK1}}^{{{\text{э ,м }}}}}} + {{{1 \mathord{\left/ {\vphantom {1 {Z_{{mN2}}^{{{\text{э ,м }}}})}}} \right. \kern-0em} {Z_{{mN2}}^{{{\text{э ,м }}}})}}}^{{ - 1}}}, \\ Z_{{mj1,2}}^{{{\text{э ,м }}}} = \\ = \frac{{Z_{{m(j - 1)1,2}}^{{{\text{э ,м }}}} + W_{{mj1,2}}^{{{\text{э ,м }}}}{\text{tg}}({{\beta }_{{mj1,2}}}\left| {{{b}_{{j1,2}}} - {{b}_{{(j - 1)1,2}}}} \right|)}}{{1 - \left( {{{Z_{{m(j - 1)1,2}}^{{{\text{э ,м }}}}} \mathord{\left/ {\vphantom {{Z_{{m(j - 1)1,2}}^{{{\text{э ,м }}}}} {W_{{mj1,2}}^{{{\text{э ,м }}}}}}} \right. \kern-0em} {W_{{mj1,2}}^{{{\text{э ,м }}}}}}} \right){\text{tg(}}{{\beta }_{{mj1,2}}}\left| {{{b}_{{j1,2}}} - {{b}_{{(j - 1)1,2}}}} \right|)}}, \\ W_{{mj1,2}}^{{\text{э }}} = {{{{\beta }_{{mj1,2}}}} \mathord{\left/ {\vphantom {{{{\beta }_{{mj1,2}}}} {{{\varepsilon }_{{j1,2}}}}}} \right. \kern-0em} {{{\varepsilon }_{{j1,2}}}}},\,\,\,\,W_{{mj1,2}}^{{\text{м }}} = {1 \mathord{\left/ {\vphantom {1 {{{\beta }_{{mj1,2}}}}}} \right. \kern-0em} {{{\beta }_{{mj1,2}}}}}. \\ \end{gathered} &{(3')} \end{array}$

Для двухслойной структуры (K = 1, N = 1) имеем

$Z_{{m11}}^{{{\text{э ,м }}}} = W_{{m11}}^{{{\text{э ,м }}}}{\text{tg}}({{\beta }_{{m11}}}c),\,\,\,\,Z_{{m12}}^{{{\text{э ,м }}}} = W_{{m12}}^{{{\text{э ,м }}}}{\text{tg}}({{\beta }_{{m12}}}(b - c)).$

2. РЕШЕНИЕ СИСТЕМЫ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ

Решаем систему уравнений (3) проекционным методом, представляя искомые функции ${{\eta }_{z}}(x)$ и ${{\eta }_{x}}(x)$ в виде разложений по полиномам Чебышева с весовыми функциями, учитывающими в явном виде краевые особенности решения [3]:

(4)

$\begin{gathered} {{\eta }_{z}}(\tilde {x}) = {{(1 - {{{\tilde {x}}}^{2}})}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sum\limits_{l = 0}^\infty {{{a}_{l}}{{T}_{l}}(\tilde {x})} , \\ i\Gamma {{\eta }_{x}}(\tilde {x}) = \frac{W}{2}\left[ {{{{(1 - {{{\tilde {x}}}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sum\limits_{l = 1}^\infty {{{b}_{l}}{{U}_{l}}(\tilde {x})} } \right], \\ \tilde {x} = {{2(x - {{x}_{0}})} \mathord{\left/ {\vphantom {{2(x - {{x}_{0}})} W}} \right. \kern-0em} W}),\,\,\,\,\left| {\tilde {x}} \right| \leqslant 1, \\ \end{gathered} $

где ${{Т }_{l}}(\tilde {x})$ – полиномы Чебышева 1-го рода, ${{U}_{l}}(\tilde {x})$ – полиномы Чебышева 2-го рода.

Подставляя (4) в систему интегральных уравнений (3) и проектируя полученные выражения на “чебышевский” базис, получим бесконечную однородную систему линейных алгебраических уравнений (СЛАУ) относительно коэффициентов разложений ${{a}_{l}},$ ${{b}_{l}}.$ Выражения для матричных коэффициентов системы имеют такой же вид, как и для экранированной микрополосковой линии, приведенные в [3]. Поэтому алгоритм расчета характеристик многослойной полосковой структуры такой же, как и соответствующий алгоритм для микрополосковой линии на однослойной подложке.

При симметричном расположении полоскового проводника относительно боковых стенок экрана: ${{x}_{0}} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$ система распадается на две независимые подсистемы относительно коэффициентов ${{a}_{{2l}}}(l = 0,1,...,),$ ${{b}_{{2l - 1}}}(l = 1,...,)$ и относительно коэффициентов ${{a}_{{2l - 1}}}(l = 1,...,),$ ${{b}_{{2(l - 1)}}}(l = 1,...,).$ Первая соответствует волнам четного типа, вторая – нечетного.

Для собственных волн четного типа коэффициенты разложения определяются из следующей бесконечной системы уравнений:

(5)

$\sum\limits_{l = 0}^\infty {{{A}_{{ql}}}{{a}_{{2l}}}} + \sum\limits_{l = 1}^\infty {{{B}_{{ql}}}{{b}_{{2l - 1}}}} = 0\,\,\,(q = 0,1,2, \ldots ),$

где

$\begin{array}{*{20}{c}} \begin{gathered} \sum\limits_{l = 0}^\infty {{{C}_{{ql}}}{{a}_{{2l}}}} + \sum\limits_{l = 1}^\infty {{{D}_{{ql}}}{{b}_{{2l - 1}}}} = 0\,\,\,\,(q = 1,2, \ldots ), \\ {{A}_{{ql}}} = {{( - 1)}^{{q + l}}}\sum\limits_{m = 1}^\infty {{{{\sin }}^{2}}\left( {m\frac{\pi }{2}} \right)\left[ {\frac{1}{{\chi _{m}^{2}}}\left( {{{\Gamma }^{2}}G_{m}^{{\text{э }}} + \alpha _{m}^{2}G_{m}^{{\text{м }}}} \right)} \right]} \times \\ \times \,\,{{J}_{{(2q)(2l)}}}\left( {m\alpha } \right),\,\,\,\,\,{{B}_{{ql}}} = {{( - 1)}^{{q + l}}}2l \times \\ \times \,\,\sum\limits_{m = 1}^\infty {{{{\sin }}^{2}}\left( {m\frac{\pi }{2}} \right)\left[ {\frac{1}{{\chi _{m}^{2}}}\left( {G_{m}^{{\text{м }}} - G_{m}^{{\text{э }}}} \right)} \right]{{J}_{{(2q)(2l)}}}\left( {m\alpha } \right)} , \\ {{C}_{{ql}}} = {{B}_{{lq}}},\,\,\,\,{{D}_{{ql}}} = {{( - 1)}^{{q + l}}}4ql \times \\ \times \,\,\sum\limits_{m = 1}^\infty {{{{\sin }}^{2}}\left( {m\frac{\pi }{2}} \right)\left[ {\frac{1}{{\chi _{m}^{2}}}\left( {\frac{{G_{m}^{{\text{э }}}}}{{{{\Gamma }^{2}}}} + \frac{{G_{m}^{{\text{м }}}}}{{\alpha _{m}^{2}}}} \right)} \right]{{J}_{{(2q)(2l)}}}\left( {m\alpha } \right),} \\ \end{gathered} &{(5')} \end{array}$

где ${{J}_{{(2q)(2l)}}}\left( {m\alpha } \right) = {{J}_{{2q}}}\left( {m\alpha } \right){{J}_{{2l}}}\left( {m\alpha } \right),$ ${{J}_{n}}(x)$ – функция Бесселя, $\alpha = {{\pi W} \mathord{\left/ {\vphantom {{\pi W} {2a}}} \right. \kern-0em} {2a}}.$

Система (5) имеет не нулевое решение только тогда, когда определитель матрицы коэффициентов этой системы D равен нулю. В выражения для матричных коэффициентов входит в качестве параметра квадрат постоянной распространения $\Gamma $. Поэтому, приравнивая к нулю определитель системы (5), получим дисперсионное уравнение, из которого численными методами определяются постоянные распространения собственных волн:

(6)

$D({{\Gamma }^{2}}) = 0.$

Бесконечные ряды для матричных коэффициентов системы (5) сходятся медленно и непосредственное их вычисление требует большого времени счета и может приводить к неустойчивым результатам даже при учете весьма большого числа членов в этих рядах. Сходимость этих рядов можно существенно улучшить, если в выражениях (5') к членам, заключенным в квадратные скобки, прибавить и вычесть их асимптотические выражения при $m \to \infty .$ Используя (3'), можно показать, что асимптотические выражения для коэффициентов $G_{m}^{{\text{э }}}$ и $G_{m}^{{\text{м }}}$ не зависят от числа слоев и, следовательно,

$G_{m}^{{\text{э }}} = - {{{{\alpha }_{m}}} \mathord{\left/ {\vphantom {{{{\alpha }_{m}}} {({{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}})}}} \right. \kern-0em} {({{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}})}},\,\,\,\,G_{m}^{{\text{м }}} = {1 \mathord{\left/ {\vphantom {1 {(2{{\alpha }_{m}})}}} \right. \kern-0em} {(2{{\alpha }_{m}})}}.$

Учитывая это, представим выражения для матричных коэффициентов системы (5) в виде:

$\begin{gathered} {{A}_{{ql}}} = {{\left( { - 1} \right)}^{{q + 1}}}\left\{ {\sum\limits_{m = 1}^\infty {{{{\sin }}^{2}}\left( {m\frac{\pi }{2}} \right)} } \right.\frac{{{{\Gamma }^{2}}G_{m}^{{\text{э }}} + \alpha _{m}^{2}G_{m}^{{\text{м }}}}}{{\chi _{m}^{2}}} - \\ - \,\,\frac{{ - \frac{{{{\Gamma }^{2}}}}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}} + \frac{1}{2}}}{{{{\alpha }_{m}}}}{{J}_{{(2q)(2l)}}}\left( {m\alpha } \right) + \\ \end{gathered} $

(7)

где

(8)

${{S}_{{ql}}}(\alpha ) = \sum\limits_{m = 1}^\infty {\frac{1}{m}{{J}_{{2q}}}\left( {m\alpha } \right){{J}_{{2l}}}\left( {m\alpha } \right)} {{\sin }^{2}}\left( {m\frac{\pi }{2}} \right).$

Ряд (8) сходится медленно, и поэтому для достижения точности расчета постоянных распространения до четырех значащих цифр в нем необходимо учитывать более 10 тысяч членов, что связано с большими вычислительными затратами. Используя формулу (8) из [3], можно получить следующие представления для функции ${{S}_{{ql}}}(\alpha )\,:$

(9)

При ν > 5 можно принять ${{S}_{{2\nu }}} \approx 1.$

Полагая в (9) $\alpha = {{\pi W} \mathord{\left/ {\vphantom {{\pi W} {2a}}} \right. \kern-0em} {2a}},$ получим следующие выражения для функции ${{S}_{{ql}}}$ при различных значениях q и l:

$\begin{gathered} {{S}_{{00}}} = \frac{1}{2}\ln \frac{8}{{\pi \left( {{W \mathord{\left/ {\vphantom {W a}} \right. \kern-0em} a}} \right)}} - 0.102808{{\left( {\frac{W}{a}} \right)}^{2}} - \\ - \,\,0.033294{{\left( {\frac{W}{a}} \right)}^{4}} - 0.016041{{\left( {\frac{W}{a}} \right)}^{6}}, \\ \end{gathered} $

$\begin{gathered} {{S}_{{01}}} = 0.025702{{\left( {\frac{W}{a}} \right)}^{2}} + 0.014797{{\left( {\frac{W}{a}} \right)}^{4}} + \\ + \,\,0.009023{{\left( {\frac{W}{a}} \right)}^{6}}, \\ \end{gathered} $

$\begin{gathered} {{S}_{{{\text{02}}}}} = - {\text{0}}{\text{.0009248}}{{\left( {\frac{W}{a}} \right)}^{{\text{4}}}} - \\ - \,\,{\text{0}}{\text{.0014436}}{{\left( {\frac{W}{a}} \right)}^{{\text{6}}}} - {\text{0}}{\text{.0014897}}{{\left( {\frac{W}{a}} \right)}^{{\text{8}}}}, \\ \end{gathered} $

${{S}_{{{\text{11}}}}} = {\text{0}}{\text{.125}} - {\text{0}}{\text{.005549}}{{\left( {\frac{W}{a}} \right)}^{{\text{4}}}} - {\text{0}}{\text{.004812}}{{\left( {\frac{W}{a}} \right)}^{{\text{6}}}},$

$\begin{gathered} {{S}_{{{\text{12}}}}} = {\text{0}}{\text{.0006015}}{{\left( {\frac{W}{a}} \right)}^{{\text{6}}}} + {\text{0}}{\text{.0008512}}{{\left( {\frac{W}{a}} \right)}^{{\text{8}}}}, \\ {{S}_{{{\text{22}}}}} = {\text{0}}{\text{.0625}} - {\text{0}}{\text{.001064}}{{\left( {\frac{W}{a}} \right)}^{{\text{8}}}}. \\ \end{gathered} $

Из полученных выражений видно, что ряд быстро сходится, и поэтому при расчете функции ${{S}_{{ql}}}$ в нем достаточно учесть несколько первых членов, а при больших значениях q и l этот ряд близок к нулю. В этом случае для функции ${{S}_{{ql}}}$ получаем следующее асимптотическое выражение:

(10)

${{S}_{{ql}}} \cong \frac{{{{\delta }_{{ql}}}}}{{4(q + l)}},\,\,\,\,{{\delta }_{{ql}}} = \left\{ \begin{gathered} 1\,\,\,\,{\text{п р и }}\,\,\,\,q = l \hfill \\ 0\,\,\,\,{\text{п р и }}\,\,\,\,q \ne l \hfill \\ \end{gathered} \right..$

Анализ выражений (7), основанный на свойстве функций Бесселя быстро убывать с ростом индекса, когда индекс больше аргумента, позволяет сделать вывод о диагональном характере матриц A, B, C, D с элементами ${{A}_{{ql}}},{{B}_{{ql}}},{{C}_{{ql}}},{{D}_{{ql}}}.$ Отсюда следует быстрая сходимость разложений (4) независимо от числа диэлектрических слоев и возможность решения бесконечной системы уравнений (5) методом редукции. При усечении этой системы следует оставлять члены с коэффициентами, имеющими одинаковый порядок малости. При этом верхние индексы суммирования в разложениях (4) для плотности продольного и поперечного тока равны L. Тогда порядок редуцированной системы уравнений равен K = 2L + 1, где L – число учитываемых членов в разложении для плотности поперечного тока, (L + 1) – число учитываемых членов в разложении для плотности продольного тока.

3. АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ БЕСКОНЕЧНОЙ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Чтобы оценить сходимость разложений (4), рассмотрим асимптотическое решение бесконечной СЛАУ при $l > L \gg 1.$ С этой целью запишем две строки СЛАУ (5) при $q = L\,:$

(11)

$\begin{gathered} \sum\limits_{l = 0}^\infty {{{A}_{{Ll}}}{{a}_{{2l}}}} + \sum\limits_{l = 1}^\infty {{{B}_{{Ll}}}{{b}_{{2L - 1}}}} = 0, \\ \sum\limits_{l = 0}^\infty {{{C}_{{Ll}}}{{a}_{{2l}}}} + \sum\limits_{l = 1}^\infty {{{D}_{{Ll}}}{{b}_{{2l - 1}}}} = 0. \\ \end{gathered} $

При больших значениях L воспользуемся асимптотическими выражениями для матричных коэффициентов:

$\begin{gathered} {{A}_{{Ll}}} \cong {{( - 1)}^{{L + 1}}}\left( {\frac{1}{2} - \frac{{{{\Gamma }^{2}}}}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}} \right)\frac{a}{\pi }{{S}_{{Ll}}}, \\ {{B}_{{ql}}} \cong {{( - 1)}^{{L + 1}}}\frac{1}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}\frac{a}{\pi }2l{{S}_{{Ll}}},\,\,\,\,{{C}_{{Ll}}} = {{B}_{{lL}}}, \\ {{D}_{{Ll}}} \cong - {{( - 1)}^{{L + 1}}}\frac{1}{{{{\Gamma }^{2}}}}\frac{1}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}4Ll\frac{1}{\pi }{{S}_{{Ll}}}. \\ \end{gathered} $

Оставляя в рядах (9) только один первый член, можно получить следующее выражение для функции ${{S}_{{Ll}}}\,:$

(12)

$\begin{gathered} {{S}_{{Ll}}} \approx \frac{{\text{1}}}{{\text{2}}}\left[ {\frac{{{{\delta }_{{Ll}}}}}{{{\text{2}}\left( {L + l} \right)}} + \frac{{{{{\left( {{\text{--1}}} \right)}}^{{L + l + 1}}}}}{{L + l}}\frac{1}{{{{{\text{2}}}^{{{\text{4}}\left( {L + l} \right)}}}}}} \right. \times \\ \times \,\,\left. {\left( \begin{gathered} 2(L + l) \hfill \\ 2L \hfill \\ \end{gathered} \right){{{\left( {\frac{W}{a}} \right)}}^{{{\text{2}}\left( {L + l} \right)}}}} \right], \\ \end{gathered} $

где $\left( \begin{gathered} n \hfill \\ m \hfill \\ \end{gathered} \right) = \frac{{n(n - 1)...(n - m + 1)}}{{1 \times 2...m}}$ = $\frac{{n!}}{{m!(n - m)!}},$ $\left( \begin{gathered} n \hfill \\ 0 \hfill \\ \end{gathered} \right) = 1.$

Оставляя в бесконечных рядах (11) лишь члены с диагональными элементами матриц A, B, C, D и члены с наименьшей степенью ${W \mathord{\left/ {\vphantom {W a}} \right. \kern-0em} a},$ получим систему из двух линейных алгебраических уравнений относительно коэффициентов ${{a}_{{2L}}}$ и ${{b}_{{2L - 1}}}\,:$

(13)

$\begin{gathered} {{A}_{{LL}}}{{a}_{{{\text{2}}L}}} + {{B}_{{LL}}}{{b}_{{{\text{2}}L - {\text{1}}}}} = - {{A}_{{L{\text{0}}}}}{{a}_{{\text{0}}}}, \\ {{C}_{{LL}}}{{a}_{{{\text{2}}L}}} + {{D}_{{LL}}}{{b}_{{{\text{2}}L - {\text{1}}}}} = - {{C}_{{L{\text{0}}}}}{{a}_{{\text{0}}}}, \\ \end{gathered} $

где

$\begin{gathered} {{A}_{{LL}}} = \left( {\frac{1}{2} - \frac{{{{\Gamma }^{2}}}}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}} \right)\frac{a}{\pi }{{S}_{{LL}}}, \\ {{B}_{{LL}}} = \frac{1}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}\frac{a}{\pi }2L{{S}_{{LL}}},\,\,\,\,{{C}_{{LL}}} = {{B}_{{LL}}}, \\ {{D}_{{LL}}} = - \frac{1}{{{{\Gamma }^{2}}}}\frac{1}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}4{{\left( L \right)}^{2}}\frac{a}{\pi }{{S}_{{LL}}}, \\ {{{\rm A}}_{{L0}}} = {{\left( { - 1} \right)}^{L}}\left( {\frac{1}{2} - \frac{{{{\Gamma }^{2}}}}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}} \right)\frac{a}{\pi }{{S}_{{L0}}}, \\ {{C}_{{L0}}} = {{B}_{{0L}}} = {{( - 1)}^{L}}\frac{1}{{{{\varepsilon }_{{K1}}} + {{\varepsilon }_{{N2}}}}}2L\frac{a}{\pi }{{S}_{{0L}}}. \\ \end{gathered} $

Решая систему (13), получим с учетом (12):

(14)

$\begin{gathered} {{{{a}_{{2L}}}} \mathord{\left/ {\vphantom {{{{a}_{{2L}}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}} \cong {{( - 1)}^{{L + 1}}}{{{{S}_{{0L}}}} \mathord{\left/ {\vphantom {{{{S}_{{0L}}}} {{{S}_{{LL}}}}}} \right. \kern-0em} {{{S}_{{LL}}}}} \cong {{2}^{{ - (2L - 1)}}}{{({W \mathord{\left/ {\vphantom {W a}} \right. \kern-0em} a})}^{{2L}}}, \\ {{{{b}_{{2L - 1}}}} \mathord{\left/ {\vphantom {{{{b}_{{2L - 1}}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}} \cong 0. \\ \end{gathered} $

Таким образом, при больших значениях $l$ $(l \geqslant L)$ коэффициенты разложений плотности тока в выражениях (4) быстро убывают и зависят только от отношения ${W \mathord{\left/ {\vphantom {W a}} \right. \kern-0em} a}.$ При этом коэффициенты ${{{{b}_{{2L - 1}}}} \mathord{\left/ {\vphantom {{{{b}_{{2L - 1}}}} {{{a}_{{\text{0}}}}}}} \right. \kern-0em} {{{a}_{{\text{0}}}}}}$ имеют более высокий порядок малости, чем коэффициенты ${{{{a}_{{2L}}}} \mathord{\left/ {\vphantom {{{{a}_{{2L}}}} {{{a}_{{\text{0}}}}}}} \right. \kern-0em} {{{a}_{{\text{0}}}}}}.$

Можно показать, что в общем случае расположения полоскового проводника $\left( {{{x}_{{\text{0}}}} \ne {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}} \right)$ матрица коэффициентов бесконечной СЛАУ также имеет диагональный характер [5] и при численном решении этой системы можно использовать метод редукции. Порядок редуцированной системы $K = 4L + 1,$ где 2L – число учитываемых членов в разложениях (4) для поперечного тока, 2L + 1 – для продольного тока. При асимптотическом решении системы она распадается на две независимые подсистемы относительно коэффициентов ${{a}_{{2l}}},$ ${{b}_{{2l - 1}}}$ и ${{a}_{{2l - 1}}},$ ${{b}_{{2l}}}.$ Для собственных волн четного типа решение определяется из системы (13), коэффициенты которой определяются через функцию

$\begin{gathered} {{S}_{{Ll}}}(\alpha ,\beta ) = \\ = \sum\limits_{m = 1}^\infty {\frac{1}{m}{{J}_{{2L}}}\left( {m\alpha } \right){{J}_{{2l}}}\left( {m\alpha } \right)} {{\sin }^{2}}\left( {m\beta } \right) \cong \frac{{{{\delta }_{{Ll}}}}}{{4(L + l)}}, \\ \end{gathered} $

где $\beta = \alpha (1 + {S \mathord{\left/ {\vphantom {S W}} \right. \kern-0em} W}),$ ${S \mathord{\left/ {\vphantom {S 2}} \right. \kern-0em} 2}$ – расстояние от полоски до ближайшей боковой стенки экрана.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО АНАЛИЗА

Численно была исследована сходимость проекционного метода и решен вопрос о выборе числа L, определяющего порядок редуцированной СЛАУ, и числа M, которое необходимо учитывать в бесконечных рядах (7) с улучшенной сходимостью для матричных коэффициентов системы (5). Погрешность расчета постоянных распространения и волновых сопротивлений основной волны и трех высших волн при $L = 2$ и $M = 50$ не превышает 0.1% в широком диапазоне изменения параметров, независимо от числа диэлектрических слоев. Однако с увеличением номера волны требуется рассматривать системы более высокого порядка. В случае когда номер волны $\nu \leqslant 50,$ число $L \leqslant 5,$ если $\xi = c\sqrt \varepsilon \leqslant \pi ,$ ${W \mathord{\left/ {\vphantom {W c}} \right. \kern-0em} c} \leqslant 20,$ ${a \mathord{\left/ {\vphantom {a c}} \right. \kern-0em} c} \leqslant 50.$

Быстрая сходимость разложений (4) подтверждается данными табл. 1, в которой представлены результаты расчета постоянных распространения и коэффициентов разложений основной $(\nu = 1)$ и пяти высших волн четного типа $(\nu = 2 - 6),$ полученные в [6] для двухслойной структуры при ${{x}_{0}} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2},$ b/a = 4/7, c/a = 1/7, W/c = 2, ${{\varepsilon }_{{11}}} = \varepsilon = 9,$ ${{\varepsilon }_{{12}}} = 1,$ с = 0.5 мм, f = 40 ГГц.

Таблица 1.

Коэффициенты разложения плотности тока по “чебышевскому базису”

$\nu $	$\Gamma _{\nu }^{2}$	a₂/a₀	a₄/a₀	a₆/a₀	b₁/a₀	b₃/a₀	b₅/a₀
1	7.746	–0.1612	0.0061	0.0000	0.3049	–0.0001	0.0000
2	0.358	0.0747	–0.0024	0.0000	–0.6020	0.0134	–0.0002
3	–2.409	2.716	–0.1277	0.0028	–11.53	0.3261	–0.0054
4	–6.396	0.453	–0.0899	0.0031	–6.054	0.3842	–0.0085
5	–7.344	1.771	–0.3757	0.0134	–24.04	1.619	–0.0377
6	–11.00	–12.14	1.833	–0.0721	116.4	–8.098	0.2165

В табл. 2 представлены результаты расчета эффективной диэлектрической проницаемости ${{\varepsilon }_{{{\text{э ф }}}}} = {{\Gamma }^{2}}$ и волнового сопротивления Z основной волны микрополосковой линии (МПЛ) при ${{x}_{0}} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2},$ b/a = 2, c/a = 0.02, $\varepsilon $ = 9.6, которые также подтверждают быструю сходимость разложений (4) в широком диапазоне изменения параметров. Из приведенных в табл. 2 данных следует, что при ${d \mathord{\left/ {\vphantom {d c}} \right. \kern-0em} c} \leqslant 1,\,\,\xi \leqslant 1$ в разложениях (4) достаточно учесть только один член для плотности продольного тока:

${{\eta }_{z}}(\tilde {x}) = {{a}_{0}}{{(1 - {{\tilde {x}}^{2}})}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{\eta }_{x}}(\tilde {x}) = 0.$

Таблица 2.

Эффективная диэлектрическая проницаемость и волновое сопротивление МПЛ

$\frac{W}{c}$	$fc$ ${\text{[Г Г ц ][м м ]}}$	${{\varepsilon }_{{{\text{э ф }}}}} = {{\Gamma }^{2}}$			$Z$
$\frac{W}{c}$	$fc$ ${\text{[Г Г ц ][м м ]}}$	K = 1 $(L = 0)$	K = 3 $(L = 1)$	K = 5 $(L = 2)$	K = 1 $(L = 0)$	K = 3 $(L = 1)$	K = 5 $(L = 2)$
1	2	6.5067	6.5079	6.5079	49.771	49.762	49.762
	6	6.7505	6.7521	6.7521	50.144	50.131	50.131
	10	7.0329	7.0356	7.0356	51.313	51.291	51.291
	14	7.3097	7.3142	7.3240	53.239	53.199	53.199
	18	7.5647	7.5715	7.5715	55.802	55.732	55.732
	22	7.7936	7.8030	7.8030	58.917	58.767	58.767
2	2	6.9640	6.9801	6.9801	33.957	33.875	33.875
	6	7.2871	7.3093	7.3093	34.292	34.188	34.188
	10	7.6200	7.6521	7.6521	35.229	35.085	35.085
	14	7.9092	7.9538	7.9538	36.587	36.376	36.376
	18	8.1476	8.2052	8.2052	38.191	37.880	37.880
	22	8.3393	8.4113	8.4113	39.939	39.476	39.476
4	2	7.4802	7.5933	7.5934	21.451	21.098	21.097
	6	7.8569	8.0060	8.0061	21.803	21.397	21.397
	10	8.1662	8.3570	8.3571	22.502	22.033	22.034
	14	8.3929	8.6193	8.6194	23.327	22.780	22.781
	18	8.5608	8.8126	8.8127	24.189	23.531	23.534
	22	8.6892	8.9569	8.9569	25.072	24.248	24.253
10	2	7.9827	8.4262	8.4268	10.895	10.115	10.114
	6	8.3017	8.8375	8.8376	11.150	10.360	10.359
	10	8.5058	9.0800	9.0798	11.435	10.674	10.676
	14	8.6549	9.2283	9.2278	11.734	10.985	10.996
	18	8.7714	9.3239	9.3233	12.052	11.268	11.296
	22	8.8652	9.3881	9.3876	12.389	11.512	11.564

Примечание: K = 2L + 1 – порядок редуцированной СЛАУ (5), L – число учитываемых членов в разложениях (4) для поперечного тока.

ЗАКЛЮЧЕНИЕ

Построенная в работе проекционным методом алгебраическая модель МПЛ в многослойной диэлектрической среде основана на строгом решении краевой задачи для уравнений Максвелла. Она позволяет получить численные результаты с малой погрешностью при небольшом числе базисных функций и небольшом числе членов в рядах для матричных коэффициентов независимо от числа диэлектрических слоев. Использование в качестве базиса полиномов Чебышева с весовыми функциями, учитывающими в явном виде особенность поля на металлическом ребре, обеспечило быструю сходимость разложений для плотности тока на полосковом проводнике. Улучшение сходимости рядов для матричных коэффициентов СЛАУ обеспечило устойчивость и высокую точность численных результатов и существенно сократило время численной реализации метода. Это позволило разработать эффективный алгоритм расчета не только основной волны, но и до 50 волн высших типов, которые необходимы для построения электродинамических моделей нерегулярных элементов ИС СВЧ на основе проекционного “сшивания” собственных волн на стыках регулярных линий.

Разработанный проекционный метод построения математических моделей полосковых линий позволяет существенно повысить качество математических моделей нерегулярных СВЧ-элементов, рассмотренных в [7].

Список литературы

Никольский В.В., Никольская Т.И. Декомпозиционный подход к задачам электродинамики. М.: Наука, 1983.
Никольский В.В. // Прикладная электродинамика. М.: Высш. школа, 1977. Вып. 1. С. 4.
Коваленко А.Н. // Изв. вузов. Радиофизика. 1978. Т. 21. № 2. С. 188.
Коваленко А.Н. // Изв. вузов. Радиофизика. 2012. Т. 55. № 12. С. 759.
Коваленко А.Н. // Рос. технол. журн. 2015. № 1(6). С. 164. https://rtj.mirea.ru/upload/medialibrary/d7d/ 14-kovalenko.pdf.
Коваленко А.Н. // Изв. вузов. Радиофизика. 1980. Т. 23. №11. С. 1388.
Никольский В.В., Никольская Т.И. // Изв. вузов. Радиофизика. 1981. Т. 24. № 12. С. 1423.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал