Радиотехника и электроника, 2019, T. 64, № 2, стр. 186-190

ВВЕДЕНИЕ

В научно-технической литературе проблема помехозащищенности систем передачи информации, ведущих обработку сигналов на фоне шумов и различного вида структурно-детерминированных помех решалась различными методами и с различной степенью полноты [1–12]. В [1–4] она разрабатывалась методами теории статистических решений на основе анализа отношения правдоподобия, с усреднением результата по априорной статистике случайных параметров наблюдения, являющимися случайными величинами. В [5] она ограниченно разрабатывалась методами линейной фильтрации в смысле Калмана–Бьюси, в [6–12] – методами теории оптимальной нелинейной фильтрации в смысле Стратоновича [13, 14]. Приведенные в [12] общие алгоритмы многоканального приема дают возможность рассматривать эффективно и с единых позиций многие варианты так называемой пространственно-временной обработки (ПВО).

Обычно [15] под ПВО понимается пространственная обработка (ПО) в некоей адаптивной антенной системе (ААС), оптимальной по какому-либо критерию, минимизирующему влияние помехи (компенсация помехи). Следующее далее устройство временной обработки (ВО) осуществляет какую-либо, по возможности оптимальную обработку сигнала на фоне лишь шума, поскольку считается, что помеха полностью скомпенсирована на этапе ПО. В [12] показано, что полная компенсация помехи возможна далеко не всегда. Поэтому процедуры ПВО надо рассматривать не раздельно, как это следует из общепринятых подходов, а совместно.

Кроме того, учитывая, что варианты обработки [12] приводят в общем случае к крайне сложным и неразделимым структурам ПВО, приведем варианты их структуризации, т.е. разделения на ПО и ВО, а также их редукции, упрощающие ход решения задачи.

1. СИНТЕЗ КВАЗИОПТИМАЛЬНОГО АЛГОРИТМА ОБРАБОТКИ

Пусть на вход многоканального приемного комплекса поступает аддитивная смесь сигнала, помехи и шума

где ${{s}_{\alpha }}(t,{{\Lambda }_{{\text{c}}}},{{\Theta }_{{\text{c}}}}),$ ${{p}_{\alpha }}(t,{{\Lambda }_{{\text{п }}}},{{\Theta }_{{\text{п }}}})$ – сигналы и помехи, являющиеся известными функциями времени ($\alpha = \overline {1,\rho } ;$ ρ – число каналов наблюдения), составных векторов непрерывных ${{\Lambda }_{{\text{c}}}}(t) = \{ {{\lambda }_{i}}(t),$ $i = \mathop {\left. {1,{{r}_{{\text{c}}}}} \right\}}\limits^{ - - - - - } ,$ ${{\Lambda }_{{\text{п }}}}(t) = \{ {{\lambda }_{j}}(t),$ $j = \mathop {1,{{r}_{{\text{п }}}}}\limits^{ - - - - - } \} $ и дискретных Θ_с,п(t) параметров; Θ_с,п(t) – многопозиционные независимые дискретные функции времени, модулирующие параметры сигнала и помехи, значения которых на разных символьных интервалах образуют модернизированную дискретную однородную цепь Маркова, с состояниями ${{\Theta }_{{{\text{c}},{\text{п }}}}} = \{ {{\Theta }_{{{\text{c}},{\text{п }}j}}},$ $j = \mathop {1,{{M}_{{{\text{c}},{\text{п }}}}}}\limits^{ - - - - - - } \} $ [12], смена которых происходит в моменты времени t_{h с,п} = t₀ + τ_с,п + h_с,пT _с,п, h_с,п = 0,1,2…, τ_с,п – время запаздывания; T_с,п – длительности символьных интервалов; матрицы переходов Θ_с,п из i_с,п-го состояния в j_с,п-е заданы, t_{h с,п} = t₀ + τ_с,п + h_с,пT_с,п, h_с,п= 0, при заданных же векторах вероятностей начальных состояний ${{n}_{{0\,\alpha }}}(t)$ – независимые белые гауссовские шумы (БГШ наблюдения) с нулевыми средними значениями и односторонними спектральными плотностями ${{N}_{{0\alpha }}}.$

Составной вектор (здесь вектор должен быть набран полужирным) ${{\Lambda }_{t}} = \{ {{\lambda }_{{i{\text{c}},{\text{п }}}}}(t);$ $i = \mathop {1,r}\limits^{ - - - } ;$ $r = {{r}_{{\text{c}}}} + {{r}_{{\text{п }}}}\} $ непрерывных параметров является многомерным марковским случайным процессом с известными коэффициентами сноса ${{a}_{i}}(t,{{\Lambda }_{t}})$ и диффузии ${{b}_{{i\,j}}}(t,{{\Lambda }_{t}})$ и может быть представлен в виде системы стохастических дифференциальных уравнений (СДУ)

где ${{a}_{i}}(t,{{\Lambda }_{t}}),$ ${{b}_{{i\,j}}}(t,{{\Lambda }_{t}})$ – непрерывные функции, ${{n}_{i}}(t)$ – БГШ, некоррелированные с ${{n}_{{0\alpha }}}(t),$ с нулевыми средними значениями и единичными спектральными плотностями, формирующие модель $\Lambda (t)$ (формирующие БГШ).

Процедура вычисления смешанной апостериорной плотности вероятности (АПВ) непрерывных параметров при произвольном $k$-м значении общего вектора дискретных параметров определяется следствием из фундаментальной теоремы Стратоновича, непосредственное использование которого вызывает большие трудности. Применение гауссовской аппроксимации АПВ позволяет получить более простые квазиоптимальные алгоритмы приема, работоспособные для типовых условий приема [11–14].

Далее, будем полагать, что имеет место соотношение

где τ_Λмин – минимальный интервал корреляции непрерывных параметров. Условие (5) означает, что непрерывные параметры мало изменяются на длительности символьных интервалов T_с,п. Это условие в современных системах передачи информации выполняется всегда, а смешанная апостериорная плотность вероятности допускает первую форму представления и имеет вид [12, 13] где $P(t,{{{{\Theta }_{k}}} \mathord{\left/ {\vphantom {{{{\Theta }_{k}}} {\Lambda _{t}^{*}}}} \right. \kern-0em} {\Lambda _{t}^{*}}})$ – апостериорная вероятность k-го дискретного состояния наблюдения. С учетом этого, для высоко- и среднескоростных систем передачи информации в соответствии с критерием максимума АПВ для $\Lambda _{t}^{*}$ – оценок непрерывных параметров $\Lambda _{t}^{{}}$ и критерием идеального наблюдателя для $\Theta _{t}^{*}$ – оценок дискретного параметра $\Theta _{t}^{{}}$ получим следующую систему стохастических дифференциальных уравнений и решающее правило, описывающие алгоритм квазиоптимального приема [12]:

Здесь ${{K}_{{i\,j}}} = {{K}_{{i\,j}}}(t)$ – элементы дисперсионной матрицы аппроксимирующего гауссовского распределения АПВ, $W({{t}_{{h + 1}}} - \varepsilon ,\Lambda _{t}^{*},{{\Theta }_{k}})$ – совместная апостериорная плотность вероятности,

– глобальный функционал правдоподобия,

$F(t,\Lambda _{t}^{*},{{\Theta }_{k}}) = \sum\nolimits_{\alpha = 1}^\rho {{{F}_{\alpha }}(t,\Lambda _{t}^{*},{{\Theta }_{k}})} $ – многоканальный функционал правдоподобия,

${{F}_{\alpha }}(t,\Lambda _{t}^{*},{{\Theta }_{k}}) = - \frac{1}{{{{N}_{{0\,\alpha }}}}}{{[{{y}_{\alpha }}(t) - {{\Phi }_{\alpha }}(t,\Lambda _{t}^{*},{{\Theta }_{k}})]}^{2}}$ – одноканальный функционал правдоподобия, являющийся производной логарифма функционала правдоподобия (если α – фиксирована), введенного В.А. Котельниковым;

${{\Phi }_{\alpha }}(t,\Lambda _{t}^{*},{{\Theta }_{k}}) = {{s}_{\alpha }}(t,\Lambda _{t}^{*},{{\Theta }_{l}}) + {{p}_{\alpha }}(t,\Lambda _{t}^{*},{{\Theta }_{m}})$ – сумма регенерированных сигнала и помехи, полученных из соответствующих эталонов, имеющихся в приемнике при ${{\Theta }_{k}}$ (k = lm), которые относятся в общем случае к l-му состоянию дискретного параметра сигнала Θ_с и $m$-му состоянию дискретного параметра помехи Θ_п.

Далее, с целью упрощения, будем полагать, что моменты времени t_h с,п, а также задержки τ_с,п, известны. Если t_{h с,п} и τ_с,п известны не точно, то это можно учесть, вводя их в составной вектор случайных параметров $\Lambda (t).$

Эволюция $P(t,{{{{\Theta }_{k}}} \mathord{\left/ {\vphantom {{{{\Theta }_{k}}} {\Lambda _{t}^{*}}}} \right. \kern-0em} {\Lambda _{t}^{*}}})$ – условной апостериорной вероятности k-го состояния составного дискретного параметра наблюдения (l-го для Θ_с(t) и m-го для Θ_п(t)) – будет описываться выражением [12, 13]

где $P(t,{{\Theta }_{l}}{\text{,}}{{{{\Theta }_{m}}} \mathord{\left/ {\vphantom {{{{\Theta }_{m}}} {\Lambda _{t}^{*}}}} \right. \kern-0em} {\Lambda _{t}^{*}}}) = P(t,{{{{\Theta }_{k}}} \mathord{\left/ {\vphantom {{{{\Theta }_{k}}} {\Lambda _{t}^{*}}}} \right. \kern-0em} {\Lambda _{t}^{*}}}),$ $t \in [{{t}_{h}},{{t}_{{h + 1}}}],$

Данное в (8) правило оценки $\Theta _{{h + 1}}^{*}$ и пределы интегрирования в (10) нуждаются в дополнительном рассмотрении, поскольку должны учитывать обстоятельства взаимного наложения двух дискретных потоков информации Θ_с(t) и Θ_п(t).

В современных системах передачи информации предпринимаются специальные меры по обеспечению равновероятности состояний дискретного параметра. Поэтому далее будем считать, что $P{{({{t}_{h}} + \varepsilon ,{{{{\Theta }_{k}}} \mathord{\left/ {\vphantom {{{{\Theta }_{k}}} {\Lambda _{t}^{*}}}} \right. \kern-0em} {\Lambda _{t}^{*}}})}_{{\varepsilon \to 0}}}$ – апостериорная условная вероятность k-го состояния составного дискретного параметра (l-го состояния Θ_с и m‑го состояния Θ_п) наблюдения в начале анализируемого символьного интервала – равна величине 1/М; т.е. любые сочетания начальных состояний дискретных параметров сигнала и помехи являются равновероятными.

Система уравнений для оценок непрерывных параметров $\lambda _{i}^{*}(t)$ в (7) и выражение для оценок $\Theta _{{h + 1}}^{*}$ (8) определяют структурную схему блоков их оценки. Система уравнений (7) для ${{K}_{{ij}}}$ определяет точность обработки. Далее основное внимание уделим некоторым общим моментам построения блоков оценки.

Подставляя (9) в (7) и (8) получим для оценок непрерывных параметров на h-м символьном интервале с l-м и m-м состояниями дискретных параметров сигнала и, соответственно, помехи, а также и для решающего правила следующие выражения:

при несовпадающих индексах $\left\{ {l,m} \right\}$ и $\left\{ {p,q} \right\}.$

Система стохастических нелинейных дифференциальных уравнений (11) и неравенств (12) и будут определять структуру требуемой квазиоптимальной обработки векторного наблюдения.

2. РЕДУКЦИЯ СТРУКТУРЫ ОБРАБОТКИ

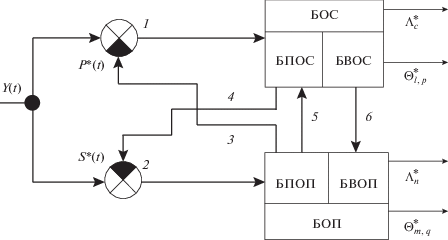
Таким образом, общий квазиоптимальный алгоритм приема дискретных сигналов на фоне подобных помех и шумов (рисунок 1) описывается выражениями (10), (11), (12). В соответствии с рисунком векторное наблюдение $Y(t) = \{ {{y}_{\alpha }}(t),$ $\alpha = \mathop {1,\rho }\limits^{ - - - } \} $ подается на вход вычитателей 1 и 2, в которых происходит взаимная компенсация (вычитание посредством векторных связей 3 и 4 из $Y(t)$) оценок векторов помехи $P{\text{*}}(t) = \{ p_{\alpha }^{*}(t),$ $\alpha = \mathop {1,\rho }\limits^{ - - - } \} $ и сигнала $S{\text{*}}(t) = \{ s_{\alpha }^{*}(t),$ $\alpha = \mathop {1,\rho }\limits^{ - - - } \} ,$ вырабатываемых в БОС и БОП. Таким образом, сами БОС и БОП, при высокой точности оценок параметров сигнала и помехи, имеют возможность работать как бы на фоне только флуктуационных шумов. Кроме того, эти блоки охвачены дополнительными связями 5 и 6, которые позволяют формировать управляющие напряжения в их цепях обратной связи, а также достаточные статистики ${{Z}_{{l,m}}}$ и апостериорные вероятности $P(t,{{\Theta }_{l}},{{{{\Theta }_{m}}} \mathord{\left/ {\vphantom {{{{\Theta }_{m}}} {\Lambda _{t}^{*}}}} \right. \kern-0em} {\Lambda _{t}^{*}}}),$ и осуществлять, таким образом, обратные связи по решениям.

Составной вектор непрерывных параметров ${{\Lambda }_{t}}$ состоит из совокупности собственных параметров сигналов и помех (амплитуды, фазы, частоты, длительность, время появления Θ_с,п(t)) и несобственных (разностных), а именно – разностей амплитуд, фаз, задержек в каналах. Собственные параметры определяют аспекты временного поведения сигналов и помех, а разностные (несобственные) – аспекты пространственного их поведения, определяемого как пространственной геометрией трасс распространения, так и неидентичностью амплитудно-частотных и фазо-частотных характеристик каналов приема. Полученные алгоритмы осуществляют в общем случае некую структурно неразделимую на составные части пространственно-временную обработку, крайне сложную в реализации в силу ее многомерности и многосвязанности. Упрощение структуризации и редукции может быть получено в случае привлечения дополнительных упрощающих предположений.

Так, используемые в стационарных системах связи каналы передачи обладают весьма большой стабильностью разностных параметров по сравнению с собственными параметрами, что определяет существенное их различие в скоростях изменения во времени. Это создает предпосылки для структурного разделения общей ПВО на медленную обработку в блоках пространственной обработки (БПО) и на быструю – в блоке временной обработки (БВО), являющегося совокупностью демодуляторов сигнала и помехи. В этом случае система уравнений (7) может быть представлена в следующем виде:

где $\vec {\lambda }{{{\kern 1pt} }_{{i{\kern 1pt} {\text{p}}}}}$ – составной вектор разностных параметров сигнала и помехи, $\vec {\lambda }{{{\kern 1pt} }_{{i{\kern 1pt} {\text{с }}}}}$ – составной вектор собственных параметров сигнала и помехи, ε_i – малые числа, определяемые малой скоростью изменения разностных параметров. Тогда БОП на рисунке будет включать в себя блок пространственной обработки помехи (БПОП), структура которого определяется соотношениями (12) и (13), а также блок временной обработки помехи (БВОП), структура которого определяется соотношениями (12) и (14). Таким же образом и БОС структурируется на два блока – БВОС и БПОС. В совокупности БПОП и БПОС определяют структуру общего блока пространственной обработки, аналогично БВОС и БВОП – общего блока временной обработки.

Из выражения (10) следует также и нетривиальная возможность раздельной демодуляции сигнала и помехи, если учесть особенности функционала правдоподобия (9) и применить критерий максимума апостериорной вероятности.

Блок пространственной обработки в общем случае реализуется в виде некой антенной решетки, в которой обрабатываются разностные параметры сигнала и помехи. В частном случае, если по какой-либо причине исчезает необходимость обрабатывать разностные параметры сигнала и собственные параметры помехи, блоки БПОС и БВОП исчезают. Тогда общая структурная схема обработки приобретает всем известную конфигурацию в составе взаимосвязанных адаптивной антенной решетки (ААР), или адаптивного компенсатора помех (АКП), а также и демодулятора сигнала, т.е. БПОП и БВОС.

Помимо приведенного здесь структурного разделения, сами блоки БОС и БОП могут быть существенно упрощены в случаях различий в мощностях сигналов и помех. В [12] достаточно подробно описаны такие варианты решения, создающие необходимое структурное многообразие вариантов обработки.

ЗАКЛЮЧЕНИЕ

Приведенные здесь квазиоптимальные алгоритмы многоканального приема дискретных сигналов на фоне структурно-детерминированной помехи создают необходимое аналитическое основание для построения оптимальных адаптивных систем совместной или раздельной пространственно-временной обработки (задачи обнаружения, оценки параметров, фильтрации, различения, разрешения сигналов и помех). В общем случае приведенные алгоритмы реализуются как разновидности нелинейных сетей синхронизации [17], а в более простых случаях из них следуют структуры различных модификаций ААР, АКП, демодуляторов, работающих как совместно, так и раздельно [12]. Учет медленности изменения разностных параметров сигналов и помех позволяет представить искомые алгоритмы обработки в виде соотношений (13) и (14), характерном для применения к их исследованию многообразных вариантов методов усреднения [16].

Предложенный в статье подход дает возможность с единых позиций статистической теории связи исследовать основные процедуры ПВО, а именно компенсацию помехи и демодуляцию сигнала как единую технологию взаимосвязанных процедур.