Радиотехника и электроника, 2019, T. 64, № 3, стр. 213-219
Алгоритм нелинейной фильтрации координат малоподвижного объекта в двухпозиционной радиосистеме
Я. О. Арешин 1, Б. А. Заикин 2, *, А. Ф. Котов 2, С. А. Решетняк 2
1 ОАО “НПК "НИИДАР”
127083 Москва, ул. 8 Марта, 10, стр. 5, Российская Федерация
2 МИРЭА – Российский технологический университет
119454 Москва, просп. Вернадского, 78, Российская Федерация
* E-mail: halfmazerkin@gmail.com
Поступила в редакцию 12.04.2018
После доработки 01.06.2018
Принята к публикации 11.06.2018
Аннотация
Представлен алгоритм фильтрации координат малоподвижного объекта в охранной двухпозиционной радиосистеме с использованием критерия максимума апостериорной вероятности. Описаны моделирование алгоритма и оценка его эффективности. Приведены графики среднеквадратического отклонения ошибки.
ВВЕДЕНИЕ
Задачи оценки и фильтрации векторов состояния объектов наблюдения являются одними из ключевых в радиотехнике. Задачу оценки можно определить следующим образом: по принятой реализации сигнала необходимо определить фиксированное на заданном интервале наблюдения значение параметра сигнала с минимальной погрешностью. Задача фильтрации является более общей и сложной: предполагается, что оцениваемый параметр наблюдения может меняться во времени, и он так же подлежит определению с минимальной погрешностью в течение заданного интервала времени. В радиотехнике эти задачи могут дополнять друг друга. Обычно представляется возможным выбрать такие интервалы наблюдения, при которых измеряемый параметр можно считать постоянным и на таких интервалах производить оценку параметра; далее при объединении таких интервалов (траекторная обработка) могут быть использованы различные методы фильтрации. Существует много подходов к реализации процедур оценки и фильтрации [1]. Они могут различаться критериями, моделями поведения объекта наблюдения (ОН), допустимой сложностью. Ниже в гауссовском приближении рассмотрен алгоритм фильтрации с использованием критерия максимума апостериорной вероятности. При этом моделью поведения объекта наблюдения служит марковская последовательность. Для упрощения вычислений использовано разложение логарифма функции правдоподобия (ЛФП) в ряд Тейлора в точке максимума правдоподобия. Представлены соотношения, необходимые для синтеза алгоритма, а также для иллюстрации приведен пример синтеза алгоритма в охранной двухпозиционной системе координатометрии. Даны описание параметров моделирования и результаты этого моделирования.
1. СИНТЕЗ АЛГОРИТМА
А. Представление алгоритма в общем виде
Предположим, что вектор состояния объекта наблюдения на ν-ом интервале может быть представлен марковской последовательностью:
(1)
${{\vec {\Lambda }}^{{\left( \nu \right)}}} = {\mathbf{Ф }}{{\vec {\Lambda }}^{{\left( {\nu - 1} \right)}}} + {\mathbf{B}}{{\vec {N}}^{{\left( \nu \right)}}},$Уравнения фильтрации по критерию максимума апостериорной вероятности (МАВ) при гауссовском приближении примут вид [2, 3]:
(3)
$\left\{ \begin{gathered} \hat {\vec {\Lambda }}_{{ps}}^{{\left( \nu \right)}} = \hat {\vec {\Lambda }}_{{\text{э }}}^{{\left( \nu \right)}} + {\mathbf{K}}_{{ps}}^{{\left( \nu \right)}}\vec {G}_{\lambda }^{{\left( \nu \right)}}, \hfill \\ {\mathbf{K}}_{{ps}}^{{\left( \nu \right)}} = {{\left[ {{{{\left( {{\mathbf{K}}_{{\text{э }}}^{{\left( \nu \right)}}} \right)}}^{{ - 1}}} - {\mathbf{H}}_{\lambda }^{{\left( \nu \right)}}} \right]}^{{ - 1}}}, \hfill \\ \end{gathered} \right.$где $\hat {\vec {\Lambda }}_{{ps}}^{{\left( \nu \right)}}$ – апостериорное значение вектора состояния на ν-ом шаге; $\hat {\vec {\Lambda }}_{{\text{э }}}^{{\left( \nu \right)}}$ – экстраполяционное значение вектора состояния на ν-ом шаге; ${\mathbf{K}}_{{ps}}^{{\left( \nu \right)}}$ – апостериорная ковариационная матрица на ν-ом шаге; $\vec {G}_{\lambda }^{{\left( \nu \right)}}$ – вектор первых частных производных логарифма функции правдоподобия по элементам вектора состояния в точке экстраполяции на ν-ом шаге; ${\mathbf{K}}_{{\text{э }}}^{{\left( \nu \right)}}$ – экстраполяционная ковариационная матрица ν-ом шаге; ${\mathbf{H}}_{\lambda }^{{\left( \nu \right)}}$ – матрица вторых частных производных логарифма функции правдоподобия по элементам вектора состояния в точке экстраполяции на ν-ом шаге. Экстраполяционные значения $\hat {\vec {\Lambda }}_{{\text{э }}}^{{\left( \nu \right)}}$ и ${\mathbf{K}}_{{\text{э }}}^{{\left( \nu \right)}}$ могут быть вычислены с помощью апостериорных значений на предыдущем шаге:
(4)
$\hat {\vec {\Lambda }}_{{\text{э }}}^{{\left( \nu \right)}} = {\mathbf{Ф }}\hat {\vec {\Lambda }}_{{ps}}^{{\left( {\nu - 1} \right)}},$(5)
${\mathbf{K}}_{{\text{э }}}^{{\left( \nu \right)}} = {\mathbf{Ф K}}_{{ps}}^{{\left( {\nu - 1} \right)}}{{{\mathbf{Ф }}}^{T}} + {\mathbf{B}}{{{\mathbf{B}}}^{T}},$где $\hat {\vec {\Lambda }}_{{ps}}^{{\left( {\nu - 1} \right)}}$ – апостериорное значение вектора состояния на предыдущем шаге; ${\mathbf{K}}_{{ps}}^{{\left( {\nu - 1} \right)}}$– апостериорная ковариационная матрица на предыдущем шаге, T – символ транспонирования.
Фильтрация по критерию максимума апостериорной вероятности сводится к вычислению вектора $\vec {G}_{\lambda }^{{\left( \nu \right)}}$ и матрицы ${\mathbf{H}}_{\lambda }^{{\left( \nu \right)}}.$ Элементы их могут быть вычислены с помощью разложения ЛФП в ряд Тейлора в точке максимального правдоподобия [2]. Таким образом, получаем:
(6)
$\vec {G}_{\lambda }^{{\left( \nu \right)}} = {\mathbf{W}}_{{q\lambda }}^{T}{{{\mathbf{H}}}_{q}}\left[ {\vec {Q}\left( {\Lambda _{э }^{{\left( \nu \right)}}} \right) - \hat {\vec {Q}}_{{м п }}^{{\left( \nu \right)}}} \right],$где ${\mathbf{W}}_{{q\lambda }}^{T}$ – транспонированная матрица первых частных производных информационных параметров по элементам вектора состояния в точке экстраполяции; ${{{\mathbf{H}}}_{q}}$ – матрица первых частных производных ЛФП по информационным параметрам (в гауссовском приближении равна отрицательной обратной ковариационной матрице информационных параметров ${{{\mathbf{H}}}_{q}} = - {\mathbf{K}}_{q}^{{ - 1}}$); $\vec {Q}\left( {\Lambda _{{\text{э }}}^{{\left( \nu \right)}}} \right)$ – вектор информационных параметров, вычисленных в точке экстраполяции; $\hat {\vec {Q}}_{{{\text{м п }}}}^{{\left( \nu \right)}}$ – вектор информационных параметров в точке максимального правдоподобия.
Элементы матрицы ${\mathbf{H}}_{\lambda }^{{\left( \nu \right)}}\,:$
(7)
$\begin{gathered} \frac{{{{\partial }^{2}}F}}{{\partial {{\lambda }_{i}}\partial {{\lambda }_{j}}}} = \\ = \sum\limits_{j = 1}^m {\sum\limits_{\mu = 1}^m {\left( {{{H}_{q}}(ij)\frac{{{{\partial }^{2}}{{q}_{j}}}}{{\partial {{\lambda }_{i}}\partial {{\lambda }_{j}}}}\left( {{{q}_{{\mu {\kern 1pt} {\text{э }}}}} - {{q}_{{\mu \,{\text{м п }}}}}} \right) + \frac{{\partial {{q}_{j}}}}{{\partial {{\lambda }_{i}}}}\frac{{\partial {{q}_{\mu }}}}{{\partial {{\lambda }_{j}}}}} \right)} } , \\ \end{gathered} $где ${{H}_{q}}(ij)$ – элемент матрицы ${{{\mathbf{H}}}_{q}};$ расположенный в i-ой строке и j-ом столбце; $\frac{{{{\partial }^{2}}{{q}_{j}}}}{{\partial {{\lambda }_{i}}\partial {{\lambda }_{j}}}}$ – вторая частная производная информационного параметра по элементам вектора состояния в точке экстраполяции; ${{q}_{{\mu \,{\text{э }}}}}$ – информационный параметр в точке экстраполяции; ${{q}_{{\mu \,{\kern 1pt} {\text{м п }}}}}$ – информационный параметр в точке максимального правдоподобия; $\frac{{\partial {{q}_{j}}}}{{\partial {{\lambda }_{i}}}}$ – первая частная производная информационного параметра по элементу вектора состояния в точке экстраполяции.
Б. Синтез алгоритма в охранной двухпозиционной радиосистеме координатометрии
Предположим, что в качестве ОН будет выступать медленно передвигающийся на плоскости объект такой, как машина или некоторые типы дронов. Тогда вектор состояния будет представлен в виде ${{\vec {\Lambda }}^{{\left( \nu \right)}}} = {{\left[ {{{x}^{{\left( \nu \right)}}}{{y}^{{\left( \nu \right)}}}} \right]}^{T}},$ при этом матрицы ${\mathbf{\Phi }}$ и ${\mathbf{B}}$ могут быть записаны как:
где ${{b}_{x}},$ ${{b}_{y}}$ – среднеквадратические отклонения траектории движения объекта по осям x и y, соответственно. Таким образом, выражение (1) может быть записано в скалярном виде:(10)
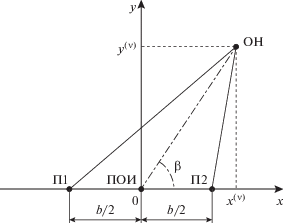
$\left\{ {\begin{array}{*{20}{c}} {{{x}^{{\left( \nu \right)}}} = {{x}^{{\left( {\nu - 1} \right)}}} + {{b}_{x}}n_{{{{b}_{x}}}}^{{\left( \nu \right)}},} \\ {{{y}^{{\left( \nu \right)}}} = {{y}^{{\left( {\nu - 1} \right)}}} + {{b}_{y}}n_{{{{b}_{y}}}}^{{\left( \nu \right)}},} \end{array}} \right.$В качестве охранной системы выбираем двухпозиционную дальномерную радиосистему координатометрии. Геометрическое построение такой системы, определяющей на ν-ом шаге координаты ОН, показано на рис. 1. На плоскости в приемных пунктах П1 и П2 расположены радиодальномеры, работающие в импульсном режиме и измеряющие на каждом ν-ом шаге временные задержки $\tau _{1}^{{\left( \nu \right)}}$ и $\tau _{2}^{{\left( \nu \right)}},$ соответственно. Временные задержки передаются по радиоканалам на пункт обработки информации ПОИ, расположенный в точке 0. Таким образом, для временных задержек, полученных на ν-ом интервале в пункте обработки, можно записать следующие выражения:
(11)
$\left\{ {\begin{array}{*{20}{c}} {\tau _{1}^{{\left( \nu \right)}} = \frac{2}{с }\sqrt {{{{\left( {{{x}^{{\left( \nu \right)}}} + \frac{b}{2}} \right)}}^{2}} + {{y}^{{\left( \nu \right)}}}} + \frac{b}{{2c}},} \\ {\tau _{2}^{{\left( \nu \right)}} = \frac{2}{с }\sqrt {{{{\left( {{{x}^{{\left( \nu \right)}}} - \frac{b}{2}} \right)}}^{2}} + {{y}^{{\left( \nu \right)}}}} + \frac{b}{{2c}},} \end{array}} \right.$Рис. 1.
Геометрическое построение охранной дальномерной двухпозиционной радиосистемы координатометрии.
Обратными формулами для выражений (11) являются:
(12)
$\left\{ {\begin{array}{*{20}{c}} {{{x}^{{\left( \nu \right)}}} = \frac{{c\left( {c\tau _{1}^{{{{{\left( \nu \right)}}^{2}}}} - c\tau _{2}^{{{{{\left( \nu \right)}}^{2}}}} - b\tau _{1}^{{\left( \nu \right)}} + b\tau _{2}^{{\left( \nu \right)}}} \right)}}{{8b}},} \\ {{{y}^{{\left( \nu \right)}}} = \sqrt {{{4}^{{ - 1}}}\left( {\tau _{2}^{{{{{\left( \nu \right)}}^{2}}}} - \frac{b}{{2c}}} \right){{c}^{2}} - {{{\left( {{{x}^{{\left( \nu \right)}}} - \frac{b}{2}} \right)}}^{2}}} .} \end{array}} \right.$При приеме каждого импульса происходит процедура оценки временной задержки, которая может быть записана, как:
(13)
$\left\{ {\begin{array}{*{20}{c}} {\hat {\tau }_{1}^{{\left( \nu \right)}} = \tau _{1}^{{\left( \nu \right)}} + {{\sigma }_{{{{\tau }_{1}}}}}n_{{{{\tau }_{1}}}}^{{\left( \nu \right)}},} \\ {\hat {\tau }_{2}^{{\left( \nu \right)}} = \tau _{2}^{{\left( \nu \right)}} + {{\sigma }_{{{{\tau }_{2}}}}}n_{{{{\tau }_{2}}}}^{{\left( \nu \right)}},} \end{array}} \right.$Для синтеза алгоритма фильтрации необходимо найти все члены выражений (3)–(7) для данного случая. Учитывая (8), выражение (4) для экстраполяционных значений можно записать в скалярном виде:
(14)
$\left\{ {\begin{array}{*{20}{c}} {x_{э }^{{\left( \nu \right)}} = \hat {x}_{{ps}}^{{\left( {\nu - 1} \right)}},} \\ {y_{э }^{{\left( \nu \right)}} = \hat {y}_{{ps}}^{{\left( {\nu - 1} \right)}},} \end{array}} \right.$Согласно [2, 3] матрица ${\mathbf{W}}_{{q\lambda }}^{T}$ определяется формулами, полученными из выражений (11) и (14):
(15)
${\mathbf{W}}_{{q\lambda }}^{T} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {{\tau }_{1}}}}{{\partial x}}}&{\frac{{\partial {{\tau }_{1}}}}{{\partial y}}} \\ {\frac{{\partial {{\tau }_{2}}}}{{\partial x}}}&{\frac{{\partial {{\tau }_{2}}}}{{\partial y}}} \end{array}} \right],$(16)
$\frac{{\partial {{\tau }_{1}}}}{{\partial x}} = \frac{2}{с }\left( {x_{{\text{э }}}^{{\left( \nu \right)}} + \frac{b}{2}} \right){{\left( {{{{\left( {x_{{\text{э }}}^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}} + y_{{\text{э }}}^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$(17)
$\frac{{\partial {{\tau }_{1}}}}{{\partial y}} = \frac{2}{с }y_{{\text{э }}}^{{\left( \nu \right)}}{{\left( {{{{\left( {x_{{\text{э }}}^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}} + y_{{\text{э }}}^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$(18)
$\frac{{\partial {{\tau }_{2}}}}{{\partial x}} = \frac{2}{с }\left( {x_{{\text{э }}}^{{\left( \nu \right)}} - \frac{b}{2}} \right){{\left( {{{{\left( {x_{{\text{э }}}^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}} + y_{{\text{э }}}^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$(19)
$\frac{{\partial {{\tau }_{2}}}}{{\partial y}} = \frac{2}{с }y_{{\text{э }}}^{{\left( \nu \right)}}{{\left( {{{{\left( {x_{{\text{э }}}^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}} + y_{{\text{э }}}^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$Ковариационная матрица информационных параметров ${{{\mathbf{K}}}_{q}}$ представляет собой диагональную матрицу из квадратов СКО измерения временной задержки ${{\sigma }_{{{{\tau }_{1}}}}},$ ${{\sigma }_{{{{\tau }_{2}}}}}.$ Обратная ковариационная матрица $K_{q}^{{ - 1}},$ записывается в виде:
(20)
$K_{q}^{{ - 1}} = \left[ {\begin{array}{*{20}{c}} {\sigma _{{{{\tau }_{1}}}}^{{ - 2}}}&0 \\ 0&{\sigma _{{{{\tau }_{2}}}}^{{ - 2}}} \end{array}} \right].$Вектор измеряемых параметров в общем случае будет состоять из временных задержек $\vec {Q} = {{\left[ {{{\tau }_{1}}{{\tau }_{2}}} \right]}^{T}},$ тогда $\left[ {\vec {Q}\left( {{\mathbf{\Lambda }}_{{\text{э }}}^{{\left( \nu \right)}}} \right) - \hat {\vec {Q}}_{{{\text{м п }}}}^{{\left( \nu \right)}}} \right]$ определяется из формул (11), (13) и (14):
(21)
$\left[ {\vec {Q}\left( {{\mathbf{\Lambda }}_{{\text{э }}}^{{\left( \nu \right)}}} \right) - \hat {\vec {Q}}_{{{\text{м п }}}}^{{\left( \nu \right)}}} \right] = \left[ {\begin{array}{*{20}{c}} {\tau _{{1{\text{э }}}}^{{\left( \nu \right)}} - \hat {\tau }_{1}^{{\left( \nu \right)}}} \\ {\tau _{{2{\text{э }}}}^{{\left( \nu \right)}} - \hat {\tau }_{2}^{{\left( \nu \right)}}} \end{array}} \right]$,Перемножив соотношения (15), взятое с отрицательным знаком (20) и (21) получаем выражение (6), которое может быть записано в скалярном виде, как:
(22)
$\left\{ {\begin{array}{*{20}{c}} {g_{{\lambda x}}^{{\left( \nu \right)}} = - \sigma _{{{{\tau }_{1}}}}^{{ - 2}}\frac{{\partial {{\tau }_{1}}}}{{\partial x}}\left( {\tau _{{1э }}^{{\left( \nu \right)}} - \hat {\tau }_{1}^{{\left( \nu \right)}}} \right) - \sigma _{{{{\tau }_{2}}}}^{{ - 2}}\frac{{\partial {{\tau }_{2}}}}{{\partial x}}\left( {\tau _{{2э }}^{{\left( \nu \right)}} - \hat {\tau }_{2}^{{\left( \nu \right)}}} \right),} \\ {g_{{\lambda y}}^{{\left( \nu \right)}} = - \sigma _{{{{\tau }_{1}}}}^{{ - 2}}\frac{{\partial {{\tau }_{1}}}}{{\partial y}}\left( {\tau _{{1э }}^{{\left( \nu \right)}} - \hat {\tau }_{1}^{{\left( \nu \right)}}} \right) - \sigma _{{{{\tau }_{2}}}}^{{ - 2}}\frac{{\partial {{\tau }_{2}}}}{{\partial y}}\left( {\tau _{{2э }}^{{\left( \nu \right)}} - \hat {\tau }_{2}^{{\left( \nu \right)}}} \right).} \end{array}} \right.$С учетом формул (14) и (22) из первого уравнения (3) можно получить:
(23)
$\left\{ {\begin{array}{*{20}{c}} {\hat {x}_{{ps}}^{{\left( \nu \right)}} = x_{э }^{{\left( \nu \right)}} + K_{{ps}}^{{\left( \nu \right)}}\left( {11} \right)g_{{\lambda x}}^{{\left( \nu \right)}} + K_{{ps}}^{{\left( \nu \right)}}\left( {12} \right)g_{{\lambda y}}^{{\left( \nu \right)}},} \\ {\hat {y}_{{ps}}^{{\left( \nu \right)}} = y_{э }^{{\left( \nu \right)}} + K_{{ps}}^{{\left( \nu \right)}}\left( {21} \right)g_{{\lambda x}}^{{\left( \nu \right)}} + K_{{ps}}^{{\left( \nu \right)}}\left( {22} \right)g_{{\lambda y}}^{{\left( \nu \right)}},} \end{array}} \right.$где $K_{{ps}}^{{\left( \nu \right)}}\left( {ij} \right)$ – элемент матрицы $K_{{ps}}^{{\left( \nu \right)}},$ расположенный в i-ой строке и j-ом столбце. Сама апостериорная ковариационная матрица $K_{{ps}}^{{\left( \nu \right)}}$ определяется из второго уравнения (3). Соответственно, учитывая формулы (8) и (9), выражение (5) можно записать в виде:
где(25)
$B{{B}^{T}} = \left[ {\begin{array}{*{20}{c}} {b_{x}^{2}}&0 \\ 0&{b_{y}^{2}} \end{array}} \right].$Таким образом, неизвестной остается матрица $H_{\lambda }^{{\left( \nu \right)}}.$ Из формулы (7) получаем элементы матрицы:
(26)
$\begin{gathered} \frac{{{{\partial }^{2}}F}}{{\partial {{x}^{2}}}} = - \sigma _{{{{\tau }_{1}}}}^{{ - 2}}\left( {\frac{{{{\partial }^{2}}{{\tau }_{1}}}}{{\partial {{x}^{2}}}}\left( {\hat {\tau }_{1}^{{\left( \nu \right)}} - \tau _{{1э }}^{{\left( \nu \right)}}} \right) + {{{\left( {\frac{{\partial {{\tau }_{1}}}}{{\partial x}}} \right)}}^{2}}} \right) - \\ - \,\,\sigma _{{{{\tau }_{2}}}}^{{ - 2}}\left( {\frac{{{{\partial }^{2}}{{\tau }_{2}}}}{{\partial {{x}^{2}}}}\left( {\hat {\tau }_{2}^{{\left( \nu \right)}} - \tau _{{2э }}^{{\left( \nu \right)}}} \right) + {{{\left( {\frac{{\partial {{\tau }_{2}}}}{{\partial x}}} \right)}}^{2}}} \right), \\ \end{gathered} $(27)
$\begin{gathered} \frac{{{{\partial }^{2}}F}}{{\partial x\partial y}} = - \sigma _{{{{\tau }_{1}}}}^{{ - 2}}\left( {\frac{{{{\partial }^{2}}{{\tau }_{1}}}}{{\partial x\partial y}}\left( {\hat {\tau }_{1}^{{\left( \nu \right)}} - \tau _{{1э }}^{{\left( \nu \right)}}} \right) + \frac{{\partial {{\tau }_{1}}}}{{\partial x}}\frac{{\partial {{\tau }_{1}}}}{{\partial y}}} \right) - \\ - \,\,\sigma _{{{{\tau }_{2}}}}^{{ - 2}}\left( {\frac{{{{\partial }^{2}}{{\tau }_{2}}}}{{\partial x\partial y}}\left( {\hat {\tau }_{2}^{{\left( \nu \right)}} - \tau _{{2э }}^{{\left( \nu \right)}}} \right) + \frac{{\partial {{\tau }_{2}}}}{{\partial x}}\frac{{\partial {{\tau }_{2}}}}{{\partial y}}} \right), \\ \end{gathered} $(28)
$\begin{gathered} \frac{{{{\partial }^{2}}F}}{{\partial {{y}^{2}}}} = - \sigma _{{{{\tau }_{1}}}}^{{ - 2}}\left( {\frac{{{{\partial }^{2}}{{\tau }_{1}}}}{{\partial {{y}^{2}}}}\left( {\hat {\tau }_{1}^{{\left( \nu \right)}} - \tau _{{1э }}^{{\left( \nu \right)}}} \right) + {{{\left( {\frac{{\partial {{\tau }_{1}}}}{{\partial y}}} \right)}}^{2}}} \right) - \\ - \,\,\sigma _{{{{\tau }_{2}}}}^{{ - 2}}\left( {\frac{{{{\partial }^{2}}{{\tau }_{2}}}}{{\partial {{y}^{2}}}}\left( {\hat {\tau }_{2}^{{\left( \nu \right)}} - \tau _{{2э }}^{{\left( \nu \right)}}} \right) + {{{\left( {\frac{{\partial {{\tau }_{2}}}}{{\partial y}}} \right)}}^{2}}} \right). \\ \end{gathered} $В выражениях (26)–(28) использованы вторые производные ЛФП по информационным параметрам, которые необходимо найти. Из уравнений (16)–(19) получаем:
(29)
$\begin{gathered} \frac{{{{\partial }^{2}}{{\tau }_{1}}}}{{\partial {{x}^{2}}}} = \frac{2}{с }{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left( {1 - {{{\left( {x_{э }^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}}{{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}}^{{ - 1}}}} \right), \\ \end{gathered} $(30)
$\frac{{{{\partial }^{2}}{{\tau }_{1}}}}{{\partial x\partial y}} = \frac{2}{с }\left( {x_{э }^{{\left( \nu \right)}} + \frac{b}{2}} \right)y_{э }^{{\left( \nu \right)}}{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}},$(31)
$\begin{gathered} \frac{{{{\partial }^{2}}{{\tau }_{1}}}}{{\partial {{y}^{2}}}} = \frac{2}{с }{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left( {1 - y_{э }^{{{{{\left( \nu \right)}}^{2}}}}{{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} + \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}}^{{ - 1}}}} \right), \\ \end{gathered} $(32)
$\begin{gathered} \frac{{{{\partial }^{2}}{{\tau }_{2}}}}{{\partial {{x}^{2}}}} = \frac{2}{с }{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left( {1 - {{{\left( {x_{э }^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}}{{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}}^{{ - 1}}}} \right), \\ \end{gathered} $(33)
$\frac{{{{\partial }^{2}}{{\tau }_{2}}}}{{\partial x\partial y}} = \frac{2}{с }\left( {x_{э }^{{\left( \nu \right)}} - \frac{b}{2}} \right)y_{э }^{{\left( \nu \right)}}{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}},$(34)
$\begin{gathered} \frac{{{{\partial }^{2}}{{\tau }_{2}}}}{{\partial {{y}^{2}}}} = \frac{2}{с }{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left( {1 - y_{э }^{{{{{\left( \nu \right)}}^{2}}}}{{{\left( {{{{\left( {x_{э }^{{\left( \nu \right)}} - \frac{b}{2}} \right)}}^{2}} + y_{э }^{{{{{\left( \nu \right)}}^{2}}}}} \right)}}^{{ - 1}}}} \right). \\ \end{gathered} $Уравнения (3)–(5) являются рекуррентными и поэтому остается открытым вопрос о начальных условиях. Координаты объекта наблюдения на первом шаге $\hat {x}_{{ps}}^{{\left( 1 \right)}},$ $\hat {y}_{{ps}}^{{\left( 1 \right)}}$ могут быть найдены с помощью подстановки оценок $\hat {\tau }_{1}^{{\left( 1 \right)}},$ $\hat {\tau }_{2}^{{\left( 1 \right)}}$ в уравнения (12). Таким образом, оценка и фильтрованное значение координат на первом шаге будут совпадать. Апостериорная ковариационная матрица ошибок фильтрации на первом шаге может быть найдена, как ковариационная матрица ошибок измерения, пересчитанная в декартову систему координат [1]:
где(36)
${{W}_{{\lambda q}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial {{\tau }_{1}}}}}&{\frac{{\partial x}}{{\partial {{\tau }_{2}}}}} \\ {\frac{{\partial y}}{{\partial {{\tau }_{1}}}}}&{\frac{{\partial y}}{{\partial {{\tau }_{2}}}}} \end{array}} \right].$Найдем элементы матрица ${{W}_{{\lambda q}}}.$ Из выражения (12) получаем:
(37)
$\frac{{\partial x}}{{\partial {{\tau }_{1}}}} = \frac{{c\left( {2c\hat {\tau }_{1}^{{\left( 1 \right)}} - b} \right)}}{{8b}},$(38)
$\frac{{\partial x}}{{\partial {{\tau }_{2}}}} = \frac{{c\left( { - 2c\hat {\tau }_{2}^{{\left( 1 \right)}} - b} \right)}}{{8b}},$(39)
$\frac{{\partial y}}{{\partial {{\tau }_{1}}}} = - \frac{{c\left( {\frac{b}{2} - \hat {x}_{{ps}}^{{\left( 1 \right)}}} \right)\left( {b - 2c\hat {\tau }_{1}^{{\left( 1 \right)}}} \right)}}{{8b\sqrt {{{4}^{{ - 1}}}{{c}^{2}}{{{\left( {\hat {\tau }_{2}^{{\left( 1 \right)}} - \frac{b}{{2c}}} \right)}}^{2}} - {{{\left( {\frac{b}{2} - \hat {x}_{{ps}}^{{\left( 1 \right)}}} \right)}}^{2}}} }},$(40)
$\begin{gathered} \frac{{\partial y}}{{\partial {{\tau }_{1}}}} = \\ = - \frac{{{{4}^{{ - 1}}}{{c}^{2}}\left( {2\hat {\tau }_{2}^{{\left( 1 \right)}} - \frac{b}{c}} \right) + {{4}^{{ - 1}}}{{b}^{{ - 1}}}c\left( {\frac{b}{2} - \hat {x}_{{ps}}^{{\left( 1 \right)}}} \right)\left( {b - 2c\hat {\tau }_{2}^{{\left( 1 \right)}}} \right)}}{{2\sqrt {{{4}^{{ - 1}}}{{c}^{2}}{{{\left( {\hat {\tau }_{2}^{{\left( 1 \right)}} - \frac{b}{{2c}}} \right)}}^{2}} - {{{\left( {\frac{b}{2} - \hat {x}_{{ps}}^{{\left( 1 \right)}}} \right)}}^{2}}} }}. \\ \end{gathered} $Таким образом, получены все необходимые соотношения для реализации нелинейного алгоритма фильтрации в охранной дальномерной двухпозиционной радиосистеме координатометрии.
2. МОДЕЛИРОВАНИЕ
А. Показатели качества
В качестве простейшей оценки может быть взята точечная ошибка по каждой координате [1]:
(41)
$\left\{ {\begin{array}{*{20}{c}} {e_{x}^{{\left( \nu \right)}} = {{x}^{{\left( \nu \right)}}} - \hat {x}_{{ps}}^{{\left( \nu \right)}},} \\ {e_{y}^{{\left( \nu \right)}} = {{y}^{{\left( \nu \right)}}} - \hat {y}_{{ps}}^{{\left( \nu \right)}}.} \end{array}} \right.$Для обобщенной оценки ошибки фильтрации по обеим координатам можно рассматривать расстояние между истинными значениями координат и значениями на выходе фильтра:
(42)
${{d}^{{\left( \nu \right)}}} = \sqrt {{{{\left( {{{x}^{{\left( \nu \right)}}} - \hat {x}_{{ps}}^{{\left( \nu \right)}}} \right)}}^{2}} + {{{\left( {{{y}^{{\left( \nu \right)}}} - \hat {y}_{{ps}}^{{\left( \nu \right)}}} \right)}}^{2}}} .$Ввиду того, что величины (41) и (42) являются случайными для численных оценок качества фильтрации могут быть взяты числовые характеристики статистических распределений – выборочное среднее, исправленная выборочная дисперсия и исправленное выборочное среднеквадратическое отклонение [4]:
(44)
${{D}_{z}} = \frac{1}{{n - 1}}\sum\limits_{\nu = 1}^n {{{{\left( {{{z}^{{\left( \nu \right)}}} - \bar {z}} \right)}}^{2}}} ,$(45)
${{\sigma }_{z}} = \sqrt {\frac{1}{{n - 1}}\sum\limits_{\nu = 1}^n {{{{\left( {{{z}^{{\left( \nu \right)}}} - \bar {z}} \right)}}^{2}}} } .$В выражениях (43)–(45) в качестве $z$ могут выступать либо точечные ошибки (41), либо расстояние (42); при этом суммы обычно ограничиваются n – числом импульсов за время наблюдения.
Б. Выбор параметров для моделирования
В общем случае, СКО измерений временной задержки представляет собой корень из суммы квадратов ошибок, возникающих по различным причинам [5]:
(46)
${{\sigma }_{\tau }} = \sqrt {\sigma _{{\tau \,ш }}^{2} + \sigma _{{\tau \,ф }}^{2} + \sigma _{{\tau \,р а с п р }}^{2}} ,$Среднеквадратическое отклонение измерения временной задержки, обусловленное внутренними шумами приемника ${{\sigma }_{{\tau \,ш }}},$ может быть вычислено по формулам потенциальной точности [5]:
(47)
${{\sigma }_{{\tau \,ш }}} = \frac{1}{{\Delta {{f}_{c}}\sqrt {{{2E} \mathord{\left/ {\vphantom {{2E} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}} }},$Полагаем, что значение величины ${{\sigma }_{{\tau \,р а с п р }}}$ и ${{\sigma }_{{\tau \,ф }}}$ с учетом небольших расстояний до объекта наблюдения не превысят величину ${{\sigma }_{{\tau \,ш }}},$ поэтому положим, что их сумма квадратов равна квадрату ${{\sigma }_{{\tau \,ш }}}.$ Таким образом, окончательно получаем:
(48)
${{\sigma }_{\tau }} = \frac{{\sqrt 2 }}{{\Delta {{f}_{c}}\sqrt {{{2E} \mathord{\left/ {\vphantom {{2E} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}} }}.$Далее зададимся некоторыми конкретными исходными параметрами радиосистемы и объекта наблюдения. В процессе моделирования будем менять некоторые из них, оценивая при этом показатели качества и, таким образом, определяя влияние конкретного параметра на эти показатели качества.
Период следования импульсов зададим равным ${{T}_{{\text{c}}}} = 0.001$ c. При этом время наблюдения будет ограничено ${{t}_{{{\text{н а б л }}}}} = 1$ с, и, соответственно, ограниченно будет и количество тактов $n = 1000.$ Ширину спектра эхосигнала принимаем равным $\Delta {{f}_{c}}$ ГГц, а ОСШ = 0 дБ (затем значение пересчитываем в энергетическое ${{2E} \mathord{\left/ {\vphantom {{2E} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}$). Среднеквадратические отклонения измерений задержек принимаем равными, так что ${{\sigma }_{{{{\tau }_{1}}}}} = {{\sigma }_{{{{\tau }_{2}}}}} = {{10}^{{ - 9}}}$ с.
Начальные координаты объекта наблюдения выбирались из условия, что ОН в начальный момент находится на расстоянии ${{R}^{{\left( 1 \right)}}} = 1500$ м от ПОИ, под углом 45° по отношению к оси x. Таким образом, начальные координаты ОН по осям x, y составили ${{x}^{{\left( 1 \right)}}} = {{y}^{{\left( 1 \right)}}} = 1061$ м. СКО флуктуаций траектории за 1 с (соизмеримый с интервалом корреляции) брались одинаковыми и равными ${{b}_{x}} = {{b}_{y}} = 1$ м (что предположительно соответствует таким объектам, как некоторые типы дронов и автомобилей). Соответственно, получаем СКО флуктуаций траектории за один такт ${{b}_{{x\;{{T}_{c}}}}} = {{b}_{{y\;{{T}_{c}}}}} = 0.001$ м.
В. Результаты моделирования
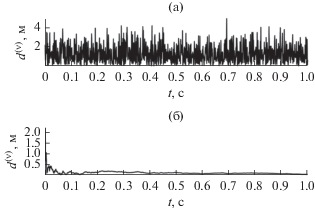
На рис. 2 представлены типовые графики обобщенных ошибок (42) оценки и фильтрации для заданных параметров.
Рис. 2.
Обобщенная ошибка расстояния между истинными значениями координат и значениями, полученными для оценки (а) и фильтрации (б).
На рис. 3а–3д показаны зависимости исправленного выборочного СКО (45) обобщенных ошибок (42) оценки и фильтрации от следующих параметров: ширины спектра эхосигнала $\Delta {{f}_{c}};$ ОСШ; начального расстояния между пунктом обработки информации и объектом наблюдения ${{R}^{{\left( 1 \right)}}};$ угла ${{\beta }^{{\left( 1 \right)}}}$ между линией, соединяющей ПОИ и ОН, и осью x; СКО формирующих воздействий цели ${{b}_{x}},$ ${{b}_{y}}.$ При этом значения СКО усреднялись по 10 000 реализациям.
Рис. 3.
Зависимости исправленного выборочного СКО ошибки от: ширины спектра эхосигнала $\Delta f$(а); ОСШ (б); начального расстояния до объекта наблюдения ${{R}^{{\left( 1 \right)}}}$ (в); угла ${{\beta }^{{\left( 1 \right)}}}$ между линией, соединяющей ПОИ и ОН, и осью x (г); СКО формирующих воздействий ${{b}_{x}},$ ${{b}_{y}}$ (д). Штриховые линии относятся к режиму оценки, сплошные линии – к режиму фильтрации.
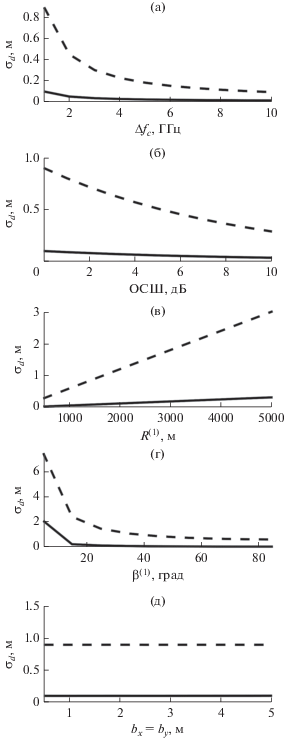
Анализ указанных зависимсотей показал, что алгоритм позволяет получить выигрыш в СКО по сравнению с оценкой по одному импульсу примерно в 9.3–9.4 раза в среднем для всех параметров, кроме ${{\beta }^{{\left( 1 \right)}}}$ при котором это уменьшение составляет 5.3 раза. Как и ожидалось, ошибки уменьшаются с увеличением ОСШ, расширением спектра эхосигнала, ростом угла наклона линии визирования. Изменение СКО формирующих воздействий в заданном при моделировании интервале практически не привело к росту ошибок.
ЗАКЛЮЧЕНИЕ
Получены выражения для реализации алгоритма фильтрации по критерию максимума апостериорной вероятности в охранной дальномерной двухпозиционной радиосистеме координатометрии. Проведено моделирование данного алгоритма и, таким образом, показана его работоспособность. При этом был оценен выигрыш в СКО ошибок при использовании алгоритма фильтрации по сравнению с использованием режима оценки.
При соответствующей корректировке алгоритм может быть реализован и в других системах.
Список литературы
Ширман Я.Д., Багдасарян С.Т., Маляренко А.С. и др. Радиоэлектронные системы: Основы построения и теория. Справочник. М.: Радиотехника, 2007. С. 319.
Гребенников В.Б. // Методы обработки сигналов в радиотехнических системах. Межвузовский сб. тр. Саратов: Изд-во Саратов. политех. ин-та, 1986. С. 16.
Котов А.Ф., Гребенников В.Б. // Радиотехника. 1987. № 6. С. 6.
Гусак А.А., Гусак Г.М., Бричникова Е.А. Справочник по высшей математике. Минск: ТетраСистемс, 1999. С. 538.
Дудник П.И., Кондратенков Г.С., Татарский Б.Г. и др. Авиационные радиолокационные комплексы и системы: учебник для слушателей и курсантов ВУЗов ВВС. М.: Изд-во ВВИА им. проф. Н.Е. Жуковского, 2006. С. 345.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


