Радиотехника и электроника, 2019, T. 64, № 3, стр. 231-245
Об искажении переднего фронта квазимонохроматического сигнала в резонансно-поглощающей среде
Н. С. Бухман *
Самарский государственный технический университет
443100 Самара, ул. Молодогвардейская, 244, Российская Федерация
* E-mail: nik3141rambler@rambler.ru
Поступила в редакцию 08.06.2017
После доработки 24.01.2018
Принята к публикации 04.03.2018
Аннотация
Изучено искажение резкого переднего фронта квазимонохроматического электромагнитного (светового или радио) сигнала (волнового пакета), распространяющегося в среде со спектральной линией (или полосой) поглощения. Показано, что фронтальный скачок комплексной огибающей радиосигнала распространяется без изменения своей величины. За передним фронтом уровень сигнала начинает снижаться, причем скорость уменьшения возрастает с ростом протяженности трассы. В результате на переднем и заднем (если он есть) фронтах сигнала формируются все более обостряющиеся с ростом протяженности трассы “зубцы”. Такие “зубцы” формируются не только в точках разрыва вещественной амплитуды сигнала, но и в точках разрыва его фазы, поэтому при распространении фазоманипулированного радиосигнала в резонансно-поглощающей среде происходит его “саморазоблачение”.
ВВЕДЕНИЕ
Данная работа посвящена проблеме деформации переднего фронта квазимонохроматического сигнала (волнового пакета), распространяющегося в резонансно-поглощающей среде, т.е. в среде с одной или несколькими спектральными линиями поглощения. Предполагается, что несущая частота этого квазимонохроматического сигнала не обязательно совпадает с центральной частотой спектральной линии (или группы линий) поглощения. Основное внимание уделяется случаю резкого переднего фронта сигнала, когда огибающая сигнала (или одна из ее производных) в стартовой точке терпит разрыв и скачком изменяется от нуля до некоторого ненулевого значения. В случае разрыва самой огибающей речь идет о сигнале с резким передним фронтом; если сама огибающая непрерывна, но скачком изменяется ее первая производная, то речь идет о линейном нарастании сигнала на фронте – и так далее.
Разумеется, само понятие комплексной огибающей узкополосного сигнала [1] предполагает медленность изменения этой огибающей в сравнении с осцилляциями несущей. Поэтому реально речь идет об изменении огибающей или ее производных за время, большое в сравнении с периодом несущей, но малое в сравнении с временем когерентности спектральной линии (или, что то же самое, с ее обратной спектральной шириной). Таким образом, нас интересует случай, когда спектральная ширина переднего фронта сигнала (практически – обратная длительность фронта сигнала) мала в сравнении с частотой несущей, но не мала в сравнении с шириной спектральной линии и в сравнении с отстройкой несущей сигнала от центра спектральной линии. Это означает, что рассматриваемый в данной работе сигнал является квазимонохроматическим “сам по себе” и поэтому можно пользоваться понятием комплексной огибающей узкополосного сигнала, но при этом тот же сигнал является “широкополосным” для данной среды и использование классической теории дисперсии (основанной на разложении показателя преломления среды в ряд Тейлора по частоте вблизи несущей сигнала, см. [1]) невозможно.
Численное и аналитическое исследование широкополосных (в указанном выше смысле) сигналов, ширина спектра которых не мала в сравнении с шириной спектральной линии (с лоренцевским или доплеровским контуром) предпринималось неоднократно (см. [2–16]). Анализ эволюции резкого переднего фронта видеосигнала (сигнала без несущей) также предпринимался неоднократно [17, 18]. Рассмотрение же эволюции резкого переднего фронта радиосигнала (сигнала с несущей) в резонансно поглощающей среде ранее не проводилось – оно и осуществляется в данной работе.
Актуальность проведенного в данной работе исследования связана с практическим использованием все более коротких электромагнитных импульсов, длительность которых часто не может считаться большой в сравнении с временем когерентности спектральной линии среды, в которой они распространяются. Ясно, что в этом случае длительность переднего и заднего фронтов сигнала тем более не может считаться большой в сравнении с временем когерентности спектральной линии и искажение фронтов сигнала может существенно изменить его характеристики.
Если говорить о распространении субмиллиметровых радиоволн в атмосфере (см. [5, 6, 12, 14]), то речь идет об импульсах с исходной длительностью фронта менее наносекунды; в оптическом диапазоне речь идет об импульсах с исходной длительностью фронта менее наносекунды (в разреженных газах или межзвездной среде) или пикосекунды (в кристаллах). Длительность самого сигнала в данном случае несущественна – она может быть и велика, и мала.
Основной целью данной работы является не конкретный расчет искажения определенного сигнала в определенной среде (каковой расчет всегда может быть осуществлен численно), а выяснение общих закономерностей, сохраняющихся для сигналов с резким передним фронтом при произвольном форм-факторе спектральной линии (или группы близко расположенных спектральных линий) поглощения. Забегая вперед, можно отметить, что основные особенности эволюции переднего фронта сигнала, как оказывается, практически не зависят не только от характера уширения спектральной линии (лоренцевский, доплеровский, фойгтовский или более сложный профиль), но и даже и от ее ширины; они определяются только концентрацией и силой осцилляторов [19], ответственных за данную спектральную линию.
1. ОСНОВНЫЕ СООТНОШЕНИЯ
Рассмотрим распространение электромагнитной волны (сигнала) $\vec {E}(x,y,z,t)$ в однородной среде с диэлектрической проницаемостью $\varepsilon (\omega )$ и показателем преломления (не обязательно вещественным) $n(\omega ) = \sqrt {\varepsilon (\omega )} .$ Предположим, что волна – плоская, распространяющаяся в положительном направлении оси z. В этом случае ее состояние поляризации в процессе распространения не изменяется и характеризуется постоянным вектором поляризации, перпендикулярным оси z (задача практически скалярна), а скалярная амплитуда $E(z,t)$ зависит только от времени t и продольной координаты z. Пусть ${{\omega }_{0}}$ – частота несущей сигнала $E(z,t),$ а $A(z,t)$ – его комплексная огибающая [1]. Предполагая, что ширина спектра сигнала мала в сравнении с частотой несущей ω0, имеем для временных и спектральных характеристик сигнала следующие очевидные соотношения:
(1)
$\begin{gathered} E(z,t) = \int\limits_{ - \infty }^{ + \infty } {{{E}_{\omega }}(z,\omega )\exp ( - i\omega t)d\omega } , \\ {{E}_{\omega }}(z,\omega ) = {{(2\pi )}^{{ - 1}}}\int\limits_{ - \infty }^{ + \infty } {E(z,t)\exp (i\omega t)dt} , \\ E(z,t) = A(z,t)\exp ( - i{{\omega }_{0}}t) + A{\text{*}}(z,t)\exp (i{{\omega }_{0}}t), \\ A(z,t) = \int\limits_{ - \infty }^{ + \infty } {{{A}_{\Omega }}(z,\Omega )\exp ( - i\Omega t)d\Omega } , \\ {{A}_{\Omega }}(z,\Omega ) = {{(2\pi )}^{{ - 1}}}\int\limits_{ - \infty }^{ + \infty } {A(z,t)\exp (i\Omega t)dt} , \\ {{A}_{\Omega }}(z,\Omega ) = {{E}_{\omega }}(z,\omega ),\,\,\,\,\omega = {{\omega }_{0}} + \Omega . \\ \end{gathered} $Задав на плоскости $z = 0$ граничные условия для распространяющейся в положительном направлении оси z волны $E(z,t)$ в виде $E(0,t) \equiv {{E}^{{(0)}}}(t),$ в произвольной точке пространства имеем
Пусть сигнал распространяется в среде с показателем преломления
где ${{n}_{0}} \geqslant 1$ – “фоновое” (“нерезонансное”) значение показателя преломления среды, частотной зависимостью которого в пределах рассматриваемой полосы частот можно пренебречь, а $\Delta n(\omega )$ – “резонансная” добавка, связанная со спектральной линией (или полосой), максимальное поглощение которой достигается на частоте11 ${{\omega }_{0}}.$Такая ситуация типична для газов, в которых обычно достаточно узкие линии или группы линий поглощения можно рассматривать как “изолированные”, в том смысле что они “окаймлены” широкими “окнами прозрачности”, в которых поглощение невелико, а диэлектрическая проницаемость практически постоянна и равна 1 (в этом случае ${{n}_{0}} = 1$) [14]. В случае же жидких и твердых сред ширина “окон прозрачности” обычно сопоставима с шириной полос поглощения; в этом случае результаты данной работы следует рассматривать лишь как оценочные (полуколичественные). Отметим, что в нашем рассмотрении “резонансная добавка” $\Delta n(\omega )$ к “фоновому” значению диэлектрической проницаемости ${{n}_{0}} \geqslant 1$ вовсе не обязательно должна быть мала22 – существенным условием является не слабость поглощения в центре спектральной линии, а достаточная узость этой линии.
С учетом (2) для комплексной передаточной функции слоя вещества толщиной $z$ имеем
(3)
$\begin{gathered} F(z,\omega ) = \exp (ikn(\omega )z) = \\ = \exp (ik{{n}_{0}}z)\exp (ik\Delta n(\omega )z), \\ \end{gathered} $(4)
${{\alpha }_{0}} \equiv - i{{k}_{0}}\Delta n({{\omega }_{0}}),\,\,\,\,{{k}_{0}} \equiv {{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} c}} \right. \kern-0em} c}$и нормированный на единицу в центре спектральной линии ${{\omega }_{0}}$ комплексный форм-фактор линии $g(\Omega )$ [7]
нетрудно представить передаточную функцию слоя в виде
где $\xi \equiv {{\alpha }_{0}}z$ – оптическая толщина слоя вещества33.В случае симметричного контура спектральной линии (например, лоренцевский или доплеровский контур) имеем $\operatorname{Re} (\Delta n({{\omega }_{0}})) = 0,$ что обеспечивает вещественность параметров α0 и ξ. В общем случае (например, если сложная спектральная линия состоит из двух близко расположенных разных спектральных линий) имеем $\operatorname{Re} (\Delta n({{\omega }_{0}})) \ne 0$ и параметры ${{\alpha }_{0}}$ и ξ комплексны. Это не приводит к существенному изменению приведенных ниже общих результатов, поскольку мнимая часть параметров ${{\alpha }_{0}}$ и ξ просто описывает общий (для всех сигналов) дополнительный набег фазы при распространении – существенна лишь вещественная часть этих параметров.
Для изучения высокочастотной составляющей спектра сигнала естественно (как и в [7]) использовать разложение функции $g(\Omega )$ в асимптотический ряд по параметру Ω в окрестности бесконечности (т.е. по параметру ${1 \mathord{\left/ {\vphantom {1 \Omega }} \right. \kern-0em} \Omega }$ в окрестности 0). Запишем соответствующее разложение в виде
где $x \equiv {{({{2\Omega } \mathord{\left/ {\vphantom {{2\Omega } {\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}})}^{{ - 1}}},$ ${{\gamma }_{n}} \equiv {{( - i)}^{n}}{{\left. {\frac{{{{d}^{n}}g}}{{d{{x}^{n}}}}} \right|}_{{x = 0}}}.$В (7) $\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – ширина спектральной линии $g(\Omega )$ на уровне 1/2 от максимума44, x – безразмерная обратная частота, набор структурных коэффициентов $\left\{ {{{\gamma }_{n}}} \right\}$ можно рассматривать как альтернативный (по отношению к прямому заданию форм-фактора линии $g(\Omega )$) способ задания профиля спектральной линии.
Используя приведенные в [15, 16, 20] формулы для комплексных форм-факторов спектральных линий, в случае лоренцевского (L) (столкновительное или радиационное уширение линии) и гауссовского (G) (доплеровское уширение) контуров спектральной линии имеем соответственно
(8)
$\begin{gathered} \gamma _{1}^{L} = 1,\,\,\,\,{\text{ }}\gamma _{2}^{L} = - 2,\,\,\,\,\gamma _{3}^{L} = 6,\,\,\,\,\gamma _{4}^{L} = - 24, \\ \gamma _{1}^{G} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {\pi \ln (2)} }}} \right. \kern-0em} {\sqrt {\pi \ln (2)} }} \approx 0.678,\,\,\,\,\gamma _{2}^{G} = 0,{\text{ }} \\ \gamma _{3}^{G} = {{ - 3} \mathord{\left/ {\vphantom {{ - 3} {(\ln (2)}}} \right. \kern-0em} {(\ln (2)}}\sqrt {\pi \ln (2)} ) \approx - 2.933,\,\,\,\,\gamma _{4}^{G} = 0. \\ \end{gathered} $Обращение в нуль четных коэффициентов разложения для гауссовского форм-фактора линии связано с экспоненциально быстрым затуханием мнимой части показателя преломления (или, что то же самое, вещественной части комплексного форм-фактора линии) по мере удаления от центральной частоты линии.
Передаточную функцию слоя (6) можно представить в виде
где – “фоновая” передаточная функция слоя вещества без учета линии поглощения,– дополнительная “резонансная” (связанная со спектральной линией) передаточная функция слоя вещества.
С учетом (7) разложение этой функции в ряд по частоте $\Omega $ в окрестности бесконечности имеет вид
(12)
${{F}^{{{\text{р е з }}}}} = 1 + \sum\limits_{n = 1}^\infty {\frac{{{{\alpha }_{n}}(\xi )}}{{n!}}{{{\left( {\frac{i}{{{{\tau }_{{\text{л }}}}\Omega }}} \right)}}^{n}}} ,$(13)
$\begin{gathered} {{\alpha }_{1}}(\xi ) = - {{\gamma }_{1}}\xi ,{\text{ }}{{\alpha }_{2}}(\xi ) = - {{\gamma }_{2}}\xi + \gamma _{1}^{2}{{\xi }^{2}}, \\ {{\alpha }_{3}}(\xi ) = - {{\gamma }_{3}}\xi + 3{{\gamma }_{1}}{{\gamma }_{2}}{{\xi }^{2}} - \gamma _{1}^{3}{{\xi }^{3}}, \\ {{\alpha }_{4}}(\xi ) = - {{\gamma }_{4}}\xi + (4{{\gamma }_{1}}{{\gamma }_{3}} + 3\gamma _{2}^{2}){{\xi }^{2}} - 6\gamma _{1}^{2}{{\gamma }_{2}}{{\xi }^{3}} + \gamma _{1}^{4}{{\xi }^{4}}. \\ \end{gathered} $В (12) ${{\tau }_{{\text{л }}}} \equiv {2 \mathord{\left/ {\vphantom {2 {\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$ имеет смысл характерного времени когерентности излучения спектральной линии. Формулы (13) для ${{\alpha }_{n}}(\xi )$ могут быть получены путем переразложения функции
Эволюция спектра огибающей сигнала по мере его распространения описывается уравнением
(14)
$\begin{gathered} {{A}_{\Omega }}(z,\Omega ) = {{A}_{\Omega }}(0,\Omega )F(z,{{\omega }_{0}} + \Omega ) = \\ = A_{\Omega }^{{{\text{п е р в }}}}(z,\Omega ) + A_{\Omega }^{{{\text{о т к л }}}}(z,\Omega ), \\ \end{gathered} $(15)
$\begin{gathered} A_{\Omega }^{{{\text{п е р в }}}}(z,\Omega ) = {{A}_{\Omega }}(0,\Omega ){{F}^{{{\text{ф о н }}}}}(z,\Omega ), \\ A_{\Omega }^{{{\text{о т к л }}}}(z,\Omega ) = {{A}_{\Omega }}(0,\Omega ){{F}^{{{\text{ф о н }}}}}(z,\Omega )\left( {{{F}^{{{\text{р е з }}}}}(z,\Omega ) - 1} \right) \\ \end{gathered} $– огибающие двух компонент сигнала, прошедших через разные фильтры и потому существенно отличающихся по своим характеристикам. Первая компонента $A_{\Omega }^{{{\text{п е р в }}}}$ (далее – первичный сигнал) соответствует исходному сигналу, распространяющемуся в среде с вещественным и не зависящим от частоты показателем преломления ${{n}_{0}}$ (непоглощающая среда без дисперсии). Вторую компоненту $A_{\Omega }^{{{\text{о т к л }}}}$ (далее – сигнал отклика) можно рассматривать как отклик спектральной линии поглощения на первичный сигнал (при ${{\alpha }_{0}} = 0$ $A_{\Omega }^{{{\text{о т к л }}}}{\text{ }} = {\text{0}}$).
Пусть в начальной точке $z = 0$ временная зависимость сигнала характеризуется функцией ${{A}^{{(0)}}}(t) \equiv A(0,t).$ Тогда из (10), (15) видно, что первичный сигнал совпадает с исходным сигналом, сдвинутым во времени на “нерезонансное” время задержки, соответствующее “фоновому” значению показателя преломления среды и набравшим соответствующую фазу:
(16)
$\begin{gathered} {{A}^{{{\text{п е р в }}}}}(z,t) = {{A}^{{(0)}}}({{t}_{{\text{с }}}})\exp (i{{k}_{0}}{{n}_{0}}z), \\ {{t}_{{\text{с }}}}(z,t) \equiv t - {{\tau }_{{{\text{п е р в }}}}}(z),\,\,\,\,{\text{ }}{{\tau }_{{{\text{п е р в }}}}}(z) \equiv {{z{{n}_{0}}} \mathord{\left/ {\vphantom {{z{{n}_{0}}} c}} \right. \kern-0em} c}. \\ \end{gathered} $В (16) ${{\tau }_{{{\text{п е р в }}}}}$ – зависящее от точки наблюдения z время задержки первичного сигнала, а ${{t}_{{\text{с }}}}(z,t)$ – сдвинутое (на “нерезонансное” время задержки) время. Использование “сдвинутого времени” ${{t}_{{\text{с }}}}(z,t)$ вместо истинного t позволяет исключить из рассмотрения “нерезонансную” задержку сигнала, различную в разных точках пространства z.
Для сигнала отклика с учетом (10), (12) и (15) нетрудно получить представление в виде ряда
(17)
$\begin{gathered} {{A}^{{{\text{о т к л }}}}}(\xi ,t) = \exp (i{{k}_{0}}{{n}_{0}}z)\sum\limits_{n = 1}^\infty {\frac{{{{\alpha }_{n}}(\xi )}}{{n!\tau _{{\text{л }}}^{n}}}A_{n}^{{{\text{о т к л }}}}({{t}_{{\text{с }}}}),} \\ A_{n}^{{{\text{о т к л }}}}(t) \equiv \int\limits_{ - \infty }^{ + \infty } {A_{\Omega }^{{(0)}}(\Omega )\exp ( - i\Omega t){{{( - i\Omega )}}^{{ - n}}}d\Omega \,.} \\ \end{gathered} $С учетом известных свойств фурье-преобразования и данных работы [22, с. 52] выражение для $A_{n}^{{{\text{о т к л }}}}(t)$ нетрудно переписать в виде
(18)
$\begin{gathered} A_{0}^{{{\text{о т к л }}}}(t) = {{A}^{{(0)}}}(t), \\ A_{n}^{{{\text{о т к л }}}}(t) = \underbrace {\int\limits_{ - \infty }^t {dt\int\limits_{ - \infty }^t {dt.....\int\limits_{ - \infty }^t {dt{{A}^{{(0)}}}(t)} } } }_{n{\text{ р а з }}} = \\ = ({1 \mathord{\left/ {\vphantom {1 {(n - 1)}}} \right. \kern-0em} {(n - 1)}}!)\int\limits_{ - \infty }^t {{{{(t - {{t}_{1}})}}^{{n - 1}}}{{A}^{{(0)}}}({{t}_{1}})d{{t}_{1}}.} \\ \end{gathered} $Тогда окончательную формулу для огибающей сигнала можно записать в виде
(19)
$\begin{gathered} A(z,t) = {{A}^{{{\text{п е р в }}}}}(z,t) + {{A}^{{{\text{о т к л }}}}}(\xi ,t), \\ {{A}^{{{\text{п е р в }}}}}(z,t) = {{A}^{{(0)}}}({{t}_{{\text{с }}}})\exp (i{{k}_{0}}{{n}_{0}}z), \\ {{A}^{{{\text{о т к л }}}}}(\xi ,t) = \exp (i{{k}_{0}}{{n}_{0}}z) \times \\ \times \,\,\sum\limits_{n = 1}^\infty {\frac{{{{\alpha }_{n}}(\xi )}}{{n!(n - 1)!\tau _{{\text{л }}}^{n}}}\int\limits_{ - \infty }^{{{t}_{{\text{с }}}}} {{{{({{t}_{{\text{с }}}} - {{t}_{1}})}}^{{n - 1}}}{{A}^{{(0)}}}({{t}_{1}})d{{t}_{1}},} } \\ {{t}_{{\text{с }}}}(z,t) = t - {{\tau }_{{{\text{п е р в }}}}}(z),\,\,\,\,{{\tau }_{{{\text{п е р в }}}}}(z) = {{z{{n}_{0}}} \mathord{\left/ {\vphantom {{z{{n}_{0}}} c}} \right. \kern-0em} c}. \\ \end{gathered} $Из (19) видно, что в случае резкого переднего фронта возникновение сигнала в точке z происходит с задержкой ${{\tau }_{{{\text{п е р в }}}}}(z) = {{z{{n}_{0}}} \mathord{\left/ {\vphantom {{z{{n}_{0}}} c}} \right. \kern-0em} c}$ по сравнению с его возникновением в точке $z = 0,$ т.е. в случае ${{A}^{{(0)}}}(t) = 0$ при $t < 0$ в точке z имеем $A(z,t) = 0$ при $t < {{\tau }_{{{\text{п е р в }}}}}(z).$
В принципе для получения точного результата в случае импульса конечной длительности необходимо проводить суммирование бесконечного количества членов ряда (19), что ничуть не проще прямого численного счета по формулам (1), (3), (14). Тем не менее ряд (19) весьма удобен для изучения поведения сигнала вблизи его резкого фронта. В частности, для оценки качественных особенностей поведения сигнала вблизи переднего фронта достаточно учета первого члена ряда (19) (следующий за ним член ряда может использоваться для контроля точности) (см. далее).
2. ИСКАЖЕНИЕ ПЕРЕДНЕГО ФРОНТА СИГНАЛА (ОБЩИЙ СЛУЧАЙ)
В работе [7] отмечено, что на переднем фронте любого сигнала, используемого для передачи информации, неизбежно имеет место разрыв комплексной огибающей сигнала или одной из его производных. В данной работе нас интересует в первую очередь именно эволюция этих разрывов в процессе распространения сигнала. Пусть в нашей среде распространяется сигнал
с частотой несущей ${{\omega }_{1}}$ (в общем случае ${{\omega }_{1}} \ne {{\omega }_{0}}$) и комплексной огибающей $A(z,t).$ Пусть сигнал имеет резкий передний фронт и возникает в стартовой точке $z = 0$ в момент времени $t = 0$ (${{A}_{0}}(t) = 0$ при $t < 0,$ ${{A}_{0}}(t) \ne 0$ при $t > 0$). Разложив временную зависимость сигнала при $t > 0$ в точке старта в ряд Тейлора
(20)
${{A}_{0}}(t) = \sum\limits_{k = 0}^\infty {\left( {{{A_{0}^{{(k)}}(0){{t}^{k}}} \mathord{\left/ {\vphantom {{A_{0}^{{(k)}}(0){{t}^{k}}} {k!}}} \right. \kern-0em} {k!}}} \right)} ,$учтя, что ${{A}_{0}}(t) = 0$ при $t < 0,$ взяв соответствующие интегралы и проведя описанное выше “переопределение” комплексной огибающей сигнала, вместо (19) имеем
(21)
$\begin{gathered} A(z,t) = {{A}^{{{\text{п е р в }}}}}(z,t) + {{A}^{{{\text{о т к л }}}}}(\xi ,t),{\text{ }} \\ {{A}^{{{\text{п е р в }}}}}(z,t) = {{A}^{{(0)}}}({{t}_{{\text{с }}}})\exp (i{{k}_{1}}{{n}_{0}}z) = \\ = \exp (i{{k}_{1}}{{n}_{0}}z)\sum\limits_{k = 0}^\infty {\left( {{{A_{0}^{{(k)}}(0)t_{{\text{с }}}^{k}} \mathord{\left/ {\vphantom {{A_{0}^{{(k)}}(0)t_{{\text{с }}}^{k}} {k!}}} \right. \kern-0em} {k!}}} \right)} , \\ {{A}^{{{\text{о т к л }}}}}(\xi ,t) = \exp (i{{k}_{1}}{{n}_{0}}z)\sum\limits_{n = 1}^\infty {\frac{{{{\alpha }_{n}}(\xi )}}{{n!\tau _{{\text{л }}}^{n}}}} \times \\ \times \,\,\left( {\sum\limits_{k = 0}^\infty {\frac{{M\left( {k + 1,k + n + 1, - i\Delta \omega {{t}_{{\text{с }}}}} \right)A_{0}^{{(k)}}(0)t_{{\text{с }}}^{{k + n}}}}{{\left( {n + k} \right)!}}} } \right), \\ {{t}_{{\text{с }}}}(z,t) = t - {{\tau }_{{{\text{п е р в }}}}}(z),\,\,\,\,{{\tau }_{{{\text{п е р в }}}}}(z) = {{z{{n}_{0}}} \mathord{\left/ {\vphantom {{z{{n}_{0}}} c}} \right. \kern-0em} c},\,\,\,\,{{k}_{1}} = {{{{\omega }_{1}}} \mathord{\left/ {\vphantom {{{{\omega }_{1}}} c}} \right. \kern-0em} c}. \\ \end{gathered} $В (21) $\Delta \omega = {{\omega }_{1}} - {{\omega }_{0}}$ – отстройка несущей сигнала от центра спектральной линии, $M(k + 1,$ $k + n + 1, - i\Delta \omega {{t}_{{\text{с }}}})$ – функция Куммера [23].
Для дальнейшего обсуждения введем (как и в [18]) соответствующую терминологию. Если в стартовой точке $z = 0$ сигнал возникает в момент времени $t = 0,$ то в этот момент комплексная огибающая сигнала или одна из ее производных имеет разрыв.
Рангом фронта огибающей сигнала мы будем называть наинизший порядок производной огибающей,
имеющей разрыв в момент возникновения сигнала. Так, например, скачкообразное возникновение
сигнала конечной величины в момент времени 0 (${{A}_{0}}(0) \ne 0$) означает, что сигнал имеет фронт нулевого ранга; начало линейного роста сигнала
в момент времени 0 (${{A}_{0}}(0) = 0,A_{0}^{'}(0) \ne 0$) означает, что сигнал имеет фронт первого ранга; начало квадратичного роста сигнала
в момент времени 0 (${{A}_{0}}(0) = A_{0}^{'}(0) = 0,$ 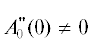 ) означает, что сигнал имеет фронт второго ранга, и т.д.
) означает, что сигнал имеет фронт второго ранга, и т.д.
Для сигнала ранга m (${{A}_{0}}(0) = A_{0}^{'}(0) = A_{0}^{{(m - 1)}} = 0,$ $A_{0}^{{(m)}}(0) \ne 0$) формулы (21) можно переписать в виде
(22)
$\begin{gathered} A(z,t) = {{A}^{{{\text{п е р в }}}}}(z,t) + {{A}^{{{\text{о т к л }}}}}(\xi ,t), \\ {{A}^{{{\text{п е р в }}}}}(z,t) = \exp (i{{k}_{1}}{{n}_{0}}z)\sum\limits_{k = m}^\infty {\left( {{{A_{0}^{{(k)}}(0)t_{{\text{с }}}^{k}} \mathord{\left/ {\vphantom {{A_{0}^{{(k)}}(0)t_{{\text{с }}}^{k}} {k!}}} \right. \kern-0em} {k!}}} \right)} , \\ {{A}^{{{\text{о т к л }}}}}(\xi ,t) = \exp (i{{k}_{1}}{{n}_{0}}z)\sum\limits_{n = 1}^\infty {\frac{{{{\alpha }_{n}}(\xi )}}{{n!\tau _{{\text{л }}}^{n}}}} \times \\ \times \,\,\left( {\sum\limits_{k = m}^\infty {\frac{{M\left( {k + 1,k + n + 1, - i\Delta \omega {{t}_{{{\text{с д в }}}}}} \right)A_{0}^{{(k)}}(0)t_{{\text{с }}}^{{k + n}}}}{{\left( {n + k} \right)!}}} } \right). \\ \end{gathered} $Тогда видно, что ранг сигнала отклика по меньшей мере на единицу больше ранга первичного сигнала. Поэтому можно утверждать, что ни ранг фронта сигнала (т.е. наинизший порядок производной огибающей, терпящей разрыв на фронте сигнала), ни амплитуда этого фронта (т.е. величина скачка этой производной на фронте сигнала) не изменяются в процессе распространения сигнала.
В общем эта ситуация вполне аналогична ситуации, имеющей место у видеосигналов [18], но “на другом материале”. А именно – передний фронт сигнала при распространении, строго говоря, не изменяется вообще – изменения, т.е. снижение его значения, наблюдаются за фронтом сигнала, причем скорость этого снижения нарастает с ростом длины трассы, что в конце концов приводит к “истончению” фронта сигнала.
Отличие состоит в том, что теперь речь идет не о перемещении разрывов волны, а о перемещении разрывов ее огибающей, и в том, что скорость перемещения этих разрывов огибающей равна не вакуумной скорости света, а “нерезонансной” скорости первичного сигнала в данной среде. Еще одно существенное отличие – несущая частота сигнала может не совпадать в точности с центральной частотой спектральной линии ($\Delta \omega = {{\omega }_{1}} - {{\omega }_{0}} \ne 0$), в [18] “несущая частота” видеосигнала была равна нулю и потому неизбежно совпадала с нулевой “центральной частотой” плазмоподобной среды.
Пренебрегая в (22) всеми членами, кроме двух старших, и учтя, что $M\left( {k + 1,k + n + 1,x} \right)$ = $1 + O(x),$ для “чисто степенного” фронта сигнала ранга
имеем
(23)
$\begin{gathered} A(z,t) = \exp (i{{k}_{1}}{{n}_{0}}z)\left( {{{A_{0}^{{(m)}}(0)t_{{\text{с }}}^{m}} \mathord{\left/ {\vphantom {{A_{0}^{{(m)}}(0)t_{{\text{с }}}^{m}} {m!}}} \right. \kern-0em} {m!}}} \right) \times \\ \times \,\,\left( {1 + \left( {{{{{\alpha }_{1}}(\xi )} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}(\xi )} {\left( {1 + m} \right)}}} \right. \kern-0em} {\left( {1 + m} \right)}}} \right)\left( {{{{{t}_{{\text{с }}}}} \mathord{\left/ {\vphantom {{{{t}_{{\text{с }}}}} {{{\tau }_{{\text{л }}}}}}} \right. \kern-0em} {{{\tau }_{{\text{л }}}}}}} \right)} \right). \\ \end{gathered} $Соотношение (23) (далее – линейная аппроксимация) позволяет оценить длительность промежутка времени, в течение которого сигнал удерживает свое “фронтальное” значение. Для этого промежутка времени с учетом (13) имеем
(24)
${{t}_{{{\text{ф р }}}}} \approx \left( {1 + m} \right){{{{\tau }_{{\text{л }}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{л }}}}} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}}} \right. \kern-0em} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}}.$Видно, что с ростом протяженности трассы “длительность фронта” ${{t}_{{{\text{ф р }}}}}$ неуклонно уменьшается и стремится к нулю.
3. ИСКАЖЕНИЕ ИМПУЛЬСА ВКЛЮЧЕНИЯ И П-ИМПУЛЬСА
Рассмотрим важный частный случай импульса включения55, т.е. сигнала, возникающего в стартовой точке скачком:
В этом случае $m = 0$ и общие формулы (22)–(24) можно переписать в следующем виде:
(25)
$\begin{gathered} A(z,t) = \exp (i{{k}_{1}}{{n}_{0}}z)\left[ {1 + \sum\limits_{n = 1}^\infty {\frac{{{{\alpha }_{n}}(\xi )}}{{n!{{{\left( { - i\Delta \omega {{\tau }_{{\text{л }}}}} \right)}}^{n}}}}} } \right. \times \\ \times \,\,\left. {\left( {\exp ( - i\Delta \omega {{t}_{{\text{с }}}}) - \sum\limits_{j = 0}^{n - 1} {({{ - i\Delta \omega {{t}_{{\text{с }}}}{{)}^{j}}} \mathord{\left/ {\vphantom {{ - i\Delta \omega {{t}_{{\text{с }}}}{{)}^{j}}} j}} \right. \kern-0em} j}!} } \right)} \right], \\ \end{gathered} $(26)
$A(z,t) = \exp (i{{k}_{1}}{{n}_{0}}z)\left( {1 + {{\alpha }_{1}}(\xi )\left( {{{{{t}_{{\text{с }}}}} \mathord{\left/ {\vphantom {{{{t}_{{\text{с }}}}} {{{\tau }_{{\text{л }}}}}}} \right. \kern-0em} {{{\tau }_{{\text{л }}}}}}} \right)} \right),$(27)
${{t}_{{{\text{ф р }}}}} \approx {{{{\tau }_{{\text{л }}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{л }}}}} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}}} \right. \kern-0em} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}}.$Из формул (25)–(27) очевидно, что с ростом протяженности трассы скачок сигнала на фронте не изменяется, но за начальным скачком сигнал все резче уменьшается, т.е. на фронте сигнала образуется острый “зубец”, толщина (но не “длина”) которого линейно уменьшается по мере роста протяженности трассы.
Разумеется, истончение этого “зубца” без уменьшения его “высоты” (т.е. амплитуды) не может происходить бесконечно – на самом деле “зубец” все-таки исчезает, но это происходит только тогда, когда его длительность становится сравнима с “настоящей” длительностью фронта исходного сигнала (которая никогда не может быть в точности равна нулю) или, в крайнем случае, тогда, когда его длительность становится соизмерима с периодом несущей.
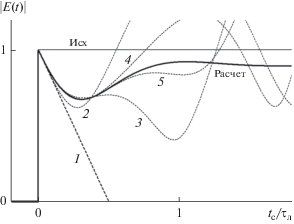
На рис. 1 проведено сравнение точности различных приближений при расчете деформации переднего фронта ступенчатого сигнала66. Следует отметить, что увеличение количества суммируемых членов ряда (25) действительно несколько повышает точность результатов и расширяет область применимости приближения (25). Тем не менее вдали от переднего фронта сигнала использование ряда (25) вряд ли оправдано. Вместе с тем даже использование простейшего “линейного приближения” (26) непосредственно за фронтом сигнала дает хорошие результаты.
Рис. 1.
Деформация переднего фронта ступенчатого сигнала при распространении. Оптическая толщина трассы $\xi = 2,$ величина сдвига несущей сигнала относительно центральной частоты спектральной линии $\Delta \omega = 2\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Временные зависимости исходной (Исх) вещественной амплитуды сигнала (функция включения) и амплитуды сигнала по данным численного расчета (Расчет); аналитическая “линейная аппроксимация” убывания амплитуды сигнала непосредственно за передним фронтом (формула (26) (кривая 1); аналитическая аппроксимация (формула (25)) при учете разного количества членов суммы: одного (кривая 2), двух (3), трех (4) и четырех (5).
Существенно, что скорость убывания сигнала непосредственно за его резким фронтом не зависит от отстройки несущей сигнала от центральной частоты спектральной линии (в формуле (26) отсутствует параметр $\Delta \omega $). Это означает, что скорость убывания сигнала сразу за его фронтом одинакова для любого значения отстройки. На рис. 2 приведены результаты расчетов деформации переднего фронта сигнала в случае одной и той же длины трассы, но различной отстройки несущей от центральной частоты спектральной линии. Следует, впрочем, отметить, что с ростом отстройки продолжительность интервала линейного убывания сигнала за передним фронтом уменьшается и линейное убывание сменяется постепенно затухающими осцилляциями огибающей. Очевидно, это связано с “расфазировкой” между “сигналом отклика” спектральной линии (характерная частота которого совпадает с центральной частотой спектральной линии) и первичным сигналом (с частотой несущей). Поэтому для длительности “переднего зубца” можно использовать оценочную формулу
(28)
${{t}_{{\text{з }}}} \approx \min \left\{ {{{{{\tau }_{{\text{л }}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{л }}}}} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}}} \right. \kern-0em} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}},{1 \mathord{\left/ {\vphantom {1 {\Delta \omega }}} \right. \kern-0em} {\Delta \omega }}} \right\},$Рис. 2.
Деформация переднего фронта функции включения (Исх) при распространении через слой фиксированной оптической толщины $\xi = 8$ (численный счет) в случае различной величины сдвига несущей сигнала относительно центральной частоты спектральной линии: $\Delta \omega = 0$ (кривая 1), $\Delta \omega = 2\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (2), $\Delta \omega = 8\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (3) и $\Delta \omega = 32\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (4). Штриховая линия – общая для всех рассмотренных случаев “линейная аппроксимация” (26) убывания амплитуды сигнала непосредственно за передним фронтом.
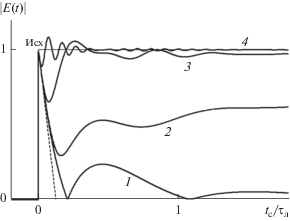
а для его относительной “высоты” со стороны сигнала–формулу
(29)
${{\Delta A} \mathord{\left/ {\vphantom {{\Delta A} A}} \right. \kern-0em} A} \approx \min \left\{ {1,{{{{\gamma }_{{\text{1}}}}\xi } \mathord{\left/ {\vphantom {{{{\gamma }_{{\text{1}}}}\xi } {\left( {\Delta \omega {{\tau }_{{\text{л }}}}} \right)}}} \right. \kern-0em} {\left( {\Delta \omega {{\tau }_{{\text{л }}}}} \right)}}} \right\}.$Теперь очевидно, что при достаточно малой протяженности трассы или достаточно большой отстройке несущей от спектральной линии (т.е. при выполнении условия ${{\gamma }_{{\text{1}}}}\xi \ll \Delta \omega {{\tau }_{{\text{л }}}}$) деформация “функции включения” невелика и сводится к возникновению неглубокой (с относительной глубиной порядка ${{{{\gamma }_{{\text{1}}}}\xi } \mathord{\left/ {\vphantom {{{{\gamma }_{{\text{1}}}}\xi } {\left( {\Delta \omega {{\tau }_{{\text{л }}}}} \right)}}} \right. \kern-0em} {\left( {\Delta \omega {{\tau }_{{\text{л }}}}} \right)}} \ll 1$ ) “ряби” (с характерной частотой $\Delta \omega $) на поверхности “ступеньки”. В случае же отсутствия отстройки несущей от центра спектральной линии искажение функции включения неизбежно становится существенным при задержке (от фронта сигнала) порядка ${{t}_{{\text{c}}}} \approx {{t}_{{{\text{ф р }}}}} \approx {{{{\tau }_{{\text{л }}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{л }}}}} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}}} \right. \kern-0em} {\left( {{{\gamma }_{{\text{1}}}}\xi } \right)}}.$
На рис. 3–5 представлена деформация исходно прямоугольного импульса длительностью ${{\tau }_{{{\text{и м п }}}}} = 2{{\tau }_{{\text{л }}}}$ при разной протяженности трассы ($\xi = 1,$ $\xi = 4$ и $\xi = 16$) в случае совпадения несущей сигнала и центральной частоты спектральной линии ($\Delta \omega = 0,$ рис. 3) и в случае их несовпадения ($\Delta \omega = 2\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ на рис. 4 и $\Delta \omega = 4\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ на рис. 5). Нетрудно заметить, что в случае $\Delta \omega = 0$ (см. рис. 3) результаты проведенных нами расчетов, как и следовало ожидать, полностью совпадают с результатами расчетов, ранее проведенных в работе [14], специально посвященной изучению дисперсионных искажений прямоугольного радиоимпульса, несущая частота которого совпадает с частотой спектральной линии. Поскольку в работе [14] использовался не спектральный (как в данной работе), а временной подход, совпадение наших результатов свидетельствует об их достаточной надежности.
Рис. 3.
Деформация прямоугольного импульса длительностью ${{\tau }_{{{\text{и м п }}}}} = 2{{\tau }_{{\text{л }}}}$ при распространении в случае совпадения несущей сигнала и центральной частоты спектральной линии при длине трассы $\xi = 1$ (а), 4 (б) и 16 (в). Кривая 1 – исходная временная зависимость вещественной амплитуды сигнала (П-импульс); кривая 2 – временная зависимость амплитуды сигнала (численный счет); кривая 3 – “линейная аппроксимация” убывания амплитуды сигнала непосредственно за передним фронтом.
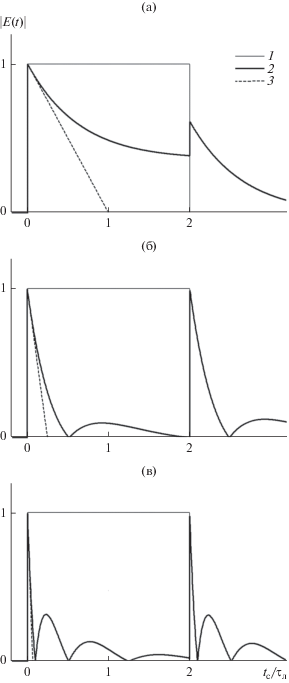
Рис. 4.
Деформация прямоугольного импульса длительностью ${{\tau }_{{{\text{и м п }}}}} = 2{{\tau }_{{\text{л }}}}$ при распространении в случае несовпадения несущей сигнала и центральной частоты спектральной линии (отстройка $\Delta \omega = 2\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$) при длине трассы $\xi = 1$ (а), 4 (б) и 16 (в). Кривая 1 – исходная временная зависимость вещественной амплитуды сигнала (П-импульс); кривая 2 – временная зависимость амплитуды сигнала (численный счет); кривая 3 – “линейная аппроксимация” убывания амплитуды сигнала непосредственно за передним фронтом, кривая 4 – амплитуда соответствующего постоянного сигнала (т.е. “чистой несущей”) при данной протяженности трассы и данной отстройке несущей.
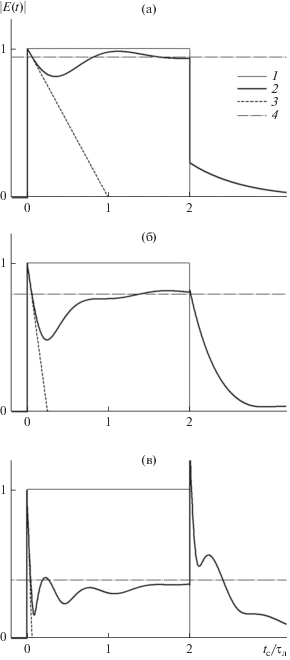
Рис. 5.
Деформация прямоугольного импульса длительностью ${{\tau }_{{{\text{и м п }}}}} = 2{{\tau }_{{\text{л }}}}$ при распространении в случае несовпадения несущей сигнала и центральной частоты спектральной линии (отстройка $\Delta \omega = 4\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$) при длине трассы $\xi = 1$ (а), 4 (б) и 16 (в). Кривая 1 – исходная временная зависимость вещественной амплитуды сигнала (П-импульс); кривая 2 – временная зависимость амплитуды сигнала (численный счет); кривая 3 – “линейная аппроксимация” убывания амплитуды сигнала непосредственно за передним фронтом, кривая 4 – амплитуда соответствующего постоянного сигнала (т.е. “чистой несущей”) при данной протяженности трассы и данной отстройке несущей.
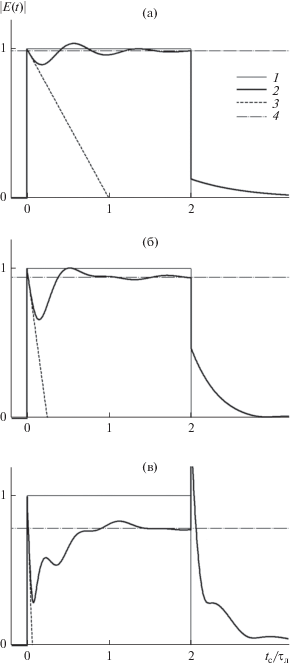
Анализ рис. 3–5 позволяет сделать следующие выводы.
1. Независимо от величины отстройки несущей от центральной частоты спектральной линии при достаточной протяженности трассы (при выполнении условия ${{{{\gamma }_{{\text{1}}}}\xi } \mathord{\left/ {\vphantom {{{{\gamma }_{{\text{1}}}}\xi } {\left( {\Delta \omega {{\tau }_{{\text{л }}}}} \right)}}} \right. \kern-0em} {\left( {\Delta \omega {{\tau }_{{\text{л }}}}} \right)}} \geqslant 1$) на переднем фронте сигнала образуется хорошо различимый “зубец”, истончающийся по мере роста протяженности трассы.
2. По прошествии времени порядка времени когерентности спектральной линии ${{\tau }_{{\text{л }}}}$ за передним фронтом сигнала сигнал выходит на стационарное значение, соответствующее уровню “чистой несущей” (при единичной амплитуде сигнала это $\exp ( - \operatorname{Re} \left[ {g({{\omega }_{1}})} \right]\xi )$ = $\exp \left( { - \alpha ({{\omega }_{1}})z} \right)$). Выход на это стационарное значение происходит с постепенно затухающими осцилляциями с частотой $\Delta \omega .$ Оба этих результата совершенно естественны – ясно, что “функция отклика” спектральной линии на внешнее воздействие в соответствии с известной связью между шириной фильтра и его постоянной времени затухает за время порядка ${{\tau }_{{\text{л }}}} \equiv {2 \mathord{\left/ {\vphantom {2 {\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$ и что интерференция этой функции отклика с первичным сигналом порождает осцилляции с частотой $\Delta \omega .$
3. На заднем фронте прямоугольного импульса по тем же самым причинам, что и на переднем фронте, возникает точно такой же скачок амплитуды сигнала и точно такой же постепенно истончающийся с ростом протяженности трассы “зубец”. В отличие от “переднего зубца”, этот “задний зубец” по прошествии времени порядка времени когерентности спектральной линии ${{\tau }_{{\text{л }}}}$ за задним фронтом сигнала выходит не на стационарное значение, соответствующее уровню “чистой несущей”, а на нуль, причем без существенных осцилляций (сигналу отклика спектральной линии в данном случае не с чем интерферировать). Еще одно отличие “заднего зубца” от переднего состоит в том, что единичный скачок амплитуды сигнала накладывается на уже имеющийся в момент подхода заднего фронта уровень комплексной огибающей сигнала, в результате чего “высота” “заднего зубца” может быть как больше, так и меньше единицы – в зависимости от фазы сигнала непосредственно перед задним фронтом ($\left| {\left| A \right| - 1} \right| \leqslant \left| {A - 1} \right| \leqslant \left| A \right| + 1$). В частности, на графике вещественной амплитуды сигнала “задний зубец” может и вовсе отсутствовать (см. рис. 4а).
4. В случае использования для передачи информации П-импульсов с длительностью, существенно превышающей время когерентности спектральной линии, искажение этих импульсов можно считать малым при любой протяженности трассы, потому что в любом случае существенному искажению подвергается только носовая и хвостовая части импульса (длительностью порядка ${{\tau }_{{\text{л }}}}$), основная же его часть остается “неповрежденной”.
В случае же использования для передачи коротких прямоугольных импульсов с длительностью ${{\tau }_{{{\text{и м п }}}}}$, сравнимой или малой в сравнении с временем когерентности спектральной линии, малым искажение импульса оказывается только при достаточно малой протяженности трассы. Условие слабого искажения сигнала имеет вид
(30)
$\xi \ll \left( {{{{{\tau }_{{\text{л }}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{л }}}}} {{{\gamma }_{{\text{1}}}}}}} \right. \kern-0em} {{{\gamma }_{{\text{1}}}}}}} \right)\max \left( {\tau _{{{\text{и м п }}}}^{{ - {\text{1}}}},\Delta \omega } \right).$Из (30) видно, что допустимая протяженность трассы возрастает как при укорочении сигнала, так и при увеличении отстройки частоты несущей от спектральной линии.
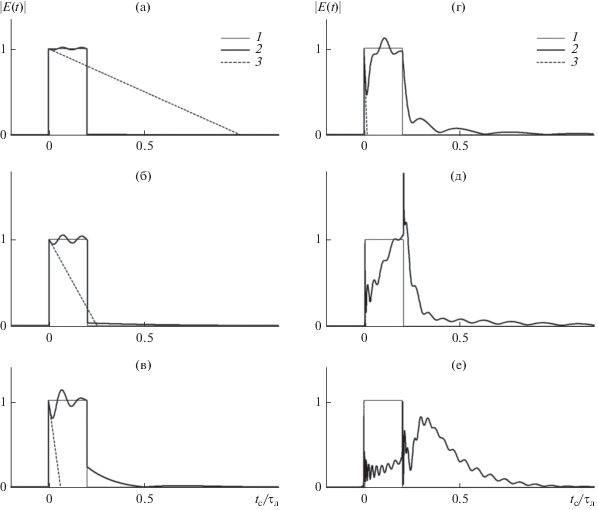
Этот вывод подтверждается и результатами расчетов, приведенными на рис. 6, 7: при достаточно большой протяженности трассы (при $\xi \geqslant 64$ и $\xi \geqslant 256$) и, соответственно, сильном искажении исходного сигнала возникают осцилляции огибающей с частотой, превышающей $\Delta \omega $ и растущей с ростом протяженности трассы. Очевидно, в данном случае мы имеем выход сигнала на режим сильно искаженного, растянутого и осциллирующего сигнала, подробно рассмотренный в [7].
Рис. 6.
Деформация короткого прямоугольного импульса длительностью ${{\tau }_{{{\text{и м п }}}}} = 0.2{{\tau }_{{\text{л }}}}$ при распространении в случае совпадения несущей сигнала и центральной частоты спектральной линии и при длине трассы $\xi = 1$ (а), 4 (б), 16 (в), 64 (г), 256 (д) и 1024 (е). Кривая 1 – исходная временная зависимость вещественной амплитуды сигнала (П-импульс); кривая 2 – временная зависимость амплитуды сигнала (численный счет); кривая 3 – “линейная аппроксимация” убывания амплитуды сигнала непосредственно за передним фронтом.
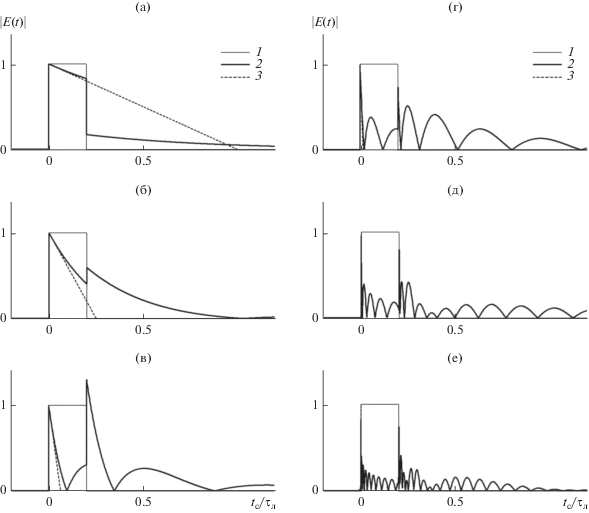
Рис. 7.
Деформация короткого прямоугольного импульса длительностью ${{\tau }_{{{\text{и м п }}}}} = 0.2{{\tau }_{{\text{л }}}}$ при распространении в случае несовпадения несущей сигнала и центральной частоты спектральной линии (отстройка $\Delta \omega = 32\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$) и при длине трассы $\xi = 1$ (а), 4 (б), 16 (в), 64 (г), 256 (д) и 1024 (е). Кривая 1 – исходная временная зависимость вещественной амплитуды сигнала (П-импульс); кривая 2 – временная зависимость амплитуды сигнала (численный счет); кривая 3 – “линейная аппроксимация” убывания амплитуды сигнала непосредственно за передним фронтом.
4. ИСКАЖЕНИЕ ФАЗОМАНИПУЛИРОВАННОГО СИГНАЛА
Существенным отличием радиосигнала от видеосигнала является возможность резкого изменения его фазы без изменения вещественной амплитуды, т.е. возможность фазовой манипуляции. Ясно, что резкое изменение фазы сигнала в точке старта даже в случае неизменности его вещественной амплитуды является разрывом его комплексной огибающей и потому обязано сопровождаться в точности таким же разрывом комплексной огибающей сигнала в точке приема. При этом даже если в точке старта разрыв комплексной огибающей сигнала не приводит к разрыву его вещественной амплитуды, то в точке наблюдения на трассе, в которой фаза и амплитуда сигнала изменились (в отличие от скачка, который измениться не может в принципе) происходит разрыв не только фазы, но и амплитуды сигнала. Поэтому при распространении фазоманипулированного сигнала в резонансно-поглощающей среде происходит его “детектирование” – в точках изменения фазы возникают “зубцы” соответствующей амплитуды и длительности (27).
На рис. 8–10 приведены результаты расчетов искажения фрагмента фазоманипулированного сигнала с квадратурной фазовой манипуляцией
гдеРис. 8.
Деформация фазоманипулированного сигнала, состоящего из пяти прямоугольных импульсов единичной амплитуды длительностью ${{\tau }_{{{\text{и м п }}}}} = 0.5{{\tau }_{{\text{л }}}}$ каждый (фаза последующего импульса увеличена на ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ относительно фазы предыдущего) в случае совпадения несущей сигнала и центральной частоты спектральной линии (отстройка $\Delta \omega = 0$). Кривая 1 – исходная временная зависимость амплитуды сигнала; кривая 2 – временная зависимость амплитуды сигнала на трассе (численный счет) при длине трассы $\xi = 1$ (а), 4 (б), 16 (в) и 64 (г).
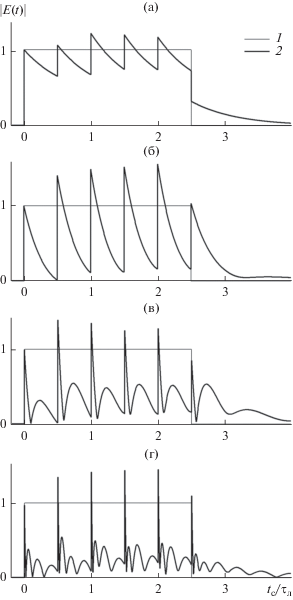
Рис. 9.
Деформация фазоманипулированного сигнала, состоящего из пяти прямоугольных импульсов единичной амплитуды длительностью ${{\tau }_{{{\text{и м п }}}}} = 0.5{{\tau }_{{\text{л }}}}$ каждый (фаза последующего импульса увеличена на ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ относительно фазы предыдущего) в случае несовпадения несущей сигнала и центральной частоты спектральной линии (отстройка $\Delta \omega = 2\Delta {{\Omega }_{{1/2}}}$). Кривая 1 – исходная временная зависимость амплитуды сигнала; кривая 2 – временная зависимость амплитуды сигнала на трассе (численный счет) при длине трассы $\xi = 1$ (а), 4 (б), 16 (в) и 64 (г).
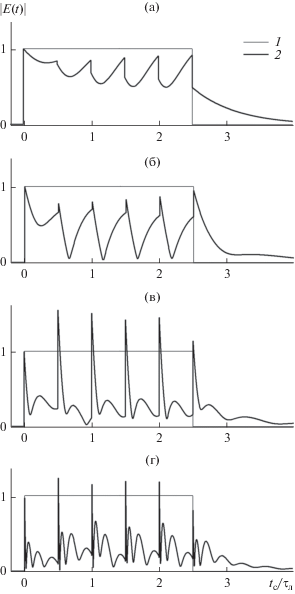
Рис. 10.
Деформация фазоманипулированного сигнала, состоящего из пяти прямоугольных импульсов единичной амплитуды длительностью ${{\tau }_{{{\text{и м п }}}}} = 0.5{{\tau }_{{\text{л }}}}$ каждый (фаза последующего импульса увеличена на ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ относительно фазы предыдущего) в случае несовпадения несущей сигнала и центральной частоты спектральной линии (отстройка $\Delta \omega = 8\Delta {{\Omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$). Кривая 1 – исходная временная зависимость амплитуды сигнала; кривая 2 – временная зависимость амплитуды сигнала на трассе (численный счет) при длине трассы $\xi = 1$ (а), 4 (б), 16 (в) и 64 (г).
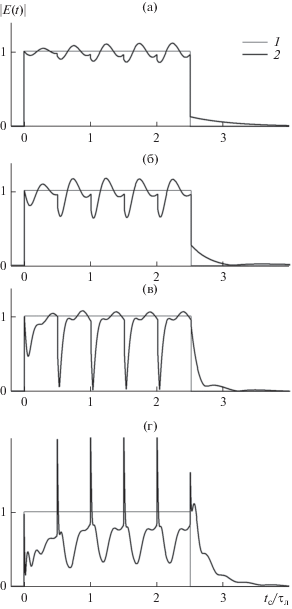
Как и следовало ожидать, при достаточной протяженности трассы в моменты смены фазы временная зависимость амплитуды сигнала резко изменяется – в точках разрыва фазы “растут зубцы”, причем их параметры (и амплитуда, и продолжительность) ничем не отличаются от того, что наблюдается в случае резкого разрыва амплитуды – их амплитуда соответствует скачкам комплексной амплитуды исходного сигнала, а продолжительность закономерно снижается по мере роста протяженности трассы. На графиках видно, что возникновение “зубца” может сопровождаться не только резким возрастанием вещественной амплитуды сигнала (см. рис. 10г), но и ее резким уменьшением (см. рис. 10в) или практически никак на ней не сказываться (см. рис. 10а, 10б). Причина этого уже обсуждалась выше и сводится к тому, что изменение вещественной амплитуды сигнала при комплексном скачке его комплексной амплитуды зависит не только от величины этого скачка (который однозначно определяется амплитудой и скачком фазы сигнала в стартовой точке), но и текущим уровнем комплексной амплитуды сигнала в момент времени, непосредственно предшествующий скачку. Интересно, что это обстоятельство может создать77 ситуацию, при которой амплитуда сигнала на трассе в момент смены фазы на краткое время значительно превышает его исходную амплитуду, несмотря на общее ослабление сигнала (см., например, рис. 10г).
Ясно, что с ростом протяженности трассы при соответствующем затухании и растягивании “основного тела” фазоманипулированного сигнала от него остаются только “зубцы” соответствующей величины (в данном случае – $\left| {1 - \exp ({{i\pi } \mathord{\left/ {\vphantom {{i\pi } 2}} \right. \kern-0em} 2})} \right| = \sqrt 2 ,$ что, кстати, в два раза выше (по интенсивности) исходного сигнала88).
Следует отметить, что аналогичный метод “детектирования” фазоманипулированного сигнала может быть применен и в “проводной” радиотехнике – ясно, что при пропускании фазоманипулированного сигнала через пассивный RLC-фильтр с резонансным поглощением типа рассмотренного в [24] или через цепочку таких фильтров также начнется “рост зубцов” в моменты смены фазы сигнала.
ЗАКЛЮЧЕНИЕ
Таким образом, на основе проведенного исследования можно сделать вывод, что при распространении радиосигнала в резонансно-поглощающей среде разрывы его комплексной огибающей (т.е. разрывы ее вещественной и мнимой части) распространяются без изменения своей величины с “нерезонансной” фазовой скоростью для данной среды (для газа это – скорость света). Это относится и к переднему фронту сигнала, если сигнал возникает скачком. Поэтому передний фронт ступенчатого сигнала распространяется без изменения. Прочие же разрывы могут проявляться по-разному, потому что они накладываются на текущее значение комплексной амплитуды сигнала. Существенно, что имевшиеся в точке старта разрывы фазы огибающей сигнала на трассе, вообще говоря, становятся разрывами и его вещественной амплитуды тоже, даже если в точке старта вещественная амплитуда и была непрерывна.
После скачка в точке разрыва значение комплексной амплитуды сигнала возвращается приблизительно к своему “доразрывному” значению. В результате на временной зависимости амплитуды сигнала возникает положительный или отрицательный “всплеск” (“зубец”), причем с ростом протяженности трассы скорость возвращения амплитуды к “доразрывному” значению увеличивается, т.е. продолжительность “всплеска” сокращается; она может быть оценена с помощью формулы (28).
Обобщение полученных результатов на случай нескольких близких спектральных линий или спектральной линии сложной формы тривиально и сводится к отысканию структурных коэффициентов $\left\{ {{{\gamma }_{n}}} \right\}$ для сложной спектральной линии. Существенно, что основные параметры возникающих на графике временной зависимости сигнала “зубцов” зависят только от первого из этих коэффициентов, т.е. от ${{\gamma }_{1}},$ причем в окончательные формулы этот параметр входит только в виде комбинации ${{{{\Gamma }_{1}} = {{\gamma }_{1}}\alpha (0)} \mathord{\left/ {\vphantom {{{{\Gamma }_{1}} = {{\gamma }_{1}}\alpha (0)} {{{\tau }_{{\text{л }}}}}}} \right. \kern-0em} {{{\tau }_{{\text{л }}}}}}.$ Так, например, оценка для длительности “зубцов”, возникающих на временной зависимости принятого сигнала при наличии разрывов амплитуды или фазы у передаваемого сигнала (28), может быть записана в виде ${{t}_{{\text{з }}}} \approx \min \left\{ {{1 \mathord{\left/ {\vphantom {1 {\left( {{{\Gamma }_{{\text{1}}}}z} \right)}}} \right. \kern-0em} {\left( {{{\Gamma }_{{\text{1}}}}z} \right)}},{1 \mathord{\left/ {\vphantom {1 {\Delta \omega }}} \right. \kern-0em} {\Delta \omega }}} \right\},$ а условие слабого искажения короткого П-импульса при распространении – в виде $z \ll \left( {{1 \mathord{\left/ {\vphantom {1 {{{\Gamma }_{{\text{1}}}}}}} \right. \kern-0em} {{{\Gamma }_{{\text{1}}}}}}} \right)\max \left( {\tau _{{{\text{и м п }}}}^{{{\text{ - 1}}}},\Delta \omega } \right).$
Сам же параметр ${{\Gamma }_{{\text{1}}}},$ как оказывается, совершенно не зависит не только от формы профиля, но даже и от ширины спектральной линии. Для того чтобы убедиться в этом, достаточно воспользоваться любой из формул
(31)
${{\Gamma }_{1}} = \left( {{1 \mathord{\left/ {\vphantom {1 \pi }} \right. \kern-0em} \pi }} \right)\int\limits_{ - \infty }^{ + \infty } {\alpha (\Omega )d\Omega } = {{\left( {\pi N{{e}^{2}}f} \right)} \mathord{\left/ {\vphantom {{\left( {\pi N{{e}^{2}}f} \right)} {\left( {mc} \right)}}} \right. \kern-0em} {\left( {mc} \right)}},$первая из которых приведена в [20], а вторая – в [19]. В формуле (31) $\alpha (\Omega )$ – зависящий от частоты коэффициент поглощения (по амплитуде) спектральной линии, N и f – концентрации и силы осцилляторов, ответственных за возникновение соответствующей спектральной линии, e и m – заряд и масса электрона99. Из формулы (31) видно, что ширина и механизм уширения спектральной линии вообще не оказывают никакого влияния на величину параметра ${{\Gamma }_{{\text{1}}}},$ а тем самым – и на параметры возникающих на месте скачков комплексной огибающей “зубцов”1010. Для оценки параметра ${{\Gamma }_{{\text{1}}}}$ можно пользоваться любой из формул (31) – в зависимости от того, какая информация о спектральной линии имеется в наличии.
Наконец, обсудим вопрос о “предвестниках” сигнала, впервые возникший более 100 лет назад [2, 3] и активно обсуждающийся до сих пор (см. [10, 11, 14]). В свете результатов данной работы и работы [18] ясно, что у любого радиосигнала их два – “предвестник сигнала” и “предвестник огибающей”. Предвестник сигнала связан с разрывом самого сигнала или одной из его производных и в соответствии с результатами [18] распространяется в точности со скоростью света в вакууме. Предвестник огибающей связан с разрывом комплексной огибающей сигнала и распространяется в точности с “нерезонансной” фазовой скоростью света в данном веществе. Действительно, любой радиосигнал в принципе является “быстро осциллирующим видеосигналом” и потому обладает всеми его атрибутами. Например, сигнал $E(t) = \cos (\omega t)\eta (t)$ ($\eta (t)$ – функция Хэвисайда) имеет на фронте разрыв сигнала и разрыв огибающей, а сигнал $E(t) = \sin (\omega t)\eta (t)$ имеет разрыв первой производной сигнала и разрыв огибающей. Оба этих сигнала имеют предвестники огибающей (причем одинаковые) и предвестники сигнала, причем разные, потому что “в качестве видеосигналов” они имеют разный ранг разрыва на переднем фронте. Для первого из этих сигналов предвестник сигнала распространяется без изменения амплитуды, а для второго амплитуда предвестника с ростом протяженности трассы уменьшается по гиперболическому закону (см. [18]). Предвестник огибающей для обоих этих сигналов распространяется без изменения амплитуды.
К сожалению, определенно решить вопрос об идентификации этих предвестников с “предвестником Зоммерфельда” и “предвестником Бриллюэна” (см. [10, 11]) автор не может ни в позитивном, ни в негативном смысле. С одной стороны, никаких иных предвестников, кроме “предвестника сигнала” и “предвестника огибающей”, в данной задаче не наблюдается. С другой стороны, свойства “предвестника сигнала” и “предвестника огибающей” (в первую очередь неизменность их амплитуды при распространении в случае скачка на переднем фронте сигнала) не слишком хорошо согласуются со свойствами, обычно приписываемыми “предвестнику Зоммерфельда” и “предвестнику Бриллюэна” (см. [10, 11]).
Список литературы
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 1979.
Sommerfeld A. // Ann. Phys. 1914. B. 44. № 10. S. 177.
Brillouin L. // Ann. Phys. 1914. B. 44. № 10. S. 203.
Apмaнд П.A. // PЭ. 2003. T. 48. № 9. C. 1045.
Cтpeлкoв Г.M. // PЭ. 1998. T. 43. № 8. C. 927.
Cтpeлкoв Г.M. // PЭ. 2000. T. 45. № 12. C. 1436.
Бyxмaн H.C. // PЭ. 2007. T. 52. № 5. C. 593.
Крюковский А.С., Зайчиков И.В. // Вестн. Рос. нового ун-та. Серия: Сложные системы: модели, анализ и управление. 2007. № 2. С. 17.
Крюковский А.С., Зайчиков И.В. // Электромагн. волны и электрон. системы. 2008. Т. 13. № 8. С. 36.
Maske B., Segard B. // Phys. Rev. A. 2012. V. 86. № 1. P. 013837.
Maske B., Segard B. // Phys. Rev. A. 2013. V. 87. № 4. P. 043830.
Cтpeлкoв Г.M. // PЭ. 2013. T. 58. № 10. C. 989.
Крюковский А.С. Равномерная асимптотическая теория краевых и угловых волновых катастроф. М.: Рос. новый ун-т, 2013.
Стрелков Г.М., Деркач О.Г. // РЭ. 2017. Т. 62. № 2. С. 99.
Бухман Н.С. Принцип причинности, неантропогенное прогнозирование и сверхсветовая скорость распространения сигнала. Самара: СГАСУ, 2005.
Бухман Н.С. Распространение узкополосного сигнала в сильно диспергирующей среде. Самара: СГАСУ, 2004.
Аллин И.В., Крюковский А.С. // Электромагн. волны и электрон. системы. 2007. Т. 12. № 8. С. 26.
Бyxмaн H.C. // PЭ. 2016. T. 61. № 12. C. 1148.
Ландсберг Г.С. Оптика. М.: Наука, 1976.
Бухман Н.С., Куликова А.В. // РЭ. 2015. Т. 60. № 5. С. 535.
Малахов А.Н. Кумулянтный анализ случайных негауссовых процессов и их преобразований. М.: Советское радио, 1978.
Смирнов В.И. Курс высшей математики. М.: Наука, 1974. Т. 2.
Справочник по специальным функциям / Под ред. Абрамовица М. и Стиган И. М.: Наука, 1979.
Бухман Н.С., Бухман С.В. // Изв. вузов. Радиофизика. 2004. Т. 47. № 1. С. 75.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


