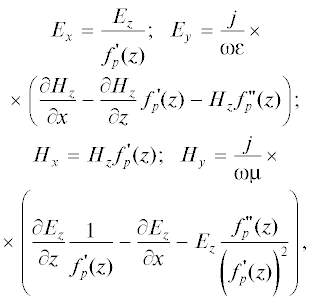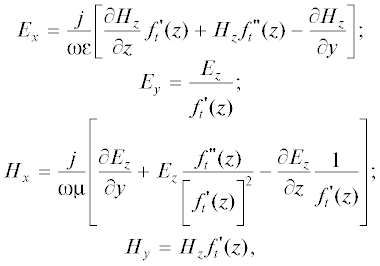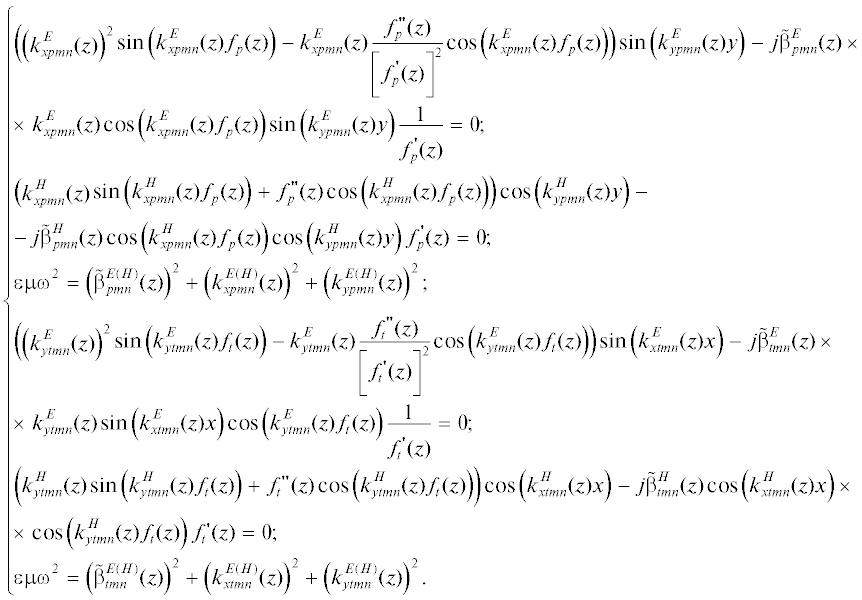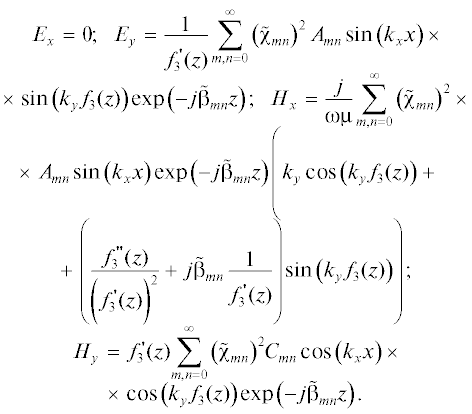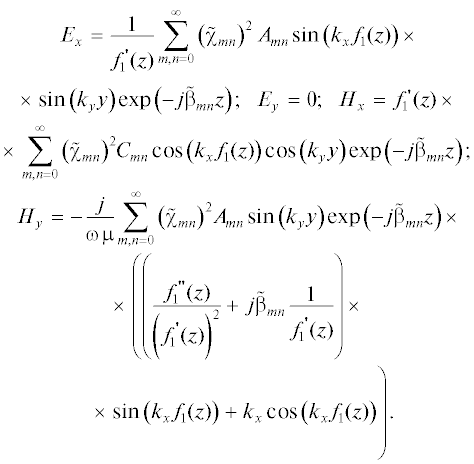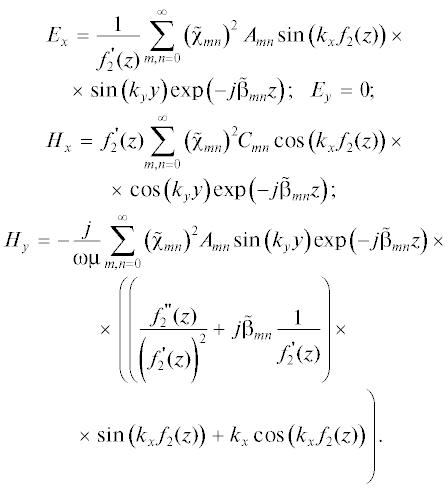Радиотехника и электроника, 2019, T. 64, № 4, стр. 317-331
Метод интегральных уравнений для расчета плавно-нерегулярных несоосных волноводных переходов
С. М. Гаранин 1, *, И. Н. Данилов 1, С. Б. Раевский 1, А. Ю. Седаков 1
1 Нижегородский государственный технический университет им. Р.Е. Алексеева
603950 Нижний Новгород, ул. Минина, 24, Российская Федерация
* E-mail: garanin_s.m@mail.ru
Поступила в редакцию 14.03.2017
После доработки 02.11.2017
Принята к публикации 02.03.2018
Аннотация
Предложен метод решения задач о расчете характеристик передачи плавных переходов между двумя несоосными экранированными волноводами различных поперечных сечений, приводящий к коллокационной алгебраизации интегральных уравнений, составленных на основе леммы Лоренца.
ВВЕДЕНИЕ
В современной технической электродинамике актуальным остается вопрос совершенствования существующих и создания новых методов решения краевых задач, к которым относятся внутренние дифракционные задачи о расчете характеристик передачи различных нерегулярных направляющих структур. При выявлении принципиальных особенностей этих характеристик являются незаменимыми аналитические и численно-аналитические строго обоснованные методы расчета, изначально развитые А.Г. Свешниковым и А.С. Ильинским (внутренние краевые задачи с нелокальными граничными условиями, метод перехода от нерегулярных волноводов к регулярным, заполненным невзаимной средой) [1, 2], Б.З. Каценеленбаумом [3] и В.В. Шевченко [4] (метод поперечных сечений), В.В. Никольским (различные вариационные методы [5]).
Строгий расчет нерегулярных участков волноводного тракта требует, как правило [6], обращения к аппарату интегральных уравнений [7], к которым можно [8] свести краевые задачи на дифференциальных уравнениях. В отличие от стандартных методов [8] в настоящей работе предлагается формулировка краевых задач о расчете нерегулярных участков волноводного тракта в виде системы интегральных уравнений, получаемых на основе леммы Лоренца [9–11]. Рассматриваемый метод впервые был предложен в работе [9].
1. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ, ОСНОВАННЫЙ НА ЛЕММЕ ЛОРЕНЦА
Краевую задачу для нерегулярного участка волноведущей структуры, каким является переход между двумя регулярными волноводами, стандартными методами [7, 8, 12] свести к интегральному уравнению (системе уравнений) трудно. Из-за зависимости амплитудных коэффициентов полей от продольной координаты [3] в уравнениях Максвелла не удается выполнить разделение переменных и сформулировать краевые покоординатные задачи, приводящие [8, 12] к уравнениям Вольтерра [13]. В настоящей работе предлагается нестандартный, можно сказать, чисто физический подход к составлению интегральных уравнений, позволяющих рассчитывать характеристики нерегулярных волноводов [9–11] и, в частности, волноводных переходов [14, 15].
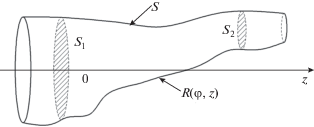
Рассматриваем пространство, ограниченное поверхностью S, описываемой функцией R(φ, z), где φ и z – цилиндрические координаты. Полагаем, что указанная поверхность идеально проводящая и не имеет разрывов. Пространство, ограниченное поверхностью S, охватывает весь интервал по продольной координате: $z \subset ( - \infty ;\infty ).$
Предположим, что поля ${{\vec {Е }}_{1}},$ ${{\vec {Н }}_{1}}$ и ${{\vec {Е }}_{2}},$ ${{\vec {Н }}_{2}}$ внутри рассматриваемого объема создаются источниками: $\vec {j}_{1}^{{e,m}}$ и $\vec {j}_{2}^{{e,m}},$ соответственно. Если объем заполнен взаимной средой, то в любой его части, ограниченной плоскостями S1, 2 (рис. 1), поля и источники согласно лемме Лоренца связаны соотношением:
(1)
$\begin{gathered} \oint\limits_{S + {{S}_{{1,2}}}} {\left( {\left( {\left( {{{{\vec {E}}}_{1}} \times {{{\vec {H}}}_{2}}} \right) - \left( {{{{\vec {E}}}_{2}} \times {{{\vec {H}}}_{1}}} \right)} \right) \cdot d\vec {S}} \right)} = \\ = \int\limits_V {\left( {\left( {\vec {j}_{1}^{e} \cdot {{{\vec {E}}}_{2}}} \right) - \left( {\vec {j}_{2}^{e} \cdot {{{\vec {E}}}_{1}}} \right) - \left( {\vec {j}_{1}^{m} \cdot {{{\vec {H}}}_{2}}} \right) + \left( {\vec {j}_{2}^{m} \cdot {{{\vec {H}}}_{1}}} \right)} \right)dV} , \\ \end{gathered} $В качестве полей ${{\vec {Е }}_{1}},$ ${{\vec {Н }}_{1}}$ возьмем решения уравнений Максвелла, удовлетворяющие на поверхности S граничным условиям:
то есть соответствующие волне, направляемой волноводной структурой.Источники $\vec {j}_{2}^{{e,m}},$ расположенные в конечной области внутри S, создают поле сферической волны, удовлетворяющее [16, 17] условию излучения.
Если сечения S1, 2 бесконечно удалить от начала координат (z1, 2 → ±∞), уравнение (1) можно будет переписать в виде:
(3)
$\begin{gathered} \oint\limits_{S + {{S}_{{1,2}}}} {\left( {\left( {{{{\vec {H}}}_{1}} \times {{{\vec {E}}}_{2}}} \right) \cdot d\vec {S}} \right)} = \\ = \int\limits_{{{V}_{\infty }}} {\left( {\left( {\vec {j}_{1}^{e} \cdot {{{\vec {E}}}_{2}}} \right)} \right. - \left( {\vec {j}_{2}^{e} \cdot {{{\vec {E}}}_{1}}} \right) - } \\ - \,\,\left( {\vec {j}_{1}^{m} \cdot {{{\vec {H}}}_{2}}} \right) + \left. {\left( {\vec {j}_{2}^{m} \cdot {{{\vec {H}}}_{1}}} \right)} \right)dV. \\ \end{gathered} $Особенностью представления леммы Лоренца в виде (3) является запись ее на решениях двух различных краевых задач для одного и того же объема. В таком виде она объединяет две краевые задачи на уравнениях Максвелла. В краевой задаче относительно поля ${{\vec {E}}_{2}},$ ${{\vec {H}}_{2}}$ в качестве граничного условия использовали условие излучения, благодаря которому положили, что источники $\vec {j}_{2}^{{e,m}}$ создают только расходящуюся сферическую волну, удовлетворяющую нулевому граничному условию на бесконечности [16, 17].
Первый поверхностный интеграл в (1) равен нулю, так как на поверхности S равна нулю тангенциальная компонента поля ${{\vec {E}}_{1}},$ а на бесконечно удаленных поверхностях S1,2 обращается в нуль поле расходящейся сферической волны, создаваемой источниками $\vec {j}_{2}^{e}$ и $\vec {j}_{2}^{m},$ расположенными в конечной области, и удовлетворяющей условию излучения. При этом учитывается условие: в волноводе, соответствующем поверхности S, на которой для поля ${{\vec {E}}_{1}},$ ${{\vec {H}}_{1}}$ выполняются граничные условия (2), при z → ±∞ имеет место неравенство ρ $ \gg $ r, где ρ – сферическая координата, связанная со вспомогательными источниками, r – цилиндрическая координата в бесконечно удаленных сечениях. За счет этого осуществляется переход от уравнения (1) к уравнению (3).
В безграничном пространстве токи $\vec {j}_{1}^{{e,m}}$ создают расходящуюся сферическую волну $\left( {{{{\vec {Е }}}_{0}},{{{\vec {Н }}}_{0}}} \right),$ удовлетворяющую [16, 17] условию излучения. В этом случае лемма Лоренца для совокупности полей: ${{\vec {E}}_{2}},$ ${{\vec {H}}_{2}}$ и ${{\vec {E}}_{0}},$ ${{\vec {H}}_{0}},$ удовлетворяющих краевым задачам с условием излучения на бесконечности принимает [17] вид:
(4)
$\begin{gathered} \int\limits_{{{V}_{\infty }}} {\left( {\left( {\vec {j}_{1}^{e} \cdot {{{\vec {E}}}_{2}}} \right)} \right. - \left( {\vec {j}_{2}^{e} \cdot {{{\vec {E}}}_{0}}} \right) - } \\ - \,\,\left( {\vec {j}_{1}^{m} \cdot {{{\vec {H}}}_{2}}} \right) + \left. {\left( {\vec {j}_{2}^{m} \cdot {{{\vec {H}}}_{0}}} \right)} \right)dV = 0. \\ \end{gathered} $Поскольку в (3) и (4) интегрирование производится по объему одних и тех же источников, значения V∞ в этих уравнениях совпадают.
Исключая из (3) с помощью (4) токи $\vec {j}_{1}^{{e,m}},$ получаем:
(5)
$\begin{gathered} \oint\limits_{S + {{S}_{{1,2}}}} {\left( {\left( {{{{\vec {H}}}_{1}} \times {{{\vec {E}}}_{2}}} \right) \cdot d\vec {S}} \right)} = \\ = \int\limits_{{{V}_{\infty }}} {\left( {\left( {\vec {j}_{2}^{e} \cdot \left( {{{{\vec {E}}}_{0}} - {{{\vec {E}}}_{1}}} \right)} \right) - \left( {\vec {j}_{2}^{m} \cdot \left( {{{{\vec {H}}}_{0}} - {{{\vec {H}}}_{1}}} \right)} \right)} \right)dV} . \\ \end{gathered} $Выбрав в качестве источников $\vec {j}_{2}^{{e,m}}$ элементарные диполи:
(6)
$\begin{gathered} \oint\limits_{S + {{S}_{{1,2}}}} {\left( {\left( {{{{\vec {H}}}_{1}} \times {{{\vec {E}}}_{2}}} \right) \cdot d\overrightarrow S } \right)} = I_{0}^{e}L\left[ {{{E}_{0}}\left( {{{{\vec {r}}}_{{j_{2}^{e}}}}} \right) - {{E}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{e}}}}} \right)} \right] - \\ - \,\,I_{0}^{m}L\left[ {{{H}_{0}}\left( {{{{\vec {r}}}_{{j_{2}^{m}}}}} \right) - {{H}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{m}}}}} \right)} \right]. \\ \end{gathered} $Поле $\left( {{{{\vec {Е }}}_{1}},{{{\vec {Н }}}_{1}}} \right)$ в (6), удовлетворяющее граничным условиям (2), можно рассматривать как поле волны в волноводе с идеально проводящей поверхностью S. В решаемой задаче это поле будет искомым. Поля $\left( {{{{\vec {Е }}}_{0}},{{{\vec {Н }}}_{0}}} \right)$ и $\left( {{{{\vec {Е }}}_{2}},{{{\vec {Н }}}_{2}}} \right)$ являются вспомогательными. Они создаются диполями $\overrightarrow j _{{1,2}}^{{e,m}}$ в неограниченном пространстве и стремятся к нулю при удалении от источников как поля расходящихся сферических волн, то есть являются решениями краевых задач с условиями излучения на бесконечности.
Расположим излучатели $\vec {j}_{2}^{{e,m}}$ в сечении z = 0, а $\vec {j}_{1}^{{e,m}}$ – в сечении z = z0, таком, для которого сечение z = 0 находится в дальней зоне источников $\vec {j}_{1}^{{e,m}}.$ При этом полагаем, что значение z0 таково, что для безграничного пространства справедлива запись леммы Лоренца в виде (4). Поскольку E0, H0 – электрическое и магнитное поля сферической волны, создаваемой источником, отнесенным в бесконечность, в месте расположения диполей $\vec {j}_{2}^{{e,m}}$ в сечении z = 0 в силу неравенств ${{E}_{0}}\left( {{{{\vec {r}}}_{{j_{2}^{{e,m}}}}}} \right) \ll {{E}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{{e,m}}}}}} \right),$ ${{H}_{0}}\left( {{{{\vec {r}}}_{{j_{2}^{{e,m}}}}}} \right) \ll {{H}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{{e,m}}}}}} \right),$ слагаемыми, пропорциональными Е0 и Н0, в (6) можно пренебречь. Тогда уравнение (6) перепишется в виде:
(7)
$\begin{gathered} \int\limits_S {\left( {\left( {{{{\vec {H}}}_{1}} \times {{{\vec {E}}}_{2}}} \right) \cdot d\vec {S}} \right)} = \\ = - I_{0}^{e}L{{E}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{e}}}}} \right) + I_{0}^{m}L{{H}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{m}}}}} \right). \\ \end{gathered} $Интегралы $\int_{{{S}_{{1,2}}}} {\left( {\left( {{{{\vec {H}}}_{1}} \times {{{\vec {E}}}_{2}}} \right) \cdot d\vec {S}} \right)} $ исчезли потому, что при z → ±∞ поле E2, создаваемое источниками, расположенными в сечении z = 0, стремится к нулю.
Таким образом, на основе леммы Лоренца сформулировали краевую задачу, объединяющую три краевых задачи относительно полей: $\left( {{{{\vec {Е }}}_{1}},{{{\vec {Н }}}_{1}}} \right);$ $\left( {{{{\vec {Е }}}_{2}},{{{\vec {Н }}}_{2}}} \right)$ и $\left( {{{{\vec {Е }}}_{0}},{{{\vec {Н }}}_{0}}} \right).$ Полученное интегральное соотношение является прямым следствием уравнений Максвелла. Поэтому указанные поля должны удовлетворять ему при выше сформулированных граничных условиях. В месте расположения экранирующей поверхности вспомогательные поля ${{\vec {Е }}_{2}},$ ${{\vec {Н }}_{2}}$ удовлетворяют произвольным граничным условиям, поскольку решение задачи ${{\vec {Е }}_{1}},$ ${{\vec {Н }}_{1}}$ должно быть инвариантным по отношению ко вспомогательным полям.
Уравнение (7) является интегральным уравнением относительно поля $\left( {\vec {E}{}_{1},{{{\vec {H}}}_{1}}} \right)$. В тех случаях, когда вводится один вспомогательный источник, получаются уравнения вида:
(8)
$\int\limits_S {\left( {\left( {{{{\vec {H}}}_{1}} \times {{{\vec {E}}}_{2}}} \right) \cdot d\vec {S}} \right)} = - I_{0}^{e}L{{E}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{e}}}}} \right);$(9)
$\int\limits_S {\left( {\left( {{{{\vec {H}}}_{1}} \times {{{\vec {E}}}_{2}}} \right) \cdot d\vec {S}} \right)} = I_{0}^{m}L{{H}_{1}}\left( {{{{\vec {r}}}_{{j_{2}^{m}}}}} \right).$И в том, и в другом случае амплитуды токов $I_{0}^{{e,m}}$ и длина диполя L, входящие в обе части уравнений, сокращаются.
В результате получили интегральные уравнения (8) и (9) относительно поля волны, распространяющейся в бесконечном, по продольной оси, нерегулярном волноводе, образованном идеально проводящей поверхностью S, описываемой непрерывной функцией R(φ, z).
Все преобразования, выполнявшиеся в процессе вывода интегральных уравнений (7), (8), (9), являются строго обоснованными в силу выполнения теорем единственности решений вспомогательных краевых задач, удовлетворяющих условиям излучения. Корректность полученных на основе этих уравнений численных результатов определяется выбором метода решения интегральных уравнений, и будет проконтролирована тестовой задачей, решение которой получено строго обоснованным методом.
2. ПРИМЕНЕНИЕ МЕТОДА ДЛЯ РЕШЕНИЯ ДИФРАКЦИОННОЙ ЗАДАЧИ О НЕСООСНОМ СОЕДИНЕНИИ ПРЯМОУГОЛЬНЫХ ВОЛНОВОДОВ
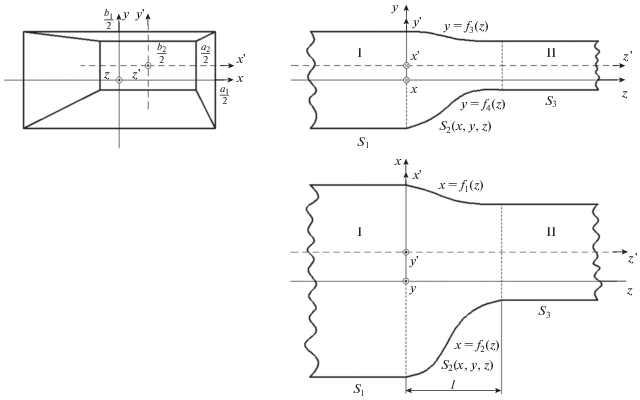
Рассмотрим трехмерно-нерегулярную направляющую структуру в виде плавного перехода между прямоугольными волноводами, имеющими параллельные оси. Внешний вид такой структуры представлен на рис. 2.
Выражения, связывающие поперечные и продольные компоненты полей на поверхности нерегулярной области направляющей структуры имеют вид, определяемый граничными условиями, соответствующими профилю этой поверхности. В плоскости XOZ:
где fp(z) – функции, описывающие профиль продольного сечения нерегулярной области в плоскости XOZ; p = 1, 2; ε и μ – диэлектрическая и магнитная проницаемости среды; ω – частота электромагнитной волны.В плоскости YOZ:
где ft(z) – функции, описывающие профиль продольного сечения нерегулярной области в плоскости YOZ; t = 3, 4.На область сочленения двух прямоугольных волноводов из z → –∞ со стороны волновода I (широкая стенка длиной a1, узкая стенка длиной b1) падает одна из собственных волн этого волновода единичной амплитуды. В результате дифракции этой волны на границе с областью II, в волноводе I возбуждается бесконечный набор отраженных волн с коэффициентами отражения $R_{{mn}}^{E}$ (для E-волн) и $R_{{mn}}^{H}$ (для H-волн), а в волноводе II образуется бесконечный набор прошедших волн с коэффициентами прохождения $B_{{mn}}^{E}$ (для E-волн) и $B_{{mn}}^{H}$ (для H‑волн).
Продольные составляющие электрического и магнитного полей в областях I и II записываются
в области I (–∞ < z ≤ 0):
(12)
$\begin{gathered} {{E}_{{z{\text{I}}}}} = {{\left( {\chi _{{mn{\text{I}}}}^{E}} \right)}^{2}}\sin \left( {\frac{{2\pi m}}{{{{a}_{1}}}}x} \right)\sin \left( {\frac{{2\pi n}}{{{{b}_{1}}}}y} \right)\exp \left( { - j\beta _{{m{{n}_{I}}}}^{E}z} \right) + \\ + \,\sum\limits_{m,n = 0}^\infty {{{{\left( {\chi _{{mn{\text{I}}}}^{E}} \right)}}^{2}}R_{{mn}}^{E}} \sin \left( {\frac{{2\pi m}}{{{{a}_{1}}}}x} \right)\sin \left( {\frac{{2\pi n}}{{{{b}_{1}}}}y} \right)\exp \left( {j\beta _{{m{{n}_{{\text{I}}}}}}^{E}z} \right); \\ {{H}_{{z{\text{I}}}}} = {{\left( {\chi _{{mn{\text{I}}}}^{H}} \right)}^{2}}\cos \left( {\frac{{2\pi m}}{{{{a}_{1}}}}x} \right)\cos \left( {\frac{{2\pi n}}{{{{b}_{1}}}}y} \right) \times \\ \times \,\,\exp \left( { - j\beta _{{m{{n}_{{\text{I}}}}}}^{H}z} \right) + \sum\limits_{m,n = 0}^\infty {{{{\left( {\chi _{{mn{\text{I}}}}^{H}} \right)}}^{2}}R_{{mn}}^{H}} \cos \left( {\frac{{2\pi m}}{{{{a}_{1}}}}x} \right) \times \\ \times \,\,\cos \left( {\frac{{2\pi n}}{{{{b}_{1}}}}y} \right)\exp \left( {j\beta _{{m{{n}_{{\text{I}}}}}}^{H}z} \right), \\ \end{gathered} $в области II (l ≤ z < ∞):
(13)
$\begin{gathered} {{E}_{{z{\text{II}}}}} = \sum\limits_{m,n = 0}^\infty {{{{\left( {{\chi }_{{mn{\text{II}}}}^{E}} \right)}}^{2}}B_{{mn}}^{E}} \sin \left( {\frac{{2{\pi }m}}{{{{a}_{2}}}}x{\text{'}}} \right) \times \\ \times \,\,\sin \left( {\frac{{2{\pi }n}}{{{{b}_{2}}}}y{\text{'}}} \right){\text{exp}}\left( { - j{\beta }_{{m{{n}_{{{\text{II}}}}}}}^{E}z} \right); \\ {{H}_{{z{\text{II}}}}} = \sum\limits_{m,n = 0}^\infty {{{{\left( {{\chi }_{{mn{\text{II}}}}^{H}} \right)}}^{2}}B_{{mn}}^{H}} \cos \left( {\frac{{2{\pi }m}}{{{{a}_{2}}}}x{\text{'}}} \right) \times \\ \times \,\,\cos \left( {\frac{{2{\pi }n}}{{{{b}_{2}}}}y{\text{'}}} \right){\text{exp}}\left( { - j{\beta }_{{m{{n}_{{{\text{II}}}}}}}^{H}z} \right), \\ \end{gathered} $Запись продольных компонент электромагнитного поля на поверхности нерегулярной области II (0 < z < l) в плоскости XOZ имеет вид:
(14)
$\begin{gathered} {{E}_{z}} = \sum\limits_{m,n = 0}^\infty {A_{{mn}}^{E}{{{\left( {{\tilde {\chi }}_{{pmn}}^{E}(z)} \right)}}^{2}}\sin \left( {k_{{xpmn}}^{E}(z){{f}_{p}}(z)} \right)} \sin \left( {k_{{ypmn}}^{E}(z)y} \right)\exp \left( { - j{\tilde {\beta }}_{{pmn}}^{E}(z)z} \right) + \\ + \,\,\sum\limits_{m,n = 0}^\infty {C_{{mn}}^{E}{{{\left( {{\tilde {\chi }}_{{pmn}}^{E}(z)} \right)}}^{2}}\sin \left( {k_{{xpmn}}^{E}(z){{f}_{p}}(z)} \right)} \sin \left( {k_{{ypmn}}^{E}(z)y} \right)\exp \left( {j{\tilde {\beta }}_{{pmn}}^{E}(z)z} \right); \\ {{H}_{z}} = \sum\limits_{m,n = 0}^\infty {A_{{mn}}^{H}{{{\left( {{\tilde {\chi }}_{{pmn}}^{H}(z)} \right)}}^{2}}\cos \left( {k_{{xpmn}}^{H}(z){{f}_{p}}(z)} \right)} \cos \left( {k_{{ypmn}}^{H}(z)y} \right)\exp \left( { - j{\tilde {\beta }}_{{pmn}}^{H}(z)z} \right) + \\ + \sum\limits_{m,n = 0}^\infty {C_{{mn}}^{H}{{{\left( {{\tilde {\chi }}_{{pmn}}^{H}(z)} \right)}}^{2}}\cos \left( {k_{{xpmn}}^{H}(z){{f}_{p}}(z)} \right)} \cos \left( {k_{{ypmn}}^{H}(z)y} \right)\exp \left( {j{\tilde {\beta }}_{{pmn}}^{H}(z)z} \right), \\ \end{gathered} $в плоскости YOZ:
(15)
$\begin{gathered} {{E}_{z}} = \sum\limits_{m,n = 0}^\infty {A_{{mn}}^{E}{{{\left( {{\tilde {\chi }}_{{tmn}}^{E}(z)} \right)}}^{2}}\sin \left( {k_{{xtmn}}^{E}(z)x} \right)} \sin \left( {k_{{ytmn}}^{E}(z){{f}_{t}}(z)} \right)\exp \left( { - j{\tilde {\beta }}_{{tmn}}^{E}(z)z} \right) + \\ + \,\,\sum\limits_{m,n = 0}^\infty {C_{{mn}}^{E}{{{\left( {{\tilde {\chi }}_{{tmn}}^{E}(z)} \right)}}^{2}}\sin \left( {k_{{xtmn}}^{E}(z)x} \right)} \sin \left( {k_{{ytmn}}^{E}(z){{f}_{t}}(z)} \right)\exp \left( {j{\tilde {\beta }}_{{tmn}}^{E}(z)z} \right); \\ {{H}_{z}} = \sum\limits_{m,n = 0}^\infty {A_{{mn}}^{H}{{{\left( {{\tilde {\chi }}_{{tmn}}^{H}(z)} \right)}}^{2}}\cos \left( {k_{{xtmn}}^{H}(z)x} \right)} \cos \left( {k_{{ytmn}}^{H}(z){{f}_{t}}(z)} \right)\exp \left( { - j{\tilde {\beta }}_{{tmn}}^{H}(z)z} \right) + \\ + \,\,\sum\limits_{m,n = 0}^\infty {C_{{mn}}^{H}{{{\left( {{\tilde {\chi }}_{{tmn}}^{H}(z)} \right)}}^{2}}\cos \left( {k_{{xtmn}}^{H}(z)x} \right)} \cos \left( {k_{{ytmn}}^{H}(z){{f}_{t}}(z)} \right)\exp \left( {j{\tilde {\beta }}_{{tmn}}^{H}(z)z} \right), \\ \end{gathered} $Здесь $k_{{xtmn}}^{{E(H)}}(z)$ и $k_{{ytmn}}^{{E(H)}}(z)$ – составляющие поперечных волновых чисел волн Е- и Н-типа, соответствующих поверхностям f3(z) и f4(z), связь между которыми имеет вид:
Связь волновых чисел в каждом поперечном сечении z = const области II (0 < z < l) записывается как:
(соответствует поверхностям f1(z) и f2(z));
(соответствует поверхностям f3(z) и f4(z)).
Для определения продольных и поперечных волновых чисел необходимо воспользоваться граничными условиями:
(16)
$\begin{gathered} {{\left. {{{E}_{y}}} \right|}_{s}}| = 0,\,\,\,\,{{\left. {\frac{{\partial {{H}_{y}}}}{{\partial x}}} \right|}_{s}} = 0 - {\text{н а }}\,\,{\text{п о в е р х н о с т я х }}\,\,x = {{f}_{1}}(z),\,\,\,\,x = {{f}_{2}}(z), \\ {{\left. {{{E}_{x}}} \right|}_{s}}| = 0,\,\,\,\,{{\left. {\frac{{\partial {{H}_{x}}}}{{\partial y}}} \right|}_{s}} = 0 - {\text{н а }}\,\,{\text{п о в е р х н о с т я х }}\,\,y = {{f}_{3}}(z),\,\,\,y = {{f}_{4}}(z), \\ \end{gathered} $Подставляя компоненты полей (10), (11) в граничные условия (16), получаем систему функциональных уравнений, связывающих продольные и поперечные волновые числа:
Функции, описывающие профиль продольного сечения x = f1(z), x = f2(z), y = f3(z) и y = f4(z), могут иметь любые гладкие зависимости от продольной координаты z. Следовательно, волновая поверхность (поверхность равных фаз) распространяющейся в нерегулярной области электромагнитной волны имеет сложную форму, в общем случае отличную от форм волновых поверхностей плоской, цилиндрической или сферической волн. В таком случае, при численной реализации разработанного алгоритма для получения результатов расчета с приемлемыми значениями относительной погрешности (не более 5%) требуется определение продольного и поперечного волновых чисел электромагнитной волны в каждой точке на поверхности нерегулярной области рассматриваемой направляющей структуры, что эквивалентно введению для каждой указанной точки своего волновода сравнения [3]. Пересечение плоскости z = zq = const и проводящей поверхности нерегулярной области образует контур поперечного сечения направляющей структуры, состоящий из четырех отрезков, описываемых соотношениями:
В каждой точке полученного контура при z = zq = = const с помощью системы уравнений (17) определяются численные значения продольного и поперечного волновых чисел. Поскольку контур поперечного сечения z = const образован четырьмя отрезками, при числе точек его аппроксимации по x и y равном K, для определения волновых чисел в указанном сечении требуется введение 4K волноводов сравнения: условно – 4K‑кратный волновод сравнения.
При p = 1 из (17) получаем две системы уравнений, связывающие поперечные и продольные волновые числа E- и H-волн на поверхности x = f1(z) нерегулярной области. Аналогичным образом получаем системы уравнений при p = 2, t = 3 и t = 4 на поверхностях x = f2(z), y = f3(z) и y = f4(z). Каждая из отмеченных систем состоит из двух трансцендентных и одного алгебраического уравнения, связывающего продольное и поперечное волновые числа. Указанная система решается численным методом Ньютона [18]. Таким образом, система (17) преобразуется в восемь независимых систем уравнений относительно неизвестных поперечных и продольных волновых чисел волн Е- и Н-типа, которые решаются независимо друг от друга.
Подставляя найденные значения поперечных и продольных волновых чисел в выражения (14) и (15), определяем компоненты Ez и Hz электромагнитных волн в нерегулярной области. Поперечные компоненты полей Е-волн регулярных волноводов I (–∞ < z ≤ 0), II (l < z ≤ ∞) выражаются через продольные (12), (13).
Связь волновых чисел в регулярных областях: $\varepsilon \mu {{\omega }^{2}} = {{\left( {\chi _{{mn}}^{Е }} \right)}^{2}} + {{\left( {\beta _{{mn}}^{Е }} \right)}^{2}}.$ В области I (–∞ < z ≤ 0): $\chi _{{mn{\text{I}}}}^{Е } = \sqrt {{{{\left( {{{\pi m} \mathord{\left/ {\vphantom {{\pi m} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}} \right)}}^{2}} + {{{\left( {{{\pi n} \mathord{\left/ {\vphantom {{\pi n} {{{b}_{1}}}}} \right. \kern-0em} {{{b}_{1}}}}} \right)}}^{2}}} ;$ в области II (l ≤ z < ∞): $\chi _{{mn{\text{II}}}}^{E} = \sqrt {{{{\left( {{{\pi m} \mathord{\left/ {\vphantom {{\pi m} {{{a}_{2}}}}} \right. \kern-0em} {{{a}_{2}}}}} \right)}}^{2}} + {{{\left( {{{\pi n} \mathord{\left/ {\vphantom {{\pi n} {{{b}_{2}}}}} \right. \kern-0em} {{{b}_{2}}}}} \right)}}^{2}}} .$
Аналогичным образом поперечные компоненты полей Н-волн регулярных волноводов I (–∞ < < z ≤ 0), II (l < z ≤ ∞) выражаем через продольные.
Волновые числа H-волн связаны соотношением: $\varepsilon \mu {{\omega }^{2}} = {{\left( {\chi _{{mn}}^{H}} \right)}^{2}} + {{\left( {\beta _{{mn}}^{H}} \right)}^{2}}.$ Волны Emn и Hmn прямоугольного волновода являются вырожденными: их волновые числа совпадают.
Получим связь поперечных компонент электромагнитного поля с продольными на поверхности нерегулярной области (0 < z < l). С учетом (10), (11), (15) и граничного условия ${{\left. {{{E}_{x}}} \right|}_{s}} = 0$ на поверхности y = f3(z) имеем:
С учетом (10), (11), (15) и граничного условия ${{\left. {{{E}_{x}}} \right|}_{s}} = 0$ на поверхности y = f4(z) имеем:
(19)
$\begin{gathered} {{E}_{x}} = 0;\,\,\,\,\,{{E}_{y}} = \frac{1}{{{{{f'}}_{4}}(z)}}\sum\limits_{m,n = 0}^\infty {{{{\left( {{{{\tilde {\chi }}}_{{mn}}}} \right)}}^{2}}{{A}_{{mn}}}\sin \left( {{{k}_{x}}x} \right)} \times \\ \times \,\,\sin \left( {{{k}_{y}}{{f}_{4}}(z)} \right)\exp \left( { - j{{{\tilde {\beta }}}_{{mn}}}z} \right);\,\,\,\,{{H}_{x}} = \frac{j}{{\omega \mu }}\sum\limits_{m,n = 0}^\infty {{{{\left( {{{{\tilde {\chi }}}_{{mn}}}} \right)}}^{2}}} \times \\ \times \,\,{{A}_{{mn}}}\sin \left( {{{k}_{x}}x} \right)\exp \left( { - j{{{\tilde {\beta }}}_{{mn}}}z} \right)\left( {{{k}_{y}}\cos \left( {{{k}_{y}}{{f}_{4}}(z)} \right) + \frac{{^{{^{{^{{}}}}}}}}{{_{{}}}}} \right. \\ \left. { + \,\,\left( {\frac{{f_{4}^{{''}}(z)}}{{{{{\left( {f_{4}^{'}(z)} \right)}}^{2}}}} + j{{{\tilde {\beta }}}_{{mn}}}\frac{1}{{f_{4}^{'}(z)}}} \right)\sin \left( {{{k}_{y}}{{f}_{4}}(z)} \right)} \right); \\ {{H}_{y}} = f_{4}^{'}(z)\sum\limits_{m,n = 0}^\infty {{{{\left( {{{{\tilde {\chi }}}_{{mn}}}} \right)}}^{2}}} {{С }_{{mn}}} \times \\ \times \,\,\cos \left( {{{k}_{x}}x} \right)\cos \left( {{{k}_{y}}{{f}_{4}}(z)} \right)\exp \left( { - j{{{\tilde {\beta }}}_{{mn}}}z} \right). \\ \end{gathered} $С учетом (10), (11), (14) и граничного условия ${{\left. {{{E}_{y}}} \right|}_{s}} = 0$ на поверхности x = f1(z) имеем:
С учетом (10), (11), (14) и граничного условия ${{\left. {{{E}_{y}}} \right|}_{s}} = 0$ на поверхности x = f2(z) имеем:
Подставляя компоненты электромагнитного поля в (8) и (9), и записывая (8), (9) в 4N точках с координатами (xu,i, yu,i, ci), где i – номер вспомогательного источника, получаем систему 4N алгебраических уравнений относительно неизвестных амплитудных коэффициентов Rmn, ${{B}_{{mn}}},$ ${{A}_{{mn}}},$ ${{С }_{{mn}}},$ которая решается в том или ином приближении в зависимости от числа учитываемых волн в стыкуемых волноводах. N – количество волн, учитываемых в направляющей структуре, по порядку следования их критических частот. N определяет номер приближения, в котором решается задача.
Левая часть интегрального уравнения (9) может быть записана следующим образом:
где S1 – боковая поверхность регулярной области I $\left( { - \infty < z \leqslant 0} \right);$ S2 – боковая поверхность нерегулярной области II $\left( {0 < z < l} \right);$ S3 – боковая поверхность регулярной области III $\left( {l \leqslant z < \infty } \right).$
Введем обозначения:
Левая часть интегрального уравнения (8) может быть записана следующим образом:
Из системы (17), корнями которой являются значения поперечных и продольных волновых чисел в нерегулярной области следует, что волновые числа имеют зависимость от декартовых координат x, y и z. В свою очередь, подынтегральные выражения Int2 и Int5 содержат поперечные и продольные волновые числа, при этом интегрирование проводится по поверхности рассматриваемой структуры в декартовой системе координат. Так как интегрирование осуществляется численным методом, то при его реализации возникает вопрос решения компромисса между количеством точек аппроксимации подынтегрального выражения и приемлемыми временными затратами. Решение этого вопроса требует исследования сходимости значений интегралов в зависимости от количества точек аппроксимации Q вдоль координаты z при фиксированном числе точек аппроксимации по поперечным координатам (равном 100). В качестве примера на рис. 3 и рис. 4 изображены графики сходимости модулей значений интегралов: Int2 – рис. 3 и Int5 – рис. 4, для двух значений нормированных частот ka1 = 4.78 и ka1 = 6.14 при соотношении размеров сочленяемых волноводов M = a2/a1= b2/b1= 0.75, a1/b1= a2/b2= 0.5, l/a1= 1. В качестве функций профиля нерегулярной области выбраны:
Рис. 3.
График сходимости значения модуля интеграла Int2 при соотношении размеров сочленяемых волноводов, M = 0.75, a1/b1 = a2/b2 = 0.5, l/a1 = 1 для нормированных частот: а – ka1 = 4.78, б – ka1 = 6.14.
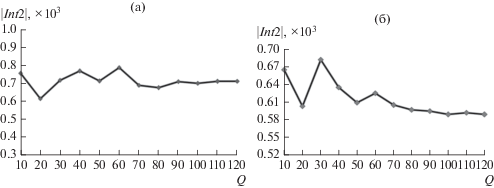
Рис. 4.
График сходимости значения модуля интеграла Int5 при соотношении размеров сочленяемых волноводов M = 0.75, a1/b1 = a2/b2 = 0.5, l/a1 = 1 для нормированных частот: а – ka1 = 4.78, б – ka1 = 6.14.
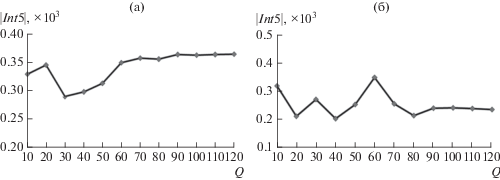
Анализ представленных зависимостей показывает, что при увеличении количества точек аппроксимации вдоль оси z начиная с Q = 100 наблюдается незначительное изменение значений модулей интегралов (порядка 1%), что дает возможность выбрать в качестве “рабочего” приближения Q = 100. При этом требуется вполне приемлемое количество машинного времени для вычисления интеграла при сохранении заданного значения точности.
3. РЕЗУЛЬТАТЫ РАСЧЕТА НЕСООСНОГО ПЛАВНОГО ПЕРЕХОДА МЕЖДУ ДВУМЯ ПРЯМОУГОЛЬНЫМИ ВОЛНОВОДАМИ В ОДНОМОДОВОМ ДИАПАЗОНЕ ЧАСТОТ
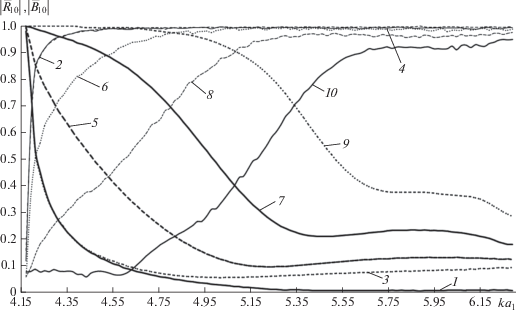
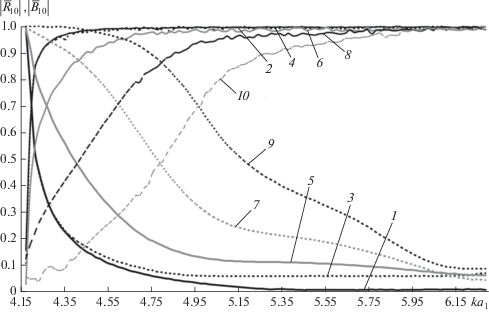
Наиболее полную качественную и количественную информацию о характеристиках направляющей структуры содержат зависимости модулей коэффициентов отражения $\left| {{{{\bar {R}}}_{{10}}}} \right|$ и прохождения $\left| {{{{\bar {B}}}_{{10}}}} \right|$ основной волны от нормированной частоты. Эти зависимости при смещении оси второго волновода вдоль координатной оси x представлены на рис. 5. Соотношения размеров соединяемых волноводов M = a2/a1 = b2/b1 = 0.75, b1/a1 = b2/a2 = 0.5, длина перехода вдоль оси z: l = a1. Кривые 1 и 2 – модули коэффициентов отражения и прохождения волны H10 при соосном соединении волноводов, кривые 3, 4 – при смещении оси второго волновода на величину ∆x = 0.4a1, где a1 – длина широкой стенки большего волновода. Кривые 5 и 6 соответствуют ∆x = 0.6a1, кривые 7 и 8 – ∆x = = 0.8a1, кривые 9 и 10 – ∆x = a1. Результаты получены в двенадцатом приближении, когда учитывалось двенадцать волн H- и Е-типа по порядку следования их критических частот. Из рис. 5 видно, что при соосном соединении двух прямоугольных волноводов, начиная с критической частоты основной волны H10 второго волновода, значение модуля коэффициента отражения резко уменьшается с ростом частоты, и далее во всем исследуемом диапазоне частот принимает значения, близкие к нулю. Модуль коэффициента прохождения, наоборот, резко увеличивается, стремясь к единице. Данный факт говорит о хорошем согласовании волноводов в рассматриваемом диапазоне частот. При возникновении и увеличении смещения оси второго волновода вдоль x, вплоть до величины ∆x = 0.4a1, наблюдается незначительное увеличение значения модуля коэффициента отражения. Однако при дальнейшем возрастании величины смещения оси второго волновода, помимо увеличения значения модуля коэффициента отражения, отчетливо наблюдается смещение критической частоты основной волны направляющей структуры в более высокочастотную область. Зависимость величины смещения критической частоты от смещения оси волновода прямо пропорциональная.
Рис. 5.
Зависимости модулей коэффициентов отражения и прохождения волны H10 от нормированной частоты при различных смещениях оси второго волновода вдоль координатной оси x.
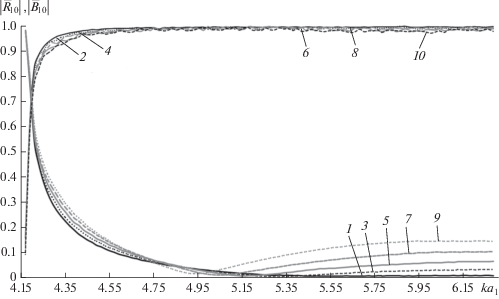
Зависимости модулей коэффициентов отражения и прохождения от нормированной частоты при смещении оси второго волновода вдоль координатной оси y представлены на рис. 6. Кривые 1 и 2 – модули коэффициентов отражения и прохождения волны H10 при соосном соединении волноводов. Кривые 3, 4 – соответствуют смещению оси второго волновода на величину ∆y = = 0.4b1, где b1 – длина узкой стенки большего волновода. Кривые 5, 6 соответствуют ∆y = 0.6b1, 7 и 8 – ∆y = 0.8b1, 9 и 10 – ∆y = b1. Из рисунка видно, что при увеличении смещения оси второго волновода вдоль координаты y, происходит возрастание величины модуля коэффициента отражения практически во всем рассматриваемом диапазоне частот.
Рис. 6.
Зависимости модулей коэффициентов отражения и прохождения волны H10 от нормированной частоты при различных смещениях оси второго волновода вдоль координатной оси y.
Зависимости модулей коэффициентов отражения и прохождения от нормированной частоты при смещении оси второго волновода одновременно вдоль осей x и y представлены на рис. 7. Кривые 1 и 2 – модули коэффициентов отражения и прохождения волны H10 при соосном соединении волноводов. Кривые 3 и 4 – соответствуют смещению оси второго волновода на величину ∆x = 0.4a1, ∆y = 0.4b1. Кривые 5 и 6 соответствуют ∆x = 0.6a1, ∆y = 0.6b1, кривые 7 и 8 – ∆x = 0.8a1, ∆y = 0.8b1, кривые 9 и 10 – ∆x = a1, ∆y = = b1. Из рисунка видно, что характер поведения зависимостей электрических характеристик данного перехода отражает свойства, присущие как переходам со смещением оси второго волновода вдоль координатной оси x, так и вдоль оси y. Приведенные зависимости показывают, что при возрастании степени нерегулярности (при увеличении расстояния между осями соединяемых регулярных волноводов) наблюдается как смещение критической частоты основной волны прямоугольного волновода вверх, так и увеличение значений модуля коэффициента отражения.
Рис. 7.
Зависимости модулей коэффициентов отражения и прохождения волны H10 от нормированной частоты при различных смещениях оси второго волновода одновременно вдоль осей x и y.
При решении системы уравнений (8) и (9) в заданном приближении при конечном числе точек, в которые помещаются вспомогательные источники, их координаты определяются из условия минимизации погрешности выполнения закона сохранения энергии (ЗСЭ), который в общем виде записывается как:
где $\bar {R}_{{mn}}^{{E,H}}$ и $\bar {B}_{{mn}}^{{E,H}}$ – нормированные коэффициенты отражения и прохождения E- и H-волн в рассматриваемой структуре, которые определяются как:
где ${{P}_{{{{H}_{{mn}}},{{E}_{{mn}}}}}}$ – поток мощности волн с амплитудными коэффициентами $R_{{mn}}^{{E,H}}$ и $B_{{mn}}^{{E,H}},$${{P}_{{{{H}_{{10}}}}}}$ – поток мощности основной волны прямоугольного волновода.
Относительная погрешность выполнения ЗСЭ вычисляется как:
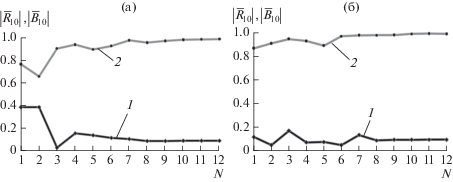
Зависимости относительной погрешности выполнения ЗСЭ от нормированной частоты представлены на рис. 8. Из рисунка видно, что величина погрешности выполнения ЗСЭ, в одномодовом диапазоне нормированных частот не превышает 5%. Для подтверждения обоснованности предлагаемого метода были исследованы зависимости величин коэффициентов отражения и прохождения от номера приближения N. Исследование проведено для плавного линейного перехода между двумя прямоугольными регулярными волноводами при смещении оси второго волновода по x и одновременно по x и y. Результаты расчетов приведены на рис. 9, из которого видно, что значения модулей коэффициентов отражения и прохождения стабилизируются при N = 12, и дальнейшее увеличение N приводит к их изменению менее, чем на 1%.
Рис. 8.
Зависимости относительной погрешности выполнения закона сохранения энергии от частоты в одномодовом диапазоне: а – при соосном соединении; б – при смещении вдоль x на величину Δx = 0.8a1; в – при смещении вдоль y на величину Δy = 0.8b1; г – при смещении одновременно вдоль обеих осей Δx = 0.4a1, Δy = 0.4b1.
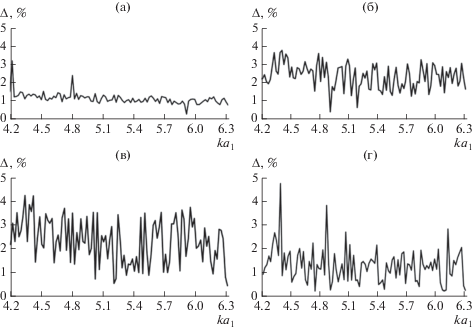
Рис. 9.
Зависимости модулей коэффициента отражения (кривая 1) и прохождения (кривая 2) волны H10 прямоугольного волновода на частоте ka1 = 6.1: а – при смещении оси второго волновода вдоль оси x на величину Δx = 0.4a1; б – при смещении одновременно вдоль осей x и y на величины Δx = 0.4a1, Δy = 0.4b1.
С целью проверки корректности получаемых предлагаемым методом результатов были рассчитаны характеристики передачи перехода с линейным профилем продольного сечения с помощью САПР CST Studio Suite. Результаты расчетов при смещении оси второго прямоугольного волновода вдоль оси x на величину ∆x = 0.6a1 приведены на рис. 10 совместно с результатами, полученными на основе разработанного алгоритма.
Рис. 10.
Сравнение результатов расчета характеристик передачи, полученных методом интегральных уравнений и с помощью САПР СВЧ для волны H10 при смещении оси второго волновода вдоль оси x на величину Δx = 0.6a1.
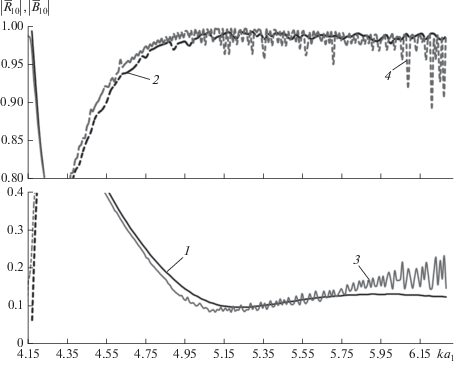
На рис. 10 кривые 1 и 3 – зависимости модулей коэффициентов отражения от частоты, полученные с помощью разработанного алгоритма и с помощью САПР СВЧ, соответственно. Кривые 2 и 4 – зависимости модулей коэффициентов прохождения от частоты, полученные с помощью разработанного алгоритма и с помощью САПР СВЧ, соответственно. Сравнение результатов, представленных на рис. 10, показывает, что имеет место хорошее качественное и количественное совпадение результатов, полученных на основе разработанного алгоритма, с результатами, полученными с использованием САПР СВЧ.
С целью подтверждения достоверности результатов, получаемых предлагаемым методом было проведено сравнение их с результатами решения задачи дифракции нормальной волны на ступенчатом сочленении двух прямоугольных регулярных волноводов с различными размерами поперечных сечений по широкой стенке и одинаковыми – по узкой. Задача ранее была решена [19] строго обоснованным методом. Внешний вид сочленения изображен на рис. 11. Соотношения размеров стыкуемых волноводов a2/a1 = 0.75, b2/b1 = 1, b1/a1 = 0.5, b2/a2 = 0.67.
Рис. 11.
Изображение ступенчатого сочленения между прямоугольными волноводами с различными размерами по широкой стенке при смещении оси второго волновода относительно первого по x на величину Δx = 0.5(a1 – a2).
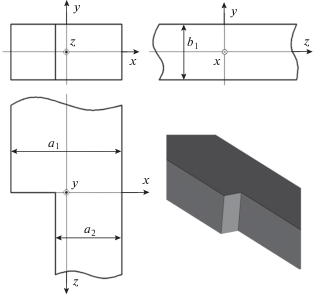
На рис. 12 представлены результаты расчета частотной зависимости модуля коэффициента отражения (сплошная линия) основной волны H10 при смещении оси второго волновода относительно первого по оси x на величину Δx = 0.5(a1 – a2). Крестиками на указанном рисунке изображены значения модуля коэффициента отражения волны H10, взятые из работы [19]. Эти результаты можно принимать за эталонные, так как задача в данной работе решалась посредством строго обоснованного метода полуобращения оператора исходной краевой задачи. Сравнение результатов расчета характеристик передачи показывает, что величина расхождения (величина относительного отклонения) между результатами, полученными на основе представленного в настоящей работе алгоритма и взятыми из работы [19], не превышают 4%. Результаты сравнения позволяют сделать вывод о действенности предлагаемого метода интегральных уравнений и корректности результатов, получаемых на его основе.
Рис. 12.
Сравнение результатов расчета модуля коэффициента отражения волны H10 несоосного сочленения двух волноводов с разными размерами по широкой стенке, полученных с помощью разработанного алгоритма (сплошная линия), с результатами, представленными в работе [17] (крестики).
4. РЕЗУЛЬТАТЫ РАСЧЕТА В МНОГОМОДОВОМ ДИАПАЗОНЕ ЧАСТОТ
С целью демонстрации возможностей предлагаемого метода были рассчитаны характеристики передачи перехода в многомодовом диапазоне нормированных частот 4.19 ≤ ka1 ≤ 12.51. На рис. 13 представлены частотные зависимости коэффициентов отражения и прохождения волн H10, H20 и H30 при смещении оси второго волновода по x на величину ∆x = 0.4a1.
Рис. 13.
Зависимости модулей коэффициентов отражения (сплошные линии) и прохождения (штриховые линии) волн Hmn от нормированной частоты при смещении оси второго волновода относительно первого по оси x на величину ∆x = 0.4a1 в многомодовом диапазоне частот.
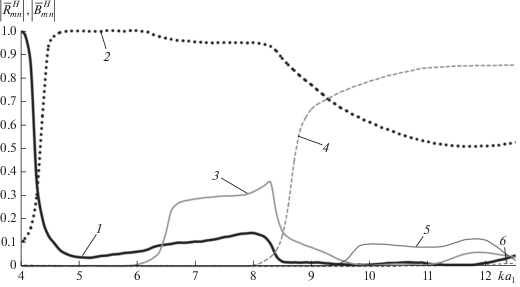
Из приведенных зависимостей видно, что в многомодовой частотной области в результате дифракции волны H10 в регулярных волноводах возбуждаются и распространяются также волны H20 и H30. Кривые 1 и 2 – модули коэффициентов отражения и прохождения волны H10, кривые 3 и 4 – волны H20, кривые 5 и 6 – волны H30. Амплитудные коэффициенты одной и той же волны высшего типа в первом и во втором согласуемых регулярных волноводах становятся отличными от нуля на различных нормированных частотах. Это связано с различными поперечными размерами этих волноводов и, соответственно, с различными в них критическими частотами возбуждаемых волн. При этом наличие ненулевых амплитудных коэффициентов волн высших типов в каждой частотной точке оказывает влияние на значения модулей коэффициентов отражения и прохождения основной волны H10, что является следствием энергетического обмена между указанными волнами.
ВЫВОДЫ
Предложен метод решения дифракционных задач о расчете плавных переходов между двумя несоосными экранированными волноводами различных поперечных сечений. Решение задачи осуществляется методом интегральных уравнений, составленных на основе леммы Лоренца. Введено понятие 4K-кратного волновода сравнения. Приведены результаты расчета зависимостей модулей коэффициентов отражения и прохождения основной волны прямоугольного волновода H10 от частоты при соосном соединении прямоугольных волноводов, а также при смещении оси второго волновода вдоль осей x, y декартовой системы координат. Исследована сходимость решения дифракционной задачи, проведено сравнение результатов, полученных на основе разработанного алгоритма и с помощью зарубежного лицензированного САПР СВЧ. Выполнены контрольные расчеты в многомодовом диапазоне частот. Достоверность полученных результатов подтверждена сравнением их с эталонными, проверкой выполнения закона сохранения энергии, демонстрацией их внутренней сходимости. Показана эквивалентность предлагаемой в представленном методе системы интегральных уравнений краевой задаче дифракции на волноводном переходе, формулируемой на уравнениях Максвелла.
Список литературы
Ильинский А.С., Свешников А.Г. // Журн. вычисл. математики и мат. физики. 1968. Т. 8. № 2. С. 363.
Альховский Э.А., Ильинский А.С., Трошин Г.И. // РЭ. 1974. Т. 19. № 6. С. 1136.
Каценеленбаум Б.З. Теория нерегулярных волноводов с медленно меняющимися параметрами. М.: Изд-во АН СССР, 1961.
Шевченко В.В. Плавные переходы в открытых волноводах. М.: Наука, 1975.
Никольский В.В. Вариационные методы для внутренних задач электродинамики. М.: Наука, 1967.
Неганов В.А., Осипов О.В., Раевский С.Б., Яровой Г.П. Электродинамика и распространение радиоволн / Под ред. Неганова В.А. и Раевского С.Б. М.: Радиотехника, 2007.
Морс Ф.М., Фешбах Г. Методы теоретической физики. Т. 1. М.: Изд-во иностр. лит., 1958.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. Т. 1. М.: Наука, 1965.
Белов Ю.Г., Раевский С.Б. // Изв. вузов СССР. Радиофизика. 1975. Т. 18. № 10. С. 1523.
Иларионов Ю.А., Раевский С.Б., Сморгонский В.Я. Расчет гофрированных и частично заполненных волноводов. М.: Сов. радио, 1980.
Иларионов Ю.А., Раевский А.С., Раевский С.Б., Седаков А.Ю. Устройства СВЧ и КВЧ диапазонов. Методы расчета. Алгоритмы. Технологии изготовления. М.: Радиотехника, 2013.
Назаров А.В., Раевский А.С., Раевский С.Б. // Антенны. 2009. № 2(141). С. 71.
Забрейко П.П., Кошелев А.И., Красносельский М.А. и др. Интегральные уравнения. М.: Наука, 1968.
Гаранин С.М., Данилов И.Н., Майстренко В.К. // Физика волновых процессов и радиотехнические системы. 2014. Т. 17. № 2. С. 18.
Данилов И.Н., Майстренко В.К. // Антенны. 2013. № 11. С. 37.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1966.
Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.
Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высш. шк., 1994.
Шестопалов В.П., Кириленко А.А., Рудь Л.А. Резонансное рассеяние волн. Т. 2. Волноводные неоднородности. Киев: Наук. думка, 1986.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника